Abstract
The analysis of the effects of magnetic or electric fields on atoms favors a deep understanding of the quantum properties of matter. Furthermore, electric or magnetic fields are tools currently used in several experimental studies.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
In fact \(({1}/{2}) \textit{rot}(\mathbf {H} \times \mathbf {r})= \hat{z} H_0\).
- 2.
Note that the field-related energy is \(\varDelta E= -\int _0^\mathcal {E} \mu _e d \mathcal {E}'\), so that for \(\mu _e= \alpha \mathcal {E}'\) Eq. (4.6) follows.
- 3.
From
$$<M_z>\,= -\frac{\partial }{\partial H} (-\frac{1}{\beta }ln Z)_T,$$with
$$\frac{\partial }{\partial H} = \frac{\beta }{H}\frac{\partial }{\partial \beta }.$$ - 4.
The single
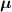 ’s are uncorrelated i.e. \(<\varDelta \mu _n\varDelta \mu _m>\,=<\varDelta \mu _n> <\varDelta \mu _m>\), for \(n\ne m\).
’s are uncorrelated i.e. \(<\varDelta \mu _n\varDelta \mu _m>\,=<\varDelta \mu _n> <\varDelta \mu _m>\), for \(n\ne m\).
Specific References and Further Reading
E.M. Purcell, Electricity and Magnetism, Berkeley Physics Course Vol.2, (McGraw-Hill, 1965).
S.J. Blundell, Magnetism in Condensed Matter, (Oxford Master Series in Condensed Matter Physics, Oxford U.P., 2001).
A. Balzarotti, M. Cini, M. Fanfoni, Atomi, Molecole e Solidi. Esercizi risolti, (Springer Verlag, 2004).
B.H. Bransden and C.J. Joachain, Physics of atoms and molecules, (Prentice Hall, 2002).
D. Budker, D.F. Kimball and D.P. De Mille, Atomic Physics - An Exploration Through Problems and Solutions, (Oxford University Press, 2004).
B. Cagnac and J.C. Pebay - Peyroula, Physique atomique, tome 2, (Dunod Université, Paris, 1971).
E.U. Condon and G.H. Shortley, The Theory of Atomic Spectra, (Cambridge University Press, London, 1959).
J.A. Cronin, D.F. Greenberg, V.L. Telegdi, University of Chicago Graduate Problems in Physics, (Addison-Wesley, 1967).
W. Demtröder, Atoms, Molecules and Photons, (Springer Verlag, 2006).
R.N. Dixon, Spectroscopy and Structure, (Methuen and Co LTD, London, 1965).
R. Eisberg and R. Resnick, Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles, (J. Wiley and Sons, 1985).
H. Eyring, J. Walter and G.E. Kimball, Quantum Chemistry, (J. Wiley, New York, 1950).
H. Haken and H.C. Wolf, Atomic and Quantum Physics, (Springer Verlag, Berlin, 1987).
C.S. Johnson and L.G. Pedersen, Quantum Chemistry and Physics, (Addison-Wesley, 1977).
M.A. Morrison, T.L. Estle and N.F. Lane, Quantum States of Atoms, Molecules and Solids, (Prentice-Hall Inc., New Jersey, 1976).
J.C. Slater, Quantum Theory of Matter, (McGraw-Hill, New York, 1968).
S. Svanberg, Atomic and Molecular Spectroscopy, (Springer Verlag, Berlin, 2003).
Author information
Authors and Affiliations
Corresponding author
Appendix 4.1 Electromagnetic Units and Gauss System
Appendix 4.1 Electromagnetic Units and Gauss System
Throughout this book we are using the CGS system of units that when involving the electromagnetic quantities is known as the Gauss system. This system corresponds to have assumed for the dielectric constant \(\varepsilon _0\) and for the magnetic permeability \(\mu _0\) of the vacuum the dimensionless values \(\varepsilon _0=\mu _0=1\), while the velocity of light in the vacuum is necessarily given by \(c=3\times 10^{10}\) cm/s.
As it is known, the most common units in practical procedures (such as Volt, Ampere, Coulomb, Ohm and Faraday) are better incorporated in the MKS system of units (and in the international SI). These systems of units are derived when in the Coulomb equation instead of assuming as arbitrary constant \(k=1\), one sets \(k=1/4\pi \varepsilon _0\), with \(\varepsilon _0=8.85\times 10^{-12}\) C\(^2\)/Nm\(^2\), as electrical permeability of the vacuum. In the SI system the magnetic field \(\mathbf {B}\), defined through the Lorentz force
is measured in Weber/m\(^2\) or Tesla.
The auxiliary field \(\mathbf {H}\) is related to the current due to the free charges by the equation \({H}= nI\), corresponding to the field in a long solenoid with n turns per meter, for a current of I Amperes. The unit of H is evidently Ampere/m. Thus in the vacuum one has \(\mathbf {B}= \mu _0 \mathbf {H}\), with \(\mu _0= 4\pi 10^{-7}\) N/A\(^2\equiv 4\pi 10^{-7}\) H/m.
In the matter the magnetic field is given by
where \(\mathbf {M}\) is the magnetic moment per unit volume.
The SI system is possibly more convenient in engineering and for some technical aspects but it is not suited in physics of matter. In fact, the Maxwell equations in the vacuum are symmetric in the magnetic and electric fields only when \(\mathbf {H}\) is used, while \(\mathbf {B}\) and not \(\mathbf {H}\) is the field involved in the matter. The SI system does not display in a straightforward way the electromagnetic symmetry. In condensed matter physics the Gauss system should be preferred.
Thus within this system the electric and magnetic fields have the same dimensions (another appealing feature), the Lorentz force is
\(\mathbf {B}\) is related to \(\mathbf {H}\) by
\(\mathbf {M}= \chi \mathbf {H}\) defines the dimensionless magnetic susceptibility \(\chi \). For \(\mu _BH\ll k_BT\), often called evanescent field condition, \(\chi \) is field independent. As already mentioned \(\mu _0\) and \(\varepsilon _0\) are equal to unit, dimensionless.
The practical units can still be used, just by resorting to the appropriate conversion factors, such as
1 volt \(\rightarrow \) | \(\frac{1}{299.8}\) statvolt or erg/esu (esu electrostatic unit) |
1 ampere | \(2.998\times 10^9\) esu/sec |
1 Amp/m | \(4\pi \times 10^{-3}\) Oersted (see below) |
1 ohm | \(1.139\times 10^{-12}\) sec/cm |
1 farad | \(0.899\times 10^{12}\) cm |
1 henry | \(1.113 \times 10^{-12}\) sec\(^2\)/cm |
1 Tesla | 10\(^4\) Gauss |
1 Weber | 10\(^8\) Gauss/cm\(^2\) |
The Bohr magneton, which is not an SI unit, is often indicated as \(\mu _B=9.274 \times 10^{-24}\) J/T, equivalent to our definition \(\mu _B=0.9274 \times 10^{-20}\) erg/Gauss. The gyromagnetic ratio is measured in the Gauss system in (rad/s.Oe) and in the SI system in (rad.m/Amp.s).
Unfortunately, some source of confusion is still present when using the Gauss system. According to Eq. (A.4.1.2), \(\mathbf {B}\) and \(\mathbf {H}\) have the same dimensions and are related to the currents in the very same way. In spite of that, while \(\mathbf {B}\) is measured in Gauss, without serious reason the unit of \(\mathbf {H}\) is called Oersted. Furthermore, there are two ways to describe electromagnetism in the framework of the CGS system. One with electrostatic units (esu) and the other with electromagnetic units (emu). The latter is usually preferred in magnetism. Thus the magnetic moment is measured in the emu unit, which is nothing else than a volume and therefore cm\(^3\). The magnetic susceptibility (per unit volume) is dimensionless and often indicated as emu/cm\(^3\). The symmetric Gauss-Hertz-Lorentz system (commonly known as Gauss system) corresponds to a mixing of the esu and of the emu systems, having assumed both \(\varepsilon _0= 1\) and \(\mu _0= 1\).
Here we do not have the aim to set the final word on the vexata quaestio of the most convenient system of units. Further details can be achieved from the books by Purcell and by Blundell .
A Table is given below for the magnetic quantities in the Gauss system and in the SI system, with the conversion factors.
Quantity | Symbol | Gauss | SI | Conversion factor* |
|---|---|---|---|---|
Magnetic Induction | \(\mathbf {B}\) | \(\text {G}\equiv Gauss\) | T | \(10^{-4}\) |
Magnetic field intensity | \(\mathbf {H}\) | Oe | A m\(^{-1}\) | \(10^{3}/4\pi \) |
Magnetization | \(\mathbf {M}\) | erg/(G cm\(^{3}\)) | A m\(^{-1}\) | \(10^{3}\) |
Magnetic moment |
| erg/G(\(\equiv \) emu) | J/T(\(\equiv \) Am\(^2\)) | \(10^{-3}\) |
Specific magnetization | \(\sigma \) | emu/g | A m\(^2\)/kg | 1 |
Magnetic flux | \(\phi \) | Mx (maxwell) | Wb (Weber) | \(10^{-8}\) |
Magnetic energy density | E | erg/cm\(^3\) | J/m\(^3\) | \(10^{-1}\) |
Demagnetizing factor | \(N_d\) | − | − | \(1/4\pi \) |
Susceptibility(unit volume) | \(\chi \) | − | − | \(4\pi \) |
Mass susceptibility | \(\chi _g\) | erg/(G g Oe) | m\(^3\)/kg | \(4\pi \times 10^{-3}\) |
Molar susceptibility | \(\chi _{mol} \) | emu/(mol Oe) | m\(^3\)/mol | \(4\pi \times 10^{-6}\) |
Magnetic permeability | \(\mu \) | G/Oe | H/m | \(4\pi \times 10^{-7}\) |
Vacuum permeability | \(\mu _0\) | G/Oe | H/m | \(4\pi \times 10^{-7}\) |
Anisotropy constant | K | erg/cm\(^3\) | J/m\(^3\) | \(10^{-1}\) |
Gyromagnetic ratio | \(\gamma \) | rad/(s Oe) | rad m/(A s) | \(4\pi \times 10^{-3}\) |
Finally a mention to the atomic units (a.u.), frequently used, is in order. In this system of units (derived from the SI system) one sets \(e=\hbar =m=1\) and \(4\pi \varepsilon _0=1\). Thus the Bohr radius for atomic Hydrogen (infinite nuclear mass) becomes \(a_0=1\), the ground state energy becomes \(E_{n=1}=- 1/2\) a.u., the a.u. for velocity is \(v_0= \alpha c\) with \(\alpha \simeq 1/137\) the fine structure constant, so that the speed of light is \(c\simeq 137\) a.u.. The Bohr magneton is 1 / 2 a.u. and the flux quantum is \(\varPhi _0= 2\pi \) (see Appendix 13.1). Less practical are the a.u.’s for other quantities. For instance the a.u. for the magnetic field corresponds to 2.35\(\times 10^5\) T and the one for the electric field to \(5.13 \times 10^9\) V/cm.
Problems
Problem 4.11
The magnetization curves for crystals containing paramagnetic ions Gd\(^{3+}\), Fe\(^{3+}\) and Cr\(^{3+}\) display the saturation (for about H / T = 20 kGauss/K) about at the values 7, 5, and 3\(\mu _B\) (per ion), respectively. From the susceptibility measurements at T= 300 K for evanescent magnetic field one evaluates the magnetic moments 7.9, 5.9, and 3.8\(\mu _B\), respectively. Comment on the differences. Then obtain the theoretical values of the magnetic moments for those ions and prove that quenching of the orbital momenta occurs (see Problem 4.12).
Solution: The susceptibility \(\chi ={Ng^2 J(J+1) \mu _B ^2}/{3k_B T}\) involves an effective magnetic moment \(\mu _{\textit{eff}}=g\mu _B \sqrt{J(J+1)}\) different from \(<\mu _z>_{\textit{max}}=g\mu _B J\) obtained from the saturation magnetization, related to the component of \(\mathbf {J}\) along the direction of the field.
For Gd\(^{3+}\), electronic configuration \((4f)^7\), one has \(S=\frac{7}{2}\), \(L=0\), \(J=\frac{7}{2}\) and \(g=2\).
Then \(\mu _{\textit{eff}}=g\mu _B \sqrt{S(S+1)}\simeq 7.9 \, \mu _B\), while \(<\mu _z>_{\textit{max}} \simeq 2 \mu _B {7}/{2}=7 \mu _B\), in satisfactory agreement with the data.
For Fe\(^{3+}\) (see Problem 4.9) \(J={5}/{2}\) and \(g=2\) and then \(\mu _{\textit{eff}}=5.92\,\mu _B\) and \( <\mu _z>_{\textit{max}} \simeq 5 \, \mu _B.\)
For Cr\(^{3+}\), electronic configuration \((3d)^3\), \(S={3}/{2}\), \(L=3\), \(J= {3}/{2}\) and \(g= {2}/{5}=0.4 \, .\) For unquenched \(\mathbf {L}\) one would have \(\mu _{\textit{eff}} = ({2}/{5}) \mu _B \sqrt{{15}/{4}} = 0.77 \, \mu _B\), while for \(L=0\), \(\mu _{\textit{eff}}= 2\mu _B \sqrt{{15}/{4}} \simeq 3.87 \, \mu _B \, .\)
Problem 4.12
By referring to the expectation value of \(l_z\) in 2p and 3d atomic states, in the assumption that the degeneracy is removed by crystal field, justify the quenching of the orbital momenta.
Solution: When the degeneracy is removed the wavefunction \(\phi _{2px,y,z}\) are real. Then, since
cannot be imaginary, one must have \(<l_z>\,=0\). Analogous consideration holds for 3d states and for any non-degenerate state. Details on the role of the crystal field in quenching the expectation values of the components of the angular momenta are given at Sect. 13.3 and at Problem 13.5.
Problem 4.13
In Hydrogen, the lines resulting from the transitions \(^2 P_{3/2} \, \longrightarrow \, ^2 S_{1/2}\) and \(^2 P_{1/2} \, \longrightarrow \, ^2 S_{1/2}\) (see Appendix 5.1) occur at (\(1210 - 3.54 \cdot 10^{-3}\)) Å and (\(1210 + 1.77 \cdot 10^{-3}\)) Å, respectively. Evaluate the effect of a magnetic field of 500 Gauss, by estimating the shifts in the wavelengths of these lines, in the weak field regime.
Solution: The relationship between the splitting of lines and the applied field is found from
namely
The values for \(dE_2\) and \(dE_1\) are given in Table below. There are 10 transitions that satisfy the electric dipole selection rule \(\varDelta M_J =\pm 1,0\). The deviation of each of these lines from \(\lambda _0 =1210\) Å is also given.
\(d\lambda _0\) \(\mathrm {\AA } \cdot 10^{-3}\) | \(dE_2\) \(\mathrm {eV} \cdot 10^{-5}\) | \(dE_1\) \(\mathrm {eV} \cdot 10^{-5}\) | \(d\lambda \) \(\mathrm {\AA } \cdot 10^{-3}\) | \(d\lambda _T =d\lambda _0 + d\lambda \) \(\mathrm {\AA } \cdot 10^{-3}\) |
|---|---|---|---|---|
−3.54 | \(+\)0.579 | \(+\)0.289 | −0.342 | −3.88 |
−3.54 | \(+\)0.193 | \(+\)0.289 | \(+\)0.114 | −3.43 |
−3.54 | \(+\)0.193 | −0.289 | −0.570 | −4.11 |
−3.54 | −0.193 | \(+\)0.289 | \(+\)0.570 | −2.97 |
−3.54 | −0.193 | −0.289 | −0.114 | −3.65 |
−3.54 | −0.579 | −0.289 | \(+\)0.342 | −3.20 |
1.77 | \(+\)0.096 | \(+\)0.289 | \(+\)0.228 | \(+\)2.00 |
1.77 | \(+\)0.096 | −0.289 | −0.456 | \(+\)1.31 |
1.77 | −0.096 | \(+\)0.289 | \(+\)0.456 | \(+\)2.23 |
1.77 | −0.096 | −0.289 | −0.228 | \(+\)1.54 |
Problem 4.14
Refer to the \(H_{\alpha }\) line in Hydrogen (see Problem 1.4). From the splitting of the s and p levels when a magnetic field of 4.5 T is applied, by taking into account that the separation between two adjacent lines is \(6.29 \cdot 10^{10}\) Hz and by ignoring the fine structure, evaluate the specific electronic charge (e / m). Compare the estimate with the one obtained from the observation that a field of 3 T induces the splitting of the spectral line in Ca atom at 4226 Å in a triplet with separation 0.25 Å (do not consider in this case the detailed structure of the energy levels).
Solution: In the Paschen-Back regime the energy correction is
with electric dipole selection rules. One observes three lines with splitting \(\varDelta \bar{\nu } =2.098\) cm\(^{-1}.\) Then from
one has
For Ca, from \(\varDelta E \simeq {e\hbar }H/{2mc} = -hc{\varDelta \lambda }/{\lambda ^2}\) again
Problem 4.15
Two particles at spin \(s=1/2\) and magnetic moments  and
and  , with
, with  spin operators, interact through the Heisenberg exchange Hamiltonian (see Sect. 2.2). Derive eigenstates and eigenvalues in the presence of magnetic field.
spin operators, interact through the Heisenberg exchange Hamiltonian (see Sect. 2.2). Derive eigenstates and eigenvalues in the presence of magnetic field.
Solution: From the Hamiltonian


one writes
The first two terms are diagonal (in the representation in which the total spin is diagonal). Both the triplet and the singlet states have definite parity for exchange of particles (even and odd respectively). Thus the only non-zero matrix element of the last term (which is odd for exchange) is the one connecting singlet and triplet states. One finds
the only non-zero matrix element being
Therefore \(S=1\), \(S_z=\pm 1\) classify the eigenstates, with eigenvalues
For the states with \(S_z =0\), the Hamiltonian can be represented by the matrix
where the out of diagonal elements involve the triplet-singlet mixture. From the secular equation the eigenvalues turn out
Problem 4.16
The saturation magnetization (per unit volume) of Iron (Fe\(^{2+}\)) is often reported to be \(1.7 \cdot 10^6 \, \mathrm {A/m}\). Derive the magnetic moment per atom and compare it to the theoretical estimate (density of iron \(7.87\,\mathrm {g}/\mathrm {cm}^3\)).
Solution: From
and \(n_{\textit{atom}} = 0.85 \cdot 10^{23} \, \mathrm {cm}^{-3}\), one derives
or equivalently \(\mu _{a} = 2.2 \mu _B\). For Fe\(^{2+}\) (\(S=2\), \(L=2\), \(J=4\) and \(g=\frac{3}{2}\)) one would expect \(\mu = g\mu _B J =6\mu _B\). For quenched orbital momentum \(\mu = 2S\mu _B = 4\mu _B\) (see Problem 4.12 and Sect. 13.3).
Problem 4.17
A bulb containing Hg vapor is irradiated by radiation propagating along the x axis and linearly polarized along z, along which a constant magnetic field is applied. When the wavelength of the radiation is 2537 Å, absorption and meantime re-emission of light along the y direction, with the same polarization, is detected. When a RF coil winding the bulb along the y direction is excited at the frequency 200 MHz one notes re-emission of light also along the z direction, light having about the same wavelength and circular polarization. Explain such a phenomenology and estimate the strength of the field.
Solution: Since spin-orbit interaction is very strong the weak-field regime holds (see Sect. 3.3 and Fig. 3.9). The electric dipole selection rule \(\varDelta M_J=0\) requires linearly polarized radiation. In the absence of radio frequency excitation, \(\pi \) radiation is re-emitted again, observed along y. Along the z direction the radiation is not observed.
The radio-frequency induces magnetic dipole transitions at \(\varDelta M_J = \pm 1\) among the Zeeman levels. The re-emission of light in such a way is about at the same wavelength \(\lambda \). In fact
On the other hand, since among the levels involved in the emission \(\varDelta M_J =\pm 1\), one has circular \(\sigma \) polarization and so the radiation along z can be observed.
From the resonance condition
with \(g= 3/2\), one deduces
The levels (in the LS classification and in the weak field regime) for the Hg \(^1 S_0\) and \(^3 P_1\) states (see Fig. 3.9) and the transitions are sketched below:


Problem 4.18
Consider a paramagnetic crystal, with non-interacting magnetic ions at \(J=1/2\). Evaluate the fluctuations \(<\varDelta M^2>\) of the magnetization and show that it is related to the susceptibility \(\chi = {\partial <M>}/{\partial H}\) by the relation \(\chi = {<\varDelta M^2>}/{k_B T}\) (particular case of the fluctuation-dissipation theorem).
Solution: The density matrix is \(\rho =({1}/{Z})e^{\beta H M_z}\) (\(\beta \equiv 1/k_BT\)) and the partition function \(Z= Tr \left[ e^{\beta H M_z}\right] \). The magnetization can be written (see also Sect. 6.1)Footnote 3
Then
Without involving the density matrix, from the single-ion fluctuations
with \(<\mu _z>\) statistical average of  , since
, since
and (see Sect. 4.4)
by taking into account that
one findsFootnote 4
and then
Problem 4.19
Consider an ensemble of N / 2 pairs of atoms at S=1/2 interacting through an Heisenberg-like coupling \(\mathcal {H}= K \mathbf {S}_1 \cdot \mathbf {S}_2\) with \(K>0\). By neglecting the interactions among different pairs, derive the magnetic susceptibility. Express the density matrix and the operator \(S_z\) on the basis of the singlet and triplet states. Finally derive the time-dependence of the statistical ensemble average \(<S^z _1 (0) \cdot S^z _1 (t)>\), known as auto-correlation function.
Solution: The eigenvalues are \(E_s= ({K}/{2})S(S+1)\), with \(S=0\) and \(S=1\). The susceptibility is
where
and
Then
On the basis given by the states
omitting irrelevant constants, one has
Then the density matrix is
By letting \(S^z _1\) act on the singlet and triplet states, one has
The autocorrelation-function is
By setting \(\omega _e=\frac{K}{\hbar }\), (Heisenberg exchange frequency), one writes
and then
For \(k_BT \gg K\)
\(1/\omega _e\) can be defined as the correlation time, in the infinite temperature limit.
Problem 4.20
By resorting to the Bohr-Sommerfeld quantization rule (Problem 1.4) for the canonical moment, derive the cyclotron frequency and the energy levels for a free electron (without spin) moving in the xy plane, in the presence of a constant homogeneous magnetic field along the z axis.
Solution: The canonical moment (see Eq. (1.26)) is \(\mathbf {p}= m\mathbf {v} - e\mathbf {A} /c\). From the quantization along the circular orbit
(R radius of the orbit). The equilibrium condition along the trajectory implies \(v= eHR/mc\) and then the quantization rule yields
The energy becomes
with
cyclotron frequency. For the quantum description, which includes \(n=0\) and the zero-point energy \(\hbar \omega _c/2\), see Appendix 13.1.
Problem 4.21
By referring to a Rydberg atom (Sect. 1.5) and considering that the diamagnetic correction to a given n-level increases with n, discuss the limit of applicability of the perturbative approach, giving an estimate of the breakdown value of n for magnetic field of 1 T (see Eq. (4.36)). Then discuss why the Rydberg atoms are highly polarizable and ionized by a relatively small electric field.
Solution: In
consider (see Table 1.4)
for large n and l and \(Z=1\), as for ideal total screen. Then, by assuming that the perturbation approach can be safely used up to a diamagnetic correction \(\varDelta E_n(H)\sim 0.2 E_n^0\), one obtains
from which a limiting value of the quantum number n turns out around \(n_{\textit{lim}}\sim 65\).
As regards the electric polarizability, by considering that in Eq. (4.8) the relevant matrix elements increase with \(n^2\) while the difference in energy at the denominator varies as \(1/n^3\) (remember the correspondence principle, Problem 1.12) one can deduce that the electric polarizability must increase as \(n^7\).
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Rigamonti, A., Carretta, P. (2015). Atoms in Electric and Magnetic Fields. In: Structure of Matter. UNITEXT for Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-17897-4_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-17897-4_4
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-17896-7
Online ISBN: 978-3-319-17897-4
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


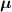 ’s are uncorrelated i.e.
’s are uncorrelated i.e. 