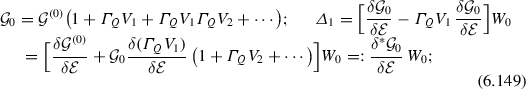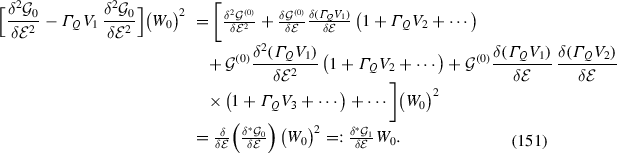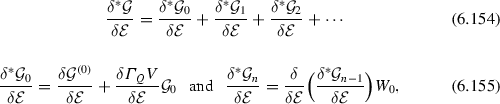Abstract
The third method we shall consider for numerical QED calculations on bound states is the Covariant-Evolution operator (CEO), developed during the last decade by the Gothenburg group (Lindgren et al., Phys. Rep. 389, 161–261, 2004) [130], (Lindgren et al., Can. J. Phys. 83, 183–218, 2005) [131], (Lindgren et al., Phys. Rev. A 73, 062–502, 2006) [132]. This procedure is based upon the non-relativistic time-evolution operator, discussed in Chap. 3, but made relativistically covariant in order to be applicable in relativistic calculations. This method has the advantage over the two methods discussed previously, the S-matrix procedure and the Green’s-function procedure, that it can be used perturbatively, and the perturbations can be included in the wave function—not only added to the energy. It then forms a convenient basis for a covariant relativistic many-body perturbation procedure, where electron correlation and quantum electrodynamics are systematically combined. For two-electron systems this is fully compatible with the Bethe–Salpeter equation. This question will be the main topic for the rest of the book.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
See footnote in the Introduction.
- 2.
An “n-body operator” is an operator with n pairs of creation/absorption operators (for particles), while an “m-particle” function or operator is an object of m particles outside our vacuum. In principle, n can take any value \(n\le m\), although we shall normally assume that \(n=m\).
- 3.
It should be observed that a Goldstone diagram is generally distinct from a “time-ordered Feynman diagram”, as is further analyzed in Appendix I.
- 4.
- 5.
As pointed out before, the numerator and denominator might here be separately singular in the limit, and only the ratio is regular.
- 6.
Also the Fock space is a form of Hilbert space, and therefore we shall refer to the Hilbert space with a constant number of photons as the restricted (Hilbert) space and the space with a variable number of photons as the (extended) photonic Fock space (see Appendix A.2).
- 7.
This equation is not completely covariant, because it has a single time, in accordance with the established quantum-mechanical picture. This is the equal-time approximation, mentioned above and further discussed later. In addition, a complete covariant treatment would require that also the interaction between the electrons and the nucleus is treated in a covariant way by means of the exchange of virtual photons (see, for instance, [227]).
- 8.
In the following we shall leave out the subscript “Rel”.
- 9.
The Green’s operator is closely related—but not quite identical—to the reduced covariant evolution operator, previously introduced by the Gothenburg group [130].
- 10.
Compare footnote in Sect. 6.4.
- 11.
We use the convention that the subscript denotes the number of model-space states (“folds”), intermediate or final, and the superscript in brackets the order of perturbation.
- 12.
\(\mathcal {G}^{(0)}(t,{\mathcal {E}})={\mathrm {e}}^{-\mathrm {i}t({\mathcal {E}}-H_0)}\) and \(\mathcal {G}_0(t,{\mathcal {E}})P_{\mathcal {E}}=\mathcal {G}^{(0)}(t,{\mathcal {E}})\,U_0(0,{\mathcal {E}})P_{\mathcal {E}}=\mathcal {G}^{(0)}(t,{\mathcal {E}})\big ((1+QU_0(0,{\mathcal {E}}))\big )P_{\mathcal {E}}\), which gives \(P_{{\mathcal {E}}'}\Big (\mathrm {i}\frac{\partial }{\partial t}\,\mathcal {G}^{(0)}(t,{\mathcal {E}})\Big )_{t=0}P_{\mathcal {E}}=P_{{\mathcal {E}}'}\Big (\mathrm {i}\frac{\partial }{\partial t}\,\mathcal {G}_0(t,{\mathcal {E}})\Big )_{t=0}P_{\mathcal {E}}=0\) and \(P_{{\mathcal {E}}'}\Big (\mathrm {i}\frac{\partial }{\partial t}\,\frac{\delta \mathcal {G}^{(0)}}{\delta {\mathcal {E}}}\Big )_{t=0}P_{\mathcal {E}}=P_{{\mathcal {E}}'}\Big (\mathrm {i}\frac{\partial }{\partial t}\,\frac{\delta \mathcal {G}_0}{\delta {\mathcal {E}}}\Big )_{t=0}P_{\mathcal {E}}=P_{{\mathcal {E}}'}P_{\mathcal {E}}\).
- 13.
From the previous footnote we have \(P_{{\mathcal {E}}''}\mathrm {i}\frac{\partial }{\partial t}\Big (\frac{\delta \mathcal {G}^{(1)}}{\delta {\mathcal {E}}}\Big )_{t=0}P_{{\mathcal {E}}'}W^{(1)}P_{\mathcal {E}}=P_{{\mathcal {E}}''}\mathrm {i}\frac{\partial }{\partial t}\Big (\frac{\delta \mathcal {G}_0^{(1)}(t,{\mathcal {E}}')}{\delta {\mathcal {E}}}+ \frac{\delta ^{2} \mathcal {G}^{(0)}(t,{\mathcal {E}}')}{\delta {\mathcal {E}}^{2}}\,W^{(1)}+\frac{\delta \mathcal {G}^{(0)}(t,{\mathcal {E}}')}{\delta {\mathcal {E}}}\frac{\delta W^{(1)}}{\delta {\mathcal {E}}}\Big )_{t=0}P_{{\mathcal {E}}'}W^{(1)}P_{\mathcal {E}}=P_{{\mathcal {E}}''}P_{{\mathcal {E}}'}W^{(1)}P_{\mathcal {E}}+P_{{\mathcal {E}}''}\frac{\delta W^{(1)}}{\delta {\mathcal {E}}}W^{(1)}P_{\mathcal {E}}\).
- 14.
The rules for differentiating are as follows
$$\begin{aligned} \frac{\delta \mathcal {G}}{\delta {\mathcal {E}}}&=\frac{\mathcal {G}_{\mathcal {E}}-\mathcal {G}_{{\mathcal {E}}'}}{{\mathcal {E}}-{\mathcal {E}}'};\quad \frac{\delta }{\delta {\mathcal {E}}}\Big (\frac{\delta \mathcal {G}}{\delta {\mathcal {E}}}V\Big ) =\frac{\big (\frac{\delta \mathcal {G}}{\delta {\mathcal {E}}}\big )_{\mathcal {E}}V_{\mathcal {E}}-\big (\frac{\delta \mathcal {G}}{\delta {\mathcal {E}}}\big )_{{\mathcal {E}}'}V_{{\mathcal {E}}'}}{{\mathcal {E}}-{\mathcal {E}}'}\nonumber \\&=\frac{\big (\frac{\delta \mathcal {G}}{\delta {\mathcal {E}}}\big )_{\mathcal {E}}V_{\mathcal {E}}-\big (\frac{\delta \mathcal {G}}{\delta {\mathcal {E}}}\big )_{{\mathcal {E}}'}V_{{\mathcal {E}}} +\big (\frac{\delta \mathcal {G}}{\delta {\mathcal {E}}}\big )_{{\mathcal {E}}'}V_{{\mathcal {E}}}-\big (\frac{\delta \mathcal {G}}{\delta {\mathcal {E}}}\big )_{{\mathcal {E}}'} V_{{\mathcal {E}}'}}{{\mathcal {E}}-{\mathcal {E}}'} =\frac{\delta ^{2} \mathcal {G}}{\delta {\mathcal {E}}^{2}}\,V+\frac{\delta \mathcal {G}}{\delta {\mathcal {E}}}\frac{\delta V}{\delta {\mathcal {E}}}\nonumber \\\frac{\delta }{\delta {\mathcal {E}}}\;V^2&=\frac{\delta }{\delta {\mathcal {E}}}V_{{\mathcal {E}}''}V_{\mathcal {E}}=V_{{\mathcal {E}}''} \frac{V_{\mathcal {E}}-V_{{\mathcal {E}}'}}{{\mathcal {E}}-{\mathcal {E}}'} =V\frac{\delta V}{\delta {\mathcal {E}}}.\nonumber \\\end{aligned}$$This can be generalized to
$$\begin{aligned} \frac{\delta ^{n} (AB)}{\delta {\mathcal {E}}^{n}}=\sum _{m=0}^n\frac{\delta ^{m} A}{\delta {\mathcal {E}}^{m}}\,\frac{\delta ^{n-m} B}{\delta {\mathcal {E}}^{n-m}} \end{aligned}$$(see further [132, Appendix B]).
- 15.
\(\frac{\delta \mathcal {G}}{\delta {\mathcal {E}}}=\frac{\delta \mathcal {G}^{(0)}}{\delta {\mathcal {E}}}+\frac{\delta \mathcal {G}^{(1)}}{\delta {\mathcal {E}}}+\cdots \); \( P_{\mathcal {E}}\Big (\mathrm {i}\frac{\partial }{\partial t}\,\mathcal {G}_0(t,{\mathcal {E}})\Big )_{t=0}P_{\mathcal {E}}=0\); \(P_{\mathcal {E}}\Big (\mathrm {i}\frac{\partial }{\partial t}\,\frac{\delta \mathcal {G}^{(0)}}{\delta {\mathcal {E}}}\Big )_{t=0}P_{\mathcal {E}}=1\); \(P_{\mathcal {E}}\Big (\mathrm {i}\frac{\partial }{\partial t}\,\frac{\delta \mathcal {G}^{(1)}}{\delta {\mathcal {E}}}\Big )_{t=0}P_{\mathcal {E}}=P_{\mathcal {E}}\mathrm {i}\frac{\partial }{\partial t}\,\frac{\delta }{\delta {\mathcal {E}}}\Big (\frac{\delta \mathcal {G}^{(0)}}{\delta {\mathcal {E}}}W^{(1)}\Big )_{t=0}P_{\mathcal {E}}=\frac{\delta W^{(1)}}{\delta {\mathcal {E}}}\);
\(P_{\mathcal {E}}\mathrm {i}\frac{\partial }{\partial t}\,\Big (\frac{\delta \mathcal {G}^{(2)}}{\delta {\mathcal {E}}}\Big )_{t=0}P_{\mathcal {E}}=\) \(P_{\mathcal {E}}\mathrm {i}\frac{\partial }{\partial t}\,\Big (\frac{\delta \mathcal {G}^{(0)}}{\delta {\mathcal {E}}}\frac{\delta W_0^{(2)}}{\delta {\mathcal {E}}}\Big )_{t=0}P_{\mathcal {E}}\)
\(+P_{\mathcal {E}}\mathrm {i}\frac{\partial }{\partial t}\,\Big (\frac{\delta ^{2} \mathcal {G}^{(1)}}{\delta {\mathcal {E}}^{2}}W^{(1)}+ \frac{\delta \mathcal {G}^{(1)}}{\delta {\mathcal {E}}}\frac{\delta W^{(1)}}{\delta {\mathcal {E}}} \Big )_{t=0}P_{\mathcal {E}}= \frac{\delta W_0^{(2)}}{\delta {\mathcal {E}}}+\frac{\delta ^{2} W^{(1)}}{\delta {\mathcal {E}}^{2}}W^{(1)}+\frac{\delta W^{(1)}}{\delta {\mathcal {E}}}^2\)
\(=\frac{\delta W_0^{(2)}}{\delta {\mathcal {E}}}+\frac{\delta W_1^{(2)}}{\delta {\mathcal {E}}}=\frac{\delta W^{(2)}}{\delta {\mathcal {E}}}\Rightarrow P_{\mathcal {E}}\mathrm {i}\frac{\partial }{\partial t}\,\Big (\frac{\delta \mathcal {G}}{\delta {\mathcal {E}}}\Big )_{t=0}P_{\mathcal {E}}= 1+\frac{\delta W^{(1)}}{\delta {\mathcal {E}}}+\frac{\delta W^{(2)}}{\delta {\mathcal {E}}}+\cdots =1+\frac{\delta W}{\delta {\mathcal {E}}}.\)
- 16.
Distinguishing the various interactions, we can write
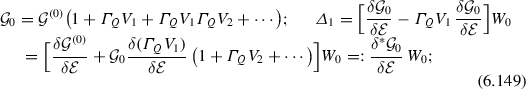
- 17.
It should be noted that an irreducible multi-photon potential is here regarded as a single interaction.
- 18.
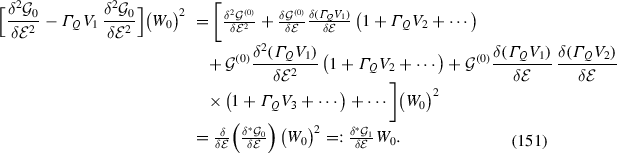
- 19.
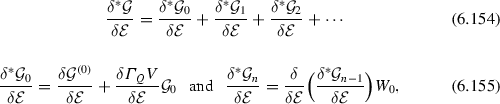
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Lindgren, I. (2016). The Covariant Evolution Operator and the Green’s-Operator Method. In: Relativistic Many-Body Theory. Springer Series on Atomic, Optical, and Plasma Physics, vol 63. Springer, Cham. https://doi.org/10.1007/978-3-319-15386-5_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-15386-5_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-15385-8
Online ISBN: 978-3-319-15386-5
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)