Inverse Problem for a Linearized Jordan–Moore–Gibson–Thompson Equation

Abstract

We consider an inverse problem for the linearized Jordan–Moore–Gibson–Thompson equation, which is a third-order (in time) PDE in the original unknown u that arises in nonlinear acoustic waves modeling high-intensity ultrasound. Both canonical recovery problems are investigated: (i) uniqueness and (ii) stability, by use of just one boundary measurement. Our approach relies on the dynamical decomposition of the Jordan–Moore–Gibson–Thompson equation given in Marchand et al. (Math. Methods Appl. Sci. 35, 1896–1929, 2012), which identified 3 distinct models in the new variable z. By using now z-model ♯3, we weaken by two units the regularity requirements on the data of the original u-dynamics over our prior effort Liu and Triggiani (J. Inverse Ill-Posed Probl. 21, 825–869, 2013), which instead employed z-model ♯1.

In memory of Alfredo Lorenzi: scholar, collaborator, friend

Appendices

Appendix 1: Admissible Geometrical Configurations in the Neumann B.C. Case

Here we present some examples in connection to the main geometrical assumptions (A.1), (A.2). We refer to Lasiecka et al. [35] for more details.

Example #1 :

(Any dimension ≥ 2): Γ ₀ is flat.

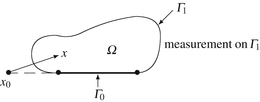
Let x ₀ ∈ hyperplane containing Γ ₀, then.

$$\displaystyle{d(x) =\| x - x_{0}\|^{2};\quad h(x) = \nabla d(x) = 2(x - x_{ 0}).}$$

Example #2 :

(A ball of any dimension ≥ 2): d(x) in [35, Theorem. A.4.1, p. 301]. 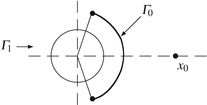Measurement on $\varGamma _{1}> \frac{1} {2}$ circumference (as in the Dirichlet case), same as for controllability.

Example #3 :

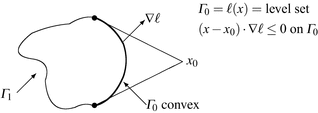
(Generalizing Ex #2: a domain Ω of any dimension ≥ 2 with unobserved portion Γ ₀ convex, subtended by a common point x ₀): d(x) in [35, Theorem. A.4.1, p. 301].

Example #4 :

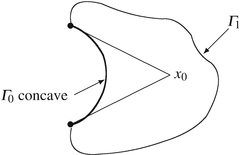
(A domain Ω of any dimension ≥ 2 with unobserved portion Γ ₀ concave, subtended by a common point x ₀): d(x) in [35, Theorem. A.4.1, p. 301].

Example #5 :

(dim = 2): Γ ₀ neither convex nor concave. Γ ₀ is described by graph

$$\displaystyle{y = \left \{\begin{array}{ll} f_{1}(x),x_{0} \leq x \leq x_{1},&y \geq 0; \\ f_{2}(x),x_{2} \leq x \leq x_{1},&y <0,\end{array} \right.}$$

f ₁, f ₂ logarithmic concave on x ₀ < x < x ₁, e.g., sinx, $-\frac{\pi }{2} <x <\frac{\pi } {2}$; cosx,  0 < x < π as the function sinx + 1 and cosx + 1 are lobarithmic concave on the corresponding x-intervals. See [35, Fig. A.3, p. 290]. The corresponding function d(x) is given in [35, (A.2.7), p. 289].

Appendix 2: Sharp Regularity Theory for Second-Order Hyperbolic Equations of Neumann Type

Consider the following second-order hyperbolic equation with non-homogeneous Neumann B.C g and I.C. {w ₀, w ₁}:

$$\displaystyle{\left \{\begin{array}{ll} w_{\mathit{tt}}(x,t) -\varDelta w(x,t) = F(w) + f(x,t)&\mbox{ in }Q =\varOmega \times [0,T]; \\ w\left (\,\cdot \,,0\right ) = w_{0}(x);\quad w_{t}\left (\,\cdot \,,0\right ) = w_{1}(x) &\mbox{ in }\varOmega; \\ \frac{\partial w} {\partial \nu } (x,t)\vert _{\varSigma } = g(x,t) &\mbox{ in }\varSigma =\varGamma \times [0,T]\end{array} \right.}$$

where the forcing term

$$\displaystyle{ f(x,t) \in L^{2}(Q), }$$

and F(w) is given by

$$\displaystyle{ F(w) = q_{1}(x,t)w + q_{2}(x,t)w_{t} + q_{3}(x,t) \cdot \nabla w, }$$

subject to the following standing assumption on the coefficients: q ₁, q ₂, | q ₃ | ∈ L ^∞(Q), so that the following pointwise estimate holds true:

$$\displaystyle{ \vert F(w)\vert \leq C_{T}[w^{2} + w_{ t}^{2} + \vert \nabla w\vert ^{2}],\quad (x,t) \in Q. }$$

We first define the parameters α and β to be the following values:

$$\displaystyle{\left \{\begin{array}{ll} \alpha = \frac{3} {5}-\epsilon,\ \beta = \frac{3} {5}:\ \mbox{ for a general smooth, bounded domain }\varOmega; \\ \alpha =\beta = \frac{2} {3}:\ \mbox{ for a sphere domain }\varOmega; \\ \alpha =\beta = \frac{3} {4}-\epsilon:\ \mbox{ for a parallelepiped domain }\varOmega \end{array} \right.}$$

where ε > 0 is arbitrary. Then we have the following sharp regularity results:

Theorem ([27, Theorem 1.2 (ii), (iii), 1.3, p. 290])

With reference to the above w-mixed problem, the following regularity results hold true, with α and β defined above:

• (i) [27, Theorem 2.0, (15.21), ( 2.9 ), p. 123; Theorem A, p. 117; Theorem  2.1, p. 124]. Suppose we have f = 0, {w ₀ ,w ₁ } ∈ H ¹ (Ω) × L ² (Ω) and g ∈ L ² (Σ). Then we have the unique solution w satisfies

  $$\displaystyle{ w \in H^{\alpha }(Q) = C([0,T];H^{\alpha }(\varOmega )) \cap H^{\alpha }(0,T;L^{2}(\varOmega ));\quad w\vert _{\varSigma }\in H^{2\alpha -1}(\varSigma ). }$$

• (ii) [27, Theorem  5.1 , (5.4), (5.5), p. 149; Theorem C, p. 118; Theorem 7.1, p. 158]. Suppose now f ∈ L ² (Q), {w ₀ ,w ₁ } ∈ H ¹ (Ω) × L ² (Ω) and g = 0. Then we have

  $$\displaystyle{ w \in C([0,T];H^{1}(\varOmega )),\ w_{ t} \in C([0,T];L^{2}(\varOmega ));\quad w\vert _{\varSigma }\in H^{\beta }(\varSigma ). }$$