Electromagnetic Waves and Propagation

Abstract

After summarizing Maxwell’s equations in Chapter 11, we are now ready to discuss their implications. In particular, we will deal directly or indirectly with the displacement current term in Maxwell’s equations.

As to the properties of electromagnetic radiation, I need first of all to come up with a little more than just words to the idea that a changing magnetic field makes an electric field, a changing electric field makes a magnetic field and that this pumping cycle produces an electromagnetic wave…

J. Robert Oppenheimer (1904–1967)

physicist in The Flying Trapeze, Oxford University Press, 1964

Problems

12.1.1 The Time-Dependent Wave Equation

• 12.1 The Wave Equation. Starting with the general time-dependent Maxwell’s equations in a linear, isotropic, homogeneous medium, write a wave equation in terms of the electric field intensity.

  • (a) Show that if you neglect displacement currents, the equation is not a wave equation.

  • (b) Write the source-free wave equation from the general equation you obtained.

• 12.2 Source-Free Wave Equation. Obtain the source-free time-dependent wave equation for the magnetic flux density in a linear, isotropic, homogeneous medium.

12.1.2 The Time-Harmonic Wave Equation

• 12.3 Time-Harmonic Wave Equation. Using the source-free Maxwell’s equations, show that a Helmholtz equation can be obtained in terms of the magnetic vector potential. Use the definition B = ∇ × A and a simple medium (linear, isotropic, homogeneous material). Justify the choice of the divergence of A.

• 12.4 The Helmholtz Equation for D. Using Maxwell’s equations, find the Helmholtz equation for the electric flux density D in a linear, isotropic, homogeneous material.

• 12.5 The Helmholtz Equation for B. Find the Helmholtz equation in terms of the magnetic flux density using the source-free time-harmonic Maxwell’s equations in a linear, isotropic, homogeneous material.

• 12.6 The Electric Hertz Potential. In a linear, isotropic, homogeneous medium, in the absence of sources, the Hertz vector potential Π _e may be defined such that H = jωε∇ × Π _e:

  • (a) Express the electric field intensity in terms of Π _e .

  • (b) Show that the Hertz potential satisfies a homogeneous Helmholtz equation provided a correct gauge is chosen. What is this appropriate gauge?

12.1.3 Solution for Plane Waves

• 12.7 Plane Wave. A plane wave propagates in the positive x direction in free space. The wave is given at x =0 as $\mathbf{E}(0)=\widehat{\mathbf{z}}5 \cos \left({10}^9\pi t\right)$ [V/m]. If properties of free space are ε = ε ₀ [F/m], μ = μ ₀ [H/m], find E(x = 20).

• 12.8 Plane Wave. A wave propagates in free space and its electric field intensity is $\mathbf{E}=\widehat{\mathbf{x}}100{e}^{-j220z}+\widehat{\mathbf{x}}100{e}^{-j220z}$ [V/m]:

  • (a) Show that E satisfies the source-free wave equation.

  • (b) What are the wave’s phase velocity and frequency?

12.1.4 The Poynting Vector

• 12.9 A simple and common use of the Poynting vector is identification of direction of propagation of a wave or the direction of fields in space. Consider the magnetic field intensity of a plane electromagnetic wave propagating in free space:

  $$ \mathbf{H}=\widehat{\mathbf{x}}{H}_0{e}^{j\beta y}+\widehat{\mathbf{z}}{H}_1{e}^{j\beta y}\kern1em \left[\mathrm{A}/\mathrm{m}\right] $$

  • (a) Calculate the electric field intensity using the properties of the Poynting vector.

  • (b) Show that the result in (a) is correct by substituting the magnetic field intensity into Maxwell’s equations and evaluating the electric field intensity through Maxwell’s equations.

• 12.10 Application: Power Relations in a Microwave Oven. The peak electric field intensity at the bottom of a microwave oven is equal to 2500 V/m. Assuming that this is uniform over the area of the oven which is equal to 400 cm², calculate the peak power the oven can deliver. Permeability and permittivity are those of free space.

• 12.11 Application: Heating Food in a Microwave Oven. A frozen pizza is marketed to be heated in a microwave oven. As an engineer you are asked to write heating instructions, specifically how long should it be heated to reach a proper temperature. The average residential microwave oven is 50 cm wide, 40 cm deep, and 30 cm high. The oven has a low and a high heating level. At low, it produces a time averaged power of 500 W, whereas at high, the power is 1000 W. We will assume the pizza is placed flat on the bottom of the oven and any power coupled into the pizza enters from above. The pizza is 25 cm in diameter, 1.5 cm thick, and is 75 % water by volume. The microwave oven heats the water in the pizza. The frozen pizza is at –20 °C and must be heated to 75 °C. Heat capacity of water is 4.1885 J/(g⋅K) and the latent heat (of melting ice) is 334 J/g (heat capacity is the energy needed to raise the temperature of one gram of substance (water in this case) by 1 degree Kelvin, and latent heat is the energy required to melt a gram of ice at 0 °C to water at 0 °C). Assume that the heat transfer from the electromagnetic waves to the pizza is 80 % efficient and calculate:

  • (a) The time it takes to heat the pizza on the low setting of the oven.

  • (b) The time it takes to heat the pizza on the high setting of the oven.

  • (c) The cost in electricity to heat the pizza if a kW⋅h costs $0.16.

• 12.12 Power Dissipation in Cylindrical Conductor. A cylindrical conductor of radius R and infinite length carries a current of amplitude I [A] and frequency f [Hz]. The conductivity of the conductor is σ [S/m] (Figure 12.23). Calculate the time-averaged dissipated power per unit length in the conductor, neglecting displacement currents in the conductor. Assume the current is uniformly distributed throughout the cross section.

  

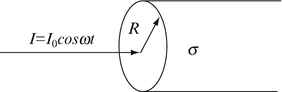
  Figure 12.23

• 12.13 Application: Power Radiated by an Antenna. An antenna produces an electric field intensity in free space as follows:

  $$ \mathbf{E}=\widehat{\boldsymbol{\uptheta}}\frac{12\pi }{R}{e}^{-j2\pi R} \sin \theta \kern1.25em \left[\frac{\mathrm{V}}{\mathrm{m}}\right] $$

  where R is the radial distance from the antenna and the field is described in a spherical coordinate system. The field of the antenna behaves as a plane wave in the spherical system of coordinates. Calculate:

  • (a) The magnetic field intensity of the antenna.

  • (b) The time-averaged power density at a distance R from the antenna.

  • (c) The total radiated power of the antenna.

• 12.14 Application: Electromagnetic Radiation Safety. The allowable time-averaged microwave power density exposure in industry in the United States is 10 mW/cm². As a means of understanding the thermal effects of this radiation level (nonthermal effects are not as well defined and are still being debated), it is useful to compare this radiation level with thermal radiation from the Sun. The Sun’s radiation on Earth is about 1,400 W/m² (time averaged). To compare the fields associated with the two types of radiation, view these two power densities as the result of a Poynting vector. Calculate:

  • (a) The electric and magnetic field intensity due to the Sun’s radiation on Earth.

  • (b) The maximum electric and magnetic field intensities allowed by the standard. Compare with that due to the Sun’s radiation.

• 12.15 Stored Energy. In a region of space where there are no currents, the time-averaged pointing vector equals 120 W/m². Assume that this power density is uniform on the surface of a sphere of radius a = 0.1 m, pointing outwards. Calculate the total stored energy in the sphere. The frequency is 1 GHz and the sphere has properties of free space.

12.1.5 Propagation in Lossless, Low-Loss, and Lossy Dielectrics

• 12.16 Energy Density in Dielectrics. A plane wave of given frequency propagates in a perfect dielectric:

  • (a) Calculate the time-averaged stored electric energy density and show that it is equal to the magnetic volume energy density.

  • (b) Suppose now the dielectric is lossy: calculate the time-averaged-stored electric and magnetic energy densities. Are they still the same?

• 12.17 Propagation in Lossy Media. Seawater has a conductivity of 4 S/m. Its permittivity depends on frequency; relative permittivity at 100 Hz is 80, at 100 MHz it is 32, and at 10 GHz it is 24:

  • (a) How can seawater be characterized in terms of its loss at these three frequencies? That is, is seawater a low-loss, high-loss, or a general lossy medium for which no approximations can be made?

  • (b) Calculate the intrinsic impedance at the three frequencies.

  • (c) What can you conclude from these calculations for the propagation properties of seawater?

• 12.18 Generation of a Plane Wave in a Lossy Dielectric. A very thin conducting layer carries a surface current density J ₀ [A/m] as shown in Figure 12.24. The frequency is f and the current is directed in the positive z direction. The layer is immersed in seawater, which has permittivity ε, permeability μ ₀, and conductivity σ. If the layer is at x = 0, calculate the electric and magnetic fields at x = x ₀. Given: J ₀ = 1 A/m, f = 100 MHz, σ = 4 S/m, ε ₀ = 8.854 × 10⁻¹² F/m, ε _r  = 80, μ ₀ = 4π × 10⁻⁷ H/m, x ₀ = 1 m.

  

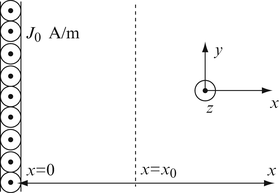
  Figure 12.24

• 12.19 Application: Communication in the Atmosphere. A parabolic antenna of radius b [m] transmits at a frequency f to a receiving antenna a distance d [m] away. The receiving antenna is also of radius b [m] and the transmission is parallel to the ground, in the atmosphere, as in Figure 12.25a. Assume that the wave propagates as a plane wave and the beam remains constant in diameter (same diameter as the antennas). Use the following values: b = 1 m, d = 200 km, ε = ε ₀ [F/m], μ = μ ₀ [H/m] σ = 2 × 10⁻⁷ S/m, and f = 300 MHz.

  • (a) Calculate the time-averaged power the transmitting antenna must supply if the receiving antenna must receive a magnetic field intensity of magnitude 1 mA/m.

  • (b) In an attempt to reduce the power required, the transmission is directed to a satellite which contains a perfect reflector, as shown in Figure 12.25b. The waves propagate through the atmosphere, into free space to the satellite and back to the receiving antenna. If the satellite is at a height h [m] and the waves propagate in the atmosphere for a distance q [m] in each direction, what is the power needed in this case for the same reception condition as in (a)? In addition to the values given in Figure 12.25a, h = 36,000 km, q = 20 km, and σ = 0 in free space. Compare the result with that in (a).

    

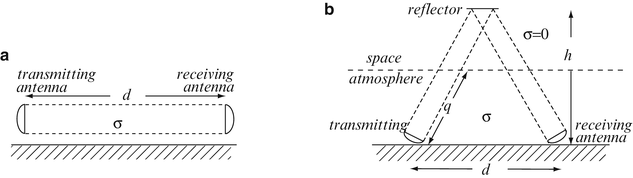
    Figure 12.25

• 12.20 Power Relations in the Atmosphere. A plane wave propagates in the atmosphere. Properties of the atmosphere are ε ₀ [F/m], μ ₀ [H/m], and σ [S/m]. The electric field intensity has an amplitude E ₀ [V/m] in the x direction and E ₀ [V/m] in the z direction. The frequency of the wave is f [Hz]. Given: E ₀ = 100 V/m, σ = 10⁻⁶ S/m, f = 100 MHz. Find:

  • (a) The direction of propagation.

  • (b) The instantaneous power per unit area in the direction of propagation.

  • (c) The magnitude of the magnetic field intensity after the wave has propagated a distance d = 10 km.

• 12.21 Application: Radar Detection and Ranging of Aircraft. A radar antenna transmits 50 kW at 10 GHz. Assume transmission is in a narrow beam, 1 m² in area, and that within the beam, waves are plane waves. The wave is reflected from an aircraft but only 1 % of the power propagates in the direction of the antenna. If the airplane is at a distance of 100 km, calculate the total power received by the antenna. Assume permittivity and permeability of free space and conductivity of 10⁻⁷ S/m.

• 12.22 Application: Fiber Optics Communication. Two optical fibers are used for communication. One is made of glass with properties μ = μ ₀ [H/m] and ε = 1.75ε ₀ [F/m] and has an attenuation of 2 dB/km. The second is made of plastic with properties μ = μ ₀ and ε = 2.5ε ₀ and attenuation of 10 dB/km. Suppose both are used to transmit signals over a length of 10 km. The input to each fiber is a laser, operating at a free-space wavelength of 800 nm and input of 0.1 W. Calculate:

  • (a) The power available at the end of each fiber.

  • (b) The wavelength, intrinsic (wave) impedance, and phase velocity in each fiber.

  • (c) The phase difference between the two fibers at their ends.

• 12.23 Application: Wave Properties and Remote Sensing in the Atmosphere. A plane wave of frequency f propagates in free space and encounters a large volume of heavy rain. The permittivity of air increases by 5 % due to the rain:

  • (a) Calculate the intrinsic impedance, phase constant, and phase velocity in rain and the percentage change in wavelength.

  • (b) Compare the properties calculated in (a) with those in free space. Can any or all of these be used to monitor atmospheric conditions (such as weather prediction)? Explain.

• 12.24 Application: Attenuation in the Atmosphere. Measurements with satellites show that the average solar radiation (solar constant) in space is approximately 1400 W/m². The total radiation reaching the surface of the Earth on a summer day is approximately 1100 W/m². 50 % of this radiation is in the visible range. To get some insight into the radiation process, assume an atmosphere which is 100 km thick. From this calculate the average attenuation constant in the atmosphere over the visible range assuming it is constant throughout the range and that attenuation is the only loss process.

12.1.6 Propagation in High-Loss Dielectrics and Conductors

• 12.25 Intrinsic Impedance in Copper. Copper at 100 MHz has the following properties: μ = μ ₀ [H/m], ε = ε ₀ [F/m], and σ = 5.7 × 10⁷ S/m. Calculate the intrinsic impedance of copper:

  • (a) Using the exact formula for general lossy materials.

  • (b) Assuming a high-loss material. Compare with (a) and with the intrinsic impedance of free space.

• 12.26 Propagation of Microwaves in Metals. A microwave oven operates at 2450 MHz and at a time-averaged power of 1000 W. The microwave beam, which can be assumed to be a plane wave, is incident on a copper foil, 1 m² in area and 10 μm thick. Assuming that the electric field is parallel to the foil and that only 2 % of the incident electric field intensity enters the foil, calculate the amplitude of the electric field intensity just below the other surface of the foil (but still in the copper foil). Use ε ₀ [F/m], μ ₀ [H/m], and σ = 0 for free space and ε ₀ [F/m], μ ₀ [H/m], and σ = 5.7 × 10⁷ S/m for copper.

• 12.27 Skin Depth and Penetration in Lossy Media. Two plane waves propagate in two materials as shown in Figure 12.26:

  • (a) What is the ratio between the distances the waves travel in each material before the electric and magnetic field intensities are attenuated to 1% of their amplitude at the surface? Assume that the waves enter the materials without losses or reflections.

  • (b) What is the ratio between the phase velocities?

    

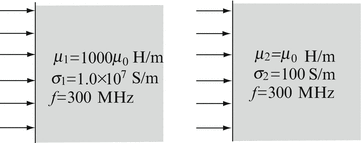
    Figure 12.26

• 12.28 Measurement of Conductivity in Lossy Materials. In an attempt to measure conductivity of a material, a plane wave is applied to one surface of a slab and measured at the other surface. Suppose the electric field intensity just below the left surface of the material is measured as E ₀ [V/m]. The electric field intensity at the right surface (again, just below the surface) is 0.1E ₀ [V/m]. Permeability and permittivity are those of free space, the material is known to have high conductivity, and the slab is d = 10 mm thick. The measurements are performed at 400 Hz. Calculate the conductivity of the material and its attenuation constant.

• 12.29 Application: Underwater Communication. Suppose a submarine could generate a plane wave and use it to communicate with another submarine in seawater. If the ratio between the amplitude at the receiver and that at the transmitter must be 10⁻¹² or higher, what is the maximum range of communication at:

  • (a) 10 MHz.

  • (b) 100 Hz.

    (Assume relative permittivity in both cases is 72 and conductivity of seawater is 4 S/m.)

• 12.30 Skin Depth in Conductors. Calculate the skin depth for the following conditions:

  • (a) Copper: f = 10¹⁰ Hz, μ = μ ₀ [H/m], σ = 5.8 × 10⁷ S/m.

  • (b) Mercury: f = 10¹⁰ Hz, μ = μ ₀ [H/m], σ = 1 × 10⁶ S/m.

• 12.31 Wave Impedance in Conductors. Calculate the intrinsic (wave) impedance of copper and iron at 60 Hz and 10 GHz. The conductivity of copper is 5.7 × 10⁷ S/m and that of iron is 1 × 10⁷ S/m. The permeability of copper is μ ₀ [H/m] and that of iron is 1,000μ ₀ [H/m] at 60 Hz and 10μ ₀ [H/m] at 10 GHz:

  • (a) Compare these with the wave impedance in free space.

  • (b) What can you conclude from these calculations for the propagation properties of conductors in general and ferromagnetic conductors in particular?

• 12.32 Classification of Lossy Materials. In a material, ε/ε ₀ = 24 and σ = 4 S/m. How do you classify this material for propagation purposes at 10 GHz? Explain.

• 12.33 Classification of Lossy Materials. A material has a conductivity of 0.01 S/m, permeability μ ₀ [H/m], and relative permittivity of 72. Is this a conductor or a dielectric at 60 Hz and at 30 GHz?

• 12.34 Application: Skin Depth and Communication in Seawater. How deep does an electromagnetic wave transmitted by a radar operating at 3 GHz propagate in seawater before its amplitude is reduced to 10⁻⁶ of its amplitude just below the surface? Use the following properties: σ = 4 S/m, ε = 24ε ₀ [F/m] (at 3 GHz), and μ = μ ₀ [H/m]. How good is radar for detection of submarines? Explain.

• 12.35 Penetration of Light in Copper. Since light is an electromagnetic wave and electromagnetic waves penetrate in any material except perfect conductors, calculate the depth of penetration of light into a sheet of copper. The conductivity of copper is 5.7 × 10⁷ S/m, and its permeability is that of free space. Assume the frequency of light (in mid-spectrum) is 5 × 10¹⁴ Hz.

• 12.36 Properties of Seawater at Different Frequencies. Seawater has relative permittivity of 81, permeability of free space, and conductivity of 4 S/m:

  • (a) Calculate the approximate range of frequencies over which seawater may be assumed to be a good conductor, assuming permittivity remains constant.

  • (b) Calculate the range of frequencies over which seawater may be assumed to be a good dielectric.

• 12.37 AC Current Distribution in a Conductor. A cable made of iron, with properties as shown in Figure 12.27, carries a current at 100 Hz. If the current density allowed (maximum) is 100 A/mm², find the current density at the center of the conductor (σ = 1 × 10⁷ S/m, μ =20 μ ₀ [H/m], r = 0.1 m).

  

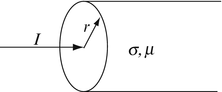
  Figure 12.27

• 12.38 Application: Skin Depth and Design of Cables for AC Power Distribution. A thick wire is made of steel as shown in Figure 12.28a. If the maximum current density allowed at any point in the material is 10 A/mm²:

  • (a) What is the total current the cable can carry at 60 Hz?

  • (b) To improve the current-carrying capability, a cable is made of 10 thinner wires (see Figure 12.28b ) such that the total cross-sectional area is equal to that of the cable in (a). What is the total current the new cable can carry for the same maximum current density, frequency, and material properties?

  • (c) Compare the results in (a) and (b) with the current the wire can carry at DC.

    Note: Assume that the solution for plane waves applies here even though the surface is curved. This is, in general, applicable if the skin depth is small compared to the radius.

    

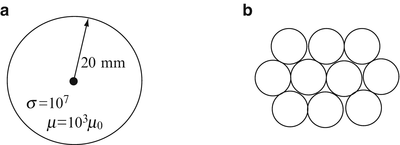
    Figure 12.28

• 12.39 Application: Electromagnetic Shielding. A shielded room is designed so that high-frequency waves cannot penetrate into the room. The shield is made of a nonconducting, nonmagnetic material with a thin coating of conducting material on the outer surface. The shield must reduce the electric field intensity by a factor of 10⁶ compared to the field outside at a frequency of 10 MHz. The conducting layer may be made of aluminum, copper, mu-metal, or a conducting polymer. Conductivities, permeabilities, cost, and mass of the three materials are given in the table below.

  	Cu	Al	Mu-metal	Polymer
  Conductivity [S/m]	5.7 × 107	3.6 × 107	0.5 × 107	0.001
  Permeability [H/m]	μ 0	μ 0	105 μ 0	μ 0
  Mass [kg/m3]	8,960	2,700	7,800	1,200
  Cost [unit/kg]	1	1.5	100	0.01

  • (a) Calculate the minimum thickness required for each of the four materials.

  • (b) Which material should we choose if the overall important parameter is: 1. Cost. 2. Mass. 3. Volume of conducting material. Use a unit area of the wall for comparison.

12.1.7 Dispersion and Group Velocity

• 12.40 Dispersion and Group Velocity. Under certain conditions, a wave propagates with the following phase constant:

  $$ \beta =\omega \sqrt{\mu \varepsilon}\sqrt{1-\frac{\omega_c^2}{\omega^2}}\kern1em \left[\frac{\mathrm{rad}}{\mathrm{m}}\right] $$

  where ω [rad/s] is the angular frequency of the wave, and ω _c [rad/s] is a fixed angular frequency. Because this gives the relation between β and ω, it is a dispersion relation:

  • (a) Plot the dispersion relation for the wave: use ω _c  = 10⁷, 10⁷ ≤ ω ≤ 2 × 10⁷ [rad/s].

  • (b) What are the phase and group velocities?

  • (c) What happens at ω = ω _c ? Explain.

• 12.41 Dispersion and Group Velocity. The dispersion relation for a wave is given as

  $$ \beta =\sqrt{\omega^2\mu \varepsilon -\frac{\uppi^2}{\mathrm{a}}}\kern1em \left[\frac{\mathrm{rad}}{\mathrm{m}}\right] $$

  • (a) Plot the dispersion relation. a is a constant.

  • (b) Find the group and phase velocities.

• 12.42 Phase and Group Velocities. Show that the following relation between group and phase velocity exists:

  $$ {v}_g={v}_p+\beta \frac{d{v}_{\mathrm{p}}}{d\beta}\kern1em \left[\frac{\mathrm{m}}{\mathrm{s}}\right] $$

• 12.43 Dispersion in Iron. Find and plot the relation between phase constant and angular frequency for a wave propagating in iron. Assume the relative permeability of iron is 1000 and its conductivity is 10⁷ S/m:

  • (a) Plot the relation for all frequencies.

  • (b) Find the phase and group velocities at 100 Hz and at 100 MHz using the plot in (a).

• 12.44 Phase and Group Velocities in Lossy Dielectrics. A plane wave with electric field intenstity E = $\widehat{\mathbf{x}}100{e}^{-j2z}\left[\mathrm{V}/\mathrm{m}\right]$ propagates in rubber, which has properties μ = μ ₀ [H/m], ε = 4ε ₀ [H/m], and σ = 0.001 S/m and may be considered to be a very low-loss dielectric. Calculate:

  • (a) The phase velocity in the material.

  • (b) The group velocity in the material.

  • (c) The energy transport velocity.

  • (d) What is the conclusion from the results in (a)–(c)?

• 12.45 Group Velocity and Dispersion in Low-Loss Media. A general low-loss medium is given in which the term σ/ωε is small but not negligible:

  • (a) Calculate the group velocity.

  • (b) Plot the group velocity as a function of frequency.

  • (c) Is the medium dispersive and, if so, is the dispersion normal or anomalous? Explain.

12.1.8 Polarization of Plane Waves

• 12.46 Polarization of Plane Waves. The magnetic field intensity of a plane wave is given as $\mathbf{H}(x)=\widehat{\mathbf{y}}10{e}^{-j\beta x}$ [A/m]. What is the polarization of this wave?

• 12.47 Polarization of Plane Waves. The magnetic field intensity of a plane wave is given as $\mathbf{H}(x)=\widehat{\mathbf{y}}10{e}^{-j\beta x}+\widehat{\mathbf{z}}10{e}^{-j\beta x}$ [A/m]. What is the polarization of this wave?

• 12.48 Polarization of Plane Waves. The electric field intensity of a wave is given as $\mathbf{E}(x) = \widehat{\mathbf{y}}10{\mathrm{e}}^{\hbox{--} 0.1x}\left({\mathrm{e}}^{\hbox{--} j\beta x}+{\mathrm{e}}^{j\beta x}\right)+\widehat{\mathbf{y}}10{\mathrm{e}}^{\hbox{--} 0.1x}\left({\mathrm{e}}^{\hbox{--} j\beta x}-{\mathrm{e}}^{j\beta x}\right)$ [V/m]. What is the polarization of this wave?

• 12.49 Polarization of Plane Waves. The electric field intensity of a wave is given as $\mathbf{E}\left(x,t\right)=\widehat{\mathbf{y}}100 \cos \left(\omega t-\beta x\right)+\widehat{\mathbf{z}}200 \cos \left(\omega t-\beta x-\pi /2\right)$ [V/m]. What is the polarization of this wave?

• 12.50 Polarization of Superposed Plane Waves. Two plane waves propagate in the same direction. Both waves are at the same frequency and have equal amplitudes. Wave A is polarized linearly in the x direction, and wave B is polarized in the direction of $\widehat{\mathbf{x}}+\widehat{\mathbf{y}}$. In addition, wave B lags behind wave A by a small angle θ. What is the polarization of the sum of the two waves?

• 12.51 Polarization of Plane Waves. The magnetic field intensity of a wave is given as $\mathbf{H}\left(x,t\right)=\widehat{\mathbf{y}}100\kern-0.1em \cos \kern-0.15em \left(\omega t-\beta x\right)+\widehat{\mathbf{z}}200 \cos \left(\omega t-\beta x+\pi /2\right)$ [V/m]. What is the polarization of this wave?