New Theory and Application for Generating Enveloping Surfaces Without Undercuts

Abstract

The design and improvement of kinematical motion transfer surfaces, namely gear surfaces, require the modeling of the surface-surface enveloping process and the visualization of contact characteristics. To analyse the quality of mesh in respect to undercuts, this study uses the special visualisation capability of the Surface Constructor (SC) system, which is intended for creating enveloped contacting surfaces. This view uses the unique Rho $=$ Rho(Fi) functions of the Reaching Model theory that have been applied earlier for different cases. Using these functions the evaluation and modification of mesh can be accomplished without the generated member of the surface pair. This study presents a new compressor type with a rotor that needs precise surface finishing. The patented grinding machine applied works with a special grinding wheel generated by the rotor surface. A novel undercut visualisation and detection method is used for the analysis of the correct grinding settings.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Nomenclature
$e$, $f$	$p$1, $p$2 parameter line indices
$g$, $h$	Indices of last $p$1, $p$2 parameter lines
$is$	Counter of intersected quadrangle edges
$k1, k2$	Contact lines
$k$x, $k$y	Constants
$p1, p2$	$F$1 surface parameters
$p1_{e}, p2_{f }$	$F$1 surface parameter values in an $F$1 grid-point, $e=$0, .., $g-1$; $f=$0, .., $h-1$
($x0_{k,l}, y0_{k,l}, z0_{k,l}$)	$P_{k}$ point in the $K$0 frame, determined at ($T_{k}$, $Z_{l})$ grid point of $F$2

($x2_{k,l}, y2_{k,l}, z2_{k,l}$)	$P_{k}$ point in the $K$2 frame, determined at ($T_{k}$, $Z_{l})$ grid point of $F$2
$A$, $B$	Points on $F$1
$F1, F1_{1}, F1_{2}$	Generating surface, 1st and 2nd intersection
$F1(p1, p2)$	Generating surface given by surface parameters $p$1 and $p$2
$F$2	Generated surface
$F2_{1}, F2_{2}$	Surfaces generated by the same $F$1 surface
Fi, Fi1, Fi2	$\varPhi$ variables of different surface generations
Ki(xi, yi, zi)	Coordinate system ($i =$ 0, 1, 2, 100)
$M$, $M_{i}$	$F$1 surface points
$M_{t}$	$F$1 surface point corresponding to $P_{k}$
$P_{k }$	Contact point$, k=$ 0, .., $r$
$P_{k}'$	Generated point of $F$2, $k=$ 0, .., $r$
$P_{n }$	Point of singularity
$R$	Space coordinate of $\kappa$ coordinate system and reaching direction, mm
$R(\varPhi )$	Reaching-coordinate function at $T_{k }$ division in $\kappa _{l}$ coordinate system associated to $Z_{l}$, mm
$R_{u}$	$R$ value of $P_{k}$ point, mm
$R_{t}$	$R$ value of $M_{t}$ point, mm
$R_{k,l }$	Minimum $R$ value determined at ($T_{k}$, $Z_{l})$ grid point of $F$2 mm
Rprev	$R$ minimum determined in previous iteration cycle for same $T-Z$ grid-point, mm
$R(x$0, $z$0)	Changeover from the ($x$0, $z$0) Descartes coordinate system to the curved $R-T$ coordinate system
$\Delta R$	Difference between the results of the last two cycles
Rho1, Rho2	$R$ variables of different surface generations
$T$, $T_{k }$	Division coordinate, $k=$ 0, .., $r$, mm or grad
$T_{A}$, $T_{B}$	Division coordinate values at points $A$ and $B$
Tau, Tau1, Tau2	$T$ variables of different surface generations
$T(x$0, $z$0)	Changeover from the ($x$0, $z$0) Descartes coordinate system to the curved $R-T$ coordinate system
$T$1, $T$1$_{1}, T$1$_{2}$	Body of the generating object, 1st and 2nd intersections
$v$, $w$	Degree of partial derivation
$Z$, $Z_{l}$	$F$2 grid-parameter value and identifying parameter of $\kappa$ coordinate system at the same time, $l=0$ , .., $s$, mm or grad
Zeta, Zeta1, Zeta2	$Z$ variables of different surface generations, mm or grad
n	Surface normal vector
r 0	Vector form of of $F$1 in $K$0 coordinate system, r 0 $=$ r 0($p$1, $p$2)
r 0 $^{(h) }$	Vector form of $F$1 in $K$0 coordinate system given by symbolic algebraic expressions
r 1 $^{(h) }$	Vector form of $F$1 in $K$1 coordinate system given by symbolic algebraic expressions
r $_{AB}$	Array of crossing points of a $p$1 or $p$2 parameter line and the $F$1 intersection curve; given in $K$0 coordinate system
v $^{1,2}$	Relative speed vector
M $_{i,j }$	Homogenous transformation matrix from Kj to Ki coordinate system given automatically by symbolic algebraic expressions
$\kappa (\varPhi , R, T)$	Non-Descartes coordinate system

$\kappa _{l}$	$\kappa$ coordinate system, associated to $Z_{l} \ F$2 grid-parameter value
$\varPhi$, $\varPhi _{i }$	Motion parameter and space coordinate of $\kappa$ coordinate system, i = 0,..,p, mm or grad
$\varPhi _{t }$	$\varPhi$ value corresponding to $P_{k}$ contact point, mm or grad

1. Remark: There is no difference between italic or normal form of above notations in the text.

1 Introduction

Most modern gear development software applies the Tooth Contact Analysis (TCA) method for optimizing the contacting properties of gears. This method involves the determination of the distance function—the ease-off topography—between the contacting tooth surfaces, and is equally suitable for conjugate and for modified, barreled or profile crowned gear surfaces. It can produce the transmission error and the bearing pattern, and is thus a very powerful tool (see e.g. [10, 11]). One of the best realizations uses real-time ease-off topography manipulation carrying out surface or kinematical system parameter alteration using a mouse and visual feedback [14]. However, such methods need the two surfaces to be previously computed, also in the case of conjugate contacting. The development in the space of motion tracks is a characteristic only of the Surface Constructor (SC) software application. Using this tool it is possible to optimize the contacting characteristics of the mesh and to avoid interference situations without the generated surface. Though many of the capabilities of SC can be found in other gear development tools (see the software comparison in Fig. 1), and especially in ZAKGEAR software, special features of SC include freedom in entering generating surfaces and kinematic relations due to the inbuilt symbolic algebraic computation capability and the software facilities based on the $R= R(\varPhi )$ functions. As these functions are very important for the detection of undercut situations, they will be the focus in this chapter.

Fig. 1

Comparison of gearing design programs

1.1 Short Introduction to the Theory of the Algorithm

To give a basis for referencing in the modeling section, we need to briefly review the theoretical fundamentals of the innovative Surface Constructor kinematical surface generating and contact analysis software. The name of the theory introduced by the author for generating conjugate surface pairs is the Reaching Model. The model solves the well-known task for gearings: the determination of the $F2$ conjugate surface if the generating $F1$ surface and the generating motion are given.

There are two well-known methods for this task:

• the differential-geometric method developed by Gochman [1], and

• the kinematical method, which applies the ${{\varvec{n}}}\cdot {{\varvec{v}}}^\mathrm{1,2 }~= 0$ scalar product where n is the normal vector and v $^\mathrm{1,2 }$ is the relative velocity vector at the contacting point. This method has two forms: the pure geometrical type and the Litvin type, which uses matrix-algebra [9].

Before the Reaching Model, the word undercut was used for various undesirable surface problems of mating surface pairs. The Reaching Model includes the capability to detect all types of local undercuts and the global cut in the same theoretical model. For a detailed explanation see [5].

The main advantage of the Reaching Model is its simplicity. In this model the generation of one of the points of the F2 surface is equivalent to solving a simple minimum value problem. The denominative reaching process will be introduced briefly based on Fig. 2.

Fig. 2

The reaching process

The Reaching Model applies a special non-Descartes coordinate system $\kappa$. The $\varPhi$ coordinate lines as well as the coordinate axis $\varPhi$ itself coincide with the motion paths of the points of a surface that is in the coordinate system $K$2, so $\varPhi$ has two roles:

• 1. motion (time) parameter,

• 2. one of the three space coordinates of coordinate system $\kappa$.

In the reaching process we choose a $\varPhi$ coordinate line that does not intersect the $T$1 body. Stepping from one $\varPhi$ coordinate line to another going in direction $R$, the generating $\varPhi$ coordinate line will be that one to reach $F$1 first. This $\varPhi$ line is the path of motion of point $P_{k}^{\prime }$ that will be one surface point of the generated surface $F$2. Point $P_{k}$ will be the contact point.

The necessary condition of connection in the Reaching Model is

$$\begin{aligned} \frac{\partial R}{\partial \varPhi }=0 \end{aligned}$$

(1)

where $R = R(\varPhi , T, Z)$ is the reaching-coordinate function, and $\varPhi$ is the space coordinate along the motion paths, $T$ is the division coordinate in the $\kappa$ slicing coordinate system, and $Z$ is the identifying parameter of the $\kappa$ coordinate system. This necessary condition is equivalent to the ${{\varvec{n}}} \cdot {{\varvec{v}}}^{{1,2}} = 0$ condition of the above-mentioned kinematical method.

The sufficient condition of the local minimum in the $\varPhi = \varPhi _{t}$ point, which is equivalent to the real mesh at the same location, given in the following form:

$$\begin{aligned} \frac{\partial ^{v} R}{\partial \varPhi ^{v}} | _{\varPhi \ = \ \varPhi _{t} } = 0 \ (v = 1, 2,..., w-1) \end{aligned}$$

(2)

and

$$\begin{aligned} \frac{\partial ^{w} R}{\partial \varPhi ^{w}} |_{\varPhi \ = \ \varPhi _{t} } >0 \end{aligned}$$

(3)

where $w$ is an even number.

This condition defines a local minimum point at $\varPhi = \varPhi _{t }$ that generates the $P_{k}'= P_{k}'(\varPhi = \varPhi _{t}; R = R(\varPhi _{t}); T=T_{k})$ point of the calculated $F$2 surface. The local nature of this condition means that it can be fulfilled in an infinitesimally small time or space domain, but a generating process with a longer $\varPhi$ (time and space) interval may destroy the generated $P_{k}'$ point.

2 Software Application for Surface Generation

Though the theory works with analytical expressions and partial derivatives, a robust, surface-independent software program for the realisation of the theory was developed on a discrete numerical basis for two reasons. Though calculations with analytical expressions are more effective, it is practically impossible to produce the explicit functions automatically in a surface- and kinematical-relation independent manner. The second reason is that the determination of global cut situations is easier using discrete computer simulation of the enveloping process.

2.1 The Calculation Algorithm

The applied iterative algorithm to determine the $P_{k}$ minimum point of the $F$1 intersection curve can be followed in Fig. 2. In this general example the applied discrete $R$ coordinate lines drawn at $\varPhi _{i} (i=0,..,t,..,p)$ intersect the $F$1 surface at points $M_{i+1},..,M_{t},..,M_{i+n}$. The $M_{t}\equiv P_{k}$ point has the minimal $R$ value among these points. The core of the algorithm determines these intersection points and the corresponding $R_{i+1},..,R_{t},..,R_{i+n}$ reaching coordinate values. Because of the discrete nature of the algorithm the exactness is not theoretical but the error can be controlled, as will be shown below. Calculating the $R_{i}$ values for ascending $\varPhi _{i}$ series makes it possible to detect not only minimum or maximum points, but also the locations of quasi-inflection places, thus detecting local undercut problems.

The algorithm developed, somewhat restricting the generality, applies a plane for slicing the space instead of a curved R-T coordinate surface. Using a plane carries some advantages, see [3].

Figure 3 shows a frequently used solution, which applies the simplest linear $R$ reaching coordinate direction and linear $T$ division coordinate direction in the $y 0 =$ 0 plane of a $K 0$ Descartes coordinate system.

Fig. 3

Example giving the position of the slicing plane in the $K$2 frame with reaching direction $R$ and $T$ division coordinate in the plane $R=R(x$0, $z$0) $= x$0; $T=T(x$0, $z$0) $= z$0

Such a $K$0 coordinate system has two roles in the Reaching Model and in the algorithm:

• It moves the $y$0 $=$ 0 coordinate plane carrying the $T$ and $R$ directions, and creates the $\varPhi$ motion tracks for every ($x$0, $z$0)—or$R, T$—point in the space, realising the fixed $\kappa =\kappa (\varPhi , R, T)$ special curved coordinate system. The start position of the $y0 = 0$ coordinate plane is identical to the $\varPhi =$ 0 coordinate surface of the $\kappa$ coordinate system and will hold the determined $P_{k}^{\prime }$, ..,$P_{r}^{\prime }$ points as the points of the $F$2 required. Cf. Fig. 2.

• Because only one curve of the $F$2 searched surface appears in the $y$0 $=$ 0 coordinate plane of the $K$0 coordinate system—and thus also in the $\varPhi =$ 0 surface of the $\kappa$ system—the installation of further $K$0—and corresponding $\kappa$—coordinate systems is necessary. These coordinate systems are positioned by the $Z$ parameter of the Reaching Model. The $y0=0$ coordinate planes of these coordinate systems, where $F$2 curves are searched for, have to slice the 3D space with single valued correspondence. To achieve this, the positive $R$ half of the plane is used in the algorithm, as in Fig. 3.

The algorithm applies two transformation chains, one of which is between the fixed $F$1 and the moving $F$2 space: this is the $K1-K$2 chain. The other gives the position of the $K$0 frame in the $K$2 as a $K2-K$0 chain. Using these transformations — given by normal and inverse homogenous transformation matrices M $_{{1,2}}$; M $_{{2,1}}$ and M $_{{2,0}}$; M $_{{0,2}}$—the position of surface $F$1 can be determined in the $K$0 frame and the series of ${\varvec{M}}_{i+1},..,{\varvec{M}}_{t},.., {\varvec{M}}_{i+n}$ points can be calculated. Using these points the grid points of surface $F2$ can be determined following the steps of the flowchart shown in Fig. 4.

Fig. 4

Calculation process of $F2$ grid points

After entering the given $F1$ surface, the relative motion of $F$2 space to $F1$ and the slicing motion symbolically, and then entering the numerical values, the $Z$ cycle value $l$ determines a slicing plane position. The $T$ cycle value $k$ selects an $R$ reaching direction in the slicing plane. The inner $\varPhi$ cycle determines the ($x0,z0$) $\equiv M_{i}$ intersection points and the corresponding $R$ values and produces the $R_{t} \equiv$ $R_{k,l}$ minimum value and the adjoined $M_{t}\equiv P_{k}$ point with its $T_{k}$ and $R_{k,l}$ coordinates in the $\kappa _{l}$ coordinate system. This core algorithm outputs $x0_{k,l}, y0_{k,l}=0$ and $z0_{k,l}$ coordinates of $P_{k}$. Taking the coordinates of this point in $K$2 frame in the $\varPhi =0$ moment, the $P_{k}'$ point is yielded. Repeating the $T$ and $Z$ cycles, the grid points of $F$2 surface can be obtained. The points of a contact line are characterised by the same time, and thus by the same $\varPhi$ value.

Fig. 5

The $M_{i}$ intersection point determination

2.1.1 Determining the $M_{i}$ Intersection Point

In the previous section it was shown that the determination of the $\mathrm{{M}}_{i}$ intersection point can be done in the $y0=0$ plane of $K$0 frame. If the coordinates of $M_{i}$ point in $K0$ frame offer themselves as $x0=x0_{i},y0=0,z0=z0_{i}$, then its coordinates in the $\kappa _{l}$ coordinate system will be $\varPhi =\varPhi _{i}, R=R(x0_{i},z0_{i}),T=T(x0_{i},z0_{i})$. To realise this, the $F1$ surface that is given by $p1$ and $p2$ surface parameters in $K1$ coordinate system has to be transformed into the $K0$ coordinate system under fixed $\varPhi _{i}$ and $\mathrm{{Z}}_{l}$ values.

If given the two-parametric vector form of $F1$ in $K1$ by homogenous coordinates:

$$\begin{aligned} {{\varvec{r}}}\mathbf 1 ^{(h)} = {{\varvec{r}}}\mathbf 1 ^{(h)}(p1, p2) = \left[ {{\begin{array}{c} {x1(p1,p2)} \\ {y1(p1,p2)} \\ {z1(p1,p2)} \\ 1 \\ \end{array} }} \right] \end{aligned}$$

(4)

then the vector form of $F1$ in $K$0 is:

$$\begin{aligned} {{\varvec{r}}}\mathbf 0 ^{(h)}&= {{\varvec{r}}}\mathbf 0 ^{(h)}(p1, p2, \varPhi _{i}, Z_{l}) \nonumber \\ = {{\varvec{M}}}_\mathrm{0,2 }(Z=Z_{l})\cdot {{\varvec{M}}}_\mathrm{2,1 }(\varPhi&=\varPhi _{i}) \cdot {{\varvec{r}}}\mathbf 1 ^{(h)} = \left[ {{\begin{array}{c} {x0(p1,p2,\varPhi _{i} ,Z_{l} )} \\ {y0(p1,p2,\varPhi _{i} ,Z_{l} )} \\ {z0(p1,p2,\varPhi _{i} ,Z_{l} )} \\ 1 \\ \end{array} }} \right] . \end{aligned}$$

(5)

To follow the subsequent steps of the algorithm, look at Fig. 5. The figure represents not only the $p$1 and $p$2 parameter lines, but the reaching direction $R$ at $T_{k}$ coordinate value. For the $M_{i}$ intersection point the $R$ value is unknown in the $\kappa _{l}$ coordinate system and so are the corresponding $x$0 and $z$0 coordinates in the $K$0 system. To determine these, the following successive approximation procedure is applied: first the algorithm seeks out that spatial quadrangle of the $p$1, $p$2 grid of $F1$ which is intersected by the $R$ reaching direction. This quadrangle is determined by the $p$1$_{e}$, $p1_{e+1}, p2_{f}, p2_{f+1}$ parameter lines in the figure. The tiles are generally bordered by arches, but the approximation applies linear interpolation between grid points. The right quadrangle is determined by the situation when the intersection points of the quadrangle edges with $y$0 plane, $A$ and $B$, embed the $T_{k}$ value in the $\kappa _{l}$ coordinate system by means of their $T_{A}$ and $T_{B}$ values.

Applying linear interpolation between $A$ and $B$ points, the $R$ value belonging to the $T_{k}$ coordinate can be calculated from the expression used for defining the reaching direction. Because of linear approximation, this value may differ from the exact $R$ value of the $M_{i}$ point. To keep this difference within a given error interval, a more precise $R$ value is calculated by refining the calculation using smaller quadrangles by halving the $p$1 and $p$2 parameter intervals. The approximation continues until the difference between the two last $R$ values becomes smaller than the given error limit. The $M_{i}$ point obtained in such a manner corresponds to the required $P_{k}$ contact point if its $R$ coordinate is the smallest among those offered by the different discrete $\varPhi _{i}$ values of the $\varPhi$ interval. The flowchart of this approximation is shown in Fig. 6. By increasing the number of $\varPhi$ steps in the $\varPhi$ interval, the error caused by the discrete enveloping simulation can be decreased.

2.2 The Surface Constructor Application

The system developed applies both symbolic and numerical representations of the objects. The symbolic algebraic computation provides the flexibility characteristic of the tool. Surface Constructor starts as an empty kinematical modelling shell and models the kinematical modelling process itself (see [6]). The system sketched in the lower right corner of Fig. 6 has three main representation levels:

• the symbolic level, which uses a symbolic algebraic representation of the objects in the kinematical model,

• the numerical level, which stores the given and computed objects using numerical form, and

• the visualisation level, which allows the analysis of views and motion of the objects.

Fig. 6

The process of $M_{i}$ point determination and the structure of the realising software

The selection and visualisation options are as follows:

• F2glob: global computational method and appropriate result

• F2lok: local computational method and appropriate result

• F2al: computation and visualisation of the occurrences of local undercuts

• $\varPhi$: computation and visualisation of moving path of selected points

• R-$\varPhi$: computation and visualisation of $R = R(\varPhi )$ functions as a special feature of this software

• v_a: computation and visualisation of the space of relative speed and acceleration

• PT: computation and visualisation of axoids.

3 The Essence of Rho = Rho(Fi) Functions

To make the following easy to understand, let us refresh the meaning of the function. The Rho is the reaching direction, a free plane curve, but in these examples lines will be applied for the sake of simplicity. It can be interpreted as a very thin telescope in the space of the required second surface $F2$. As the given surface $F1$ moves in this space, it compresses and releases the telescope, so the length of the telescope changes in time. This $length =length(time)$ function corresponds to the $Rho = Rho(Fi)$ function. Instead of time, usually the motion parameter Fi is used. The minimum value of the length plays an important role because this creates a surface point of $F2$. Points of the function having a horizontal tangent—minimum, maximum, inflection, constant—satisfy the necessary but not the sufficient kinematical condition of mesh. The sufficient condition is also fulfilled if such a point is a minimum point. So minimum points play a central role in the evaluation of good mesh by the $Rho =Rho(Fi)$ functions.

Fig. 7

Simple surface generation

A Simple Example of Rho $=$ Rho(Fi) Functions. In the following example the Rho reaching direction will be vertical and the motion horizontal. The given $F1$ surface in the K100 coordinate system has the form: $z100={ kx*x}100\ {*\ x}100+{ky*y}100\ {*\ y}100$, where kx and ky are constants. Figure 7 shows both the given $F1$ and the generated $F2$ surfaces. The boat-form $F2$ has a middle enveloped part and two footprint-like parts at the ends. Such footprint-like areas are not advantageous in gears mesh. In the Surface Constructor system there is a ${Rho }={Rho(Fi)}$ function visualisation window that maps the generated $F2 = F2({Zeta, Tau})$ parametric surface into its own rectangle area. Moving the sliders or simply the mouse cursor in the window, the (Zeta, Tau) parameter regions can be scanned and for every (Zeta, Tau) pair, as well as for every $F2$ surface point, a ${Rho} ={Rho}({Fi})$ function can be shown. The Zeta direction is parallel to Fi direction, Tau is perpendicular to the Zeta and Rho directions in this example. Figure 8 gives window shots for ${Tau index }= 100$ and Fig. 9 for ${Tau index }= 50$. Functions not having minimum with the horizontal tangent indicate footprint-like contact. Arrows emphasize window shots where surface-surface enveloping starts and ends $({Zeta }= 0; {Zeta }= -100)$.

Fig. 8

$Rho ={Rho}({Fi})$ functions at ${Tau index}= 100$

Fig. 9

${Rho }={ Rho}({Fi})$ functions at ${Tau index}= 50$

Fig. 10

${Rho }={ Rho}({Fi, Tau})$ surfaces at ${Zeta }= 20$ and ${Zeta }= -50$

It is also possible to plot the Rho = Rho(Fi,Tau), Zeta=const and the Rho= Rho(Fi, Zeta), Tau = const surfaces, as shown in Fig. 10. The valley form indicates surface-surface enveloping.

It is important that the characteristics—horizontal tangent, minimum point, inflection, horizontal line segment—indicating different contacting situations that are the same both for simple and complex relative surface motions do not depend on the complexity of shape of the given generating surface. To realise this advantage of the Rho = Rho(Fi) functions, the set of carrying planes of Rho reaching directions has to fill in the space of $F2$ single manner. Coordinate systems such as Descartes, cylindrical, and spherical satisfy this requirement. For details refer to [4].

3.1 Examples on Detection and Elimination of Undercuts

In the examples the parabolic $F1$ generating surface works as a tooth of a gear and generates different $F2$ surfaces depending on the relative kinematics, motion interval and parameters of the generating surface applied.

Figure 11 shows the situation when two enveloped local minimum points exist. If the motion is not limited, the deeper minimum destroys, or cuts the point of generated surface produced by the higher minimum occurring first, usually resulting in an edge on the surface.

Fig. 11

Generated surface having edges because of global cut, the characterising Rho = Rho(Fi) function and Rho = Rho(Fi, Tau) surface

3.1.1 The Possibilities of Avoiding Undercuts and Cut

The undercut is an infinitesimal happening opposite to the cut which requires a given space and time interval to occur. Local undercuts are usually followed and hided by global cuts.

The First Possibility: Limitation of the Generated Surface, so the Zeta Interval. This is a restrictive method and its use is limited, because the limited surface area does not have the same functionality and loadability as the original surface area. Figure 12 shows an example.

Fig. 12

Left There is a small remained undercut part after limiting Zeta = $-90 ...$ ${+}90$ to Zeta $=+60 ...$ ${+}90$. Right There is not undercut at Zeta $= +61...$ ${+}90$

The Second Possibility: Limitation of the Motion, so the Fi Interval. A better method is to limit the motion interval in order to prevent an undercut region from appearing. This modification may result in a larger loadable, usable area of the generated surface because by limiting the undercutting motion the maximum of the generated enveloped surface can be saved. In the course of demonstrating this, let us stop for a minute to introduce the detection of the inflection type local undercut. This type of undercut occurs at a point that is more difficult to detect. Figure 13 shows the situation when the generating motion is limited so the dangerous global cut cannot fully appear. (The Zeta interval was also limited by half.) Scanning the Zeta-Tau parameter region, the appearing inflections can be caught. Following these points, the border of Zeta-Tau region of enveloped points can be drawn. The outer points characterised by clear enveloping while the inner ones produced by cut or footprint formation.

Fig. 13

Limited motion interval. Detection of border points of not enveloped region (hatched)

To emphasise the advantage of Fi limitation opposite to Zeta, a generating surface in a deeper position was applied and caused a large undercut. Comparing the effects of the Zeta and Fi limitations it can be proved that Fi limitation provides a larger enveloped surface, see Fig. 14.

Fig. 14

Left Conspicuous cut formation of the Rho = Rho(Fi, Tau) surface. Right: Comparing Zeta and Fi limitations: Fi results in a somewhat longer cut-free enveloped surface

The Third Possibility: Modification of Kinematic Relation of Motion. By positioning the $F1$ surface to a higher position in the relative rolling motion, the resulting undercut becomes smaller. At a given parameter setting, enveloping of an edge can be observed: the sliding velocity of contacting point on $F1$ becomes zero for a short time, indicated by horizontal Rho = Rho(Fi) function segment, see Fig. 15.

Fig. 15

Edge enveloping on Rho = Rho(Fi, Tau) surface. Edge enveloping means stopping points of the contacting line. The two pictures on the right show different moments

The Fourth Possibility: Modification of the Generating Surface F1. Applying smaller kx and ky constants at F1 it becomes more flat. There is a little edge enveloping at kx = 0.02; ky = 0.008. Decreasing the values, the edge can be eliminated as shown in Fig. 16.

Fig. 16

Edge enveloping at kx = 0.02; ky = 0.008. Using smaller values at $F1$ results in $F2$ without an edge. The horizontal segment of Rho = Rho(Fi) function disappeared

4 Grinding Wheel Surface Generation

In this section a demonstrative example often use of the Surface Constructor for determination of a special grinding wheel surface enveloped by the rotor surface of a new type of compressor will be given. The grinding of this non-regular helical surface requires a non-conventional grinding machine and technology [8] to which the author holds a patent [2].

The result of the pump innovation is a new construction that has rotary parts only. The design method can be extended to compressors and expansion machines if the spiral angle of the helical surface is not equable. These new constructions, patented in recent years [13], are characterized by a rotary housing and rotor that form closed spaces or cavities. As the rotary parts rotate these cavities move parallel to the axes of the rotating machine elements. The required gap between the housing and the rotor has to be as small as possible to provide good sealing. This is essential for pumps and for expansion machines that work with steam energy. The airtight sealing is achieved by thick-film lubrication and the dynamic inertia effect of the oil [15]. The best way to ensure an airtight seal is to grind the working surfaces, but this raises problems. In the case of fluid pumps with normal helical surfaces, as shown in Fig. 17, the solution for rotor 1 is well known and is similar to the grinding of worms. The grinding of rotary house 2 is more complicated because of the inner surface, but is also possible [3]. The determination of grinding wheel profile is possible using modern software, like HeliCAD [3] or Surface Constructor [6, 7], and the profile of the determined surface of a revolution grinding wheel can be dressed by CNC dressers.

Fig. 17

FORCYL type water pump [12]

Fig. 18

New grinding machine construction for grinding non-conventional helical surfaces [2]

The grinding of helical surfaces having a non-constant lead requires the special technology and machine introduced in [3]. This machine has a constant wheel/workpiece ratio. The grinding machine shown in Fig. 18 is also needed for the finishing process of spiroid and globoid worms. The theoretically exact grinding of such worms was an unresolved task in the past, except for some special types of spiroid and globoid worms, e.g. involute spiroid worms. The problem is that a surface of revolution shaped classical grinding wheel cannot change its shape during grinding. However, the grinding of helical surfaces characterized by a changing diameter along the threads or a having non-constant lead requires this ability, because the contact line between the machined surface and the grinding wheel changes shape during grinding. The changing shape of the contact line means a different form of the surface of revolution of the wheel, but conventional wheels can-not change. One way to solve this problem is if the different surface parts of the worm can connect with different parts of the wheel, such as a special grinding wheel that has a working surface generated theoretically by the worm surface.

Fig. 19

Generation of grinding wheel for spiroid worm

Fig. 20

Full-width grinding of the rotor

The modeling of the grinding of a spiroid worm with the new machine construction is presented in Fig. 19. Here the calculated wheel surface reminds us of a Reishauer-type gear-grinder wheel but with a conical base. The grinding of normal helicoids like the rotor of the pump shown in Fig. 17 is also possible with the new technology. As the width of the grinding wheel is equal to the length of the rotor there is no need for axial feed. Figure 20 shows two moments of the modeled grinding process. The disadvantage of the method is the complicated production process of the wheel. Because of this, the non-conventional method introduced here can be used efficiently for mass production.

4.1 Grinding of Special Rotors

The new, innovative compressors and expansion machines have a rotor and rotary housing characterized by special helicoids with changing pitch. The difference between the rotors of the pump and the compressor is shown in Fig. 21. The compressor can be used as an expansion machine by changing the direction of the rotation of the elements. As the construction of such machines is fairly new, first a short introduction of the construction is given. The rotor and the rotary housing have their own, parallel axes.

Figure 22 shows the rotor and the opened rotary housing. Between the two axes there is a distance. The two parts rotate around their individual axes in the same direction and form cavities in every moment. These cavities move parallel to the axes, along the length of the machine. In the case of a compressor or an expansion machine these cavities become smaller or larger, respectively, as the parts rotate. The compression or expansion ratio depends on the pitch variation along the axis, not on the angle velocity of the rotation. The grinding of the rotary housing is problematic because of the length and relatively small diameter. Possibilities and limitations require further analysis, not presented here.

The grinding of the rotor is also problematic because of the undercut possibility. From earlier experiments on the grinding of worms having constant pitch it seems to be evident that the grinding wheel tilt angle has to be set close to the lead of the thread that has the smallest pitch value. To model the grinding process the special gear CAD software named Surface Constructor (SC) is used.

Fig. 21

Rotor of the pump and rotor of the compressor

Fig. 22

Rotor and the rotary housing of the expansion or compression machine

SC generates the grinding wheel surface as an enveloped surface, generated by the rotor in the relative motion. Thus the wheel surface and the rotor surface are conjugate surfaces. To check machinability and to successfully avoid undercut, two methods are applied:

• contact line visualization and

• visualization of $R=R(\varPhi )$ functions.

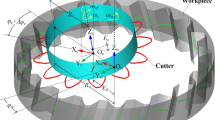
Using contact line visualization, the surface-surface contact has to be found every-where in the enveloping process. The surface-surface contact is important because the edge-surface contact may mean generating the surface by sweeping, not by envelop-ing, or an edge can be enveloped by the surface of the rotor. One moment of the checking can be seen on the right-hand side of Fig. 23. Because of the undercut possibility the continuity of the contact curve is essential. A discontinuity or ’jumping’ on the contact line means that the jumped-over area will not be ground accurately. To achieve the perfect result shown in Fig. 23, some trial-and-error runs were applied, and the model parameters, mainly the angle between the rotational axes, were fine tuned.

The problem with contact line visualization is that it has to be applied in every moment of the rotation. As Fig. 23 shows, the checking requires proper angle and zoom settings at every moment. Though the user interface of the visualization is very user friendly, the checking process is time consuming. Fortunately SC has a unique visualization capability.

Fig. 23

Calculated grinding wheel surface (left) and checking of perfect grinding by the contact line (view from the inside of the rotor) (right). Gamma = $5^{\circ }$

The exclusive capability of the Surface Constructor software, as well as the visualization of the $R=R(\varPhi )$ functions, were discussed in the previous section. The visualization of the $R=R(\varPhi )$ functions uses the relative kinematical relation of the rotor and the wheel as basic information and optimizes the grinding wheel surface and its setting in the space of relative velocity. Instead of relative velocity vectors it uses the motion tracks because these lines are tangential to the velocity vectors.

4.2 Undercut Control by the R = R($\varPhi$) Functions

In most cases the given generating surface is changeable, or the kinematical relations have some flexibility. In these situations we can optimize the contacting properties by changing the value of one of the parameters of the generating surface or the kinematical system. In the particular situation when the derivation of the grinding wheel surface is required without undercut problems, the main parameter that can be varied is the angle between the rotation axes. The distance of these axes, and thus the grinding wheel diameter, can also be modified, but angle modification is preferred.

Fig. 24

$R=R(\varPhi )$ function at Gamma = $5^{\circ }$ indicates a problem in grinding wheel generation

Fig. 25

$R=R( \varPhi )$ functions at Gamma = $0^{\circ }$

Fig. 26

Surface of $R=R(\varPhi )$ functions at Gamma = $0^{\circ }$

The first idea was that the best angle is the smallest lead angle of the rotor, which appears where the pitch is the smallest. This means an angle between the axes of about Gamma = $5^{\circ }$. The calculations showed good contact and enveloping surface by surface using the contact line visualization method for checking against undercut. This can be seen in Fig. 23. However, using the second checking method the visualization of the $R=R(\varPhi )$ functions gave a more precise solution. The more accurate investigation showed that there is an undercut problem at the $T=0$ coordinate indicated by the inflexion form, as can be seen in Fig. 24. The $T$ axis coincides with the wheel axis and $Z$ angle is measured like in Fig. 3. It was somewhat surprising that the best result appeared at Gamma = $0^{\circ }$, as proven by Figs. 25 and 26. Figure 25 shows the $R=R(\varPhi )$ functions in some peripheral and internal locations of the investigation area. The cursor position determines the $T$ and $Z$ values. Figure 26 shows all function curves as a surface and proves that every curve has a smooth minimum point, so the curves form a valley shape. This means that all the generated points of the grinding wheel surface are produced by surface-surface enveloping, so there is no undercut.

The investigations proved that the given rotor can be grinded accurately. Unfortunately, the production of such a grinding wheel is expensive, and its use is reasonable in the mass production of rotors only. The suitable type of grinding wheel is not a dressable sort, but another, coated by an abrasive layer.

The performance of the investigations was aided by the Surface Constructor kinematical modeling and surface generating software tool. In the investigation process the computer program modeled the rotor surface, then the first generating process calculated the surface of the rotary housing, after which the second generating process determined the special grinding wheel. The generating processes applied enveloping of the calculated surface by the rotor surface. During the investigation the visualization of the surface objects helped check the results and monitor the modeling process. The software handles a maximum of eleven visualization windows at the same time. The content of any window can be freely animated, zoomed, or rotated. This freedom and the ease of entering the generator curves, e.g. ellipse for the rotor, and entering the kinematical relations using symbolic expressions made the investigation process convenient.

Fig. 27

The surface constructor development tool in use

One screenshot of the investigation screen is given in Fig. 27. The upper part shows the generating surface entering window with the rotor, the first derivation window with the derived rotary housing and the second derivation window with the generated grinding wheel surface. The lower part of the screen shows additional visualization windows.

5 Summary

This chapter presented a new theory for the determination of enveloped surfaces. An algorithm that realizes the theory was introduced in detail. A short description was given of the Surface Constructor application that applies the algorithm and is suitable for the determination of enveloped surfaces and for detecting undercut problems. The unique $R=R(\varPhi )$ function visualization capability makes it possible to reveal the problematic generated surface regions and helps to avoid undercut problems. The study analyzed the grindability of the rotor of special pumps, innovative compressors and expansion machines from a geometrical point of view. The conclusion is that pump machine elements can be ground without a problem, and that the special rotors with a changing pitch for compressors or for expansion machines can be ground using a special machine, grinding wheel and technology. However, grinding of the inner surface of a rotary housing raises problems and requires further investigation and analysis. The investigation was performed by the Surface Constructor kinematical simulation and surface modeling tool, which has proved its applicability many times. The discrete simulation of the generating process offers an advantage when the determination of the real surface is required, but has a disadvantage when mathematical analysis is needed.