Abstract
The first purpose of this chapter is to provide a deep intuition of formal notions like the metric tensor, the Christoffel symbols, the Riemann tensor, vector fields, the covariant derivative, and so on: an intuition based on the consideration of surfaces in the three dimensional real space. We switch next to the study of geodesics, geodesic curvature and systems of geodesic coordinates. As an example of a Riemann surface, we develop the study of the Poincaré half plane and prove that it is a model of non-Euclidean geometry. We conclude with the Gauss–Codazzi–Mainardi equations and the related question of the embeddability of Riemann surfaces in the three dimensional real space.
As the title indicates, the purpose of this chapter is not to develop Riemannian geometry as such. The idea is to first re-visit the theory of surfaces in \(\mathbb{R}^{3}\), as studied in Chap. 5, adopting a different point of view and different notation. One of the objectives of this somehow unusual exercise—besides proving some important new theorems—is to provide a good intuition for the basic notions and techniques involved in general Riemannian geometry.
The idea of Riemannian geometry is to consider a surface as a universe in itself, not as a part of a “bigger universe”, for example as a part of \(\mathbb{R}^{3}\). Thus Riemannian geometry is interested in the study of those properties of the surface which can be established by measures performed directly “within” the surface, without any reference to the possible surrounding space. The “key” to performing measures on the surface will be the consideration of its first fundamental form (see Sect. 5.4), called the metric tensor in Riemannian geometry.
In Chap. 5, our main concern regarding surfaces in \(\mathbb {R}^{3}\) has been the study of their curvature. The normal curvature of a given curve on the surface is the orthogonal projection of its “curvature” vector on the normal vector to the surface (see Sect. 5.8). This normal curvature cannot be determined by measures performed on the surface, but the geodesic curvature can: the geodesic curvature is “the other component” of the curvature vector, that is, the length of the orthogonal projection of the curvature vector on the tangent plane to the surface. When you have the impression of “moving without turning” on a given surface—like when you follow a great circle on the surface of the Earth—you are in fact following a curve with zero geodesic curvature. Such a curve is called a geodesic: we pay special attention to the study of these geodesics.
In Sect. 5.16 we also studied the Gaussian curvature, which provides less precise information than the normal curvature. But in Riemannian geometry—where the normal curvature no longer makes sense—the Gaussian curvature assumes its full importance: the Gaussian curvature can be determined by measures performed on the surface itself. This is the famous Theorema Egregium of Gauss.
We characterize—in terms of the coefficients E, F, G, L, M, N of their two fundamental quadratic forms—those Riemann surfaces which arise from a surface embedded in \(\mathbb{R}^{3}\), as studied in Chap. 5. As an example of a Riemann surface not obtained from a surface in \(\mathbb{R}^{3}\), we describe the so-called Poincaré half plane, which is a model of non-Euclidean geometry.
We conclude with a first discussion of what a tensor is and a precise definition of a Riemann surface. This last definition refers explicitly to topological notions: the reader not familiar with them is invited to consult Appendix A.
Let us close this introduction with an observation which, in this chapter, will play an important role in supporting our intuition. Consider a surface represented by
and suppose that f is injective, not just locally injective. Consider a point P=f(u,v), for (u,v)∈U. The injectivity of f allows us to speak equivalently of the point P of the surface or the point with parameters (u,v) on the surface. In this case, the points of the open subset U describe precisely the points of the surface: f is a bijection between these two sets of points.
6.1 What Is Riemannian Geometry?
Turning through the pages of Chap. 5, we find many pictures of surfaces, as if we had taken photographs of these surfaces. But of course when you take a photograph of a surface, you do not put the lens of the camera on the surface itself: you stay outside the surface, sufficiently far, at some point from which you have a good view of the shape of the surface. Doing this, you study your surface from the outside, taking full advantage of the fact that the surface is embedded in \(\mathbb{R}^{3}\) and that you are able to move in \(\mathbb{R}^{3}\), outside the surface.
Let us proceed to a completely different example. We are three dimensional beings living in a three-dimensional world. We are interested in studying the world in which we are living. Of course if we are interested in only studying our solar system, we can take \(\mathbb{R}^{3}\) as a reliable mathematical model of our universe and use the rules of classical mechanics to study the trajectories of the planets. But we know that if we are interested in cosmology and the theory of the expansion of the universe, the very “static” model \(\mathbb{R}^{3}\) is no longer appropriate to the question. Physicists perform a lot of experiments to study our universe: they use large telescopes to capture very remote information. But these telescopes are inside our universe and take pictures of things that are inside our universe. This time—we have no other choice—we study our universe from the inside. From this study inside the universe itself physicists try to determine—for example—the possible curvature of our universe.
The topic of Riemannian geometry is precisely this: the study of a universe from the inside, from measures taken inside that universe. In this book we shall focus on Riemann surfaces, that is, two dimensional universes. Thus we imagine that we are very clever two-dimensional beings, living in a two-dimensional universe and knowing a lot of geometry. We do our best to study our universe from the inside, since of course there is no way for us to escape and look at it from the outside.
Our first challenge is to mathematically model this idea. For that, we shall rely on our study of surfaces embedded in \(\mathbb {R}^{3}\) in order to guess what it can possibly mean to study these surfaces from the inside. The above discussion suggests a first answer:
A Riemannian property of a surface in \(\mathbb{R}^{3}\) is a property which can be established by measures performed on the support of the surface, without any reference to its parametric representation.
Of course a two-dimensional being living on a surface of \(\mathbb {R}^{3}\) is able to measure the length of an arc of a curve on this surface, or the angle between two curves on the surface. These operations can trivially be done inside the surface, without any need to escape from the surface.
But given a regular curve
on a regular surface
we have seen (see Proposition 5.4.3) how to calculate its length:
where the three functions E(u,v), F(u,v), G(u,v) are the coefficients of the first fundamental form of the surface. The same matrix also allows us to calculate the angle between two curves on the surface (see Proposition 5.4.4). The matrix
thus allows us to compute lengths and angles on the surface: it is intuitively the “mathematical measuring tape” on the surface.
However, we must stress the following: knowledge of this “mathematical measuring tape” is (somehow) equivalent to being able to perform measures inside the surface. That is, only from measures performed inside the surface, you can infer the values of the three functions E(u,v), F(u,v), G(u,v). In this statement, the “somehow” restriction is the fact that to reach this goal, you have to perform infinitely many measures, because there are infinitely many points on the surface.
Indeed consider the curve v=v 0
for some fixed value v 0. The length on this curve from an origin u 0 to the point with parameter u is thus
The two dimensional being living on the surface can thus measure the value ℓ(u) for any value of the parameter u, and so “somehow” determine the function ℓ(u). If he makes the additional effort to attend a first calculus course, he will be able to compute the derivative
of that function and thus eventually, get the value of E(u,v 0). An analogous argument holds for G(u 0,v). Notice further that the angle θ between the two curves u=u 0 and v=v 0 is given by
Since E(u 0,v 0) and G(u 0,v 0) are already known, the two-dimensional being gets the value of F(u 0,v 0) from the measure of the angle θ.
All this suggests reformulating the above statement as follows:
The Riemannian geometry of a surface
$$f\colon U \longrightarrow\mathbb{R}^3,\qquad(u,v)\mapsto f(u,v) $$embedded in \(\mathbb{R}^{3}\) is the study of those properties of the surface which can be inferred from the sole knowledge of the three functions
$$E,F,G\colon U \longrightarrow\mathbb{R}. $$
Now working with three symbols E, F, G and two parameters u, v remains technically quite tractable. But imagine that you are no longer interested in “two dimensional universes” (surfaces), but in “three dimensional universes”, such as the universe in which we are living! Instead of two parameters, you now have to handle three parameters; analogously, as we shall see in Definition 6.17.6, the corresponding “mathematical measuring tape” will become a 3×3-matrix. If you are interested—for example—in studying relativity, you will have to handle a fourth dimension, “time”. Thus four parameters and a 4×4-matrix. In such higher dimensions, one has to use “notation with indices” in order to cope with all the quantities involved! We shall do this in the case of surfaces and introduce the classical notation of Riemannian geometry.
The Riemannian notation for the first fundamental form is:
Having changed the notation, we shall also change the terminology.
Definition 6.1.1
Consider a regular parametric representation of a surface
The matrix of functions
defined by
is called the metric tensor of the surface.
The “magic word” tensor suddenly appears! The reason for such a terminology will be “explained” in Sect. 6.12. For the time being, this is just a point of terminology which does not conceal any hidden properties and so formally, does not require any justification.
Using symbols like g ij to indicate the various elements of the “tensor”—which after all is just a matrix—sounds perfectly reasonable, as does using symbols (x 1,x 2) to indicate the two parameters. The use of upper indices x 1 and x 2 might seem like an invitation for confusion at this point, but we shall come back to this in Sect. 6.12. For the time being, we just decide to use the unusual notation (x 1,x 2).
Even if we do not yet know the reason for using these “upper indices”, let us at least be consistent. Given a curve
on the surface, we should now write
for the two components of the function c.
We have thus described the “challenge” of Riemannian geometry, as far as surfaces embedded in \(\mathbb{R}^{3}\) are concerned, and we have introduced the classical notation and terminology of Riemannian geometry. But to help us guess which properties have a good chance to be Riemannian, we shall add a “slogan”.
Consider again our friendly and clever two-dimensional being living on the surface. This two-dimensional being should have full knowledge of what happens “at the level of the surface” but no knowledge at all of what happens “outside the surface”. From a quantity that lives in the “outside world \(\mathbb{R}^{3}\)”, the two-dimensional being should only see its “shadow on the surface”, its “component at the level of the surface”, that is, its “orthogonal projection at the level of the surface”. Let us write this quantity of \(\mathbb{R}^{3}\) in terms of the basis comprising the two partial derivatives of the parametric representation and the normal vector to the surface. What happens along the normal to the surface, that is, what projects as “zero” on the surface, is the part of the information that the two-dimensional being cannot possibly access. So the rest of the information, that is, the components along the partial derivatives, should probably be accessible to our two-dimensional being. Let us take this as a slogan for discovering Riemannian properties.
Slogan:
The component of a geometric quantity along the normal vector to the surface is not Riemannian, but its components along the tangent plane should be Riemannian.
This is of course just a “slogan”, not a precise mathematical statement!
6.2 The Metric Tensor
Let us first recall (Proposition 5.5.4) that at each point of a regular surface
the matrix
is that of the scalar product in the tangent plane at \(f(x^{1}_{0},x^{2}_{0})\), with respect to the affine basis
This matrix is thus symmetric, definite and positive (Proposition 5.4.6).
We are now ready to give a first (restricted) definition of a Riemann surface, a definition which no longer refers to any parametric representation:
Definition 6.2.1
A Riemann patch of class \(\mathcal{C}^{k}\) consists of:
-
1.
a connected open subset \(U\subseteq\mathbb{R}^{2}\);
-
2.
four functions of class \(\mathcal{C}^{k}\)
$$g_{i,j}\colon U \longrightarrow\mathbb{R},\qquad \bigl(x^1,x^2 \bigr)\mapsto g_{ij}\bigl(x^1,x^2\bigr),\quad 1 \leq i,j\leq2 $$
so that at each point (x 1,x 2)∈U, the matrix
is symmetric definite positive. The matrix of functions
is called the metric tensor of the Riemann patch.
The observant reader will have noticed that if we start with a regular parametric representation f of class \(\mathcal{C}^{k}\) of a surface in \(\mathbb{R}^{3}\), the corresponding metric tensor as in Definition 6.2.1 is only of class \(\mathcal{C}^{k-1}\). This is the reason why some authors declare a Riemann patch to be of class \(\mathcal{C}^{k+1}\) when the functions g ij are of class \(\mathcal {C}^{k}\). This is just a matter of taste!
The term Riemann patch instead of Riemann surface underlines the fact that in this chapter, we shall again essentially work “locally”. The more general notion of Riemann surface is investigated in Sect. 6.17. We can now express will full precision the concern of Riemannian geometry:
Local Riemannian geometry is the study of the properties of a Riemann patch.
Of course what has been explained above suggests that we should think of the metric tensor intuitively as being that of a hypothetical surface in \(\mathbb {R}^{3}\). This can indeed support our intuition but this is perhaps not the best way to look at a Riemann patch.
Let us go back to the example of the sphere (or part of it) in terms of the “longitude” and “latitude”, as in Example 5.1.6:
Assume that we have restricted our attention to an open subset U on which f is injective. Think of the sphere as being the Earth. The open subset \(U\subseteq \mathbb{R}^{2}\) is then the geographical map of the corresponding piece of the Earth. The two coordinates of a point of \(U\subseteq \mathbb{R}^{2}\) are the longitude and the latitude of the corresponding point of the Earth. But how can you—for example—determine the distance between two points of the Earth, simply by inspecting your map? Certainly not by measuring the distance on the map using your ruler! Indeed on the map, the further one moves away from the equator, the more distorted the distances on the map become. Of course we can determine the longitude and the latitude of the two points on the map and use our knowledge of spherical trigonometry to calculate the corresponding distance on the surface of the Earth. However, to do this, one has to know that the Earth is approximately a sphere in the surrounding universe \(\mathbb{R}^{3}\): an attitude which does not make sense in Riemannian geometry.
What would be better would be to have an elastic ruler which is able to adjust itself to the correct length, depending on where it has been placed on the map. We are in luck, such an elastic ruler exists: it is the metric tensor. The metric tensor is at each point the matrix of a scalar product, but a scalar product which varies from point to point, compensating for the distortion of the map.
It is better to imagine that the map is of some unknown planet, the shape of which is totally unknown to us. From only the longitude and the latitude of points on this planet, as given by the map, we cannot draw any conclusions since we have no idea of the shape of the planet and thus of the distortion of the map together with the “elastic ruler” (the metric tensor), to “calculate” from the map the actual distances on the planet (we shall make this precise in Definitions 6.3.2 and 6.3.3). This probably gives a clearer intuitive way to think about Riemann patches.
Let us return to our formal definition of a Riemann patch.
Proposition 6.2.2
Given a Riemann patch as in Definition 6.2.1, the metric tensor is at each point (x 1,x 2) an invertible matrix with strictly positive determinant. Moreover at each point, g 11>0 and g 22>0.
Proof
By Proposition G.3.4 in [4], Trilogy II, the determinant of the matrix is strictly positive, thus the matrix is invertible. On the other hand
thus this quantity is strictly positive by positivity and definiteness. An analogous argument holds for g 22. □
Definition 6.2.3
Given a Riemann patch as in Definition 6.2.1, the inverse metric tensor
is at each point (x 1,x 2) the inverse of the metric tensor.
The matrix (g ij) ij has again received the label tensor and the indices have now been put “upstairs”. Once more, this is for the moment simply a matter of terminology and notation. We will comment further on this in Sect. 6.12.
Proposition 6.2.4
Given a Riemann patch of class \(\mathcal{C}^{k}\), the coefficients g ij of the inverse metric tensor are still functions of class \(\mathcal{C}^{k}\).
Proof
From any algebra course, we know that the inverse metric tensor is equal to
This forces the conclusion because the denominator is never zero (Proposition 6.2.2) while by Definition 6.2.1, the functions g ij are of class \(\mathcal{C}^{k}\). □
Let us conclude this section with a useful point of notation. Since at each point of a Riemann patch, the metric tensor is a 2×2 symmetric definite positive matrix (Definition 6.2.1), it is the matrix of a scalar product in \(\mathbb{R}^{2}\). Let us introduce a notation for this scalar product.
Notation 6.2.5
Given a Riemann patch
and a point (x 1,x 2)∈U, we shall write
for the corresponding scalar product on \(\mathbb{R}^{2}\), and by analogy
6.3 Curves on a Riemann Patch
The notion of a curve on a Riemann patch is the most obvious one.
Definition 6.3.1
A curve on a Riemann patch
is simply a plane curve in the sense of Sect. 2.1, admitting a parametric representation
The curve on the Riemann patch is regular when the plane curve represented by c is regular.
Using Notation 6.2.5 and in view of Propositions 5.4.3 and 5.4.4, we define:
Definition 6.3.2
Consider a regular curve
on a Riemann patch
Given a<k<l<b, the length of the arc of the curve between the points with parameters k and l is defined as being
Definition 6.3.3
Consider two regular curves
on a Riemann patch
When these two curves have a common point
the angle between these two curves at their common point is the real number θ∈[0,2π[ such that
Let us now, for a curve in a Riemann patch, investigate the existence of a normal representation.
Definition 6.3.4
Consider a Riemann patch
and a regular curve
in it. The parametric representation c is said to be a normal representation when at each point
One should be well aware that in Definition 6.3.4, c is not a normal representation of the ordinary plane curve in U of which it is a parametric representation. In the case of a surface of \(\mathbb{R}^{3}\) represented by f, the condition in Definition 6.3.4 requires in fact that f∘c be a normal representation of the corresponding skew curve.
The existence of normal representations in the case of a Riemann patch can be established just as in the case of plane or skew curves (see Propositions 2.8.2 and 4.2.7).
Proposition 6.3.5
Consider a Riemann patch
and a regular curve
Fixing a point t 0∈]a,b[, the function
is a change of parameter of class \(\mathcal{C}^{1}\) making c∘σ −1 a normal representation.
Proof
The derivative of σ is simply σ′=∥c′∥ c . This derivative is strictly positive at each point because the matrix (g ij ) ij is symmetric definite positive (see Definition 6.2.1) and by regularity, the vector c′ is never zero. Therefore σ′—thus also σ—is still of class \(\mathcal {C}^{1}\), since so are the g ij and c, as well as the square root function “away from zero”. Since its derivative is always strictly positive, σ is a strictly increasing function. Therefore σ admits an inverse σ −1, still of class \(\mathcal {C}^{1}\), whose first derivative is given by
Let us write \(\overline{c}=c\circ\sigma^{-1}\). We must prove that \(\|\overline{c}'\|_{\overline{c}}=1\) (see Definition 6.3.4). But
which forces at once the conclusion. □
Of course, we have:
Proposition 6.3.6
Consider a Riemann patch
and a regular curve
given in normal representation. Then for a<k<l<b
Proof
In Definition 6.3.2, the integral is that of the constant function 1. □
6.4 Vector Fields Along a Curve
Following the “slogan” at the end of Sect. 6.1, what happens in the tangent plane to a surface should be a Riemannian notion. In the theory of skew curves (see Chap. 3) we have considered several vectors attached to each point of a curve: its successive derivatives, the tangent vector, the normal vector, the binormal vector, and so on. When the curve is drawn on a surface, our “slogan” suggests that only the components of these vectors in the tangent plane should be relevant in Riemannian geometry. Therefore we make the following definition.
Definition 6.4.1
Let us consider a curve c on a surface f
both being regular and of class \(\mathcal{C}^{k}\). A vector field of class \(\mathcal{C}^{k}\) along the curve, tangent to the surface, is a function of class \(\mathcal{C}^{k}\)
where for each t∈]a,b[, ξ(t) belongs to the direction of the tangent plane to the surface at the point (f∘c)(t) (see Definition 2.4.1 in [4], Trilogy II).
Of course, working as usual in the affine basis of the partial derivatives in each tangent plane, we can re-write (with upper indices)
The knowledge of the vector field ξ is of course equivalent to the knowledge of its two components ξ 1 and ξ 2. This suggests at once that being a tangent vector field can easily be made a Riemannian notion:
Definition 6.4.2
Consider a Riemann patch of class \(\mathcal{C}^{k}\)
and a regular curve of class \(\mathcal{C}^{k}\) in it
A vector field ξ of class \(\mathcal{C}^{k}\) along this curve consists of giving two functions of class \(\mathcal{C}^{k}\)
Of course in Definition 6.4.2 we intuitively think of the two functions ξ 1, ξ 2 as being the two components of a vector in the tangent plane (see Definition 6.4.1), even if in the case of a Riemann patch, no such tangent plane is a priori defined. Let us conclude this section with a very natural definition:
Example 6.4.3
Consider a Riemann patch of class \(\mathcal{C}^{k}\)
and a regular curve of class \(\mathcal{C}^{k}\)
The vector field τ of class \(\mathcal{C}^{k-1}\) with components
is called “the” tangent vector field to the curve; it is such that ∥τ∥ c =1. When c is given in normal representation, one has further τ=c′.
Proof
At each point, the vector field τ is the vector \(c'\in\mathbb {R}^{2}\) divided by its norm for the scalar product (−|−) c (see Notation 6.3.4). The result follows by Definition 6.3.4. □
In Example 6.4.3, it is clear that equivalent parametric representations of the same curve can possibly give corresponding tangent vector fields opposite in sign.
Definition 6.4.4
Consider a Riemann patch
and a regular curve
With Notation 6.2.5:
-
1.
The norm of a vector field ξ along c is the positive real valued function
$$\|\xi\|(t)=\bigl\| \xi(t)\bigr\| _{c(t)}. $$ -
2.
Two vector fields ξ and χ along c are orthogonal when at each point
$$\bigl(\xi(t)\bigl|\chi(t)\bigr)_{c(t)}=0. $$
6.5 The Normal Vector Field to a Curve
We are now interested in transposing, to the context of a Riemann patch, the notion of the normal vector to a curve in the sense of the Frenet trihedron (see Definition 4.4.1).
Proposition 6.5.1
Consider a Riemann patch of class \(\mathcal{C}^{k}\)
and a regular curve of class \(\mathcal{C}^{k}\)
There exists a vector field of class \(\mathcal{C}^{k-1}\)
along c with the properties:
-
1.
η is orthogonal to the tangent vector field of c;
-
2.
∥η∥ c =1;
-
3.
the basis (c′,η) has at each point direct orientation (see Sect. 3.2 in [4], Trilogy II).
This vector field is called “the” normal vector field to the curve.
Proof
To get a vector field μ satisfying the orthogonality condition of the statement, at each point we must have (see Definition 6.4.4)
or in other words
It suffices to put
or—of course—the opposite choice
This can be re-written as
In this formula, the square matrix is regular at each point (it has the same determinant as the metric tensor) and c′ is non-zero at each point, by regularity of c. Thus μ is non-zero at each point and the expected normal vector field is
Observe that the two-fold possibility in the choice of the vector field μ yields two bases (c′,η) with opposite orientations: it remains to choose the basis with direct orientation. □
6.6 The Christoffel Symbols
Chapter 5 has provided evidence that all important properties of the surface can be expressed in terms of the six functions E, F, G, L, M, N defined in Proposition 5.4.3 and Theorem 5.8.2. As emphasized in Sect. 6.2, the functions E, F, G constitute the metric tensor of the surface. But what about the functions L, M, N. Are they Riemannian quantities, quantities that we can determine by measures performed on the surface? The answer is definitely “No”:
Counterexample 6.6.1
The coefficients L, M, N of the second fundamental form of a surface cannot be deduced from the sole knowledge of the coefficients E, F, G of the first fundamental form.
Proof
At each point of the plane with parametric representation
we have trivially
At each point of the circular cylinder (see Sect. 1.14 in [4], Trilogy II) with parametric representation
we have
from which again
On the other hand
and
from which
The two surfaces have the same functions E, F, G, but not the same functions L, M, N. □
So L, M, N are not Riemannian quantities. Let us recall that they are obtained from the second partial derivatives of the parametric representation, by performing the scalar product with the normal vector \(\overrightarrow{n}\) to the surface (see Theorem 5.8.2). Applying the “slogan” at the end of Sect. 6.1 to the case of the second partial derivatives of the parametric representation, the following definition sounds sensible:
Definition 6.6.2
Consider a regular parametric representation
of class \(\mathcal{C}^{k}\) of a surface.
-
1.
The Christoffel symbols of the first kind are the functions
$$\varGamma_{ijk} = \biggl( \frac{\partial^2 f}{\partial x^i\partial x^j} \bigg\vert \frac{\partial f}{\partial x^k} \biggr),\quad 1\leq i,j,k\leq2. $$ -
2.
The Christoffel symbols of the second kind are the quantities \(\varGamma_{ij}^{k}\), the components of the second partial derivatives of f with respect to the basis comprising the first partial derivatives and the normal to the surface:
$$\frac{\partial^2 f}{\partial x^i\partial x^j} = \varGamma_{ij}^1\frac{\partial f}{\partial x^1} +\varGamma_{ij}^2\frac{\partial f}{\partial x^2} +h_{ij}\overrightarrow{n}. $$
The observant reader will have noticed the use of the word “symbols”, not “tensor”; and the presence of upper and lower indices! Again, we shall comment upon this later.
Proposition 6.6.3
Under the conditions of Definition 6.6.2,
Proof
Simply take the scalar product of
with \(\overrightarrow{n}\), keeping in mind that
□
From now on, we shall use the notation h ij instead of L, M, N. Let us also make the following easy observations:
Proposition 6.6.4
Under the conditions of our Definition 6.6.2, the Christoffel symbols are functions of class \(\mathcal{C}^{k-2}\) with the following properties:
Proof
The first two equalities hold because
The third equality is obtained by expanding the scalar product
keeping in mind that \((\overrightarrow{n}|\frac{\partial f}{\partial x^{k}})=0\).
This third equality can be re-written in matrix form as
Multiplying both sides by the inverse metric tensor, we obtain the fourth formula.
By Definition 6.6.2, the Christoffel symbols of the first kind are functions of class \(\mathcal{C}^{k-2}\). By Proposition 6.2.4 and the fourth equality in the statement, the same conclusion holds for the symbols of the second kind. □
The key observation is now:
Proposition 6.6.5
Under the conditions of Definition 6.6.2, the Christoffel symbols of the first kind are also equal to
Proof
First (see Lemma 1.11.3)
Therefore
by the first formula in Proposition 6.6.4. □
Proposition 6.6.6
Under the conditions of Definition 6.6.2, the Christoffel symbols of the first and second kind can be expressed as functions of the coefficients of the metric tensor.
Proof
Proposition 6.6.5 proves the result for the symbols of the first kind. But the inverse metric tensor can itself be expressed in terms of the metric tensor (see Definition 6.2.3 or the proof of Proposition 6.2.4 for an explicit formula). By the fourth equality in Proposition 6.6.5, the result for the symbols of the second kind follows immediately. □
To stress the fact that the Christoffel symbols are Riemannian quantities, let us conclude this section with a definition inspired by Proposition 6.6.6:
Definition 6.6.7
Given a Riemann patch of class \(\mathcal{C}^{1}\) as in Definition 6.2.1, the Christoffel symbols of the first kind are by definition the quantities
while the Christoffel symbols of the second kind are the quantities
Proposition 6.6.4 carries over to this generalized context.
Proposition 6.6.8
Consider a Riemann patch of class \(\mathcal{C}^{k}\)
The Christoffel symbols are functions of class \(\mathcal{C}^{k-1}\) satisfying the following properties:
Proof
The last condition is just Definition 6.6.7. This same definition forces at once the first condition, because the metric tensor is symmetric. This immediately implies the second condition. Finally Definition 6.6.7 can be expressed as the matrix formula
Multiplying both sides by the metric tensor yields condition 4 in the statement. □
6.7 Covariant Derivative
Our experience of doing mathematics tells us how important the derivative of a function can be. Going back to Definition 6.4.1, we therefore want to consider the derivative of the function ξ describing a vector field. However, since we are working in Riemannian geometry, our “slogan” of Sect. 6.6 suggests that we should focus on the component of this derivative in the tangent plane.
Definition 6.7.1
Consider a regular curve c on a regular surface f
Consider further a vector field of class \(\mathcal{C}^{1}\) along this curve, tangent to the surface
The covariant derivative of this vector field is the vector field
defined at each point as the orthogonal projection of the derivative of ξ on the direction of the tangent plane to the surface.
Our job is now to explicitly calculate this covariant derivative.
Proposition 6.7.2
In the situation described in Definition 6.7.1, when the surface is of class \(\mathcal{C}^{2}\), the covariant derivative of the vector field ξ is equal to
Proof
Let us first differentiate the function
We obtain, keeping in mind Definition 6.6.2 and writing \(\overrightarrow{n}\) for the normal vector to the surface:
where for short, we have used the abbreviated notation
and analogously for the partial derivatives of f. The orthogonal projection on the direction of the tangent plane is constituted of the first two lines of this last expression, which is indeed the formula in the statement. □
The observant reader will have noticed that Definition 6.7.1 of the covariant derivative makes perfect sense in class \(\mathcal{C}^{1}\), while its expression given in Proposition 6.7.2 requires the class \(\mathcal{C}^{2}\) because of the presence of the Christoffel symbols (see Definition 6.6.2).
The Christoffel symbols are Riemannian quantities (see Definition 6.6.7), thus by Proposition 6.7.2, so is the covariant derivative:
Definition 6.7.3
Consider a Riemann patch of class \(\mathcal{C}^{1}\)
and a regular curve
The covariant derivative of a tangent vector field ξ of class \(\mathcal{C}^{1}\) along this curve is the tangent vector field \(\frac{\nabla\xi}{dt}\) whose two components are
The covariant derivative inherits the classical properties of an “ordinary” derivative. For example:
Proposition 6.7.4
Consider a Riemann patch of class \(\mathcal{C}^{1}\)
and a regular curve
in it. Consider two tangent vector fields ξ and χ of class \(\mathcal{C}^{1}\) along this curve, as well as an additional function of class \(\mathcal{C}^{1}\)
and a change of parameter of class \(\mathcal{C}^{1}\)
The following properties hold:
-
1.
\(\frac{\nabla(\xi+\chi)}{dt} =\frac{\nabla\xi}{dt}+\frac{\nabla\chi}{dt}\);
-
2.
\(\frac{\nabla(\alpha\cdot\xi)}{dt} =\frac{d\alpha}{dt}\xi+\alpha\frac{\nabla\xi}{dt}\);
-
3.
\(\frac{\nabla(\xi\circ\varphi)}{ds} =(\frac{\nabla\xi}{dt}\circ\varphi) \cdot\varphi'\);
-
4.
\(\frac{d(\xi|\chi)_{c}}{dt} =(\frac{\nabla\xi}{dt}|\xi)_{c} +(\xi|\frac{\nabla\chi}{dt})_{c}\).
Proof
Condition 1 of the statement is trivial. Condition 2 is immediate: the components of \(\frac{\nabla(\alpha\cdot\xi)}{dt}\) are
which is the second formula of the statement. Condition 3 is proved in exactly the same straightforward way: the components of \(\frac{\nabla(\xi\circ\varphi)}{ds}\) are
which is again the announced statement.
Proving the fourth formula in the statement is a more involved task. First let us observe that the components of \(\frac{d(\xi|\chi )_{c}}{dt}\) are
On the other hand the components of \((\frac{\nabla\xi}{dt}|\chi) +(\xi|\frac{\nabla\xi}{dt})\) are
Comparing both expressions, it remains to prove that
Using Proposition 6.6.8 and Definition 6.6.7, we obtain
which is the expected equality concluding the proof. □
Corollary 6.7.5
Consider a Riemann patch of class \(\mathcal{C}^{2}\)
and a regular curve of class \(\mathcal{C}^{2}\)
given in normal representation. The tangent vector field c′ to the curve and its covariant derivative \(\frac{\nabla c'}{ds}\) are orthogonal vector fields (see Definition 6.4.4).
Proof
By Definition 6.3.4, (c′|c′) c =1. By Proposition 6.7.4.4, this implies \(2(\frac{\nabla c'}{ds}\bigl|c')_{c}=0\). □
Under the conditions of Corollary 6.7.5, when the covariant derivative of c′ is non-zero at each point, the normal vector field of Proposition 6.5.1 is given by
Let us conclude this section by noticing that the notion of covariant derivative provides the notion of covariant partial derivative:
Definition 6.7.6
Consider a Riemann patch (U,(g ij ) ij ) of class \(\mathcal{C}^{k}\) (k≥1).
-
1.
A 2-dimensional tangent vector field ξ of class \(\mathcal {C}^{k}\) on this Riemann patch consists of two functions of class \(\mathcal{C}^{k}\)
$$\xi^1,\xi^2\colon U \longrightarrow\mathbb{R}. $$ -
2.
The covariant partial derivatives of this vector field ξ at a point \((x^{1}_{0},x^{2}_{0})\) are:
-
\(\frac{\nabla\xi}{\partial x^{1}}(x^{1}_{0},x^{2}_{0})\), the covariant partial derivative at \(x^{1}_{0}\) of the vector field \(\xi (x^{1},x^{2}_{0})\) along the curve \(x^{2}=x^{2}_{0}\);
-
\(\frac{\nabla\xi}{\partial x^{2}}(x^{1}_{0},x^{2}_{0})\), the covariant partial derivative at \(x^{2}_{0}\) of the vector field \(\xi (x^{1}_{0},x^{2})\) along the curve \(x^{1}=x^{1}_{0}\).
-
As expected, one has:
Proposition 6.7.7
Consider:
-
a Riemann patch (U,(g ij ) ij ) of class \(\mathcal{C}^{1}\) (k≥1);
-
a 2-dimensional tangent vector field ξ=(ξ 1,ξ 2) of class \(\mathcal{C}^{1}\);
-
a regular curve represented by c:]a,b[⟶U.
Under these conditions, writing t∈]a,b[ for the parameter,
Proof
Since \(\frac{\nabla\xi}{\partial x^{1}}\) is computed along a curve \(h(x^{1})=(x^{1},x^{2}_{0})\), one has
and analogously for the other partial derivative. Thus by Definition 6.7.3 \(\frac{\nabla\xi}{\partial x^{j}}\) has for components
On the other hand, still by Definition 6.7.3, the vector field ξ(c(t)) along c has a covariant derivative whose components are given by
This proves the announced formula. □
6.8 Parallel Transport
In the plane \(\mathbb{R}^{2}\), we know at once how to “transport” a fixed vector \(\overrightarrow{v}\) along a curve represented by c(t) (see Fig. 6.1): at each point of the curve, simply consider the point
that is the point P(t) such that \(\overrightarrow{c(t)\, P(t)}=\overrightarrow{v}\) (see Definition 2.1.1 in [4], Trilogy II).

Fig. 6.1
This construction in \(\mathbb{R}^{2}\) thus yields a “constant vector field” along c
But saying that this function is constant is equivalent to saying that its derivative is equal to zero. The corresponding Riemannian notion is now clear:
Definition 6.8.1
Consider a Riemann patch of class \(\mathcal{C}^{1}\)
and a regular curve
in it. A vector field ξ of class \(\mathcal{C}^{1}\) along c is said to be parallel when its covariant derivative is everywhere zero.
Let us observe that
Lemma 6.8.2
Being a parallel vector field along a curve is independent of the regular parametric representation chosen for the curve.
Proof
Let φ be a change of parameters of class \(\mathcal{C}^{1}\) for the curve. Differentiating the equality \(\varphi\circ\varphi ^{_{1}}=\mathsf{id}\), we get
proving that φ′ is never zero. The conclusion then follows immediately from Proposition 6.7.4.3. □
Proposition 6.8.3
Consider a Riemann patch of class \(\mathcal{C}^{1}\)
and a regular curve in it:
-
1.
A parallel vector field ξ of class \(\mathcal{C}^{1}\) along c has a constant norm.
-
2.
A parallel vector field ξ of class \(\mathcal{C}^{1}\) along c is orthogonal to its covariant derivative \(\frac{\nabla\xi}{dt}\).
-
3.
Two non-zero parallel vector fields ξ, χ of class \(\mathcal{C}^{1}\) along c make a constant angle.
Proof
By Proposition 6.7.4
This proves that the scalar product (ξ|χ) c is constant. Putting ξ=χ we conclude that ∥ξ∥ c and ∥χ∥ c are constant. Together with the scalar product being constant, this proves that the angle is constant as well (see Notation 6.2.5).
But when \(\|\xi\|_{c}^{2}=(\xi|\xi)_{c}\) is constant, its derivative is zero and by Proposition 6.7.4.4, this yields \(2(\frac {\nabla\xi}{dt}|\xi)_{c}=0\), thus the orthogonality of ξ and \(\frac{\nabla\xi}{dt}\). □
The existence of parallel vector fields is attested by the following theorem:
Theorem 6.8.4
Consider a Riemann patch of class \(\mathcal{C}^{k}\) (k≥2)
and a regular curve of class \(\mathcal{C}^{k}\) in it:
Given a vector \(\overrightarrow{v}\in\mathbb{R}^{2}\) and a point t 0∈]a,b[, there exists a sub-interval ]r,s[⊆]a,b[ still containing t 0 and a unique parallel vector field ξ of class \(\mathcal{C}^{k}\) along c
such that \(\xi(t_{0})=\overrightarrow{v}\). For each value t∈]r,s[, the vector ξ(t) is called the parallel transport of \(\overrightarrow{v}\) along c.
Proof
This is an immediate consequence of the theorem for the existence and uniqueness of a solution of the system of differential equations (see Proposition B.1.1)
together with the initial conditions
(see Definition 6.7.3). Observe that all the coefficients of the differential equations are indeed of class \(\mathcal{C}^{k-1}\) (see Proposition 6.6.8). □
6.9 Geodesic Curvature
Let us now switch to the study of the curvature of a curve in a Riemann patch.
Let us first recall the situation studied in Sect. 5.8. Given a curve on a surface
we write h=f∘c for the corresponding skew curve and \(\overline{h}\) for its normal representation. The normal curvature (up to its sign) is the length of the orthogonal projection of the “curvature vector” \(\overline{h}''\) on the normal vector \(\overrightarrow{n}\) to the surface. Following our “slogan” at the end of Sect. 6.1, this normal curvature is probably not a Riemannian notion. Indeed we have the following:
Counterexample 6.9.1
The normal curvature of a surface cannot be deduced from the sole knowledge of the three coefficients E, F, G.
Proof
In Counterexample 6.6.1, the two surfaces have the same coefficients E, F, G but not the same normal curvature. Indeed by Theorem 5.8.2, the normal curvature of the cylinder is equal to −1 in the direction (1,0) while in the case of the plane, the normal curvature is equal to 0 in all directions. □
However, as our “slogan” of Sect. 6.1 suggests, in the discussion above, the orthogonal projection of the “curvature vector” \(\overline{h}''\) on the tangent plane should be a Riemannian notion. That projection—called the geodesic curvature of the curve—is intuitively what the two-dimensional being living on the surface sees of the curvature of the curve (see Sect. 6.1).
Definition 6.9.2
Consider a curve on a surface
both being regular and of class \(\mathcal{C}^{2}\). Write \(\overline {f\circ c}\) for the normal representation of the corresponding skew curve. The geodesic curvature of the curve on the surface is the length of the orthogonal projection of the vector \(\overline{f\circ c}''\) on the tangent plane to the surface.
We thus get at once:
Proposition 6.9.3
Consider a curve on a surface, both being regular and of class \(\mathcal{C}^{2}\). Then at each point of this curve
where
-
κ indicates the curvature of the curve;
-
κ n indicates the normal curvature of the curve;
-
κ g indicates the geodesic curvature of the curve.
Proof
This follows by Pythagoras’ Theorem (see Theorem 4.3.5 in [4], Trilogy II) and Definitions 5.8.1 and 6.9.2. □
Definition 6.9.2 can easily be rephrased:
Proposition 6.9.4
Consider a curve on a surface
both being regular and of class \(\mathcal{C}^{2}\). Write \(\overline {f\circ c}\) for the normal representation of the corresponding skew curve. The geodesic curvature of the curve on the surface is the norm of the covariant derivative of the tangent vector field \(\overline {f\circ h}'\).
Proof
This follows by Definitions 6.9.2 and 6.7.1. □
By Proposition 6.9.4, the geodesic curvature is thus a Riemannian notion. Therefore we make the following definition:
Definition 6.9.5
Consider a Riemann patch of class \(\mathcal{C}^{2}\)
and a regular curve of class \(\mathcal{C}^{2}\)
given in normal representation. The geodesic curvature of that curve is—with Notation 6.2.5—the norm of the covariant derivative of its tangent vector field:
Of course one can refine Definition 6.9.5 and provide the geodesic curvature with a sign, as we did for plane curves (see Definition 2.9.8). For that purpose, let us make the following observation:
Proposition 6.9.6
Consider a Riemann patch of class \(\mathcal{C}^{2}\)
and a regular curve of class \(\mathcal{C}^{2}\)
given in normal representation. The geodesic curvature is also equal to
where η is the normal vector field to the curve (see Proposition 6.5.1).
Proof
At a point where \(\frac{\nabla c'}{ds}(s)=(0,0)\), both the geodesic curvature and the scalar product of the statement are equal to zero. Otherwise we have
where θ(s) is the angle between \(\frac{\nabla c'}{ds}(s)\) and η(s). By Proposition 6.5.1, η(s) is of length 1. But by Proposition 6.7.5, since c is given in normal representation, \(\frac{\nabla c}{ds}(s)\) is proportional to η(s), thus cosθ(s)=±1. Therefore
which forces the conclusion. □
Definition 6.9.7
Consider a Riemann patch of class \(\mathcal{C}^{2}\)
and a regular curve of class \(\mathcal{C}^{2}\)
given in normal representation. The relative geodesic curvature is the quantity
where η is the normal vector field to the curve (see Proposition 6.5.1).
Clearly, the sign of the geodesic curvature as in Definition 6.9.7 is not an intrinsic property of the curve: for example, it is reversed when considering the equivalent normal parametric representation \(\widetilde{c}(\widetilde{s})\) obtained via the change of parameter \(\widetilde{s}=-s\).
Of course the following proposition is particularly useful:
Proposition 6.9.8
Consider a Riemann patch of class \(\mathcal{C}^{2}\)
and a regular curve of class \(\mathcal{C}^{2}\)
given in arbitrary representation. The geodesic curvature of c is equal to
where η is the normal vector field of the curve (see Proposition 6.5.1).
Proof
Let us freely use the notation and the results in the proof of Proposition 6.3.5: we thus write s=σ(t) and \(\overline{c}(s)=(c\circ\sigma^{-1})(s)\) for the normal representation of the curve. Analogously, we write \(\overline{\eta}(s)\) for the normal vector expressed as a function of the parameter s (see Proposition 6.5.1). Thus, by the proof of Proposition 6.3.5, we already know that
By Proposition 6.9.6, and using Proposition 6.7.4, the normal curvature in terms of the parameter s is then given by
where the last but one equality holds because c′ is orthogonal to η.
Putting σ −1(s)=t in these equalities, we get the formula of the statement. □
6.10 Geodesics
Imagine that you traveling on the Earth, around the equator. To achieve this, you have to proceed “straight on”, without ever turning left or right. But nevertheless, by doing this you travel along a circle, because the equator is a circle. The point is that the “curvature vector” of this circle—the second derivative of a normal representation (see Example 2.9.5)—is oriented towards the center of the circle, and in the case of the equator, the center of the circle is also the center of the Earth. The “curvature vector” is thus perpendicular to the tangent plane to the Earth and so its orthogonal projection on that tangent plane is zero. The geodesic curvature of the equator is zero and this is the reason why you have the false impression of not turning at all when you proceed along the equator.
Definition 6.10.1
A geodesic in a Riemann patch of class \(\mathcal{C}^{2}\) is a regular curve of class \(\mathcal{C}^{2}\) whose geodesic curvature is zero at each point.
Notice at once that
Proposition 6.10.2
In a Riemann patch of class \(\mathcal{C}^{2}\), a regular curve of class \(\mathcal{C}^{2}\) is a geodesic if and only if its tangent vector field is a parallel vector field.
Proof
By Lemma 6.8.2, there is no loss of generality in assuming that the curve is given in normal representation. By Definitions 6.10.1 and 6.9.5, being a geodesic is then equivalent to \(\|\frac{\nabla c'}{ds}\|=0\), which is the condition for being a parallel vector field (see Definition 6.8.1). □
The results that we already have yield at once a characterization of the geodesics:
Theorem 6.10.3
Consider a Riemann patch of class \(\mathcal{C}^{2}\)
and a regular curve of class \(\mathcal{C}^{2}\)
given in normal representation. That curve is a geodesic if and only if
Proof
By Definition 6.9.5, we must prove that \(\bigl\|\frac{\nabla c'}{ds}\bigr\|=0\), which is of course equivalent to \(\frac{\nabla c'}{ds}=0\), since at each point of U, the norm is that given by a scalar product (see Definition 6.4.4 and Notation 6.2.5). The result follows by Definition 6.7.3, putting ξ=c′. □
Example 6.10.4
The geodesics of a sphere are the great circles.
Proof
The argument concerning the equator, at the beginning of this section, works for every great circle, proving that these are geodesics of the sphere.
Conversely, consider a geodesic on a sphere. There is no loss of generality in assuming that the center of the sphere is the origin of \(\mathbb{R}^{3}\). Given a normal representation h of that geodesic viewed as a skew curve, we have h′ in the tangent plane to the sphere (Lemma 5.5.1) and h″ perpendicular to that tangent plane (Definition 6.9.2). Therefore h″ is oriented along the radius of the sphere and the osculating plane (Definition 4.1.6) to the curve passes through the center of the sphere. But, since the center of the sphere is the origin of \(\mathbb{R}^{3}\), h″ is also proportional to h. Let us write
By Proposition 4.5.1, the torsion of the geodesic is equal to
because h′×h″ is orthogonal to h′, but also to h which is proportional to h″. So the torsion of the curve is equal to zero and by Proposition 4.5.3, the geodesic is a plane curve. The plane of this curve is thus also its osculating plane, which passes through the center of the sphere. So the geodesic lies on the intersection of the sphere with a plane through the center of the sphere. Therefore the geodesic is (a piece of) a great circle. □
Example 6.10.5
A straight line contained in a surface is always a geodesic.
Proof
A straight line has a zero curvature vector (see Example 2.9.4). □
Example 6.10.6
The geodesics of the plane are the straight lines.
Proof
The straight lines are geodesics by Example 6.10.5. Now as a surface, the plane is its own tangent plane at each point. But given a curve in the plane, its curvature vector is already in the plane, thus coincides with its orthogonal projection on the tangent plane. Therefore the curve is a geodesic if and only if its curvature vector is zero at each point. The result follows by Example 2.12.7. □
Example 6.10.7
The geodesics of the circular cylinder
are:
-
1.
for each fixed value θ 0, the rulings
$$z\mapsto(\cos\theta_0,\sin\theta_0,z); $$ -
2.
for each fixed value z 0, the circular sections
$$\theta\mapsto(\cos\theta,\sin\theta,z_0); $$ -
3.
for all values r≠0, \(s\in\mathbb{R}\), the circular helices (see Example 4.5.4)
$$\theta\mapsto(\cos\theta,\sin\theta,r\theta+s). $$
Proof
Going back to the proof of Example 6.6.1, we observe at once that the second partial derivatives of g are orthogonal to the first partial derivatives. Therefore the Christoffel symbols of the first kind are all equal to zero (Definition 6.6.2). By the fourth formula in Proposition 6.6.4, the Christoffel symbols of the second kind are all zero as well. This trivializes the equations in Theorem 6.10.3: a curve on the cylinder
such that g∘c is in normal representation is a geodesic when
Integrating twice, we conclude that c 1 and c 2 are polynomials of degree 1. The geodesics are thus obtained as the deformations by g of the plane curves
The case a=0=c is excluded, since it is not a curve. When a=0, \(c\not=0\), we obtain the ruling corresponding to θ 0=b. When \(a\not=0\), c=0 we obtain the circular section corresponding to z 0=d. When \(a\not=0\not=c\), the change of parameter t=as+b yields in the plane the parametric representation
Putting
this curve yields on the cylinder the circular helix of the statement. □
In fact, all surfaces admit geodesics, not just these obvious examples which tend to be the ones we immediately think of. Indeed:
Proposition 6.10.8
Consider a Riemann patch of class \(\mathcal{C}^{k}\), with k≥3
For each point of \((x^{1}_{0},x^{2}_{0})\in U\) and every direction \((\alpha ,\beta)\not=(0,0)\), there exists in a neighborhood of this point a unique geodesic of class \(\mathcal{C}^{k}\)
such that
Proof
We are looking for two functions c 1, c 2 of class \(\mathcal{C}^{k}\) which are solutions of the second order differential equations in Theorem 6.10.3 and satisfy the initial conditions of the statement. Since all coefficients of the differential equations are of class \(\mathcal{C}^{k-1}\), such a solution exists and is unique (see Proposition B.2.1). □
6.11 The Riemann Tensor
Both the normal curvature and the Gaussian curvature of a surface are expressed in terms of the six coefficients E, F, G, L, M, N (see Propositions 5.8.4 and 5.16.3). We have seen in Counterexample 6.6.1 that the three functions L, M, N are not Riemannian quantities and, in Counterexample 6.9.1, that the normal curvature is not a Riemannian notion. This might suggest that the Gaussian curvature is also not a Riemannian quantity. Perhaps unexpectedly, it is!
A very striking result, due to Gauss himself, is that the Gaussian curvature can be expressed as a function of E, F, G. So the Gaussian curvature is a Riemannian notion, while the normal curvature is not. To prove this, in view of the formula
of Proposition 5.16.3, it suffices of course to prove that the quantity LN−M 2 can be expressed as a function of E, F, G. For this, let us switch back to the notation h ij and g ij of Definitions 6.6.2 and 6.1.1.
Definition 6.11.1
Consider a regular parametric representation of class \(\mathcal {C}^{3}\) of a surface:
The Riemann tensor of this surface consists of the family of functions
where
are the coefficients of the second fundamental form of the surface (see Theorem 5.8.2).
Notice once more the appearance of the term tensor.
Lemma 6.11.2
Under the conditions of Definition 6.11.1, all the components R ijkl of the Riemann tensor are equal to one of the following quantities:
Thus, knowing the metric tensor, the knowledge of the Riemann tensor is equivalent to the knowledge of the Gaussian curvature.
Proof
Simply observe that
while all other components are zero. □
Theorem 6.11.3
(Theorema Egregium, Gauss)
Under the conditions of Definition 6.11.1, the Riemann tensor is equal to
In particular, the Riemann tensor can be expressed as a function of the sole coefficients of the metric tensor.
Proof
Of course the last sentence in the statement will follow at once from the formula in the statement, since we already know the corresponding result for the Christoffel symbols (see Proposition 6.6.6). Let us therefore prove this formula.
Since the normal vector \(\overrightarrow{n}\) has length 1, we can write equivalently
But by Definition 6.6.2
Let us then replace \(h_{ij}\overrightarrow{n}\) by the quantity on the right hand side, keeping in mind Definition 6.1.1 of the coefficients of the metric tensor and Definition 6.6.2 of the Christoffel symbols.
Let us now use the third formula in Proposition 6.6.4 to simplify this last expression. This formula allows us to combine the first and the third terms in the fourth line to obtain
That quantity is then exactly the opposite of the first term in the second line. The same process allows us to simplify the second and fourth terms in the fourth line with the second term in the second line. Next, we can apply this process again to the last line and the first two terms in the third line. Eventually, the last four lines reduce to
This is exactly the sum in α in the formula of the statement.
To conclude, it remains to check that
Indeed
by the well-known property of commutation of partial derivatives. □
As you might now expect, we conclude this section with a corresponding definition:
Definition 6.11.4
Given a Riemann patch of class \(\mathcal{C}^{2}\), the Riemann tensor is defined as being the family of functions
(See Definition 6.6.7.)
It is worth adding a comment.
Definition 6.11.5
Given a Riemann patch of class \(\mathcal{C}^{2}\), the quantity
is called the Gaussian curvature of the Riemann patch.
This terminology is clearly inspired by Lemma 6.11.2 and its proof. This notion of Gaussian curvature makes perfect sense in the “restricted” context of our Definition 6.2.1, simply because Lemma 6.11.2 remains valid in this context (see Problem 6.18.1). However, the possibility of reducing the information given by the metric tensor to a single quantity κ τ is a very specific peculiarity of the Riemann patches of dimension 2. This notion of Gaussian curvature does not extend to higher dimensional Riemann patches, as defined in Definition 6.17.6: in higher dimensions, the correct notion to consider is the full Riemann tensor.
6.12 What Is a Tensor?
The time has come to discuss the magic word tensor. A family of functions receives this “honorary label” when it transforms “elegantly” along a change of parameters. In fact, a formal, general and elegant theory of tensors must rely on a good multi-linear algebra course; but this is beyond the scope of this book.
In Sect. 6.1 we have exhibited the Riemann patch corresponding to a specific parametric representation of a surface in \(\mathbb{R}^{3}\), and we know very well that a given surface admits many equivalent parametric representations. However, up to now, we have not paid attention to the question: What are equivalent Riemann patches?
Consider a regular surface of class \(\mathcal{C}^{3}\) admitting two equivalent parametric representations
To be able to handle the corresponding change of parameters in our arguments, we have to fix a notation for it. Up to now, we have always used a notation like
Of course if you have many changes of parameters to handle, using various notations such as φ, ψ, θ, τ and so on rapidly becomes unwieldy. Riemannian geometry uses a very standard and efficient notation for a change of parameters:
Of course such a notation is a little ambiguous, since it uses the same symbol for the coordinates \(\widetilde{x}^{i}\) and for the functions \(\widetilde{x}^{i}\). However, in practice no confusion occurs. In fact, this notation significantly clarifies the language. When you have several changes of coordinates, the notation \(\widetilde{x}^{i}(x^{1},x^{2})\) reminds you at once of both systems of coordinates involved in the question, while a notation such as φ i(x 1,x 2) recalls only one of them.
Proposition 6.12.1
Consider a regular surface of class \(\mathcal{C}^{3}\) admitting the equivalent parametric representations
Write further
for the corresponding metric tensors. Under these conditions
Proof
With the notation just explained for the changes of coordinates, we have
It follows that
This implies
that is
which is the formula of the statement. □
This elegant formula is what one calls the transformation formula for a tensor which is twice covariant. Forgetting about this new jargon “covariant” for the time being, let us repeat the same for the inverse metric tensor (see Definition 6.2.3).
Proposition 6.12.2
Consider a regular surface of class \(\mathcal{C}^{3}\) admitting the equivalent parametric representations
Write further
for the corresponding inverse metric tensors. Under these conditions
Proof
As already observed in the proof of Proposition 6.12.1:
The matrix
is thus the change of coordinates matrix between the two bases of partial derivatives in the tangent plane (see Sect. 2.20 in [4], Trilogy II).
For the needs of this proof, let us write T for the matrix given by the metric tensor. The formula of Proposition 6.12.1 becomes simply
Taking the inverses of both sides, we get
since (B t)−1=(B −1)t. But the same argument as above shows that
Therefore the transformation formula for the inverse metric tensor is
as announced in the statement. □
Compare now the two formulas in Propositions 6.12.1 and 6.12.2. They are very similar of course, but nevertheless with a major difference! It will be convenient for us to call \((\widetilde{x}^{1},\widetilde{x}^{2})\) the “new” coordinates and (x 1,x 2) the “old” coordinates.
-
In the case of the metric tensor, the coefficients in the change of parameters formula are the derivatives of the “old” coordinates with respect to the “new” coordinates. One says that the tensor is covariant in both variables or simply, twice covariant. One uses lower indices to indicate the covariant indices of a tensor.
-
In the case of the inverse metric tensor, the coefficients in the change of parameters formula are the derivatives of the “new” coordinates with respect to the “old” coordinates. One says that the tensor is contravariant in both variables or simply, twice contravariant. One uses upper indices to indicate the contravariant indices of a tensor.
This already clarifies some points of notation and terminology. However, this still does not tell us what a tensor is. As mentioned earlier, in order to give an elegant definition we would need some multi-linear algebra. Nevertheless, as far as surfaces in \(\mathbb{R}^{3}\) are concerned, we can at least take as our definition a famous criterion characterizing the tensors of Riemannian geometry. For simplicity, we state the definition in the particular case of a tensor two times covariant and three times contravariant, but the generalization is obvious.
Definition 6.12.3
Suppose that for each parametric representation of class \(\mathcal {C}^{3}\) of a given surface of \(\mathbb{R}^{3}\) you have a corresponding family of continuous functions
with two lower indices and three upper indices. These families of continuous functions are said to constitute a tensor covariant in the indices i, j and contravariant in the indices k, l, m when, given any two equivalent parametric representations f, \(\widetilde{f}\)—and with obvious notation—these functions transform into each other via the formulas
Of course, an analogous definition holds for a tensor α times covariant and β times contravariant, for any two integers α, β.
You should now have a clear idea why some quantities are designated as tensors and others are not. For example, the Riemann tensor of Theorem 6.11.3 is a tensor four times covariant (Problem 6.18.2) while the Christoffel symbols do not constitute a tensor (Problem 6.18.4). This also indicates why some indices are put upside and others downside.
One should be able to guess now why we use upper indices to indicate the coordinates of a point or the coordinates of a tangent vector field.
Proposition 6.12.4
Consider a regular curve c on a regular surface of class \(\mathcal {C}^{3}\) in \(\mathbb{R}^{3}\). In a change of parameters and with obvious notation, a vector field ξ along the curve c, tangent to the surface, transforms via the formula
Proof
One has
and this proves the formula of the statement. □
Of course a vector field along a curve is not a tensor in the sense of Definition 6.12.3, because it is not defined on the whole subset U. Nevertheless, its transformation law along the curve is exactly that of a tensor one time contravariant. This explains the use of upper indices.
In particular, the components of the tangent vector field to the curve c itself should be written with upper indices: c′=((c 1)′,(c 2)′). But then of course, the components of c should use upper indices as well c=(c 1,c 2). To be consistent, when writing the parametric equations of the curve c
we should use upper indices as well for the two coordinates x 1 and x 2.
Let us conclude this long discussion on tensors by giving the answer to the question raised at the beginning of this section: What are equivalent Riemann patches? Keeping in mind that for a surface of class \(\mathcal{C}^{k+1}\) in \(\mathbb{R}^{3}\) the coefficients g ij of the metric tensor are functions of class \(\mathcal{C}^{k}\) (see Definition 6.1.1), we make the following definition:
Definition 6.12.5
Two Riemann patches of class \(\mathcal{C}^{k}\)
are equivalent in class \(\mathcal{C}^{k}\) when there exists a change of parameters of class \(\mathcal{C}^{k+1}\) (that is, a bijection of class \(\mathcal{C}^{k+1}\) with inverse of class \(\mathcal {C}^{k+1}\))
such that
As expected:
Proposition 6.12.6
A change of parameters φ as in Definition 6.12.5 is a Riemannian isometry, that is, respects lengths and angles in the sense of the Riemannian metric.
Proof
Consider a curve
Under the conditions of Definition 6.12.5, the length of an arc of the curve in \(\widetilde{U}\) represented by φ∘c is given by
and this last formula expresses precisely the length of the curve c in U.
The proof concerning the preservation of angles is perfectly analogous. □
Notice that already for a Riemann patch of class \(\mathcal{C}^{0}\), the form of the change of parameters requires that it be of class \(\mathcal {C}^{1}\). This is another way to justify the “jump” of one unit in the classes of differentiability.
We are almost done. But you are still entitled to ask an intriguing question. If the Christoffel symbols are not tensors, how do we decide to use upper or lower indices? There is another convention in Riemannian geometry: a convention which, deliberately, has not been used in this chapter, and which requires an appropriate choice of position of the indices.
Convention 6.12.7
(Abbreviated Notation)
In Riemannian geometry, when in a given term of a formula, the same index appears once as an upper index and once as a lower index, it is understood that a sum is taken over all the possible values of this index.
For example, following this convention, the formula giving the components of the covariant derivative of a tangent vector field (see Definition 6.7.3)
is generally simply written as
because both indices i and j appear once as an upper index and once as a lower index in the “second” term. Notice that the index k appears twice as an upper index and moreover in two different terms: thus no sum is to be taken on this index. It is easy to see why we did not use this convention in this first approach of Riemannian geometry.
6.13 Systems of Geodesic Coordinates
Once again, let us support our intuition with the case of the Earth, regarded as a sphere. The most traditional system of coordinates is in terms of the latitude and the longitude. Consider the corresponding “geographical map” as in Example 5.1.6
where τ is the latitude and θ is the longitude.
-
The equator is really the “base curve” of the whole system of coordinates: the curve given by τ=0; this is a great circle on the sphere, that is, a geodesic (see Example 6.10.4). Observe that f(0,θ) is a normal representation of the equator, because the radius of the sphere has been chosen to be equal to 1.
-
The curves θ=k on the sphere, with k constant, are the meridians: they are great circles, thus geodesics, and moreover they are orthogonal to the equator. Observe that f(τ,θ 0) is again a normal representation of the meridian with fixed longitude θ 0, again because the radius of the sphere is equal to 1.
-
The curves τ=k on the sphere, with k constant, are the so-called parallels; they are not great circles (except for the equator), thus they are not geodesics; but they are orthogonal to all the meridians.
This is thus a very particular system of coordinates of which we can expect many properties and advantages. One calls such a system a system of geodesic coordinates.
A system of geodesic coordinates exists in a neighborhood of each point of a “good” surface. Let us establish this result in the general context of a Riemann patch.
Theorem 6.13.1
Consider a regular curve \(\mathcal{C}\) passing through a point P in a Riemann patch. Assume that both the Riemann patch and the curve are of class \(\mathcal{C}^{m}\), with m≥2. There exists a connected open neighborhood of P such that the Riemann patch, restricted to this neighborhood, is equivalent in class \(\mathcal{C}^{m-1}\) to a Riemann patch
with the following properties:
-
1.
the point P has coordinates (0,0);
-
2.
the curve \(\mathcal{C}\) is the curve x 1=0 and is now given in normal representation;
-
3.
the curves x 2=k, with k constant, are geodesics in normal representation;
-
4.
the curves x 1=l, with l constant, are orthogonal to the curves x 2=k, with k constant;
-
5.
at all points of U
$$g_{11}=1,\qquad g_{21}=0=g_{12},\qquad g_{22}>0 $$and also
$$g^{11}=1,\qquad g^{21}=0= g^{12},\qquad g^{22}>0; $$ -
6.
at all points of U
$${\varGamma}_{211}={\varGamma}_{121}= {\varGamma}_{112}={\varGamma}_{111}=0; \qquad {\varGamma}^2_{11}={\varGamma}^1_{11} ={\varGamma}_{21}^1={\varGamma}_{12}^1 =0 $$while
$${\varGamma}_{222} =\frac{1}{2} \frac{\partial g_{22}}{\partial x^2} ,\qquad {\varGamma}_{212} ={\varGamma}_{122} = \frac{1}{2} \frac{\partial g_{22}}{\partial x^1},\qquad {\varGamma}_{221} =-\frac{1}{2} \frac{\partial g_{22}}{\partial x^1}, $$and
$${\varGamma}_{22}^2 =\frac{1}{2 g_{22}} \frac{\partial g_{22}}{\partial x^2} ,\qquad {\varGamma}_{21}^2 ={\varGamma}_{12}^2 =\frac{1}{2 g_{22}} \frac{\partial g_{22}}{\partial x^1},\qquad {\varGamma}_{22}^1= -\frac{1}{2}\frac{\partial g_{22}}{\partial x^1}; $$ -
7.
when moreover the original curve c is a geodesic
$$g_{22}(0,x^2)=1,\qquad \frac{\partial g_{22}}{\partial x^1}(0, x^2)=0 $$and
$${\varGamma}_{ij}^k(0, x^2)=0,\qquad {\varGamma}_{ijk}(0, x^2)=0,\quad 1\leq i,j,k\leq2. $$
A system of coordinates satisfying conditions 1 to 6 is called a geodesic system of coordinates. When moreover it satisfies condition 7, it is called a Fermi system of geodesic coordinates.
Proof
Let us write
for the original Riemann patch and
for the given curve \(\mathcal{C}\). Let us write further P=c(t 0). Follow the construction above on Fig. 6.2.

Fig. 6.2
By Proposition 6.3.5, there is no loss of generality in assuming that the curve \(\mathcal{C}\) is given in normal representation with P as origin, thus P=c(0). Under these conditions c′(t) becomes a vector of norm 1 (see Definition 6.3.4).
For each value t∈]a,b[, we consider the normal vector η(t) to the curve (see Proposition 6.5.1), which is thus a vector of norm 1 orthogonal to c′(t). By Proposition 6.10.8, in a neighborhood of c(t), there exists in the Riemann patch a unique geodesic h t (s) of class \(\mathcal{C}^{m}\) through c(t) in the direction η(t), satisfying an initial condition that we choose to be h t (0)=c(t). We are interested in the function
which we want to become the expected change of parameters of class \(\mathcal{C}^{m-2}\) in a neighborhood of c(0). Since the coefficients of the equations in Proposition 6.10.8 are of class \(\mathcal{C}^{m-1}\) and c is of class \(\mathcal{C}^{m}\), the function φ is indeed defined, and of class \(\mathcal{C}^{m}\), on a neighborhood of (0,0) (see Proposition B.3.2). But to be a good change of parameters, the inverse of φ should also be of class \(\mathcal{C}^{m}\).
Let us compute the partial derivatives of the function φ at the point (0,0):
By regularity of c and Proposition 6.5.1, c′(0) and η(0) are perpendicular and of length 1 with respect to the scalar product (−|−) c(0), thus linearly independent. By the Local Inverse Theorem (see Theorem 1.3.1), the function φ is thus invertible on some neighborhood U′ of (0,0), with an inverse which is still of class \(\mathcal{C}^{m}\). There is no loss of generality in choosing U′ open and connected. In this way φ becomes a homeomorphism
We simply define U=φ(U′) and use the notation \(\bigl(x^{1}, x^{2})\) instead of (s,t). Thus our change of parameters φ is now
Of course there is no difficulty in providing U with the structure of a Riemann patch equivalent to that given by the \(\widetilde{g}_{ij}\) on \(\widetilde{U}\). With Definition 6.12.5 in mind, simply define
With the notation of Proposition 6.12.3, this definition can be re-written as
As observed in the proof of Proposition 6.12.3, the matrix B is that of a change of basis, while \(\widetilde{T}\) is at each point the matrix of a scalar product in \(\mathbb{R}^{2}\) (see Notation 6.2.5). By Corollary G.1.4 in [4], Trilogy II, T is then at each point the matrix of the same scalar product expressed in another base: it is thus a symmetric definite positive matrix. Therefore the g ij on U constitute a Riemann patch equivalent in class \(\mathcal{C}^{m-1}\) to that of the \(\widetilde{g}_{ij}\) on U′.
By construction, the curve x 1=0 is the curve h t (0), that is the original curve c(t).
Also by construction, the curves x 2=k, with k constant, are the curves h k (s), which are geodesics given in normal representation.
Next, we prove that g 11=1. With Notation 6.2.5,
because each h t (s) is in normal representation (see Definition 6.3.4).
Next, we turn our attention to the Christoffel symbols. The curve x 2=k is represented by
Differentiating with respect to s=x 1, we obtain
Since this curve x 2=k is a geodesic in normal representation, it satisfies the system of differential equations of Theorem 6.10.3. The observations that we have just made show that this system reduces simply to its terms in (i,j)=(1,1), that is,
Since this holds for every value k, this proves condition 5 of the statement.
Now the case of g 12=g 21. By Definition 6.6.7, we have at all points
Keeping in mind that g 11=1 while g 12=g 21, which also forces g 12=g 21 (the inverse of a symmetric matrix is symmetric), this equality reduces to
Introducing the value of g 21 (see the proof of Proposition 6.2.4) into this equality, we obtain
We know that \(g_{11} g_{22}- g_{12} g_{21}\not=0\) (Proposition 6.2.1); the equality is thus equivalent to
But this can be re-written as
This proves that g 21(x 1,x 2) is a constant function of x 1: thus to conclude that g 21=0, it suffices thus to prove that g 21(0,x 2)=0. By definition of g 21 and using the values of the partial derivatives of the change of parameters φ, we indeed obtain
So g 21(0,x 2)=0 and as we have seen, this implies g 21=g 12=0. Since we know already that g 11=1, this forces g 22>0 by positivity of the metric tensor (see Definition 6.2.1).
The metric tensor is thus a diagonal matrix; therefore its inverse (see Definition 6.2.3) is obtained by taking the inverses of the diagonal elements and thus
Since g 11, g 12 and g 21 are constant, their partial derivatives are zero. Considering the definition of the Christoffel symbols of the first kind (see Definition 6.6.7), only the partial derivatives of g 22 remain: this gives at once the formulas of the statement concerning the symbols Γ ijk and as an immediate consequence, the formulas concerning the symbols \({\varGamma}_{ij}^{k}\).
Saying that the curves x 1=l, x 2=k, are orthogonal means
which is trivially the case since g 12=0=g 21. This concludes the proof in the case of an arbitrary base curve c.
Let us now suppose that this curve c is itself a geodesic. In terms of the coordinates (x 1,x 2), we have t=x 2 and the curve c is simply c(x 2)=(0,x 2). By Theorem 6.10.3 we have
But since c(x 2)=(0,x 2), this reduces to
By Proposition 6.7.4.4
On the other hand by Proposition 6.7.4
the last equality holds because c(t) is a geodesic in normal representation: this implies that c′ is a parallel vector field (see Proposition 6.10.2), thus \(\frac{\nabla c'}{dt}=0\) by Definition 6.8.1. But, still by Proposition 6.5.1 and normality of the representation, c′ and η constitute at each point an orthonormal basis of \(\mathbb{R}^{2}\) for the scalar product (−|−) c . The orthogonality of \(\frac{\nabla\eta}{dt}\) to both c′ and η implies
for all values of t=x 2. By Definition 6.7.3 we have
But in terms of the coordinates (x 1,x 2), η(x 2)=(1,0) while c(x 2)=(0,x 2). Therefore the two equalities reduce to
Of course this also forces
by Proposition 6.6.8. The third condition in this same proposition also shows that Γ ijk (0,x 2)=0 for all indices. □
Corollary 6.13.2
Consider a Riemann patch of class \(\mathcal{C}^{m}\), with m≥2
Suppose that:
-
1.
the curves x 2=k are geodesics in normal representation;
-
2.
each of these curves cuts the curve x 1=0 orthogonally.
Under these conditions, (x 1,x 2) is already a system of geodesic coordinates.
Proof
Simply observe that in the proof of Theorem 6.13.1, the change of parameters φ is the identity and therefore, is trivially valid on the whole of V. □
At the beginning of Sect. 6.10, we introduced geodesics via the intuition that they are the curves on the surface along which you have the impression of travelling in a straight line without ever turning left or right. As a consequence of the existence of systems of geodesic coordinates, let us now prove a precise result which reinforces the intuition that geodesics are “the best substitute for straight lines” on a surface.
Theorem 6.13.3
Locally, in a Riemann patch of class \(\mathcal{C}^{2}\), a geodesic is the shortest regular curve joining two of its points.
Proof
We consider a Riemann patch
and a geodesic
There is no loss of generality in assuming that h is at once given in normal representation, with 0∈]a,b[.
By Proposition 6.10.8, let us consider the geodesic
such that
where η is the normal vector field of h (see Proposition 6.5.1). By Theorem 6.13.1, there exists in a neighborhood U⊆V of c(0) a Fermi system of geodesic coordinates admitting the curve c as base curve. There is no loss of generality in assuming that we are working in this system of coordinates. The curve h is a geodesic perpendicular to the base curve c at c(0)=h(0): it is thus the geodesic x 2=0.
Consider now an arbitrary regular curve
joining two points
of the geodesic h. Let us compute its length (see Definition 6.12.3); in view of Theorem 6.13.1
where the last equality holds by Proposition 6.3.6. □
6.14 Curvature in Geodesic Coordinates
Let us now investigate some simplifications of formulas when working in a system of geodesic coordinates.
Proposition 6.14.1
Consider a Riemann patch of class \(\mathcal{C}^{2}\)
and assume that we are working in a system of geodesic coordinates. Under these conditions the length of an arc of the curves x 1=k, with k a constant, is given by \(\int\sqrt{g_{22}}\).
Proof
These curves admit the parametric representation c k (x 2)=(k,x 2). Therefore \(c'_{k}=(0,1)\) and (see Definition 6.3.2 and Theorem 6.13.1)
□
Proposition 6.14.2
Consider a Riemann patch of class \(\mathcal{C}^{2}\)
and assume that we are working in a system of geodesic coordinates. Under these conditions the relative geodesic curvature of the curves x 1=k, with k a constant, is given by
Proof
Proposition 6.14.1 explains how to pass to normal representation for these curves x 1=k, but we shall instead Proposition 6.9.8 which allows us to work at once with the representation h(x 2)=(k,x 2). Notice that h′=(0,1), from which \(\|h'\|_{h}=\sqrt{g_{22}}\) at each point.
Let us first compute the covariant derivative of h′(x 2)=(0,1) along h(x 2)=(k,x 2). The formula in Definition 6.7.3 reduces to
The curves x 2=l (with l a constant) are in normal representation and orthogonal to the curve x 1=k (Theorem 6.13.1), that is, the curve h. The tangent vector field to the curves x 2=l is thus of constant length 1 (Definition 6.3.4) and orthogonal to h′. Therefore, up to the sign, it is the normal vector field η to h. The “minus sign” must be chosen since (h′,η) must have direct orientation. But the curve x 2=l admits the parametric representation x 1↦(x 1,l); therefore its tangent vector field is (1,0) and the normal vector field η to d is given by η=(−1,0).
By Proposition 6.9.8, the geodesic curvature is then given by
□
Our next concern is to exhibit a formula, in geodesic coordinates, for the geodesic curvature of an arbitrary regular curve. It is based on the so-called Liouville formula, which does not require the full strength of geodesic coordinates and—after all—is more elegant under these weaker assumptions.
Theorem 6.14.3
(Liouville Formula)
Consider a Riemann patch
of class \(\mathcal{C}^{3}\) and a regular curve in this patch
given in normal representation. Suppose that at each point of the Riemann patch, the curves x 1=l, with l constant, are orthogonal to the curves x 2=k, with k constant. At a point with coordinates \((x^{1}_{0},x^{2}_{0})\), let us write
-
\(\kappa_{1}(x^{1}_{0},x^{2}_{0})\) for the relative geodesic curvature at \((x^{1}_{0},x^{2}_{0})\) of the curve \(x^{1}\mapsto(x^{1},x^{2}_{0})\);
-
\(\kappa_{2}(x^{1}_{0},x^{2}_{0})\) for the relative geodesic curvature at \((x^{1}_{0},x^{2}_{0})\) of the curve \(x^{2}\mapsto(x^{1}_{0},x^{2})\);
-
θ(s 0) for the angle at c(s 0) between the curve c and the curve x 1↦(x 1,c 2(s 0)).
Under these conditions, the geodesic curvature of the curve c is given by
Proof
To keep the notation as “light” as possible, let us make the convention that every norm, length, angle, scalar product or orthogonal condition met in this proof has to be understood in the Riemann sense, that is, with respect to the metric tensor. Except when absolutely necessary, we thus avoid repeating the notation introduced in Notation 6.2.5.
Let us fix once and for all a value s 0 of the parameter. We consider the two changes of parameters
putting the two curves
in normal representations (see Proposition 6.3.5). This yields a mapping
which is bijective, of class \(\mathcal{C}^{3}\), with an inverse of class \(\mathcal{C}^{3}\), since this is the case for each of the two components of this function. This is thus a very special change of parameters of class \(\mathcal{C}^{3}\), acting component-wise. Notice that the equivalent Riemann patch is then simply given by (see Definition 6.12.5)
because
Let us write
for the parametric representation of the surface in terms of the new parameters \(\widetilde{x}^{1}\), \(\widetilde{x}^{2}\). With respect to this new system of coordinates, the curve c becomes
and is still in normal representation, since the parameter s is still the length s on the curve. The curves x 1=l are transformed into the curves \(\widetilde{x}^{1}=\widetilde{x}^{1}(l)\) (that is, \(\widetilde{x}^{1}\) is equal to a constant) and analogously for the curves x 2=k. Therefore the angle θ(s) and the geodesic curvatures κ 1 and κ 2 are the same in the new system of coordinates as in the original system. Consequently, it suffices to prove the formula of the statement in the new system of coordinates. Or in other words, there is no loss of generality in assuming that the two curves
are in normal representation. This is what we shall do from now on.
With that convention, let us now consider the two “2-dimensional” vector fields (see Definition 6.7.6) given by the normed tangent vectors to the curves x 2=k, x 1=l:
Since the curves x 2=k, x 1=l are orthogonal at each point, e 1(x 1,x 2) and e 2(x 1,x 2) constitute at each point an orthonormal basis for the metric tensor. Notice that since the two curves x 1=c 1(s 0) and x 2=c 2(s 0) are in normal representation
On the other hand the curve c is in normal representation and at each point (e 1,e 2) is an orthonormal basis. Thus the normed vector c′(s) has at each point the form
Let us compute the covariant derivative along the curve c(s) of both sides of this equality, using freely the results of Sect. 6.7.
where η ( s) is the normal vector to the curve c (see Proposition 6.5.1).
Let us now compute the relative geodesic curvature of the two curves
which are thus in normal representation. We have
which implies that the corresponding normal vectors are
The relative geodesic curvatures κ 1 and κ 2 involved in the statement are thus given by
Covariantly differentiating the equalities
(see Proposition 6.7.4), the κ 1 and κ 2 can also be re-written as
Notice also that covariantly differentiating the equality
yields
Analogously we obtain
Using these various equalities and keeping in mind that
we compute further, at the point c(s 0) and with obvious abbreviated notation, that
Now the relative geodesic curvature of the curve c is given by (see Definition 6.9.7)
Introducing into this formula the various quantities calculated above, we obtain still at the point c(s 0) and still with abbreviated notation,
This concludes the proof. □
Corollary 6.14.4
Consider a Riemann patch of class \(\mathcal{C}^{3}\)
given in geodesic coordinates and a regular curve in it
given in normal representation. Write θ(s 0) for the angle at c(s 0) between the curve c and the curve x 1↦(x 1,c 2(s 0)). Under these conditions, the geodesic curvature of the curve c at the point with parameter s 0 is given by
Proof
The curves x 2=l are geodesics by Theorem 6.13.1 thus, with the notation of Theorem 6.14.3, κ 1=0 (see Definition 6.10.1). On the other hand, Proposition 6.14.2 gives the value of κ 2. Then, still following Theorem 6.14.3
It remains to compute sinθ. But
that is at each point, the cosine of the angle between the curve c and the curves x 1=c 1(s 0). Therefore
Thus finally
□
Let us conclude this section with the case of the Gaussian curvature (see Definition 5.16.1).
Proposition 6.14.5
In a geodesic system of coordinates, the Gaussian curvature of a regular surface of class \(\mathcal{C}^{3}\) in \(\mathbb{R}^{3}\) is given by
Proof
In view of condition 5 in Theorem 6.13.1, the formula in Theorem 6.11.3 reduces to
Applying Proposition 6.6.8 and Theorem 6.13.1 again
These various observations, together with Lemma 6.11.2, show that
On the other hand
Dividing by \(\sqrt{g_{22}}\) and changing the sign indeed yields the formula that we have obtained for κ τ . □
6.15 The Poincaré Half Plane
Our basic example of a Riemann patch is that induced by a surface of \(\mathbb{R}^{3}\) (see Sect. 6.1). Up to now, we have not provide any other examples. Let us fill this gap by describing the so-called Poincaré half plane: a Riemann patch which was introduced in order to provide a model of non-Euclidean geometry. Non-Euclidean geometries have been given full attention in Chap. 7 of [3], Trilogy I. Therefore we shall only very briefly remark upon them later in this section.
Definition 6.15.1
Let U be the “upper half plane” in \(\mathbb{R}^{2}\), that is
The Poincaré half plane is the Riemann patch of class \(\mathcal{C}^{\infty}\)
given by
Trivially, the matrix (g ij ) ij is symmetric definite positive, since x 2>0 at all points of U.
Proposition 6.15.2
In the Poincaré half plane:
-
1.
g 11=g 22=x 2 while g 12=g 21=0;
-
2.
Γ 111=Γ 122=Γ 212=Γ 221=0 while \(\varGamma_{112}=\frac{1}{(x^{2})^{3}}\) and \(\varGamma_{121}=\varGamma_{211}=\varGamma_{222} =-\frac{1}{(x^{2})^{3}}\);
-
3.
\(\varGamma_{11}^{1}=\varGamma_{12}^{2}=\varGamma_{21}^{2} =\varGamma_{22}^{1}=0\) while \(\varGamma_{11}^{2}=\frac{1}{x^{2}}\) and \(\varGamma_{12}^{1}=\varGamma_{21}^{1}=\varGamma_{22}^{2} =-\frac{1}{x^{2}}\).
Proof
This is just a routine application of the formulas in Definitions 6.6.7 and 6.11.4. □
Corollary 6.15.3
The Poincaré half plane is such that
at all points.
Proof
This follows by Proposition 6.15.2 and Definition 6.11.4. □
Let us recall that the quantity in Corollary 6.15.3, in the case of a 2-dimensional Riemann patch, is sometimes called the Gaussian curvature of the Riemann patch (see the comment at the end of Sect. 6.11). The Poincaré half plane thus has a constant negative Gaussian curvature equal to −1, just as the pseudo-sphere of pseudo-radius 1 (see Example 5.16.7). Notice that nevertheless, the metric tensor of the pseudo-sphere does not have the same form as that of the Riemann patch (see the proof of Example 5.16.7).
Proposition 6.15.4
The Riemannian angles of the Poincaré half plane coincide with the Euclidean angles.
Proof
At a given point (x 1,x 2), consider the two vectors
Their Riemannian angle θ is such that
and this last formula is precisely the value of the cosine of the Euclidean angle. □
Let us now turn our attention to the geodesics:
Proposition 6.15.5
The geodesics of the Poincaré half plane are:
-
1.
the parallels to the x 2-axis;
-
2.
the half circles with center on the x 1-axis.
Of course in this statement “parallel” and “circle” should be understood in the sense of the ordinary Euclidean geometry of \(\mathbb {R}^{2}\) (see Fig. 6.3).

Fig. 6.3
Proof
In view of Proposition 6.15.2, the conditions of Theorem 6.10.3 for being a geodesic c in normal representation reduce to
that is
From now on, let us use instead the more concise notation
Integrating a system of differential equations is not such an easy task. But we shall nevertheless take it easy, since the statement suggests at once the answer! We shall prove that the curves given in the statement are geodesics and we shall prove further that they exhaust all the possibilities.
The parallels to the x 2-axis are the curves c(t)=(k,t) with k a constant. The change of parameter to pass in normal representation (see Proposition 6.3.5) is
when choosing t 0=1. Therefore σ −1(s)=e s and we obtain as normal representation
and it is immediate that these data satisfy the above system of differential equations for being a geodesic.
The upper half circle of center (α,0) and radius R admits the parametric representation
Notice in particular that sint>0 for all t. The change of parameter for passing to normal representation is this time
Unfortunately, the explicit form of this last integral is in terms of hyperbolic functions, so we shall avoid calculating it and calculate instead its inverse function. This is not really a problem because the differential equations for being a geodesic refer only to the derivatives of the normal representation \(\overline{c}\). Therefore, as already observed several times in this book, only the derivatives of σ and σ −1 are needed explicitly. We have
The normal representation and its derivatives are thus
It is now trivial that these data satisfy the above differential equations for being a geodesic.
So: all the curves mentioned in the statement are geodesics. Are they the only ones? Let us recall that by Proposition 6.10.8, at each point of U, in each direction, there exists a unique geodesic. If we prove that at each point, in each direction, there is already a geodesic of the statement, these geodesics will thus exhaust all the possibilities and the proof will be complete. Of course in the “vertical” direction, we always have the corresponding parallel to the x 2-axis. Consider next a point P∈U and a line d passing through P in a non-vertical direction (see Fig. 6.4). The line d ⊥, passing through P and orthogonal to d, intersects the x 1-axis at some point C. The circle with center C passing through P has a tangent at P perpendicular to its radius CP: this is precisely the given line d. So the half circle is a geodesic having at P the direction d.

Fig. 6.4
□
Axiomatic geometries were the topic of [3], Trilogy I. Roughly speaking, for the reader who is not familiar with these theories, let us say that a Euclidean plane consists of:
-
a set Π—called the plane—whose elements are called points;
-
a choice of subsets of Π, called lines;
-
various binary or ternary relations involving points and lines;
-
axioms to be satisfied by those data.
Among the relations, some express “geometric configurations” (a point is on a line, a point is between two other points) and others express “congruences”: congruence of two segments or congruence of two angles (see [3], Trilogy I, for the definition of these notions).
Among the axioms, one has expected statements such as
Through two distinct points passes exactly one line.
But one also has the famous parallel postulate (two lines are called parallel when their intersection is empty):
Given a point P not on a line d, there passes through P exactly one line parallel to d.
The full list of axioms on these geometric data force Π to be isomorphic to the Euclidean space \(\mathbb{R}^{2}\), with its usual lines. See for example Hilbert’s axiomatization of the Euclidean plane in Chap. 8 of [3], Trilogy I.
Dropping the “parallel axiom” from Hilbert’s axiomatization of the plane yields what is called absolute geometry. Let us stress that in absolute geometry, the existence of a parallel is already a theorem (see Corollary 8.3.36 in [3], Trilogy I): a parallel can be constructed via two perpendiculars. Thus the parallel axiom is not needed to prove the existence of a parallel and therefore passing from absolute geometry to Euclidean geometry requires only to state as an axiom the uniqueness of the parallel:
Given a point P not on a line d, there passes through P at most one line parallel to d.
Non-Euclidean geometry is obtained when adding instead to absolute geometry the negation of this uniqueness requirement:
Given a point P not on a line d, there pass through P several lines parallel to d.
It can then be proved that the number of possible parallel lines is necessarily infinite.
The Poincaré half plane is a model of non-Euclidean geometry obtained by choosing as lines the geodesics. The rest of this section is devoted to proving this result.
Proposition 6.15.6
Through two distinct points of the Poincaré half plane passes exactly one geodesic.
Proof
We freely refer to Theorem 6.16.2. If two points A and B are on the same vertical line, this vertical line is a geodesic joining them. Of course no other vertical line contains these two points A, B and no half circle contains them either: indeed, a half circle never contains two points on the same vertical. So the vertical line through A and B is the unique geodesic joining these two points.
If two points A and B are not on the same vertical line, we must prove the existence of a unique half circle joining them. The necessary and sufficient condition for a circle to pass through A and B is that its center C lies on the median perpendicular m of the segment AB (see Fig. 6.5 and Proposition 8.4.10 in [3], Trilogy I; the median perpendicular is the perpendicular to AB at its middle point). But when the half circle is a geodesic, the center C of the circle must also be on the x 1-axis, thus finally it must be at the intersection of the median m and the x 1-axis. Since A and B are not on the same vertical, the median m is not horizontal, thus it indeed meets the x 1-axis at some unique point C. The half circle with center C passing through A and B is then the expected unique geodesic.

Fig. 6.5
□
Now the “parallel axiom”:
Proposition 6.15.7
In the Poincaré half plane, given a point P not on a geodesic d, there pass through P infinitely many geodesics not intersecting d. All these geodesics are contained between two “limit” geodesics.
Proof
We freely refer to Theorem 6.16.2. Consider first as geodesic a vertical line d (see Fig. 6.6). Consider also a point P∉d, thus on the left or the right of d; the same argument applies in both cases. Write Q for the intersection in \(\mathbb{R}^{2}\) of d and the x 1-axis. Consider the median m of the segment PQ which—since PQ is not vertical—meets the x 1-axis at some point C in \(\mathbb{R}^{2}\). The half circle with center C passing through P thus also “passes” through Q: this is a first geodesic c 1 which does not meet d in the Poincaré half plane. Of course the vertical line through P is another geodesic c 2 not intersecting d. But there are infinitely many others! Every half circle passing through P and whose center is “on the other side of C with respect to Q”, intersects the x 1-axis at some point situated between C and Q: thus it does not meet d. In other words, “all geodesics situated between c 1 and c 2 do not intersect the geodesic d”.

Fig. 6.6
Next consider as geodesic d a half circle “cutting” in \(\mathbb {R}^{2}\) the x 1-axis at two points A and B. Consider further a point P not on this geodesic d. The point P can thus be “under” or “above” the half circle, but the proof applies to both cases (see Figs. 6.7 and 6.8). Again we consider the median of the segment PA and its intersection C A with the x 1-axis. In \(\mathbb{R}^{2}\), the half circle with center C A passing through P “cuts” the x 1-axis at A; this is thus a first geodesic c A not intersecting the geodesic d in the Poincaré half plane. Analogously the median of PB cuts the x 1-axis at a point C B and the half circle with center C B passing through P is a second geodesic c B not intersecting d. Of course all half circles passing through P “between c A and c B ” are geodesics not intersecting d.

Fig. 6.7

Fig. 6.8
□
Next, we observe that
Lemma 6.15.8
In the Poincaré half-plane, every normal representation of a geodesic induces a bijection between the real line and the geodesic.
Proof
Consider first a parallel to the x 2-axis:
and choose \(x^{2}_{0}\) as origin for computing lengths along the geodesic. Since c′(x 2)=(0,1), we obtain (see Proposition 6.3.5)
As x 2 tends to zero, this quantity tends to −∞ and when x 2 tends to infinity, it tends to +∞. This yields the announced bijection.
Consider next as geodesic a half circle centered on the x 1-axis.
and fix t 0 as origin for computing lengths along this geodesic. Since
we obtain (see Proposition 6.3.5 again)
As t tends to 0 this quantity tends to −∞ and as t tends to π, it tends to +∞. Again this yields the announced bijection. □
Notice that the bijection in Lemma 6.15.8 allows us to transpose onto every geodesic the natural order of the real line and in particular, the relation “a point is between two other points”. It thus makes perfect sense to speak of segments and half lines (see Sect. 8.2 in [3], Trilogy I). It therefore also makes sense to consider the congruence (in the sense of the Riemannian metric) between two segments or two angles. Notice that:
Corollary 6.15.9
In the Poincaré half plane, every half-line has infinite length.
Proof
This follows by Lemma 6.15.8. □
To be able to check the validity of all congruence axioms for non-Euclidean geometry (see Sect. 8.3 in [3], Trilogy II), we need to exhibit some Riemannian isometries of the Poincaré half plane onto itself: that is, bijections which respect the Riemannian metric.
Proposition 6.15.10
Every Euclidean horizontal translation is a Riemannian isometry of the Poincaré half plane.
Proof
Such a translation is a bijection having another such translation as inverse. It has the form
The matrix of partial derivatives of τ is the identity matrix. The value of the Riemann tensor is the same at (x 1,x 2) and τ(x 1,x 2), since it depends only on the coordinate x 2. The conditions of Definition 6.12.5 are then trivially satisfied and by Corollary 6.12.6, τ is an isometry. □
Proposition 6.15.11
Every Euclidean symmetry with respect to a vertical axis is a Riemannian isometry of the Poincaré half plane.
Proof
It suffices to prove the result when the axis of symmetry is the x 2-axis. Indeed, first translating the axis of symmetry onto the x 2-axis, performing the orthogonal symmetry around the x 2-axis and translating the axis back, yields the symmetry indicated. We know already by Proposition 6.15.10 that horizontal translations are Riemannian isometries.
The orthogonal symmetry around the x 2-axis is its own inverse and has the form
The matrix of partial derivatives of σ thus has the form
The value of the Riemann tensor is the same at (x 1,x 2) and σ(x 1,x 2), since it depends only on the coordinate x 2. The conditions of Definition 6.12.5 are then trivially satisfied and by Corollary 6.12.6, σ is an isometry. □
However, the crucial fact is (see Sect. 5.7 in [3], Trilogy I, for the theory of inversions):
Proposition 6.15.12
The Euclidean inversions with center on the x 1-axis are Riemannian isometries.
Proof
It suffices to prove the result when the center of inversion is the point (0,0). Indeed, first translating the center of inversion to (0,0), performing the inversion and translating the center of inversion back to its original position, yields the inversion indicated. We know already by Proposition 6.15.10 that horizontal translations are Riemannian isometries.
The inversion with center (0,0) and power R 2 is its own inverse and is defined everywhere on the Poincaré half plane, since (0,0) is not a point of the Poincaré half plane. With the notation of Definition 6.12.5, it has the form
The matrix of partial derivatives of ι is thus
while, with the notation of Corollary 6.12.6,
It is then immediate to compute that
The result follows by Corollary 6.12.6. □
We are now ready to conclude that:
Theorem 6.15.13
The Poincaré half plane is a model of non-Euclidean geometry.
Proof
We freely refer to Chap. 8 of [3], Trilogy I. We recall that our points are those of the Poincaré half plane, with the geodesics as lines. The incidence of a point and a line is just the membership relation. The “between” relation is that transposed from the real line via Lemma 6.15.8. The congruence relation for segments and angles is the congruence in terms of the Riemannian metric.
Proposition 6.15.6 attests the validity of the first incidence axiom; the other two incidence axioms are trivially satisfied. The first four axioms concerning the “between” relation follow at once from the corresponding properties of the real line, via Lemma 6.15.8. The last axiom on this “between” relation—the so-called Pasch axiom—is a routine exercise on lines and circles in the Euclidean plane, but is also an easy consequence of our Proposition 7.11.1. When a geodesic not containing a vertex of a triangle “enters” the triangle along one side, it must leave it (Proposition 7.11.1) along another side (Proposition 6.15.6).
The first five axioms concerning the congruence of segments or angles are immediate consequences of Lemma 6.15.8 and Proposition 6.15.4. Let us thus check the validity of the sixth congruence axiom: the so called case of equality of two triangles; writing ≡ for the congruence relation:
If two triangles ABC and A′B′C′ are such that
$$AB\equiv A'B',\qquad \measuredangle ABC\equiv\measuredangle A'B'C',\qquad \measuredangle BAC\equiv\measuredangle B'A'C' $$then
$$AC\equiv A'C',\qquad BC\equiv B'C',\qquad \measuredangle ACB\equiv\measuredangle A'C'B'. $$
To prove this, we shall show that the triangle ABC is congruent to a triangle \(\tilde{A}\tilde{B}\tilde{C}\) “in canonical position”, that is, a triangle such that:
-
\(\tilde{A}=(0,1)\);
-
\(\tilde{B}=(0,b)\) with b>1;
-
\(\tilde{C}=(a,c)\) with a>0.
Analogously, the triangle A′B′C′ will be congruent to a triangle \(\tilde{A}'\tilde{B}'\tilde{C}'\) in canonical position:
-
\(\tilde{A}'=(0,1)\);
-
\(\tilde{B}'=(0,b')\) with b′>1;
-
\(\tilde{C}'=(a',c')\) with a′>0.
When this has been proved, since AB≡A′B′, necessarily b=b′. Thus
But since ∡ABC≡∡A′B′C′, we also have \(\measuredangle\tilde{A}\tilde{B}\tilde{C} \equiv\measuredangle\tilde{A}'\tilde{B}'\tilde{C}'\). Since moreover \(\tilde{C}\) and \(\tilde{C}'\) are both on the right hand side of the x 2-axis, the two geodesics through \(\tilde{B}\), \(\tilde{C}\) and \(\tilde{B}'\), \(\tilde{C}'\) coincide. Analogously, the two geodesics through \(\tilde{A}\), \(\tilde{C}\) and \(\tilde{A}'\), \(\tilde{C}'\) coincide. Eventually, the two triangles \(\tilde{A}\tilde{B}\tilde{C}\) and \(\tilde{A}'\tilde{B}'\tilde{C}'\) coincide. Since they are respectively congruent to the original triangles ABC and A′B′C′, the proof will be complete.
So we must now prove that every triangle ABC is congruent to a triangle in canonical position.
-
1.
First, if it is not already the case, we force the geodesic AB to become a parallel to the x 2 axis. For this it suffices to perform an inversion of arbitrary power whose center P is one the two “intersection” points of the x 1-axis with the half circle through A and B. By Proposition 5.7.5 in [3], Trilogy I, the Euclidean (half)-circle through A and B becomes a Euclidean (half)-line perpendicular to the line joining the center P of inversion and the center of the circle, that is, perpendicular to the x 1-axis. By Proposition 6.15.12, the triangle ABC then becomes congruent to a triangle A 1 B 1 C 1 such that the geodesic A 1 B 1 is a Euclidean parallel to the x 2-axis.
-
2.
Second, if necessary, translate the triangle A 1 B 1 C 1 horizontally to get, by Proposition 6.15.10, a congruent triangle A 2 B 2 C 2 now with A 2 and B 2 on the x 2-axis.
-
3.
Third, if necessary, perform an orthogonal symmetry around the x 2-axis to transform the triangle A 2 B 2 C 2 into a congruent triangle A 3 B 3 C 3 (see Proposition 6.15.11) now with C 3 on the right hand side of the x 2-axis.
-
4.
Fourth, if this is not already the case, we shall force A 3 to become the point (0,1). If A 3=(α,0), it suffices to apply an inversion with center (0,0) and power α. By Proposition 6.15.12, we thus obtain a new triangle A 4 B 4 C 4, still congruent to ABC, now with A 4=(0,1), B 4 still on the x 2-axis and C 4 still on the right hand side of this axis.
-
5.
Finally, if it turns out that B 4 is below A 4, use Proposition 6.15.12 again and perform an inversion with center (0,0) and power 1 to obtain a triangle \(\tilde{A}\tilde{B}\tilde{C}\) still congruent to ABC but now in canonical position.
This concludes the proof of the last congruence axiom.
The continuity axiom is an immediate consequence of Lemma 6.15.8. And the non-Euclidean axiom of parallels is Proposition 6.15.7. □
6.16 Embeddable Riemann Patches
We have seen that a plane curve can be “intrinsically” described—up to an isometry—by an arbitrary continuous function κ(s): the curvature in terms of the arc length s (see Sect. 2.12). An analogous result holds for skew curves, this time using two sufficiently differentiable arbitrary functions κ(s) and τ(s): the curvature and the torsion (see Sect. 4.6). Is there an analogous result for surfaces?
The fundamental theorem of the theory of surfaces tells us in a first approach that
A surface of \(\mathbb{R}^{3}\) is entirely determined—up to an isometry—by the six coefficients E, F, G, L, M, N of its two fundamental quadratic forms.
(See Definitions 5.4.5 and 5.8.6). However, in contrast to the case of curves, we can no longer expect six such arbitrary functions to always define a surface. Indeed in the case of a surface, these six functions are not “independent”: we already know some specific properties relating them. Among other things:
-
the coefficients E, F, G are those of a symmetric definite positive quadratic form (see Proposition 5.4.6);
-
LN−M 2=R 1212 (see Lemma 6.11.2) where R 1212 can be written as a function of E, F, G (see Theorem 6.11.3).
And so on. So in fact, the fundamental theorem of the theory of surfaces must also answer the following question:
Give necessary and sufficient conditions on six functions E, F, G, L, M, N for being the coefficients of the two fundamental quadratic forms of a surface of \(\mathbb{R}^{3}\).
As we have just recalled, one necessary condition is the fact that E, F, G are the coefficients of a symmetric definite positive quadratic form: in other words, they must define a Riemann patch (see Definition 6.2.1). But this is certainly not sufficient, as our second observation LN−M 2=R 1212 shows. Thus our question can be rephrased as
What are the additional conditions on a Riemann patch which will ensure that it is the patch associated with a surface of \(\mathbb{R}^{3}\)?
This section is devoted to an answer to this question.
It is well-known that given a function ψ(u,v,w) of class \(\mathcal{C}^{3}\), the continuity of the partial derivatives forces the equality
This simple fact is the key to solving our problem. As is often the case in the context of Riemannian geometry, such an easy formula can take an unexpectedly involved form. It will be convenient for us to switch back to the notation g ij and h ij of Definition 6.2.1 and Proposition 6.6.3.
Proposition 6.16.1
Consider a regular parametric representation of class \(\mathcal {C}^{3}\) of a surface
The following equalities hold:
The Gauss Equations
The Codazzi–Mainardi Equations
Proof
Write n for the normal vector to the surface (see Definition 5.5.7). Differentiating the equality (n|n)=0 we get \((\frac{\partial n}{\partial x^{i}} |n)=0\) proving that \(\frac{\partial n}{\partial x^{i}}\) is in the tangent plane. Let us write
Since n is orthogonal to \(\frac{\partial f}{\partial x^{j}}\), differentiating the equality \((\frac{\partial f}{\partial x^{j}}| n)=0\) with respect to x i with respect to x i we obtain
that is
From Definition 6.6.2, we then deduce
This equality can be re-written as
from which we deduce
(see Definition 6.2.3), that is
As a consequence
Let us now consider the third partial derivatives of f and introduce, for the needs of this proof, an explicit notation for its components:
Considering the definition of the Christoffel symbols of the second kind (Definition 6.6.2)
and differentiating this equality with respect to x i we obtain
The three components of the third partial derivatives of f are then
and
The Gauss equations translate simply as the equality \(\varUpsilon_{ijk}^{l}=\varUpsilon_{jik}^{l}\), while the Codazzi–Mainardi equations translate as the equality Ω ijk =Ω jik . □
We are now ready to state the expected result. Its proof is highly involved and uses deep results from the theory of partial differential equations. This clearly runs outside the normal context for this introductory textbook. Therefore—even if not formally needed for the proof—we often rely on the intuition hidden behind the arguments involving the solutions of systems of partial differential equations.
Theorem 6.16.2
A Riemann patch of class \(\mathcal{C}^{2}\)
is, in a neighborhood V of each point, induced by a regular parametric representation
of a surface if and only if there exist three functions of class \(\mathcal{C}^{1}\)
satisfying the Gauss–Codazzi–Mainardi equations of Proposition 6.16.1.
Proof
Proposition 6.16.1 proves the necessity of the condition. Conversely, we are thus looking for a parametric representation f(x 1,x 2), which—if it exists—will have two partial derivatives
satisfying the requirements (see Definition 6.6.2)
where μ will be the normal vector to the surface. From what we have observed in the proof of Proposition 6.16.1, we shall further have, if f exists,
We therefore consider the following system of partial differential equations, with three unknown functions
that is, in terms of the components of these functions, nine functions \(U\longrightarrow\mathbb{R}\):
In these equations, g ij is of course the inverse metric tensor of the Riemann patch and the \(\varGamma_{ij}^{k}\) are its Christoffel symbols. We are first interested in finding a solution φ 1, φ 2, μ of this system.
A general theorem on systems of partial differential equations (see Proposition B.4.1) asserts the existence of a solution of class \(\mathcal{C}^{2}\) to the system above, provided some integrability conditions are satisfied. These conditions require that the given equations force the relations
Let us prove that this is the case.
Since eventually, we want φ 1 and φ 2 to be the partial derivatives of the parametric representation f we are looking for, the first integrability condition should translate as the classical formula
But this equality expresses exactly the Gauss–Codazzi–Mainardi equations, as we have seen in the proof of Proposition 6.16.1. Therefore the first integrability condition should follow from these equations. Let us observe that this is indeed the case.
From our system of partial differential equations, we obtain
The corresponding formula for \(\frac{\partial^{2}\varphi_{k}}{\partial x^{j}\partial x^{i}}\) is obtained simply by permuting the indices i and j in the formula above. To prove the necessary equality of the two expressions (while we do not yet know the existence of φ 1, φ 2 and μ), it suffices to prove the equality of the respective coefficients of these unknown functions. But this is precisely what the Gauss–Codazzi–Mainardi equations say.
We still have to take care of the integrability condition concerning the function μ. Since we eventually want μ to become the normal vector to a surface whose parametric representation admits φ 1 and φ 2 as partial derivatives, we expect to have
where × indicates the cross product (see Sect. 1.7 in [4], Trilogy II). Therefore the permutability of the partial derivatives of μ should be a consequence of the permutability of the partial derivatives of φ 1, φ 2, that is, of the Gauss–Codazzi–Mainardi equations. It is indeed so.
We have at once
We must therefore prove that the three coefficients of φ 1, φ 2 and μ are equal to those obtained when permuting the indices i and j. This is of course trivial for the coefficient of μ. We shall now prove the same for the coefficient of φ 1, the proof being analogous in the case of φ 2.
To achieve this, we first replace the coefficients g ij by their values calculated in the proof of Proposition 6.2.4. We also replace the partial derivatives of the coefficients g ij by their values given in Problem 6.18.6 (the proof is an easy routine calculation). Introducing all these values into the coefficient of φ 1, we obtain
The last but one equality is obtained just by simplifying equal terms appearing with opposite signs. By the Codazzi–Mainardi equations, the coefficients of g 22 and g 12 in the last line are equal to those obtained when permuting the roles of the indices i and j. This concludes the proof of the integrability conditions.
Since the integrability conditions are satisfied, our system of partial differential equations admits solutions of class \(\mathcal{C}^{2}\) in a neighborhood of each point. As usual, many solutions exist a priori, but we can force the uniqueness of the solution by imposing initial conditions at some fixed point \((x^{1}_{0},x^{2}_{0})\in U\). The idea is to choose initial conditions which force, at the given point \((x^{1}_{0},x^{2}_{0})\), the properties that we eventually want to be satisfied, at all points, by the three functions φ 1, φ 2 and μ. More precisely, we want to have
since we want φ 1 and φ 2 to become the partial derivatives of a parametric representation, while μ should become the corresponding normal vector of length 1.
To force these requirement, let us first arbitrarily choose three vectors e 1, e 2, e 3 of \(\mathbb{R}^{3}\) such that:
-
e 3 is an arbitrary vector of length 1;
-
e 1 and e 2 are perpendicular to e 3 and of lengths
$$\|e_1\|=\sqrt{g_{11}\bigl(x^1_0,x^2_0\bigr)},\qquad \|e_2\|=\sqrt{g_{22}\bigl(x^1_0,x^2_0\bigr)}; $$ -
the angle θ between e 1 and e 2 is given by
$$\cos\theta=\frac{g_{12}(x^1_0,x^2_0)}{\sqrt{g_{11}(x^1_0,x^2_0)} \sqrt{g_{22}(x^1_0,x^2_0)}}; $$ -
the basis (e 1,e 2,e 3) of \(\mathbb{R}^{3}\) has direct orientation
(see Definition 3.2.3 in [4], Trilogy II). Notice that all this makes sense by Proposition 6.2.2. Indeed g 11>0 and g 22>0; moreover cos2 θ=1 would imply that the determinant of the metric tensor is zero, which is not the case; thus θ≠kπ and therefore e 1 and e 2 are not proportional.
The initial conditions that we impose on our system of partial differential equations are then simply
By Proposition B.4.1, we conclude the unique existence of three functions φ 1, φ 2 and μ of class \(\mathcal{C}^{2}\), solutions of the system of partial differential equations above, and satisfying these initial conditions.
We are next interested in finding the expected function f(x 1,x 2) such that
This is another system of partial differential equations, which admits solutions in a neighborhood of our fixed point \((x^{1}_{0},x^{2}_{0})\) as soon as the integrability conditions
are forced by the system of partial differential equations (see Proposition B.4.1 again). These integrability conditions thus mean
that is, considering the system of partial differential equations defining φ 1, φ 2 and μ
These equalities hold by the assumption h ij =h ji and because \(\varGamma_{ij}^{k}=\varGamma_{ji}^{k}\), by Proposition 6.6.8.
But we know at once the general form of the solutions of the very simple system of partial differential equations defining f:
where v 0, w 0 are arbitrary constant vectors. (Of course, by taking the integral of a function with values in \(\mathbb{R}^{3}\) we mean taking the integrals of its three components.) Fixing v 0 (or equivalently, w 0) as initial condition thus forces the uniqueness of the solution. Notice that since φ 1 and φ 2 are of class \(\mathcal{C}^{2}\), f is of class \(\mathcal{C}^{3}\).
Our next job is to prove that f is the parametric representation of a surface admitting precisely, as coefficients of its two fundamental quadratic forms, the coefficients g ij and h ij . For that, we need once more to rely on systems of partial differential equations.
We observe first that
This proves that the functions
satisfy the system of partial differential equations
Observe that the initial conditions put on the system in φ 1, φ 2 and μ force precisely the satisfaction of the initial conditions:
Again Proposition B.4.1 on systems of partial differential equations asserts the uniqueness of a solution satisfying these initial conditions (this time there is no need to check the integrability conditions). Therefore to conclude that
it suffices to prove that
is also solution of the above system, satisfying the same initial conditions. By Proposition 6.6.8 and Definition 6.6.7
and this takes care of the first equation. The second equation reduces to
which reduces further to
since the g lm are the coefficients of the matrix inverse to that of the g im . The third equation is trivially satisfied: it reduces to \(\frac{\partial1}{\partial x^{k}}=0\). Moreover, the initial conditions indicated are trivially satisfied.
By uniqueness of the solution, we thus have at each point
In particular, μ is at each point a vector of length 1 orthogonal to the partial derivatives of f.
When two vectors are linearly dependent, the matrix of their scalar products has zero determinant:
By Proposition 6.2.2, the condition
implies that the matrix of the scalar products of the partial derivatives of f is regular; these partial derivatives are thus linearly independent. Then by Proposition 5.2.4, f is a regular parametric representation of a surface. Since μ is of length 1 and orthogonal to the partial derivatives of f, it is the normal vector \(\overrightarrow{n}\) to the surface.
We must still prove that the coefficients h ij are those of the second fundamental quadratic form of f. We have already
where the \(\varGamma_{ij}^{k}\) are the Christoffel symbols of the original Riemann patch and the h ij are the functions given in the statement. Comparing with Definition 6.6.2, these equalities prove that the \(\varGamma_{ij}^{k}\) are also the Christoffel symbols of the surface represented by f, and the symbols h ij are the coefficients of the second quadratic fundamental form. This concludes the proof of the existence of a surface f admitting the g ij and h ij of the statement as coefficients of its two fundamental quadratic forms. □
The proof of Theorem 6.16.2 indicates that the parametric representation f is unique for the given choices of initial conditions. Changing these initial conditions results simply in applying an isometry to the surface (see Problem 6.18.8). Thus the surface in Theorem 6.16.2 is in fact unique up to an isometry.
6.17 What Is a Riemann Surface?
The time has come to give an elegant solution to the problem raised in Sect. 5.1:
The sphere does not admit a parametric representation in the sense of Definition 5.1.1.
In other words, once more thinking of the sphere as being the Earth, we cannot draw a “geographical map” of the whole Earth while respecting the requirements of Definition 5.1.1. Even if we were to forget the requirements in Definition 5.1.1, there is no particular practical interest in having a single geographical map of the whole Earth. Such a map would necessarily feature extreme distortions, so the sensible thing to do is to map the Earth using a full atlas of geographical maps. This is also how we define a surface in full generality.
Now let us be aware that every geographical map of a portion of the Earth—no matter how small—will necessarily have some distortions, because the Earth is not flat! If we have a full atlas of maps to describe the Earth, the same portion of the Earth may appear on several maps, with different distortions. As a consequence the “elastic rulers” called metric tensors will then be different for the same portion of the Earth on different maps. Nevertheless, these metric tensors will be equivalent, in order to calculate from the various maps the same actual result at the surface of the Earth.
Thus a surface should be a “universe” which can be mapped by an atlas of Riemann patches, in such a way that when two Riemann patches of the atlas describe a same portion of the “universe”, they are equivalent as Riemann patches (see Definition 6.12.5). It remains to say what “universe” means: this is simply the very general notion of topological space (see Definition A.5.1). However, if you prefer not to enter into this level of generality, simply think of a “universe” as being a subset of \(\mathbb {R}^{3}\) as in Chap. 5, provided with the usual notions of openness, continuity, and so on.
Definition 6.17.1
A Riemann surface of class \(\mathcal{C}^{k}\) consists of:
-
1.
a topological space \((X,\mathcal{T})\);
-
2.
a covering X=⋃ i∈I U i of X by open subsets \(U_{i}\in\mathcal{T}\);
-
3.
for each index i∈I, a Riemann patch of class \(\mathcal{C}^{k}\)
$$g_{jl}\colon V_i\longrightarrow\mathbb{R},\quad 1\leq j,l\leq2; $$ -
4.
for each index i∈I, a homeomorphism
$$\varphi_i\colon V_i\longrightarrow U_i $$which is called a local map.
These data must satisfy the following compatibility axiom. For every pair i, j of indices and every connected open subset U⊆U i ∩U j ,
is an equivalence of Riemann patches of class \(\mathcal{C}^{k}\).
Extending the geographical terminology, the set of local maps is often called the atlas of local maps. In this book we shall mainly be interested in the following class of surfaces:
Definition 6.17.2
By a Riemann surface in \(\mathbb{R}^{3}\) is meant a subset \(X\subseteq\mathbb{R}^{3}\) provided with the induced topology (see Proposition A.5.4) and the structure of a Riemann surface (see Definition 6.17.1), in such a way that for each local map
the corresponding metric tensor is
Notice that in Definition 6.17.2, the local map φ i is a regular parametric representation of U i viewed as an ordinary surface in \(\mathbb{R}^{3}\) (see Definitions 5.1.1 and 5.2.1); the last requirement indicates that the Riemann structure on U i is precisely that induced by the parametric representation (see Definition 6.1.1).
As expected:
Example 6.17.3
The sphere is a Riemann surface of \(\mathbb{R}^{3}\).
Proof
We know a parametric representation of the sphere of radius 1
punctured at its two poles (0,0,±1) (see Example 5.1.6):
As we have seen, to be locally injective, this function must be considered on the open subset
On this open subset of \(\mathbb{R}^{3}\) we thus have four functions of class \(\mathcal{C}^{\infty}\) defining at each point the metric tensor:
namely
By Proposition A.9.4, each point P i ∈V has a neighborhood V i on which f is injective and moreover
is a homeomorphism. Let us choose arbitrarily a family (V i ) i∈I of these V i ’s such that the corresponding U i cover the whole punctured sphere.
Let us now make some remarks which will help to support our intuition.
When producing a geographical atlas of the Earth, each map of the atlas generally corresponds to some fixed ranges of longitudes and latitudes, thus to some open rectangle in \(\mathbb{R}^{2}\). Although it is not needed for the proof, to make the language more intuitive, we will freely choose each open subset V i to be an open rectangle in \(\mathbb{R}^{2}\).
Now we might be concerned that near the poles, the distortion of the maps “tends to infinity”. First, we should be aware that such a distortion is mathematically not a problem at all, even if “geographically” it is certainly not recommended. Nevertheless if our intuition insists on avoiding excessive distortions, we are free to replace in what follows the “punctured sphere” by a “widely punctured sphere”: for example,
In such a case, we consider only those points whose latitude is “less than 60 degrees North or South”.
Finally we might wonder how many maps we will have in our atlas. This depends on our choices, in particular on the size that we fix for each map. For example if we insist on covering the whole punctured sphere with individual maps whose distortion remains below some “geographically acceptable” bound, then near the poles, we will have to consider smaller and smaller maps, eventually ending up with infinitely many maps! Mathematically this is not a problem at all, since we do not have to physically print all these maps!
So long for this digression. Whatever our choice is: the punctured sphere or a “widely punctured” sphere, a finite or an infinite atlas, let us now observe that each U i is an open subset of the sphere. By choice of the open subsets V i (open rectangles in \(\mathbb{R}^{2}\)), U i is thus the portion of the sphere situated between two meridians and two parallels. Join all points of the four edges of U i (i.e. the portions of meridians and parallels limiting U i ) to the center of the sphere. The interior of the “generalized pyramid” obtained in this way is an open subset of \(\mathbb{R}^{3}\), whose intersection with the sphere is precisely U i . Therefore U i is indeed an open subset of the sphere with respect to the induced topology, by Proposition A.5.4. (Of course V i being a rectangle is unessential in this argument.)
Now the same point of the sphere can be written as
if and only if τ 1=τ 2 while θ 1=θ 2+2kπ. Therefore if \(U_{i}\cap U_{j}\not=\emptyset\), then the corresponding mapping
is simply given by
This is a bijection of class \(\mathcal{C}^{\infty}\) with inverse
still of class \(\mathcal{C}^{\infty}\). This is thus a change of parameters of class \(\mathcal{C}^{\infty}\) and therefore, by Proposition 6.12.2, it induces on each connected open subset an equivalence between the corresponding Riemann patches, as required by Definition 6.12.5.
This already presents the sphere, punctured (or widely punctured) at its two poles (0,0,±1), as a Riemann surface in the sense of Definition 6.17.1.
In a perfectly analogous way, interchanging the roles of the second and the third components, the function
is now a parametric representation of the sphere punctured (or widely punctured) at the two points (0,±1,0). Just as above, this allows a presentation of this alternative punctured (or widely punctured) sphere as a Riemann surface. Let us write \(\widetilde{V}_{j}\), \(\widetilde{U}_{j}\) for the corresponding open subsets of \(\mathbb{R}^{2}\) and of the sphere.
Considered together, these two punctured (or widely punctured) spheres cover the whole sphere. Therefore considered together, all the open subsets U i and \(\widetilde{U}_{j}\) cover the whole sphere. To conclude that we have so obtained a presentation of the sphere as a Riemann surface in the sense of Definition 6.17.1, it remains to prove the required compatibility condition when \(U_{i}\cap\widetilde{U}_{j}\neq \emptyset\). Again by Proposition 6.12.2, this reduces to proving that the bijection
is a change of parameters of class \(\mathcal{C}^{\infty}\), that is, is of class \(\mathcal{C}^{\infty}\) as is its inverse.
So we must investigate the form of the change of parameters \(\varphi(\theta,\tau) =(\widetilde{\theta},\widetilde{\tau})\) such that \(f(\theta,\tau) =\widetilde{f}(\widetilde{\theta},\widetilde{\tau})\). This means
But since in any case
we always necessarily have
Dividing the second component by the third one, on both sides of the equality, we then obtain
while the third components give at once
This proves that, at those points where both parametric representations are defined
This is indeed a formula of class \(\mathcal{C}^{\infty}\). An analogous proof holds for the inverse change of parameters, interchanging θ and \(\widetilde{\theta}\), and analogously τ and \(\widetilde{\tau}\). □
The example of the sphere should nevertheless not mislead the reader:
Warning 6.17.4
Being a Riemann surface of \(\mathbb{R}^{3}\) is a property which is neither stronger nor weaker than being a surface in the sense of Chap. 5.
Proof
The sphere is an example of a Riemann surface of \(\mathbb{R}^{3}\) which does not admit a parametric representation in the sense of Chap. 5 (see Example 6.17.3).
On the other hand the surface of \(\mathbb{R}^{3}\) (see Fig. 6.9) represented by
is not a Riemann surface: at each “multiple” point f(−1,v)=f(1,v) (a point where the surface “crosses itself”), every neighborhood of the point on the surface is constituted of two sheets, thus is not homeomorphic to an open subset of \(\mathbb{R}^{2}\).

Fig. 6.9
□
Warning 6.17.5
Even the support of an injective regular parametric representation
need not be a Riemann surface in \(\mathbb{R}^{3}\).
Proof
Observe that in the proof of Warning 6.17.4, restricting the parametric representation to the open subset
avoids having multiple points, but the problem remains the same at all points f(1,v). For the topology induced by \(\mathbb{R}^{3}\) on the support of the surface, each neighborhood of the point f(1,v) is still comprised of two sheets. See also the comment at the end of Sect. 6.4. □
Let us conclude with a definition which gives evidence of the power of the notions and techniques developed in this chapter.
Definition 6.17.6
An n-dimensional Riemann patch of class \(\mathcal{C}^{k}\) consists of a connected open subset \(U\subseteq\mathbb{R}^{n}\), together with functions of class \(\mathcal{C}^{k}\)
which, at each point (x 1,…,x n), constitute a symmetric definite positive matrix.
The only differences with Definition 6.2.1 are:
-
the replacement of \(\mathbb{R}^{2}\) by \(\mathbb{R}^{n}\);
-
the fact that the indices vary from 1 to n.
If you want to develop n-dimensional Riemannian geometry, simply repeat all the definitions in dimension 2 by letting the indices vary from 1 to n. For example, if you are interested in Riemannian geometry of dimension 5, you will now have 53=125 Christoffel symbols \(\varGamma_{ij}^{k}\) of the second kind, and 54=625 components for the Riemann tensor. Nevertheless, the formulas remain “identical” to those in dimension 2: for example
Of course you can also transpose Definition 6.17.1 to dimension n, obtaining what is called a Riemann manifold of dimension n.
6.18 Problems
6.18.1
In a Riemann patch of class \(\mathcal{C}^{2}\), prove that
while all other components of the Riemann tensor are equal to zero. Explain why your argument no longer works for Riemann patches of higher dimensions (see Definition 6.17.6).
6.18.2
Prove that the Riemann tensor is indeed a four times covariant tensor.
6.18.3
The Riemann tensor of Definition 6.11.4 is also called the Riemann tensor of the second kind. As you easily imagine, there is also a so-called Riemann tensor of the first kind:
Prove that this is indeed a tensor three times covariant and one time contravariant. Prove further that
while
6.18.4
Prove that the Christoffel symbols, in a change of parameters, transform according to the formulas
Therefore, they do not constitute a tensor.
6.18.5
With the comment at the end of Sect. 6.11 in mind, generalize Proposition 6.14.5 to express, in a system of geodesic coordinates, the Gaussian curvature of a Riemann patch.
6.18.6
Consider a Riemann patch of class \(\mathcal{C}^{2}\)
Prove that
-
1.
\(\displaystyle\frac{\partial g_{ij}}{\partial x^k} =\varGamma_{ikj}+\varGamma_{jki} =\sum_l\varGamma_{ik}^lg_{lj}+\sum_l\varGamma_{jk}^lg_{li} \);
-
2.
\(\displaystyle\frac{\partial(g_{11}g_{22}-g_{21}g_{12})}{\partial x^k} = 2(\varGamma_{1k}^1+\varGamma_{2k}^2) (g_{11}g_{22}-g_{21}g_{12}) \);
-
3.
\(\displaystyle\frac{\partial g^{11}}{\partial x^k} =2\frac{\varGamma_{2k}^1g_{12}-\varGamma_{1k}^1g_{22}}{g_{11}g_{22}-g_{21}g_{12}}\), \(\displaystyle\frac{\partial g^{22}}{\partial x^k} =2\frac{\varGamma_{1k}^2g_{21}-\varGamma_{2k}^2g_{11}}{g_{11}g_{22}-g_{21}g_{12}}\), \(\displaystyle\frac{\partial g^{12}}{\partial x^k} = \frac{\partial g^{21}}{\partial x^k} =-\frac{\varGamma_{1k}^2g_{22}+\varGamma_{2k}^1g_{11} -\varGamma_{1k}^1g_{21}-\varGamma_{2k}^2g_{12}}{g_{11}g_{22}-g_{21}g_{12}}\).
(See Proposition 6.2.4 for the explicit values of the symbols g ij.)
6.18.7
Prove that given a regular surface \(f\colon U \longrightarrow\mathbb{R}^{3}\) of class \(\mathcal{C}^{2}\) and an isometry \(\varphi\colon\mathbb{R}^{3}\longrightarrow\mathbb {R}^{3}\), the composite φ∘f is still a regular parametric representation of a surface. Prove that both fundamental quadratic forms of these surfaces have the same coefficients g ij and h ij .
6.18.8
Show that in the proof of Theorem 6.16.2:
-
another choice of the vector v 0 (or equivalently, w 0) results in a translation of the surface;
-
another choice of the vector e 3 keeps the point \(f(x^{1}_{0},x^{2}_{0})\) fixed and results (via Theorem 4.12.4 in [4], Trilogy II) in a rotation of the surface around an axis passing through \(f(x^{1}_{0},x^{2}_{0})\);
-
another choice of the vectors e 1, e 2 in the plane perpendicular to e 3 results in a rotation of the surface around the axis of direction e 3 passing through \(f(x^{1}_{0},x^{2}_{0})\);
-
the choice of the inverse orientation for the basis (e 1,e 2,e 3) results in an orthogonal symmetry of the surface with respect to the plane passing through \(f(x^{1}_{0},x^{2}_{0})\) and whose direction is that of the plane (e 1,e 2).
We conclude that the surface in Theorem 6.16.2 is defined uniquely up to an isometry (see Sect. 4.11 in [4], Trilogy II).
6.19 Exercises
6.19.1
Determine if the following pairs (U,g) are Riemann patches; if so, determine their class of differentiability.
-
1.
\(U=\mathbb{R}^{2}\); \(g\colon U\longrightarrow\mathbb{R}^{2\times2}\),
 .
. -
2.
\(U=\mathbb{R}^{2}\setminus\{(0,0)\}\); \(g\colon U \longrightarrow\mathbb{R}^{2\times2}\),
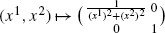 .
. -
3.
\(U=\mathbb{R}^{2}\); \(g\colon U\longrightarrow\mathbb{R}^{2\times2}\),
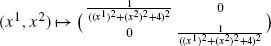 .
. -
4.
\(U=\mathbb{R}^{2}\); \(g\colon U\longrightarrow\mathbb{R}^{2\times2}\),
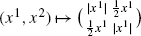 .
. -
5.
\(U=\mathbb{R}^{2}\); \(g\colon U\longrightarrow\mathbb{R}^{2\times2}\),
 .
.
6.19.2
Construct a Riemann patch induced by:
-
1.
the so-called inverse plane
$$\left\{ \begin{array}{@{}l} x=\frac{u}{u^2+v^2}\\ y=\frac{v}{u^2+v^2}\\ z=0; \end{array} \right. $$ -
2.
the hyperbolic paraboloid.
6.19.3
Consider the Riemann patch
Consider further
Determine \(\widetilde{g}\) so that \(\varphi\colon\widetilde{U} \longrightarrow U\) becomes an equivalence of Riemann patches between \((\widetilde{U},\widetilde{g})\) and (U,g). What are the corresponding classes of differentiability?
6.19.4
Consider the cone \(\mathcal{S}\) with parametric representation
-
1.
Give a Riemann patch induced by \(\mathcal{S}\).
-
2.
In this Riemann patch, determine the tangent and the normal vector fields to the curves x 1=k and x 2=k, with k a constant.
6.19.5
Compute the Riemann tensor of the Riemann patch defined in Exercise 6.19.1.3.
6.19.6
Compute the Christoffel symbols of the first and the second kind:
-
1.
of the sphere of radius R centered at the origin;
-
2.
of the cone.
6.19.7
On the circular cylinder
consider the curve \(\mathcal{E}\) represented by
-
1.
Show that this curve is an ellipse in \(\mathbb{R}^{3}\).
-
2.
Calculate the covariant derivative along \(\mathcal{E}\) of the following vector fields, defined by their components with respect to the canonical basis of \(\mathbb{R}^{3}\)
$$\xi(t)= \begin{pmatrix}0\\0\\1 \end{pmatrix},\qquad \xi(t)= \begin{pmatrix}-\sin t\\\cos t\\0 \end{pmatrix}. $$
6.19.8
On the sphere represented by
consider the “parallel” \(\mathcal{P}\) determined by u=k, \(k\in\mathbb{R}\). Consider along \(\mathcal{P}\) the vector field ξ admitting the components  with repect to the basis of partial derivatives of f. Compute the covariant derivative of ξ along \(\mathcal{P}\). Is ξ a parallel vector field?
with repect to the basis of partial derivatives of f. Compute the covariant derivative of ξ along \(\mathcal{P}\). Is ξ a parallel vector field?
6.19.9
Consider the helicoid with parametric representation
-
1.
Construct a Riemann patch induced by the helicoid.
-
2.
Compute the Christoffel symbols of the first and the second kind of the helicoid.
-
3.
Consider the skew curve
$$f\colon\mathbb{R}\longrightarrow\mathbb{R}^3,\qquad f(t)= \biggl(t^2\sin t,t^2\cos t,\frac{\pi}{2}-t \biggr). $$Is this curve a geodesic of the helicoid?
6.19.10
Let
be a normal parametric representation of class \(\mathcal{C}^{3}\) of a 2-regular skew curve \(\mathcal{C}\) (see Definition 4.1.3). Write n and b for the normal and the binormal vectors (see Definition 4.4.1). Given \(a\in\mathbb{R}\), consider the surface \(\mathcal{S}\) represented by
-
1.
Determine a parametric representation of the surface \(\mathcal{S}\) defined by choosing
$$a=0,\qquad g(s)=\bigl(e^s\cos s,e^s\sin s,e^s\bigr). $$ -
2.
Determine a constant a so that \(\mathcal{C}\) becomes a geodesic of \(\mathcal{S}\).
-
3.
Construct a Riemann patch induced by \(\mathcal{S}\) in the case \(a=\frac{\pi}{2}\).
-
4.
Choose again \(a=\frac{\pi}{2}\). Compute the covariant derivative along \(\mathcal{C}\) of the tangent vector field ξ having components
 with respect to the basis of partial derivatives of f.
with respect to the basis of partial derivatives of f.
References and Further Reading
F. Borceux, An Axiomatic Approach to Geometry. Geometric Trilogy, vol. I (Springer, Berlin, 2014)
F. Borceux, An Algebraic Approach to Geometry. Geometric Trilogy, vol. II (Springer, Berlin, 2014)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Borceux, F. (2014). Towards Riemannian Geometry. In: A Differential Approach to Geometry. Springer, Cham. https://doi.org/10.1007/978-3-319-01736-5_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-01736-5_6
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-01735-8
Online ISBN: 978-3-319-01736-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 .
.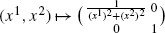 .
.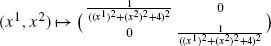 .
.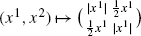 .
. .
. with respect to the basis of partial derivatives of f.
with respect to the basis of partial derivatives of f.