Abstract
The idea of a Potential Energy Surface (PES) forms the basis of almost all accounts of the mechanisms of chemical reactions, and much of theoretical molecular spectroscopy. It is assumed that, in principle, the PES can be calculated by means of clamped-nuclei electronic structure calculations based upon the Schrödinger Coulomb Hamiltonian. This article is devoted to a discussion of the origin of the idea, its development in the context of the Old Quantum Theory, and its present status in the quantum mechanics of molecules. It is argued that its present status must be regarded as uncertain.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
René Marcelin was killed in action fighting for France in September 1914.
- 2.
That a molecule must reach a certain region of space at a suitable angle, that its speed must exceed a certain limit, that its internal structure must correspond to an unstable configuration etc.; …
- 3.
Nevertheless it seems proper to regard Marcelin’s introduction of phase-space variables and a critical reaction surface into chemical dynamics as the beginning of a formulation of the Transition State Theory that was developed by Wigner in the 1930’s [12–15]. The 2n phase-space variables q,p were identified with the n nuclei specified in the chemical formula of the participating species, and the Hamiltonian
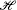 was that for classical nuclear motion on a Potential Energy Surface; this dynamics was assumed to give rise to a critical surface which was such that reaction trajectories cross the surface precisely once. The classical nature of the formalism was quite clear because the Uncertainty Principle precludes the precise specification of position on the critical surface simultaneously with the momentum of the nuclei.
was that for classical nuclear motion on a Potential Energy Surface; this dynamics was assumed to give rise to a critical surface which was such that reaction trajectories cross the surface precisely once. The classical nature of the formalism was quite clear because the Uncertainty Principle precludes the precise specification of position on the critical surface simultaneously with the momentum of the nuclei. - 4.
This is strictly true only for integrable Hamiltonians [26].
- 5.
- 6.
This is the earliest reference we know of where the idea of adiabatic separation of the electrons and the nuclei is proposed explicitly.
- 7.
This also deals with the uninteresting overall translation of the molecule.
- 8.
The rotational and vibrational energies occur together because of the choice of the parameter λ; as is well-known, Born and Oppenheimer later showed that a better choice is to take the quarter power of the mass ratio as this separates the vibrational and rotational energies in the orders of the perturbation expansion [38].
- 9.
- 10.
If one sets κ=0…one obtains a differential equation in the x k alone, the X l appearing as parameters:…. Evidently, this represents the electronic motion for stationary nuclei.
- 11.
W(X) in the notation of the above quotation.
- 12.
The reader may find it helpful to refer to the Appendix which summarizes some mathematical notions that are needed here, and illustrates them in a simple model of coupled oscillators with two degrees of freedom.
- 13.
It is always possible to split off the kinetic energy of the centre-of-mass without any approximation; with this choice we retain the separation of the electronic and nuclear kinetic energies as well, as in (1.24). Explicit formulae are given in e.g. [3] where it is shown that the nuclear kinetic energy terms involve reciprocals of the nuclear masses, so that overall, the nuclear kinetic energy is proportional to κ 4.
- 14.
After the elimination of the centre-of-mass variables \(\hat{\mathsf{H}}^{\mathrm{elec}}\) is playing the role of \(\hat{H}_{o}\) in (1.20).
- 15.
We assume that the centre-of-mass contributions are eliminated as usual.
- 16.
The multiminima case can also be treated in this way.
- 17.
The Lorentz Theory of the electron for example [77].
- 18.
A similar requirement must be placed on the denominator in (12) of [85] for the equation to provide a secure definition.
- 19.
In its original form b=b o , the equilibrium configuration, on the right-hand side of (1.50).
- 20.
The variables are expressed in dimensionless form for simplicity. The quantum oscillator \(\hat{\mathsf{h}}=\frac{1}{2}(\hat{\mathsf{p}}^{2}+\hat{\mathsf{q}}^{2})\) has eigenvalues \(n+\frac{1}{2}\).
References
Löwdin P-O (1989) Pure Appl Chem 61:2065–2074
Thomson JJ (1899) Philos Mag 48:547–567
Woolley RG, Sutcliffe BT (2003) In: Brändas EJ, Kryachko ES (eds) Fundamental world of quantum chemistry, vol 1. Kluwer Academic, Dordrecht
Sutcliffe BT, Woolley RG (2012) J Chem Phys 137:22A544
Marcelin R (1914) Contribution à l’étude de la cinétique physico-chimique. Gauthier-Villars, Paris
Marcelin R (1915) Ann Phys 3:120–231
Marcelin R (1914) C R Hebd Séances Acad Sci 158:116–118
Marcelin R (1914) C R Hebd Séances Acad Sci 158:407–409
Gibbs JW (1902) Elementary principles in statistical mechanics. C. Scribner, New York
Navarro L (1998) Arch Hist Exact Sci 53:147–180
Duhem P (1911) Traité d’énergétique, 2 vols. Gauthier-Villars, Paris
Pelzer H, Wigner EP (1932) Z Phys Chem Abt B 15:445–471
Wigner EP (1938) Trans Faraday Soc 34:29–41
Laidler KJ, King MC (1983) J Phys Chem 87:2657–2664
Waalkens H, Schubert R, Wiggins S (2008) Nonlinearity 21:R1–R118
Earnshaw S (1842) Trans Camb Philos Soc 7:97–112
Bohr N (1922) The structure of the atom. Nobel Lecture, December 11. Available online as http://www.nobelprize.org/nobel_prizes/physics/laureates/1922/Bohr-lecture.html
Bohr N (1913) Philos Mag 26:1–25
Schwarzschild K (1916) Sitzber Preuss Akad Wiss 1:548–561
Heurlinger T (1919) Z Phys 20:188–190
Born M (1925) Vorlesungen über Atommechanik. Springer, Berlin. The mechanics of the atom. Translated by JW Fisher (1927). George Bell and Sons, London
Sommerfeld A (1919) Atombau und Spektrallinien. Verlag F Vieweg und Sohn, Braunschweig
Ehrenfest P (1916) Ann Phys 356:327–352
Bohr N (1918) Kgl Danske Vid Selskab 4:1–36
Bohr N (1923) Z Phys 13:117–165
Berry MV (1984) J Phys A, Math Gen 17:1225–1233
Gutzwiller M (1998) Rev Mod Phys 70:589–639
Percival IC (1973) J Phys B, Atom Mol Phys 6:L229–L232
Thirring W (1987) In: Kilmister CW (ed) Schrödinger, centenary celebrations of a polymath. Cambridge University Press, Cambridge
Poincaré H (1899) Les méthodes nouvelles de la mécanique céleste. Gauthier-Villars, Paris
Einstein A (1917) Verh Dtsch Phys Ges 19:82–92
Pauli W (1922) Ann Phys 68:177–240
Nordheim L (1923) Z Phys 19:69–93
Kemble EC (1926) Molecular spectra of gases. Bull NRC 11(57):303–304
Kragh H (2012) Neils Bohr and the quantum atom: the Bohr model of atomic structure, 1913–1925. Oxford University Press, Oxford, p 239
Born M, Heisenberg W (1924) Ann Phys 74:1–31
Eckart C (1935) Phys Rev 47:552–558
Born M, Oppenheimer JR (1927) Ann Phys 84:457–484
Heitler W, London F (1927) Z Phys 44:455–472
London F (1928) In: Quantentheorie und Chemie. Hirzel, Leipzig, p 59
London F (1928) In: Probleme der modernen Physik. Hirzel, Leipzig, p 104
Slater JC (1927) Proc Natl Acad Sci 13:423–430
Born M, Fock V (1928) Z Phys 51:165–180
Born M, Huang K (1954) Dynamical theory of crystal lattices. Clarendon, Oxford
Lathouwers L, van Leuven P (1982) Adv Chem Phys 49:115–189
An English language translation of the original paper can be found at www.ulb.ac.be/cpm/people/scientists/bsutclif/main.html
Sutcliffe BT (1990) In: Maksic ZB (ed) Theoretical models of chemical bonding, part 1. Springer, Berlin, pp 1–28
Pauling L, Wilson EB Jr. (1935) Introduction to quantum mechanics. McGraw-Hill, New York. See especially Chap X, p 262
Born M (1951) Nachr. Akad. Wiss. Göttingen. Math-Phys. Klasse IIa. Math Phys Chem Abt, S Art Nr 6:1–3
O’Malley TF (1971) Adv At Mol Phys 7:223–249
Hall GG (1987) Int J Quant Chem XXXI:383–391
Loss M, Miyao T, Spohn H (2007) J Funct Anal 243:353–393
Reed M, Simon B (1978) Analysis of operators. Methods of modern mathematical physics, vol IV. Academic Press, New York
Kato T (1951) Trans Am Math Soc 70:195–218
Frolov AM (1999) Phys Rev A 59:4270–4280
Messiah A (1961) Quantum mechanics. North-Holland, Amsterdam
Bastiaan JB, Bowman JM (2009) Int Rev Phys Chem 28:577–606
Broeckhove J, Lathouwers L, van Leuven P (1991) J Math Chem 6:207–241
Mead CA (1992) Rev Mod Phys 64:51–85
Faure F, Zhilinskii B (2002) Phys Lett A 302:242–252
Combes J-M (1975) In: International symposium on mathematical physics, Kyoto University, Kyoto. Lecture notes in physics, vol 39, pp 467–471
Combes J-M (1977) Acta Phys Austriaca Suppl XVII:139–159
Combes J-M, Seiler R (1980) Quantum dynamics of molecules. In: Woolley RG (ed) NATO ASI B57. Plenum, New York
Combes J-M, Duclos P, Seiler R (1981) In: Velo G, Wightman A (eds) Rigorous atomic and molecular physics. Plenum, New York
Löwdin P-O (1966) Perturbation theory and its application in quantum mechanics. In: Wilcox CH (ed) Proceedings of Madison symposium. Wiley, New York
Zhislin G (1960) Tr Mosc Mat Obsc 9:81–128
van Winter C (1964) Kgl Danske Vid Selskab 1:1–60
Hunziker W (1966) Helv Phys Acta 39:451–462
Hagedorn GA, Joye A (2007) In: Gesztezy F, Deift P, Galvez C, Perry P, Schlag GW (eds) Spectral theory and mathematical physics. A festschrift in honor of Barry Simon’s 60th birthday. Oxford University Press, London, p 203
Klein M, Martinez A, Seiler R, Wang XP (1992) Commun Math Phys 143:607–639
Feffermann CL (1983) Bull Am Math Soc 9:129–206
Hagedorn GA, Joye A (1999) Rev Math Phys 11:41–101
Primas H (1983) Chemistry, quantum mechanics and reductionism, 2nd edn. Springer, Berlin
Woolley RG (1980) Isr J Chem 19:30–46
Woolley RG (1982) Struct Bond (Springer) 52:1–35
Anderson PW (1984) Basic notions of condensed matter physics. Benjamin-Cummings, Redwood City
Lorentz HA (1909) The theory of electrons and its applications to the phenomena of light and radiant heat. Teubner, Leipzig
Lieb EH, Loss M (2003) Adv Theor Math Phys 7:667–710
Lieb EH, Loss M (2005) Commun Math Phys 258:675–695
Hasler D, Herbst I (2008) Commun Math Phys 279:769–787
Loss M, Miyao T, Spohn H (2009) Lett Math Phys 89:21–31
Lieb EH, Seiringer R (2010) The stability of matter in quantum mechanics. Cambridge University Press, Cambridge
Hunter G (1975) Int J Quant Chem 9:237–242
Abedi A, Matra NT, Gross EKU (2010) Phys Rev Lett 105:123002
Kutzelnigg W (2007) Mol Phys 105:2627–2647
Hunter G (1981) Int J Quant Chem 19:755–761
Czub J, Wolniewicz L (1978) Mol Phys 36:1301–1305
Wilson EB Jr. (1979) Int J Quantum Chem, Symp 13:5–14
Cassam-Chenai P (2006) Chem Phys Lett 420:354–357
Pachuki K, Komasa J (2009) J Chem Phys 130:164113
Henderson JR, Tennyson J, Sutcliffe BT (1993) J Chem Phys 98:7191–7203
Miller S, Tennyson J (1988) Chem Phys Lett 145:117–120
Sutcliffe BT, Woolley RG (2005) Phys Chem Chem Phys 7:3664–3676
Dixmier J (1981) Von Neumann algebras. Elsevier/North-Holland, Amsterdam
Ballentine LE (1990) Quantum mechanics. Prentice-Hall, Englewood Cliffs
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
In this appendix we give an heuristic account of the mathematical notion of the direct integral of Hilbert spaces, and then study a simple model problem to illustrate the general ideas discussed in the paper.
Consider a self-adjoint operator T that depends on a parameter X, so T=T(X). The parameter X=−∞≤X≤+∞, covers the whole real line  , and T(X) is assumed to be defined for all X. T(X) is an operator on a Hilbert space, which is denoted
, and T(X) is assumed to be defined for all X. T(X) is an operator on a Hilbert space, which is denoted  ; its eigenfunctions {ϕ} defined by
; its eigenfunctions {ϕ} defined by
form a complete orthogonal set for the space  . The scalar product is
. The scalar product is
T may have discrete eigenvalues below a continuous spectrum that starts at Λ, that is
Now let’s introduce a ‘big’ Hilbert space  as a direct integral over the {
as a direct integral over the { },
},

and correspondingly the operator  acting on
acting on  defined by
defined by

The scalar product on the big space  is defined explicitly in terms of (1.51) by
is defined explicitly in terms of (1.51) by

In (1.51) one can always chose the functions {ϕ k } to be orthonormalized independently of X,
However this choice is not consistent with (1.53), which requires f(X) to decrease sufficiently fast as |X|→∞ for the integral to exist. The mathematical motivation for this construction is this: the cartesian product of the spaces { },
},

is a field of Hilbert spaces over  which has a natural vector space structure. In modern geometric language, the Hilbert space
which has a natural vector space structure. In modern geometric language, the Hilbert space  is a fibre over a point X in a fibre bundle;
is a fibre over a point X in a fibre bundle;  is the vector space of sections of this bundle. The subspace of
is the vector space of sections of this bundle. The subspace of  consisting of square integrable sections is the direct integral (1.52). The direct integral is the generalization to the continuous infinite dimensional case of the notion of the direct sum of finite dimensional vector spaces.
consisting of square integrable sections is the direct integral (1.52). The direct integral is the generalization to the continuous infinite dimensional case of the notion of the direct sum of finite dimensional vector spaces.
Purely as a heuristic explanation suppose initially that the parameter X has only two discrete values {X 1,X 2}. There are then two eigenvalue equations to consider, and two associated Hilbert spaces. In the direct sum space we have

The eigenfunctions of  are then two-dimensional column vectors, and so
are then two-dimensional column vectors, and so

The spectrum of  is the union of the spectra of T(X
1) and T(X
2). This discussion is trivially extended to n points {X
k
:k=1,…,n}, with the spectrum of
is the union of the spectra of T(X
1) and T(X
2). This discussion is trivially extended to n points {X
k
:k=1,…,n}, with the spectrum of  given by the union of the n operators T(X
1),…,T(X
n
). The limit n→∞ is not trivial since it brings in important notions from topology and integration (measure theory) which we gloss over [94]. When these are taken into consideration however the result is that the spectrum σ of
given by the union of the n operators T(X
1),…,T(X
n
). The limit n→∞ is not trivial since it brings in important notions from topology and integration (measure theory) which we gloss over [94]. When these are taken into consideration however the result is that the spectrum σ of  is purely continuous since its direct integral representation implies that its spectrum is the union of the spectra of the infinite set of T(X) operators,
is purely continuous since its direct integral representation implies that its spectrum is the union of the spectra of the infinite set of T(X) operators,

where L
0 is the minimum value of λ
0(X). The eigenvalue equation for  is,
is,

with Λ a continuous index for the {Φ}. Even if T(X) is self-adjoint, it doesn’t follow that its direct integral  is self-adjoint; that depends on specifics and has to be investigated. So the {Φ} cannot be assumed to be complete.
is self-adjoint; that depends on specifics and has to be investigated. So the {Φ} cannot be assumed to be complete.
In the application of this mathematics to the Born-Oppenheimer approximation, the role of x is taken by the electronic coordinates t
e, and X is to be identified with definite choices of the nuclear coordinates b. If there are M nuclei the parameters b are elements of  . The operator T(X) is the clamped-nuclei Hamiltonian \(\hat{\mathsf{K}}(\mathbf{b},\hat{\mathbf{t}}^{\mathrm{e}})_{o}=\hat{\mathsf{K}}_{o}\). With the conventional normalization of clamped-nuclei electronic eigenfunctions independent of the nuclear positions b, the formal eigenvectors, (1.36), [56] of \(\hat{\mathsf{H}}^{\mathrm{elec}}\) do not belong to the Hilbert space
. The operator T(X) is the clamped-nuclei Hamiltonian \(\hat{\mathsf{K}}(\mathbf{b},\hat{\mathbf{t}}^{\mathrm{e}})_{o}=\hat{\mathsf{K}}_{o}\). With the conventional normalization of clamped-nuclei electronic eigenfunctions independent of the nuclear positions b, the formal eigenvectors, (1.36), [56] of \(\hat{\mathsf{H}}^{\mathrm{elec}}\) do not belong to the Hilbert space  ; this simply reflects the loose use of the Dirac delta function for the position operator eigenfunctions.
; this simply reflects the loose use of the Dirac delta function for the position operator eigenfunctions.
We now consider a concrete model consisting of coupled harmonic oscillators with two degrees of freedom; we try to mimic the steps taken in the usual Born-Oppenheimer discussion. Consider the following Hamiltonian where κ and a are dimensionless constantsFootnote 20
The only non-zero commutators of the operators are
Following the conventional discussion of electron-nuclear separation outlined in Sects. 1.3.1, 1.3.2, define
so that
with Schrödinger equation
We note that
so the two parts cannot be simultaneously diagonalized. A principal axis transformation of the whole expression \(\hat{\mathsf{H}}\) brings it to separable form, but we do not need to pursue explicitly the full solution here.
On the other hand
so these two operators may be simultaneously diagonalized, and consider \(\hat{\mathsf{H}}_{o}\) at a definite eigenvalue of \(\hat{\mathsf{X}}\), say X
This is the Hamiltonian (in the variables \(\hat{\mathsf{x}},\hat{\mathsf{p}}\)) of a displaced oscillator in which X is a (c-number) parameter, with Schrödinger equation in position representation
\(\hat{\mathsf{K}}_{o}\) is the analogue in this model of the ‘clamped-nuclei’ electronic Hamiltonian.
The solution is immediate; we make a unitary transformation by introducing a displaced coordinate involving X
so that the transformed \(\hat{\mathsf{K}}_{o}\) in the new variables is
which has oscillator eigenvalues and eigenfunctions
where \(x'=x-\frac{aX}{2}\), the {φ n } are the usual harmonic oscillator eigenfunctions and \(E_{n}^{0}\) is the energy of the free oscillator \(2(n+\frac{1}{2})\). For fixed n the spectrum σ(X) is discrete and, as a function of the X parameters, would be conventionally interpreted as a ‘potential energy curve’. As far as (1.58) is concerned, \(\hat{\mathsf{K}}_{o}\), evaluated at some point X 0 cannot be regarded as an ‘approximation’ to \(\hat{\mathsf{H}}_{o}\), since obviously
so they can be simultaneously diagonalized, and \(\hat{\mathsf{H}}_{1}\) has purely continuous spectrum (free motion). So we have to consider X in the full problem in its operator form, \(\hat{\mathsf{X}}\).
We make the same unitary transformation of the \(\hat{\mathsf{x}},\hat{\mathsf{p}}\) variables in \(\hat{\mathsf{H}}_{o}\) as before, and it is still brought to diagonal form; however \(\hat{\mathsf{H}}_{1}\) will be modified because \(\hat{\mathsf{P}}\) is also translated by the operator \(\hat{\mathsf{U}}\) in (1.65) that generates the coordinate displacement (cf. (1.60)); thus
so the transform of \(\hat{\mathsf{H}}_{1}\) contains linear and quadratic terms in \(\hat{\mathsf{p}}\).
Nevertheless (1.61) is still valid, and formally we may write \(\hat{\mathsf{H}}_{0}\) as a direct integral
The Schrödinger equation for \(\hat{\mathsf{H}}_{o}\) in position representation is now an equation involving functions of x and X
Just as before (see (1.54)) the direct integral decomposition (1.67) implies that the spectrum is purely continuous, explicitly
ε in (1.68) takes all positive values ≥1, where 1 is the minimum value of the oscillator eigenvalue \(2(n+\frac{1}{2})\). The associated continuum eigenfunctions {Φ} may formally be written as products of oscillator eigenfunctions (in x′), and delta functions (in X). They don’t lie in Hilbert space of course and one needs the Gel’fand construction of a rigged space to make sense of the formal calculation [95]. If one returns to the x variable, the {φ n } are functions of x and X, since x′=x′(X).
One can’t do anything very useful with the direct integral expression (1.67) for \(\hat{\mathsf{H}}_{o}\) apart from adding it onto the κ 4 term, which just returns us to the full problem. The full wavefunction in (1.59) can be expanded as

which obviously leads towards a variational approach [56]; such expansions rely on the completeness of the states employed. In this simple problem there is no difficulty, but as noted earlier, in realistic Coulomb systems it is much less clear that a complete set of states is available.
However that may be, let us rehearse again the argument due to Born summarized in Sect. 1.3.2. We substitute (1.71) in (1.59), left multiply by \(\varphi_{m}^{*}\) and integrate out the x′ variables to leave an equation for the coefficients {c(X) n },
At this point in the conventional account, \(\hat{\mathsf{H}}_{o}\) is replaced by \(\hat{\mathsf{K}}_{o}\), (1.62), and then the action of \(\hat{\mathsf{K}}_{o}\) on the functions {φ} in (1.72) can be evaluated using (1.63) in the well-known way,
From the foregoing discussion it is clear that the substitution of \(\hat{\mathsf{H}}_{o}\) by \(\hat{\mathsf{K}}_{o}\) makes a qualitative change in the theory. This change does seem to be the ‘right’ thing to do, but so far there is no explanation as to why this is so.
Rights and permissions
Copyright information
© 2013 Springer International Publishing Switzerland
About this paper
Cite this paper
Sutcliffe, B., Woolley, R.G. (2013). The Potential Energy Surface in Molecular Quantum Mechanics. In: Hotokka, M., Brändas, E., Maruani, J., Delgado-Barrio, G. (eds) Advances in Quantum Methods and Applications in Chemistry, Physics, and Biology. Progress in Theoretical Chemistry and Physics, vol 27. Springer, Cham. https://doi.org/10.1007/978-3-319-01529-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-01529-3_1
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-01528-6
Online ISBN: 978-3-319-01529-3
eBook Packages: Chemistry and Materials ScienceChemistry and Material Science (R0)


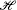 was that for classical nuclear motion on a Potential Energy Surface; this dynamics was assumed to give rise to a critical surface which was such that reaction trajectories cross the surface precisely once. The classical nature of the formalism was quite clear because the Uncertainty Principle precludes the precise specification of position on the critical surface simultaneously with the momentum of the nuclei.
was that for classical nuclear motion on a Potential Energy Surface; this dynamics was assumed to give rise to a critical surface which was such that reaction trajectories cross the surface precisely once. The classical nature of the formalism was quite clear because the Uncertainty Principle precludes the precise specification of position on the critical surface simultaneously with the momentum of the nuclei.