Abstract
The last chapter introduced the exterior product, which multiplied a p-vector and a q-vector to yield a (p+q)-vector. By directly summing the spaces of all such vectors, we obtained a vector space which was closed under multiplication. This led to a 2n-dimensional algebra, which we called the exterior algebra (see Theorem 26.3.6).
In the meantime we revisited inner product and considered non-Euclidean inner products, which are of physical significance. In this chapter, we shall combine the exterior product with the inner product to create a new type of algebra, the Clifford algebra, which happens to have important applications in physics.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
We are using the natural units for which the Planck constant (over 2π) and the speed of light are set to 1: ħ=1=c.
- 2.
Here we define an inner product simply as a symmetric bilinear map as in Definition 2.4.2.
- 3.
Many other notations are also used to denote this algebra. Among them are \(\mathbf {C}_{\mu,\nu}(\mathbb{R})\), C(μ,ν), \(C\ell_{\mu,\nu}(\mathbb{R})\), \(C\ell_{p,q}(\mathbb{R})\), and C(p,q) where q=ν and p=μ. Occasionally, we’ll use one of these notations as well.
- 4.
It is worth noting that, by using
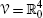 or
or 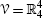 , we could obtain formulas for \(\textbf{C}_{n+4}^{0}(\mathbb{R})\) and \(\textbf{C}^{n+4}_{0}(\mathbb{R})\) analogous to (27.50) and (27.51). However, as entries 5, 6, and 7 of Table 27.1 can testify, they would not be as appealing as the formulas obtained above. This is primarily because
, we could obtain formulas for \(\textbf{C}_{n+4}^{0}(\mathbb{R})\) and \(\textbf{C}^{n+4}_{0}(\mathbb{R})\) analogous to (27.50) and (27.51). However, as entries 5, 6, and 7 of Table 27.1 can testify, they would not be as appealing as the formulas obtained above. This is primarily because 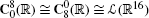 .
. - 5.
Here we are using the physicists’ convention of numbering the basis vectors from 0 to 3 with \(\hat {\mathbf {e}}_{0}=\hat {\mathbf {e}}_{4}\) and using Greek letters for indices.
References
Greub, W.: Multilinear Algebra, 2nd edn. Springer, Berlin (1978)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Hassani, S. (2013). Clifford Algebras. In: Mathematical Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-01195-0_27
Download citation
DOI: https://doi.org/10.1007/978-3-319-01195-0_27
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-01194-3
Online ISBN: 978-3-319-01195-0
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


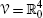 or
or 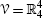 , we could obtain formulas for
, we could obtain formulas for 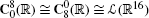 .
.