Abstract
Until around 1970s, tensors were almost completely synonymous with (general) relativity except for a minor use in hydrodynamics. Students of physics did not need to study tensors until they took a course in the general theory of relativity. Then they would read the introductory chapter on tensor algebra and analysis, solve a few problems to condition themselves for index “gymnastics”, read through the book, learn some basic facts about relativity, and finally abandon it (unless they became relativists).
Today, with the advent of gauge theories of fundamental particles, the realization that gauge fields are to be thought of as geometrical objects, and the widespread belief that all fundamental interactions (including gravity) are different manifestations of the same superforce, the picture has changed drastically.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
We denote vectors by roman boldface, and tensors of higher rank by sans serif bold letters.
- 2.
Here, we are assuming that
 acts on an object (such as v) by “pairing it up” with an appropriate factor of which
acts on an object (such as v) by “pairing it up” with an appropriate factor of which 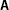 is composed (such as \({\pmb{\epsilon}}^{j}\)).
is composed (such as \({\pmb{\epsilon}}^{j}\)). - 3.
When there is no risk of confusion, we shall delete
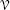 from
from  , it being understood that all tensors are defined on some given underlying vector space.
, it being understood that all tensors are defined on some given underlying vector space. - 4.
The use of
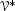 in
in 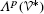 is by convention. Since a member of
is by convention. Since a member of 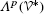 acts on p
dual vectors, it is more natural to use
acts on p
dual vectors, it is more natural to use 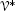 .
. - 5.
The reader should be warned that different authors may use different numerical coefficients in the definition of the exterior product.
- 6.
Note that
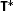 is the extension of the pullback operator introduced at the end of Chap. 2.
is the extension of the pullback operator introduced at the end of Chap. 2. - 7.
See also Problem 5.37.
- 8.
It turns out to be more natural to consider J as a 3-form. However, such a fine distinction is not of any consequence for the present discussion.
References
Abraham, R., Marsden, J., Ratiu, T.: Manifolds, Tensor Analysis, and Applications, 2nd edn. Springer, Berlin (1988)
Bishop, R., Goldberg, S.: Tensor Analysis on Manifolds. Dover, New York (1980)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Hassani, S. (2013). Tensors. In: Mathematical Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-01195-0_26
Download citation
DOI: https://doi.org/10.1007/978-3-319-01195-0_26
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-01194-3
Online ISBN: 978-3-319-01195-0
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


 acts on an object (such as v) by “pairing it up” with an appropriate factor of which
acts on an object (such as v) by “pairing it up” with an appropriate factor of which 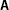 is composed (such as
is composed (such as 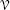 from
from  , it being understood that all tensors are defined on some given underlying vector space.
, it being understood that all tensors are defined on some given underlying vector space.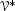 in
in 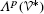 is by convention. Since a member of
is by convention. Since a member of 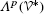 acts on p
dual vectors, it is more natural to use
acts on p
dual vectors, it is more natural to use 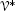 .
.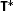 is the extension of the pullback operator introduced at the end of Chap.
is the extension of the pullback operator introduced at the end of Chap.