Abstract
The linear operators discussed in the last two chapters were exclusively integral operators. Most applications of physical interest, however, involve differential operators (DO). Unfortunately, differential operators are unbounded. We noted that complications arise when one abandons the compactness property of the operator, e.g., sums turn into integrals and one loses one’s grip over the eigenvalues of noncompact operators. The transition to unbounded operators complicates matters even more. Fortunately, the formalism of one type of DOs that occur most frequently in physics can be studied in the context of compact operators. Such a study is our aim for this chapter.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
A linear manifold of an infinite-dimensional normed vector space
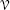 is a proper subset that is a vector space in its own right, but is not necessarily closed.
is a proper subset that is a vector space in its own right, but is not necessarily closed. - 2.
As opposed to on
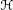 .
. - 3.
This subtle difference between hermitian and self-adjoint is stated here merely to warn the reader and will be confined to the present discussion. The two qualifiers will be (ab)used interchangeably in the rest of the book.
- 4.
The sum of two bounded operators is bounded.
- 5.
We shall depart from our convention here and shall not use the Dirac bar-ket notation although the use of abstract operators encourages their use. The reason is that in this example, we are dealing with functions, and it is more convenient to undress the functions from their Dirac clothing.
- 6.
Although this will change q—and the original operator—no information will be lost because the eigenvectors will be the same and all eigenvalues will be changed by α.
- 7.
The reader recalls that when
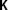 acts on
acts on 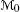 , it yields zero.
, it yields zero. - 8.
This is because n, m, and l are all positive.
References
DeVito, C.: Functional Analysis and Linear Operator Theory. Addison-Wesley, Reading (1990)
Hassani, S.: Mathematical Methods for Students of Physics and Related Fields, 2nd edn. Springer, Berlin (2008)
Hellwig, G.: Differential Operators of Mathematical Physics. Addison-Wesley, Reading (1967)
Lorrain, P., Corson, D., Lorrain, F.: Electromagnetic Fields and Waves, 3rd edn. Freeman, New York (1988)
Marion, J., Heald, M.: Classical Electromagnetic Radiation, 2nd edn. Academic Press, New York (1980)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Hassani, S. (2013). Sturm-Liouville Systems. In: Mathematical Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-01195-0_19
Download citation
DOI: https://doi.org/10.1007/978-3-319-01195-0_19
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-01194-3
Online ISBN: 978-3-319-01195-0
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


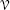 is a proper subset that is a vector space in its own right, but is not necessarily closed.
is a proper subset that is a vector space in its own right, but is not necessarily closed.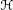 .
.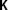 acts on
acts on 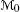 , it yields zero.
, it yields zero.