Abstract
The first two parts of the book dealt almost exclusively with algebraic techniques. The third and fourth part were devoted to analytic methods. In this introductory chapter, we shall try to unite these two branches of mathematics to gain insight into the nature of some of the important equations in physics and their solutions. Let us start with a familiar problem.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The precise definition uses “supremum” instead of “maximum”. Rather than spending a lot of effort explaining the difference between the two concepts, we use the less precise, but more intuitively familiar, concept of “maximum”.
- 2.
Here the two Hilbert spaces coincide, so that the derivative operator acts on a single Hilbert space.
- 3.
One can simply choose a λ whose absolute value is greater than
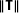 .
. - 4.
Note how critical finite-dimensionality is for this implication. In infinite dimensions, an operator can be one-to-one (thus having a zero kernel) without being onto.
- 5.
In topological jargon one says that (a,b) and \(\mathbb{R}\) are homeomorphic.
- 6.
The spectrum of a bounded operator need not occupy any “area” in the complex plane. It may consist of isolated points or line segments, etc., in which case the spectrum will constitute the entire boundary.
- 7.
BWHB stands for Bolzano, Weierstrass, Heine, and Borel. Bolzano and Weierstrass proved that any closed and bounded subset of \(\mathbb{R}\) has the Bolzano-Weierstrass property. Heine and Borel abstracted the notion of compactness in terms of open sets, and showed that a closed bounded subset of \(\mathbb{R}\) is compact. The BWHB theorem as applied to \(\mathbb{R}\) is usually called the Heine-Borel theorem (although some authors call it the Bolzano-Weierstrass theorem). Since the Bolzano–Weierstrass property and compactness are equivalent, we have decided to choose BWHB as the name of our theorem.
- 8.
Our conclusion is valid only in infinite dimensions. In finite dimensions, all operators, including
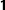 , are compact.
, are compact. - 9.
We have not discussed multiple integrals of complex functions. A rigorous study of such integrals involves the theory of functions of several complex variables—a subject we have to avoid due to lack of space. However, in the simple case at hand, the theory of real multiple integrals is an honest guide.
- 10.
This is possible because the poles are isolated.
References
Birkhoff, G., MacLane, S.: Modern Algebra, 4th edn. Macmillan, London (1977)
Dennery, P., Krzywicki, A.: Mathematics for Physicists. Harper and Row, New York (1967)
DeVito, C.: Functional Analysis and Linear Operator Theory. Addison-Wesley, Reading (1990)
Halmos, P.: Finite Dimensional Vector Spaces, 2nd edn. Van Nostrand, Princeton (1958)
Richtmyer, R.: Principles of Advanced Mathematical Physics. Springer, Berlin (1978)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Hassani, S. (2013). Introductory Operator Theory. In: Mathematical Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-01195-0_17
Download citation
DOI: https://doi.org/10.1007/978-3-319-01195-0_17
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-01194-3
Online ISBN: 978-3-319-01195-0
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


 .
.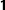 , are compact.
, are compact.