Abstract
Though Wallis’s Arithmetica infinitorum was one of Newton’s major sources of inspiration during the first years of his mathematical education, indivisibles were not a central feature of his mathematical production.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The original Newton’s manuscript is conserved at the University Library of Cambridge (now available online on the Cambridge Digital Library): Add. 3996 (the entry “Of Quantity” is at p. 90r) A printed edition, supplemented by a large commentary, is provided in McGuire and Tammy (1983).
- 2.
The original is included in another manuscript conserved at the University Library of Cambridge (and now available online on the Cambridge Digital Library): Add. 4000, p. 82r and 83r-84r. At top of page 82r there is a date: ‘\( 166\frac{3}{4} \) January’, which refers to January 1663 old style, the month of January 1663 in the Julian calendar still used in Great Britain at that time, equivalent to the month going from January 11th 1664 to February 10th 1664 of our Gregorian calendar, which were then used on the Continent. Still, the blank dividing this date from the beginning of the note suggests that the former could not be that of the latter. A detailed analysis of the note is offered in Panza (2005, pp. 134–149). We come back here on the main points that are made there.
- 3.
As observed by Whiteside (Newton 1967, I, 1, 3, § 2, p. 92, footnote 8), the last remark in Lemma 2 concerned with “a crookedlined figure” is a generalisation of Wallis’s construction of conical Pyramidoides (Wallis 1655, propp. IX, XIV, and XVIII), and is then adding something new to Newton’s readings, though this addition is, as such, quite natural.
- 4.
In stating these arguments, Newton makes no explicit mention of his three lemmas. Our appeal to them in our reconstruction pertains then to our own understanding of these arguments.
- 5.
For the difference between Lemma 2 and Lemma 3, cf. footnote 9.
- 6.
Though formally equivalent to ‘\( {\displaystyle {\int}_0^{\xi }}\frac{x^2}{a}\;dx=\frac{\xi^3}{3a} \)’, the equality (16.2) deeply differs also from it both for its justification and its intended interpretation.
- 7.
Following Whiteside’s suggestion (Newton 1967, I, 94–97, footnote 29), we take Newton’s main diagram—which seems to represent an equilateral hyperbola of centre d—as inaccurate and we amend it. To this purpose, we only consider the branch of hyperbola which Newton tries to square.
- 8.
On this mistake, cf. Newton (1967, I, 1, 3, § 2, 94–97, notes 16, 21 et 29).
- 9.
As it is stated, Lemma 3 is reminiscent of the rule of ductus plani in planum (cf. (Newton 1967), I, 1, 3, § 2, p. 93, footnote 10). But it is still not clear how this lemma is supposed to differ from Lemma 2, according to Newton understanding. I take Lemma 2 to concern the multiplication of the parallel chords of a certain figure either by themselves or by the same constant segment, respectively, and Lemma 3 to concern the multiplication of the parallel chords of a certain figure by the corresponding values of a variable segment (which are taken in turn as the parallel chords of another figure), respectively.
- 10.
As a matter of fact, Newton does not explicitly mention the whole solid yxvwz and draws no diagram of it, by confining himself to consider its half yxvz.
- 11.
Unpublished in Newton’s lifetime, the first page of Newton’s holograph copy of this tract is missing. On the title we use we follow Whiteside’s suggestion (Newton 1967, vol. III, p. 32, footnotes 2 and 3), based on one of Newton’s manuscript in which he mentions the treatise as “Tractatu[s] de methodis serierum et fluxionum anno 1671 composito”. When it was printed in Latin in 1779, in Newton’s Opera, edited by S. Horsley, it was given the title “Artis analyticæ specimina vel Geometria analytica” (Newton 1779, vol. 1, pp. 389–518; in the table of contents, ibid., p. XVII, the title becomes: “Geometria analytica sive specimina artis analyticæ”). This Latin edition was preceded by an English translation, edited by J. Colson, in 1736, titled after the mentioned manuscript, namely “The Method of Fluxions and Infinite Series” (Newton 1736). We quote from Newton (1967, vol. III, pp. 32–328). For the datation, cf. ibid., Introduction, pp. 3–18. The treatise results from a deep revision, involving many significant changes and additions, of a previous tract, composed in October–November 1666, today known, after Whiteside’s edition, as the October 1666 Tract on Fluxions (Newton 1967, vol. I, pp. 400–448). All translations from these and other Newton’s works included in Newton (1967) are Whiteside’s, unless mention to the contrary.
- 12.
- 13.
The term ‘fluxion’ was introduced by Newton for the first time just in the De methodis, to designate (with a significant conceptual stretching) what he had previously identified as punctual speed.
- 14.
For the composition and circulation of De analysi, cf. Whiteside’s comments in footnotes 1, 2, pp. 206–207 of Newton (1967, vol. II). The third substantial tract is the October 1666 Tract on Fluxions, mentioned in footnote (11).
- 15.
Cf. footnote 13, above.
- 16.
Cf. Collins (1712), p. 14: “N. B. Hic describitur Methodus per Fluentes et earum Momenta. Haec momenta à D. Leibnitio Differentiae postmodum vocata sunt: Et inde nomen Methodi Differentialis.” (We slightly modify Whiteside’s translation).
- 17.
This specification (“unitas ista quæ pro momento ponitur”, in Newton’s original Latin) is intended to distinguish the unity “which is set for the moment” from another one, which is rather set for the diameter of the circle (and later for its radius), of which the moment is merely a (infinitesimal) portion. This double use of the unity makes clear that taking the moment of the abscissa to be equal to 1 is not, for Newton, a way to ascribe a measure to it, but rather a way to identify the abscissa as the principal variable of the problem, and its moment as a sort of (infinitesimal) parameter to which the other relevant moments are to be compared.
- 18.
Notice that, though a moment is here indubitably conceived as an infinitesimal amount of time, rather than as a portion of space, as in De Analysis and De Methodis, once more, no definition or clarification is given for this crucial notion.
- 19.
Newton’s philosophy of mathematics, with special attention to the problems posed by infinitesimals and indivisibles, is analysed in detail in Guicciradini (2009, p. 179–219).
- 20.
According to Whiteside, the text originated as an augmented replacement for a couple pages in De methodis. Apparently this replacement was left behind when copies of the tract were taken in the early eighteenth century to be never included instead of the two pages it was meant to replace: cf. (Newton 1967, vol. III, p. 329, notes 1 and 2).
- 21.
Notice that the whole tract occupies pp. 32–328 of volume III of Newton (1967).
- 22.
For the scanty information available, cf. Whiteside’s introduction and footnote in Newton (1967, vol. IV, pp. 411 ff).
- 23.
F. De Gandt has stressed the importance that indivisibles, or, more generally infinitely smalls, have in the mathematics of the Principia: cf. Gandt (1995, Chap. III, pp. 159–264).
- 24.
- 25.
This geometrical configuration can be constructed by rule and compass even supposing that the positions of corpuscles P and p with respect to the shells is given in advance. Take, indeed, any great circle of the first shell, and draw two segments PHK and PIL from P to it. The chords HK, IL are then given in length. Take then any great circle of the second shell. To get the points h and i such that \( \overset{\frown }{\mathtt{HK}}=\overset{\frown }{\mathtt{hk}} \) and \( \overset{\frown }{\mathtt{IL}}=\overset{\frown }{\mathtt{il}} \), it is enough to insert within this great circles two chords hk, il respectively equal to the chords HK, IL, verging to p. This is a quite simple neusis problem tackled by Apollonius in the first book of On verging constructions (Heath 1961, vol. II, pp. 189–190), which is easily solvable by rule and compass, as shown, for example, by S. Horsley, in solving problem I of his Apollonii Pergæi Inclinationum (Horsley 1770, pp. 1–2).
- 26.
Corollary III to Lemma VII is appealed here in order to warrant the replacement of RI and ri with \( \overset{\frown }{\mathtt{IH}} \) and \( \overset{\frown }{\mathtt{ih}} \) in PI × pf : PF × pi :: RI : ri. On the cogency of this derivation, cf. Weinstock (1984), Sect. III (p. 886)—which wrongly denies that this corollary does actually warrant this replacement—and Erlichson (1990)—which rightly argues for the opposite, by showing how the ultimate equalities of RI and \( \overset{\frown }{\mathtt{IH}} \), and of ri and \( \overset{\frown }{\mathtt{ih}} \) follows from this corollary.
- 27.
On the ultimate equality \( \frac{\overset{\frown }{\mathtt{IH}}\times \mathtt{I}\mathtt{Q}}{\overset{\frown }{\mathtt{ih}}\times \mathtt{i}\mathtt{q}}=\frac{St.\left(\overset{\frown }{\mathtt{IH}}\right)}{St.\left(\overset{\frown }{\mathtt{ih}}\right)} \), cf. Weinstock (1984, pp. 884 and 889, footnote 15). Weinstock’s suggestion is that Newton is here relying on the equalities \( St.\;\left(\overset{\frown }{\mathtt{IH}}\right)=2\pi \left(\overset{\frown }{\mathtt{IH}}\right)\left(\mathtt{I}\mathtt{Q}\right) \) and \( St.\;\left(\overset{\frown }{\mathtt{ih}}\right)=2\pi \left(\overset{\frown }{\mathtt{ih}}\right)\left(\mathtt{i}\mathtt{q}\right) \), which result, by appropriate replacements (licensed by the supposition that the angles \( \widehat{\mathtt{DPE}} \), \( \widehat{\mathtt{dpe}} \) vanish), from the equalities Tr.Cn. (IH) = 2π(IH) (MN) and Tr.Cn. (ih) = 2π (ih) (mn), where Tr.Cn. (IH) and Tr.Cn. (ih) are the truncated cones respectively generated by IH and ih under the revolution of the semicircles AHKB and ahkb about the diameters AB and ab, and MN and mn are the radii of the mean circumferences of these truncated cones.
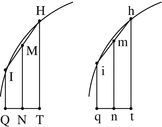
- 28.
Indeed, as the two shells are equal, this is the same as saying that the attractive forces exerted by these shells upon the two corpuscles are inversely proportional to the square of the distances between these corpuscles and the centres of the shells.
References
J. Collins, editor. Commercium epistolicum D. Johannis Collins et aliorum de Analysi promota, jussu Societatis Regiæ in lucem editum. typis Pærsonianis, Londini, 1712.
S. Ducheyne. The Main Business of Natural Philosophy. Isaac Newton’s Natural-Philosophical Methodology. Springer, Dorcrecht, etc., 2011.
F. De Gandt. Force and Geometry in Newton’s Principia. Princeton Univ. Press, Princeton, 1995.
H. Erlichson. Comment on “Newton’s Principia and the external gravitational field of a spherically symmetric mass distribution” by R. Weinstock. American Journal of Physics, 58:274–276, 1990.
N. Guicciardini. Reading the Principia. The Debate on Newton’s Mathematical Methods for Natural Philosophy from 1687 to 1736. Cambridge Univ. Press, Cambridge, etc., 1999.
N. Guicciradini. Isaac Newton on Mathematical Certainty and Method. Thde MIT Press, Cambridge (Mass), London, 2009.
T. Heath. A History of Greek Mathematics. Clarendon Press, Oxford, 1961. 2 volumes.
S. Horsley. Apolloni Pergæi Inclinationom Libri duo. E Typographeo Clarendoniano, Oxonii, 1770.
J.E. McGuire and M. Tammy. Certain Philosophical Questions. Newton’s Trinity Notebook. Cambridge University Press, Cambridge, 1983.
I. Newton. Philosophiæ naturalis principia mathematica. Jussu Societatis Regiæ ac Typis Josephi Streater, Londoni, 1687.
I. Newton. The Method of Fluxions and Infinite Series. Printed by H. Woodfall, and sold by J. Nourse, London, 1736. Translated from the Author’s Latin Original by John Colson.
I. Newton. Isaci Newtoni Opera quæ extant omnia. Excudebat J. Nichols, Londini, 1779–1785. Commentariis illustrabat S. Horseley. 5 vols.
I. Newton. The Mathematical Papers of Isaac Newton. Cambridge University Press, Cambridge, 1967–1981. Edited by D. T. Whiteside (8 vols.).
I. Newton. The Principia. Mathematical Principles of Natural Philosophy. University of California Press, Berkeley, Los Angeles and London, 1999. A new translation by I. B. Cohen and A. Whitman, assisted by J. Budenz; preceded by a guide to Newton’s Principia by I. B. Cohen.
M. Panza. Newton et les origines de l’analyse: 1664–1666. Blanchard, Paris, 2005.
J. Wallis. De Sectionibus Conicis Nova Methodo Expositis, Tractatus. typis L. Lichfield, Academiæ Typographi, Impensis T. Robinson, Oxonii, 1655. Included with separate pagination in Wallis (1656). Also in Wallis (1693–1699), vol. I, pp. 291–354.
J. Wallis. De Angulo Cantactus et Semicirculis Disquisitio Geometrica. typis L. Lichfield, Academiæ Typographi, Impensis T. Robinson, Oxonii, 1656. Included with separate pagination in Wallis (1656). Also in Wallis (1693–1699), vol. II, pp. 603–630.
J. Wallis. Operum Mathematicorum. Pars Altera […]. typis L. Lichfield, Impensis T. Robinson, Oxonii, 1656.
J. Wallis. Opera Mathematica. E. Theatro Sheldoniano, Oxoniaæ, 1693–1699. 3 vols.
R. Weinstock. Newton’s Principia and the external gravitational field of a spherically symmetric mass distribution. American Journal of Physics, 52:883–890, 1984.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Malet, A., Panza, M. (2015). Newton on Indivisibles. In: Jullien, V. (eds) Seventeenth-Century Indivisibles Revisited. Science Networks. Historical Studies, vol 49. Birkhäuser, Cham. https://doi.org/10.1007/978-3-319-00131-9_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-00131-9_16
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-319-00130-2
Online ISBN: 978-3-319-00131-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


