Abstract
Let K be a global field. The aim of this paper is to study the basic properties of the global non-Abelian norm-residue symbol \(\mathsf{NR}_{K}^{\underline{\varphi }^{\mathrm{Weil}} }\) of K, which is defined following the Chevalley-Miyake philosophy of idèles by “glueing” the local non-Abelian norm-residue symbol \(\{\bullet,K_{\nu }\}_{\varphi _{\nu }}\) of K ν in the sense of Koch, for each \(\nu \in\mathbb{h}_{K}\).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The author would like to thank Pierre Cartier, A. D. Raza Choudary, and Michel Waldschmidt for inviting him to deliver a talk in the 6th World Conference on 21st Century Mathematics 2013, which took place in the Abdus Salam School of Mathematical Sciences, Lahore, on March 6–9, 2013. He would also like to thank the Abdus Salam School of Mathematical Sciences for arranging his stay and for the hospitality he received in Lahore on March 4–11, 2013, which he enjoyed very much. Finally, the author thanks the referee for his or her suggestions, which improved the presentation of this work a lot.
- 2.
By Čebotarev density theorem, \(\mathrm{Spl}: L/K\mapsto \mathrm{Spl}(L/K)\) is an injective and order-reversing mapping from finite Galois extensions L of the global field K into the power set of \(\mathbb{h}_{K}\cup\mathbb{a}_{K}\). The image of the map “Spl” for finite Abelian extensions L of K has a description in terms of the Abelian global reciprocity map (•, L∕K) relative to the extension L∕K.
- 3.
Initially, Koch started this theory for metabelian extensions of local fields (look at [9]) using explicit computations with formal Lubin-Tate groups, unlike the more general approach of Fesenko, Laubie, Serbest, and others, which uses APF-extensions and the fields of norm construction of Fontaine and Wintenberger.
- 4.
If {G i } i ∈ I is a collection of topological groups and
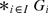 is the free product of this collection together with the canonical embeddings
is the free product of this collection together with the canonical embeddings 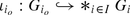 , for each i
o
∈ I, then the universal mapping property of free products states that, if for each i
o
∈ I, \(\phi _{i_{o}}: G_{i_{o}} \rightarrow H\) is a continuous homomorphism, then there exists a unique continuous homomorphism
, for each i
o
∈ I, then the universal mapping property of free products states that, if for each i
o
∈ I, \(\phi _{i_{o}}: G_{i_{o}} \rightarrow H\) is a continuous homomorphism, then there exists a unique continuous homomorphism 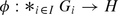 , such that \(\phi \circ \iota _{i_{o}} =\phi _{i_{o}}\), for every i
o
∈ I.
, such that \(\phi \circ \iota _{i_{o}} =\phi _{i_{o}}\), for every i
o
∈ I. - 5.
Which is unique if K is a function field and unique up to composition with an inner automorphism of W K defined by an element of the connected component W K o of W K if K is a number field.
- 6.
In fact, if \(\mathsf{s}_{K} = \mathsf{a}_{K}\), then \(\mathcal{J}_{K}^{\underline{\varphi }_{K}^{c}} = \mathsf{s}_{K}^{-1}\left (K^{\times }\right )\) by Theorem 2.
References
Auer, R.: Ray class fields of global function fields with many rational places. Acta Arith. 95, 97–122 (2000)
Fesenko, I.B.: Noncommutative local reciprocity maps. In: Miyake, K. (ed.) Class Field Theory–Its Centenary and Prospect, Tokyo 1998. Advanced Studies in Pure Mathematics, vol. 30, pp. 63–78. Mathematical Society of Japan, Tokyo (2001)
Hilton, P., Wu, Y.-C.: A Course in Modern Algebra. Wiley-Interscience, New York (1989)
Ikeda, K.I.: On the non-Abelian global class field theory. Annales mathématiques du Quebec 37, 129–172 (2013)
Ikeda, K.I., Kazancıoǧlu, S., Serbest, E.: On the relationship between the generalized Fesenko and the Laubie reciprocity maps (submitted)
Ikeda, K.I., Serbest, E.: Non-Abelian local reciprocity law. Manuscripta Math. 132, 19–49 (2010)
Ikeda, K.I., Serbest, E.: Ramification theory in non-Abelian local class field theory. Acta Arith. 144, 373–393 (2010)
Iwasawa, K.: On solvable extensions of algebraic number fields. Ann. Math. 58, 548–572 (1953)
Koch, H.: Local class field theory for metabelian extensions. In: Behara M., Fritsch R., Lintz R.G. (eds.) Symposia Gaussiana, Conference A: Mathematics and Theoretical Physics, pp. 287–300. de Gruyter, Berlin/New York (1995)
Laubie, F.: Une théorie non abélienne du corps de classes local. Composit. Math. 143, 339–362 (2007)
Manin Yu.I., Panchishkin, A.A.: Introduction to Modern Number Theory: Fundamental Problems, Ideas and Theories. Encyclopedia of Mathematical Sciences, vol. 49, 2nd edn. Springer, Berlin/Heidelberg (2005)
Miyake, K.: The arithmetic structure of the Galois group of the maximal nilpotent extension of an algebraic number field. Proc. Jpn. Acad. Ser. A 67, 55–59 (1991)
Miyake, K.: Galois theoretic local-global relations in nilpotent extensions of algebraic number fields. In: David, S. (ed.) Séminaire de Théorie des Nombres, Paris 1989–90. Progress in Mathematics vol. 102, pp. 191–207. Birkhäuser, Boston (1992)
Morris, S.A.: Free products of topological groups. Bull. Aust. Math. Soc. 4, 17–29 (1971)
Neukirch, J.: Algebraic Number Theory. Grundlehren Math. Wiss., vol. 322. Springer, Berlin/Heidelberg (1999)
Tate, J.: Number theoretic background. In: Borel, A., Casselman W. (eds.) Automorphic Forms, Representations, and L-Functions. Proceedings of the Symposium in Pure Mathematics, vol. 33, Part 2, pp. 3–26. American Mathematical Society, Providence (1979)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Additional information
Dedicated to my teacher Goro Shimura.
Rights and permissions
Copyright information
© 2015 Springer Basel
About this paper
Cite this paper
İkeda, K.İ. (2015). Basic Properties of the Non-Abelian Global Reciprocity Map. In: Cartier, P., Choudary, A., Waldschmidt, M. (eds) Mathematics in the 21st Century. Springer Proceedings in Mathematics & Statistics, vol 98. Springer, Basel. https://doi.org/10.1007/978-3-0348-0859-0_5
Download citation
DOI: https://doi.org/10.1007/978-3-0348-0859-0_5
Published:
Publisher Name: Springer, Basel
Print ISBN: 978-3-0348-0858-3
Online ISBN: 978-3-0348-0859-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


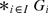 is the free product of this collection together with the canonical embeddings
is the free product of this collection together with the canonical embeddings 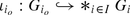 , for each i
o
∈ I, then the universal mapping property of free products states that, if for each i
o
∈ I,
, for each i
o
∈ I, then the universal mapping property of free products states that, if for each i
o
∈ I, 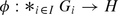 , such that
, such that