Abstract
A k-Counter Net (k-CN) is a finite-state automaton equipped with k integer counters that are not allowed to become negative, but do not have explicit zero tests. This language-recognition model can be thought of as labelled vector addition systems with states, some of which are accepting. Certain decision problems for k-CNs become easier, or indeed decidable, when the dimension k is small. Yet, little is known about the effect that the dimension k has on the class of languages recognised by k-CNs. Specifically, it would be useful if we could simplify algorithmic reasoning by reducing the dimension of a given CN.
To this end, we introduce the notion of dimension-primality for k-CN, whereby a k-CN is prime if it recognises a language that cannot be decomposed into a finite intersection of languages recognised by d-CNs, for some \(d<k\). We show that primality is undecidable. We also study two related notions: dimension-minimality (where we seek a single language-equivalent d-CN of lower dimension) and language regularity. Additionally, we explore the trade-offs in expressiveness between dimension and non-determinism for CN.
S. Almagor was supported by the ISRAEL SCIENCE FOUNDATION (grant No. 989/22), G. Avni was supported by the ISRAEL SCIENCE FOUNDATION (grant No. 1679/21), H. Sinclair-Banks was supported by EPSRC Standard Research Studentship (DTP), grant number EP/T5179X/1.
The full version can be found on https://arxiv.org/abs/2307.14492
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
A k-dimensional Counter Net (k-CN) is a finite-state automaton equipped with k integer counters that are not allowed to become negative, but do not have explicit zero tests (see Fig. 1a for an example). This language-recognition model can be thought of as an alphabet-labelled Vector Addition System with States (VASS), some of whose states are accepting [7]. A k-CN \(\mathcal {A}\) over alphabet \(\varSigma \) accepts a word \(w\in \varSigma ^*\) if there is a run of \(\mathcal {A}\) on w that ends in an accepting state in which the counters stay non-negative. The language of \(\mathcal {A}\) is the set \(\mathcal {L}(\mathcal {A})\) of words accepted by \(\mathcal {A}\).
Counter nets are a natural model of concurrency and are closely related — and equivalent, in some senses — to labelled Petri Nets. These models have received significant attention over the years [6, 7, 13, 14, 17, 19, 27], with specific interest in the one-dimensional case, often referred to as one-counter nets [1, 2, 20, 21]. Unfortunately, most decision problems for k-CNs are notoriously difficult and are often undecidable [1, 2]. In particular, k-CNs subsume VASS and Petri nets, for which many problems are known to be Ackermann-complete, for example see the recent breakthrough in the complexity of reachability in VASS [11, 25].
In many cases, the complexity of decision problems for VASS, sometimes with extensions, depends on the dimension, with low dimensions admitting more tractable solutions. [8,9,10, 16]. For example, reachability in dimensions one and two is NP-complete [18] and PSPACE-complete [4], respectively, when counter updates are encoded in binary.
A natural question, therefore, is whether we can decrease the dimension of a given a k-CN whilst maintaining its language, to facilitate reasoning about it. More generally, the trade-off between expressiveness and the dimension of Counter Nets is poorly understood. We tackle this question in this work by introducing two approaches. The first is straightforward dimension-minimality: given a k-CN, does there exist a d-CN \(\mathcal {B}\) recognising the same language for some \(d<k\)?
The second approach is primality: given a k-CN, does there exist some \(d<k\) and d-CNs \(\mathcal {B}_1, \ldots , \mathcal {B}_n\) such that \(L(\mathcal {A})=\bigcap _{i=1}^n \mathcal {L}(\mathcal {B}_i)\)? That is, we ask whether the language of \(\mathcal {A}\) can be decomposed as an intersection of languages recognised by several lower-dimension CNs. We also consider compositeness, the dual of primality. Intuitively, in a composite k-CN the usage of the counters can be “split” across several lower-dimension CNs, allowing for properties (such as universality) to be checked on each conjunct separately.
Example 1
We illustrate the model and the definition of compositeness. Consider the 2-CN \(\mathcal {A}\) depicted in Fig. 1a, and consider a word \(w = a^m \# b^n \# c^k\). We have that \(\mathcal {A}\) has an accepting run on w iff \(m \ge n\) and \(m \ge k\). Indeed, if \(m < n\), the first counter drops below 0 while cycling in the second state and so the run is “stuck”, and similarly if \(m<k\). It is not hard to show that there is no 1-CN that recognizes the language of \(\mathcal {A}\). However, Fig. 1b shows two 1-CNs \(\mathcal {B}_1\) and \(\mathcal {B}_2\) such that \(\mathcal {L}(\mathcal {B}) = \mathcal {L}(\mathcal {B}_1) \cap \mathcal {L}(\mathcal {B}_2)\). Indeed, a word \(w = a^m \# b^n \# c^k \in \mathcal {L}(\mathcal {B}_1)\) iff \(m \ge n\), and \(w \in \mathcal {L}(\mathcal {B}_2)\) iff \(m \ge k\).
Note that the decomposition in Example 1 is obtained by “splitting” the counters between the two 1-CNs. This raises the question of whether such splittings are always possible. As we show in Proposition 1, for deterministic k-CNs (k-DCNs) this is indeed the case. In general, however, it is not hard to find examples where a k-CN cannot simply be split to an intersection by projecting on each counter. This however, does not rule out that other decompositions are possible. Our main result, Theorem 1, gives an example of a prime 2-CN. That is, a 2-CN whose language cannot be expressed as an intersection of 1-CNs.
The notion of primality has been studied for regular languages in [22,23,24], the exact complexity of deciding primality is still open. There, an automaton is composite if it can be written as an intersection of finite automata with fewer states. In this work we introduce primality for CNs. We focus on dimension as a measure of size, a notion which does not exist for regular languages. Thus, unlike regular languages, the differences between prime and composite CNs is not only in succinctness, but actually in expressiveness, as we later demonstrate.
We parameterise primality and compositeness by the dimension d and the number n of lower-dimension factors. Thus, a k-CN \(\mathcal {A}\) is (d, n)-composite if it can be written as the intersection above. Then, \(\mathcal {A}\) is composite if it is (d, n)-composite for some \(d<k\) and \(n\in \mathbb {N}\). Under this view, dimension-minimality is a special case of compositeness, namely \(\mathcal {A}\) is dimension-minimal if it is not \((k-1,1)\)-composite. Another particular problem captured by compositeness is regularity. Indeed, \(\mathcal {L}(\mathcal {A})\) is regular if and only if \(\mathcal {A}\) is (0, 1)-composite, since 0-CNs are just NFAs. Since regularity is already undecidable for 1-CNs [2, 28], it follows that deciding whether a k-CN is (d, n)-composite is undecidable. Moreover, it follows that both primality and dimension-minimality are undecidable for 1-CNs.
The undecidability of the above problems is not surprising, as the huge difference in expressive power between 1-CNs and regular languages is well understood. In contrast, even the expressive power difference between 1-CNs and 2-CNs is poorly understood, let alone what effect the dimension has on the expressive power beyond regular languages. Already, 1-VASS and 2-VASS are known to have flat equivalents with respect to reachability [4, 26], but the complexity differs greatly.
Our goal in this work is to shed light on these differences. In Section 4, we give a concrete example of a prime 2-CN, which turns out to be technically challenging. This example is the heart of our technical contribution, and we emphasise that we do not currently have a proved example of a prime 3-CN, let alone for general k-CN (although we conjecture a candidate for such languages). We consider this an interesting open problem, as it highlights the type of pumping machinery that is currently missing from the VASS/CN reasoning arsenal. The technical intricacy in proving our example suggests that generalising it is highly nontrivial. Indeed, proving this claim would require intricate pumping arguments, which are notoriously difficult even for low-dimensional CNs [9].
Using our example, we obtain in Section 5, the undecidability of primality and of dimension-minimality for 2-CNs. To complement this, we show in Theorem 3, that regularity of k-DCNs is decidable. In Section 6, we explore trade-offs in expressiveness of CNs with increasing dimension and with nondeterminism. In particular, we show that there is a strict hierarchy of expressiveness with respect to the dimension. We conclude with a discussion in Section 7. For brevity, some proofs only appear in the full version of the paper.
2 Preliminaries
We denote the non-negative integers \(\{0,1,\ldots \}\) by \(\mathbb {N}\). We write vectors in bold, e.g., \(\boldsymbol{e}\in \mathbb {Z}^k\), and \(\boldsymbol{e}[i]\) is the i-th coordinate. We use \([k]=\{1,\ldots ,k\}\) for \(k\ge 1\). We use \(\varSigma ^*\) to denote the set of all words over an alphabet \(\varSigma \), and |w| is the length of \(w\in \varSigma ^*\).
A k-dimensional Counter Net (k-CN) \(\mathcal {A}\) is a quintuple \(\mathcal {A}=\langle \varSigma , Q, Q_0, \delta , F \rangle \) where \(\varSigma \) is a finite alphabet, Q is a finite set of states, \(Q_0 \subseteq Q\) is the set of initial states, \(\delta \subseteq Q \times \varSigma \times \mathbb {Z}^k \times Q\) is a set of transitions, and \(F \subseteq Q\) are the accepting states. A k-CN is deterministic, denoted k-DCN, if \(|Q_0| = 1\), and for every \(p \in Q\) and \(\sigma \in \varSigma \) there is at most one transition of the form \((p, \sigma , \boldsymbol{v}, q) \in \delta \). For a transition \((p, \sigma , \boldsymbol{v}, q)\in \delta \), we refer to \(\boldsymbol{v} \in \mathbb {Z}^k\) as its effect.
An \(\mathbb {N}\)-configuration (resp. \(\mathbb {Z}\)-configuration) of a k-CN \(\mathcal {A}\) is a pair \((q,\boldsymbol{v})\in Q\times \mathbb {N}^k\) (resp. \((q,\boldsymbol{v})\in Q\times \mathbb {Z}^k\)) representing the current state and values of the counters. A transition \((p, \sigma , \boldsymbol{e}, q) \in \delta \) is valid from \(\mathbb {N}\)-configuration \((q, \boldsymbol{v})\) if \(\boldsymbol{v} + \boldsymbol{e} \in \mathbb {N}^k\), i.e., if all k counters remain non-negative after the transition. A \(\mathbb {Z}\)-run \(\rho \) of \(\mathcal {A}\) on w is a sequence of \(\mathbb {Z}\)-configurations \(\rho =(q_0, \boldsymbol{v}_0), (q_1, \boldsymbol{v}_1), \ldots , (q_n, \boldsymbol{v}_n)\) such that \((q_i, \sigma _i, \boldsymbol{v}_{i+1} - \boldsymbol{v}_i, q_{i+1}) \in \delta \) for every \(0 \le i \le n-1\), we may also say that \(\rho \) reads \(w = \sigma _0 \sigma _1 \cdots \sigma _n\). An \(\mathbb {N}\)-run is a \(\mathbb {Z}\)-run that visits only \(\mathbb {N}\)-configurations. Note that all the transitions in an \(\mathbb {N}\)-run are valid. We may omit \(\mathbb {N}\) or \(\mathbb {Z}\) from the run when it does not matter. For a run \(\rho = (q_0, \boldsymbol{v}_0), (q_1, \boldsymbol{v}_1), \ldots , (q_n, \boldsymbol{v}_n)\) of \(\mathcal {A}\), we denote \((q_0,\boldsymbol{v}_0){\mathop {\rightarrow }\limits ^{\rho }}(q_n, \boldsymbol{v}_n)\). We define the effect of \(\rho \) to be \(\textsf {eff}(\rho )=\boldsymbol{v}_n - \boldsymbol{v}_0\).
An \(\mathbb {N}\)-run \(\rho \) is accepting if \(q_0 \in Q_0\), \(\boldsymbol{v}_0 = \boldsymbol{0}\), and \(q_n \in F\). We say that \(\mathcal {A}\) accepts w if there is an accepting \(\mathbb {N}\)-run of \(\mathcal {A}\) on w. The language of \(\mathcal {A}\) is \(\mathcal {L}(\mathcal {A})=\{w\in \varSigma ^* \mid \mathcal {A}\text { accepts } w\}\). We say that \(\mathcal {A}\) is \(unambiguous \) if it has at most one accepting run on any given word. Otherwise we say that it is ambiguous.
An infix \(\pi = (q_k, \boldsymbol{v}_k), (q_{k+1}, \boldsymbol{v}_{k+1}), \ldots , (q_{k+n}, \boldsymbol{v}_{k+n})\) of a run \(\rho \) is a cycle if \(q_k = q_{k+n}\) and is a simple cycle if it does not contain a cycle as a proper infix. When discussing an infix \(\pi \) of a 1-CN – we write that \(\pi \) is  ,
,  , or
, or  if \(\textsf {eff}(\pi ) > 0\), \(\textsf {eff}(\pi ) \ge 0\), or \(\textsf {eff}(\pi ) < 0\), respectively.
if \(\textsf {eff}(\pi ) > 0\), \(\textsf {eff}(\pi ) \ge 0\), or \(\textsf {eff}(\pi ) < 0\), respectively.
3 Primality and Compositeness
We begin by presenting our main definitions, followed by some introductory properties.
Definition 1 (Compositeness, Primality, and Dimension-Minimality)
[Compositeness, Primality, and Dimension-Minimality] Consider a k-CN \(\mathcal {A}\), and let \(d,n\in \mathbb {N}\). We say that \(\mathcal {A}\) is (d, n)-composite if there exist d-CNs \(\mathcal {B}_1,\ldots ,\mathcal {B}_n\) such that \(\mathcal {L}(\mathcal {A})=\bigcap _{i=1}^n\mathcal {L}(\mathcal {B}_i)\). If \(\mathcal {A}\) is (d, n)-composite for some \(d<k\) and \(n\in \mathbb {N}\), we say \(\mathcal {A}\) is composite. Otherwise, \(\mathcal {A}\) is prime. If \(\mathcal {A}\) is not \((k-1,1)\)-composite, we say that \(\mathcal {A}\) is dimension-minimal. We also extend the definition of primality to languages, and say that a language \(\mathcal {L}\) is prime if there is an integer \(d>0\) such that \(\mathcal {L}=\mathcal {L}(\mathcal {A})\) for some d-CN \(\mathcal {A}\), but there are no \((d-1)\)-CNs \(\mathcal {B}_1, \ldots \mathcal {B}_n\) such that \(\mathcal {L}=\bigcap _{i=1}^n\mathcal {L}(\mathcal {B}_i)\).
Remark 1
Note that the special case where \(\mathcal {A}\) is (0, n)-composite coincides with the regularity of \(\mathcal {L}(\mathcal {A})\), and hence also with being (0, 1)-composite.
Observe that in Fig. 1 we in fact show a composite 2-DCN. We now show that every k-DCN is (1, k)-composite, by projecting to each of the counters separately. In particular, a k-DCN is prime only when \(k=1\) and it recognises a non-regular language, or when \(k=0\). Formally, consider a k-DCN \(\mathcal {D}=\langle \varSigma ,Q,Q_0,\delta ,F \rangle \) and let \(1\le i\le k\). We define the i-projection to be the 1-DCN \(\mathcal {D}|_i=\langle \varSigma ,Q,Q_0,\delta |_i,F \rangle \) where \(\delta |_i = \{ (p, \sigma , \boldsymbol{v}[i], q) \mid (p, \sigma , \boldsymbol{v}, q) \in \delta \}\).
Proposition 1
Every k-DCN \(\mathcal {D}\) is (1, k)-composite, and \(\mathcal {L}(\mathcal {D})=\bigcap _{i=1}^k\mathcal {L}(\mathcal {D}|_i)\).
Proof
Let \(w\in \mathcal {L}(\mathcal {D})\) and let \(\rho \) be the accepting run of \(\mathcal {D}\) on w, then the projection of \(\rho \) on counter i induces an accepting run of \(\mathcal {D}|_i\) on w, thus \(w\in \bigcap _{i=1}^k\mathcal {L}(\mathcal {D}|_i)\). Note that this direction does not use the determinism of \(\mathcal {D}\).
Conversely, let \(w\in \bigcap _{i=1}^k\mathcal {L}(\mathcal {D}|_i)\), then each \(\mathcal {D}|_i\) has an accepting run \(\rho _i\) on w. Since the structure of all the \(\mathcal {D}|_i\) is identical to that of \(\mathcal {D}\), all the runs \(\rho _i\) have identical state sequences, and therefore are also a \(\mathbb {Z}\)-run of \(\mathcal {D}\) on w. Moreover, due to this being a single \(\mathbb {N}\)-run in each \(\mathcal {D}|_i\), it follows that all counter values remain non-negative in the corresponding run of \(\mathcal {D}\) on w. Hence, this is an accepting \(\mathbb {N}\)-run of \(\mathcal {D}\) on w, so \(w\in \mathcal {L}(\mathcal {D})\). \(\square \)
Remark 2 (Unambiguous Counter Nets are Composite)
[Unambiguous Counter Nets are Composite] The proof of Proposition 1 applies also to structurally unambiguous CNs, i.e. CNs whose underlying automaton, disregarding the counters, is unambiguous. Thus, every unambiguous CN is (1, k)-composite.
Consider k-CNs \(\mathcal {B}_1,\ldots ,\mathcal {B}_n\). By taking their product, we can construct a \(k\cdot n\)-CN \(\mathcal {A}\) such that \(\mathcal {L}(\mathcal {A}) = \bigcap _{i=1}^n \mathcal {L}(\mathcal {B}_i)\). In particular, if each \(\mathcal {B}_i\) is a 1-DCN, then \(\mathcal {A}\) is an n-DCN. Combining this with Proposition 1, we can deduce the following (proof can be found in the full version).
Proposition 2
A k-DCN is dimension-minimal if and only if it is not \((1,k-1)\)-composite.
4 A Prime Two-Counter Net
In this section we present our main technical contribution, namely an example of a prime 2-CN. The technical difficulty arises from the need to prove that this example cannot be decomposed as an intersection of nondeterministic 1-CNs. Since intersection has a “universal flavour”, and nondeterminism has an “existential flavour”, we have a sort of “quantifier alternation” which is often a source of difficulty.
The importance of this example is threefold. First, it enables us to show that primality is undecidable in Section 5. Second, it offers intuition on what makes a language prime. Third, we suspect that the techniques developed here will be useful in other settings when reasoning about nondeterministic automata, perhaps with counters.
We start by presenting the prime 2-CN, followed by an overview of the proof, before delving into the details.
Example 2
Consider the 2-CN \(\mathcal {P}\) over alphabet \(\varSigma =\{a,b,c,\#\}\) depicted in Fig. 2. Intuitively, \(\mathcal {P}\) starts by reading segments of the form \(a^m\#\), where in each segment it nondeterministically chooses whether to increase the first or second counter by m. Then, it reads \(b^{m_b}c^{m_c}\) and accepts if the value of the first and second counter is at least \(m_b\) and \(m_c\), respectively. Thus, \(\mathcal {P}\) accepts a word if its \(a^m\#\) segments can be partitioned into two sets I and \(\overline{I}\) so that the combined lengths of the segments in I (resp. \(\overline{I}\)) is at least the length of the b segment (resp. c segment). For example, \(a^{10}\#a^{20}\#a^{15}\#b^{15}c^{30}\in \mathcal {L}(\mathcal {P})\), since segments 1 and 2 have length 30, matching \(c^{30}\) and segment 3 matches \(b^{15}\). However, \(a^{10}\#a^{20}\#a^{15}\#b^{21}c^{21}\notin \mathcal {L}(\mathcal {P})\), since in any partition of \(\{10,20,15\}\), one set will have sum lower than 21. More precisely, we have the following:
Theorem 1
\(\mathcal {P}\) is prime.
The high-level intuition behind Theorem 1 is that any 1-CN can either guess a subset of segments that covers \(m_b\) or \(m_c\), but not both, and in order to make sure the choices between two 1-CNs form a partition, we need to fix the partition in advance. This is only possible if the number of segments is a priori fixed, which is not true (c.f., Remark 3). This intuition, however, is far from a proof.
4.1 Overview of the Proof of Theorem 1
Assume by way of contradiction that \(\mathcal {P}\) is not a prime 2-CN. Thus, there exist 1-CNs \(\mathcal {V}_1,\ldots \mathcal {V}_k\) such that \(\mathcal {L}(\mathcal {P})=\bigcap _{1 \le j \le k}\mathcal {L}(\mathcal {V}_j)\). Throughout the proof, we focus on words of the form \(a^{m_1} \# a^{m_2} \# \cdots \# a^{m_{k+1}} \# b^{m_b} c^{m_c}\) for positive integers \(\left\{ m_i \right\} _{i=1}^{k+1}, m_b, m_c\). We index the \(a^{m_i}\) segments of these words, so \(a^{m_i}\) is the i-th segment. Note that we focus on words with \(k+1\) many a segments, one more than the number of \(\mathcal {V}_j\) factors in the intersection. It is useful to think about each segment as “paying” for either b or c. Then, a word is accepted if there is a way to choose for each segment whether it pays for b or c, such that there is sufficient budget for both.
Let \(i\in [k+1]\) and \(j\in [k]\). We say that the i-th segment is bad in \(\mathcal {V}_j\) if, intuitively, we can pump the length \(m_i\) of segment i whilst pumping both \(m_b\) and \(m_c\) to unbounded lengths, such that the resulting words are accepted by \(\mathcal {V}_j\) (see Definition 2 for the formal definition). For example, consider the word \(a^{10} \# a^{10} \# a^{10} \# b^{20} c^{10} \in \mathcal {L}(\mathcal {P})\). If the second segment is bad for \(\mathcal {V}_j\) then there exist \(x, y, z > 0\) such that for every \(t, t_b, t_c \in \mathbb {N}\) it holds that the word \(a^{10} \# a^{10+tx} \# a^{10} \# b^{20+t_b y} c^{10+t_c z}\) is in \(\mathcal {L}(\mathcal {V}_j)\). Observe that such behaviour is undesirable, since for large enough \(t, t_b, t_c\), the resulting word is not in \(\mathcal {L}(\mathcal {P})\). Note, however, that the existence of such a bad segment is not a contradiction by itself, since the resulting pumped words might not be accepted by some other 1-CN \(\mathcal {V}_{j'}\).
In order to reach a contradiction, we need to show the existence of a segment i that is bad for every \(\mathcal {V}_j\). Moreover, we must also show that arbitrarily increasing \(m_i, m_b, m_c\) can be simultaneously achieved in all the \(\mathcal {V}_j\) together (i.e., the above \(x, y, z > 0\) are the same for all \(V_j\)). This would create a contradiction since all the \(\mathcal {V}_j\) accept a word that is not in \(\mathcal {L}(\mathcal {P})\). Our goal is therefore to establish a robust and precise definition of a “bad” segment, then find a word w comprising \(k+1\) segments where one of the segments is bad for every \(\mathcal {V}_j\), and pumping the words in each segment can be done synchronously.
4.2 Pumping Arguments in One-Counter Nets
In this section we establish some pumping results for 1-CN which will be used in the proof of Theorem 1. Throughout this section, we consider a 1-CN \(\mathcal {V}=\langle \varSigma ,Q,Q_0,\delta ,F \rangle \).
Our first lemma states the intuitive fact that without  cycles, the counter value of a run is bounded (proof can be found in the full version).
cycles, the counter value of a run is bounded (proof can be found in the full version).
Lemma 1
Let (q, n) be a configuration of \(\mathcal {V}\), let W be the maximal positive update in \(\mathcal {V}\), \(\sigma \in \varSigma \), and \(N\in \mathbb {N}\). If an \(\mathbb {N}\)-run \(\rho \) of \(\mathcal {V}\) on \(\sigma ^N\) from configuration (q, n) does not traverse any  cycle, then the maximal possible counter value anywhere along \(\rho \) is \(n+W|Q|\).
cycle, then the maximal possible counter value anywhere along \(\rho \) is \(n+W|Q|\).
The next lemma shows that long-enough runs must contain  cycles.
cycles.
Lemma 2
Let \(\sigma \in \varSigma \) and (q, n) be an \(\mathbb {N}\)-configuration of \(\mathcal {V}\). Then there exists \(N\in \mathbb {N}\) such that for all \(N' \ge N\), every \(\mathbb {N}\)-run of \(\mathcal {V}\) on \(\sigma ^{N'}\) from (q, n) traverses a  cycle.
cycle.
Proof
Let W be the maximal positive transition update in \(\mathcal {V}\), we show that \(N=|Q|(n+|Q| \cdot W)\) satisfies the requirements. Assume by way of contradiction that \(\mathcal {V}\) can read \(\sigma ^{N}\) via an \(\mathbb {N}\)-run \(\rho =(q_0,n_0=n){\mathop {\rightarrow }\limits ^{\rho }} (q_N,n_N)\) that only traverses  cycles.
cycles.
Since \(\rho \) visits \(N+1\) states, then by the Pigeonhole Principle, there exists a state \(p \in Q\) that is visited \(m \ge (N+1)/|Q| > N/|Q|\) many times in \(\rho \).
Consider all the indices \(0 \le i_1 < i_2 < \ldots < i_m \le N\) such that \(p = q_{i_1} = \ldots = q_{i_m}\). Each run segment \((q_{i_1}, n_{i_1}) \rightarrow (q_{i_2}, n_{i_2}), \ldots , (q_{i_{m-1}}, n_{i_{m-1}}) \rightarrow (q_{i_m}, n_{i_m})\) is a cycle in \(\rho \), and therefore must have negative effect. Thus \(n_{i_1} > n_{i_2} > \ldots > n_{i_m} \ge 0\), so in particular \(n_{i_1} \ge n_{i_m} + m-1 \ge 0\) (as each cycle has effect at most \(-1\)). Moreover, \(n_{i_1} < n + |Q|\cdot W\) since the prefix \((q_0, n) \rightarrow (q_{i_1}, n_{i_1})\) cannot contain a non-negative cycle. However, since \(m >N/|Q| = n + |Q|\cdot W\) and \(n_{i_1} \ge n_{i_m} + m - 1 \ge n + |Q|\cdot W\), we get \(n+|Q|\cdot W<n+ |Q| \cdot W\) which is a contradiction.
\(\square \)
Next, we show that runs with  and
and  cycles have “pumpable” infixes.
cycles have “pumpable” infixes.
Lemma 3
Let \(\sigma \in \varSigma \) and consider a  (resp.
(resp.  ) cycle \(\pi =(q_0,c_0){\mathop {\rightarrow }\limits ^{\sigma }} (q_1,c_1) {\mathop {\rightarrow }\limits ^{\sigma }} \ldots (q_n=q_0,c_n)\) on \(\sigma ^n\) that induces an \(\mathbb {N}\)-run. Then, there is a sequence of (not necessarily contiguous) indices \(0 \le i_1 \le \ldots \le i_k \le n\) such that \(q_{i_1}{\mathop {\rightarrow }\limits ^{\sigma }} q_{i_2}{\mathop {\rightarrow }\limits ^{\sigma }}\cdots q_{i_k}\) is a simple
) cycle \(\pi =(q_0,c_0){\mathop {\rightarrow }\limits ^{\sigma }} (q_1,c_1) {\mathop {\rightarrow }\limits ^{\sigma }} \ldots (q_n=q_0,c_n)\) on \(\sigma ^n\) that induces an \(\mathbb {N}\)-run. Then, there is a sequence of (not necessarily contiguous) indices \(0 \le i_1 \le \ldots \le i_k \le n\) such that \(q_{i_1}{\mathop {\rightarrow }\limits ^{\sigma }} q_{i_2}{\mathop {\rightarrow }\limits ^{\sigma }}\cdots q_{i_k}\) is a simple  (resp.
(resp.  ) cycle with some effect \(e>0\) (resp. \(e \ge 0\)). In addition, this simple cycle is “pumpable” from the first occurrence of \(q_{i_1}\) in \(\pi \); namely, for all \(m \in \mathbb {N}\) there is a run \(\pi _m\) obtained from \(\pi \) by traversing the cycle m times so that \(\textsf {eff}(\pi _m)=\textsf {eff}(\pi )+em\).
) cycle with some effect \(e>0\) (resp. \(e \ge 0\)). In addition, this simple cycle is “pumpable” from the first occurrence of \(q_{i_1}\) in \(\pi \); namely, for all \(m \in \mathbb {N}\) there is a run \(\pi _m\) obtained from \(\pi \) by traversing the cycle m times so that \(\textsf {eff}(\pi _m)=\textsf {eff}(\pi )+em\).
Proof
We prove the  case, the
case, the  case can be proved mutatis mutandis.
case can be proved mutatis mutandis.
We define \(\pi _m=(q_0,c_0){\mathop {\rightarrow }\limits ^{\sigma }} \ldots (q_{i_1},c_{i_1}) {\mathop {\rightarrow }\limits ^{\sigma }} \ldots (q_{i_1},c_{i_1}+em){\mathop {\rightarrow }\limits ^{\sigma }} \ldots (q_n,c_n+em)\). The proof is now by induction on the length of \(\pi \).
The base of the induction is a cyclic \(\mathbb {N}\)-run of length 2. In this case \(\pi =(q_0,c_0) {\mathop {\rightarrow }\limits ^{\sigma }} (q_1=q_0, c_1)\) is itself a  simple cycle that is infinitely pumpable from \((q_0,c_0)\).
simple cycle that is infinitely pumpable from \((q_0,c_0)\).
We now assume correctness for length n, and discuss \(\pi =(q_0,c_0){\mathop {\rightarrow }\limits ^{\sigma }} (q_1,c_1) {\mathop {\rightarrow }\limits ^{\sigma }} \ldots (q_n=q_0,c_n)\) of length \(n+1\). Let \(0\le j_1<j_2\le n\) be indices such that \(q_{j_1}=q_{j_2}\), for a maximal \(j_1\). Note that the cycle \(\tau =(q_{j_1},c_{j_1}){\mathop {\rightarrow }\limits ^{\sigma }} \ldots (q_{j_2},c_{j_2})\) must be simple. If \(j_1=0\) and \(j_2=n\), then \(\pi \) itself is a simple  cycle, and the pumping argument is straightforward. Otherwise \(\tau \) is nested. We now split into two cases, based on whether \(\textsf {eff}(\tau ) \ge 0\).
cycle, and the pumping argument is straightforward. Otherwise \(\tau \) is nested. We now split into two cases, based on whether \(\textsf {eff}(\tau ) \ge 0\).
-
1.
\(\tau \) is
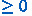 : then the induction hypothesis applies on \(\tau \). We take the guaranteed constants \(j_1 \le i_1 \le \ldots \le i_k \le j_2\), which apply to \(\pi \) as well.
: then the induction hypothesis applies on \(\tau \). We take the guaranteed constants \(j_1 \le i_1 \le \ldots \le i_k \le j_2\), which apply to \(\pi \) as well. -
2.
\(\tau \) is
 : then we remove \(\tau \) from \(\pi \) to obtain \(\pi '=(q_0,c_0){\mathop {\rightarrow }\limits ^{\sigma }} \ldots (q_{j_1},c_{j_1}) {\mathop {\rightarrow }\limits ^{\sigma }} (q_{j_2+1},c'_{j_2+1}) {\mathop {\rightarrow }\limits ^{\sigma }} \ldots (q_n,c'_n)\), such that \(c'_i \ge c_i\) for all \(j_2+1 \le i \le n\). The induction hypothesis applies on \(\pi '\), so let \(i_1, \ldots , i_k\) be the guaranteed constants. Note that \(i_1 \le j_1\), since the cycle removed when obtaining \(\pi '\) from \(\pi \) is the last occurrence of a repetition of states in \(\pi \). We therefore know that \(q_{i_1}{\mathop {\rightarrow }\limits ^{\sigma }} q_{i_2}{\mathop {\rightarrow }\limits ^{\sigma }}\cdots q_{i_k}\) is a simple
: then we remove \(\tau \) from \(\pi \) to obtain \(\pi '=(q_0,c_0){\mathop {\rightarrow }\limits ^{\sigma }} \ldots (q_{j_1},c_{j_1}) {\mathop {\rightarrow }\limits ^{\sigma }} (q_{j_2+1},c'_{j_2+1}) {\mathop {\rightarrow }\limits ^{\sigma }} \ldots (q_n,c'_n)\), such that \(c'_i \ge c_i\) for all \(j_2+1 \le i \le n\). The induction hypothesis applies on \(\pi '\), so let \(i_1, \ldots , i_k\) be the guaranteed constants. Note that \(i_1 \le j_1\), since the cycle removed when obtaining \(\pi '\) from \(\pi \) is the last occurrence of a repetition of states in \(\pi \). We therefore know that \(q_{i_1}{\mathop {\rightarrow }\limits ^{\sigma }} q_{i_2}{\mathop {\rightarrow }\limits ^{\sigma }}\cdots q_{i_k}\) is a simple  cycle in \(\pi '\) – which applies to \(\pi \) as well. In addition, it is infinitely pumpable from \(\mathbb {N}\)-configuration \((q_{i_1},c_{i_1})\) in \(\pi '\) for \(i_1 \le j_1\). Indeed, since \(\pi \) and \(\pi '\) coincide up to and including \((q_{j_1},c_{j_1})\) between \(\pi \) and \(\pi '\) - this cycle is infinitely pumpable in \(\pi \) as well. \(\square \)
cycle in \(\pi '\) – which applies to \(\pi \) as well. In addition, it is infinitely pumpable from \(\mathbb {N}\)-configuration \((q_{i_1},c_{i_1})\) in \(\pi '\) for \(i_1 \le j_1\). Indeed, since \(\pi \) and \(\pi '\) coincide up to and including \((q_{j_1},c_{j_1})\) between \(\pi \) and \(\pi '\) - this cycle is infinitely pumpable in \(\pi \) as well. \(\square \)
The simple cycle in Lemma 3 has length \(k<|Q|\). By pumping it \(\frac{|Q|!}{k}\) times we obtain a pumpable cycle of length |Q|!, allowing us to conclude with the following.
Corollary 1
Let \(\rho \) be an \(\mathbb {N}\)-run of \(\mathcal {V}\) on \(\sigma ^n\) that traverses a  cycle. For every \(m\in \mathbb {N}\), we can construct an \(\mathbb {N}\)-run \(\rho '\) of \(\mathcal {V}\) on \(\sigma ^{n+m|Q|!}\) such that \(\textsf {eff}(\rho ') \ge \textsf {eff}(\rho )\) by pumping a
cycle. For every \(m\in \mathbb {N}\), we can construct an \(\mathbb {N}\)-run \(\rho '\) of \(\mathcal {V}\) on \(\sigma ^{n+m|Q|!}\) such that \(\textsf {eff}(\rho ') \ge \textsf {eff}(\rho )\) by pumping a  simple cycle in \(\rho \).
simple cycle in \(\rho \).
4.3 Good and Bad Segments
We lift the colour schemeFootnote 1 of  and
and  to words and runs as follows. For a word \(w=uv\) and a run \(\rho \), we write e.g.,
to words and runs as follows. For a word \(w=uv\) and a run \(\rho \), we write e.g.,  to denote that \(\rho \) traverses a
to denote that \(\rho \) traverses a  cycle when reading u, then a
cycle when reading u, then a  cycle when reading v. Note that this does not preclude other cycles, e.g., there could also be negative cycles in the u part, etc. That is, the colouring is not unique, but represents elements of the run.
cycle when reading v. Note that this does not preclude other cycles, e.g., there could also be negative cycles in the u part, etc. That is, the colouring is not unique, but represents elements of the run.
Recall our assumption that \(\mathcal {L}(\mathcal {P}) = \bigcap _{1 \le j \le k}\mathcal {L}(\mathcal {V}_j)\), and for all \(j \in [k]\) denote \(\mathcal {V}_j = \langle \varSigma , Q_j, I_j, \delta _j, F_j \rangle \). Let \(Q_{\max } = \max \{|Q_j|\}_{j=1}^k\) and denote \(\alpha =Q_{\max }!\). Further recall that we focus on words of the form \(a^{m_1} \# a^{m_2} \# \cdots \# a^{m_{k+1}} \# b^{m_b} c^{m_c}\) for integers \(\left\{ m_i \right\} _{i=1}^{k+1}, m_b, m_c \in \mathbb {N}\), and that we refer to the infix \(a^{m_i}\) as the i-th segment, for \(1 \le i \le k+1\). We proceed to formally define good and bad segments.
Definition 2 (Good and Bad Segments)
[Good and Bad Segments] The i-th segment is bad in \(\mathcal {V}_j\) if there exist constants \(\left\{ m_i\right\} _{i=1}^{k+1},m_b,m_c \in \mathbb {N}\) such that the following hold.
-
(a)
\(\left\{ m_i \right\} _{i=1}^{k+1}, m_b,m_c\) are multiples of \(\alpha \), and
-
(b)
there is an accepting \(\mathbb {N}\)-run \(\rho \) of \(\mathcal {V}_j\) on \(w = a^{m_1} \# a^{m_2} \# \cdots \# a^{m_{k+1}} \# b^{m_b} c^{m_c}\) that adheres to one of the three forms:
-
(i)
 ,
, -
(ii)
 , or
, or -
(iii)
 .
.
-
(i)
The i-th segment is good in \(\mathcal {V}_j\) if it is not bad in \(\mathcal {V}_j\).
Lemma 4 formalises the intuition that a bad segment can be pumped simultaneously with both the b and c segments, giving rise to a word accepted by \(\mathcal {V}_j\) but rejected by \(\mathcal {P}\).
Intuitively, Forms (ii) and (iii) indicate that all segments are bad. Indeed, the i-th segment has a  cycle, so it can be pumped safely, and in Form (ii) both b and c can be pumped using
cycle, so it can be pumped safely, and in Form (ii) both b and c can be pumped using  cycles. Whereas in Form (iii) we can pump b using a
cycles. Whereas in Form (iii) we can pump b using a  cycle, and can use it to compensate for pumping c, even if the latter requires iterating a negative cycle.
cycle, and can use it to compensate for pumping c, even if the latter requires iterating a negative cycle.
Form (i) is the interesting case, where we use a  cycle in the i-th segment to compensate for pumping both b and c. The requirement that all segments up to the i-th are
cycle in the i-th segment to compensate for pumping both b and c. The requirement that all segments up to the i-th are  is at the core of our proof and is explained in Section 4.4.
is at the core of our proof and is explained in Section 4.4.
Lemma 4
Suppose the l-th segment is bad in \(\mathcal {V}_j\), then there exist \(x, y, z \in \mathbb {N}\), that are multiples of \(\alpha \), such that for every \(n \in \mathbb {N}\) the following word w is accepted by \(\mathcal {V}_j\).
Proof
We can choose \(z=\alpha \), then take y to be large enough so that Form (iii) runs can compensate for negative cycles in \(c^z\) using  cycles in \(b^y\), whilst not decreasing the counters in Form (ii) runs. We can indeed find such a \(y \in \mathbb {N}\) that is a multiple of \(\alpha \), since \(\alpha \) is divisible by all lengths of simple cycles. Finally, we choose x so that Form (i) runs can compensate for \(c^z\) and \(b^y\) using
cycles in \(b^y\), whilst not decreasing the counters in Form (ii) runs. We can indeed find such a \(y \in \mathbb {N}\) that is a multiple of \(\alpha \), since \(\alpha \) is divisible by all lengths of simple cycles. Finally, we choose x so that Form (i) runs can compensate for \(c^z\) and \(b^y\) using  cycles on \(a^x\) in the l-th segment, again whilst not decreasing the counters in Forms (ii) and (iii). \(\square \)
cycles on \(a^x\) in the l-th segment, again whilst not decreasing the counters in Forms (ii) and (iii). \(\square \)
Recall that our goal is to show that there is a segment \(l \in [k+1]\) that is bad in every \(V_j\), for \(j \in [k]\). In Lemma 5, We show that each \(V_j\) has at most one good segment. Therefore, there are at most k good segments in total, leaving at least one segment that is bad in every \(\mathcal {V}_j\), as desired.
Lemma 5
Let \(j \in [k]\) and \(0 \le r < s \le k+1\). Then the r-th or s-th segment is bad in \(\mathcal {V}_j\).
Proof
Since j is fixed, denote \(\mathcal {V}_j=\langle \varSigma ,Q,Q_0,\delta ,F \rangle \). We inductively define constants \(\left\{ n_i\right\} _{i=1}^{k+1},n_b,n_c \in \mathbb {N}\) as follows. Suppose that \(n_1\) is a large-enough multiple of \(\alpha \) so that Lemma 2 guarantees a  cycle in any accepting run of \(\mathcal {V}_j\) on \(a^{n_1}\) from some \((q_0,0)\) with \(q_0\in Q_0\). Now, assume that we have defined \(n_1, \ldots n_{l-1}\), and consider the word \(u = a^{n_1} \# a^{n_2} \# \cdots \# a^{n_{l-1}} \#\). Define \(n=|u| \cdot W\) where W is the maximal update of any transition of \(\mathcal {V}_j\). Since u consists of \(\frac{n}{W}\) letters, \(n+1\) is greater than any counter value that can be observed in any run of \(\mathcal {V}_j\) on u. We define \(n_l\) to be a multiple of \(\alpha \) large enough so that Lemma 2 guarantees a
cycle in any accepting run of \(\mathcal {V}_j\) on \(a^{n_1}\) from some \((q_0,0)\) with \(q_0\in Q_0\). Now, assume that we have defined \(n_1, \ldots n_{l-1}\), and consider the word \(u = a^{n_1} \# a^{n_2} \# \cdots \# a^{n_{l-1}} \#\). Define \(n=|u| \cdot W\) where W is the maximal update of any transition of \(\mathcal {V}_j\). Since u consists of \(\frac{n}{W}\) letters, \(n+1\) is greater than any counter value that can be observed in any run of \(\mathcal {V}_j\) on u. We define \(n_l\) to be a multiple of \(\alpha \) large enough so that Lemma 2 guarantees a  cycle when reading \(a^{n_l}\) from any configuration of the form \(\{(q,n') \mid q \in Q,\ n' \le n+1\}\). We set \(n_b=n_c=\alpha \), the choice of \(n_b,n_c\) is somewhat arbitrary. Finally, we set \(w = a^{n_1} \# \cdots \# a^{n_{k+1}} \# b^{n_b} c^{n_c}\).
cycle when reading \(a^{n_l}\) from any configuration of the form \(\{(q,n') \mid q \in Q,\ n' \le n+1\}\). We set \(n_b=n_c=\alpha \), the choice of \(n_b,n_c\) is somewhat arbitrary. Finally, we set \(w = a^{n_1} \# \cdots \# a^{n_{k+1}} \# b^{n_b} c^{n_c}\).
Now, for every \(x\in \mathbb {N}\), we obtain from w a word \(w_x\) by pumping \(x\alpha \) many a’s in the r-th and s-th segments and pumping \(x\alpha \) many b’s and c’s in their segments. That is, let \(n'_i = n_i + x\alpha \) for \(i \in \{r, s\}\) and \(n'_i=n_i\) for \(i\notin \{r,s\}\), and let \(n'_b=n_b+x \alpha \) and \(n'_c=n_c+x \alpha \), then \(w_x = a^{n'_1} \# \cdots \# a^{n'_{k+1}} \# b^{n'_b} c^{n'_c}\). Observe that \(w_x\in \mathcal {L}(\mathcal {P})\). Indeed, since \(n_{r} \ge n_b = \alpha \) and \(n_{s} \ge n_c=\alpha \) we have that \(n_{r}+x\alpha \ge n_b+x\alpha \) and \(n_{s}+x\alpha \ge n_c+x\alpha \), so the r-th and s-th segments can already pay for the b’s and c’s, respectively. In particular, \(w_x\in \mathcal {L}(\mathcal {V}_j)\) via some accepting \(\mathbb {N}\)-run \(\rho _x\).
We choose a particular value of x, as follows. Consider x and suppose some accepting \(\mathbb {N}\)-run \(\rho _x\) as above does not traverse a  cycle neither in r-th nor s-th segment. By Lemma 1, the maximal possible counter value of \(\rho _x\) after reading
cycle neither in r-th nor s-th segment. By Lemma 1, the maximal possible counter value of \(\rho _x\) after reading
is \(M_b = (k+1+\sum _{z \in [k+1]\setminus \{r,s\}}n_z) \cdot W + 2|Q| \cdot W\). Crucially, this value does not depend on x. Further, if there is no  cycle in the segment of b’s as well, again the maximal counter value of \(\rho \) up to the c segment is bounded by \(M_c = (k+2 + \sum _{z\in [k+1]\setminus \{r,s\}}n_z) \cdot W + 3|Q| \cdot W\), that is independent of x and \(M_b\). By Lemma 2, we can now choose x large enough to satisfy that for every accepting \(\mathbb {N}\)-run \(\rho _x\) on \(w_x\):
cycle in the segment of b’s as well, again the maximal counter value of \(\rho \) up to the c segment is bounded by \(M_c = (k+2 + \sum _{z\in [k+1]\setminus \{r,s\}}n_z) \cdot W + 3|Q| \cdot W\), that is independent of x and \(M_b\). By Lemma 2, we can now choose x large enough to satisfy that for every accepting \(\mathbb {N}\)-run \(\rho _x\) on \(w_x\):
-
1.
If \(\rho _x\) does not traverse any
 cycle in the r-th or s-th segments, then \(\rho _x\) has a
cycle in the r-th or s-th segments, then \(\rho _x\) has a  cycle reading \(b^{(n_b+x\alpha )}\) from any configuration in \(\{ (q,M') \mid q\in Q,\ M' \le M_b \}\).
cycle reading \(b^{(n_b+x\alpha )}\) from any configuration in \(\{ (q,M') \mid q\in Q,\ M' \le M_b \}\). -
2.
If \(\rho _x\) does not traverse any
 cycle in the r-th or s-th segment, nor in the b segment, then \(\rho _x\) has a
cycle in the r-th or s-th segment, nor in the b segment, then \(\rho _x\) has a  cycle reading \(c^{(n_c+x\alpha )}\) from any configuration in \(\{ (q,M') | q\in Q,\ M'\le M_c \}\).
cycle reading \(c^{(n_c+x\alpha )}\) from any configuration in \(\{ (q,M') | q\in Q,\ M'\le M_c \}\).
Having fixed x, we claim that for the constants of \(w_x\), one of the r-th or s-th segment is bad in \(\mathcal {V}_j\). By construction, Lemma 2 guarantees that \(\rho _x\) has  cycles in segments \(1,\ldots r-1\). If \(\rho _x\) has a
cycles in segments \(1,\ldots r-1\). If \(\rho _x\) has a  cycle in segment r, then \(\rho _x\) is of Form (i):
cycle in segment r, then \(\rho _x\) is of Form (i):

and so the r-th segment must be bad in \(\mathcal {V}_j\).
Otherwise, if \(\rho _x\) does not have a  cycle in the r-th segment, then the construction in Lemma 2 guarantees
cycle in the r-th segment, then the construction in Lemma 2 guarantees  cycles in segments indexed \(r, r+1, \ldots , s-1\). Indeed, for the r-th segment, we are guaranteed a
cycles in segments indexed \(r, r+1, \ldots , s-1\). Indeed, for the r-th segment, we are guaranteed a  cycle reading \(a^{n_{r}}\), all the more for \(a^{n_{r}+x\alpha }\). As for segments indexed \(r+1, \ldots s-1\), if \(\rho _x\) does not have a
cycle reading \(a^{n_{r}}\), all the more for \(a^{n_{r}+x\alpha }\). As for segments indexed \(r+1, \ldots s-1\), if \(\rho _x\) does not have a  cycle in the r-th segment, then the maximal effect of segment r is \(|Q| \cdot W\). However, \(n_{r+1}\) was constructed to guarantee a
cycle in the r-th segment, then the maximal effect of segment r is \(|Q| \cdot W\). However, \(n_{r+1}\) was constructed to guarantee a  cycle even in case the effect of segment r is \(Wn_{r} \ge W\alpha \ge W|Q|\).
cycle even in case the effect of segment r is \(Wn_{r} \ge W\alpha \ge W|Q|\).
If there is a  cycle in segment s, then \(\rho _x\) is again of Form (i):
cycle in segment s, then \(\rho _x\) is again of Form (i):

and so the s-th segment must be bad in \(\mathcal {V}_j\).
Otherwise, using the same arguments as for the r-th segment, we have that segments indexed \(s+1,\ldots ,k+1\) each contain a  cycle. In this case we are left with the b and c segments. The choice of x guarantees a
cycle. In this case we are left with the b and c segments. The choice of x guarantees a  cycle in the b segment. If \(\rho _x\) traverses a
cycle in the b segment. If \(\rho _x\) traverses a  cycle in the b segment, then \(w_x\) is of Form (iii).
cycle in the b segment, then \(w_x\) is of Form (iii).

Finally, if there are no  cycles in the b segment, then the choice of x again guarantees a
cycles in the b segment, then the choice of x again guarantees a  cycle in the c segment, so \(w_x\) is of Form (ii).
cycle in the c segment, so \(w_x\) is of Form (ii).

In the two latter cases, both the r-th and the s-th segments are bad in \(\mathcal {V}_j\). \(\square \)
4.4 Proof of Theorem 1
Given Lemma 5, we now know that each \(\mathcal {V}_j\) has at most one good segment. Therefore, all 1-CNs \(\mathcal {V}_1,\ldots ,\mathcal {V}_k\) together have at most k good segments. Recall that the words we focus on have \(k+1\) segments, and therefore there is at least one segment, say the l-th segment, that is bad in every \(\mathcal {V}_j\). Note, however, that this segment may correspond to different constants in each \(\mathcal {V}_j\). That is, there exists constants \(\{ m_i^j, m_b^j, m_c^j \mid i \in [k+1], j \in [k] \}\) witnessing that the l-th segment is bad for each \(\mathcal {V}_j\). We group the \(\mathcal {V}_j\) according to the form of their accepting runs \(\rho _j\) (see Definition 2):
-
(i)
 ,
, -
(ii)
 , or
, or -
(iii)
 .
.
We now find constants resulting in a single word for which the l-th segment is bad in every \(\mathcal {V}_j\). First, for \(i \in [k+1] \setminus \{l\}\), we define \(M_i = \max \{m^j_i \mid j \in [k]\}\), note that these values are still multiples of \(\alpha \). Similarly, we define \(M_c = \max \{m^j_c \mid j \in [k]\}\). It remains to fix new constants \(L\) and \(B\), which we do in phases in the following. The resulting word is then
Most steps in the analysis below are based on Lemma 3 and Corollary 1. We first, partially, handle Form (iii) runs. For such \(\mathcal {V}_j\), there is an accepting \(\mathbb {N}\)-run \(\rho _j\) on

By pumping  cycles as per Corollary 1 in all segments except l we obtain an accepting \(\mathbb {N}\)-run \(\rho '_j\) on
cycles as per Corollary 1 in all segments except l we obtain an accepting \(\mathbb {N}\)-run \(\rho '_j\) on

We now pump arbitrary cycles in the c segment to construct a \(\mathbb {Z}\)-run \(\rho ''_j\) on

Next, we compensate for possible negative cycles in the c segment by pumping a  cycle in the b segment. Thus, we construct an \(\mathbb {N}\)-run \(\rho '''_j\) on
cycle in the b segment. Thus, we construct an \(\mathbb {N}\)-run \(\rho '''_j\) on

where \(B\) is chosen to be large enough such that \(\rho '''_j\) is an \(\mathbb {N}\)-run for all \(\mathcal {V}_j\), \(j \in [k]\). Note that it remains to fix \(L\).
We now turn to Form (i) with a similar process we start with an accepting \(\mathbb {N}\)-run \(\rho _j\) on

Pump  cycles in segments indexed \(1, \ldots , l-1\) to obtain an accepting \(\mathbb {N}\)-run \(\rho '_j\) on
cycles in segments indexed \(1, \ldots , l-1\) to obtain an accepting \(\mathbb {N}\)-run \(\rho '_j\) on

Now, obtain a \(\mathbb {Z}\)-run \(\rho ''_j\) by pumping arbitrary cycles in the remaining segments, including the b segment.

Again, compensate for negative cycles by taking \(L\) large enough so that pumping  cycles in the l-th segment yields an accepting \(\mathbb {N}\)-run \(\rho '''_j\) on
cycles in the l-th segment yields an accepting \(\mathbb {N}\)-run \(\rho '''_j\) on

We now return to Form (iii) and fix the l-th segment by pumping  cycles to construct an accepting \(\mathbb {N}\)-run on
cycles to construct an accepting \(\mathbb {N}\)-run on

We are left with Form (ii), which are the most straightforward to handle. We simply pump  cycles in all segments to construct an accepting \(\mathbb {N}\)-run \(\rho '_j\) on
cycles in all segments to construct an accepting \(\mathbb {N}\)-run \(\rho '_j\) on

Note that the requirement for all segments before the l-th to be  is crucial, otherwise we won’t be able to pump all the cycles in all forms simultaneously.
is crucial, otherwise we won’t be able to pump all the cycles in all forms simultaneously.
We now have that w is accepted by every \(\mathcal {V}_j\), and the l-th segment is bad for all \(\mathcal {V}_j\). By applying Lemma 4 for each of the \(\mathcal {V}_j\) and taking global constants to be the products of the respective constants \(x, y, z > 0\) for each \(\mathcal {V}_j\), we now obtain \(X, Y, Z \in \mathbb {N}\), multiples of \(\alpha \), such that for every \(n\in \mathbb {N}\) the word
is accepted by every \(\mathcal {V}_j\), for every \(j \in [k]\).
Finally, we choose n large enough to satisfy \(\sum _{i\in [k+1] \setminus \{l\}} M_i < \min \{B+Yn, M_c+Zn\}\), so that \(w_n\notin \mathcal {L}(\mathcal {P})\). This is possible because, w.l.o.g, the l-th segment can only pay for b, and the remaining segments \([k+1] \setminus \{l\}\) cannot pay for c. This contradicts the assumption that \(\mathcal {L}(\mathcal {P}) = \bigcap _{j\in [k]}\mathcal {L}(\mathcal {V}_j)\), concluding the proof of Theorem 1. \(\square \)
Remark 3 (Unbounded Compositeness)
[Unbounded Compositeness] The proof of Theorem 1 shows that if words with \(k+1\) segments are allowed, then the language is not (1, k)-composite, we use this to establish primality. By intersecting \(\mathcal {L}(\mathcal {P})\) with words that allow at most \(k+1\) segments, we obtain a language that is not (1, k)-composite, but it is not hard to show that it is \((1,2^{k+1})\)-composite. This demonstrates that a 2-CN can be composite, but may require unboundedly many factors.
The intuition behind Theorem 1 is that separate counters are needed to keep track of the elements that “cover” \(b^{m_b}\) and \(c^{m_c}\). Extending this idea to k-CN, we require that the a segments are partitioned to k different sets that cover k “targets”.
Conjecture 1
The following language is the language of a prime k-CN:
While constructing a k-CN for \(L_k\) is a simple extension of Example 2, proving that it is indeed prime does not seem to succumb to our techniques, and we leave it as an important open problem (see Section 7).
5 Primality of Counter Nets is Undecidable
In this section we consider the primality and dimension-minimality decision problems: given a k-CN \(\mathcal {A}\), decide whether \(\mathcal {A}\) is prime and whether \(\mathcal {A}\) is dimension-minimal, respectively.
We use our prime 2-CN from Example 2 and the results of Section 4 to show that both problems are undecidable. Our proof is by reduction from the containment problemFootnote 2 for 1-CN: given two 1-CN \(\mathcal {A},\mathcal {B}\) over alphabet \(\varSigma \), decide whether \(\mathcal {L}(\mathcal {A})\subseteq \mathcal {L}(\mathcal {B})\). This problem was shown to be undecidable in [20].
We begin by describing the reduction that applies to both problems. Consider an instance of 1-CN containment with two 1-CNs \(\mathcal {A}\) and \(\mathcal {B}\) over the alphabet \(\varSigma \). We construct a 2-CN \(\mathcal {C}\) as follows. Let \(\varLambda \) be the alphabet of the 2-CN from Example 2 and Theorem 1, and let \(\$ \notin \varSigma \cup \varLambda \) be a fresh symbol. Intuitively, \(\mathcal {C}\) accepts words of the form \(u\$v\) when either \(u\in \mathcal {L}(\mathcal {A})\) and v is accepted by \(\mathcal {P}\) starting from the maximal counter \(\mathcal {A}\) ended with on u, or when \(u\in \mathcal {L}(\mathcal {B})\) and \(v\in \varLambda ^*\).
Formally, we convert \(\mathcal {A}\) and \(\mathcal {B}\) to 2-CNs \(\mathcal {A}'\) and \(\mathcal {B}'\) by adding a counter and never modifying its value, so a transition \((p, \sigma , v, q)\) in \(\mathcal {A}\) becomes \((p, \sigma , (v,0), q))\) in \(\mathcal {A}'\), for example. We construct a 2-CN \(\mathcal {C}\) as follows (see Fig. 3). We take \(\mathcal {A}'\), \(\mathcal {B}'\), and \(\mathcal {P}\), and for every accepting state q of \(\mathcal {A}'\) we introduce a transition \((q, \$, \boldsymbol{0}, p_0)\) where \(p_0\) is an initial state of \(\mathcal {P}\). We then add a new accepting state \(q_\top \) and add the transitions \((q_\top , \lambda , \boldsymbol{0}, q_\top )\) for every letter \(\lambda \in \varLambda \), in other words \(q_\top \) is an accepting sink for \(\varLambda \). We also add transitions \((s, \$, \boldsymbol{0}, q_\top )\) from every accepting state s of \(\mathcal {B}'\). The initial states are those of \(\mathcal {A}'\) and \(\mathcal {B}'\), and the accepting states are those of \(\mathcal {P}\) and \(q_\top \).
Theorem 2
Primality and dimension-minimality are undecidable, already for 2-CN.
Proof
We prove the theorem by establishing that \(\mathcal {C}\) is not prime if and only if \(\mathcal {L}(\mathcal {A})\subseteq \mathcal {L}(\mathcal {B})\), and \(\mathcal {C}\) is not dimension-minimal if and only if \(\mathcal {L}(\mathcal {A})\subseteq \mathcal {L}(\mathcal {B})\).
Assume that \(\mathcal {L}(\mathcal {A}) \subseteq \mathcal {L}(\mathcal {B})\), then the component of \(\mathcal {C}\) containing \(\mathcal {A}'\) and \(\mathcal {P}\) (Fig. 3 left) becomes redundant. Since the component containing \(\mathcal {B}'\) and \(q_\top \) only makes use of one counter, \(\mathcal {C}\) is composite. Formally, we claim that \(\mathcal {L}(\mathcal {C}) =\{ u\$v \mid u \in \mathcal {L}(\mathcal {B}) \wedge v \in \varLambda ^*\}\). Indeed, if \(w\in \mathcal {L}(\mathcal {C})\) then \(w=u\$v\) so either \(u \in \mathcal {L}(\mathcal {A}') = \mathcal {L}(\mathcal {A})\) or \(u \in \mathcal {L}(\mathcal {B})\), but since \(\mathcal {L}(\mathcal {A})\subseteq \mathcal {L}(\mathcal {B})\), this is equivalent to \(u \in \mathcal {L}(\mathcal {B})\), and in this case there is simply no condition on \(v \in \varLambda ^*\). Since the second counter is not used in component containing \(\mathcal {B}'\) and \(q_\top \) (Fig. 3 right), we can construct a 1-CN equivalent to \(\mathcal {C}\) by projecting on the first counter and just deleting the component containing \(\mathcal {A}'\) and \(\mathcal {P}\) completely. It follows that in this case \(\mathcal {C}\) is not dimension-minimal, and therefore is not prime either.
For the converse, assume that \(\mathcal {L}(\mathcal {A}) \not \subseteq \mathcal {L}(\mathcal {B})\), and let \(u \in \mathcal {L}(\mathcal {A}) \setminus \mathcal {L}(\mathcal {B})\). Denote \(m = \max \{ \textsf {eff}(\rho ) \mid \rho \text { is an accepting run of } \mathcal {A}\text { on } u \}\). Thus, for a word \(v \in \varLambda ^*\) we have that \(u\$v \in \mathcal {L}(\mathcal {C})\) if and only if v is accepted in \(\mathcal {P}\) with initial counter m. Assume by way of contradiction that \(\mathcal {C}\) is not prime, then we can write \(\mathcal {L}(\mathcal {C})\) as an intersection of languages of 1-CNs. Loosely speaking, this will create a contradiction as we will be able to argue that \(\mathcal {P}\) is not prime. More precisely, take \(v = a^{m_1} \# a^{m_2} \# \cdots \# a^{m_{k+1}} \# b^{m_b} c^{m_c}\) for integers \(\left\{ m_i \right\} _{i=1}^{k+1}, m_b, m_c \in \mathbb {N}\) and consider words of the form \(u\$v\). Our analysis from Section 4—specifically the arguments used in the proof Lemma 5—on \(u\$v\) can show, mutatis mutandis, that the language of \(\mathcal {P}\) is not composite regardless of any fixed initial counter value (an analogue of Theorem 1).
We thus have that \(\mathcal {C}\) is prime, and in particular \(\mathcal {C}\) is dimension-minimal, concluding the correctness of the reduction. \(\square \)
To contrast the undecidability of primality in nondeterministic CNs, we turn our attention to a decidable fragment of primality, for which we focus on deterministic CNs. Recall that by Proposition 1, a k-DCN is dimension minimal if and only if it is not \((1, k-1)\)-composite. Thus, dimension-minimality “captures” primality. We show that regularity, which is equivalent to being (0, 1)-composite, is decidable for k-DCNs for every dimension k.
For dimension one, regularity is already known to be decidable in EXPSPACE, even for history-deterministic 1-CNs [5, Theorem 19]. History-determinism is a restricted form of nondeterminism; history-deterministic CNs are less expressive than nondeterministic CNs but more expressive than DCNs. However, already for \(k\ge 2\), regularity is undecidable for history-deterministic k-CNs [5, Theorem 20].
Theorem 3
Regularity of k-DCN is decidable and is in \(\textsf{EXPSPACE}\).
We provide further details, including a proof of Theorem 3, in the full version. In short, we translate our k-DCN into a regularity preserving Vector Addition System (VAS) and use results on VAS regularity from [3, Theorem 4.5]. We remark that an alternative approach may be taken by adapting the results of [12] on regularity of VASS, although this seems more technically challenging because CNs have accepting states.
6 Expressiveness Trade-Offs between Dimensions and Nondeterminism
Theorem 1 implies that 2-CNs are more expressive than 1-CNs, and that nondeterministic models are more expressive than deterministic ones. In particular, a k-DCN can be decomposed by projection (Proposition 1), and have decidable regularity (Theorem 3). It is therefore interesting to study the interplay between increasing the dimension and introducing nondeterminism. In this section we present two results: first, we show that dimension and nondeterminism, are incomparable notions, in a sense. Second, we show that increasing the dimension strictly increases expressiveness, for both CNs and DCNs. We remark that the latter may seem like an intuitive and simple claim. However, to the best of our knowledge it has never been proved, and moreover, it requires a nontrivial approach to pumping with several counters.
We start by showing that nondeterminism can sometimes compensate for low dimension. Let \(k \in \mathbb {N}\) and \(\varSigma = \{ a_1, \ldots , a_k, b_1, \ldots , b_k, c \}\); consider the language \(L_k =\{ a_1^{n_1} a_2^{n_2} \cdots a_k^{n_k} b_i c^m \mid i \in [k] \wedge n_i \ge m \}\). It is easy to construct a k-DCN as well as a 1-CN for \(L_k\), as depicted by Figs. 4 and 5 for \(k=3\). To construct a 1-CN we guess which \(b_i\) will be later read, and verify the guess using the single counter in the \(a_i^{n_i}\) part.
We now show that \(\mathcal {L}_k\)’s dimension cannot be minimised whilst maintaining determinism.
Theorem 4
\(L_k\) is not recognisable by a \((k-1)\)-DCN.
Proof
Assume by way of contradiction that there exists a \((k-1)\)-DCN \(\mathcal {D}= \langle \varSigma , Q, Q_0, \delta , F \rangle \) such that \(\mathcal {L}(\mathcal {D}) = L_k\). Let \(n > |Q|\) and for every \(i \in [k]\) consider the word \(w_i = a_1^n a_2^n \cdots a_k^n b_i c^n \in L_k\). Since \(\mathcal {D}\) is deterministic and \(n > |Q|\), all of the accepting runs on the \(w_i\) coincide up to the \(b_i\) part and have cycles in each \(a_i^n\) segment as well as in the \(c^n\) segment (the latter may differ according to i). Let M be the product of the lengths of all these cycles.
First, observe that the cycles in all of the \(a_i^n\) segments cannot decrease any counter. Indeed, otherwise by pumping such a cycle for large enough \(t>0\) times, there would not exist an \(\mathbb {N}\)-run on words with the prefix \(a_1^n \cdots a_{i-1}^n a_i^{n+tM}\). This creates a contradiction since, with an appropriate suffix, such words can be accepted.
Thus, all \(a_i\) cycles have non-negative effects for all counters. Indeed, for each counter i – associate with i the minimal segment index whose cycle strictly increases i. Since there are \(k-1\) counters and k segments this map is not surjective, in other words, there is a segment (without loss of generality, the \(a_k\) segment) such that every counter that is increased in the \(a_k\) cycle is also increased in a previous segment. Therefore, there exist \(s,t>0\) such that the word
is accepted by \(\mathcal {D}\), which is a contradiction.
We now turn to show that conversely, dimension can sometimes compensate for nondeterminism. Moreover, we show that there is a strict hierarchy of expressiveness with respect to dimension. Specifically, for \(k\in \mathbb {N}\) consider the language \(H_k=\{a_1^{m_1}a_2^{m_2}\cdots a_k^{m_k}b_1^{n_1}b_2^{n_2}\cdots b_k^{n_k}\mid \forall 1\le i\le k,\ m_i\ge n_i\}\).
Theorem 5
\(H_k\) is recognisable by a k-DCN, but not by a \((k-1)\)-CN.
Proof (sketch)
[sketch] Constructing a k-DCN for \(H_k\) is straightforward, by using the i-th counter to check that \(m_i\ge n_i\), for each \(i\in [k]\).
We turn to argue that \(H_k\) is not recognisable by a \((k-1)\)-CN (See the full version for a complete proof). Assume by way of contradiction that \(\mathcal {A}=\langle \varSigma ,Q,Q_0,\delta ,F \rangle \) is a \((k-1)\)-CN with \(L(\mathcal {A})=H_k\). We first observe that there exists \(m_1\in \mathbb {N}\) large enough so that every run of \(\mathcal {A}\) on \(a_1^{m_1}\) must traverse a non-negative cycle, i.e., a cycle whose overall effect is \(\boldsymbol{u_1}\in \mathbb {Z}^{k-1}\) such that \(\boldsymbol{u_1}[i]\ge 0\) for all \(i\in [k-1]\). Indeed, this is immediate by a “uniformly bounded” version of Dickson’s lemma [15]; any long-enough “controlled” sequence of vectors in \(\mathbb {N}^{k-1}\) must contain an r-increasing chain, for any \(r\in \mathbb {N}\).
By repeating this argument we can ultimately find \(m_1,\ldots ,m_k\) such that any run of \(\mathcal {A}\) on \(a_1^{m_1}a_2^{m_2}\cdots a_k^{m_k}\) traverses a non-negative cycle in each \(a_j\) segment for \(j\in [k]\). Consider now the word \(w=a_1^{m_1}a_2^{m_2}\cdots a_k^{m_k}b_1^{m_1}b_2^{m_2}\cdots b_k^{m_k}\in H_k\), then there exists an accepting run \(\rho \) of \(\mathcal {A}\) on w such that for each \(j\in [k]\), the run \(\rho \) traverses a non-negative cycle in segment \(a_j\), with effect \(\boldsymbol{u_j}\in \mathbb {N}^{k-1}\).
Consider the vectors \(\boldsymbol{u_1},\ldots ,\boldsymbol{u_k}\). We claim that there exists \(\ell \in [k]\) such that the support of \(\boldsymbol{u_\ell }\) is covered by \(\boldsymbol{u_1},\ldots ,\boldsymbol{u_{\ell -1}}\) in the following sense: for every counter \(i\in [k-1]\), if \(\boldsymbol{u_\ell }[i]>0\), then there exists \(j<\ell \) such that \(\boldsymbol{u_j}[i]>0\). Indeed, this holds since otherwise every \(\boldsymbol{u_j}\) must contribute a fresh positive coordinate to the union of supports of the previous vectors, but there are k vectors and only \(k-1\) coordinates.
Next, observe that since each \(\boldsymbol{u_j}\) is a non-negative cycle taken in \(\rho \), then it can be pumped without decreasing any following counters, and hence induce an accepting run on a pumped word. Intuitively, we now proceed by pumping all the \(\boldsymbol{u_j}\) cycles for \(j<\ell \) for some large-enough number of times M, which enables us to remove one iteration of the cycle with effect \(\boldsymbol{u_\ell }\) while maintaining an accepting run on a word of the form:
Since \(m_\ell >m_\ell -d_\ell \), the \(b_\ell \) segment is longer than the \(a_\ell \) segment. Thus \(w'\notin H_k\), this yields a contradiction. \(\square \)
Apart from showing that nondeterminism cannot always compensate for increased dimension, Theorem 5 also shows that for every dimension k, there are languages recognisable by a \((k+1)\)-DCN (and in particular by a \((k+1)\)-CN), but not by any k-CN (and in particular not by any k-DCN). Thus, we obtain the following hierarchy.
Corollary 2
For every \(k\in \mathbb {N}\), k-CNs (resp. k-DCNs) are strictly less expressive than \((k+1)\)-CNs (resp. \((k+1)\)-DCNs).
7 Discussion
Broadly, this work explores the interplay between the dimension of a CN and its expressive power. This is done by studying the dimension-minimality problem, where we ask whether the dimension of a given CN can be decreased while preserving its language, and by the more involved primality problem, which allows a decomposition to multiple CNs of lower dimension. We show that both primality and dimension-minimality are undecidable. Moreover, they remain undecidable even when we discard the degenerate dimension 0 case, which corresponds to finite memory, i.e., regular languages. On the other hand, this degenerate case is one where we can show decidability for DCNs.
This work also highlights a technical shortcoming of current understanding of high-dimensional CNs: pumping arguments in the presence of k dimensions and nondeterminism are very involved, and are (to our best efforts) insufficient to prove Conjecture 1. To this end, we present novel pumping arguments in the proof of Theorem 1 and to some extent in the proof of Theorem 5, which make progress towards pumping in the presence of k dimensions and nondeterminism.
Notes
- 1.
The colours were chosen as accessible for the colourblind. For a greyscale-friendly version, see the full paper.
- 2.
Actually, the complement thereof.
References
Shaull Almagor, Udi Boker, Piotr Hofman, and Patrick Totzke. Parametrized universality problems for one-counter nets. In 31st International Conference on Concurrency Theory (CONCUR 2020). Schloss Dagstuhl-Leibniz-Zentrum für Informatik, 2020.
Shaull Almagor and Asaf Yeshurun. Determinization of one-counter nets. In 33rd International Conference on Concurrency Theory (CONCUR 2022). Schloss Dagstuhl-Leibniz-Zentrum für Informatik, 2022.
Michel Blockelet and Sylvain Schmitz. Model checking coverability graphs of vector addition systems. In Filip Murlak and Piotr Sankowski, editors, Mathematical Foundations of Computer Science 2011 - 36th International Symposium, MFCS 2011, Warsaw, Poland, August 22-26, 2011. Proceedings, volume 6907 of Lecture Notes in Computer Science, pages 108–119. Springer, 2011.https://doi.org/10.1007/978-3-642-22993-0_13.
Michael Blondin, Matthias Englert, Alain Finkel, Stefan Göller, Christoph Haase, Ranko Lazić, Pierre McKenzie, and Patrick Totzke. The reachability problem for two-dimensional vector addition systems with states. Journal of the ACM (JACM), 68(5):1–43, 2021.
Sougata Bose, David Purser, and Patrick Totzke. History-deterministic vector addition systems. arXiv preprint arXiv:2305.01981, 2023.
Maria Paola Cabasino, Alessandro Giua, and Carla Seatzu. Diagnosability of discrete-event systems using labeled Petri nets. IEEE Transactions on Automation Science and Engineering, 11(1):144–153, 2013.
Wojciech Czerwiński, Diego Figueira, and Piotr Hofman. Universality problem for unambiguous vass. In 31st International Conference on Concurrency Theory (CONCUR 2020). Schloss Dagstuhl-Leibniz-Zentrum für Informatik, 2020.
Wojciech Czerwiński, Sławomir Lasota, Ranko Lazić, Jérôme Leroux, and Filip Mazowiecki. Reachability in fixed dimension vector addition systems with states. In 31st International Conference on Concurrency Theory (CONCUR 2020). Schloss Dagstuhl-Leibniz-Zentrum für Informatik, 2020.
Wojciech Czerwiński, Slawomir Lasota, Christof Löding, and Radoslaw Piórkowski. New pumping technique for 2-dimensional VASS. In 44th International Symposium on Mathematical Foundations of Computer Science (MFCS 2019). Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 2019.
Wojciech Czerwiński, Sławomir Lasota, and Łukasz Orlikowski.Improved lower bounds for reachability in vector addition systems. In 48th International Colloquium on Automata, Languages, and Programming (ICALP 2021). Schloss Dagstuhl-Leibniz-Zentrum für Informatik, 2021.
Wojciech Czerwiński and Łukasz Orlikowski. Reachability in vector addition systems is Ackermann-complete. In 2021 IEEE 62nd Annual Symposium on Foundations of Computer Science (FOCS), pages 1229–1240. IEEE, 2022.
Stéphane Demri. On selective unboundedness of VASS. J. Comput. Syst. Sci., 79(5):689–713, 2013. https://doi.org/10.1016/j.jcss.2013.01.014.
Javier Esparza. Decidability and complexity of petri net problems–an introduction. Lectures on Petri Nets I: Basic Models: Advances in Petri Nets, pages 374–428, 2005.
Diego Figueira. Co-finiteness of VASS coverability languages. working paper or preprint, July 2019. URL: https://hal.science/hal-02193089.
Diego Figueira, Santiago Figueira, Sylvain Schmitz, and Philippe Schnoebelen. Ackermannian and primitive-recursive bounds with dickson’s lemma. In 2011 IEEE 26th Annual Symposium on Logic in Computer Science, pages 269–278. IEEE, 2011.
Alain Finkel, Jérôme Leroux, and Grégoire Sutre. Reachability for two-counter machines with one test and one reset. In FSTTCS 2018-38th IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science, volume 122, pages 31–1. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 2018.
Sheila A. Greibach. Remarks on blind and partially blind one-way multicounter machines. Theoretical Computer Science, 7(3):311–324, 1978.
Christoph Haase, Stephan Kreutzer, Joël Ouaknine, and James Worrell.Reachability in succinct and parametric one-counter automata. In CONCUR 2009-Concurrency Theory: 20th International Conference, CONCUR 2009, Bologna, Italy, September 1-4, 2009. Proceedings 20, pages 369–383. Springer, 2009.
Michel Henri Theódore Hack. Petri net language. Computation Structures Group Memo 124, 1976. URL: http://publications.csail.mit.edu/lcs/pubs/pdf/MIT-LCS-TR-159.pdf.
Piotr Hofman, Richard Mayr, and Patrick Totzke. Decidability of weak simulation on one-counter nets. In 2013 28th Annual ACM/IEEE Symposium on Logic in Computer Science, pages 203–212. IEEE, 2013.
Piotr Hofman and Patrick Totzke. Trace inclusion for one-counter nets revisited. In Reachability Problems: 8th International Workshop, RP 2014, Oxford, UK, September 22-24, 2014. Proceedings 8, pages 151–162. Springer, 2014.
I. Jecker, N. Mazzocchi, and P. Wolf. Decomposing permutation automata. In Proc. 32nd CONCUR, volume 203 of LIPIcs, pages 18:1–18:19. Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2021.
Ismael R Jecker, Orna Kupferman, and Nicolas Mazzocchi. Unary prime languages. In 45th International Symposium on Mathematical Foundations of Computer Science, volume 170, 2020.
Orna Kupferman and Jonathan Mosheiff. Prime languages. Information and Computation, 240:90–107, 2015.
Jérôme Leroux. The reachability problem for petri nets is not primitive recursive. In 2021 IEEE 62nd Annual Symposium on Foundations of Computer Science (FOCS), pages 1241–1252. IEEE, 2022.
Jérôme Leroux and Grégoire Sutre. On flatness for 2-dimensional vector addition systems with states. In CONCUR, volume 4, pages 402–416. Springer, 2004.
Elaine Render and Mark Kambites. Rational subsets of polycyclic monoids and valence automata. Information and Computation, 207(11):1329–1339, 2009.
Rüdiger Valk and Guy Vidal-Naquet. Petri nets and regular languages.Journal of Computer and system Sciences, 23(3):299–325, 1981.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Almagor, S., Avni, G., Sinclair-Banks, H., Yeshurun, A. (2024). Dimension-Minimality and Primality of Counter Nets. In: Kobayashi, N., Worrell, J. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2024. Lecture Notes in Computer Science, vol 14575. Springer, Cham. https://doi.org/10.1007/978-3-031-57231-9_11
Download citation
DOI: https://doi.org/10.1007/978-3-031-57231-9_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-57230-2
Online ISBN: 978-3-031-57231-9
eBook Packages: Computer ScienceComputer Science (R0)




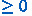 : then the induction hypothesis applies on
: then the induction hypothesis applies on  : then we remove
: then we remove  cycle in
cycle in  ,
, , or
, or .
. cycle in the r-th or s-th segments, then
cycle in the r-th or s-th segments, then  cycle reading
cycle reading  cycle in the r-th or s-th segment, nor in the b segment, then
cycle in the r-th or s-th segment, nor in the b segment, then  cycle reading
cycle reading  ,
, , or
, or .
.


