Abstract
We introduce a first-order quantum programming language, named foq, whose terminating programs are reversible. We restrict foq to a strict and tractable subset, named pfoq, of terminating programs with bounded width, that provides a first programming language-based characterization of the quantum complexity class fbqp. We finally present a tractable semantics-preserving algorithm compiling a pfoq program to a quantum circuit of size polynomial in the number of input qubits.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Motivations. Quantum computing is an emerging and promising computational model that has been in the scientific limelight for several decades. This phenomenon is mainly due to the advantage of quantum computers over their classical competitors, based on the use of purely quantum properties such as superposition and entanglement. The most notable example being Shor’s algorithm for finding the prime factors of an integer [15], which is exponentially faster than the most efficient known classical factoring algorithm and which is expected to have implications in cryptography (RSA encryption, etc.).
Whether due to the fragility of quantum systems, namely the engineering problem of maintaining a large number of qubits in a coherent state, or by lack of reliable technological alternatives, quantum computing is typically described at a level close to hardware. Without any hope of being exhaustive, one can think to quantum circuits [9, 11], to measurement-based quantum computers [4, 7] or to circuit description languages [13]. This low-level machinery restricts drastically the abstraction and programming ease offered by these models and quantum programs currently suffer from the comparison with their classical competitors, which have many high-level tools and formalisms based on more than 50 years of scientific research, engineering development, and practical and industrial applications.
In order to solve these issues, a major effort is made to realize the promise of a quantum computer, which requires the development of different layers of hardware and software, together referred to as the quantum stack. Our paper is part of this line of research. We focus on the highest layers of the quantum stack: quantum programming languages and quantum algorithms. We seek to better understand what can be done efficiently on a quantum computer and we are particularly interested in the development of quantum programming languages where program complexity can be certified automatically by some static analysis technique.
Contribution. Towards this end, we take the notion of polynomial time computation as our main object of study. Our contributions are the following.
-
We introduce a quantum programming language, named foq, that includes first-order recursive procedures. The input of a foq program consist in a sorted set of qubits, a list of pairwise distinct qubit indexes. A foq program can apply to each of its qubits basic operators corresponding to unary unitary operators. The considered set of operators has been chosen in accordance with [16] to form a universal set of gates.
-
After showing that terminating foq programs are reversible (Theorem 1), we restrict programs to a strict subset, named pfoq, for polynomial time foq. The restrictions put on a pfoq programs are tractable (i.e., can be decided in polynomial time, see Theorem 2), ensure that programs terminate on any input (Lemma 1), and prevent programs from having any exponential blow up (Lemma 2).
-
We show that the class of functions computed by pfoq programs is sound and complete for the quantum complexity class fbqp. fbqp is the functional extension of bounded-error quantum polynomial time, known as bqp [2], the class of decision problems solvable by a quantum computer in polynomial time with an error probability of at most \(\frac{1}{3}\) for all instances. Hence the language \(\textsc {pfoq} \) is, to our knowledge, the first programming language characterizing quantum polynomial time functions. Soundness (Theorem 3) is proved by showing that any pfoq program can be simulated by a quantum Turing machine running in polynomial time [2]. The completeness of our characterization (Theorem 6) is demonstrated by showing that pfoq programs strictly encompass Yamakami’s function algebra, known to be fbqp-complete [16].
-
We also describe a polynomial-time deterministic algorithm \({\textbf {compile}} \) (based on the subroutines described in Algorithms 1 and 2), that takes in a \(\textsc {pfoq} \) program \(\textrm{P}\) and an integer n and outputs a quantum circuit of size polynomial in n that simulates \(\textrm{P}\) on an input size of n qubits. The existence of such circuits is not surprising, as a direct consequence of Yao’s characterization of the class \(\textsc {bqp} \) in terms of uniform families of circuits of polynomial size [17]. However, a constructive generation based on Yao’s algorithm is not satisfactory because of the use of quantum Turing machines which makes the circuits complex and not optimal (in size). We show that, in our setting, circuits can be effectively computed and that the \({\textbf {compile}} \) algorithm is tractable (Theorem 9).
Our programming language \(\textsc {foq} \) and the restriction to \(\textsc {pfoq} \) are illustrated throughout the paper, using the Quantum Fourier Transform \(\textrm{QFT}\) as a leading algorithm (Example 1).
Related work. This paper belongs to a long standing line of works trying to specify, understand, and analyze the semantics of quantum programming languages, starting with the cornerstone work of Selinger [14]. The motivations in restricting the considered programs to pfoq were inspired by the works on implicit computational complexity, that seek to characterize complexity classes by putting restrictions (type systems or others) on standard programming languages and paradigms [1, 5, 12]. These restrictions have to be implicit (i.e., not provided by the programmer) and tractable. Among all these works, we are aware of two results [16] and [6] studying polynomial time computations on quantum programming languages, works from which our paper was greatly inspired. [6] provides a characterization of bqp based on a quantum lambda-calculus. Our work is an extension to fbqp with a restriction to first-order procedures. Last but not least, [6] is based on Yao’s simulation of quantum Turing machines [17] while we provide an explicit algorithm for generating circuits of polynomial size. Our work is also inspired by the function algebra of [16], that characterizes fbqp: our completeness proof shows that any function in [16] can be simulated by a pfoq program (Theorem 6). However, we claim that foq is a more general language for fbqp in so far that it is much less constraining (in terms of expressive power) than the function algebra of [16]: any function of [16] can be, by design, transformed into a pfoq program, whereas the converse is not true. We can take as example the quantum Fourier transform (QFT) which, as noted in [16], cannot be exactly computed by the function algebra without an additional initial quantum function. Furthermore, the multi-qubit recursion construction described in [16] is more restrictive than what we allow in pfoq, since we may only call the same recursive function in each branch.
2 First-order quantum programming language
Syntax and well-formedness. We consider a quantum programming language, called foq for First-Order Quantum programming language, that includes basic data types such as Integers, Booleans, Qubits, Operators, and Sorted Sets of qubits, lists of finite length where all elements are different. A foq program has the ability to call first-order (recursive) procedures taking a sorted set of qubits as a parameter. Its syntax is provided in Figure 1.
Let \(\textrm{x}\) denote an integer variable and \(\bar{\textrm{p}}\), \(\bar{\text {q}}\) denote sorted sets variables. The size of the sorted set stored in \(\bar{\text {q}}\) will be denoted by \(| \bar{\text {q}} |\). We can refer to the i-th qubit in \(\bar{\text {q}}\) as \(\bar{\text {q}}{\small [i]}\), with \(1 \le i \le | \bar{\text {q}} |\). Hence, each non-empty sorted set variable \(\bar{\text {q}}\) can be viewed as a list \([\bar{\text {q}}{\small [1]},\dots , \bar{\text {q}}{\small [| \bar{\text {q}} |]}]\). The empty sorted set, of size 0, will be denoted by \(\text {nil}\) and \(\bar{\text {q}}\ominus {\small [i]}\) will denote the sorted set obtained by removing the qubit of index i in \(\bar{\text {q}}\). For notational convenience, we extend this notation by \(\bar{\text {q}} \ominus {\small [i_1,\dots ,i_k]}\), for the list obtained by removing the qubits of indexes \(i_1,\dots ,i_k\) in the sorted set \(\bar{\text {q}}\).
The language also includes some constructs \(\textrm{U}^f\) to represent (unary) unitary operators, for some total function \(f \in \mathbb {Z}\rightarrow [0,2\pi )\cap \tilde{\mathbb {R}}\). The function f is required to be polynomial-time approximable: its output is restricted to \(\tilde{\mathbb {R}}\), the set of real numbers that can be approximated by a Turing machine for any precision \(2^{-k}\) in time polynomial in k.
A foq program \(\textrm{P}(\bar{\text {q}})\) consists of a sequence of procedure declarations \(\textrm{D}\) followed by a program statement S, \(\varepsilon \) denoting the empty sequence. In what follows, we will sometimes refer to program \(\textrm{P}(\bar{\text {q}})\) simply as \(\textrm{P}\). Let \(var(\textrm{S})\) be the set of variables appearing in the statement \(\textrm{S}\). Let \(| \textrm{P} |\) be the size of program \(\textrm{P}\), that is the total number of symbols in \(\textrm{P}\).
A procedure declaration \({\textbf {decl }}\textrm{proc}{\small [\textrm{x}]}(\bar{\textrm{p}})\{\textrm{S}\}\) takes a sorted set parameter \(\bar{\textrm{p}}\) and some optional integer parameter \(\textrm{x}\) as inputs. \(\textrm{S}\) is called the procedure statement, \(\textrm{proc}\) is the procedure name and belongs to a countable set Procedures. We will write \(\textrm{S}^{\textrm{proc}}\) to refer to \(\textrm{S}\) and \(\textrm{proc}\in \textrm{P}\) holds if \(\textrm{proc}\) is declared in \(\textrm{D}\).
Statements include a no-op instruction, applications of a unitary operator to a qubit (
 ), sequences, (classical) conditionals, quantum cases, and procedure calls (\({\textbf {call }}\textrm{proc}{\small [\textrm{i}]}(\textrm{s});\)). A quantum case \({\textbf {qcase }} \text {q} {\textbf { of }}\{0\rightarrow \textrm{S}_0, 1\rightarrow \textrm{S}_1\}\) provides a quantum control feature that will execute statements \(\textrm{S}_0\) and \(\textrm{S}_1\) in superposition. For example, the CNOT gate on qubits \(\bar{\text {q}}{\small [i]}\) and \(\bar{\text {q}}{\small [j]}\), for \(i,j \in \mathbb {N}\), \(i \ne j\), can be simulated by the following statement:
), sequences, (classical) conditionals, quantum cases, and procedure calls (\({\textbf {call }}\textrm{proc}{\small [\textrm{i}]}(\textrm{s});\)). A quantum case \({\textbf {qcase }} \text {q} {\textbf { of }}\{0\rightarrow \textrm{S}_0, 1\rightarrow \textrm{S}_1\}\) provides a quantum control feature that will execute statements \(\textrm{S}_0\) and \(\textrm{S}_1\) in superposition. For example, the CNOT gate on qubits \(\bar{\text {q}}{\small [i]}\) and \(\bar{\text {q}}{\small [j]}\), for \(i,j \in \mathbb {N}\), \(i \ne j\), can be simulated by the following statement:

Throughout the paper, we restrict our study to well-formed programs, that is, programs \(\textrm{P}=\textrm{D}::\textrm{S}\) satisfying the following properties: \(var(\textrm{S}) \subseteq \{\bar{\text {q}}\}\); \(\forall \textrm{proc}\in \textrm{P}\), \(var(\textrm{S}^{\textrm{proc}})\subseteq \{\textrm{x},\bar{\textrm{p}}\}\); procedure names declared in \(\textrm{D}\) are pairwise distinct; for each procedure call, the procedure name is declared in \(\textrm{D}\).
Semantics. Let \(\mathcal {H}_{2^n}\) be the Hilbert space \(\mathbb {C}^{2^n}\) of n qubits. We use Dirac notation to denote a quantum state
 . Each
. Each
 can be written as a superposition of bitstrings of size n:
can be written as a superposition of bitstrings of size n:
 , with \(\alpha _w \in \mathbb {C}\) and \(\sum _w |\alpha _w|^2=1\). The length
, with \(\alpha _w \in \mathbb {C}\) and \(\sum _w |\alpha _w|^2=1\). The length
 of the state
of the state
 is n. Given two matrices M, N, we denote by \(M^\dagger \) the transpose conjugate of M and by \(M \otimes N\) the tensor product of M by N.
is n. Given two matrices M, N, we denote by \(M^\dagger \) the transpose conjugate of M and by \(M \otimes N\) the tensor product of M by N.
 is equal to
is equal to
 and
and
 and
and
 are respectively the inner product and outer product of
are respectively the inner product and outer product of
 and
and
 . Let \(I_{n}\) be the identity matrix in \(\mathbb {C}^{n \times n}\). Given \(m \le n\) and \(i \in \{0,1\}\), define
. Let \(I_{n}\) be the identity matrix in \(\mathbb {C}^{n \times n}\). Given \(m \le n\) and \(i \in \{0,1\}\), define
 and
and
 .
.
A function \(\llbracket \textrm{U}^f \rrbracket \in \mathbb {\mathbb {Z}}\rightarrow \tilde{\mathbb {C}}^{2 \times 2}\) is associated to each \(\textrm{U}^f\) as follows:
\(\llbracket \text {NOT} \rrbracket (n)\triangleq \begin{pmatrix} 0 &{} 1\\ 1 &{} 0 \end{pmatrix}\!, \ \llbracket \text {R}_Y^f \rrbracket (n)\triangleq \begin{pmatrix} \cos (f(n)) &{} -\sin (f(n))\\ \sin (f(n)) &{} \cos (f(n)) \end{pmatrix}\!, \ \llbracket \text {Ph}^f \rrbracket (n)\triangleq \begin{pmatrix} 1 &{} 0\\ 0 &{} e^{i f(n)} \end{pmatrix}\!, \)
where \(\tilde{\mathbb {C}}\) is the set of complex numbers whose both real and imaginary parts are in \(\tilde{\mathbb {R}}\). One can check easily that each matrix \(M\triangleq \llbracket \textrm{U}^f \rrbracket (n) \in \tilde{\mathbb {C}}^{2 \times 2}\) is unitary, i.e., it satisfies \(M^\dagger \,M = M\,M^\dagger =I_2\).
Let \(\mathbb {B}\) to be the set of Boolean values \(b \in \{{\textbf {false}},{\textbf {true}}\}\). For a given set X, let \(\mathcal {L}(X)\) be the set of lists of elements in X. Let \(l=[x_1,\ldots ,x_m]\), with \(x_1,\ldots ,x_m \in X\), denote a list of m-elements in \(\mathcal {L}(X)\) and \([\,]\) be the empty list (when \(m=0\)). For \(l,l' \in \mathcal {L}(X)\),
 denotes the concatenation of l and \(l'\). hd(l) and tl(l) represent the tail and the head of l, respectively. Lists of integers will be used to represent Sorted Sets. They contain pointers to qubits (i.e., indexes) in the global memory.
denotes the concatenation of l and \(l'\). hd(l) and tl(l) represent the tail and the head of l, respectively. Lists of integers will be used to represent Sorted Sets. They contain pointers to qubits (i.e., indexes) in the global memory.
We interpret each basic data type \(\tau \) as follows: \(\llbracket \textrm{Integers} \rrbracket \triangleq \mathbb {Z}\), \(\llbracket \textrm{Booleans} \rrbracket \triangleq \mathbb {B}\), \(\llbracket \textrm{Sorted Sets} \rrbracket \triangleq \mathcal {L}(\mathbb {N})\), \(\llbracket \textrm{Qubits} \rrbracket \triangleq \mathbb {N}\), and \(\llbracket \textrm{Operators} \rrbracket \triangleq \tilde{\mathbb {C}}^{2\times 2}\). Each basic operation
 of arity n, with \(1 \le n \le 2\), has a type signature \(\tau _1 \times \ldots \times \tau _n \rightarrow \tau \) fixed by the program syntax. For example, the operation \(+\) has signature \(\textrm{Integers}\times \textrm{Integers} \rightarrow \textrm{Integers}\). A total function
of arity n, with \(1 \le n \le 2\), has a type signature \(\tau _1 \times \ldots \times \tau _n \rightarrow \tau \) fixed by the program syntax. For example, the operation \(+\) has signature \(\textrm{Integers}\times \textrm{Integers} \rightarrow \textrm{Integers}\). A total function
 is associated to each op.
is associated to each op.
For each basic type \(\tau \), the reduction \(\Downarrow _{\llbracket \tau \rrbracket }\) is a map in \(\tau \times \mathcal {L}(\mathbb {N}) \rightarrow \llbracket \tau \rrbracket \). Intuitively, it maps an expression of type \(\tau \) to its value in \(\llbracket \tau \rrbracket \) for a given list l of pointers in memory. These reductions are defined in Figure 2, where \(\textrm{e}\) and \(\textrm{d}\) denote either an integer expression \(\textrm{i}\) or a boolean expression \(\textrm{b}\).
Note that in rule (Rm\(_{\notin }\)), if we try to delete an undefined index then we return the empty list, and in rule (Qu\(_{\notin }\)), if we try to access an undefined qubit index then we return the value 0 (defined indexes will always be positive). The standard gates \({R}_Y(\pi /4)\), \({P}(\pi /4)\), and CNOT, form a universal set of gates [3], which justifies the choice of \(\text {NOT}\), \(\text {R}_Y^f(\textrm{i})\), and \(\text {Ph}^f(\textrm{i})\) as basic operators. For instance, we can simulate the application of an Hadamard gate H on \(\text {q}\) by the following statement
 , with the function f defined by \(\forall n, f(n)=\pi /4 \in [0,2\pi )\cap \tilde{\mathbb {R}}\). By abuse of notation, we will sometimes use
, with the function f defined by \(\forall n, f(n)=\pi /4 \in [0,2\pi )\cap \tilde{\mathbb {R}}\). By abuse of notation, we will sometimes use
 to denote this statement. Using \(\text {CNOT}\), we can also define the \(\text {SWAP}\) operation swapping the state between two qubits \(\bar{\text {q}}{\small [i]}\) and \(\bar{\text {q}}{\small [j]}\), with \(i,j \in \mathbb {N},\ i \ne j\):
to denote this statement. Using \(\text {CNOT}\), we can also define the \(\text {SWAP}\) operation swapping the state between two qubits \(\bar{\text {q}}{\small [i]}\) and \(\bar{\text {q}}{\small [j]}\), with \(i,j \in \mathbb {N},\ i \ne j\):
Let \(\top \) and \(\bot \) be two special symbols for termination and error, respectively, and let \(\diamond \) stand for a symbol in \(\{\top ,\bot \}\). The set of configurations of dimension \(2^n\), denoted \(\text {Conf}_n\), is defined by
with \(\mathcal {P}(\mathbb {N})\) being the powerset over \(\mathbb {N}\). A configuration
 contains a statement \(\textrm{S}\) to be executed (provided that \(\textrm{S}\notin \{\top , \bot \}\)), a quantum state
contains a statement \(\textrm{S}\) to be executed (provided that \(\textrm{S}\notin \{\top , \bot \}\)), a quantum state
 of length n, a set A containing the indexes of qubits that are allowed to be accessed by statement \(\textrm{S}\), and a list l of qubit pointers.
of length n, a set A containing the indexes of qubits that are allowed to be accessed by statement \(\textrm{S}\), and a list l of qubit pointers.
The program big-step semantics \({\mathop {\longrightarrow }\limits ^{}}\), described in Figure 3, is defined as a relation in \(\bigcup _{n \in \mathbb {N}} \text {Conf}_n \times \text {Conf}_n\). In the rules of Figure 3, \({\mathop {\longrightarrow }\limits ^{}}\) is annotated by an integer, called level. For example, the level of the conclusion in the (Call\(_{[\,]}\)) rule is 1. The level is used to count the total number of procedure calls that are not in superposition (i.e., in distinct branches of a quantum case).
We now give a brief intuition on the rules of Figure 3. Rules (Asg\(_\bot \)) and (Asg\(_\top \)) evaluate the application of a unitary operator, corresponding to \(\textrm{U}^f(\textrm{j})\), to a qubit \(\textrm{s}[\textrm{i}]\). For that purpose, they evaluate the index n of \(\textrm{s}[\textrm{i}]\) in the global memory. Rule (Asg\(_\bot \)) deals with the error case, where the corresponding qubit is not allowed to be accessed. Rule (Asg\(_\top \)) deals with the success case: the new quantum state is obtained by applying the result of tensoring the evaluation of \(\textrm{U}^f(\textrm{j})\) to the right index. Rules (Seq\(_\diamond \)) and (Seq\(_\bot \)) evaluate the sequence of statements, depending on whether an error occurs or not. The (If) rule deals with classical conditionals in a standard way. The three rules (Case\(_\top \)), (Case\(_\bot \)), and (Case\(_{\notin }\)) evaluate the qubit index n of the control qubit \(\textrm{s}{\small [\textrm{i}]}\). Then they check whether this index belongs to the set of accessible qubits (is n in A?). If so, the two statements \(\textrm{S}_0\) and \(\textrm{S}_1\) are intuitively evaluated in superposition, on the projected state
 and
and
 , respectively. During these evaluations, the index n cannot be accessed anymore. The rule (Call\(_{[\,]}\)) treats the base case of a procedure call when the sorted set parameter is empty. In the non-empty case, rule (Call\(_\diamond \)) evaluates the sorted set parameter \(\textrm{s}\) to \(l'\) and the integer parameter \(\textrm{x}\) to n. It returns the result of evaluating the procedure statement \(\textrm{S}^{\textrm{proc}}\{n/\textrm{x}\}\), where n has been substituted to \(\textrm{x}\), w.r.t. the updated qubit pointers list \(l'\).
, respectively. During these evaluations, the index n cannot be accessed anymore. The rule (Call\(_{[\,]}\)) treats the base case of a procedure call when the sorted set parameter is empty. In the non-empty case, rule (Call\(_\diamond \)) evaluates the sorted set parameter \(\textrm{s}\) to \(l'\) and the integer parameter \(\textrm{x}\) to n. It returns the result of evaluating the procedure statement \(\textrm{S}^{\textrm{proc}}\{n/\textrm{x}\}\), where n has been substituted to \(\textrm{x}\), w.r.t. the updated qubit pointers list \(l'\).
For a given program \(\textrm{P}=\textrm{D}::\textrm{S}\) and a given quantum state
 , the initial configuration for input
, the initial configuration for input
 is
is
 . A program is error-free if there is no initial configuration
. A program is error-free if there is no initial configuration
 such that
such that
 . We write
. We write
 , whenever
, whenever
 holds for some m.
holds for some m.
 is called a terminal configuration. Let \(\mathcal {H}=\bigcup _n\mathcal {H}_{2^n}\), a program terminates if \(\llbracket \textrm{P} \rrbracket \) is a total function in \(\mathcal {H} \rightarrow \mathcal {H}\). Note that if a program terminates then it is obviously error-free but the converse property does not hold. Every program \(\textrm{P}\) can be efficiently transformed into an error-free program \(\textrm{P}_{\lnot \bot }\) such that
is called a terminal configuration. Let \(\mathcal {H}=\bigcup _n\mathcal {H}_{2^n}\), a program terminates if \(\llbracket \textrm{P} \rrbracket \) is a total function in \(\mathcal {H} \rightarrow \mathcal {H}\). Note that if a program terminates then it is obviously error-free but the converse property does not hold. Every program \(\textrm{P}\) can be efficiently transformed into an error-free program \(\textrm{P}_{\lnot \bot }\) such that
 , if
, if
 is defined then
is defined then
 . For example, an assignment
. For example, an assignment
 can be transformed into the conditional statement
can be transformed into the conditional statement
 .
.
Example 1
A notable example of quantum algorithm is the Quantum Fourier Transform (QFT), used as a subroutine in Shor’s algorithm [15], and whose quantum circuit is provided below, with \(R_n \triangleq \llbracket \text {Ph}^{\lambda x . \pi /2^{x-1}} \rrbracket (n)\), for \(n \ge 2\). After applying Hadamard and controlled \(R_n\) gates, the circuit performs a permutation of qubits using swap gates.

Note that \(\lambda x . \pi /2^{x-1}\) is a total function in \(\mathbb {Z}\rightarrow [0, 2\pi ) \cap \tilde{\mathbb {R}}\). Hence, it is polynomial time approximable. The above circuit can be simulated for any number of qubits \(| \text {q} |\) by the following foq program \(\textrm{QFT}\).

Derivation tree and level. Given a configuration c wrt a fixed program \(\textrm{P}\),
 denotes the derivation tree of \(\textrm{P}\), the tree of root c whose children are obtained by applying the rules of Figures 2 and 3 on configuration c with respect to \(\textrm{P}\). We write \(\pi \) instead of
denotes the derivation tree of \(\textrm{P}\), the tree of root c whose children are obtained by applying the rules of Figures 2 and 3 on configuration c with respect to \(\textrm{P}\). We write \(\pi \) instead of
 when \(\textrm{P}\) and c are clear from the context. Note that a derivation tree \(\pi \) can be infinite in the particular case of a non-terminating computation. When \(\pi '\) is finite, \(\pi \unlhd \pi '\) denotes that \(\pi \) is a subtree of \(\pi '\).
when \(\textrm{P}\) and c are clear from the context. Note that a derivation tree \(\pi \) can be infinite in the particular case of a non-terminating computation. When \(\pi '\) is finite, \(\pi \unlhd \pi '\) denotes that \(\pi \) is a subtree of \(\pi '\).
In the case of a terminating computation
 , there exists a terminal configuration \(c'\) and a level \(m\in \mathbb {N}\) such that \(c {\mathop {\longrightarrow }\limits ^{m}} c'\) holds. In this case, the level of \(\pi \) is defined as \(\text {lv}_\pi \triangleq m\). Given a foq program \(\textrm{P}\) that terminates, \(\text {level}_\textrm{P}\) is a total function in \(\mathbb {N}\rightarrow \mathbb {N}\) defined as
, there exists a terminal configuration \(c'\) and a level \(m\in \mathbb {N}\) such that \(c {\mathop {\longrightarrow }\limits ^{m}} c'\) holds. In this case, the level of \(\pi \) is defined as \(\text {lv}_\pi \triangleq m\). Given a foq program \(\textrm{P}\) that terminates, \(\text {level}_\textrm{P}\) is a total function in \(\mathbb {N}\rightarrow \mathbb {N}\) defined as
 .
.
Intuitively, \(\text {level}_\textrm{P}(n)\) corresponds to the maximal number of non-superposed procedure calls in any program execution on an input of length n.
Example 2
Consider the program \(\textrm{QFT}\) of example 1. Assume temporarily that \(\textrm{QFT}\) terminates (this will be shown in Example 3). For all \(n \in \mathbb {N}\), \(\text {level}_{\textrm{QFT}}(n)= \frac{(n+1)(n+2)}{2}+\lfloor {\frac{n}{2}} \rfloor +1\). Indeed, on sorted sets of size n, procedure \(\textrm{rec}\) is called recursively \(n+1\) times and makes \(n+1\) calls to procedure \(\textrm{rot}\) on sorted sets of size n, \(n-1\), \(\ldots \), and 1. On sorted sets of size n, \(\textrm{rot}\) performs n recursive calls. Hence the total number of calls to \(\textrm{rot}\) is equal to \(\sum _{i=1}^{n} i\). Finally, on a sorted set of size n, procedure \(\textrm{inv}\) does \(\lfloor {\frac{n}{2}} \rfloor +1\) recursive call.
A program \(\textrm{P}\) is reversible if it terminates and there exists a program \(\textrm{P}^{-1}\) such that \(\llbracket \textrm{P}^{-1} \rrbracket \circ \llbracket \textrm{P} \rrbracket = Id\).
Theorem 1
All terminating foq programs are reversible.
3 Polynomial time soundness
In this section, we restrict the set of foq programs to a strict subset, named pfoq, that is sound for the quantum complexity class fbqp. For this, we define two criteria: a criterion ensuring that a program terminates and a criterion preventing a terminating program from having an exponential runtime.
Polynomial-time foq. Given two statements \(\textrm{S},\textrm{S}'\), we write \(\textrm{S}\in \textrm{S}'\) to mean that \(\textrm{S}\) is a substatement of \(\textrm{S}'\) and \(\textrm{proc}\in \textrm{S}\) holds if there are \(\textrm{i}\) and \(\textrm{s}\) such that \({\textbf {call }}\textrm{proc}{\small [\textrm{i}]}(\textrm{s}); \in \textrm{S}.\) Given a program \(\textrm{P}=\textrm{D}::\textrm{S}\), we define the relation \(>_{\textrm{P}} \subseteq \text {Procedures} \times \text {Procedures}\) by \(\textrm{proc}_1 >_{\textrm{P}} \textrm{proc}_2\) if \(\textrm{proc}_2 \in \textrm{S}^{\textrm{proc}_1}\), for any two procedures \(\textrm{proc}_1,\) \(\textrm{proc}_2 \in \textrm{S}\). Let the partial order \(\succeq _{\textrm{P}}\) be the transitive and reflexive closure of \(>_{\textrm{P}}\) and define the equivalence relation \(\sim _{\textrm{P}}\) by \(\textrm{proc}_1 \sim _{\textrm{P}} \textrm{proc}_2 \) if \(\textrm{proc}_1\succeq _{\textrm{P}} \textrm{proc}_2\) and \(\textrm{proc}_2 \succeq _{\textrm{P}} \textrm{proc}_1\) both hold. Define also the strict order \(\succ _{\textrm{P}}\) by \(\textrm{proc}_1 \succ _{\textrm{P}} \textrm{proc}_2 \) if \(\textrm{proc}_1\succeq _{\textrm{P}} \textrm{proc}_2\) and \(\textrm{proc}_1 \not \sim _{\textrm{P}} \textrm{proc}_2\) both hold.
Definition 1
Let wf be the set of foq programs \(\textrm{P}\) that are error-free and satisfy the well-foundedness constraint: \(\forall \textrm{proc}\in \textrm{P},\ \forall {\textbf {call }}\textrm{proc}'{\small [\textrm{i}]}(\textrm{s}); \in \textrm{S}^{\textrm{proc}},\)
Lemma 1
If \(\textrm{P}\in \textsc {wf} \), then \(\textrm{P}\) terminates.
Example 3
Consider the program \(\textrm{QFT}\) of Example 1. The statements of the procedure declarations define the following relation: \(\textrm{rec}>_{\textrm{QFT}} \textrm{rec}\), \(\textrm{rec}>_{\textrm{QFT}} \textrm{rot}\), \(\textrm{rot}>_{\textrm{QFT}} \textrm{rot}\), and \(\textrm{inv}>_{\textrm{QFT}} \textrm{inv}\). Consequently, \(\textrm{rec}\sim _{\textrm{QFT}} \textrm{rec}\), \(\textrm{rot}\sim _{\textrm{QFT}} \textrm{rot}\), \(\textrm{inv}\sim _{\textrm{QFT}} \textrm{inv}\), and \(\textrm{rec}\succ _{\textrm{QFT}} \textrm{rot}\) hold. For each call to an equivalent procedure, we check that the argument decreases: \(\bar{\textrm{p}}\ominus {\small [1]}\) in \(\textrm{rec}\), \(\bar{\textrm{p}}\ominus {\small [2]}\) in \(\textrm{rot}\), and \(\bar{\textrm{p}}\ominus {\small [1,| \bar{\textrm{p}} |]}\) in \(\textrm{inv}\). Consequently, \(\textrm{QFT}\in \textsc {wf} \). We deduce from Theorem 1 that \(\textrm{QFT}\) terminates.
We now add a further restriction on mutually recursive procedure calls for guaranteeing polynomial time using a notion of width.
Definition 2
Given a program \(\textrm{P}\) and a procedure \(\textrm{proc}\in \textrm{P}\), the width of \(\textrm{proc}\) in \(\textrm{P}\), noted \(\text {width}_{\textrm{P}}(\textrm{proc})\), and the width of \(\textrm{proc}\) in \(\textrm{P}\) relatively to statement \(\textrm{S}\), noted \(w_{\textrm{P}}^{\textrm{proc}}(\textrm{S})\), are two positive integers in \(\mathbb {N}\). They are defined inductively by:

Definition 3
(PFOQ). Let pfoq be the set of programs \(\textrm{P}\) in wf that satisfy the following constraint: \(\forall \textrm{proc}\in \textrm{P}, \text {width}_{\textrm{P}}(\textrm{proc})\le 1\).
Example 4
In the program of Example 1, \(\text {width}_{\textrm{QFT}}(\textrm{rec}) = \text {width}_{\textrm{QFT}}(\textrm{rot}) = \text {width}_{\textrm{QFT}}(\textrm{inv}) =1\), since \(\textrm{rec}\succ _{\textrm{QFT}} \textrm{rot}\) holds. Since \(\textrm{QFT}\in \textsc {wf} \), by Example 3, we conclude that \(\textrm{QFT}\) is a pfoq program.
We now show that the level of a pfoq program is bounded by a polynomial in the length of its input.
Lemma 2
For each \(\textsc {pfoq} \) program \(\textrm{P}\), there exists a polynomial \(Q \in \mathbb {N}[X]\) such that \(\forall n \in \mathbb {N},\ \text {level}_\textrm{P}(n) \le Q(n)\).
Moreover, checking whether a program is pfoq is tractable.
Theorem 2
For each foq program \(\textrm{P}\), it can be decided in time \(O(| \textrm{P} |^2)\) whether \(\textrm{P}_{\lnot \bot } \in \textsc {pfoq} \).
Quantum Turing machines and FBQP. Following Bernstein and Vazirani [2], a k-tape Quantum Turing Machine (QTM), with \(k \ge 1\), is defined by a triplet \((\varSigma ,Q,\delta )\) where \(\varSigma \) is a finite alphabet including a blank symbol \(\#\), Q is a finite set of states with an initial state \(s_0\) and a final state \(s_\top \ne s_0\), and \(\delta \) is the quantum transition function in \(Q\times \varSigma ^k \rightarrow \tilde{\mathbb {C}}^{Q\times \varSigma ^k\times \{L,N,R\}^k}\); \(\{L,N,R\}\) being the set of possible movements of a head on a tape. Each tape of the QTM is two-way infinite and contains cells indexed by \(\mathbb {Z}\). A QTM successfully terminates if it reaches a superposition of only the final state \(s_\top \). A QTM is said to be well-formed if the transition function \(\delta \) preserves the norm of the superposition (or, equivalently, if the time evolution of the machine is unitary). The starting position of the tape heads is the start cell, the cell indexed by 0. If the machine terminates with all of its tape heads back on the start cells, it is called stationary. We will use stationary in the case where the machine terminates with its input tape head in the first cell, and all other tape heads in the last non-blank cell. We will further refer to a QTM as being in normal form if the only transitions from the final state \(s_\top \) are towards the initial state \(s_0\). These will be important conditions for the composition and branching constructions of QTMs. If a QTM is well-formed, stationary, and in normal form, we will call it conservative [16] (N.B.: our notion of stationary QTM differs but can be shown to be equivalent to the definition of stationary QTM in [16]).
A configuration \(\gamma \) of a k-tape QTM is a tuple \((s,\overline{w},\overline{n})\), where s is a state in Q, \(\overline{w}\) is a k-tuple of words in \(\varSigma ^*\), and \(\overline{n}\) is a k-tuple of indexes (head positions) in \(\mathbb {Z}\). An initial (final) configuration \(\gamma _{init}\) (resp. \(\gamma _{fin}\)) is a configuration of the shape \((s_0,\overline{w},\overline{0})\) (resp. \((s_\top ,\overline{w},\overline{0})\)). We use \(\gamma (w)\) to denote a configuration \(\gamma \) where the word w is written on the input/output tape. Following [2], we write \(\mathcal {S}\) to represent the inner-product space of finite complex linear combinations of configurations of the QTM M with the Euclidean norm. A QTM M defines a linear time operator \(U_M : \mathcal {S} \rightarrow \mathcal {S}\), that outputs a superposition of configurations
 obtained by applying a single-step transition of M to a configuration
obtained by applying a single-step transition of M to a configuration
 (i.e.,
(i.e.,
 ). Let \(U_M^t\), for \(t \ge 1\), be the t-steps transition obtained from \(U_M\) as follows: \(U_M^1 \triangleq U_M\) and \(U_M^{t+1} \triangleq U_M \circ U_M^t\). Given a quantum state
). Let \(U_M^t\), for \(t \ge 1\), be the t-steps transition obtained from \(U_M\) as follows: \(U_M^1 \triangleq U_M\) and \(U_M^{t+1} \triangleq U_M \circ U_M^t\). Given a quantum state
 and a configuration \(\gamma \), let
and a configuration \(\gamma \), let
 be the quantum configuration defined by
be the quantum configuration defined by
 .
.
A quantum function \(f : \mathcal {H} \rightarrow \mathcal {H}\) is computed by the QTM M in time t if for any
 ,
,
 . Given \(T:\mathbb {N}\rightarrow \mathbb {N}\) and a quantum function f, we say that the QTM M computes f in time T if for inputs of length n, M computes f in time T(n).
. Given \(T:\mathbb {N}\rightarrow \mathbb {N}\) and a quantum function f, we say that the QTM M computes f in time T if for inputs of length n, M computes f in time T(n).
Definition 4
Given two functions \(f:\{0, 1\}^\star \rightarrow \{0, 1\}^\star \), \(F:\mathcal {H}\rightarrow \mathcal {H}\), and a value \(p\in [0,1]\), we say that f is computed by F with probability p if
 .
.
The class fbqp is the functional extension of the complexity class bqp.
Definition 5
([2]). A function \(f \in \{0,1\}^\star \rightarrow \{0,1\}^\star \) is in fbqp iff there exist a QTM M and a polynomial \(P \in \mathbb {N}[X]\) s.t. M computes f in time P with probability \(\frac{2}{3}\).
A function \(f\in \{0,1\}^\star \rightarrow \{0,1\}^\star \) has a polynomial bound \(P\in \mathbb {N}[X]\) if \(\forall n \in \mathbb {N}, \forall x\in \{0,1\}^n, \exists k \le P(n),\ f(x)\in \{0, 1\}^{k}\). Functions in fbqp have a polynomial bound as the size of their output is smaller than the polynomial time bound.
Soundness. We show that QTMs can simulate the function computed by any terminating foq program. The time complexity of this simulation depends on the length of the input quantum state and on the level of the considered program.
Lemma 3
For any terminating foq program \(\textrm{P}\), there exists a conservative QTM M that computes \(\llbracket \textrm{P} \rrbracket \) in time \(O(n+n \times \text {level}_\textrm{P}(n))\).
Now we show that any \(\textsc {pfoq} \) program computes a fbqp function.
Theorem 3
Given a pfoq program \(\textrm{P}\), a function \(f:\{0, 1\}^\star \rightarrow \{0, 1\}^\star \), and a value \(p\in (\frac{1}{2},1]\). If f is computed by \(\llbracket \textrm{P} \rrbracket \) with probability p then \(f \in \textsc {fbqp} \).
Proof
4 FBQP completeness
In this section we show that any function in fbqp can be faithfully approximated by a pfoq program. Toward this end, we show that Yamakami’s [16] fbqp -complete function algebra can be exactly simulated in pfoq.
Yamakami’s function algebra. A characterization of fbqp was provided in [16] using a function algebra, named \(\widehat{\square ^{\textrm{QP}}_1}\). Given a quantum state
 and a word \(w \in \{0,1\}^n\), with
and a word \(w \in \{0,1\}^n\), with
 .
.
 can be written as
can be written as
 , with \(w_i \in \{0,1\}^n\) and
, with \(w_i \in \{0,1\}^n\) and
 . We write
. We write
 as an abuse of notation for the quantum state defined by
as an abuse of notation for the quantum state defined by

Definition 6
\(\widehat{\square ^{\textrm{QP}}_1}\) is the smallest class of functions including the basic initial functions \(\{I,Ph_\theta , Rot_\theta , NOT, SWAP \}\), with \(\theta \in [0,2\pi )\cap \tilde{\mathbb {C}}\),
and closed under schemes Comp, Branch, and \(kQRec_t\), for \(k,t \in \mathbb {N}\),
-

-

-
 where each \(F_w \in \{kQRec_t[F,G,H],I\}\).
where each \(F_w \in \{kQRec_t[F,G,H],I\}\).
To handle general fbqp functions, [16] defines the extended encoding of an input \(x\in \{0,1\}^\star \) as
 , for some polynomial \(P \in \mathbb {N}[X]\) that is an upper bound on the output size of the desired fbqp function. \(\phi _P\) simply consists in the quantum state
, for some polynomial \(P \in \mathbb {N}[X]\) that is an upper bound on the output size of the desired fbqp function. \(\phi _P\) simply consists in the quantum state
 preceded by a polynomial number of ancilla qubits. These ancilla provide space for internal computations and account for the polynomial bound associated to polynomial time QTMs.
preceded by a polynomial number of ancilla qubits. These ancilla provide space for internal computations and account for the polynomial bound associated to polynomial time QTMs.
Theorem 4
([16]). Given \(f : \{0,1\}^\star \rightarrow \{0,1\}^\star \) with polynomial bound \(P\in \mathbb {N}[X]\), the following statements are equivalent.
-
1.
The function f is in fbqp.
-
2.
There exists \(F \in \widehat{\square ^{\textrm{QP}}_1}\) such that \(F \circ \phi _P\) computes f with probability \(\frac{2}{3}\).
We show the following result by structural induction on a function in \(\widehat{\square ^{\textrm{QP}}_1}\).
Theorem 5
Let F be a function in \(\widehat{\square ^{\textrm{QP}}_1}\). Then there exists a pfoq program \(\textrm{P}\) such that \(\llbracket \textrm{P} \rrbracket = F\).
We are now ready to state the completeness result.
Theorem 6
For every function f in fbqp with polynomial bound \(Q \in \mathbb {N}[X]\), there is a pfoq program \(\textrm{P}\) such that \(\llbracket \textrm{P} \rrbracket \circ \phi _Q\) computes f with probability \(\frac{2}{3}\).
Proof
5 Compilation to polynomial-size quantum circuits
In this section, we provide an algorithm that compiles a pfoq program on a given input length \(n \in \mathbb {N}\) into a quantum circuit of size polynomial in n.
Quantum circuits [8] are a well-known graphical computational model for describing quantum computations. Qubits are represented by wires. Each unitary transformation U acting on n qubits can be represented as a gate U with n inputs and n outputs. A circuit C is an element of a PROP category ([10], a symmetric strict monoidal category) whose morphisms are generated by gates G and wires. Let \(\mathbbm {1}\) be the identity circuit (for any length) and \(\circ \) and \(\otimes \) be the composition and product, respectively. By abuse of notation, given k circuits \(C^1, \ldots , C^k\), \(\circ _{i=1}^k C^i\) will denote the circuit \(\tilde{C}^1 \circ \dots \circ \tilde{C}^k\), where each circuit \(\tilde{C^i}\) is obtained by tensoring \(C^i\) appropriately with identities so that the output of \(C^i\) matches the input of \(C^{i+1}\). By construction, a circuit is acyclic. Each circuit \(C_n\) can be indexed by its number \(n \in \mathbb {N}\) of input wires (i.e., non ancilla qubits) and computes a function \(\llbracket C_n \rrbracket \in \mathcal {H}_{2^n} \rightarrow \mathcal {H}_{2^n}\). To deal with functions in \(\mathcal {H}\rightarrow \mathcal {H}\), we consider families of circuits \((C_n)_{n\in \mathbb {N}}\), that are sequences of circuits such that each \(C_n\) encodes computation on quantum states of length n. Hence each circuit has n input qubits plus some extra ancilla qubits. These ancillas can be used to perform intermediate computations but also to represent functions whose output size is strictly greater than their input size. To avoid the consideration of families encoding undecidable properties, we put a uniformity restriction.
Definition 7
A family of circuits \((C_n)_{n\in \mathbb {N}}\) is said to be uniform if there exists a polynomial time Turing machine that takes n as input and outputs a representation of \(C_n\), for all \(n\in \mathbb {N}\).
In quantifying the complexity of a circuit, it is necessary to specify the considered elementary gates, and define the complexity of an operation as the number of elementary gates needed to perform it. In our setting, we consider the following set of universal elementary gates \(\{ {R}_Y(\pi /4), {P}(\pi /4),{CNOT}\}\). The size \(\# C\) of a circuit C is equal to the number of its gates and wires.
Definition 8
A family of circuits \((C_n)_{n\in \mathbb {N}}\) is said to be polynomial-size with \(\alpha \in \mathbb {N}\rightarrow \mathbb {N}\) ancilla qubits if there exists a polynomial \(P \in \mathbb {N}[X]\) such that, for each \(n\in \mathbb {N}\), \(\# C_n \le P(n)\) and the number of ancilla qubits in \(C_n\) is exactly \(\alpha (n)\).
Let \(\chi _m:\mathcal {H}_{2^n}\rightarrow \mathcal {H}_{2^{n+m}}\) be defined by
 , for a state
, for a state
 of size n. Let \(\xi _m: \mathcal {H}_{2^n}\rightarrow \mathcal {H}_{2^m}\), with \(m\le n\), be defined by
of size n. Let \(\xi _m: \mathcal {H}_{2^n}\rightarrow \mathcal {H}_{2^m}\), with \(m\le n\), be defined by
 . Finally, let \(| w |\), for \(w \in \{0,1\}^\star \), be the size of the word w.
. Finally, let \(| w |\), for \(w \in \{0,1\}^\star \), be the size of the word w.
Theorem 7
(Adapted from [17] and [11]) A function \(f: \{0, 1\}^{\star }\rightarrow \{0, 1\}^{\star }\) is in fbqp iff there exists a uniform polynomial-size family of circuits \((C_n)_{n\in \mathbb {N}}\) with \(\alpha \) ancilla qubits s.t. \(\forall x\in \{0,1\}^\star \),
 .
.
In Theorem 7, \(\llbracket C_{| x |} \rrbracket \) is a function in \(\mathcal {H}_{2^{| x | + \alpha (| x |)}} \rightarrow \mathcal {H}_{2^{| x | + \alpha (| x |)}}\) The function \(\chi _{\alpha (| x |)}\) pads the input with ancilla in state
 to match the circuit dimension. The function \(\xi _{| f(x) |}\) projects the output of the circuit to match the length of the function output \(| f(x) |\). Hence, for
to match the circuit dimension. The function \(\xi _{| f(x) |}\) projects the output of the circuit to match the length of the function output \(| f(x) |\). Hence, for
 ,
,
 .
.
Compilation to circuits. For each pfoq program \(\textrm{P}\), the existence of a polynomial-size uniform family of circuits \((C_n)_{n\in \mathbb {N}}\) that computes \(\llbracket \textrm{P} \rrbracket \) is entailed by the combination of Lemma 2 and Theorem 7. However, due to the complex machinery of QTM, the constructions of both proofs cannot be used in practice to generate a circuit. In this section, we exhibit an algorithm that compiles directly a pfoq program to a polynomial-size circuit. Note that this compilation process requires some care since recursive procedure calls in quantum cases may yield an exponential number of calls. The remainder of this section will be devoted to presenting an algorithm, named compile, which, for a given pfoq program \(\textrm{P}\) and a given integer n produces a circuit \(C_n\) such that
 .
.
The compile algorithm uses two subroutines, named compr and optimize, and is defined by \({\textbf {compile}} (\textrm{P},n) \triangleq {\textbf {compr}} (\textrm{P},[1,\ldots ,n],\cdot )\).
The subroutine compr (Algorithm 1) generates the circuit inductively on the program statement. It takes as inputs: a program \(\textrm{P}\), a list of qubit pointers l, and a control structure \(cs\). A control structure cs is a partial function in \(\mathbb {N}\rightarrow \{0,1\}\), mapping a qubit pointer to a control value (of a quantum case). Let \(\cdot \) be the control structure of empty domain. For \(n \in \mathbb {N}\) and \(k \in \{0,1\}\), \(cs[n := k]\) is the control structure obtained from cs by setting \(cs(n) \triangleq k\). For a given \(x\in \{0,1\}^\star \), we say that state
 satisfies cs if, \(\forall n\in dom(cs)\),
satisfies cs if, \(\forall n\in dom(cs)\),
 . Two control structures cs and \(cs'\) are orthogonal if there does not exist a state
. Two control structures cs and \(cs'\) are orthogonal if there does not exist a state
 that satisfies cs and \(cs'\). Note that if \(\exists i \in dom(cs) \cap dom(cs'),\ cs(i)+cs'(i)=1\) then cs and \(cs'\) are orthogonal.
that satisfies cs and \(cs'\). Note that if \(\exists i \in dom(cs) \cap dom(cs'),\ cs(i)+cs'(i)=1\) then cs and \(cs'\) are orthogonal.

Given a control structure cs and a statement \(\textrm{S}\), a controlled statement is a pair \((cs,\textrm{S}) \in \textrm{Cst}\triangleq (\mathbb {N}\rightarrow \{0,1\}) \times \text {Statements}\). Intuitively, a controlled statement \((cs,\textrm{S})\) denotes a statement controlled by the qubits whose indices are in dom(cs). For a unitary gate \(U\in \mathcal {H}_{2^n}\rightarrow \mathcal {H}_{2^n}\), a control structure cs, and a list of pointers \(l=[x_1,\ldots ,x_n] \in \mathcal {L}(\mathbb {N})\) such that \(\{x_1,\ldots ,x_n\}\cap dom(cs)=\emptyset \), \(U(cs,l)\) denotes the circuit applying gate U on qubits \(\bar{\text {q}}{\small [x_1]}, \ldots , \bar{\text {q}}{\small [x_n]}\), whenever \(\forall m \in dom(cs),\) \(\bar{\text {q}}{\small [m]}\) is in state
 . As demonstrated in [11], this circuit can be built with O(card(dom(cs))) elementary gates and ancillas, and a single controlled-U gate.
. As demonstrated in [11], this circuit can be built with O(card(dom(cs))) elementary gates and ancillas, and a single controlled-U gate.
Example 5
As an illustrative example, consider a binary gate U and a control structure cs such that \(dom(cs)=\{1,2,3\}\), \(cs(1)=cs(2)=1\), and \(cs(3)=0\). Also consider a list \(l=[4,5] \in \mathcal {L}(\mathbb {N})\). The circuit \(U(cs,l)\) is provided in Figure 4.
Similarly, we can define a generalized Toffoli gate as a circuit of the shape NOT(cs, n). Since card(dom(cs)) will not scale with the size of the input, such a circuit has a constant cost in gates and ancillas and can thus be considered as an elementary gate. We will also be interested in rearranging wires under a given control structure. For two lists of qubit pointers \(l_1=[x_1,\ldots ,x_n],\ l_2=[x'_1,\ldots ,x'_n] \in \mathcal {L}(\mathbb {N})\), define \({SWAP}(cs,l_1,l_2)\) as the circuit that swaps the wires in \(l_1\) with wires in \(l_2\), controlled on cs. This circuit needs in the worst case one ancilla and O(n) controlled SWAP gates (also known as Fredkin gates).
Let \(\mathcal {D}\triangleq \mathcal {D}(\text {Procedures}\times \mathbb {Z}\times \mathbb {N}\rightarrow \mathbb {N}\times \mathcal {L}(\mathbb {N}))\) be the set of dictionaries mapping keys of the shape \((\textrm{proc},i,j)\) to pairs of the shape (a, l), where i is the value of a classical parameter, j is the size of a sorted set, and a is a qubit index. We will denote the empty dictionary by \(\{\}\). Let also \(a \leftarrow {{\textbf {new }}} ancilla()\) be an instruction that sets a to a fresh qubit index.
The subroutine optimize (Algorithm 2) treats the complex cases where circuit optimizations (merging) are needed, that is for recursive procedure calls. It takes as input a sequence of procedure declarations \(\textrm{D}\), a list of controlled statements \(l_{\textrm{Cst}}\), a procedure name \(\textrm{proc}\), a list of qubit pointers l, and a dictionary \(\text {Anc}\). The subroutine iterates on list \(l_{\textrm{Cst}}\) of controlled statements, indicating the statements left to be treated together with their control qubits. When recursive procedure calls appear in distinct branches of a quantum case, the algorithm merges these calls together. For that purpose, it uses new ancilla qubits as control qubits. Given procedure calls of shape \({\textbf {call }}\textrm{proc}[\textrm{i}](\textrm{s});\), with respect to a given list \(l \in \mathcal {L}(\mathbb {N})\), such that \((\textrm{i},l) \Downarrow _\mathbb {Z}i\), \((\textrm{s}, l)\Downarrow _{\mathcal {L}(\mathbb {N})} l'\), and \((| \textrm{s} |,l) \Downarrow _\mathbb {N}j\). If the key \((\textrm{proc},i,j)\) already exists in the dictionary \(\text {Anc}\), the associated ancilla is re-used, otherwise, \(\text {Anc}[\textrm{proc}, i, j]\) is set to \((a,l')\). We can assume w.l.o.g. that the statement controlled on the ancilla can be treated only after all the re-uses of the ancilla. This can be done without increasing the total complexity of optimize.
Some extra ancillas e are also created for swapping wires and are not explicitly indexed since they are not revisited by the subroutine, and are just considered unique. Ancillas a and e are indexed and treated as input qubits, therefore they can be part of the domain of control structures.

Theorem 8
For any \( \textrm{P}\) in pfoq, there is \(Q \in \mathbb {N}[X]\), \(\forall n \in \mathbb {N}\),

 and \( \# {\textbf {compile}}(\textrm{P},n) \le Q(n)\).
and \( \# {\textbf {compile}}(\textrm{P},n) \le Q(n)\).
Example 6
\({\textbf {compile}} (\textrm{QFT},n)\) outputs the circuit provided in Example 1. Notice that there is no extra ancilla as no procedure call appears in the branch of a quantum case.
Polynomial-size circuits. We show Theorem 8 by exhibiting that any exponential growth of the circuit can be avoided by the compile algorithm using an argument based on orthogonal control structures. With a linear number of gates and a constant number of extra ancillas, we can merge calls referring to the same procedure, on different branches of a quantum case, when they are applied to sorted sets of equal size. An example of the construction is given in Figure 5 where two instances of a gate U are merged into one using SWAP gates and gates controlled by orthogonal control structures.
The following proposition shows that multiple uses of a gate can be merged in one provided they are applied to orthogonal control structures.
Lemma 4
For any circuit \(C_n \triangleq \circ _{i=1}^k U(cs_i,l_i)\), with a unitary gate U, pairwise orthogonal \(cs_1, \dots , cs_k\in \textrm{Cst}\), and \(l_1, \dots l_k\in \mathcal {L}(\mathbb {N})\), there exists a circuit C using one controlled gate U, O(kn) gates, and O(k) ancillas, and such that \(\llbracket C \rrbracket = \llbracket C_n \rrbracket \).
Now we show that orthogonality is an invariant property of compile.
Lemma 5
Orthogonality is an invariant property of the control structures in \(l_{\textrm{Cst}}\) of the subroutine optimize. In other words, for any two distinct pairs \((cs, \textrm{S})\), \((cs', \textrm{S}')\) in \(l_{\textrm{Cst}}\), cs and \(cs'\) are orthogonal.
Theorem 9
For any \(\textrm{P}\) in pfoq, compile\((\textrm{P},n)\) runs in time \(O(n^{2| \textrm{P} |+1})\).
Proof
Using Lemma 4 and Lemma 5. \(\square \)
As there is no circuit duplication in the assignments of compile, we can deduce from Theorem 9 that the compiled circuit is of polynomial size.
Corollary 1
For any \(\textrm{P}\) in pfoq, there exists a polynomial \(Q\in \mathbb {N}[X]\) such that \(\#{{\textbf {compile}}}(\textrm{P},n) \le Q(n)\).
References
Bellantoni, S., Cook, S.: A new recursion-theoretic characterization of the polytime functions. computational complexity 2(2), 97–110 (Jun 1992). https://doi.org/10.1007/BF01201998.
Bernstein, E., Vazirani, U.: Quantum complexity theory. SIAM Journal on Computing 26(5), 1411–1473 (1997). https://doi.org/10.1137/S0097539796300921
Boykin, P.O., Mor, T., Pulver, M., Roychowdhury, V., Vatan, F.: On universal and fault-tolerant quantum computing (1999). https://doi.org/10.48550/ARXIV.QUANT-PH/9906054
Briegel, H.J., Browne, D.E., Dür, W., Raussendorf, R., Van den Nest, M.: Measurement-based quantum computation. Nature Physics 5(1), 19–26 (2009). https://doi.org/10.1038/nphys1157
Dal Lago, U.: A short introduction to implicit computational complexity. In: ESSLLI 2010. pp. 89–109 (2011). https://doi.org/10.1007/978-3-642-31485-8_3
Dal Lago, U., Masini, A., Zorzi, M.: Quantum implicit computational complexity. Theoretical Computer Science 411(2), 377–409 (2010). https://doi.org/10.1016/j.tcs.2009.07.045
Danos, V., Kashefi, E.: Determinism in the one-way model. Physical Review A 74(5), 052310 (2006). https://doi.org/10.1103/PhysRevA.74.052310
Deutsch, D.E.: Quantum computational networks. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 425(1868), 73–90 (1989)
Feynman, R.P.: Simulating physics with computers. International Journal of Theoretical Physics 21(6), 467–488 (Jun 1982). https://doi.org/10.1007/BF02650179
MacLane, S.: Categorical algebra. Bulletin of the American Mathematical Society 71(1), 40–106 (1965). https://doi.org/10.1090/S0002-9904-1965-11234-4
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press (2011)
Péchoux, R.: Implicit computational complexity: past and future. Mémoire d’habilitation á diriger des recherches (2020), https://tel.archives-ouvertes.fr/tel-02978986, université de Lorraine
Ross, N.J.: Algebraic and logical methods in quantum computation. PhD thesis (2015). https://doi.org/10.48550/ARXIV.1510.02198
Selinger, P.: Towards a quantum programming language. Mathematical Structures in Computer Science 14(4), 527–586 (2004). https://doi.org/10.1017/S0960129504004256
Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In: Proceedings 35th Annual Symposium on Foundations of Computer Science. pp. 124–134 (1994). https://doi.org/10.1109/SFCS.1994.365700
Yamakami, T.: A schematic definition of quantum polynomial time computability. J. Symb. Log. 85(4), 1546–1587 (2020). https://doi.org/10.1017/jsl.2020.45
Yao, A.C.C.: Quantum circuit complexity. In: Proceedings of 1993 IEEE 34th Annual Foundations of Computer Science. pp. 352–361 (1993). https://doi.org/10.1109/SFCS.1993.366852
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Hainry, E., Péchoux, R., Silva, M. (2023). A Programming Language Characterizing Quantum Polynomial Time. In: Kupferman, O., Sobocinski, P. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2023. Lecture Notes in Computer Science, vol 13992. Springer, Cham. https://doi.org/10.1007/978-3-031-30829-1_8
Download citation
DOI: https://doi.org/10.1007/978-3-031-30829-1_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-30828-4
Online ISBN: 978-3-031-30829-1
eBook Packages: Computer ScienceComputer Science (R0)


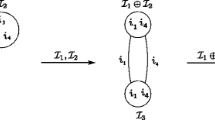












 where each
where each 
