Abstract
We propose a superposition-based proof procedure to reason on equational first order formulas defined over graphs. First, we introduce the considered graphs that are directed labeled graphs with lists of roots standing for pins or interfaces for replacements. Then the syntax and semantics of the considered logic are defined. The formulas at hand are clause sets built on equations and disequations on graphs. Afterwards, a sound and complete proof procedure is provided, and redundancy criteria are introduced to dismiss useless clauses and improve the efficiency of the procedure. In a first step, a set of inferences rules is provided in the case of uninterpreted labels. In a second step, the proposed rules are lifted to take into account labels defined as terms interpreted in some arbitrary theory. Particular formulas of interest are Horn clauses, for which stronger redundancy criteria can be devised. Essential differences with the usual term superposition calculus are emphasized.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Graphs are ubiquitous structures in computer science. They are used to model several notions such as data, program runs (transition systems), networks, software and hardware architectures. They are also often used as foundational structures to model knowledge or data bases, cognitive or intelligent systems as well as physical, chemical or biological phenomena. They constitute, in addition, the basis of operational research or combinatorics. Graphs are, definitely, fundamental structures for modelling, computing and reasoning. Graph transformations have been studied since the early 70’s [29]. Some of their applications can be found in [16, 18]. In the literature, one can distinguish two main streams of approaches for graph transformation, namely the algebraic approaches [12, 15] where category theory is used to define structure transformations in a very abstract and elegant way and the algorithmic approaches where graph transformations are defined by means of the actual algorithms involved in the transformations [13, 20].
During the last decade, a very interesting application of graph transformations has emerged in the area of quantum models of computation, see e.g., the calculi ZX [11], ZH [3], ZW [24] or PBS [10]. In these calculi, one can specify quantum algorithms using particular graphs and can make some equational reasoning on them to verify correctness of quantum algorithms, see e.g. the Quantomatic tool [25]. In such situations, making automated equational reasoning over graphs is very desirable even though equational theories over graphs are not recursively enumerable in general (see e.g. [7]).
The superposition calculus [1] is one of the most successful automated proof procedures which handles equational theories (on terms) which is being actually implemented in various theorem provers such as Vampire [28], Spass [32], or E [30]. The calculus operates on finite sets of equational clauses. It is defined as a set of inference rules, which deduce new clauses from previous ones. To prune the search space, strong restrictions (based on term orderings and literal selection functions) are imposed on the inferences, and redundancy criteria are provided to detect and dismiss useless clauses. The rules are applied until a contradiction (i.e., the empty clause) is derived or until the set is saturated, i.e., no further non-redundant clause may be deduced. The calculus is refutationally complete, in the sense that it is able to derive a contradiction from any unsatisfiable clause set. In a recent work [14], we proposed a superposition calculus for testing the unsatisfiability of sets of equations and disequations between graphs whose shapes are inspired by those used in the ZX calculus, where nodes are labeled by first-order (uninterpreted) terms. In the present paper we extend this work in several directions: (i) We tackle full clauses, i.e., disjunctions of equations and disequations. This extension turned out to be much more difficult than we initially expected, due to the fact that no reduction order exists on the considered graphs (see Examples 19 and 22), which complicates the completeness proof. We introduce redundancy criteria that cover some usual deletion and simplification rules. (ii) We lift the obtained calculus into a constrained calculus operating on graphs labeled by terms interpreted in some base theory. The procedure is a semi-decision procedure for unsatisfiability if the underlying theory is (semi) decidable and compact. (iii) We consider a slightly different class of graphs, where multi-edges are allowed. The new framework has the advantage of being both more general and simpler, and it also improves the efficiency of the calculus (more precisely for the computation of “merges” between graphs, see Remark 9).
Why defining a graph superposition calculus is difficult. We wish to emphasize some important differences between term and graph superposition. (i) It is well-known that term rewrite systems that are terminating and in which all critical pairs are joinable are confluent. This property plays a key rôle in the completeness proof of the superposition calculus. However, such a property does not hold for graph rewrite systems, and, worse, confluence is undecidable for terminating graph rewrite rules (if confluence is meant modulo isomorphism). As it is done in [14] we overcome this issue by considering a special class of graphs, for which the above property holds. This class is obtained by restricting the way graphs can be composed and replaced, using a sequence of distinguished nodes in the graphs, called roots. (ii) The usual superposition calculus is based on the use of a reduction order, i.e., a well-founded order on terms that is total on ground terms and closed under instantiation and embedding. Unfortunately no such order exists for graphs in general (see Example 19). Thus the model construction algorithm used to establish refutational completeness must cope with non terminating systems (indeed, since a ground equation \(\mathfrak {g}\approx \mathfrak {h}\) cannot always be oriented, one must consider both rules: \(\mathfrak {g}\rightarrow \mathfrak {h}\) and \(\mathfrak {h}\rightarrow \mathfrak {g}\), which entails that the system does not terminate). Confluence is harder to establish for non terminating systems and we need to devise a new confluence criterion. (iii) The usual redundancy criterion of [1] (where a clause is considered redundant if it is implied by smaller clauses) does not apply to graphs. For instance the conclusion of an inference may be strictly bigger than all the premises (see Example 21). This is due to the fact that two graphs may overlap without one of them being included in the other. Such a behavior cannot be avoided, since, as proven in [14, Theorem 45], satisfiability is undecidable for sets of ground equational clauses defined on graphs (whereas it is well known to be decidable for standard ground clauses based on terms), thus superposition cannot terminate on ground graphs. Furthermore, we show (see Example 22) that the calculus is – rather surprisingly – not compatible with tautology deletion in general (tautology deletion is possible for Horn clauses).
Related work. The graphs we are considering are intended to capture (possibly cyclic) circuit shaped structures such as those used in the ZX or related calculi. They are close to hypergraphs with interfaces as used in some papers (see, e.g. [5]) where the roots or interfaces are used in the gluing process while transforming a graph. We follow an algorithmic approach when transforming the graphs. This approach eases the completeness proofs of the proposed superposition calculus. However, the performed graph transformations used in the present paper can be encoded as simple double pushout (DPO) [19] steps of the form \(L \longleftarrow Roots \longrightarrow R \) with some additional constraints on matched subgraphs. It is also a particular case of DPOI steps (DPO with interfaces) where the roots play the rôle of the interfaces [5]. Automated reasoning in presence of graph structures is not an easy task in general. Several authors did tackle this problem and one can distinguish different approaches in the literature. Variants of Hoare-like calculi have been proposed for the verification of graph transformation systems see, e.g., [6, 8, 23, 26]. Likewise, model checking procedures have also been devised in presence of graph structures see, e.g. [27, 31]. In these works, a dynamic logic underlying program execution is assumed. In addition, a dedicated logic is used to express graph properties to be proven. Other techniques have been used to prove graph equivalences such as bisimulation [17] or normalization using terminating and confuent graph rewriting systems [9]. In the paper at hand, we are rather concerned by a refutational proof technique based on superposition dedicated to a class of graphs. Thus our proof procedure departs from all the aforementioned works. To our knowledge, only the report [22] presents a refutational procedure dedicated to ZX diagrams which is close to ours. However, the authors use the classical superposition calculus [1] over first-order terms and provide a translation from the considered graphs to first-order terms. Such translation needs the use of additional axioms encoding some graph properties such as associativity and commutativity of graph constructor operations. Such additional axioms are useless in our framework. The class of graph rewriting systems handled in our proof procedure are not necessarily terminating and thus we had to devise new criteria to ensure their (ground) confluence instead of using joinability of pre-critical pairs as done in [4].
The paper is organized as follows. Section 2 introduces some basic notations and defines the considered graphs and the operations used over them. In Section 3 the syntax and semantics of the formulas are introduced. In Section 4, a first set of inference rules is defined to test the satisfiability of sets of clauses where graphs are endowed with uninterpreted labels and its completeness is established modulo a redundancy criterion that captures usual deletion or simplification rules (such as subsumption). In Section 5 the obtained calculus is lifted to graphs labeled with terms that can be interpreted in some arbitrary theory and possibly containing variables. Completeness is guaranteed if the theory is semi-decidable and compact. This last calculus is proven complete and an enhanced redundancy test is proposed. Concluding remarks are given in Section 6. Due to lack of space, proofs are omitted.
2 Graphs and Graph Operations
We briefly review some usual definitions and notations. For any partial function f, we denote by \( dom (f)\) the domain of f. If f and g are partial functions, we write \(f(x) = g(x)\) to state that either \(x \not \in dom (f) \cup dom (g)\) or that \(x \in dom (f) \cap dom (g)\) and the images of x by f and g are identical. Given a multiset \({\mathfrak m}\) and an element e, \({\mathfrak m}(e)\) denotes the multiplicity of e in \({\mathfrak m}\). For all multisets \({\mathfrak m}_1\) and \({\mathfrak m}_2\), we denote by \({\mathfrak m}_1 +{\mathfrak m}_2\) and \({\mathfrak m}_1 -{\mathfrak m}_2\) the sum and difference of \({\mathfrak m}_1\) and \({\mathfrak m}_2\), respectively. We write \({\mathfrak m}_1 \sqsubseteq {\mathfrak m}_2\) to state that \({\mathfrak m}_1\) is included in \({\mathfrak m}_2\). A multiset containing exactly the elements \(e_1,\dots ,e_n\) is written \(\boldsymbol{\{}e_1,\dots ,e_n\boldsymbol{\}}\). We denote by \({\mathfrak m}_1 \sqcup {\mathfrak m}_2\) the union of \({\mathfrak m}_1\) and \({\mathfrak m}_2\) (i.e., the minimal multiset containing \({\mathfrak m}_1\) and \({\mathfrak m}_2\)) defined as follows: for all elements e, \(({\mathfrak m}_1 \sqcup {\mathfrak m}_2)(e) = \max ({\mathfrak m}_1(e), {\mathfrak m}_2(e))\). Finite sequences may sometimes be identified with sets if the order is not important, e.g., if \(\boldsymbol{y} = (y_1,\dots ,y_n)\), we may write \(x \in \boldsymbol{y}\) to state that \(x = y_i\), for some \(i = 1,\dots ,n\). We recall that a preorder is a binary relation that is reflexive and transitive. Any preorder \(\le \) may be associated with a strict order < defined as follows: \(x < y \iff (x \le y \wedge y \not \le x)\).
The graphs we consider are directed, labeled graphs enriched with a sequence of distinguished nodes, called roots:
Definition 1
Let \(\mathcal{N}\) be a countably infinite set of nodes and let \(\mathcal{L}\) be a set of labels, disjoint from \(\mathcal{N}\). An \(\mathcal{L}\)-graph \(\mathfrak {g}\) is a tuple \(\langle N,\,E,\,R,\,L \rangle \), where:
-
\(N\subseteq \mathcal{N}\) is a finite set of nodes in \(\mathcal{N}\), called vertices or nodes;
-
\(E\) is a finite multiset of pairs in \(N\times N\), called edges;
-
\(R\) is a sequence of nodes in \(N\), with no repetition, called the roots of \(\mathfrak {g}\);
-
\(L\) is a function mapping every node in \(N\setminus R_{}\) to a label in \(\mathcal{L}\).
The components \(N\), \(E\), \(R\) and \(L\) of a graph \(\mathfrak {g}\) are denoted by \(N_{\mathfrak {g}}\), \(E_{\mathfrak {g}}\), \(R_{\mathfrak {g}}\) and \(L_{\mathfrak {g}}\), respectively. We denote by \(\widehat{N}_{\mathfrak {g}}\) the set of nodes \(\alpha \in N_{\mathfrak {g}}\) that do not occur in \(R_{\mathfrak {g}}\). The profile of a graph \(\mathfrak {g}\), written \( pr (\mathfrak {g})\), is the length of \(R_{\mathfrak {g}}\).
Example 2
The \(\mathcal{L}\)-graph \(\mathfrak {g}\) with \(N_{\mathfrak {g}} = \{ \rho _1, \alpha , \beta \}\), \(E_{\mathfrak {g}} = \boldsymbol{\{}(\rho _1,\alpha ), (\rho _1,\beta ), (\alpha ,\beta ) \boldsymbol{\}}\), \(R_{\mathfrak {g}} = (\rho _1)\), \( dom (L_{\mathfrak {g}}) = \{ \alpha ,\beta \}\), \(L_{\mathfrak {g}}(\alpha ) = 0\) and \(L_{\mathfrak {g}}(\beta ) = 1\) is depicted graphically as follows:

We write \(\alpha : \ell \) to state that a node named \(\alpha \) is labeled by \(\ell \). In many cases, the names of the non-root nodes will be irrelevant, and will thus be omitted. When possible, root nodes will be named \(\rho _1,\rho _2,\rho _3\),...in this order.
In the following, \(\mathcal{L}\)-graphs will be considered up to a renaming of nodes. More precisely, the isomorphism relation on \(\mathcal{L}\)-graphs is defined as follows.
Definition 3
An \(\mathcal{N}\)-renaming \(\mu \) is an injective mapping from \(\mathcal{N}\) to \(\mathcal{N}\). It is extended to any \(\mathcal{L}\)-graph \(\mathfrak {g}\) by replacing every occurrence of a node \(\alpha \) by \(\mu (\alpha )\). In particular, the function \(L_{\mu (\mathfrak {g})}\) is defined as follows: \(L_{\mu (\mathfrak {g})}(\alpha ) = \ell \) iff \(L_{\mathfrak {g}}(\beta ) = \ell \) for some \(\beta \in N_{\mathfrak {g}}\) such that \(\mu (\beta ) = \alpha \) (\(L_{\mu (\mathfrak {g})}\) is well-defined since \(\mu \) is injective). We write \(\mathfrak {g}\equiv \mathfrak {h}\) if \(\mathfrak {h}= \mu (\mathfrak {g})\), for some \(\mathcal{N}\)-renaming \(\mu \). It is easy to check that \(\equiv \) is an equivalence relation. Two \(\mathcal{L}\)-graphs \(\mathfrak {g},\mathfrak {h}\) such that \(\mathfrak {g}\equiv \mathfrak {h}\) are isomorphic.
2.1 Subgraphs and Replacement
We define the notion of a subgraph. The definition is slightly stronger than the usual one in graph theory because it imposes that only nodes that are roots in the subgraph can be connected to a node outside the subgraph. These roots can be viewed as an “interface” which restricts the way graphs may be connected and composed.
Definition 4
(Subgraph). A graph \(\mathfrak {h}\) is a subgraph of \(\mathfrak {g}\) (written \(\mathfrak {h}\le ^{g}\mathfrak {g}\)) if \(N_{\mathfrak {h}} \subseteq N_{\mathfrak {g}}\), \(E_{\mathfrak {h}} \sqsubseteq E_{\mathfrak {g}}\), \(\widehat{N}_{\mathfrak {h}} \subseteq \widehat{N}_{\mathfrak {g}}\), \(L_{\mathfrak {h}}(\alpha ) = L_{\mathfrak {g}}(\alpha )\) for all \(\alpha \in \widehat{N}_{\mathfrak {h}}\) and if a node \(\alpha \) occurs in an edge in \(E_{\mathfrak {g}}-E_{\mathfrak {h}}\) then \(\alpha \not \in \widehat{N}_{\mathfrak {h}}\).
Example 5
Consider the \(\mathcal{L}\)-graphs \(\mathfrak {h}\), \(\mathfrak {i}\), \(\mathfrak {j}\) and \(\mathfrak {k}\) with respective roots \((\alpha ,\beta )\), \((\beta )\), \((\alpha )\) and \((\rho _1)\), defined as follows:

The \(\mathcal{L}\)-graph \(\mathfrak {h}\) is a subgraph of the \(\mathcal{L}\)-graph \(\mathfrak {g}\) from Example 2, but \(\mathfrak {i}\), \(\mathfrak {j}\) and \(\mathfrak {k}\) are not. Indeed, \(\alpha \) has different labels in \(\mathfrak {g}\) and \(\mathfrak {i}\); \(\mathfrak {g}\) contains an edge between \(\rho _1\) and \(\beta \) that does not occur in \(\mathfrak {j}\) and \(\beta \) is not a root node in \(\mathfrak {j}\); and \(E_{\mathfrak {g}} -E_{\mathfrak {k}}\) contains the edge \((\alpha ,\beta )\) between nodes that are not roots in \(\mathfrak {k}\).
The replacement operation is defined in a natural way: all vertices and edges occurring from the replaced subgraph are deleted and replaced by those in the replacing graph (we assume that the considered graphs share the same roots).
Definition 6
(Subgraph replacement). Let \(\mathfrak {g}\) be an \(\mathcal{L}\)-graph and let \(\mathfrak {h}\) be a subgraph of \(\mathfrak {g}\). An \(\mathcal{L}\)-graph \(\mathfrak {i}\) is substitutable for \(\mathfrak {h}\) in \(\mathfrak {g}\) if \(R_{\mathfrak {i}} = R_{\mathfrak {h}}\) and \(N_{\mathfrak {g}} \cap \widehat{N}_{\mathfrak {i}} = \emptyset \). If \(\mathfrak {i}\) is substitutable for \(\mathfrak {h}\) in \(\mathfrak {g}\), then we denote by \(\mathfrak {g}\{ \mathfrak {h} \leftarrow \mathfrak {i} \}\) (the \(\mathcal{L}\)-graph obtained by replacing \(\mathfrak {h}\) by \(\mathfrak {i}\) in \(\mathfrak {g}\)) the tuple \(\langle N',\,E',\,R',\,L' \rangle \), where:
-
 . Note that since \(R_{\mathfrak {i}} = R_{\mathfrak {h}}\) we have \(N' = (N_{\mathfrak {g}} \setminus \widehat{N}_{\mathfrak {h}}) \cup \widehat{N}_{\mathfrak {i}}\).
. Note that since \(R_{\mathfrak {i}} = R_{\mathfrak {h}}\) we have \(N' = (N_{\mathfrak {g}} \setminus \widehat{N}_{\mathfrak {h}}) \cup \widehat{N}_{\mathfrak {i}}\). -
 .
. -
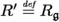 .
. -
 .
.
Example 7
Let \(\mathfrak {i}'\) be the \(\mathcal{L}\)-graph with root \((\alpha ,\beta )\) defined below. Using the \(\mathcal{L}\)-graphs \(\mathfrak {g}\) and \(\mathfrak {h}\) from Examples 2 and 5, we get the following \(\mathcal{L}\)-graph \(\mathfrak {g}\{ \mathfrak {h} \leftarrow \mathfrak {i}' \}\) (the edge \((\alpha ,\beta )\) occurs twice because it occurs both in \(E_{\mathfrak {i}'}\) and in \(E_{\mathfrak {g}} -E_{\mathfrak {h}}\)):

The notation \(\mathfrak {g}\{ \mathfrak {h} \leftarrow \mathfrak {i} \}\) is extended to the case where \( pr (\mathfrak {i}) = pr (\mathfrak {h})\) as follows:
 , where \(\mathfrak {i}'\) is any \(\mathcal{L}\)-graph substitutable for \(\mathfrak {h}\) in \(\mathfrak {g}\) such that \(\mathfrak {i}\equiv \mathfrak {i}'\). Thus the replacement operation possibly involves a renaming step, to avoid conflicts on the names of the nodes. The next proposition states a straightforward property of subgraph replacement:
, where \(\mathfrak {i}'\) is any \(\mathcal{L}\)-graph substitutable for \(\mathfrak {h}\) in \(\mathfrak {g}\) such that \(\mathfrak {i}\equiv \mathfrak {i}'\). Thus the replacement operation possibly involves a renaming step, to avoid conflicts on the names of the nodes. The next proposition states a straightforward property of subgraph replacement:
Proposition 8
Let \(\mathfrak {g}, \mathfrak {h}, \mathfrak {i}, \mathfrak {j}\) be \(\mathcal{L}\)-graphs, where \(\mathfrak {i}\le ^{g}\mathfrak {h}\le ^{g}\mathfrak {g}\) and \( pr (\mathfrak {i}) = pr (\mathfrak {j})\). Then \(\mathfrak {g}\{ \mathfrak {h} \leftarrow \mathfrak {h}\{ \mathfrak {i} \leftarrow \mathfrak {j} \} \} \equiv \mathfrak {g}\{ \mathfrak {i} \leftarrow \mathfrak {j} \}\).
Remark 9
Note that Proposition 8 would not hold if edges were defined as sets and not as multisets. For instance, consider \(\mathcal{L}\)-graphs \(\mathfrak {g},\mathfrak {h}\) with two root nodes \(\rho _1,\rho _2\), where \(\mathfrak {g}\) contains an edge \((\rho _1,\rho _2)\) and \(\mathfrak {h}\) contains no edges. If edges are taken as sets then we get \(\mathfrak {g}\{ \mathfrak {h} \leftarrow \mathfrak {g} \} = \mathfrak {g}\) and \(\mathfrak {g}\{ \mathfrak {g} \leftarrow \mathfrak {h} \} = \mathfrak {h}\), whereas \(\mathfrak {g}\{ \mathfrak {h} \leftarrow \mathfrak {h} \} = \mathfrak {g}\). In our previous work [14], this problem was overcome by restricting ourselves to induced subgraphs (which prevents the replacement of \(\mathfrak {h}\) by \(\mathfrak {g}\) in \(\mathfrak {g}\)), but this causes a combinatorial explosion in the definition of the calculus: when one “merges” two subgraphs, it is necessary to add every possible combination of edges connecting a root of the first \(\mathcal{L}\)-graph to a root of the second one, yielding exponentially many solutions w.r.t. the number of roots (see [14, Definition 30]). Such a behavior is avoided in the new framework.
We now introduce a notion of orthogonality between graphs. The intuition is that two \(\mathcal{L}\)-graphs will be considered orthogonal if they share no edges and no nodes other than roots.
Definition 10
(Orthogonal graphs). Let \(\mathfrak {g}\) be an \(\mathcal{L}\)-graph. Two subgraphs \(\mathfrak {h}\) and \(\mathfrak {i}\) of \(\mathfrak {g}\) are orthogonal in \(\mathfrak {g}\), or simply orthogonal, if \(\widehat{N}_{\mathfrak {h}} \cap \widehat{N}_{\mathfrak {i}} = \emptyset \) and \(E_{\mathfrak {h}} +E_{\mathfrak {i}} \sqsubseteq E_{\mathfrak {g}}\).
Note that \(\mathfrak {h}\) and \(\mathfrak {i}\) may share root nodes. Proposition 11 states that the result of the replacement of two orthogonal subgraphs does not depend on the order in which the \(\mathcal{L}\)-graphs are considered.
Proposition 11
Let \(\mathfrak {g}\) be an \(\mathcal{L}\)-graph, and let \(\mathfrak {h}_1\), \(\mathfrak {h}_2\) be orthogonal subgraphs of \(\mathfrak {g}\). For all \(\mathcal{L}\)-graphs \(\mathfrak {i}_1,\mathfrak {i}_2\) of respective profiles \( pr (\mathfrak {h}_1)\) and \( pr (\mathfrak {h}_2)\), \(\mathfrak {h}_2\) and \(\mathfrak {h}_1\) are subgraphs of \(\mathfrak {g}\{ \mathfrak {h}_1 \leftarrow \mathfrak {i}_1 \}\) and \(\mathfrak {g}\{ \mathfrak {h}_2 \leftarrow \mathfrak {i}_2 \}\), respectively, and \(\mathfrak {g}\{ \mathfrak {h}_1 \leftarrow \mathfrak {i}_1 \}\{ \mathfrak {h}_2 \leftarrow \mathfrak {i}_2 \} \equiv \mathfrak {g}\{ \mathfrak {h}_2 \leftarrow \mathfrak {i}_2 \}\{ \mathfrak {h}_1 \leftarrow \mathfrak {i}_1 \}\).
2.2 Graph Merging
Intuitively, a merge of two \(\mathcal{L}\)-graphs \(\mathfrak {g}_1\) and \(\mathfrak {g}_2\) denotes any minimal \(\mathcal{L}\)-graph containing all vertices, labels and edges in \(\mathfrak {g}_1\) and \(\mathfrak {g}_2\). More formally:
Definition 12
A merge of two \(\mathcal{L}\)-graphs \(\mathfrak {g}_1\) and \(\mathfrak {g}_2\) is an \(\mathcal{L}\)-graphs \(\mathfrak {h}\) such that: (i) \(\mathfrak {g}_i \le ^{g}\mathfrak {h}\), for all \(i = 1,2\); (ii) \(N_{\mathfrak {h}} = N_{\mathfrak {g}_1} \cup N_{\mathfrak {g}_2}\), \(E_{\mathfrak {h}} = E_{\mathfrak {g}_1} \sqcup E_{\mathfrak {g}_2}\) and \(\widehat{N}_{\mathfrak {h}} = \widehat{N}_{\mathfrak {g}_1} \cup \widehat{N}_{\mathfrak {g}_2}\); (iii) for all \(i = 1,2\) and for all \(\alpha \in \widehat{N}_{\mathfrak {g}_i}\), \(L_{\mathfrak {h}}(\alpha ) = L_{\mathfrak {g}_i}(\alpha )\).
Note that in contrast to [14, Definition 30], the merge contains no node and edge other than those occurring in \(\mathfrak {g}_1\) or \(\mathfrak {g}_2\). Moreover, the multiplicity of edges is minimal (\(E_{\mathfrak {h}}\) is defined as \(E_{\mathfrak {g}_1} \sqcup E_{\mathfrak {g}_2}\) instead of \(E_{\mathfrak {g}_1} +E_{\mathfrak {g}_2}\)). It is easy to check that a merge of \(\mathfrak {g}_1\), \(\mathfrak {g}_2\) exists iff \(L_{\mathfrak {g}_1}(\alpha ) = L_{\mathfrak {g}_2}(\alpha )\) holds for all \(\alpha \in \widehat{N}_{\mathfrak {g}_1}\cap \widehat{N}_{\mathfrak {g}_2}\). Moreover, all the merges are equal up to a permutation of their roots.
Example 13
Consider the following \(\mathcal{L}\)-graphs \(\mathfrak {g}\) and \(\mathfrak {h}\) below of respective roots \((\rho _1,\rho _2)\) and \((\rho _2,\rho _3)\), where the nodes \(\alpha ,\beta ,\gamma \) are labeled by 0, 1 and 2, respectively. These \(\mathcal{L}\)-graphs admit the following merge \(\mathfrak {i}\), of root \((\rho _1,\rho _2,\rho _3)\):

Example 14
Let \(\mathfrak {g}\), \(\mathfrak {h}\), \(\mathfrak {i}\) and \(\mathfrak {j}\) be the \(\mathcal{L}\)-graphs, defined as follows:

The \(\mathcal{L}\)-graph \(\mathfrak {g}\) has roots \((\alpha ,\beta )\) and \(\mathfrak {h},\mathfrak {i},\mathfrak {j}\) have roots \((\alpha )\). Then \(\mathfrak {g}\) and \(\mathfrak {h}\) admit the following merge, of root \((\alpha )\):

In contrast, \(\mathfrak {g}\) and \(\mathfrak {i}\) admit no merge (since \(\gamma \) has different labels in the two graphs), and neither do \(\mathfrak {g}\) and \(\mathfrak {j}\) (due to the edge connecting the non-root node \(\gamma \) to \(\delta \), that is outside of \(\mathfrak {g}\)).
Lemma 15
Let \(\mathfrak {g}\) be an \(\mathcal{L}\)-graph and let \(\mathfrak {h}, \mathfrak {i}\) be subgraphs of \(\mathfrak {g}\). Then \(\mathfrak {h}\) and \(\mathfrak {i}\) admit a merge \(\mathfrak {j}\), and for all merges \(\mathfrak {j}\) of \(\mathfrak {h}\) and \(\mathfrak {i}\) we have \(\mathfrak {j}\le ^{g}\mathfrak {g}\).
3 An Equational Logic on Graphs
We now define equational clauses built on \(\mathcal{L}\)-graphs and their semantics.
Definition 16
An equation is an unordered pair written \(\mathfrak {g}\approx \mathfrak {h}\), where \(\mathfrak {g},\mathfrak {h}\) are \(\mathcal{L}\)-graphs such that \(R_{\mathfrak {g}} = R_{\mathfrak {h}}\). A literal is either an equation (positive literal) or the negation of an equation, written \(\mathfrak {g}\not \approx \mathfrak {h}\) (negative literal). A clause is a disjunction of literals. The disjunction may be empty, in which case the clause is written \(\Box \). A clause is Horn if it contains at most one positive literal. A set of clauses is Horn if it contains only Horn clauses.
Note that we assume for technical convenience that the two members of an equation share the same roots. \(\mathcal{N}\)-renamings \(\mu \) are extended to equations, literals and clauses in a straightforward way:
 ,
,
 and
and
 . The relation \(\equiv \) is extended accordingly.
. The relation \(\equiv \) is extended accordingly.
Sets of clauses built on \(\mathcal{L}\)-graphs will be interpreted w.r.t. a congruence on \(\mathcal{L}\)-graphs. Graph congruences are defined in same way as for terms, except that we also assume that they are closed under isomorphism.
Definition 17
(Graph Congruence). A binary relation \(\bowtie \) on \(\mathcal{L}\)-graphs is closed under isomorphisms if \(\mathfrak {i}\bowtie \mathfrak {h}\) when \(\mathfrak {g}\bowtie \mathfrak {h}\) and \(\mathfrak {g}\equiv \mathfrak {i}\). It is closed under embeddings if \(\mathfrak {h}\bowtie \mathfrak {i}\) entails \(\mathfrak {g}\{ \mathfrak {h} \leftarrow \mathfrak {i} \} \bowtie \mathfrak {g}\). A congruence is an equivalence relation on \(\mathcal{L}\)-graphs that is closed under isomorphisms and embeddings.
Definition 18
A congruence \(\sim \) validates an expression \(E\) (written \({\sim }{\models }\,E\)) iff one of the following conditions holds: (i) \(E\) is an equation \(\mathfrak {g}\approx \mathfrak {h}\) and \(\mathfrak {g}\sim \mathfrak {h}\); (ii) \(E\) is a literal \(\mathfrak {g}\not \approx \mathfrak {h}\) and \(\mathfrak {g}\not \sim \mathfrak {h}\); (iii) \(E\) is a clause \(C\) and \(\sim \) validates at least one literal in \(C\); (iv) \(E\) is a set of clauses \(\varGamma \) and \(\sim \) validates all the clauses in \(\varGamma \). A congruence \(\sim \) is a model of \(E\) if \({\sim }{\models }\,E\). An expression is satisfiable if it admits a model and unsatisfiable otherwise. A tautology is a clause that is true in all congruences.
4 Superposition Calculus with Uninterpreted Labels
We define a superposition calculus for testing the satisfiability of sets of clauses. This calculus is strict (see, e.g., [2]) in the sense that it does not use the equational factorization rule (as defined in [1]), but uses instead the standard factorization rule that unifies both members of two equations. This choice is motivated by the fact that, as shown in Example 22, graph superposition is not compatible with tautology deletion (except when the clauses are Horn). Since tautology deletion is disabled for non-Horn clauses, equational factorization is not needed anyway. Selection functions are not considered, since they are not compatible with the redundancy criterion.
The usual superposition calculus [1] is parameterized by a reduction order, i.e., an order on terms that is well-founded, total on ground terms, and closed under substitutions and embeddings. In the case of \(\mathcal{L}\)-graphs, no such order possibly exists, if we also add the natural requirement that the order must be closed under renamings, as evidenced by the following example:
Example 19
Assume that an order exists, satisfying the following properties: is well-founded, closed under isomorphisms and embeddings, and total up to isomorphism (i.e., if \(\mathfrak {g}\not \equiv \mathfrak {h}\) then either \(\mathfrak {g}<\mathfrak {h}\) or \(\mathfrak {h}<\mathfrak {g}\)). Consider the \(\mathcal{L}\)-graphs \(\mathfrak {g}\) and \(\mathfrak {h}\) with roots \((\rho _1,\rho _2,\rho _3,\rho _4)\) and containing no labels, as well as the \(\mathcal{L}\)-graphs \(\mathfrak {i},\mathfrak {j}\) with an empty sequence of roots, where all nodes are labeled by 0:

It is clear that \(\mathfrak {g}\not \equiv \mathfrak {h}\). Indeed, if \(\mu (\mathfrak {g}) = \mathfrak {h}\) holds for some \(\mathcal{N}\)-renaming \(\mu \), then \(\mu (R_{\mathfrak {g}}) = R_{\mathfrak {h}}\), i.e., \(\mu ((\rho _1,\rho _2,\rho _3,\rho _4)) = (\rho _1,\rho _2,\rho _3,\rho _4)\), which entails that \(\mu \) is the identity on these nodes. Thus we cannot have \(\mu (E_{\mathfrak {g}}) = E_{\mathfrak {h}}\), as the first root \((\rho _1)\) is connected to the third root (\(\rho _3\)) in \(\mathfrak {g}\) and to the fourth one \((\rho _4)\) in \(\mathfrak {h}\). Consequently, we have either \(\mathfrak {g}<\mathfrak {h}\) or \(\mathfrak {h}<\mathfrak {g}\). Now we also have \(\mathfrak {g}\le ^{g}\mathfrak {i}\) and \(\mathfrak {h}\le ^{g}\mathfrak {j}\), and it is easy to check that \(\mathfrak {i}\{ \mathfrak {g} \leftarrow \mathfrak {h} \} = \mathfrak {j}\) and \(\mathfrak {j}\{ \mathfrak {h} \leftarrow \mathfrak {g} \} = \mathfrak {i}\). Thus we have either \(\mathfrak {i}<\mathfrak {j}\) or \(\mathfrak {j}<\mathfrak {i}\). But since \(R_{\mathfrak {i}} = R_{\mathfrak {j}} = ()\) we have \(\mathfrak {i}\equiv \mathfrak {j}\): indeed, if \(\mu (\rho _1) = \rho _1\), \(\mu (\rho _2) = \rho _2\), \(\mu (\rho _3) = \rho _4\) and \(\mu (\rho _4) = \rho _3\), then \(\mu (\mathfrak {i}) = \mathfrak {j}\).
We thus slightly relax the requirement of having a reduction order, and consider instead a pre-order on \(\mathcal{L}\)-graphs, that is well-founded, closed under isomorphisms and embeddings, and contains \(\le ^{g}\). We write \(\mathfrak {g}<\mathfrak {h}\) if \(\mathfrak {g}\le \mathfrak {h}\) and \(\mathfrak {h}\not \le \mathfrak {g}\), and we write \(\mathfrak {g}\simeq \mathfrak {h}\) if \(\mathfrak {g}\le \mathfrak {h}\) and \(\mathfrak {h}\le \mathfrak {g}\). We also assume that the equivalence classes of \(\simeq \) are finite, up to isomorphism. It is clear that such pre-orders exist, for instance, the pre-order: \(\mathfrak {g}\le \mathfrak {h}\iff card (N_{\mathfrak {g}})\le card (N_{\mathfrak {h}})\) fulfills the above properties.
Similarly to the usual superposition calculus, we associate every literal \(L\) with a multiset defined as follows:
 and
and
 . For every clause \(C= L_1 \vee \dots \vee L_n\), we define:
. For every clause \(C= L_1 \vee \dots \vee L_n\), we define:
 . Any order or preorder \(\triangleright \) on \(\mathcal{L}\)-graphs may then be extended into an order on clauses as follows: \(C\triangleright D\iff mset (C) \triangleright _m mset (D)\), where \(\triangleright _m\) denotes the multiset extension of \(\triangleright \) (note that \(\triangleright _m\) is also a (pre)order). A literal \(L\) is -maximal in a clause \(C\) if there is no literal \(L'\in C\) such that \(L' >L\). An \(\mathcal{L}\)-graph \(\mathfrak {g}\) is -maximal in a literal \(L\) if \(L\) contains no \(\mathcal{L}\)-graph \(\mathfrak {g}'\) such that \(\mathfrak {g}' >\mathfrak {g}\). A literal \(L\) is eligible in a clause \(C\) if \(L\) is a -maximal literal in \(C\). Intuitively, eligible literals are those that may be considered for performing inferences. For instance, given a clause \((\mathfrak {g}\approx \mathfrak {h}) \vee (\mathfrak {i}\approx \mathfrak {j})\), if \((\mathfrak {g}\approx \mathfrak {h}) >(\mathfrak {i}\approx \mathfrak {j})\), then \(\mathfrak {g}\approx \mathfrak {h}\) is eligible but not \(\mathfrak {i}\approx \mathfrak {j}\). Consequently the inference rules (as defined in Section 4.1) will be allowed to replace \(\mathfrak {g}\) by \(\mathfrak {h}\) using the equation \(\mathfrak {g}\approx \mathfrak {h}\) (provided \(\mathfrak {g}\not <\mathfrak {h}\)) but not, e.g., \(\mathfrak {i}\) by \(\mathfrak {j}\) (this restricts the number of inferences and prune the search space). Non eligible literals are simply attached to the conclusion of the inference but they play no active role until they (eventually) become eligible.
. Any order or preorder \(\triangleright \) on \(\mathcal{L}\)-graphs may then be extended into an order on clauses as follows: \(C\triangleright D\iff mset (C) \triangleright _m mset (D)\), where \(\triangleright _m\) denotes the multiset extension of \(\triangleright \) (note that \(\triangleright _m\) is also a (pre)order). A literal \(L\) is -maximal in a clause \(C\) if there is no literal \(L'\in C\) such that \(L' >L\). An \(\mathcal{L}\)-graph \(\mathfrak {g}\) is -maximal in a literal \(L\) if \(L\) contains no \(\mathcal{L}\)-graph \(\mathfrak {g}'\) such that \(\mathfrak {g}' >\mathfrak {g}\). A literal \(L\) is eligible in a clause \(C\) if \(L\) is a -maximal literal in \(C\). Intuitively, eligible literals are those that may be considered for performing inferences. For instance, given a clause \((\mathfrak {g}\approx \mathfrak {h}) \vee (\mathfrak {i}\approx \mathfrak {j})\), if \((\mathfrak {g}\approx \mathfrak {h}) >(\mathfrak {i}\approx \mathfrak {j})\), then \(\mathfrak {g}\approx \mathfrak {h}\) is eligible but not \(\mathfrak {i}\approx \mathfrak {j}\). Consequently the inference rules (as defined in Section 4.1) will be allowed to replace \(\mathfrak {g}\) by \(\mathfrak {h}\) using the equation \(\mathfrak {g}\approx \mathfrak {h}\) (provided \(\mathfrak {g}\not <\mathfrak {h}\)) but not, e.g., \(\mathfrak {i}\) by \(\mathfrak {j}\) (this restricts the number of inferences and prune the search space). Non eligible literals are simply attached to the conclusion of the inference but they play no active role until they (eventually) become eligible.
4.1 Inference Rules
The Superposition calculus \(\texttt{SC}\) is defined by the following rules: \(\texttt{Sp}^+\) (positive superposition), \(\texttt{Sp}^-\) (negative superposition), \(\texttt{R}\) (Reflection) and \(\texttt{F}\) (Factoring). The rules and their side conditions are very similar to those of the usual (ground) superposition calculus, except for the use of the merging operation for positive superposition. To simplify notations, the rules are defined modulo isomorphims, which means that one has to find a renaming of the premises such that the considered rule applies (this can be done using standard algorithms for finding graph homomorphisms). For instance, with this convention, the Reflection rule \(\texttt{R}\) actually removes all equations of the form \(\mathfrak {g}\not \approx \mathfrak {h}\), with \(\mathfrak {g}\equiv \mathfrak {h}\).
where:
-
1.
\(\mathfrak {i}\) is a merge of \(\mathfrak {g}_1\) and \(\mathfrak {g}_2\), and \(\mathfrak {g}_1,\mathfrak {g}_2\) are not orthogonal;
-
2.
\(\mathfrak {g}_i \approx \mathfrak {h}_i\) is eligible in \(\mathfrak {g}_i \approx \mathfrak {h}_i \vee C_i\) for \(i = 1,2\).
-
3.
\(\mathfrak {g}_i \not <\mathfrak {h}_i\) for \(i = 1,2\).
The non-orthogonality condition is the analogous of the non-variable condition of the usual calculus, it dismisses trivial replacements.
where:
-
1.
\(\mathfrak {g}\le ^{g}\mathfrak {i}\);
-
2.
\(\mathfrak {g}\approx \mathfrak {h}\) and \(\mathfrak {i}\not \approx \mathfrak {j}\) are eligible in \(\mathfrak {g}\approx \mathfrak {h}\vee C\) and \(\mathfrak {i}\not \approx \mathfrak {j}\vee D\), respectively.
-
3.
\(\mathfrak {g}\not <\mathfrak {h}\) and \(\mathfrak {i}\not <\mathfrak {j}\).
Lemma 20
The rules \(\texttt{Sp}^+\), \(\texttt{Sp}^-\), \(\texttt{F}\) and \(\texttt{R}\) are sound, i.e., for all congruences \(\sim \) and for all clauses \(C\) deducible from a set of premises \(\varGamma \), we have \({\sim }{\models }\,\varGamma \,\implies \,{\sim }{\models }\,C\).
4.2 Redundancy
In the usual superposition calculus [1], a clause is redundant if all its ground instances are entailed by smaller clauses (w.r.t. the considered order). Such clauses can be deleted without threatening refutational completeness, which reduces the search space. In our context, such a definition cannot be used, because one of the inference rules –namely \(\texttt{Sp}^+\)– may generate clauses that are strictly larger than the premises (hence such clauses would be considered as redundant if the usual criterion were to be used).
Example 21
Consider the clauses: \(\mathfrak {g}\approx \mathfrak {h}\) and \(\mathfrak {i}\approx \mathfrak {j}\), where \(\mathfrak {g},\mathfrak {h},\mathfrak {i}, \mathfrak {j}\) are \(\mathcal{L}\)-graphs with root \((\rho _1)\) that are defined as follows:

The \(\mathcal{L}\)-graphs \(\mathfrak {g}\) and \(\mathfrak {i}\) admit the following merge (of root \((\rho _1)\)):

Therefore, rule \(\texttt{Sp}^+\) applies, yielding \(\mathfrak {g}' \approx \mathfrak {g}''\), where:

If \(\mathcal{L}\)-graphs are ordered according to their number of nodes, then we have \((\mathfrak {g}' \approx \mathfrak {g}'') >(\mathfrak {g}\approx \mathfrak {h})\) and \((\mathfrak {g}' \approx \mathfrak {g}'') >(\mathfrak {i}\approx \mathfrak {j})\).
Worse, the calculus is actually incomplete if tautologies are deleted, as shown in the following example.
Example 22
Consider the \(\mathcal{L}\)-graphs \(\mathfrak {g}_1,\mathfrak {g}_2\) and \(\mathfrak {g}_3\) with roots \((\rho _1,\rho _2,\rho _3)\):

Let \(\dot{\mathfrak {g}}_i\) denote the graph obtained from \(\mathfrak {g}_i\) by adding one additional non root node \(\alpha \) distinct from \(\rho _1,\rho _2,\rho _3\), with some arbitrary (but fixed) label, e.g., 0. Assume that the graphs are ordered by the number of nodes, so that \(\dot{\mathfrak {g}}_i >\mathfrak {g}_j\), \(\dot{\mathfrak {g}}_i \simeq \dot{\mathfrak {g}}_j\) and \(\mathfrak {g}_i \simeq \mathfrak {g}_j\) (for all \(i,j \in \{ 1,2,3 \}\)). Let \(\varGamma = \{ \dot{\mathfrak {g}}_1 \approx \mathfrak {g}_2 \vee \dot{\mathfrak {g}}_2 \approx \mathfrak {g}_3 \vee \dot{\mathfrak {g}}_3 \approx \mathfrak {g}_1, \dot{\mathfrak {g}}_1 \not \approx \mathfrak {g}_2 \vee \dot{\mathfrak {g}}_2 \not \approx \mathfrak {g}_3 \vee \dot{\mathfrak {g}}_3 \not \approx \mathfrak {g}_1 \}\). Intuitively, every equation \(\dot{\mathfrak {g}}_i \approx \mathfrak {g}_j\) where \((i,j) \in \{ (1,2), (2,3), (3,1) \}\) states that the semantics of the graph is preserved when the isolated node is deleted and the graph is rotated by 90 degrees clockwise, for each possible position of the loop. Since the graphs are invariant by rotation, all these transformations are actually equivalent. It is easy to check that every clause that can be generated from \(\varGamma \) by applying the negative superposition rule from the first clause into the second clause contains two complementary literals (i.e. two literals of the form \(\dot{\mathfrak {g}}_i \approx \mathfrak {g}_j\) and \(\dot{\mathfrak {g}}_i \not \approx \mathfrak {g}_j\)) hence is a tautology. Moreover, the clauses obtained by superposition using the first clause only either are subsumed by the first clause (if the superposition rule is applied on two different literals) or contains a literal \(\mathfrak {g}_i \approx \mathfrak {g}_i\) (hence is a tautology). The equational factorization rule (as defined in [1]) does not apply since \(\dot{\mathfrak {g}}_i\) and \(\dot{\mathfrak {g}}_j\) are not isomorphic if \(i \not =j\). However, consider the \(\mathcal{L}\)-graphs \(\mathfrak {g}_i',\dot{\mathfrak {g}}_i'\) which contain the same nodes and edges as \(\mathfrak {g}_i\) and \(\dot{\mathfrak {g}}_i\) respectively, but with roots \((\rho _2,\rho _3,\rho _1)\). It is clear that \(\mathfrak {g}_2' \equiv \mathfrak {g}_1\) and \(\mathfrak {g}_3' \equiv \mathfrak {g}_2\), so that \(\dot{\mathfrak {g}}_1 \approx \mathfrak {g}_2 \,\models \, \dot{\mathfrak {g}}_2' \approx \mathfrak {g}_3'\). However, \(\dot{\mathfrak {g}}_2' \le ^{g}\dot{\mathfrak {g}}_2\) and \(\dot{\mathfrak {g}}_2\{ \dot{\mathfrak {g}}_2' \leftarrow \mathfrak {g}_3' \} = \mathfrak {g}_3\), thus \(\dot{\mathfrak {g}}_1 \approx \mathfrak {g}_2 \,\models \, \dot{\mathfrak {g}}_2 \approx \mathfrak {g}_3\). By a similar reasoning, we may show that \(\dot{\mathfrak {g}}_2 \approx \mathfrak {g}_3 \,\models \, \dot{\mathfrak {g}}_3 \approx \mathfrak {g}_1\) and \(\dot{\mathfrak {g}}_3 \approx \mathfrak {g}_1 \,\models \, \dot{\mathfrak {g}}_1 \approx \mathfrak {g}_2\), so that the equations \(\dot{\mathfrak {g}}_1 \approx \mathfrak {g}_2\), \(\dot{\mathfrak {g}}_2 \approx \mathfrak {g}_3\), and \(\dot{\mathfrak {g}}_3 \approx \mathfrak {g}_1\), are actually pairwise equivalent, which entails that \(\varGamma \) is unsatisfiable. However, \(\Box \) cannot be derived from \(\varGamma \) if the clauses containing complementary literals are discarded.
Thus, the conditions that ensure that a clause is redundant must be stronger than those of the usual superposition calculus. The definition proposed below covers usual deletion rules such as subsumption. Actually, two different criteria will be used, namely non-strict and strict redundancy, depending on whether the considered clauses are Horn or not. Indeed, in the former case a slightly less restrictive definition can be used, which permits the deletion of (some) tautological clauses.
Definition 23
Let \(C,D\) be two clauses and let \(\varGamma \) be a set of clauses. We say that \(C\) is subsumed by \(D\) and write \(C\ge ^{ sub }D\) if \(C= D\vee C'\), up to associativity and commutativity of \(\vee \) and isomorphism. We write \(C\rightarrow _{\varGamma } D\) (\(C\) demodulates to \(D\) w.r.t. \(\varGamma \)) if \(C\) is of the form \(\mathfrak {g}\bowtie \mathfrak {h}\vee E\) (with \(\bowtie \in \{ \approx , \not \approx \}\)), \(D= \mathfrak {g}\{ \mathfrak {i} \leftarrow \mathfrak {j} \} \bowtie \mathfrak {h}\vee E\), and there exists a clause \(F\in \varGamma \) such that \(F= (\mathfrak {i}\approx \mathfrak {j}) \vee F'\), with \(F' \le ^{ sub }E\), \(\mathfrak {i}>\mathfrak {j}\), \(F' <(\mathfrak {i}\approx \mathfrak {j})\) and \((\mathfrak {i}\approx \mathfrak {j}) <(\mathfrak {g}\bowtie \mathfrak {h})\).
The set of clauses that are redundant w.r.t. a set of clauses \(\varGamma \) is defined inductively as follows. A clauses \(C\) is redundant w.r.t. \(\varGamma \) iff one of the following conditions holds: (1) \(C\) contains two literals \(\mathfrak {g}_1 \approx \mathfrak {g}_2\) and \(\mathfrak {g}_1' \not \approx \mathfrak {g}_2'\), with \(\mathfrak {g}_i \equiv \mathfrak {g}_i'\) for \(i = 1,2\); (2) \(C\) contains a literal of the form \(\mathfrak {g}\approx \mathfrak {h}\) with \(\mathfrak {g}\equiv \mathfrak {h}\); (3) \(C\ge ^{ sub }D\), for some \(D\in \varGamma \); (4) \(C\rightarrow _{\varGamma } D\) and \(D\) is redundant. The set of strictly redundant ground clauses is defined in a similar way, except that Item 1 is removed.
Intuitively, the conditions ensuring that \(C\) demodulates to \(D\) in Definition 23 are meant to ensure that \(D\) may be deduced from \(C\) by applying the rule \(\texttt{Sp}^+\) or \(\texttt{Sp}^-\) using the clause \(F\) (with \(D<C\) and \(F<C\)) and that \(\{ D\} \cup \varGamma \) is equivalent to \(\{ C\} \cup \varGamma \). In particular, the condition \(F' \le ^{ sub }E\) ensures that all the literals added by the inference already occur in \(C\).
Definition 24
A set of clauses \(\varGamma \) is saturated (resp. strictly saturated) if every clause that can be deduced from premises in \(\varGamma \) using one of the rules of \(\texttt{SC}\) (in one step) is redundant (resp. strictly redundant) w.r.t. \(\varGamma \).
We prove that \(\texttt{SC}\) is refutationally complete. We actually establish two completeness results, the first one for general clauses and the second one for Horn clauses. The latter is stronger since it uses the weaker non-strict saturatedness criterion instead of strict saturatedness.
Theorem 25
Let \(\varGamma \) be a set of clauses. If \(\Box \not \in \varGamma \) and \(\varGamma \) is strictly saturated or both Horn and saturated then \(\varGamma \) is satisfiable.
5 A Constrained Graph Superposition Calculus
We now lift the calculus \(\texttt{SC}\) defined in Section 4 into a constrained calculus. The goal is to handle graphs labeled by terms interpreted in some arbitrary theory, and possibly containing variables. To this aim, we attach constraints to the clauses, which are formulas interpreted in the considered theory, asserting conditions on the labels. Such constraints will be updated when inference rules will be applied, by asserting the conditions that are required by the rule applications.
5.1 Constrained Clauses
Let \(\mathcal{V}\) be a countably infinite set of variables and let \(\varSigma \) be a set of function symbolsFootnote 1. Each symbol \(f\) in \(\varSigma \) is associated with a unique arity \(\#(f)\). We denote by \(\mathcal{T}\) the set of terms built inductively as usual on \(\mathcal{V}\) and \(\varSigma \), and by \(\mathcal{C}\) the set of first-order formulas, called constraints, built inductively as usual on atoms of the form \(t \doteq s\), where \(t,s \in \mathcal{T}\) using the logical connectives \(\vee ,\wedge ,\lnot ,\Rightarrow ,\Leftrightarrow \), the quantifiers \(\exists ,\forall \) and two logical constants \(\bot \) and \(\top \).
A substitution \(\sigma \) is a function mapping all variables x to a term \(x\sigma \). The domain \( dom (\sigma )\) of \(\sigma \) is the set of variables x such that \(x\sigma \not = x\). For every term or formula e, we denote by \(e\sigma \) the term or formula obtained from e by replacing every (free) variable x by \(x\sigma \). A term is ground if it contains no variables, and a substitution \(\sigma \) is ground if \(x\sigma \) is ground for all \(x\in dom (\sigma )\).
\(\mathcal{T}\)-graphs are \(\mathcal{L}\)-graph with labels in \(\mathcal{T}\). A \(\mathcal{T}\)-clause is a clause defined on \(\mathcal{T}\)-graphs. Substitutions are extended to \(\mathcal{T}\)-graphs and \(\mathcal{T}\)-clauses as follows. For every \(\mathcal{T}\)-graph \(\mathfrak {g}\), we denote by \(\mathfrak {g}\sigma \) the \(\mathcal{T}\)-graph such that: \(F_{\mathfrak {g}\sigma } = F_{\mathfrak {g}}\) for all \(F\in \{ N_{}, E_{}, R_{} \}\) and \(L_{\mathfrak {g}\sigma }(\alpha ) = L_{\mathfrak {g}}(\alpha )\sigma \), for all \(\alpha \in \widehat{N}_{\mathfrak {g}}\). Then:
 ,
,
 and
and
 . A \(\mathcal{T}\)-graph \(\mathfrak {g}\) is ground if for all \(\alpha \in \widehat{N}_{\mathfrak {g}}\), \(L_{\mathfrak {g}}(\alpha )\) is ground. A \(\mathcal{T}\)-clause is ground if all the \(\mathcal{T}\)-graphs occurring in it are ground. For every expression (term, \(\mathcal{T}\)-graph, constraint or \(\mathcal{T}\)-clause) \(E\), we denote by \(\mathcal{V}(E)\) the set of variables (freely) occurring in \(E\).
. A \(\mathcal{T}\)-graph \(\mathfrak {g}\) is ground if for all \(\alpha \in \widehat{N}_{\mathfrak {g}}\), \(L_{\mathfrak {g}}(\alpha )\) is ground. A \(\mathcal{T}\)-clause is ground if all the \(\mathcal{T}\)-graphs occurring in it are ground. For every expression (term, \(\mathcal{T}\)-graph, constraint or \(\mathcal{T}\)-clause) \(E\), we denote by \(\mathcal{V}(E)\) the set of variables (freely) occurring in \(E\).
Definition 26
A constrained clause (or c-clause) is a pair \([C\ |\ \phi ]\), where \(C\) is a \(\mathcal{T}\)-clause and \(\phi \in \mathcal{C}\).
Let \(\mathcal{I}\) be some fixed set of first-order interpretations on the signature \(\varSigma \). For all \(I\in \mathcal{I}\), we denote by \( dom (I)\) the domain of \(I\) and by \(f^I\) the interpretation of the function \(f\) (with \(f\in \varSigma \)). For every ground term t and for all \(I\in \mathcal{I}\), we denote by \([t]^I\) the value of t in \(I\), inductively defined as usual. To simplify notations, we assume that for every \(I\in \mathcal{I}\) and for every \(e\in dom (I)\), there exists a ground term t such that \([t]^I = e\).
The satisfiability relation \(\models \) relating interpretations in \(\mathcal{I}\) and constraints in \(\mathcal{C}\) is defined as usual, where \(\doteq \) is interpreted as the identity, and \(\bot \) and \(\top \) are interpreted as false and true, respectively. We write \(\phi \models _{\mathcal{I}}\psi \) if the implication \(I\models \phi \sigma \implies I\models \psi \sigma \) holds for all \(I\in \mathcal{I}\) and for all ground substitutions of domain \(\mathcal{V}(\phi ) \cup \mathcal{V}(\psi )\); and \(\phi \equiv _{\mathcal{I}}\psi \) iff \(\phi \models _{\mathcal{I}}\psi \) and \(\psi \models _{\mathcal{I}}\phi \). For any set of constraints, we write \(I\models S\) iff \(I\models \phi \) for all \(\phi \in S\). For any constraint (or set of constraints) \(\phi \), if there exists a ground substitution \(\sigma \) with domain \(\mathcal{V}(\phi )\) and an interpretation \(I\in \mathcal{I}\) such that \(I\models \phi \sigma \), then \(\phi \) is \(\mathcal{I}\)-satisfiable (and \(\mathcal{I}\)-satisfiable otherwise). For instance, the fixed set of first-order interpretations may be the set \(\mathcal{I}_1\) of first-order interpretations on \(\varSigma \) that satisfy the above condition on the domain (this is not restrictive provided there are infinitely many ground terms), in which case \(\mathcal{I}\)-satisfiability is simply the standard satisfiability in first-order clausal logic, or the set
 of interpretations of domain
of interpretations of domain
 interpreting the functions \(0,1,+\) as usual. We say that \(\mathcal{I}\) is compact if for every \(\mathcal{I}\)-unsatisfiable set of constraints S there exists a finite set \(S' \subseteq S\) such that \(S'\) is \(\mathcal{I}\)-unsatisfiable. It is well-known that \(\mathcal{I}_1\) is compact [21] and that
interpreting the functions \(0,1,+\) as usual. We say that \(\mathcal{I}\) is compact if for every \(\mathcal{I}\)-unsatisfiable set of constraints S there exists a finite set \(S' \subseteq S\) such that \(S'\) is \(\mathcal{I}\)-unsatisfiable. It is well-known that \(\mathcal{I}_1\) is compact [21] and that
 is not compactFootnote 2.
is not compactFootnote 2.
Any ground \(\mathcal{T}\)-graph may be transformed into a \( dom (I)\)-graph by replacing the labels by their interpretations in \(I\). More formally:
Definition 27
For all \(I\in \mathcal{I}\) and for all ground \(\mathcal{L}\)-graphs \(\mathfrak {g}\) we denote by \([\mathfrak {g}]^I\) the graph such that \(F_{[\mathfrak {g}]^I} = F_{\mathfrak {g}}\) for all \(F\in \{ N_{}, E_{}, R_{} \}\) and \(L_{[\mathfrak {g}]^I}(\alpha ) = [L_{\mathfrak {g}}(\alpha )]^I\), for all \(\alpha \in \widehat{N}_{\mathfrak {g}}\). For every ground \(\mathcal{T}\)-clause \(C\), we denote by \([C]^I\) the clause obtained from \(C\) by replacing every \(\mathcal{T}\)-graph \(\mathfrak {g}\) by \([\mathfrak {g}]^I\). For all sets of c-clauses \(\varGamma \), we denote by \([\varGamma ]^I\) the set of clauses of the form \([C\sigma ]^I\), where \(C\in \varGamma \) and \(\sigma \) is a substitution mapping every variable in \(C\) to a ground term.
Note that by definition, all the labels of \([\mathfrak {g}]^I\) are elements of the domain of \(I\). Proposition 28 follows immediately from Definition 27.
Proposition 28
Let \(\mathfrak {g}, \mathfrak {h}\) be \(\mathcal{T}\)-graphs, let \(I\in \mathcal{I}\) and let \(\sigma \) be a ground substitution with domain \(\mathcal{V}(\mathfrak {g}) \cup \mathcal{V}(\mathfrak {h})\). If \(\mathfrak {g}\equiv \mathfrak {h}\) then \([\mathfrak {g}\sigma ]^I \equiv [\mathfrak {h}\sigma ]^I\).
Definition 29
An \(\mathcal{I}\)-interpretation is a pair \((I,\sim )\), where \(I\in \mathcal{I}\) and \(\sim \) is a congruence on dom(I)-graphs. An \(\mathcal{I}\)-interpretation \((I,\sim )\) validates a set of c-clauses \(\varGamma \) (written \((I,\sim ) \,\models \,\varGamma \)) if \({\sim }{\models }\,[\,]^\varGamma {I}\).
5.2 Lifting the Calculus
In the constrained calculus, the equality of labels will not be checked when an inference rule is applied. Instead, the corresponding conditions will be extracted from the considered graphs and added to the constraints of the conclusion. We first introduce a relation stating that two \(\mathcal{T}\)-graphs are identical up to their labels. This relation is parameterized by a constraint that asserts conditions on the labels ensuring that the graphs are identical (modulo \(\mathcal{I}\)).
Definition 30
Let \(\mathfrak {g},\mathfrak {h}\) be two \(\mathcal{T}\)-graphs and let \(\phi \in \mathcal{C}\). We write \(\mathfrak {g}=_{\phi } \mathfrak {h}\) if \(N_{\mathfrak {g}} = N_{\mathfrak {h}}\), \(E_{\mathfrak {g}} = E_{\mathfrak {h}}\), \(R_{\mathfrak {g}} = R_{\mathfrak {h}}\), and \(\phi = \bigwedge _{\alpha \in \widehat{N}_{\mathfrak {g}}} (L_{\mathfrak {g}}(\alpha ) \doteq L_{\mathfrak {h}}(\alpha ))\) (up to associativity and commutativity of \(\wedge \)).
Example 31
Consider the \(\mathcal{T}\)-graphs \(\mathfrak {g}\) and \(\mathfrak {h}\) below, of root \((\rho _1)\). We have \(\mathfrak {g}=_{\phi } \mathfrak {h}\), with \(\phi = (x \doteq 0 \wedge 0 \doteq y)\).

Every relation between \(\mathcal{T}\)-graphs or \(\mathcal{T}\)-clauses may be adapted in a similar way, keeping the conditions on the nodes, edges and roots, and asserting conditions ensuring that the label of every given node is unique (up to equality modulo \(\mathcal{I}\)). Definitions 32 and 33 lift the subgraph and subsumption relations, respectively:
Definition 32
We write \(\mathfrak {h}\le ^{g}_{\phi } \mathfrak {g}\) if \(N_{\mathfrak {h}} \subseteq N_{\mathfrak {g}}\); \(E_{\mathfrak {h}} \sqsubseteq E_{\mathfrak {g}}\); every node \(\alpha \in N_{\mathfrak {h}}\) occurring in \(R_{\mathfrak {g}}\) also occurs in \(R_{\mathfrak {h}}\); if \(\alpha \in N_{\mathfrak {h}}\) occurs in an edge in \(E_{\mathfrak {g}}\setminus E_{\mathfrak {h}}\) then \(\alpha \in R_{\mathfrak {h}}\), and \(\phi = \bigwedge _{\alpha \in \widehat{N}_{\mathfrak {h}}} L_{\mathfrak {h}}(\alpha ) \doteq L_{\mathfrak {g}}(\alpha )\). The notation \(\mathfrak {g}\{ \mathfrak {h} \leftarrow \mathfrak {i} \}\) may be extended to the case where \(\mathfrak {h}\le ^{g}_{\phi } \mathfrak {g}\) (following Definition 6). Orthogonality is extended accordingly (as it does not depend on labels).
Definition 33
We write \(C\le ^{ sub }_{\phi } D\) if \(C\) and \(D\) are respectively of the form (up to associativity and commutativity of \(\vee \) and isomorphism): \(\bigvee _{i=1}^n \mathfrak {g}_i \bowtie _i\mathfrak {h}_i\), and \(\bigvee _{i=1}^n \mathfrak {g}_i' \bowtie _i \mathfrak {h}_i' \vee D'\), with \(\mathfrak {g}_i =_{\phi _i} \mathfrak {g}_i'\), \(\mathfrak {h}_i =_{\psi _i} \mathfrak {h}_i'\) (for all \(i = 1,\dots ,n\)) and \(\phi = \bigwedge _{i=1}^n (\phi _i \wedge \psi _i)\).
The notion of a merge is extended analogously:
Definition 34
A \(\phi \)-merge of two \(\mathcal{T}\)-graphs \(\mathfrak {g}_1\) and \(\mathfrak {g}_2\) is a \(\mathcal{T}\)-graph \(\mathfrak {h}\) such that:
-
\(N_{\mathfrak {h}} = N_{\mathfrak {g}_1} \cup N_{\mathfrak {g}_2}\), \(E_{\mathfrak {h}} = E_{\mathfrak {g}_1} \sqcup E_{\mathfrak {g}_2}\), and \(\widehat{N}_{\mathfrak {h}} = \widehat{N}_{\mathfrak {g}_1} \cup \widehat{N}_{\mathfrak {g}_2}\).
-
For every node \(\alpha \in \widehat{N}_{\mathfrak {h}}\), we have \(L_{\mathfrak {h}}(\alpha ) = L_{\mathfrak {g}_i}(\alpha )\), for some (arbitrarily chosen) \(i = 1,2\) such that \(L_{\mathfrak {g}_i}(\alpha )\) is defined.
-
\(\phi = \bigwedge _{\alpha \in \widehat{N}_{\mathfrak {g}_1} \cap \widehat{N}_{\mathfrak {g}_2}} L_{\mathfrak {g}_1}(\alpha ) \doteq L_{\mathfrak {g}_2}(\alpha )\).
We now lift the order relation. Let \(\le _{I}\) (for \(I\in \mathcal{I}\)) be a family of well-founded preorders on \( dom (I)\)-\(\mathcal{T}\)-graphs that are closed under isomorphisms and embeddings and contain \(\le ^{g}\). Let \(\le _{\phi }\) (for \(\phi \in \mathcal{C}\)) be a family of pre-orders on \(\mathcal{T}\)-graphs satisfying the following conditions: \(\mathfrak {g}>_{\phi } \mathfrak {h}\implies \mathfrak {g}>_{\psi } \mathfrak {h}\), for all constraints \(\phi ,\psi \) such that \(\psi \models _{\mathcal{I}}\phi \), and \((I\models \phi \wedge \mathfrak {g}>_{\phi } \mathfrak {h}) \implies [\mathfrak {g}]^I >_{I} [\mathfrak {h}]^I\). The simplest solution in practice is to order \(\mathcal{T}\)-graphs according to their number of nodes, in which case the order does not depend on \(I\) or \(\phi \): \(\mathfrak {g}\le _{I} \mathfrak {h}\iff \mathfrak {g}\le _{\phi } \mathfrak {h}\iff card (N_{\mathfrak {g}}) \le card (N_{\mathfrak {h}})\). However, our framework is meant to be general enough to cope with orders that take labels into account.
A literal \(L\) is maximal in a c-clause \([C\ |\ \phi ]\) if there is no literal \(L'\in C\) such that \(L' >_{\phi } L\). It is eligible in a c-clause \([C\ |\ \phi ]\) if \(L\) is a \(>_{\phi }\)-maximal literal in \(C\).
We are now in the position to define the constrained inference rules. As for the rules in Section 4.1, they apply modulo isomorphism. We assume as for the standard resolution or superposition calculus that the premises share no variables. In every rule, the conclusion inherits the constraints of the premises together with additional conditions on the labels which makes the inference valid. In all rules, the eligibility condition is tested after adding all the constraints enabling the inference, as this yields the most restrictive condition, thus reducing the branching factor.
where:
-
1.
\(\mathfrak {i}\) is a \(\psi \)-merge of \(\mathfrak {g}_1\) and \(\mathfrak {g}_2\) and \(\mathfrak {g}_1\) and \(\mathfrak {g}_2\) are not orthogonal;
-
2.
\(\mathfrak {g}_i \approx \mathfrak {h}_i\) is eligible in \([\mathfrak {g}_i \approx \mathfrak {h}_i \vee C_i\ |\ \phi _1 \wedge \phi _2 \wedge \psi ]\) (for all \(i = 1,2\));
-
3.
\(\mathfrak {g}_i \not <_{\phi _1 \wedge \phi _2 \wedge \psi } \mathfrak {h}_i\) (for all \(i = 1,2\)).
where:
-
1.
\(\mathfrak {g}\le ^{g}_{\xi } \mathfrak {i}\) (note that \(\xi \) is uniquely defined by Definition 32);
-
2.
\(\mathfrak {g}\approx \mathfrak {h}\) and \(\mathfrak {i}\not \approx \mathfrak {j}\) are eligible in \([\mathfrak {g}\approx \mathfrak {h}\vee C\ |\ \phi \wedge \psi \wedge \xi ]\) and \([\mathfrak {i}\not \approx \mathfrak {j}\vee D\ |\ \phi \wedge \psi \wedge \xi ]\), respectively;
-
3.
\(\mathfrak {g}\not <_{\phi \wedge \psi \wedge \xi } \mathfrak {h}\) and \(\mathfrak {i}\not <_{\phi \wedge \psi \wedge \xi } \mathfrak {j}\).
where \(\mathfrak {g}\approx \mathfrak {h}\) is eligible in \([\mathfrak {g}\approx \mathfrak {h}\vee \mathfrak {g}' \approx \mathfrak {h}' \vee C\ |\ \phi \wedge \psi \wedge \psi ']\), \(\mathfrak {g}=_{\psi } \mathfrak {g}'\), and \(\mathfrak {h}=_{\psi '} \mathfrak {h}'\).
where \(\mathfrak {g}\not \approx \mathfrak {h}\) is eligible in \([\mathfrak {g}\not \approx \mathfrak {h}\vee C\ |\ \phi \wedge \psi ]\) and \(\mathfrak {g}=_{\psi } \mathfrak {h}\).
5.3 Soundness and Refutational Completeness
We establish the soundness and completeness of the constrained calculus, by lifting the corresponding properties for the base calculus. Note that semi decidability holds only if the base theory is semi-decidableFootnote 3 and compact (otherwise it is easy to see that unsatisfiability is not semi-decidable in general).
Lemma 35
The rules \(\texttt{Sp}^+\), \(\texttt{Sp}^-\), \(\texttt{F}\) and \(\texttt{R}\) (applied on c-clauses) are sound, i.e., for all \(\mathcal{I}\)-interpretations \((I,\sim )\) and for all c-clauses \([C\ |\ \phi ]\) deducible for a set of premises \(\varGamma \), we have \((I,\sim ) \,\models \, \varGamma \implies (I,\sim ) \,\models \, [C\ |\ \phi ]\).
The redundancy criterion may be lifted as follows:
Definition 36
A c-clause \([C\ |\ \phi ]\) is (strictly) \(\mathcal{I}\)-redundant in a set of c-clauses \(\varGamma \) if for all ground substitutions \(\sigma \) of domain \(\mathcal{V}(C) \cup \mathcal{V}(\phi )\) and for all \(I\in \mathcal{I}\) such that \(I\models \phi \sigma \), the clause \([C\sigma ]^I\) is (strictly) redundant in \([\varGamma ]^I\).
A set of c-clauses \(\varGamma \) is (strictly) saturated if every c-clause that is deducible from \(\varGamma \) by the rules above is (strictly) \(\mathcal{I}\)-redundant in \(\varGamma \).
Theorem 37
Let \(\varGamma \) be a set of c-clauses. If \(\varGamma \) is unsatisfiable and strictly saturated or Horn and saturated, then \(\varGamma \) contains a set of c-clauses \(\{ [\Box \ |\ \phi _I] \mid I\in \mathcal{I}\}\) such that for every \(I\in \mathcal{I}\), \(I\models \exists \boldsymbol{x}_I. \phi _i\), with \(\boldsymbol{x}_I= \mathcal{V}(\phi _I)\). If, moreover, \(\mathcal{I}\) is compact, then \(\varGamma \) contains a finite set of c-clauses \(\{ [\Box \ |\ \phi _i] \mid i = 1,\dots ,n \}\) such that \(\bigwedge _{i = 1}^n \lnot (\exists \boldsymbol{x}. \phi _i)\) is \(\mathcal{I}\)-unsatisfiable, with \(\boldsymbol{x}_i = \mathcal{V}(\phi _i)\).
5.4 Redundancy Testing
The redundancy criterion in Definition 36 is very general, but it may be difficult to test in practice. We thus introduce a second notion of redundancy, defined directly on constrained clauses, that is stronger and easier to decide.
Definition 38
Let \([C\ |\ \phi ],[D\ |\ \psi ]\) be two clauses and let \(\varGamma \) be a set of clauses. Let \(\boldsymbol{x}\) and \(\boldsymbol{y}\) be the vectors of variables occurring in \([C\ |\ \phi ]\) and \([D\ |\ \psi ]\), respectively (we assume by renaming that \(\boldsymbol{x}\) and \(\boldsymbol{y}\) share no variable).
We say that \([C\ |\ \phi ]\) is subsumed by \([D\ |\ \psi ]\) and we write \([C\ |\ \phi ] \ge ^{ sub }[D\ |\ \psi ]\) if there exists \(\xi \in \mathcal{C}\) such that \(D\le ^{ sub }_{\xi } C\) and \(\phi \models _{\mathcal{I}}\exists \boldsymbol{y}. (\psi \wedge \xi )\).
We write \([C\ |\ \phi ] \rightarrow _{\varGamma } [D\ |\ \psi ]\) (\([C\ |\ \phi ]\) demodulates to \([D\ |\ \psi ]\) w.r.t. \(\varGamma \)) if \(C\) is of the form \(\mathfrak {g}\bowtie \mathfrak {h}\vee E\), \(D= \mathfrak {g}\{ \mathfrak {i} \leftarrow \mathfrak {j} \} \bowtie \mathfrak {h}\vee E\), and there exists a c-clause \([F\ |\ \xi ] \in \varGamma \) (with free variables \(\boldsymbol{z}\)) such that \(F= (\mathfrak {i}\approx \mathfrak {j}) \vee F'\), \(\mathfrak {i}\le ^{g}_{\xi '} \mathfrak {g}\), \(F' \le ^{ sub }_{\xi ''} E\), \(\phi \models _{\mathcal{I}}\exists \boldsymbol{y}. \exists \boldsymbol{z}. (\psi \wedge \xi \wedge \xi ' \wedge \xi '')\), \(\mathfrak {i}>_{\xi } \mathfrak {j}\), \(F' <_{\xi } (\mathfrak {i}\approx \mathfrak {j})\) and \((\mathfrak {i}\approx \mathfrak {j}) <_{\xi } (\mathfrak {g}\bowtie \mathfrak {h})\).
A c-clause \([C\ |\ \phi ]\) is redundant w.r.t. \(\varGamma \) iff one of the following conditions holds: (1) \(\exists \boldsymbol{x}. \phi \) is \(\mathcal{I}\)-unsatisfiable, with \(\boldsymbol{x} = \mathcal{V}(\phi )\). (2) \(C\) contains two literals \(\mathfrak {g}_1 \approx \mathfrak {g}_2\) and \(\mathfrak {g}_1' \not \approx \mathfrak {g}_2'\), with \(\mathfrak {g}_i =_{\phi _i} \mathfrak {g}_i'\), and \(\phi \models _{\mathcal{I}}\phi _i\) (for all \(i = 1,2\)); (3) \(C\) contains a literal of the form \(\mathfrak {g}\approx \mathfrak {h}\) with \(\mathfrak {g}=_{\psi } \mathfrak {h}\) and \(\phi \models _{\mathcal{I}}\psi \); (4) \([C\ |\ \phi ] \ge ^{ sub }[D\ |\ \psi ]\), for some \([D\ |\ \psi ]\in \varGamma \); (5) \([C\ |\ \phi ] \rightarrow _{\varGamma } [D\ |\ \psi ]\) and \([D\ |\ \psi ]\) is redundant. The notion of strictly redundant c-clause is defined in a similar way, removing Item 2.
Example 39
Consider the following \(\mathcal{T}\)-graphs, of root ():

We have \(\mathfrak {g}\approx \mathfrak {i}\le ^{ sub }_{\phi } \mathfrak {h}\approx \mathfrak {i}\), with \(\phi = (x \doteq 0 \wedge y \doteq z+1 \wedge 0 \doteq 0)\). Thus, if \(\mathcal{I}\) only contains the standard model of Presburger arithmetic, then \([\mathfrak {g}\approx \mathfrak {i}\ |\ y \not \approx 0]\) subsumes \([\mathfrak {h}\approx \mathfrak {i}\ |\ \top ]\).
The following lemma states the relation between the new notion of redundancy and \(\mathcal{I}\)-redundancy (as defined in Definition 36).
Lemma 40
Let \(\varGamma \) be a set of c-clauses. If \([C\ |\ \phi ]\) is (strictly) redundant w.r.t. \(\varGamma \) then it is (strictly) \(\mathcal{I}\)-redundant w.r.t. \(\varGamma \).
Remark 41
By the previous definitions, checking whether a given c-clause is (strictly) redundant involves testing the validity of entailments of the form \(\phi \models _{\mathcal{I}}\exists \boldsymbol{y}. \psi \), which may be infeasible in practice (for instance the problem is undecidable if \(\mathcal{I}\) contains all interpretations). Stronger conditions may be used instead, e.g., one may check whether there exists a substitution \(\sigma \) such that \(\phi \) is of the form \(\psi \sigma \wedge \psi \), which is decidable.
6 Conclusion
We devised a constrained superposition calculus to test the satisfiability of sets of clauses defined over graphs. Its soundness and refutational completeness was established, modulo a redundancy criterion that captures the usual deletion and simplification rules: subsumption, demodulation, deletion of clauses with trivial equations and – in the case of Horn clauses only – deletion of clauses containing complementary literals. The considered structures are rooted directed labeled graphs, which are general enough to capture most existing equational graph theories, such as those developed for quantum circuits. In contrast to [14], the calculus is able to handle disjunctions as well as interpreted labels, and in contrast to [22], our solution avoids any encoding of graphs into terms, by defining inference rules operating directly on graphs.
From a practical point of view, it would be interesting to get more general redundancy criteria, to reduce the branching factor and improve the efficiency of the procedure. In particular, is it possible to define a version of the calculus in which tautology deletion is allowed, even for non Horn clauses? As evidenced by Example 22, this would require to define a new equational factorization rule, allowing for non trivial superposition inferences within a single clause.
Another interesting issue is to add variables denoting not only labels, but also graphs. This would allow for instance to synthesize graphs satisfying some properties. As graphs can be viewed as functions with multiple inputs and outputs (denoted by the roots) such an addition would yield a second order logic.
Finally, it would be interesting to identify fragments for which the calculus terminates, ensuring decidability of the satisfiability problem. In contrast to terms, the calculus does not terminate (and the satisfiability problem is undecidable) for ground unit clauses [14], hence strong restrictions on the shape of the graphs are required to ensure termination.
Notes
- 1.
As usual, predicates may be encoded as functions.
- 2.
For instance, the set
 is unsatisfiable if n is interpreted as a natural number, but admits no finite unsatisfiable subset.
is unsatisfiable if n is interpreted as a natural number, but admits no finite unsatisfiable subset. - 3.
in the sense that there exists a semi-decision procedure to check whether a formula in \(\mathcal{C}\) is unsatisfiable.
References
L. Bachmair and H. Ganzinger. Rewrite-based equational theorem proving with selection and simplification. Journal of Logic and Computation, 3(4):217–247, 1994.
L. Bachmair and H. Ganzinger. Strict basic superposition. In C. Kirchner and H. Kirchner, editors, Automated Deduction - CADE-15, 15th International Conference on Automated Deduction, Lindau, Germany, July 5-10, 1998, Proceedings, volume 1421 of Lecture Notes in Computer Science, pages 160–174. Springer, 1998.
M. Backens and A. Kissinger. ZH: A complete graphical calculus for quantum computations involving classical non-linearity. arXiv preprint arXiv:1805.02175, 2018.
F. Bonchi, F. Gadducci, A. Kissinger, P. Sobocinski, and F. Zanasi. Confluence of graph rewriting with interfaces. In 26th European Symposium on Programming (21/04/17 - 28/04/17), February 2017.
F. Bonchi, F. Gadducci, A. Kissinger, P. Sobocinski, and F. Zanasi. String diagram rewrite theory I: rewriting with frobenius structure. J. ACM, 69(2):14:1–14:58, 2022.
J. H. Brenas, R. Echahed, and M. Strecker. Verifying graph transformation systems with description logics. In Graph Transformation - 11th International Conference, ICGT 2018, Held as Part of STAF 2018, Toulouse, France, June 25-26, 2018, Proceedings, volume 10887 of Lecture Notes in Computer Science, pages 155–170. Springer, 2018.
R. Caferra, R. Echahed, and N. Peltier. A term-graph clausal logic: Completeness and incompleteness results. Journal of Applied Non-classical Logics, 18(4):373–411, 2008.
C. Chareton, S. Bardin, F. Bobot, V. Perrelle, and B. Valiron. An automated deductive verification framework for circuit-building quantum programs. In N. Yoshida, editor, Programming Languages and Systems - 30th European Symposium on Programming, ESOP 2021, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2021, Luxembourg City, Luxembourg, March 27 - April 1, 2021, Proceedings, volume 12648 of Lecture Notes in Computer Science, pages 148–177. Springer, 2021.
A. Clément, N. Heurtel, S. Mansfield, S. Perdrix, and B. Valiron. Lo_v-calculus: A graphical language for linear optical quantum circuits. In S. Szeider, R. Ganian, and A. Silva, editors, 47th International Symposium on Mathematical Foundations of Computer Science, MFCS 2022, August 22-26, 2022, Vienna, Austria, volume 241 of LIPIcs, pages 35:1–35:16. Schloss Dagstuhl - Leibniz-Zentrum fürInformatik, 2022.
A. Clément and S. Perdrix. PBS-calculus: A graphical language for quantum-controlled computations. arXiv preprint arXiv:2002.09387, 2020.
B. Coecke and R. Duncan. Tutorial: Graphical calculus for quantum circuits. In International Workshop on Reversible Computation, pages 1–13. Springer, 2012.
A. Corradini, D. Duval, R. Echahed, F. Prost, and L. Ribeiro. The PBPO graph transformation approach. J. Log. Algebraic Methods Program., 103:213–231, 2019.
R. Echahed. Inductively sequential term-graph rewrite systems. In H. Ehrig, R. Heckel, G. Rozenberg, and G. Taentzer, editors, Graph Transformations, 4th International Conference, ICGT 2008, Leicester, United Kingdom, September 7-13, 2008. Proceedings, volume 5214 of Lecture Notes in Computer Science, pages 84–98. Springer, 2008.
R. Echahed, M. Echenim, M. Mhalla, and N. Peltier. A superposition-based calculus for diagrammatic reasoning. In N. Veltri, N. Benton, and S. Ghilezan, editors, PPDP 2021: 23rd International Symposium on Principles and Practice of Declarative Programming, Tallinn, Estonia, September 6-8, 2021, pages 10:1–10:13.ACM, 2021.
H. Ehrig, K. Ehrig, U. Prange, and G. Taentzer. Fundamentals of Algebraic Graph Transformation. Monographs in Theoretical Computer Science. An EATCS Series. Springer, 2006.
H. Ehrig, G. Engels, H.-J. Kreowski, and G. Rozenberg, editors. Handbook of Graph Grammars and Computing by Graph Transformations, Volume 2: Applications, Languages and Tools. World Scientific, 1999.
H. Ehrig and B. König. Deriving bisimulation congruences in the DPO approach to graph rewriting. In I. Walukiewicz, editor, Foundations of Software Science and Computation Structures, 7th International Conference, FOSSACS 2004, Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2004, Barcelona, Spain, March 29 - April 2, 2004, Proceedings, volume 2987 of Lecture Notes in Computer Science, pages 151–166.Springer, 2004.
H. Ehrig, H.-J. Kreowski, U. Montanari, and G. Rozenberg, editors. Handbook of Graph Grammars and Computing by Graph Transformations, Volume 3: Concurrency, Parallelism and Distribution. World Scientific, 1999.
H. Ehrig, M. Pfender, and H. J. Schneider. Graph-grammars: An algebraic approach. In 14th Annual Symposium on Switching and Automata Theory, Iowa City, Iowa, USA, October 15-17, 1973, pages 167–180, 1973.
J. Engelfriet and G. Rozenberg. Node replacement graph grammars. In G. Rozenberg, editor, Handbook of Graph Grammars and Computing by Graph Transformations, Volume 1: Foundations, pages 1–94. World Scientific, 1997.
M. Fitting. First-Order Logic and Automated Theorem Proving. Texts and Monographs in Computer Science. Springer-Verlag, 1990.
J. Gorard, M. Namuduri, and X. D. Arsiwalla. Zx-calculus and extended wolfram model systems II: fast diagrammatic reasoning with an application to quantum circuit simplification. CoRR, abs/2103.15820, 2021.
A. Habel and K. Pennemann. Correctness of high-level transformation systems relative to nested conditions. Math. Struct. Comput. Sci., 19(2):245–296, 2009.
A. Hadzihasanovic. The algebra of entanglement and the geometry of composition. arXiv preprint arXiv:1709.08086, 2017.
A. Kissinger and V. Zamdzhiev. Quantomatic: A proof assistant for diagrammatic reasoning. In International Conference on Automated Deduction, pages 326–336. Springer, 2015.
C. M. Poskitt and D. Plump. A hoare calculus for graph programs. In H. Ehrig, A. Rensink, G. Rozenberg, and A. Schürr, editors, Graph Transformations - 5th International Conference, ICGT 2010, Enschede, The Netherlands, September 27 - - October 2, 2010. Proceedings, volume 6372 of Lecture Notes in Computer Science, pages 139–154.Springer, 2010.
A. Rensink. The GROOVE simulator: A tool for state space generation. In Second International Workshop on Applications of Graph Transformations with Industrial Relevance, AGTIVE 2003, volume 3062 of LNCS, pages 479–485. Springer, 2003.
A. Riazanov and A. Voronkov. Vampire 1.1 (system description). In R. Goré, A. Leitsch, and T. Nipkow, editors, Automated Reasoning, First International Joint Conference, IJCAR 2001, Siena, Italy, June 18-23, 2001, Proceedings, volume 2083 of Lecture Notes in Computer Science, pages 376–380. Springer, 2001.
G. Rozenberg, editor. Handbook of Graph Grammars and Computing by Graph Transformations, Volume 1: Foundations. World Scientific, 1997.
S. Schulz, S. Cruanes, and P. Vukmirovic. Faster, higher, stronger: E 2.3. In P. Fontaine, editor, Automated Deduction - CADE 27 - 27th International Conference on Automated Deduction, Natal, Brazil, August 27-30, 2019, Proceedings, volume 11716 of Lecture Notes in Computer Science, pages 495–507. Springer, 2019.
D. Varró. Automated formal verification of visual modeling languages by model checking. Journal of Software and Systems Modeling, 3(2):85–113, May 2004.
C. Weidenbach, D. Dimova, A. Fietzke, R. Kumar, M. Suda, and P. Wischnewski. SPASS version 3.5. In R. A. Schmidt, editor, Automated Deduction - CADE-22, 22nd International Conference on Automated Deduction, Montreal, Canada, August 2-7, 2009. Proceedings, volume 5663 of Lecture Notes in Computer Science, pages 140–145. Springer, 2009.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Echahed, R., Echenim, M., Mhalla, M., Peltier, N. (2023). A Strict Constrained Superposition Calculus for Graphs. In: Kupferman, O., Sobocinski, P. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2023. Lecture Notes in Computer Science, vol 13992. Springer, Cham. https://doi.org/10.1007/978-3-031-30829-1_7
Download citation
DOI: https://doi.org/10.1007/978-3-031-30829-1_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-30828-4
Online ISBN: 978-3-031-30829-1
eBook Packages: Computer ScienceComputer Science (R0)





 . Note that since
. Note that since  .
.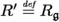 .
. .
. is unsatisfiable if n is interpreted as a natural number, but admits no finite unsatisfiable subset.
is unsatisfiable if n is interpreted as a natural number, but admits no finite unsatisfiable subset.