Abstract
The concept of must testing is naturally parametrised with a chosen completeness criterion, defining the complete runs of a system. Here I employ justness as this completeness criterion, instead of the traditional choice of progress. The resulting must-testing preorder is incomparable with the default one, and can be characterised as the fair failure preorder of Vogler. It also is the coarsest precongruence preserving linear time properties when assuming justness.
As my system model I here employ Petri nets with read arcs. Through their Petri net semantics, this work applies equally well to process algebras. I provide a Petri net semantics for a standard process algebra extended with signals; the read arcs are necessary to capture those signals.
Supported by Royal Society Wolfson Fellowship RSWF\(\backslash \)R1\(\backslash \)221008
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
May- and must-testing was proposed by De Nicola & Hennessy in [9]. It yields semantic equivalences where two processes are distinguished if and only if they react differently on certain tests. The tests are processes that additionally feature success states. A test \(\mathcal{T}\) is applied to a process N by taking the CCS parallel composition \(\mathcal{T}|N\), and implicitly applying a CCS restriction operator to it that removes the remnants of unsuccessful communication. Applying \(\mathcal{T}\) to N is deemed successful if and only if this composition yields a process that may, respectively must, reach a success state. It is trivial to recast this definition using the CSP parallel composition \(\Vert _\mathcal{A}\) [39] instead of the one from CCS.
It is not a priori clear how a given process must reach a success state. For all we know it might stay in its initial state and never take any transition leading to this success state. To this end one must employ an assumption saying that under appropriate circumstances certain enabled transitions will indeed be taken. Such an assumption is called a completeness criterion [18]. The theory of testing from [9] implicitly employs a default completeness criterion that in [25] is called progress. However, one can parameterise the notion of must testing by the choice of any completeness criterion, such as the many notions of fairness classified in [25]. Here I employ justness, a completeness criterion that is better justified than either progress or fairness [25].
The resulting must-testing equivalence is incomparable to the progress-based one from [9]. On the one hand, it no longer distinguishes deadlock and livelock, i.e., the Petri nets N and \(N'\) of Ex. 3; on the other hand, it keeps recording information past a divergence. I characterise the corresponding preorder as the fair failure preorder of Vogler [43], which using my terminology ought to be called the just failures preorder. I show that it also is the coarsest precongruence preserving linear time properties when assuming justness. Finally I show that the same preorder originates from the timed must-testing framework explored in [43], but only if all quantitative information is removed from that approach.
I carry out this work within the model of Petri nets extended with read arcs [7, 35], so that it also applies to process algebras through their standard Petri net semantics. The extension with read arcs is necessary to capture signalling, a process algebra operator that cannot be adequately modelled by standard Petri nets. Signalling, or read arcs, can be used to accurately model mutual exclusion without making a fairness assumption [8, 11, 43]. This is not possible in standard Petri nets [24, 31, 43], or in process algebras with a standard Petri net semantics [24]. Here I give a Petri net semantics of signalling, and illustrate its use in modelling a traffic light, interacting with passing cars.
2 Labelled Petri nets with read arcs
I will employ the following notations for multisets.
Definition 1
Let X be a set.
-
A multiset over X is a function
 , i.e.
, i.e.
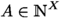 .
. -
\(x \in X\) is an element of A, notation \(x \in A\), iff \(A(x) > 0\).
-
For multisets A and B over X I write \(A \subseteq B\) iff \(A(x) \le B(x)\) for all \(x \mathbin \in X\);
\(A\cup B\) denotes the multiset over X with \((A\cup B)(x):=\text {max}(A(x), B(x))\),
\(A\cap B\) denotes the multiset over X with \((A\cap B)(x):=\text {min}(A(x), B(x))\),
\(A + B\) denotes the multiset over X with \((A + B)(x):=A(x)+B(x)\),
\(A - B\) is given by \((A - B)(x):=\text {max}(A(x)-B(x),0)\), and
for
 the multiset \(k\cdot A\) is given by \((k \cdot A)(x):=k\cdot A(x)\).
the multiset \(k\cdot A\) is given by \((k \cdot A)(x):=k\cdot A(x)\). -
The function
 , given by \(\emptyset (x):=0\) for all \(x \mathbin \in X\), is the empty multiset over X.
, given by \(\emptyset (x):=0\) for all \(x \mathbin \in X\), is the empty multiset over X. -
The cardinality |A| of a multiset A over X is given by \(|A| := \sum _{x\in X}A(x)\).
-
A multiset A over X is finite iff \(|A|<\infty \), i.e., iff the set \(\{x \mid x \mathbin \in A\}\) is finite.
With \(\{x,x,y\}\) I denote the multiset over \(\{x,y\}\) with \(A(x)\mathbin =2\) and \(A(y)\mathbin =1\), rather than the set \(\{x,y\}\) itself. A multiset A with \(A(x) \le 1\) for all x is identified with the set \(\{x \mid A(x)=1\}\).
I employ general labelled place/transition systems extended with read arcs [7, 35].
Definition 2
Let \(\mathcal{A}\) be a set of visible actions and \(\tau \mathbin {\not \in }\mathcal{A}\) be an invisible action. Let
 . A (labelled) Petri net (over \(\mathcal{A}_\tau \)) is a tuple \((S, T, F, R, M_0, \ell )\) where
. A (labelled) Petri net (over \(\mathcal{A}_\tau \)) is a tuple \((S, T, F, R, M_0, \ell )\) where
-
S and T are disjoint sets (of places and transitions),
-
 (the flow relation including arc weights),
(the flow relation including arc weights), -
 (the read relation),
(the read relation), -
 (the initial marking), and
(the initial marking), and -
\(\ell : T \rightarrow \mathcal{A}_\tau \) (the labelling function).
Petri nets are depicted by drawing the places as circles and the transitions as boxes, containing their label. Identities of places and transitions are displayed next to the net element. When \(F(x,y)>0\) for \(x,y \mathbin \in S\cup T\) there is an arrow (arc) from x to y, labelled with the arc weight F(x, y). Weights 1 are elided. An element (s, t) of the multiset R is called a read arc. Read arcs are drawn as lines without arrowhead. When a Petri net represents a concurrent system, a global state of this system is given as a marking, a multiset M of places, depicted by placing M(s) dots (tokens) in each place s. The initial state is \(M_0\).
The behaviour of a Petri net is defined by the possible moves between markings M and \(M'\), which take place when a finite multiset G of transitions fires. In that case, each occurrence of a transition t in G consumes F(s, t) tokens from each place s. Naturally, this can happen only if M makes all these tokens available in the first place. Moreover, for each \(t\in G\) there need to be at least R(s, t) tokens in each place s that are not consumed when firing G. Next, each t produces F(t, s) tokens in each place s. Definition 4 formalises this notion of behaviour.
Definition 3
Let \(N = (S, T, F, R, M_0, \ell )\) be a Petri net. The multisets
 are given by \(\widehat{t}(s)=R(s,t)\), \({}^\bullet t(s)=F(s,t)\) and \({t}^\bullet (s)=F(t,s)\) for all \(s \mathbin \in S\). The elements of \(\widehat{t}\), \({}^\bullet t\) and \({t}^\bullet \) are called read-, pre- and postplaces of t, respectively. These functions extend to finite multisets
are given by \(\widehat{t}(s)=R(s,t)\), \({}^\bullet t(s)=F(s,t)\) and \({t}^\bullet (s)=F(t,s)\) for all \(s \mathbin \in S\). The elements of \(\widehat{t}\), \({}^\bullet t\) and \({t}^\bullet \) are called read-, pre- and postplaces of t, respectively. These functions extend to finite multisets
 by \(\widehat{G} \mathbin {:=} \bigcup _{t \in G}\;\widehat{t}\), \({}^\bullet \!G \mathbin {:=} \sum _{t \in T}G(t)\cdot {}^\bullet t\) and \({G}^\bullet \mathbin {:=} \sum _{t \in T}G(t)\cdot {t}^\bullet \!\).
by \(\widehat{G} \mathbin {:=} \bigcup _{t \in G}\;\widehat{t}\), \({}^\bullet \!G \mathbin {:=} \sum _{t \in T}G(t)\cdot {}^\bullet t\) and \({G}^\bullet \mathbin {:=} \sum _{t \in T}G(t)\cdot {t}^\bullet \!\).
Definition 4
([7]) Let \(N \mathbin = (S, T, F, R, M_0, \ell )\) be a Petri net,
 non-empty and finite, and
non-empty and finite, and
 . G is a step from M to \(M'\), written \(M~[G\rangle _N~ M'\), iff
. G is a step from M to \(M'\), written \(M~[G\rangle _N~ M'\), iff
-
\({}^\bullet G + \widehat{G} \subseteq M\) (G is enabled) and
-
\(M' = (M - {}^\bullet G) + {G}^\bullet \).
Note that steps are (finite) multisets, thus allowing self-concurrency, i.e. the same transition can occur multiple times in a single step. One writes \(M~[t\rangle _N~ M'\) for \(M\mathrel {[\{t\}\rangle _N} M'\), whereas \(M [t\rangle _N\) abbreviates \(\exists M'.~ M \mathrel {[t\rangle _N} M'\). The subscript N may be omitted if clear from context.
In my Petri nets transitions are labelled with actions drawn from a set
 . This makes it possible to see these nets as models of reactive systems that interact with their environment. A transition t can be thought of as the occurrence of the action \(\ell (t)\). If \(\ell (t)\mathbin \in \mathcal{A}\), this occurrence can be observed and influenced by the environment, but if \(\ell (t)\mathbin =\tau \), it cannot and t is an internal or silent transition. Transitions whose occurrences cannot be distinguished by the environment carry the same label. In particular, since the environment cannot observe the occurrence of internal transitions at all, they are all labelled \(\tau \).
. This makes it possible to see these nets as models of reactive systems that interact with their environment. A transition t can be thought of as the occurrence of the action \(\ell (t)\). If \(\ell (t)\mathbin \in \mathcal{A}\), this occurrence can be observed and influenced by the environment, but if \(\ell (t)\mathbin =\tau \), it cannot and t is an internal or silent transition. Transitions whose occurrences cannot be distinguished by the environment carry the same label. In particular, since the environment cannot observe the occurrence of internal transitions at all, they are all labelled \(\tau \).
In [24, 31, 43] it was established that mutual exclusion protocols cannot be correctly modelled in standard Petri nets (without read arcs, i.e., satisfying \(R(s,t)\mathbin =0\) for all \(s\mathbin \in S\) and \(t\mathbin \in T\)), unless their correctness becomes contingent on making a fairness assumption. In [24] it was concluded from this that mutual exclusion protocols can likewise not be correctly expressed in standard process algebras such as CCS [34], CSP [6] or ACP [4], at least when sticking to their standard Petri net semantics. Yet Vogler showed that mutual exclusion can be correctly modelled in Petri nets with read arcs [43], and [8, 11] demonstrate how mutual exclusion can be correctly modelled in a process algebra extended with signalling [3]. Thus signalling adds expressiveness to process algebra that cannot be adequately modelled in terms of standard Petri nets. This is my main reason to use Petri nets with read arcs as system model in this paper.
In many papers on Petri nets, the sets of places and transitions are required to be finite, or at least countable. Here I need a milder restriction, and will limit attention to nets that are finitary in the following sense.
Definition 5
A Petri net \(N = (S, T, F, R, M_0, \ell )\) is finitary if \(M_0\) is countable, \({t}^\bullet \) is countable for all \(t\in T\), and moreover the set of transitions t with \({}^\bullet t=\emptyset \) is countable.
3 A Petri net semantics of CCSP with signalling
CCSP [37] is a natural mix of the process algebras CCS [34] and CSP [6], often used in connection with Petri nets. Here I will present a Petri net semantics of a version CCSPS of CCSP enriched with signalling [3]. This builds on work from [10, 27, 29, 37, 38, 44]; the only novelty is the treatment of signalling. Petri net semantics of other process algebras, like CCS [34], CSP [6] or ACP [4], are equally well known. This Petri net semantics lifts any semantic equivalence on Petri nets to CCSPS, or to any other process algebra, so that the results of this work apply equally well to process algebras.
CCSPS is parametrised by the choice of sets \(\mathcal{A}\) of visible actions and \(\mathcal K\) of agent identifiers. Its syntax is given by

with \(a,a_i \mathbin \in \mathcal{A}\), \(A \mathbin \subseteq \mathcal{A}\), \(f\!:\mathcal{A}\rightarrow \mathcal{A}\) and \(K \in \mathcal K\). Here the guarded choice \(\sum _{i \in I}a_i P_i\) executes one of the actions \(a_i\), followed by the process \(P_i\). The process \(a \triangleright P\) behaves as P, except that in its initial state it it is sending the signal a.Footnote 1 Footnote 2The process \(P \Vert _A Q\) is the partially synchronous parallel composition of processes P and Q, where actions from A can take place only when both P and Q can engage in such an action, while other actions of P and Q occur independently. The abstraction operator \(\tau _A\) hides action from A from the environment by renaming them into \(\tau \), whereas f is a straightforward relabelling operator (leaving internal actions alone). Each agent identifier K comes with a defining equation \(K{\mathop {=}\limits ^{ def}}P\), with P a guarded CCSPS expression; it behaves exactly as the body of its defining equation. Here P is guarded if each occurrence of an agent identifier within P lays in the scope of a guarded choice \(\sum _{i \in I}a_i P_i\) or \(a \triangleright \sum _{i \in I}a_i P_i\).
A formal Petri net semantics of CCSPS, and of each of the operators \(\sum \), \(\triangleright \), \(\Vert _A\), \(\tau _A\) and f, appears in [22, Appendix A]. Here I give an informal summary.
Given nets \(N_i\) for \(i \mathbin \in I\), the net \(\sum _{i \in I}a_i N_i\) is obtained by taking their disjoint union, but without their initial markings \((M_0)_i\), and adding a single marked place r, and for each \(i \in I\) a fresh transition \(t_i\), labelled \(a_i\), with \({}^\bullet t_i=\{r\}\), \(\widehat{t_i}=\emptyset \) and \({(}^\bullet t_i)=(M_0)_i\).
The parallel composition \(N\Vert _A N'\) is obtained out of the disjoint union of N and \(N'\) by dropping from N and \(N'\) all transitions t with \(\ell (t)\in A\), and instead adding synchronisation transitions \((t,t')\) for each pair of transitions t and \(t'\) from N and \(N'\) with \(\ell (t)=\ell (t')\in A\). One has
 , and similarly for \(\widehat{(t,t')}\) and \({(t,t')}^\bullet \), i.e., all arcs are inherited.
, and similarly for \(\widehat{(t,t')}\) and \({(t,t')}^\bullet \), i.e., all arcs are inherited.
\(\tau _A\) and f are renaming operators that only affect the labels of transitions.
The net \(a \triangleright N\) adds to the net N a single transition u, labelled a, that may fire arbitrary often, but is enabled in the initial state of N only. To this end, take \({}^\bullet u={u}^\bullet =\emptyset \) and \(\widehat{u} = M_0\), the initial marking of N. I apply this construction only to nets for which its initially marked places have no incoming arcs.
Example 1
A traffic light can be modelled by the recursive equation
Here the actions \({ tr}\), \({ tg}\) and \({ ty}\) stand for “turn red”, “turn green” and “turn yellow”, and \({ drive}\) indicates a state where it is OK to drive through. A sequence of two passing cars is modelled as \({ Traffic}{\mathop {=}\limits ^{ def}} { drive}.{ drive}.\textbf{0}\). Here \(\textbf{0}\) stands for the empty sum \(\sum _{i\in \emptyset }a_i.E_i\) and models inaction. In the parallel composition \({ TL}~\Vert _{\{{ drive}\}}~ { Traffic}\) the cars only drive through when the light is green. All three processes are displayed in Fig. 1.
4 Justness and other completeness criteria
Definition 6
Let \(N = (S, T, F, R, M_0, \ell )\) be a Petri net. An execution path \(\pi \) is an alternating sequence \(M_0 t_1 M_1 t_2 M_2 \dots \) of markings and transitions of N, starting with \(M_0\), and either being infinite or ending with a marking, such that \(M_{i}~[t_{i+1}\rangle _N~ M_{i+1}\) for all \(i<{ length}(\pi )\). Here
 is the number of transitions in \(\pi \).
is the number of transitions in \(\pi \).
Let \(\ell (\pi )\in \mathcal{A}_\tau ^\infty \) be the string \(\ell (t_1) \ell (t_2) \dots \). Here \(\mathcal{A}_\tau ^\infty \) denotes the collection of finite and infinite sequences of actions. Moreover, \({ trace}(\pi ) \in \mathcal{A}^\infty \) is obtained from \(\ell (\pi )\) by dropping all occurrences of \(\tau \).
The execution path \(\pi \) is said to enable a transition t, notation \(\pi [t\rangle \), if \(M_k[ t\rangle \) for some
 and for all \(k \le j < { length}(\pi )\) one has \(t_j \ne t\) and \(({}^\bullet t + \widehat{t}\,) \cap {}^\bullet t_{j+1} = \emptyset \).
and for all \(k \le j < { length}(\pi )\) one has \(t_j \ne t\) and \(({}^\bullet t + \widehat{t}\,) \cap {}^\bullet t_{j+1} = \emptyset \).
Path \(\pi \) is B-just, for some \(B \subseteq \mathcal{A}\), if \(\ell (t)\in B\) for all \(t\in T\) with \(\pi [t\rangle \).
In the definition of \(\pi [ t\rangle \) above one also has \(M_{j+1}[ t\rangle \) for all \(k \le j < { length}(\pi )\). Hence, a finite execution path enables a transition iff its final marking does so.
Informally, \(\pi [t\rangle \) holds iff transition t is enabled in some marking on the path \(\pi \), and after that state no transition of \(\pi \) uses any of the resources needed to fire t. Here the read- and preplaces of t count as such resources. The clause \(t_j \ne t\) moreover counts the transition itself as one of its resources, in the sense that a transition is no longer enabled when it occurs. This clause is redundant for transitions t with \({}^\bullet t\ne \emptyset \). One could interpret this clause as saying that a transition t with \({}^\bullet t=\emptyset \) comes with implicit marked private preplace \(p_t\), and arcs \((p_t,t)\) as well as \((t,p_t)\).
In [18] I posed that Petri nets or transition systems constitute a good model of concurrency only in combination with a completeness criterion: a selection of a subset of all execution paths as complete executions, modelling complete runs of the represented system. The default completeness criterion, called progress in [25], declares an execution path complete iff it either is infinite, or its final marking enables no transition. An alternative, called justness in [25], declares an execution path complete iff it enables no transition. Justness is a stronger completeness criterion than progress, in the sense that it deems fewer execution paths complete. The difference is illustrated by the Petri net of Fig. 2(a). There, the execution of an infinite sequence of b-transitions, not involving the a-transition, is complete when assuming progress, but not when assuming justness. In the survey paper [25], 20 different completeness criteria are ordered by strength: progress, justness, and 18 kinds of fairness. Most of the latter are stronger than justness: in Fig. 2(b) the infinite sequence of b-transitions is just but unfair—i.e. incomplete according to these notions of fairness. Whereas justness was a new idea in the context of transition systems [25], it was used as an unnamed default assumption in much work on Petri nets [40]. That justness is better warranted in applications than other completeness criteria has been argued in [17, 18, 24, 25].
The mentioned completeness criteria from [25] are all stronger than progress, in the sense that not all infinite execution paths are deemed complete; on the finite execution paths they judge the same. An orthogonal classification is obtained by varying the set \(B \subseteq \mathcal{A}\) of actions that may be blocked by the environment. This fits the reactive viewpoint, in which a visible action can be regarded as a synchronisation between the modelled system and its environment. An environment that is not ready to synchronise with an action \(b\in \mathcal{A}\) can be regarded as blocking b. Now B-progress is the criterion that deems a path complete iff it is either infinite, or its final marking M enables only transitions with labels from B. When the environment may block such transitions, it is possible for the system to not progress past M. In Fig. 2(c) the execution that performs only the \(\tau \)-transition is complete when assuming \(\{b\}\)-progress, but not when assuming \(\emptyset \)-progress. Definition 6 defines B-justness accordingly, and [25] furthermore defines 18 different notions of B-fairness, for any choice of \(B \subseteq \mathcal{A}\). The internal action \(\tau \notin B\) can never be blocked by the environment. The default forms of progress and justness described above correspond with \(\emptyset \)-progress and \(\emptyset \)-justness. In [40] blocking and non-blocking transitions are called cold and hot, respectively.
Two subtly different computational interpretations of Petri nets appear in the literature [14]: in the individual token interpretation multiple tokens appearing in the same place are seen as different resources, whereas in the collective token interpretation only the number of tokens in a place is semantically relevant. The difference is illustrated in Fig. 3.
The idea underlying justness is that once a transition t is enabled, eventually either t will fire, or one of the resources necessary for firing t will be used by some other transition. The execution path \(\pi \) in the net of Fig. 3 that fires the action a infinitely often, but never the action b, is \(\emptyset \)-just by Def. 6. Namely, \(t^b\) is not enabled by \(\pi \), as \(({}^\bullet t^b + \widehat{t}^b) \cap {}^\bullet t^a \ne \emptyset \). This fits with the individual token interpretation, as in this run it is possible to eventually consume each token that is initially present, and each token that stems from firing transition \(t^a\). This way any resource available for firing \(t^b\) will eventually be used by some other transition.
When adhering to the collective token interpretation of nets, execution path \(\pi \) could be deemed \(\emptyset \)-unjust, since transition \(t^b\) can fire when there is at least one token in its preplace, and this state of affairs can be seen as a single resource that is never taken away. This might be formalised by adapting the definition of \(\pi [t\rangle \), a path enabling a transition, namely by changing the condition \(({}^\bullet t + \widehat{t}\,) \cap {}^\bullet t_{j+1} = \emptyset \) from Def. 6 into \({}^\bullet t + \widehat{t} + {}^\bullet t_{j+1} \subseteq M_j\). However, this formalisation doesn’t capture that after dropping place s from the net of Fig. 3 there is still an infinite run in which b does not occur, namely when regularly firing two as simultaneously. This contradicts the conventional wisdom that firing multiple transitions at once can always be reduced to firing them in some order. To avoid that type of complication, I here stick to the individual token interpretation. Alternatively, one could restrict attention to 1-safe nets [40], on which there is no difference between the individual and collective token interpretations, or to the larger class of structural conflict nets [21, 23], on which the conditions \(({}^\bullet t + \widehat{t}\,) \cap {}^\bullet t_{j+1} = \emptyset \) and \({}^\bullet t + \widehat{t} + {}^\bullet t_{j+1} \subseteq M_j\) are equivalent [21, Section 23.1], so that Def. 6 applies equally well to the collective token interpretation.
5 Feasibility
A standard requirement on fairness assumptions, or completeness criteria in general, is feasibility [2], called machine closure in [33]. It says that any finite execution path can be extended into a complete one. The following theorem shows that B-justness is feasible indeed.
Theorem 1
For any \(B\subseteq \mathcal{A}\), each finite execution path of a finitary Petri net can be extended into a B-just path.
Proof
Without loss of generality I restrict attention to nets without transitions t with \({}^\bullet t=\emptyset \). Namely, an arbitrary net can be enriched with marked private preplaces \(p_t\) for each such t, and arcs \((p_t,t)\) and \((t,p_t)\). In essence, this enrichment preserves the collection of execution path of the net, ordered by the relation “is an extension of”, the validity of statements \(\pi [t\rangle \), and the property of B-justness.
I present an algorithm extending any given path \(M_0 t_1 M_1 t_2 \dots t_{k-1} M_k\) into a B-just path \(\pi = M_0 t_1 M_1 t_2 M_2 \dots \). The extension only uses transitions \(t_i\) with \(\ell (t_i)\notin B\). As data structure my algorithm employs an
 -matrix with columns named i, for \(i\ge k\), where each column has a head and a body. The head of column k contains \(M_k\) and its body lists the places \(s\in M_k\), leaving empty most slots if there are only finitely many such places. Since the given net is finitary, \(M_k\) has only countable many elements, so that they can be listed in the
-matrix with columns named i, for \(i\ge k\), where each column has a head and a body. The head of column k contains \(M_k\) and its body lists the places \(s\in M_k\), leaving empty most slots if there are only finitely many such places. Since the given net is finitary, \(M_k\) has only countable many elements, so that they can be listed in the
 slots of column k.
slots of column k.
The head of each column \(i>k\) with \(i{-}1<{ length}(\pi )\) will contain the pair \((t_i,M_i)\) and its body will list the places \(s\in M_i\), again leaving empty most slots if there are only finitely many such places. Once more, finitariness ensures that there are enough slots in column i.
An entry in the body of the matrix is either (still) empty, filled in with a place, or crossed out. Let
 be an enumeration of the entries in the body of this matrix.
be an enumeration of the entries in the body of this matrix.
At the beginning only column k is filled in; all subsequent columns of the matrix are empty. At each step \(i> k\) I first cross out all entries s in the body of the matrix for which there is no transition t with \(\ell (t)\notin B\), \(M_{i-1} [t\rangle \) and \(s \in {}^\bullet t\). In case all entries of the matrix are crossed out, the algorithm terminates, with output \(M_0 t_1 M_1 t_2 \dots M_{i-1}\). Otherwise I fill in column i as follows and cross out some more places occurring in body of the matrix.
I take n to be the smallest value such that entry
 is already filled in, say with place r, but not yet crossed out. By the previous step of the algorithm, \(M_{i-1} [t_i\rangle \) for some transition \(t_i\) with \(\ell (t_i)\notin B\) and \(r \in {}^\bullet t_i\). I now fill in \((t_i,M_i)\) in the head of column i; here \(M_i\) is the unique marking such that \(M_{i-1} [t_i\rangle M_i\). Subsequently I cross out all entries in the body of the matrix containing a place \(r'\in {}^\bullet t_i\). This includes the entry f(n). Finally, I fill in the body of column i with the places \(s\in M_i\).
is already filled in, say with place r, but not yet crossed out. By the previous step of the algorithm, \(M_{i-1} [t_i\rangle \) for some transition \(t_i\) with \(\ell (t_i)\notin B\) and \(r \in {}^\bullet t_i\). I now fill in \((t_i,M_i)\) in the head of column i; here \(M_i\) is the unique marking such that \(M_{i-1} [t_i\rangle M_i\). Subsequently I cross out all entries in the body of the matrix containing a place \(r'\in {}^\bullet t_i\). This includes the entry f(n). Finally, I fill in the body of column i with the places \(s\in M_i\).
In case the algorithm doesn’t terminate, the desired path \(\pi \) is the sequence \(\pi = M_0 t_1 M_1 t_2 M_2 \dots \) that is constructed in the limit. It remains to show that \(\pi \) is B-just.
Towards a contradiction, suppose \(\pi [t\rangle \) for a transition t with \(\ell (t)\notin B\). By Def. 6 there is an
 such that \(M_m[t\rangle \) and \(({}^\bullet t + \widehat{t}\,) \cap {}^\bullet t_{j+1} = \emptyset \) for all \(m \le j < { length}(\pi )\). Let h be the smallest such m with \(m\ge k\). Then there is a place \(r \in {}^\bullet t\) appearing in column h. Here I use that \({}^\bullet t\ne \emptyset \). This place was not yet crossed out when column h was constructed. Since \(r \notin {}^\bullet t_{j+1}\) and \(M_{j+1}[t\rangle \) for all \(h \le j < { length}(\pi )\), place r will never be crossed out. It follows that \(\pi \) must be infinite. The entry r in column h is enumerated as f(n) for some
such that \(M_m[t\rangle \) and \(({}^\bullet t + \widehat{t}\,) \cap {}^\bullet t_{j+1} = \emptyset \) for all \(m \le j < { length}(\pi )\). Let h be the smallest such m with \(m\ge k\). Then there is a place \(r \in {}^\bullet t\) appearing in column h. Here I use that \({}^\bullet t\ne \emptyset \). This place was not yet crossed out when column h was constructed. Since \(r \notin {}^\bullet t_{j+1}\) and \(M_{j+1}[t\rangle \) for all \(h \le j < { length}(\pi )\), place r will never be crossed out. It follows that \(\pi \) must be infinite. The entry r in column h is enumerated as f(n) for some
 , and is eventually reached by the algorithm and crossed out. In this regard the matrix acts as a priority queue. This yields the required contradiction. \(\square \)
, and is eventually reached by the algorithm and crossed out. In this regard the matrix acts as a priority queue. This yields the required contradiction. \(\square \)
The above proof is a variant of [18, Thm. 1], which itself is a variant of [25, Thm. 6.1]. The side condition of finitariness is essential, as the below counterexample shows.
Example 2
Let \(N = (S, T, F, R, M_0, \ell )\) be the net with
 ,
,
 , \(M_0(s_r)=1\), \(\ell (t_r)=\tau \), \({}^\bullet t_r=\{s_r\}\) and \(\widehat{t}_r = {t}^\bullet _r= \emptyset \) for each
, \(M_0(s_r)=1\), \(\ell (t_r)=\tau \), \({}^\bullet t_r=\{s_r\}\) and \(\widehat{t}_r = {t}^\bullet _r= \emptyset \) for each
 . It contains uncountably many action transitions, each with a marked private preplace. As each execution path \(\pi \) contains only countably many transitions, many transitions remain enabled by \(\pi \).
. It contains uncountably many action transitions, each with a marked private preplace. As each execution path \(\pi \) contains only countably many transitions, many transitions remain enabled by \(\pi \).
6 The coarsest preorders preserving linear time properties
A linear time property is a predicate on system runs, and thus also on the execution paths of Petri nets. One writes \(\pi \models \varphi \) if the execution path \(\pi \) satisfies the linear-time property \(\varphi \). As the observable behaviour of an execution path \(\pi \) of a Petri net is deemed to be \({ trace}(\pi )\), in this context one studies only linear time properties \(\varphi \) such that
For this reason, a linear time property can be defined or characterised as a subset of \(\mathcal{A}^\infty \).
Linear time properties can be used to formalise correctness requirements on systems. They are deemed to hold for (or be satisfied by) a system iff they hold for all its complete runs. Following [20] I write \(\mathscr {D}\models ^{CC} \varphi \) iff property \(\varphi \) holds for all runs of the distributed system \(\mathscr {D}\)—and \(N \models ^{CC} \varphi \) iff it holds for all execution paths of the Petri net N—that are complete according to the completeness criterion CC. Prior to [20], \(\models \) was a binary predicate predicate between systems—or system representations such as Petri nets—and properties; in this setting the default completeness criterion of Section 4 was used. When using a completeness criterion B-C, where C is one of the 20 completeness criteria classified in [25] and \(B \subseteq \mathcal{A}\) is a modifier of C based on the set B of actions that may be blocked by the environment,
 is written \(N \models _{B}^C \varphi \) [20]. In this paper I am mostly interested in the values Pr and J of C, standing for progress and justness, respectively. To be consistent with previous work on temporal logic, \(N \models \varphi \) is a shorthand for \(N \models _\emptyset ^{ Pr} \varphi \).
is written \(N \models _{B}^C \varphi \) [20]. In this paper I am mostly interested in the values Pr and J of C, standing for progress and justness, respectively. To be consistent with previous work on temporal logic, \(N \models \varphi \) is a shorthand for \(N \models _\emptyset ^{ Pr} \varphi \).
For each completeness criterion B-C, let \(\sqsubseteq ^C_B\) be the coarsest preorder that preserves linear time properties when assuming B-C. Moreover, \(\sqsubseteq ^C\) is the coarsest preorder that preserves linear time properties when assuming completeness criterion C in each environment, meaning regardless which set of actions B can be blocked.
Definition 7
Write \(N \sqsubseteq ^C_B N'\) iff \(N \models _{B}^C \varphi ~\Rightarrow ~ N' \models _{B}^C \varphi \) for all linear time properties \(\varphi \). Write \(N \sqsubseteq ^C N'\) iff \(N \sqsubseteq ^C_B N'\) for all \(B \subseteq \mathcal{A}\).
It is trivial to give a more explicit characterisation of these preorders. To preserve the analogy with the failure pairs of CSP [6], instead of sets \(B \subseteq \mathcal{A}\) I will record their complements \(\overline{B} := \mathcal{A}{\setminus } B\). As \(\overline{\overline{B}}=B\), such sets carry the same information. Since B contains the actions that may be blocked by the environment, meaning that we consider environments that in any state may decide which actions from B to block, the set \(\overline{B}\cup \{\tau \}\) contains actions that may not be blocked by the environment. This means that we only consider environments that in any state are willing to synchronise with any action in \(\overline{B}\).
Definition 8
For completeness criterion C, B ranging over \(\mathscr {P}(\mathcal{A})\), and Petri net N, let

An element \((\sigma ,X)\) of \(\mathscr {F}^C(N)\) could be called a C-failure pair of N, because it indicates that the system represented by N, when executing a path with visible content \(\sigma \), may fail to execute additional actions from X, even when all these actions are offered by the environment, in the sense that the environment is perpetually willing to partake in those actions. Note that if \((\sigma ,X)\in \mathscr {F}^C(N)\) and \(Y \subseteq X\) then \((\sigma ,Y)\in \mathscr {F}^C(N)\).
Proposition 1
\(N \mathbin \sqsubseteq ^C_B N'\) iff \(\mathscr {F}^C_B(N) \mathbin \supseteq \mathscr {F}^C_B(N')\).
Likewise, \(N \mathbin \sqsubseteq ^C N'\) iff \(\mathscr {F}^C(N) \mathbin \supseteq \mathscr {F}^C(N')\).
Proof
Suppose \(N \sqsubseteq ^C_B N'\) and \(\sigma \notin \mathscr {F}^C_B(N)\). Let \(\varphi \) be the linear time property satisfying \(\pi \models \varphi \) iff \({ trace}(\pi ) \ne \sigma \). Then \(N \models ^C_B \varphi \) and thus \(N' \models ^C_B \varphi \). Hence \(\sigma \notin \mathscr {F}^C_B(N')\).
Suppose \(N \not \sqsubseteq ^C_B N'\). There there exists a linear time property \(\varphi \) such that \(N \models ^C_B \varphi \), yet \(N' \not \models ^C_B \varphi \). Let \(\pi '\) be a B-C-complete execution path of \(N'\) such that \(\pi '\not \models \varphi \), and let \(\sigma ={ trace}(\pi ')\). By (1) \(\pi \not \models \varphi \) for any execution path \(\pi \) (of any net) such that \({ trace}(\pi )=\sigma \). Hence \(\sigma \in \mathscr {F}^C_B(N')\), yet \(\sigma \notin \mathscr {F}^C_B(N)\). It follows that \(\mathscr {F}^C_B(N) \not \supseteq \mathscr {F}^C_B(N')\).
The second statement follows as a corollary of the first, using that \(\mathscr {F}^C(N) \supseteq \mathscr {F}^C(N')\) iff \(\mathscr {F}^C_B(N) \supseteq \mathscr {F}^C_B(N')\) for all \(B\subseteq \mathcal{A}\). \(\square \)
The preorders \(\sqsubseteq ^C_B\) can be classified as linear time semantics [12], as they are characterised through reverse trace inclusions. The preorders \(\sqsubseteq ^C\) on the other hand capture a minimal degree of branching time. This is because they should be ready for different choices of a system’s environment at runtime.
Note that \(\sqsubseteq ^C\) is contained in \(\sqsubseteq ^C_B\) for each \(B\subseteq \mathcal{A}\), in the sense that \(N \sqsubseteq ^C N'\) implies \(N \sqsubseteq ^C_B N'\). There is a priori no reason to assume inclusions between preorders \(\sqsubseteq ^C\) and \(\sqsubseteq ^D\) when D is a stronger completeness criterion than C.
To relate the preorders \(\sqsubseteq ^C_B\) and \(\sqsubseteq ^C\) with ones established in the literature, I consider the case \(C \mathbin = { Pr}\), i.e., taking progress as the completeness criterion C. The preorder \(\sqsubseteq ^{ Pr}_\emptyset \) is characterised as reverse inclusion of complete traces, where completeness is w.r.t. the default completeness criterion of Section 4. These complete traces include
-
the infinite traces of a system,
-
its divergence traces (stemming from execution paths that end in infinitely many \(\tau \)-transitions), and
-
its deadlock traces (stemming from finite execution paths that end in a marking enabling no transitions).
Deadlock and divergence traces are not distinguished. This corresponds with what is called divergence sensitive trace semantics (\(T^\lambda \)) in [12]. The above concept of complete traces of a process p is the same as in [15], there denoted \({ CT}(p)\).
The preorder \(\sqsubseteq ^{ Pr}_\mathcal{A}\) is characterised as reverse inclusion of infinite and partial traces, i.e., the traces of all execution paths. This corresponds with what is called infinitary trace semantics (\(T^\infty \)) in [12]. It is strictly coarser (making more identifications) than \(T^\lambda \).
To analyse the preorder \(\sqsubseteq ^{ Pr}\), one has \((\sigma ,X)\in \mathscr {F}^{ Pr}(N)\) if either
-
\(\sigma \) is an infinite trace of N—the set X plays no rôle in that case,
-
\(\sigma \) is a divergence trace of N, or
-
\(\sigma \) is the trace of a finite path of N whose end-marking enables no transition t with \(\ell (t)\in X\).
The resulting preorder does not occur in [12]—it can be placed strictly between divergence sensitive failure semantics (\(F^\varDelta \)) and divergence sensitive trace semantics (\(T^\lambda \)).
The entire family of preorders \(\sqsubseteq ^C_B\) and \(\sqsubseteq ^C\) proposed in this section was inspired by its most interesting family member, \(\sqsubseteq ^J\) (i.e., taking justness as the completeness criterion C), proposed earlier by Walter Vogler [43, Def. 5.6], also on Petri nets with read arcs. Vogler [43] uses the word fair for what I call just. I believe the choice of the word “just” is warranted to distinguish the concept from the many other kinds of fairness that appear in the literature, which are all of a very different nature. Accordingly, Vogler calls the semantics induced by \(\sqsubseteq ^J\) the fair failure semantics, whereas I call it the just failures semantics. My set \(\mathscr {F}^J(N)\) is called \(\mathscr {F}\mathscr {F}(N)\) in [43], and Vogler addresses \(\sqsupseteq ^J\) simply as \(\mathscr {F}\mathscr {F}\)-inclusion, thereby defining it via the right-hand side of Prop. 1.
7 Congruence properties
A preorder \(\sqsubseteq \) is called a precongruence for an n-ary operator \({ Op}\), if \(N_i \sqsubseteq N'_i\) for \(i=1,\dots ,n\) implies that \({ Op}(N_1,\dots ,N_n) \sqsubseteq { Op}(N'_1,\dots ,N'_n)\). In this case the operator \({ Op}\) is said to be monotone w.r.t. the preorder \(\sqsubseteq \). Being a precongruence for important operators is known to be a valuable tool in compositional verification [41].
I write \(\equiv \) for the kernel of \(\sqsubseteq \), that is, \(N \equiv N'\) iff \(N\sqsubseteq N' \wedge N' \sqsubseteq N\). Here I also imply that \(\equiv _B^C\) is the kernel of \(\sqsubseteq ^C_B\). If \(\sqsubseteq \) is a precongruence for \({ Op}\), then \(\equiv \) is a congruence for \({ Op}\), meaning that \(N_i \equiv N'_i\) for \(i=1,\dots ,n\) implies that \({ Op}(N_1,\dots ,N_n) \equiv { Op}(N'_1,\dots ,N'_n)\).
The preorder \(\sqsubseteq ^{ Pr}_\mathcal{A}\), characterised as reverse inclusion of infinite and partial traces, is well-known to be precongruence for the operators of CCSP. However, none of the other preorders \(\sqsubseteq ^{ Pr}_B\), nor \(\sqsubseteq ^{ Pr}\), is a precongruence for parallel composition.
Example 3
Let
 and
and
 . The definition of \(\Vert _\emptyset \) yields
. The definition of \(\Vert _\emptyset \) yields
 and
and
 . One has \(N \equiv ^{ Pr} N'\), and thus also \(N \equiv ^{ Pr}_B N'\), for each \(B\subseteq \mathcal{A}\). Namely \(\mathscr {F}^{ Pr}(N) =\mathscr {F}^{ Pr}(N') = \{(\varepsilon ,X)\mid X \subseteq \mathcal{A}\}\). Here \(\varepsilon \) denotes the empty string. When fixing B such that \(B\ne \mathcal{A}\) one may choose \(w \notin B\). Now \(\varepsilon \in \mathscr {F}_B^{ Pr}(\mathcal{T} \Vert _\emptyset N')\), for this process has an infinite execution path that avoids the w-transition, which generates a divergence trace \(\varepsilon \). Yet \(\varepsilon \notin \mathscr {F}_B^{ Pr}(\mathcal{T} \Vert _\emptyset N)\). Hence \(\mathcal{T} \Vert _\emptyset N \not \sqsubseteq ^{ Pr}_B \mathcal{T} \Vert _\emptyset N'\), and thus also \(\mathcal{T} \Vert _\emptyset N \not \sqsubseteq ^{ Pr} \mathcal{T} \Vert _\emptyset N'\). So neither \(\sqsubseteq ^{ Pr}_B\) nor \(\sqsubseteq ^{ Pr}\) are precongruences for \(\Vert _\emptyset \).
. One has \(N \equiv ^{ Pr} N'\), and thus also \(N \equiv ^{ Pr}_B N'\), for each \(B\subseteq \mathcal{A}\). Namely \(\mathscr {F}^{ Pr}(N) =\mathscr {F}^{ Pr}(N') = \{(\varepsilon ,X)\mid X \subseteq \mathcal{A}\}\). Here \(\varepsilon \) denotes the empty string. When fixing B such that \(B\ne \mathcal{A}\) one may choose \(w \notin B\). Now \(\varepsilon \in \mathscr {F}_B^{ Pr}(\mathcal{T} \Vert _\emptyset N')\), for this process has an infinite execution path that avoids the w-transition, which generates a divergence trace \(\varepsilon \). Yet \(\varepsilon \notin \mathscr {F}_B^{ Pr}(\mathcal{T} \Vert _\emptyset N)\). Hence \(\mathcal{T} \Vert _\emptyset N \not \sqsubseteq ^{ Pr}_B \mathcal{T} \Vert _\emptyset N'\), and thus also \(\mathcal{T} \Vert _\emptyset N \not \sqsubseteq ^{ Pr} \mathcal{T} \Vert _\emptyset N'\). So neither \(\sqsubseteq ^{ Pr}_B\) nor \(\sqsubseteq ^{ Pr}\) are precongruences for \(\Vert _\emptyset \).
A common solution to the problem of a preorder \(\sqsubseteq \) not being a precongruence for certain operators is to instead consider its congruence closure, defined as the largest precongruence contained in \(\sqsubseteq \).
In [15, 30] the congruence closure of \(\sqsubseteq ^{ Pr}\) is characterised as the so-called NDFD preorder \(\sqsubseteq _{ NDFD}\). Here \(N \sqsubseteq _{ NDFD} N'\) iff \(N \sqsubseteq ^{ Pr} N'\) (characterised in the previous section) and moreover the divergence traces of \(N'\) are included in those of N. As remarked in [15], here it does not matter whether one requires congruence closure merely w.r.t. parallel composition and injective relabelling, or w.r.t. all operators of CSP (or CCSP, or anything in between).
Unlike \(\sqsubseteq ^{ Pr}\), the preorder \(\sqsubseteq ^J\) is a precongruence for parallel composition. Although this has been proven already by Vogler [43, 22, in Appendix B] I provide a proof that bypasses the auxiliary notion of urgent transitions, and provides more details.
Proposition 2
([43]) \(\sqsubseteq ^J\) is a precongruence for relabelling and abstraction.
Proof
This follows since \(\mathscr {F}^J(f(N)) = \{(f(\sigma ),X) \mid (\sigma , f^{-1}(X))\in \mathscr {F}^J(N)\}\) and moreover \(\mathscr {F}^J(\tau _I(N)) = \{(\tau _I(\sigma ),X) \mid (\sigma , X\cup I)\in \mathscr {F}^J(N)\}\). Here \(\tau _I(\sigma )\) is the result of pruning all I-actions from \(\sigma \in \mathcal{A}^\infty \). \(\square \)
Trivially, \(\sqsubseteq ^J\) also is a precongruence for \(\sum a_i P_i\) and \(a \triangleright \sum a_i P_i\).
The preorder \(\sqsubseteq ^{ J}_\mathcal{A}\) can be seen to coincide with \(\sqsubseteq ^{ Pr}_\mathcal{A}\), characterised as reverse inclusion of infinite and partial traces, and thus is a precongruence for the operators of CCSP. Leaving open the case \(|\mathcal{A}{\setminus }B|=1\), the preorders \(\sqsubseteq ^{ J}_B\) with \(|\mathcal{A}{\setminus }B|\ge 2\) fail to be precongruences for parallel composition.
Example 4
Take \(b,c \notin B\). Let N, \(N'\) and \(\mathcal{T}\) be as shown in Fig. 4. Then \(N \mathbin \equiv ^J_B N'\), as \(\mathscr {F}^J_B(N)\mathbin =\mathscr {F}^J_B(N')\mathbin =\{\varepsilon , ab, ac\}\). (Whether \(\varepsilon \) is included depends on whether \(a \mathbin \in B\).) Yet \(\mathcal{T}\Vert _\mathcal{A}N \not \equiv ^J_B \mathcal{T}\Vert _\mathcal{A}N'\), as \(a \mathbin \in \mathscr {F}^J_B(\mathcal{T}\Vert _\mathcal{A}N')\), yet \(a \mathbin {\notin } \mathscr {F}^J_B(\mathcal{T}\Vert _\mathcal{A}N)\).
Moreover, as illustrated below, the preorders \(\sqsubseteq ^{ J}_B\) with \(B\ne \emptyset \) and \(|\mathcal{A}{\setminus }B|\ge 1\) fail to be precongruences for abstraction. In the next section I will show that, for \(\mathcal{A}\) infinite and \(B\ne \mathcal{A}\), the congruence closure of \(\sqsubseteq ^J_B\) for parallel composition, abstraction and relabelling is \(\sqsubseteq ^J\).
Example 5
Take \(b \in B\) and \(c\notin B\). Let N and \(N'\) be as shown in Fig. 5. Then \(N \equiv ^J_B N'\), as \(\mathscr {F}^J_B(N)=\mathscr {F}^J_B(N')=\{\varepsilon , bc\}\). Yet \(\tau _{\{b\}}(N) \not \equiv ^J_B \tau _{\{b\}}(N')\), since \(\varepsilon \in \mathscr {F}^J_B(\tau _{\{b\}}(N'))\), yet \(\varepsilon \notin \mathscr {F}^J_B(\tau _{\{b\}}(N))\).
8 Must Testing
A test is a Petri net, but featuring a special action \(w\notin \mathcal{A}_\tau \), not used elsewhere. This action is used to mark success markings: those in which w is enabled. If \({\mathcal{T}}\) is a test and N a net then \(\tau _{\mathcal{A}}(\mathcal{T}\Vert _\mathcal{A}N)\) is also a test. An execution path of \(\tau _{\mathcal{A}}(\mathcal{T}\Vert _\mathcal{A}N)\) is successful iff it contains a success marking.
Definition 9
A Petri net N may pass a test \(\mathcal{T}\!\), notation \(N~{\textbf {may}}~\mathcal{T}\!\), if \(\tau _{\!\mathcal{A}}(\mathcal{T}\Vert _\mathcal{A} N)\) has a successful execution path. It must pass \(\mathcal{T}\), notation \(N~{\textbf {must}}~\mathcal{T}\), if each complete execution path of \(\tau _{\mathcal{A}}(\mathcal{T}\Vert _\mathcal{A}N)\) is successful. It should pass \(\mathcal{T}\), notation \(N~{\textbf {should}}~\mathcal{T}\), if each finite execution path of \(\tau _{\mathcal{A}}(\mathcal{T}\Vert _\mathcal{A}N)\) can be extended into a successful execution path.
Write \(N \sqsubseteq _\textrm{must} N'\) if \(N~{\textbf {must}}~\mathcal{T}\) implies \(N'~{\textbf {must}}~\mathcal{T}\) for each test \(\mathcal{T}\). The preorders \(\sqsubseteq _\textrm{may}\) and \(\sqsubseteq _\textrm{should}\) are defined similarly.
The may- and must-testing preorders stem from De Nicola & Hennessy [9], whereas should-testing was added independently in [5] and [36].
In the original work on testing [9] the CCS parallel composition \(\mathcal{T}|N\) was used instead of the concealed CCSP parallel composition \(\tau _{\mathcal{A}}(\mathcal{T}\Vert _\mathcal{A}N)\); moreover, only those execution paths consisting solely of internal actions mattered for the definitions of passing a test. The present approach is equivalent. First of all, restricting attention to execution paths of \(\mathcal{T}|N\) consisting solely of internal actions is equivalent to putting \(\mathcal{T}|N\) is the scope of a CCS restriction operator \(\backslash \mathcal{A}\) [34], for that operator drops all transitions of its argument that are not labelled \(\tau \) or w. Secondly, CCS features a complementary action \(\bar{a}\) for each \(a\in \mathcal{A}\), and one has \(\bar{\bar{a}}=a\). For \(\mathcal{T}\) a test, let \(\overline{\mathcal{T}}\) denote the complementary test in which each action \(a\in \mathcal{A}\) is replaced by \(\bar{a}\); again \(\overline{\overline{\mathcal{T}}}=\mathcal{T}\). It follows directly from the definitions of the operators involved that \(\tau _{\mathcal{A}}(\mathcal{T}\Vert _\mathcal{A}N)\) is identicalFootnote 3 to \((\overline{\mathcal{T}}| N)\backslash \mathcal{A}\). This proves the equivalence of the two approaches.
Unlike may- and should-testing, the concept of must-testing is naturally parametrised with a completeness criterion, deciding what counts as a complete execution. To make this choice explicit I use the notation \(\sqsubseteq _\textrm{must}^C\), where C could be any of the completeness criteria surveyed in [25]. Since processes \(\tau _{\mathcal{A}}(\mathcal{T}\Vert _\mathcal{A}N)\) (or \((\mathcal{T}| N)\backslash \mathcal{A}\)) do not feature any actions other than \(\tau \) and w, where w is used merely to point to the success states, the modifier \(B\subseteq \mathcal{A}\) of a completeness criteria B-C has no effect, i.e., any two choices of this modifier are equivalent.
In the original work of [9] the default completeness criterion progress from Section 4 was employed. Interestingly, \(\sqsubseteq _\textrm{must}^{ Pr}\) is a congruence for the operators of CCSP that does not preserve all linear time properties. It is strictly coarser than \(\sqsubseteq _{ NDFD}\). In fact, it is the coarsest precongruence for the CCSP parallel composition and injective relabelling that preserves those linear time properties that express that a system will eventually reach a state in which something [good] has happened [15]. (In [15], following [32], but deviating from the standard terminology of [1], such properties are called liveness properties.)
In this paper I investigate the must-testing preorder when taking justness as the underlying completeness criterion, \(\sqsubseteq _\textrm{must}^{ J}\). Thm. 2 below shows that it can be characterised as the just failures preorder \(\sqsubseteq ^{ J}\) of Section 6.
First note that Def. 9 can be simplified. When dealing with justness as completeness criterion, the word “complete” in Def. 9 is instantiated by “just” or “B-just”, for some \(B\subseteq \mathcal{A}\) (not including w). As the result is independent of B, one may take \(B:=\emptyset \). Since the labelling of a net has no bearing on its execution paths, or on whether such a path is \(\emptyset \)-just, or successful, one may now drop the operator \(\tau _A\) from Def. 9 without affecting the resulting notion of must testing.
Theorem 2
\(N \sqsubseteq _\textrm{must}^{ J} N'\) iff \(N \sqsubseteq ^J N'\).
Proof
The “if” direction is established in [22, Appendix C].
For “only if”, suppose \(N \sqsubseteq _\textrm{must}^{ J} N'\). Using Prop. 1, it suffices to show that \(\mathscr {F}^J(N) \supseteq \mathscr {F}^J(N')\). Let \((\sigma ,X) \in \mathscr {F}^J(N')\), where \(\sigma = a_1 a_2 \dots \in \mathcal{A}^\infty \) is a finite or infinite sequence of actions. Let \(\mathcal{T}\) be the test displayed in Fig. 6. The drawing is for the case that \(\sigma = a_1 a_2 \dots a_n\) finite; in the infinite case, there is no need to display \(a_n\) separately. Now \(K ~{\textbf {must}}~ \mathcal{T}\), for any net K, when using justness as completeness criterion, iff each \(\emptyset \)-just execution path of \(\mathcal{T}\Vert _\mathcal{A}K\) is successful, which is the case iff \((\sigma ,X)\notin \mathscr {F}^J(K)\). (In other words, \(\mathcal{T}\Vert _\mathcal{A}K\) has an unsuccessful \(\emptyset \)-just execution path iff \((\sigma ,X)\in \mathscr {F}^J(K)\). For the meaning of \((\sigma ,X)\in \mathscr {F}^J(K)\) is that K has an execution path \(\pi \) with \({ trace}(\pi )=\sigma \) such that \(\ell _K(t)\in X \Rightarrow \lnot \pi [t\rangle \).) Hence \(N' ~{\textbf {must}}~{\textbf {not}}~ \mathcal{T}\) and thus \(N ~{\textbf {must}}~{\textbf {not}}~ \mathcal{T}\), and thus \((\sigma ,X)\in \mathscr {F}^J(N)\). \(\square \)
Proposition 3
Let \(\mathcal{A}\) be infinite and \(B \ne \mathcal{A}\). Then \(\sqsubseteq ^J\) is the congruence closure of \(\sqsubseteq ^J_B\) for parallel composition, abstraction and injective relabelling.
Proof
Pick an action \(w \in \mathcal{A}{\setminus }B\). Assume \(N \not \sqsubseteq ^J N'\). By applying an injective relabelling, one can assure that w does not occur in N or \(N'\). Let \((\sigma ,X)\in \mathscr {F}^J(N')\), yet \((\sigma ,X)\notin \mathscr {F}^J(N)\), with \(w \notin X\). Let T be the net of Fig. 6. Then, writing \(A:=\mathcal{A}{\setminus }\{w\}\), \((\sigma ,\mathcal{A})\in \mathscr {F}^J(\mathcal{T}\Vert _A N')\), yet \((\sigma ,\mathcal{A})\notin \mathscr {F}^J(\mathcal{T}\Vert _A N)\). Moreover, \((\rho ,\mathcal{A})\notin \mathscr {F}^J(\mathcal{T}\Vert _A N')\) and \((\rho ,\mathcal{A})\notin \mathscr {F}^J(\mathcal{T}\Vert _A N)\) for any \(\rho \ne \sigma \) not containing the action w. Hence, applying the proof of Prop. 2, using that \(A \cup \overline{B} = \mathcal{A}\), one has \((\varepsilon ,\overline{B})\in \mathscr {F}^J(\tau _{A}(\mathcal{T}\Vert _A N'))\), yet \((\varepsilon ,\overline{B})\notin \mathscr {F}^J(\tau _{A}(\mathcal{T}\Vert _A N))\). Thus \(\varepsilon \in \mathscr {F}^J_B(\tau _{A}(\mathcal{T}\Vert _A N'))\), yet \(\varepsilon \notin \mathscr {F}^J_B(\tau _{A}(\mathcal{T}\Vert _A N))\). It follows that \(\tau _{A}(\mathcal{T}\Vert _A N) \not \sqsubseteq ^J_B \tau _{A}(\mathcal{T}\Vert _A N')\). \(\square \)
9 Timed must-testing
A timed form of must-testing was proposed by Vogler in [43]. Justness says that each transition that gets enabled must fire eventually, unless one of its necessary resources will be taken away. In Vogler’s framework, each transition t must fire within 1 unit of time after it becomes enabled, even though it can fire faster. The implicit timer is reset each time t becomes disabled and enabled again, by another transition taken a token and returning it to one of the replaces of t. Since there is no lower bound on the time that may elapse before a transition fires, this view encompasses the same asynchronous behaviour of nets as under the assumption of justness.
Vogler’s work only pertains to safe nets: those with the property that no reachable marking allocates multiple tokens to the same place. Here a marking is reachable if it occurs in some execution path. Transitions t with \({}^\bullet t=\emptyset \) are excluded. Although he only considered finite nets, here I apply his work unchanged to finitely branching nets: those in which only finitely many transitions are enabled in each reachable marking.
Definition 10
([43]) A continuous(ly timed ) instantaneous description (CID) of a net N is a pair \((M,\xi )\) consisting of a marking M of N and a function \(\xi \) mapping the transitions enabled under M to [0, 1]; \(\xi \) describes the residual activation time of an enabled transition.
The initial CID is CID\(_0 = (M_0 ; \xi _0)\) with \(\xi _0 (t) = 1\) for all t with \(M_0[t\rangle \).
One writes \((M,\xi )[\eta \rangle (M',\xi ')\) if one of the following cases applies:
-
(1)
\(\eta = t \in T\), \(M [t\rangle M'\), \(\xi '(t):=\xi (t)\) for those transitions t enabled under \(M - {}^\bullet t\) and \(\xi '(t):=1\) for the other transitions enabled under \(M'\).
-
(2)
 , \(M' = M\) and \(\xi ' = \xi - r\).
, \(M' = M\) and \(\xi ' = \xi - r\).
A timed execution path \(\pi \) is an alternating sequence of CIDs and elements \(t\in T\) or
 , defined just like an execution path in Def. 6. Let
, defined just like an execution path in Def. 6. Let
 be the sum of all time steps in a timed execution path \(\pi \), the duration of \(\pi \).
be the sum of all time steps in a timed execution path \(\pi \), the duration of \(\pi \).
A timed test is a pair \((\mathcal{T}, D)\) of a test \(\mathcal{T}\) and a duration
 . A net must pass a timed test \((\mathcal{T}, D)\), notation N must \((\mathcal{T}, D)\), if each timed execution path \(\pi \) with \(\zeta (\pi )> D\) contains a transition labelled w. Write \(N \sqsubseteq _\textrm{must}^\textrm{timed} N'\) if \(N~{\textbf {must}}~(\mathcal{T},D)\) implies \(N'~{\textbf {must}}~(\mathcal{T},D)\) for each timed test \((\mathcal{T},D)\).
. A net must pass a timed test \((\mathcal{T}, D)\), notation N must \((\mathcal{T}, D)\), if each timed execution path \(\pi \) with \(\zeta (\pi )> D\) contains a transition labelled w. Write \(N \sqsubseteq _\textrm{must}^\textrm{timed} N'\) if \(N~{\textbf {must}}~(\mathcal{T},D)\) implies \(N'~{\textbf {must}}~(\mathcal{T},D)\) for each timed test \((\mathcal{T},D)\).
Vogler shows that the preorder \(\sqsubseteq _\textrm{must}^\textrm{timed}\) is strictly finer than \(\sqsubseteq ^J\). In fact, although \(\tau .a.\textbf{0}\equiv ^J a.\textbf{0}\), one has \(\tau .a.\textbf{0}\not \equiv _\textrm{must}^\textrm{timed} a.\textbf{0}\), since only the latter process must pass the timed test (a.w, 2). Here I use that each of the actions \(\tau \), a and w may take up to 1 unit of time to occur. A statement \(N \sqsubseteq _\textrm{must}^\textrm{timed} N'\) says that \(N'\) is faster than N, in the sense that composed with a test it is guaranteed to reach success states in less time than N.
Here I show that when abstracting from the quantitative dimension of timed must-testing, it exactly characterises \(\sqsubseteq ^J\).
Definition 11
A net must eventually pass a test \(\mathcal{T}\) if there exists a
 such that N must \((\mathcal{T}, D)\). Write \(N \sqsubseteq _\textrm{must}^\mathrm{ev.} N'\) if when N must eventually pass a test \(\mathcal{T}\), then so does \(N'\).
such that N must \((\mathcal{T}, D)\). Write \(N \sqsubseteq _\textrm{must}^\mathrm{ev.} N'\) if when N must eventually pass a test \(\mathcal{T}\), then so does \(N'\).
Theorem 3
Let \(N,N'\) be finitely branching safe nets. Then \(N \sqsubseteq _\textrm{must}^\mathrm{ev.} N'\) iff \(N \sqsubseteq ^J N'\).
A proof can be found in [22, Appendix D].
10 Conclusion
The just failures preorder \(\sqsubseteq ^J\) was introduced by Walter Vogler [43] in 2002. Since then it has not received much attention in the literature, and has not been used as the underlying semantic principle justifying actual verifications. In my view this can be seen as a fault of the subsequent literature, as \(\sqsubseteq ^J\) captures exactly what is needed—no more and no less—for the verification of safety and liveness properties of realistic systems.
I substantiate this claim by pointing out that \(\sqsubseteq ^J\) is the coarsest preorder preserving safety and liveness properties when assuming justness, that is a congruence for basic process algebra operators, such as the partially synchronous parallel composition, abstraction from internal actions, and renaming. As argued in [17, 18, 24, 25], justness is better motivated and more suitable for applications than competing completeness criteria, such as progress or the many notions of fairness surveyed in [24].
Moreover, I adapt the well-known must-testing preorder of De Nicola & Hennessy [9], by using justness as the underlying completeness criterion, instead of the traditional choice of progress. By showing that the resulting must-testing preorder \(\sqsubseteq _\textrm{must}^{ J}\) coincides with \(\sqsubseteq ^J\) I strengthen the case that this is a natural and fundamental preorder.
This conclusion is further strengthened by my result that it also coincides with a qualitative version \(\sqsubseteq _\textrm{must}^\mathrm{ev.}\) of the timed must-testing preorder \(\sqsubseteq _\textrm{must}^\textrm{timed}\) of Vogler [43]. (Although \(\sqsubseteq _\textrm{must}^\textrm{timed}\) and \(\sqsubseteq ^J\) stem from the same paper [43], this connection was not made there.)
All this was shown in the setting of Petri nets extended with read arcs, and therefore also applies to the settings of standard process algebras such as CCS, CSP or ACP. Since I cover read arcs, it also applies to process algebras enriched with signalling, an operator that extends the expressiveness of standard process algebras and is needed to accurately model mutual exclusion. I leave it for future work to explore these matters for probabilistic models of concurrency, or other useful extensions.
Fig. 7 situates \(\sqsubseteq _\textrm{must}^{ J}\) w.r.t. the some other semantic preorders from the literature. The lines indicate inclusions. Here \({\sqsubseteq _\textrm{must}^{ Pr}}\), \({\sqsubseteq _\textrm{may}}\) and \({\sqsubseteq _\textrm{should}}\) are the classical must-, may- and should-testing preorders from [9] and [5, 36]—see Def. 9—and \(\sqsubseteq _\textrm{reward}^{ Pr}\) is the reward-testing preorder introduced by me in [19]. The failures-divergences preorder of CSP [6, 42], defined in a similar way as \(\sqsubseteq _\textrm{must}^{ J}\), coincides with \({\sqsubseteq _\textrm{must}^{ Pr}}\) [9, 19].
 denotes the classical notion of strong bisimilarity [34], and
denotes the classical notion of strong bisimilarity [34], and
 ,
,
 are essentially the only other preorders (in fact equivalences) that preserve linear time properties when assuming justness: the enabling preserving bisimilarity of [26] and the structure preserving bisimilarity of [16].
are essentially the only other preorders (in fact equivalences) that preserve linear time properties when assuming justness: the enabling preserving bisimilarity of [26] and the structure preserving bisimilarity of [16].
The inclusions follow directly from the definitions—see refs. —and counterexamples against further inclusions appear below.

Notes
- 1.
- 2.
Here I require P to be a guarded choice in order to avoid the need for a root condition [13] to make the equivalences of this paper into congruences. This is also the reason my language features a guarded choice, instead of action prefixing and general choice.
- 3.
The standard definition of | on Petri nets [28] is given only up to isomorphism. By choosing the names of places and transitions similar to those in the definition of \(\Vert _\mathcal{A}\) from [22, Appendix A] one can obtain \(\tau _{\mathcal{A}}(\mathcal{T}\Vert _\mathcal{A}N)=(\overline{\mathcal{T}}| N)\backslash \mathcal{A}\).
References
Alpern, B., Schneider, F.B.: Defining liveness. Infromation Processing Letters 21(4), 181–185 (1985). https://doi.org/10.1016/0020-0190(85)90056-0
Apt, K.R., Francez, N., Katz, S.: Appraising fairness in languages for distributed programming. Distributed Computing 2(4), 226–241 (1988). https://doi.org/10.1007/BF01872848
Bergstra, J.A.: ACP with signals. In: Grabowski, J., Lescanne, P., Wechler, W. (eds.) Proc. International Workshop on Algebraic and Logic Programming. LNCS, vol. 343, pp. 11–20. Springer (1988). https://doi.org/10.1007/3-540-50667-5_53
Bergstra, J.A., Klop, J.W.: Algebra of communicating processes with abstraction. Theor. Comput. Sci. 37(1), 77–121 (1985). https://doi.org/10.1016/0304-3975(85)90088-X
Brinksma, E., Rensink, A., Vogler, W.: Fair testing. In: Lee, I., Smolka, S.A. (eds.) Proc. 6th International Conference on Concurrency Theory, CONCUR’95. LNCS, vol. 962, pp. 313–327. Springer (1995). https://doi.org/10.1007/3-540-60218-6_23
Brookes, S.D., Hoare, C.A.R., Roscoe, A.W.: A theory of communicating sequential processes. J. ACM 31(3), 560–599 (1984). https://doi.org/10.1145/828.833
Busi, N., Pinna, G.M.: Non sequential semantics for contextual P/T nets. In: Billington, J., Reisig, W. (eds.) Proc. 17th Int. Conf. on Application and Theory of Petri Nets. LNCS, vol. 1091, pp. 113–132. Springer (1996). https://doi.org/10.1007/3-540-61363-3_7
Corradini, F., Di Berardini, M.R., Vogler, W.: Time and fairness in a process algebra with non-blocking reading. In: Nielsen, M., Kucera, A., Miltersen, P.B., Palamidessi, C., Tuma, P., Valencia, F.D. (eds.) Theory and Practice of Computer Science, SOFSEM’09. LNCS, vol. 5404, pp. 193–204. Springer (2009). https://doi.org/10.1007/978-3-540-95891-8_20
De Nicola, R., Hennessy, M.: Testing equivalences for processes. Theor. Comput. Sci. 34, 83–133 (1984). https://doi.org/10.1016/0304-3975(84)90113-0
Degano, P., De Nicola, R., Montanari, U.: CCS is an (augmented) contact free C/E system. In: Venturini Zilli, M. (ed.) Advanced School on Mathematical Models for the Semantics of Parallelism, 1986. LNCS, vol. 280, pp. 144–165. Springer (1987). https://doi.org/10.1007/3-540-18419-8_13
Dyseryn, V., van Glabbeek, R.J., Höfner, P.: Analysing mutual exclusion using process algebra with signals. In: Peters, K., Tini, S. (eds.) Proceedings Combined 24th International Workshop on Expressiveness in Concurrency and 14th Workshop on Structural Operational Semantics. EPTCS, vol. 255, pp. 18–34 (2017). https://doi.org/10.4204/EPTCS.255.2
van Glabbeek, R.J.: The linear time – branching time spectrum II; the semantics of sequential systems with silent moves. In: Best, E. (ed.) Proc. CONCUR’93, 4\(^{th}\) Int. Conf. on Concurrency Theory. LNCS, vol. 715, pp. 66–81. Springer (1993). https://doi.org/10.1007/3-540-57208-2_6
van Glabbeek, R.J.: A characterisation of weak bisimulation congruence. In: Middeldorp, A., van Oostrom, V., van Raamsdonk, F., de Vrijer, R. (eds.) Processes, Terms and Cycles: Steps on the Road to Infinity: Essays Dedicated to Jan Willem Klop on the Occasion of His 60th Birthday. LNCS, vol. 3838, pp. 26–39. Springer (2005). https://doi.org/10.1007/11601548_4
van Glabbeek, R.J.: The individual and collective token interpretations of Petri nets. In: Abadi, M., de Alfaro, L. (eds.) Proc. CONCUR’05, 16\(^{th}\) Int. Conf. on Concurrency Theory. LNCS, vol. 3653, pp. 323–337. Springer (2005). https://doi.org/10.1007/11539452_26
van Glabbeek, R.J.: The coarsest precongruences respecting safety and liveness properties. In: Calude, C., Sassone, V. (eds.) Proc. 6th IFIP TC 1/WG 2.2 Int. Conf. on Theoretical Computer Science, TCS’10; held as part of the World Computer Congress. IFIP, vol. 323, pp. 32–52. Springer (2010). https://doi.org/10.1007/978-3-642-15240-5_3, http://arxiv.org/abs/1007.5491
van Glabbeek, R.J.: Structure preserving bisimilarity, supporting an operational petri net semantics of CCSP. In: Meyer, R., Platzer, A., Wehrheim, H. (eds.) Proceedings Correct System Design - Symposium in Honor of Ernst-Rüdiger Olderog on the Occasion of His 60th Birthday. LNCS, vol. 9360, pp. 99–130. Springer (2015). https://doi.org/10.1007/978-3-319-23506-6_9, http://arxiv.org/abs/1509.05842
van Glabbeek, R.J.: Ensuring liveness properties of distributed systems: Open problems. Journal of Logical and Algebraic Methods in Programming 109, 100480 (2019). https://doi.org/10.1016/j.jlamp.2019.100480
van Glabbeek, R.J.: Justness: A completeness criterion for capturing liveness properties. In: Bojańczyk, M., Simpson, A. (eds.) Proc. 22st Int. Conf. on Foundations of Software Science and Computation Structures, FoSSaCS’19; held as part of ETAPS’19. LNCS, vol. 11425, pp. 505–522. Springer (2019). https://doi.org/10.1007/978-3-030-17127-8_29, https://arxiv.org/abs/1909.00286
van Glabbeek, R.J.: Reward testing equivalences for processes. In: Boreale, M., Corradini, F., Loreti, M., Pugliese, R. (eds.) Models, Languages, and Tools for Concurrent and Distributed Programming, Essays Dedicated to Rocco De Nicola on the occasion of his 65th Birthday, LNCS, vol. 11665, pp. 45–70. Springer (2019). https://doi.org/10.1007/978-3-030-21485-2_5, https://arxiv.org/abs/1907.13348
van Glabbeek, R.J.: Reactive temporal logic. In: Dardha, O., Rot, J. (eds.) Proc. Combined 27th Int. Workshop on Expressiveness in Concurrency and 17th Workshop on Structural Operational Semantics. EPTCS, vol. 322, pp. 51–68 (2020). https://doi.org/10.4204/EPTCS.322.6
van Glabbeek, R.J.: Modelling mutual exclusion in a process algebra with time-outs (2021), https://arxiv.org/abs/2106.12785
van Glabbeek, R.J.: Just Testing (2022), version of this paper extended with four appendices, https://arxiv.org/abs/2212.08829
van Glabbeek, R.J., Goltz, U., Schicke, J.W.: Abstract processes of place/transition systems. Information Processing Letters 111(13), 626–633 (2011). https://doi.org/10.1016/j.ipl.2011.03.013, https://arxiv.org/abs/1103.5916
van Glabbeek, R.J., Höfner, P.: CCS: it’s not fair! – fair schedulers cannot be implemented in CCS-like languages even under progress and certain fairness assumptions. Acta Informatica 52(2-3), 175–205 (2015). https://doi.org/10.1007/s00236-015-0221-6, https://arxiv.org/abs/1505.05964
van Glabbeek, R.J., Höfner, P.: Progress, justness and fairness. ACM Computing Surveys 52(4), 69 (August 2019). https://doi.org/10.1145/3329125, https://arxiv.org/abs/1810.07414
van Glabbeek, R.J., Höfner, P., Wang, W.: Enabling preserving bisimulation equivalence. In: Haddad, S., Varacca, D. (eds.) Proc. 32nd Int. Conference on Concurrency Theory, CONCUR’21. Leibniz International Proceedings in Informatics (LIPIcs), vol. 203. Schloss Dagstuhl–Leibniz-Zentrum für Informatik (2021). https://doi.org/10.4230/LIPIcs.CONCUR.2021.33, https://arxiv.org/abs/2108.00142
van Glabbeek, R.J., Vaandrager, F.W.: Petri net models for algebraic theories of concurrency. In: Bakker, J.W.d., Nijman, A.J., Treleaven, P.C. (eds.) Proc. PARLE, Parallel Architectures and Languages Europe, Vol. II. LNCS, vol. 259, pp. 224–242. Springer (1987). https://doi.org/10.1007/3-540-17945-3_13
Goltz, U.: CCS and Petri nets. In: Guessarian, I. (ed.) Proc. Semantics of Systems of Concurrent Processes, LITP Spring School on Theoretical Computer Science. LNCS, vol. 469, pp. 334–357. Springer (1990). https://doi.org/10.1007/3-540-53479-2_14
Goltz, U., Mycroft, A.: On the relationship of CCS and Petri nets. In: Paredaens, J. (ed.) Proc. \(11^{th}\) Colloquium on Automata, Languages and Programming, ICALP84. LNCS, vol. 172, pp. 196–208. Springer (1984). https://doi.org/10.1007/3-540-13345-3_18
Kaivola, R., Valmari, A.: The weakest compositional semantic equivalence preserving nexttime-less linear temporal logic. In: Cleaveland, R. (ed.) Proc. CONCUR’92. LNCS, vol. 630, pp. 207–221. Springer (1992). https://doi.org/10.1007/BFb0084793
Kindler, E., Walter, R.: Mutex needs fairness. Inf. Process. Lett. 62(1), 31–39 (1997). https://doi.org/10.1016/S0020-0190(97)00033-1
Lamport, L.: Proving the correctness of multiprocess programs. IEEE Transactions on Software Engineering 3(2), 125–143 (1977). https://doi.org/10.1109/TSE.1977.229904
Lamport, L.: Fairness and hyperfairness. Distributed Computing 13(4), 239–245 (2000). https://doi.org/10.1007/PL00008921
Milner, R.: Communication and Concurrency. Prentice-Hall (1989), alternatively see A Calculus of Communicating Systems, LNCS 92, Springer, 1980, https://doi.org/10.1007/3-540-10235-3
Montanari, U., Rossi, F.: Contextual nets. Acta Informatica 32(6), 545–596 (1995). https://doi.org/10.1007/BF01178907
Natarajan, V., Cleaveland, R.: Divergence and fair testing. In: Fülöp, Z., Gécseg, F. (eds.) Proc. 22nd Int. Colloquium on Automata, Languages and Programming, ICALP’95. LNCS, vol. 944, pp. 648–659. Springer (1995). https://doi.org/10.1007/3-540-60084-1_112
Olderog, E.R.: Operational Petri net semantics for CCSP. In: Rozenberg, G. (ed.) Advances in Petri Nets 1987. LNCS, vol. 266, pp. 196–223. Springer (1987). https://doi.org/10.1007/3-540-18086-9_27
Olderog, E.R.: Nets, Terms and Formulas: Three Views of Concurrent Processes and Their Relationship. Cambridge Tracts in Theoretical Computer Science 23, Cambridge University Press (1991)
Olderog, E.R., Hoare, C.A.R.: Specification-oriented semantics for communicating processes. Acta Inf. 23, 9–66 (1986). https://doi.org/10.1007/BF00268075
Reisig, W.: Understanding Petri Nets — Modeling Techniques, Analysis Methods, Case Studies. Springer (2013). https://doi.org/10.1007/978-3-642-33278-4
Roever, W.P.d., de Boer, F.S., Hannemann, U., Hooman, J., Lakhnech, Y., Poel, M., Zwiers, J.: Concurrency Verification: Introduction to Compositional and Noncompositional Methods, Cambridge Tracts in TCS, vol. 54. Cambridge University Press (2001)
Roscoe, A.W.: The Theory and Practice of Concurrency. Prentice-Hall (1997), http://www.comlab.ox.ac.uk/bill.roscoe/publications/68b.pdf
Vogler, W.: Efficiency of asynchronous systems, read arcs, and the MUTEX-problem. Theor. Comput. Sci. 275(1-2), 589–631 (2002). https://doi.org/10.1016/S0304-3975(01)00300-0
Winskel, G.: A new definition of morphism on Petri nets. In: Fontet, M., Mehlhorn, K. (eds.) Proc. Symposium on Theoretical Aspects of Computer Science, STACS’84. LNCS, vol. 166, pp. 140–150. Springer (1984). https://doi.org/10.1007/3-540-12920-0_13
Acknowledgement
I am grateful to Weiyou Wang for valuable feedback.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
van Glabbeek, R. (2023). Just Testing. In: Kupferman, O., Sobocinski, P. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2023. Lecture Notes in Computer Science, vol 13992. Springer, Cham. https://doi.org/10.1007/978-3-031-30829-1_24
Download citation
DOI: https://doi.org/10.1007/978-3-031-30829-1_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-30828-4
Online ISBN: 978-3-031-30829-1
eBook Packages: Computer ScienceComputer Science (R0)





 , i.e.
, i.e.
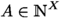 .
. the multiset
the multiset  , given by
, given by  (the flow relation including arc weights),
(the flow relation including arc weights), (the read relation),
(the read relation), (the initial marking), and
(the initial marking), and





 ,
, 