Abstract
Pebble transducers are nested two-way transducers which can drop marks (named “pebbles”) on their input word. Such machines can compute functions whose output size is polynomial in the size of their input. They can be seen as simple recursive programs whose recursion height is bounded. A natural problem is, given a pebble transducer, to compute an equivalent pebble transducer with minimal recursion height. This problem has been open since the introduction of the model.
In this paper, we study two restrictions of pebble transducers, that cannot see the marks (“blind pebble transducers” introduced by Nguyên et al.), or that can only see the last mark dropped (“last pebble transducers” introduced by Engelfriet et al.). For both models, we provide an effective algorithm for minimizing the recursion height. The key property used in both cases is that a function whose output size is linear (resp. quadratic, cubic, etc.) can always be computed by a machine whose recursion height is 1 (resp. 2, 3, etc.). We finally show that this key property fails as soon as we consider machines that can see more than one mark.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Pebble transducers
- Polyregular functions
- Blind pebble transducers
- Last pebble transducers
- Factorization forests.
1 Introduction
Transducers are finite-state machines obtained by adding outputs to finite automata. They are very useful in a lot of areas like coding, computer arithmetic, language processing or program analysis, and more generally in data stream processing. In this paper, we consider deterministic transducers which compute functions from finite words to finite words. In particular, a
 is a two-way automaton with outputs. This model describes the class of
is a two-way automaton with outputs. This model describes the class of
 , which is often considered as one of the functional counterparts of regular languages. It has been intensively studied for its properties such as closure under composition [5], equivalence with logical transductions [12] or regular expressions [7], decidable equivalence problem [14], etc.
, which is often considered as one of the functional counterparts of regular languages. It has been intensively studied for its properties such as closure under composition [5], equivalence with logical transductions [12] or regular expressions [7], decidable equivalence problem [14], etc.
Pebble transducers and polyregular functions.
 can only describe functions whose output size is at most linear in the input size. A possible solution to overcome this limitation is to consider nested
can only describe functions whose output size is at most linear in the input size. A possible solution to overcome this limitation is to consider nested
 . In particular, the model of
. In particular, the model of
 has been studied for a long time [13]. For \(k=1\), a
has been studied for a long time [13]. For \(k=1\), a
 is just a
is just a
 . For \(k \geqslant 2\), a
. For \(k \geqslant 2\), a
 is a
is a
 that, when on any position i of its input word, can call a
that, when on any position i of its input word, can call a
 . The latter takes as input the original input where position i is marked by a “pebble”. The main
. The latter takes as input the original input where position i is marked by a “pebble”. The main
 then outputs the concatenation of all the outputs produced along its calls. The intuitive behavior of a
then outputs the concatenation of all the outputs produced along its calls. The intuitive behavior of a
 is depicted in fig. 1. It can be seen as a recursive program whose recursion stack has height 3. The class of functions computed by
is depicted in fig. 1. It can be seen as a recursive program whose recursion stack has height 3. The class of functions computed by
 is known as
is known as
 . It has been intensively studied due to its properties such as closure under composition [11], equivalence with logical interpretations [4], etc.
. It has been intensively studied due to its properties such as closure under composition [11], equivalence with logical interpretations [4], etc.
Optimization of pebble transducers. Given a
 computing a function f, a very natural problem is to compute the least possible \(1 \leqslant \ell \leqslant k\) such that f can be computed by an
computing a function f, a very natural problem is to compute the least possible \(1 \leqslant \ell \leqslant k\) such that f can be computed by an
 . Furthermore, we can be interested in effectively building an
. Furthermore, we can be interested in effectively building an
 for f. Both questions are open, but they are meaningful since they ask whether we can optimize the recursion height (i.e. the running time) of a program.
for f. Both questions are open, but they are meaningful since they ask whether we can optimize the recursion height (i.e. the running time) of a program.
It is easy to observe that if f is computed by a
 , then \(|f(u)| = \mathcal {O}(|u|^k)\). It was first claimed in a LICS 2020 paper that the minimal recursion height \(\ell \) of f (i.e. the least possible \(\ell \) such that f can be computed by an
, then \(|f(u)| = \mathcal {O}(|u|^k)\). It was first claimed in a LICS 2020 paper that the minimal recursion height \(\ell \) of f (i.e. the least possible \(\ell \) such that f can be computed by an
 ) was exactly the least possible \(\ell \) such that \(|f(u)| = \mathcal {O}(|u|^{\ell })\). However, Bojańczyk recently disproved this statement in [3, Theorem 6.3]: the function
) was exactly the least possible \(\ell \) such that \(|f(u)| = \mathcal {O}(|u|^{\ell })\). However, Bojańczyk recently disproved this statement in [3, Theorem 6.3]: the function
 can be computed by a
can be computed by a
 and is such that
and is such that
 , but it cannot be computed by a
, but it cannot be computed by a
 . Other counterexamples were given in [16] using different proof techniques. Therefore, computing the minimal recursion height of f is believed to be hard, since this value not only depends on the output size of f, but also on the word combinatorics of this output.
. Other counterexamples were given in [16] using different proof techniques. Therefore, computing the minimal recursion height of f is believed to be hard, since this value not only depends on the output size of f, but also on the word combinatorics of this output.
Optimization of blind pebble transducers. A subclass of
 , named
, named
 , was recently introduced in [17]. A
, was recently introduced in [17]. A
 is somehow a
is somehow a
 , with the difference that the positions are no longer marked when making recursive calls. The behavior of a
, with the difference that the positions are no longer marked when making recursive calls. The behavior of a
 is depicted in fig. 2. The class of functions computed by
is depicted in fig. 2. The class of functions computed by
 is strictly included in
is strictly included in
 [10, 17]. The main result of [17] shows that for
[10, 17]. The main result of [17] shows that for
 , the minimal recursion height for computing a function only depends on the growth of its output. More precisely, if f is computed by a
, the minimal recursion height for computing a function only depends on the growth of its output. More precisely, if f is computed by a
 , then the least possible \(1 \leqslant \ell \leqslant k\) such that f can be computed by an
, then the least possible \(1 \leqslant \ell \leqslant k\) such that f can be computed by an
 is the least possible \(\ell \) such that \(|f(u)| = \mathcal {O}(|u|^{\ell })\).
is the least possible \(\ell \) such that \(|f(u)| = \mathcal {O}(|u|^{\ell })\).
Contributions. In this paper, we first give a new proof of the connection between minimal recursion height and growth of the output for
 . Furthermore, our proof provides an algorithm that, given a function computed by a
. Furthermore, our proof provides an algorithm that, given a function computed by a
 , builds a
, builds a
 which computes it, for the least possible \(1 \leqslant \ell \leqslant k\). This effective result is not claimed in [17], and our proof techniques significantly differ from theirs. Indeed, we make a heavy use of
which computes it, for the least possible \(1 \leqslant \ell \leqslant k\). This effective result is not claimed in [17], and our proof techniques significantly differ from theirs. Indeed, we make a heavy use of
 , which have already been used as a powerful tool in the study of
, which have already been used as a powerful tool in the study of
 [2, 8, 10].
[2, 8, 10].
Secondly, the main contribution of this paper is to show that the (effective) connection between minimal recursion height and growth of the output also holds for the class of
 (introduced in [13]). Intuitively, a
(introduced in [13]). Intuitively, a
 is a
is a
 where a called submachine can only see the position of its call, but not the full stack of the former positions. The behavior of a
where a called submachine can only see the position of its call, but not the full stack of the former positions. The behavior of a
 is depicted in fig. 3. Observe that a
is depicted in fig. 3. Observe that a
 is a restricted version of a
is a restricted version of a
 . Formally, we show that if f is computed by a
. Formally, we show that if f is computed by a
 , then the least possible \(\ell \) such that f can be computed by a
, then the least possible \(\ell \) such that f can be computed by a
 is the least possible \(\ell \) such that \(|f(u)| = \mathcal {O}(|u|^{\ell })\). Furthermore, our proof gives an algorithm that effectively builds a
is the least possible \(\ell \) such that \(|f(u)| = \mathcal {O}(|u|^{\ell })\). Furthermore, our proof gives an algorithm that effectively builds a
 computing f.
computing f.
As a third theorem, we show that our result for
 is tight, in the sense that the connection between minimal recursion height and growth of the output does not hold for more powerful models. More precisely, we define the model of
is tight, in the sense that the connection between minimal recursion height and growth of the output does not hold for more powerful models. More precisely, we define the model of
 , which extends
, which extends
 by allowing them to see the two last positions of the calls (and not only the last one). We show that for all \(k \geqslant 1\), there exists a function f such that \(|f(u)| = \mathcal {O}(|u|^2)\) and that is computed by a
by allowing them to see the two last positions of the calls (and not only the last one). We show that for all \(k \geqslant 1\), there exists a function f such that \(|f(u)| = \mathcal {O}(|u|^2)\) and that is computed by a
 , but cannot be computed by a
, but cannot be computed by a
 . The proof of this result relies on a counterexample presented by Bojańczyk in [2].
. The proof of this result relies on a counterexample presented by Bojańczyk in [2].
Outline. We introduce
 in section 2. In section 3 we describe
in section 2. In section 3 we describe
 and
and
 . We also state our main results that connect the minimal recursion height of a function to the growth of its output. Their proof goes over sections 4 to 6. In section 7, we finally show that these results cannot be extended to two visible marks.
. We also state our main results that connect the minimal recursion height of a function to the growth of its output. Their proof goes over sections 4 to 6. In section 7, we finally show that these results cannot be extended to two visible marks.
2 Preliminaries on two-way transducers
Capital letters A, B denote alphabets, i.e. finite sets of letters. The empty word is denoted by \(\varepsilon \). If \(u \in A^*\), let \(|u| \in \mathbb {N}\) be its length, and for \(1 \leqslant i \leqslant |u|\) let u[i] be its i-th letter. If \( i \leqslant j\), we let u[i : j] be \(u[i]u[i{+}1] \cdots u[j]\) (empty if \(j <i\)). If \(a \in A\), let \(|u|_a\) be the number of letters a occurring in u. We assume that the reader is familiar with the basics of automata theory, in particular two-way automata and monoid morphisms. The type of total (resp. partial, i.e. possibly undefined on some inputs) functions is denoted \(S \rightarrow T\) (resp. \(S \rightharpoonup T\)).
The machines described in this paper are always
 .
.
Definition 2.1
A
 \(\mathscr {T}= (A,B,Q,q_0,F,\delta ,\lambda )\) consists of:
\(\mathscr {T}= (A,B,Q,q_0,F,\delta ,\lambda )\) consists of:
-
an input alphabet A and an output alphabet B;
-
a finite set of states Q with \(q_0 \in Q\) initial and \(F \subseteq Q\) final;
-
a transition function
 ;
; -
an output function
 with same domain as \(\delta \).
with same domain as \(\delta \).
The semantics of a
 \(\mathscr {T}\) is defined as follows. When given as input a word \(u \in A^*\), \(\mathscr {T}\) disposes of a read-only input tape containing
\(\mathscr {T}\) is defined as follows. When given as input a word \(u \in A^*\), \(\mathscr {T}\) disposes of a read-only input tape containing
 . The marks
. The marks
 and
and
 are used to detect the borders of the tape, by convention we denote them by positions 0 and \(|u|{+}1\) of u. Formally, a configuration over
are used to detect the borders of the tape, by convention we denote them by positions 0 and \(|u|{+}1\) of u. Formally, a configuration over
 is a tuple (q, i) where \(q \in Q\) is the current state and \(0 \leqslant i \leqslant |u|{+}1\) is the position of the reading head. The transition relation
is a tuple (q, i) where \(q \in Q\) is the current state and \(0 \leqslant i \leqslant |u|{+}1\) is the position of the reading head. The transition relation
 is defined as follows. Given a configuration (q, i), let \((q',\star ):= \delta (q,u[i])\). Then
is defined as follows. Given a configuration (q, i), let \((q',\star ):= \delta (q,u[i])\). Then
 whenever either
whenever either
 and \(i' = i{-}1\) (move left), or
and \(i' = i{-}1\) (move left), or
 and \(i' = i{+}1\) (move right), with \(0 \leqslant i' \leqslant |u|{+}1\). A run is a sequence of configurations
and \(i' = i{+}1\) (move right), with \(0 \leqslant i' \leqslant |u|{+}1\). A run is a sequence of configurations
 . Accepting runs are those that begin in \((q_0, 0)\) and end in a configuration of the form \((q, |u|{+}1)\) with \(q \in F\) (and never visit such a configuration before).
. Accepting runs are those that begin in \((q_0, 0)\) and end in a configuration of the form \((q, |u|{+}1)\) with \(q \in F\) (and never visit such a configuration before).
The partial function \(f: A^* \rightharpoonup B^*\) computed by the
 \(\mathscr {T}\) is defined as follows: for \(u \in A^*\), if there exists an accepting run on
\(\mathscr {T}\) is defined as follows: for \(u \in A^*\), if there exists an accepting run on
 , then it is unique, and f(u) is defined as
, then it is unique, and f(u) is defined as
 . The class of functions computed by
. The class of functions computed by
 is called
is called
 .
.
Example 2.2
Let \(\widetilde{u}\) be the mirror image of \(u \in A^*\). Let \(\# \not \in A\) be a fresh symbol. The function
 can be computed by a
can be computed by a
 , that reads each factor \(u_j\) from right to left.
, that reads each factor \(u_j\) from right to left.
It is well-known that the domain of a
 is always a
is always a
 (see e.g. [18]). From now on, we assume without losing generalities that our
(see e.g. [18]). From now on, we assume without losing generalities that our
 only compute total functions (in other words, they have exactly one accepting run on each
only compute total functions (in other words, they have exactly one accepting run on each
 ). Furthermore, we assume that
). Furthermore, we assume that
 for all \(q \in Q\) (we only lose generality for the image of \(\varepsilon \)).
for all \(q \in Q\) (we only lose generality for the image of \(\varepsilon \)).
In the rest of this section, \(\mathscr {T}\) denotes a
 with input alphabet A, output alphabet B and output function \(\lambda \). Now, we define the
with input alphabet A, output alphabet B and output function \(\lambda \). Now, we define the
 in a position \(1 \leqslant i \leqslant |u|\) of input
in a position \(1 \leqslant i \leqslant |u|\) of input
 . Intuitively, it regroups the states of the accepting run which are visited in this position.
. Intuitively, it regroups the states of the accepting run which are visited in this position.
Definition 2.3
Let \(u \in A^*\) and \(1 \leqslant i \leqslant |u|\) . Let
 be the accepting run of \(\mathscr {T}\) on
be the accepting run of \(\mathscr {T}\) on
 . The
. The
 of \(\mathscr {T}\) in i, denoted
of \(\mathscr {T}\) in i, denoted
 , is defined as the sequence
, is defined as the sequence
 .
.
If \(\mu : A^* \rightarrow \mathbb {M}\) is a monoid morphism, we say that any \(m,m' \in \mathbb {M}\) and \(a \in A\) define a
 that we denote by \(m {\boldsymbol{\llbracket } a\boldsymbol{\rrbracket }} m'\). It is well-known that the
that we denote by \(m {\boldsymbol{\llbracket } a\boldsymbol{\rrbracket }} m'\). It is well-known that the
 in a position of the input only depends on the
in a position of the input only depends on the
 of this position, for a well-chosen monoid, as claimed in proposition 2.4 (see e.g. [7]).
of this position, for a well-chosen monoid, as claimed in proposition 2.4 (see e.g. [7]).
Proposition 2.4
One can build a finite monoid \(\mathbb {T}\) and a monoid morphism \(\mu : A^* \rightarrow \mathbb {T}\), called the
 of \(\mathscr {T}\), such that for all \(u \in A^*\) and \(1 \leqslant i \leqslant |u|\),
of \(\mathscr {T}\), such that for all \(u \in A^*\) and \(1 \leqslant i \leqslant |u|\),
 only depends on \(\mu (u[1{:}i{-}1]), u[i]\) and \(\mu (u[i{+}1{:}|u|])\).
only depends on \(\mu (u[1{:}i{-}1]), u[i]\) and \(\mu (u[i{+}1{:}|u|])\).
Thus we denote it
 .
.
Finally, let us define “the output produced below position i”.
Definition 2.5
Let \(u \in A^*\) and \(1 \leqslant i \leqslant |u|\) and
 . We define the
. We define the
 of \(\mathscr {T}\) in i, denoted
of \(\mathscr {T}\) in i, denoted
 , as \(\lambda (q_1, u[i]) \cdots \lambda (q_n, u[i])\).
, as \(\lambda (q_1, u[i]) \cdots \lambda (q_n, u[i])\).
By proposition 2.4, it also makes sense to define
 to be
to be
 whenever \(m = \mu (u[1{:}i{-}1])\), \(m' = \mu (u[i{+}1{:}|u|])\) and \(a = u[i]\).
whenever \(m = \mu (u[1{:}i{-}1])\), \(m' = \mu (u[i{+}1{:}|u|])\) and \(a = u[i]\).
3 Blind and last pebble transducers
Now, we are ready to define formally the models of
 and
and
 . Intuitively, they correspond to
. Intuitively, they correspond to
 which make a tree of recursive calls to other
which make a tree of recursive calls to other
 .
.
Definition 3.1
(Blind pebble transducer [17]). For \(k \geqslant 1\), a
 with input alphabet A and output alphabet B is:
with input alphabet A and output alphabet B is:
-
if \(k =1\), a
 with input alphabet A and output B;
with input alphabet A and output B; -
if \(k \geqslant 2\), a tree \(\mathscr {T}\langle \mathscr {B}_1, \cdots ,\mathscr {B}_p \rangle \) where the subtrees \(\mathscr {B}_1, \dots , \mathscr {B}_p\) are
 with input A and output B; and the root label \(\mathscr {T}\) is a
with input A and output B; and the root label \(\mathscr {T}\) is a
 with input A and output alphabet \(\{\mathscr {B}_1, \dots , \mathscr {B}_p\}\).
with input A and output alphabet \(\{\mathscr {B}_1, \dots , \mathscr {B}_p\}\).
The (total) function \(f:A^* \rightarrow B^*\) computed by the
 of definition 3.1 is built in a recursive fashion, as follows:
of definition 3.1 is built in a recursive fashion, as follows:
-
for \(k=1\), f is the function computed by the
 ;
; -
for \(k\geqslant 2\), let \(u \in A^*\) and
 be the accepting run of \(\mathscr {T}= (A,B,Q,q_0,F,\delta ,\lambda )\) on
be the accepting run of \(\mathscr {T}= (A,B,Q,q_0,F,\delta ,\lambda )\) on
 . For all \(1 \leqslant j \leqslant n\), let \(f_j : A^* \rightarrow B^*\) be the concatenation of the functions recursively computed by the sequence
. For all \(1 \leqslant j \leqslant n\), let \(f_j : A^* \rightarrow B^*\) be the concatenation of the functions recursively computed by the sequence
 . Then \(f(u) {:}{=}f_1 (u) \cdots f_n(u)\).
. Then \(f(u) {:}{=}f_1 (u) \cdots f_n(u)\).
The behavior of a
 is depicted in fig. 2.
is depicted in fig. 2.
Example 3.2
The function
 can be computed by a
can be computed by a
 . This machine has shape \(\mathscr {T}\langle \mathscr {T}' \rangle \): \(\mathscr {T}\) calls \(\mathscr {T}'\) on each position \(1 \leqslant i \leqslant |u|\) of its input u, and \(\mathscr {T}'\) outputs \(u\#\).
. This machine has shape \(\mathscr {T}\langle \mathscr {T}' \rangle \): \(\mathscr {T}\) calls \(\mathscr {T}'\) on each position \(1 \leqslant i \leqslant |u|\) of its input u, and \(\mathscr {T}'\) outputs \(u\#\).
The class of functions computed by a
 for some \(k \geqslant 1\) is called
for some \(k \geqslant 1\) is called
 [10]. They form a strict subclass of
[10]. They form a strict subclass of
 [8, 10, 17] which is closed under composition [17, Theorem 6.1].
[8, 10, 17] which is closed under composition [17, Theorem 6.1].
Now, let us define
 . They corresponds to
. They corresponds to
 enhanced with the ability to mark the current position of the input when doing a recursive call. Formally, this position is underlined and we define
enhanced with the ability to mark the current position of the input when doing a recursive call. Formally, this position is underlined and we define
 for \(u \in A^*\) and \(1 \leqslant i \leqslant |u|\).
for \(u \in A^*\) and \(1 \leqslant i \leqslant |u|\).
Definition 3.3
(Last pebble transducer [13]). For \(k \geqslant 1\), a
 with input alphabet A and output alphabet B is:
with input alphabet A and output alphabet B is:
-
if \(k =1\), a
 with input alphabet
with input alphabet
 and output B;
and output B; -
if \(k \geqslant 2\), a tree \(\mathscr {T}\langle \mathscr {L}_1, \cdots ,\mathscr {L}_p \rangle \) where the subtrees \(\mathscr {L}_1, \dots , \mathscr {L}_p\) are
 with input A and output B; and the root label \(\mathscr {T}\) is a
with input A and output B; and the root label \(\mathscr {T}\) is a
 with input
with input
 and output alphabet \(\{\mathscr {L}_1, \dots , \mathscr {L}_p\}\).
and output alphabet \(\{\mathscr {L}_1, \dots , \mathscr {L}_p\}\).
The (total) function
 computed by the
computed by the
 of definition 3.3 is defined in a recursive fashion, as follows:
of definition 3.3 is defined in a recursive fashion, as follows:
-
for \(k=1\), f is the function computed by the
 ;
; -
for \(k\geqslant 2\), let \(u \in A^*\) and
 be the accepting run of
be the accepting run of
 on
on
 . For all \(1 \leqslant j \leqslant n\), let \(f_j : A^* \rightarrow B^*\) be the concatenation of the functions recursively computed by
. For all \(1 \leqslant j \leqslant n\), let \(f_j : A^* \rightarrow B^*\) be the concatenation of the functions recursively computed by
 . Let
. Let
 be the morphism which erases the underlining (i.e. \(\tau (\underline{a})=a\)), then
be the morphism which erases the underlining (i.e. \(\tau (\underline{a})=a\)), then
 .
.
The behavior of a
 is depicted in fig. 3. Observe that our definition builds a function of type
is depicted in fig. 3. Observe that our definition builds a function of type
 , but we shall in fact consider its restriction to \(A^*\) (the marks are only used within the induction step).
, but we shall in fact consider its restriction to \(A^*\) (the marks are only used within the induction step).
Example 3.4
([1]). The function
 can be computed by a
can be computed by a
 , which successively marks and makes recursive calls in positions 1, 2, etc. However this function is not
, which successively marks and makes recursive calls in positions 1, 2, etc. However this function is not
 [17].
[17].
We are ready to state our main result. Its proof goes over Sections 4 to 6.
Theorem 3.5
(Minimization of the recursion height). Let \(1 \leqslant \ell \leqslant k\). Let \(f : A^* \rightarrow B^*\) be computed by a
 (resp. by a
(resp. by a
 ). Then f can be computed by a
). Then f can be computed by a
 (resp. by a
(resp. by a
 ) if and only if \(|f(u)| = \mathcal {O}(|u|^{\ell })\).
) if and only if \(|f(u)| = \mathcal {O}(|u|^{\ell })\).
This property is decidable and the construction is effective.
As an easy consequence, the class of functions computed by
 form a strict subclass of the
form a strict subclass of the
 (because theorem 3.5 does not hold for the full model of
(because theorem 3.5 does not hold for the full model of
 [3, Theorem 6.3]) and therefore it is not closed under composition (because any
[3, Theorem 6.3]) and therefore it is not closed under composition (because any
 can be obtained as a composition of
can be obtained as a composition of
 and
and
 s [1]).
s [1]).
Even if a (non-effective) theorem 3.5 was already known for
 [17, Theorem 7.1], we shall first present our proof of this case. Indeed, it is a new proof (relying on
[17, Theorem 7.1], we shall first present our proof of this case. Indeed, it is a new proof (relying on
 ) which is simpler than the original one. Furthermore, understanding the techniques used is a key step for understanding the proof for
) which is simpler than the original one. Furthermore, understanding the techniques used is a key step for understanding the proof for
 presented afterwards.
presented afterwards.
4 Factorization forests
In this section, we introduce the key tool of
 . Given a monoid morphism \(\mu :A^* \rightarrow \mathbb {M}\) and \(u \in A^*\), a
. Given a monoid morphism \(\mu :A^* \rightarrow \mathbb {M}\) and \(u \in A^*\), a
 of u is an unranked tree structure defined as follows. We use the brackets \(\langle \cdots \rangle \) to build a tree.
of u is an unranked tree structure defined as follows. We use the brackets \(\langle \cdots \rangle \) to build a tree.
Definition 4.1
(Factorization forest [19]). Given a morphism \(\mu : A^* \rightarrow \mathbb {M}\) and \(u\in A^*\), we say that
 is a
is a
 of u if:
of u if:
-
either \(u = \varepsilon \) and \(\mathcal {F}= \varepsilon \); or \(u = \langle a \rangle \in A \) and \(\mathcal {F}= a\);
-
or \(\mathcal {F}= \langle \mathcal {F}_1, \cdots ,\mathcal {F}_n \rangle \), \(u = u_1 \cdots u_n\), for all \(1 \leqslant i \leqslant n\), \(\mathcal {F}_i\) is a
 of \(u_i \in A^+\), and if \(n \geqslant 3\) then \(\mu (u) = \mu (u_1) = \dots = \mu (u_n)\) is idempotent.
of \(u_i \in A^+\), and if \(n \geqslant 3\) then \(\mu (u) = \mu (u_1) = \dots = \mu (u_n)\) is idempotent.
We use the standard tree vocabulary of height, child, sibling, descendant and ancestor (a node being itself one of its ancestors/descendants), etc. We denote by
 the set of nodes of \(\mathcal {F}\). In order to simplify the statements, we identify a node
the set of nodes of \(\mathcal {F}\). In order to simplify the statements, we identify a node
 with the subtree rooted in this node. Thus
with the subtree rooted in this node. Thus
 can also be seen as the set of subtrees of \(\mathcal {F}\), and
can also be seen as the set of subtrees of \(\mathcal {F}\), and
 . We say that a node is
. We say that a node is
 if it has at least 3 children. We denote by
if it has at least 3 children. We denote by
 (resp.
(resp.
 ) the set of
) the set of
 of \(u \in A^*\) (resp.
of \(u \in A^*\) (resp.
 of \(u \in A^*\) of height at most d). We write
of \(u \in A^*\) of height at most d). We write
 and
and
 of all
of all
 (of any word).
(of any word).
A \(\mu \)-forest of \(u \in A^*\) can also be seen as “the word u with brackets” in definition 4.1. Therefore
 can be seen as a language over
can be seen as a language over
 . In this setting, it is well-known that
. In this setting, it is well-known that
 of bounded height can effectively be computed by a
of bounded height can effectively be computed by a
 , i.e. a particular case of
, i.e. a particular case of
 that can be computed by a non-deterministic one-way transducer (see e.g. [8]).
that can be computed by a non-deterministic one-way transducer (see e.g. [8]).
Theorem 4.2
(Simon [6, 19]). Given a morphism \(\mu : A^* \rightarrow \mathbb {M}\) into a finite monoid \(\mathbb {M}\), one can effectively build a

 such that for all \(u \in A^*\),
such that for all \(u \in A^*\),
 .
.
Building
 of bounded height is especially useful for us, since it enables to decompose any word in a somehow bounded way. This decomposition will be guided by the following definitions, that have been introduced in [8, 10]. First, we define
of bounded height is especially useful for us, since it enables to decompose any word in a somehow bounded way. This decomposition will be guided by the following definitions, that have been introduced in [8, 10]. First, we define
 as the middle children of
as the middle children of
 .
.
Definition 4.3
Let
 . Its
. Its
 , denoted
, denoted
 , are:
, are:
-
if \(\mathcal {F}= \langle a \rangle \in A\) or \(\mathcal {F}= \varepsilon \), then
 ;
; -
otherwise if \(\mathcal {F}= \langle \mathcal {F}_1, \cdots ,\mathcal {F}_n \rangle \), then:
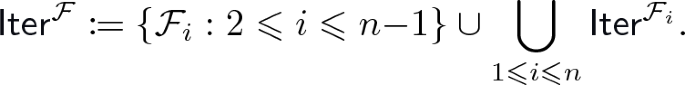
Now, we define the notion of
 of a node \(\mathfrak {t}\), which contains all the descendants of \(\mathfrak {t}\) except those which are
of a node \(\mathfrak {t}\), which contains all the descendants of \(\mathfrak {t}\) except those which are
 .
.
Definition 4.4
(Skeleton, frontier).
Let
 ,
,
 , we define the
, we define the
 of \(\mathfrak {t}\), denoted
of \(\mathfrak {t}\), denoted
 , by:
, by:
-
if \(\mathfrak {t}= \langle a \rangle \in A\) is a leaf, then
 ;
; -
otherwise if \(\mathfrak {t}= \langle \mathcal {F}_1, \cdots , \mathcal {F}_n \rangle \), then
 .
.
The
 of \(\mathfrak {t}\) is the set
of \(\mathfrak {t}\) is the set
 containing the positions of u which belong to
containing the positions of u which belong to
 (when seen as leaves of the
(when seen as leaves of the
 \(\mathcal {F}\) over u).
\(\mathcal {F}\) over u).
Example 4.5
Let \(\mathbb {M}{:}{=}(\{-1,1,0\}, \times )\) and \(\mu : \mathbb {M}^* \rightarrow \mathbb {M}\) the product. A
 \(\mathcal {F}\) of the word \((-1)(-1)0(-1)000000\) is depicted in Figure 4. Double lines denote
\(\mathcal {F}\) of the word \((-1)(-1)0(-1)000000\) is depicted in Figure 4. Double lines denote
 . The set of blue nodes is the
. The set of blue nodes is the
 of the topmost blue node.
of the topmost blue node.
It is easy to observe that for
 , the size of a
, the size of a
 , or of a
, or of a
 , is bounded independently from \(\mathcal {F}\). Furthermore, the set of
, is bounded independently from \(\mathcal {F}\). Furthermore, the set of

 is a partition of
is a partition of
 [8, Lemma 33]. As a consequence, the set of
[8, Lemma 33]. As a consequence, the set of

 is a partition of [1 : |u|]. Given a position \(1 \leqslant i \leqslant |u|\), we can thus define the
is a partition of [1 : |u|]. Given a position \(1 \leqslant i \leqslant |u|\), we can thus define the
 of i in \(\mathcal {F}\), denoted
of i in \(\mathcal {F}\), denoted
 , as the unique
, as the unique
 such that
such that
 .
.
Definition 4.6
(Observation). Let
 and
and
 . We say that
. We say that


 if either \(\mathfrak {t}'\) is an ancestor of \(\mathfrak {t}\), or \(\mathfrak {t}'\) is the immediate right or left sibling of an ancestor of \(\mathfrak {t}\).
if either \(\mathfrak {t}'\) is an ancestor of \(\mathfrak {t}\), or \(\mathfrak {t}'\) is the immediate right or left sibling of an ancestor of \(\mathfrak {t}\).
The intuition behind the notion of
 (which is not symmetrical) is depicted in fig. 5. Note that in a forest of bounded height, the number of nodes that some \(\mathfrak {t}\)
(which is not symmetrical) is depicted in fig. 5. Note that in a forest of bounded height, the number of nodes that some \(\mathfrak {t}\)
 is bounded. This will be a key argument in the following. We say that \(\mathfrak {t}\) and \(\mathfrak {t}'\) are
is bounded. This will be a key argument in the following. We say that \(\mathfrak {t}\) and \(\mathfrak {t}'\) are
 if either \(\mathfrak {t}\)
if either \(\mathfrak {t}\)
 \(\mathfrak {t}'\) or the converse. Given \(\mathcal {F}\), we can translate these notions to the positions of u: we say that i
\(\mathfrak {t}'\) or the converse. Given \(\mathcal {F}\), we can translate these notions to the positions of u: we say that i
 (resp.
(resp.
 on) \(i'\) if
on) \(i'\) if

 (resp.
(resp.
 on)
on)
 .
.
5 Height minimization of blind pebble transducers
In this section, we show theorem 3.5 for
 . We say that a
. We say that a
 \(\mathscr {T}\) is a
\(\mathscr {T}\) is a
 of a
of a
 \(\mathscr {B}\) if \(\mathscr {T}\) labels a node in the tree description of \(\mathscr {B}\). If \(\mathscr {B}= \mathscr {T}\langle \mathscr {B}_1, \dots , \mathscr {B}_n \rangle \), we say that the
\(\mathscr {B}\) if \(\mathscr {T}\) labels a node in the tree description of \(\mathscr {B}\). If \(\mathscr {B}= \mathscr {T}\langle \mathscr {B}_1, \dots , \mathscr {B}_n \rangle \), we say that the
 \(\mathscr {T}\) is the
\(\mathscr {T}\) is the
 of \(\mathscr {B}\). We let the
of \(\mathscr {B}\). We let the
 of \(\mathscr {B}\) be the cartesian product of all the
of \(\mathscr {B}\) be the cartesian product of all the
 of all the
of all the
 of \(\mathscr {B}\). Observe that it makes sense to consider the
of \(\mathscr {B}\). Observe that it makes sense to consider the
 of a
of a
 \(\mathscr {T}\) in a
\(\mathscr {T}\) in a
 defined using the
defined using the
 of \(\mathscr {B}\).
of \(\mathscr {B}\).
5.1 Pumpability
We first give a sufficient condition, named
 , for a
, for a
 to compute a function f such that \(|f(u)| \ne \mathcal {O}(|u|^{k-1})\). The behavior of a
to compute a function f such that \(|f(u)| \ne \mathcal {O}(|u|^{k-1})\). The behavior of a

 is depicted in fig. 6 over a well-chosen input: it has a factor in which the
is depicted in fig. 6 over a well-chosen input: it has a factor in which the
 \(\mathscr {T}_1\) calls a
\(\mathscr {T}_1\) calls a
 \(\mathscr {T}_2\), and a factor in which \(\mathscr {T}_2\) produces a non-empty output. Furthermore both factors can be iterated without destroying the runs of these machines (due to idempotents).
\(\mathscr {T}_2\), and a factor in which \(\mathscr {T}_2\) produces a non-empty output. Furthermore both factors can be iterated without destroying the runs of these machines (due to idempotents).
Definition 5.1
Let \(\mathscr {B}\) be a
 whose
whose
 is \(\mu : A^* \rightarrow \mathbb {T}\). We say that the transducer \(\mathscr {B}\) is
is \(\mu : A^* \rightarrow \mathbb {T}\). We say that the transducer \(\mathscr {B}\) is
 if there exists:
if there exists:
-
 \(\mathscr {T}_1, \dots , \mathscr {T}_k\) of \(\mathscr {B}\), such that \(\mathscr {T}_1\) is the
\(\mathscr {T}_1, \dots , \mathscr {T}_k\) of \(\mathscr {B}\), such that \(\mathscr {T}_1\) is the
 of \(\mathscr {B}\);
of \(\mathscr {B}\); -
\(m_0, \dots , m_k, {\ell }_1, \dots , {\ell _k}, r_1, \dots , r_k \in \mu (A^*)\);
-
\(a_1,\dots , a_k \in A\) such that for all \(1 \leqslant j \leqslant k\), \(e_j {:}{=}{\ell }_j \mu (a_j) r_j\) is an idempotent;
-
a permutation \(\sigma : [{1}{:}{k}] \rightarrow [{1}{:}{k}]\);
such that if \(\mathcal {M}_{i}^{j} {:}{=}m_{i} e_{i + 1} m_{i + 1} \cdots e_{j} m_{j}\) for all \(0 \leqslant i \leqslant j \leqslant k\), and if we define the following
 for all \(1 \leqslant j \leqslant k\):
for all \(1 \leqslant j \leqslant k\):
then for all \(1 \leqslant j \leqslant k{-}1\),
 , and
, and
 .
.
Lemma 5.2 follows by choosing inverse images in \(A^*\) for the \(m_i\), \(\ell _i\) and \(r_i\).
Lemma 5.2
Let f be computed by a

 . There exists words \(v_0, \dots , v_k, u_1, \dots , u_k\) such that \(|f(v_0 u_1^{X} \cdots u_k^{X} v_k)| = \Theta (X^k)\).
. There exists words \(v_0, \dots , v_k, u_1, \dots , u_k\) such that \(|f(v_0 u_1^{X} \cdots u_k^{X} v_k)| = \Theta (X^k)\).
Now, we use
 as a key ingredient for showing theorem 3.5, which directly follows by induction from the more precise theorem 5.3.
as a key ingredient for showing theorem 3.5, which directly follows by induction from the more precise theorem 5.3.
Theorem 5.3
(Removing one layer). Let \(k \geqslant 2\) and \(f : A^* \rightarrow B^*\) be computed by a
 \(\mathscr {B}\). The following are equivalent:
\(\mathscr {B}\). The following are equivalent:
-
1.
\(|f(u)| = \mathcal {O}(|u|^{k-1})\);
-
2.
\(\mathscr {B}\) is not
 ;
; -
3.
f can be computed by a
 .
.
Furthermore, this property is decidable and the construction is effective.
Proof
Item 3 \(\Rightarrow \) item 1 is obvious. Item 1 \(\Rightarrow \) item 2 is lemma 5.2. Furthermore,
 can be tested by an enumeration of \(\mu (A^*)\) and A. It remains to show item 2 \(\Rightarrow \) item 3 (in an effective fashion): this is the purpose of section 5.2.
can be tested by an enumeration of \(\mu (A^*)\) and A. It remains to show item 2 \(\Rightarrow \) item 3 (in an effective fashion): this is the purpose of section 5.2.
5.2 Algorithm for removing a recursion layer
Let \(k \geqslant 2\) and \(\mathscr {U}\) be a
 that is not
that is not
 , and that computes \(f : A^* \rightarrow B^*\). We build a
, and that computes \(f : A^* \rightarrow B^*\). We build a
 \(\overline{\mathscr {U}}\) for f.
\(\overline{\mathscr {U}}\) for f.
Let \(\mu : A^* \rightarrow \mathbb {T}\) be the
 of \(\mathscr {U}\). We shall consider that, on input \(u \in A^*\), the
of \(\mathscr {U}\). We shall consider that, on input \(u \in A^*\), the
 of \(\overline{\mathscr {U}}\) can in fact use
of \(\overline{\mathscr {U}}\) can in fact use
 as input. Indeed
as input. Indeed
 is a
is a
 (by theorem 4.2), hence its information can be recovered by using a
(by theorem 4.2), hence its information can be recovered by using a
 . Informally, the
. Informally, the
 feature enables a
feature enables a
 to chose its transitions not only depending on its current state and current letter u[i] in position \(1 \leqslant i \leqslant |u|\), but also on a regular property of the prefix \(u[1{:}i{-}1]\) and the suffix \(u[i{+1}{:}|u|]\). It is well-known that given a
to chose its transitions not only depending on its current state and current letter u[i] in position \(1 \leqslant i \leqslant |u|\), but also on a regular property of the prefix \(u[1{:}i{-}1]\) and the suffix \(u[i{+1}{:}|u|]\). It is well-known that given a
 \(\mathscr {T}\) with
\(\mathscr {T}\) with
 , one can build an equivalent \(\mathscr {T}'\) that does not have this feature (see e.g. [12, 15]). Furthermore, even if the accepting runs of \(\mathscr {T}\) and \(\mathscr {T}'\) may differ, they produce the same outputs from the same positions (this observation will be critical for
, one can build an equivalent \(\mathscr {T}'\) that does not have this feature (see e.g. [12, 15]). Furthermore, even if the accepting runs of \(\mathscr {T}\) and \(\mathscr {T}'\) may differ, they produce the same outputs from the same positions (this observation will be critical for
 , in order to ensure that the marked positions of the recursive calls will be preserved).
, in order to ensure that the marked positions of the recursive calls will be preserved).
Now, we describe the
 that are the
that are the
 of \(\overline{\mathscr {U}}\). First, it has
of \(\overline{\mathscr {U}}\). First, it has

 for \(\mathscr {T}\) a
for \(\mathscr {T}\) a
 of \(\mathscr {U}\), which are described in algorithm 1. Intuitively,
of \(\mathscr {U}\), which are described in algorithm 1. Intuitively,
 is just a copy of \(\mathscr {T}\). It is clear that if \(\mathscr {T}\) is a
is just a copy of \(\mathscr {T}\). It is clear that if \(\mathscr {T}\) is a
 of \(\mathscr {U}\), then
of \(\mathscr {U}\), then
 is the concatenation of the outputs produced by (the recursive calls of) \(\mathscr {T}\) along its accepting run on
is the concatenation of the outputs produced by (the recursive calls of) \(\mathscr {T}\) along its accepting run on
 .
.

\(\overline{\mathscr {U}}\) also has

 for \(\mathscr {T}\) a
for \(\mathscr {T}\) a
 of \(\mathscr {U}\), which are described in algorithm 2. Intuitively,
of \(\mathscr {U}\), which are described in algorithm 2. Intuitively,
 simulates \(\mathscr {T}\) while trying to inline recursive calls in its own run. More precisely, let \(u \in A^*\) be the input and
simulates \(\mathscr {T}\) while trying to inline recursive calls in its own run. More precisely, let \(u \in A^*\) be the input and
 . If \(\mathscr {T}\) calls \(\mathscr {B}'\) in \(1 \leqslant i \leqslant |u|\) that belongs to the
. If \(\mathscr {T}\) calls \(\mathscr {B}'\) in \(1 \leqslant i \leqslant |u|\) that belongs to the
 of the root node \(\mathcal {F}\) of \(\mathcal {F}\), then
of the root node \(\mathcal {F}\) of \(\mathcal {F}\), then
 inlines the behavior of the
inlines the behavior of the
 of \(\mathscr {B}'\). Otherwise it makes a recursive call, except if \(\mathscr {B}'\) is a leaf of \(\mathscr {U}\). Hence if \(\mathscr {T}\) is a
of \(\mathscr {B}'\). Otherwise it makes a recursive call, except if \(\mathscr {B}'\) is a leaf of \(\mathscr {U}\). Hence if \(\mathscr {T}\) is a
 of \(\mathscr {U}\) which is not a leaf,
of \(\mathscr {U}\) which is not a leaf,
 is the concatenation of the outputs produced by the calls of \(\mathscr {T}\) along its accepting run.
is the concatenation of the outputs produced by the calls of \(\mathscr {T}\) along its accepting run.

Finally, the transducer \(\overline{\mathscr {U}}\) is obtained by defining
 to be its
to be its
 , where \(\mathscr {T}\) is the
, where \(\mathscr {T}\) is the
 of \(\mathscr {U}\). Furthermore, we remove the
of \(\mathscr {U}\). Furthermore, we remove the

 or
or
 which are never called. Observe that \(\overline{\mathscr {U}}\) indeed computes the function f. Furthermore, we observe that \(\overline{\mathscr {U}}\) has recursion height (i.e. the number of nested Call instructions, plus 1 for the
which are never called. Observe that \(\overline{\mathscr {U}}\) indeed computes the function f. Furthermore, we observe that \(\overline{\mathscr {U}}\) has recursion height (i.e. the number of nested Call instructions, plus 1 for the
 ) \(k{-}1\), since each inlining of lines 9, 10 and 12 in algorithm 2 removes exactly one recursion layer of \(\mathscr {U}\).
) \(k{-}1\), since each inlining of lines 9, 10 and 12 in algorithm 2 removes exactly one recursion layer of \(\mathscr {U}\).
It remains to justify that each
 can be implemented by a
can be implemented by a
 (i.e. with
(i.e. with
 but a bounded memory). We represent variable i by the current position of the transducer. Since it has access to \(\mathcal {F}\), the
but a bounded memory). We represent variable i by the current position of the transducer. Since it has access to \(\mathcal {F}\), the
 can be used to check whether
can be used to check whether
 or not (since the size of
or not (since the size of
 is bounded). It remains to explain how the inlinings are performed:
is bounded). It remains to explain how the inlinings are performed:
-
if
 , the
, the
 inlines
inlines
 by executing the same moves and calls as \(\mathscr {T}'\) does. Once its computation is ended, it has to go back to position i. This is indeed possible since belonging to
by executing the same moves and calls as \(\mathscr {T}'\) does. Once its computation is ended, it has to go back to position i. This is indeed possible since belonging to
 is a property that can be detected by using the
is a property that can be detected by using the
 , hence the machine only needs to remember that i was the \(\ell \)-th position of
, hence the machine only needs to remember that i was the \(\ell \)-th position of
 (\(\ell \) being bounded);
(\(\ell \) being bounded); -
else if \(\mathscr {B}' = \mathscr {T}'\) is a
 , we produce the output of \(\mathscr {T}'\) without moving. This is possible since for all
, we produce the output of \(\mathscr {T}'\) without moving. This is possible since for all
 ,
,
 (hence the output of \(\mathscr {T}'\) on u is bounded, and its value can be determined without moving, just by using the
(hence the output of \(\mathscr {T}'\) on u is bounded, and its value can be determined without moving, just by using the
 ). Indeed, if
). Indeed, if
 for such an
for such an
 when reaching line 12 of algorithm 2, then the conditions of lemma 5.4 hold, which yields a contradiction. This lemma is the key argument of this proof, relying on the non-
when reaching line 12 of algorithm 2, then the conditions of lemma 5.4 hold, which yields a contradiction. This lemma is the key argument of this proof, relying on the non-
 of \(\mathscr {U}\).
of \(\mathscr {U}\).
Lemma 5.4
(Key lemma). Let \(u \in A^*\) and
 . Assume that there exists a sequence \(\mathscr {T}_1, \dots , \mathscr {T}_k\) of
. Assume that there exists a sequence \(\mathscr {T}_1, \dots , \mathscr {T}_k\) of
 of \(\mathscr {U}\) and a sequence of positions \(1 \leqslant i_1, \dots , i_k \leqslant |u|\) such that:
of \(\mathscr {U}\) and a sequence of positions \(1 \leqslant i_1, \dots , i_k \leqslant |u|\) such that:
-
\(\mathscr {T}_1\) is the
 of \(\mathscr {U}\);
of \(\mathscr {U}\); -
for all \(1 \leqslant j \leqslant k{-}1\),
 and
and
 ;
; -
for all \(1 \leqslant j \leqslant k\),
 (i.e.
(i.e.
 ).
).
Then \(\mathscr {B}\) is
 .
.
Proof
(idea). We first observe that
 follows as soon as the nodes
follows as soon as the nodes
 are pairwise
are pairwise
 . We then show that this
. We then show that this
 condition can always be obtained, up to duplicating some
condition can always be obtained, up to duplicating some
 subtrees of \(\mathcal {F}\) (and some factors of u), because the behavior of a
subtrees of \(\mathcal {F}\) (and some factors of u), because the behavior of a
 in a
in a
 does not depend on the positions of the above recursive calls.
does not depend on the positions of the above recursive calls.
6 Height minimization of last pebble transducers
In this section, we show theorem 3.5 for
 . The notions of
. The notions of
 ,
,
 and
and
 for a
for a
 are defined as in section 5. The
are defined as in section 5. The
 is now defined over
is now defined over
 .
.
6.1 Pumpability
The sketch of the proof is similar to section 5. We first give an equivalent of
 for
for
 . The intuition behind this notion is depicted in fig. 7. The formal definition is however more cumbersome, since we need to keep track of the fact that the calling position is marked.
. The intuition behind this notion is depicted in fig. 7. The formal definition is however more cumbersome, since we need to keep track of the fact that the calling position is marked.
Definition 6.1
Let \(\mathscr {L}\) be a
 whose
whose
 is \(\mu : (A \cup \underline{A})^* \rightarrow \mathbb {T}\). We say that the transducer \(\mathscr {L}\) is
is \(\mu : (A \cup \underline{A})^* \rightarrow \mathbb {T}\). We say that the transducer \(\mathscr {L}\) is
 if there exists:
if there exists:
-
 \(\mathscr {T}_1, \dots , \mathscr {T}_k\) of \(\mathscr {L}\), such that \(\mathscr {T}_1\) is the
\(\mathscr {T}_1, \dots , \mathscr {T}_k\) of \(\mathscr {L}\), such that \(\mathscr {T}_1\) is the
 of \(\mathscr {L}\);
of \(\mathscr {L}\); -
\(m_0, \dots , m_k, {\ell }_1, \dots , {\ell _k}, r_1, \dots , r_k \in \mu (A^*)\);
-
\(a_1,\dots , a_k \in A\) such that for all \(1 \leqslant j \leqslant k\), \(e_j {:}{=}{\ell }_j \mu (a_j) r_j\) is idempotent;
-
a permutation \(\sigma : [{1}{:}{k}] \rightarrow [{1}{:}{k}]\);
such that if we let \(\mathcal {M}_{i}^{j} {:}{=}m_{i} e_{i + 1} m_{i + 1} \cdots e_{j} m_{j}\) for all \(0 \leqslant i \leqslant j \leqslant k\), and if we define the following
 :
:

and for all \(1 \leqslant j \leqslant k{-}1\) the
 :
:

then for all \(1 \leqslant j \leqslant k{-}1\),
 , and
, and
 .
.
We obtain lemma 6.2 by a proof which is similar to that of lemma 5.2.
Lemma 6.2
Let f be computed by a

 . There exists words \(v_0, \dots , v_k, u_1, \dots , u_k\) such that \(|f(v_0 u_1^{X} \cdots u_k^{X} v_k)| = \Theta (X^k)\).
. There exists words \(v_0, \dots , v_k, u_1, \dots , u_k\) such that \(|f(v_0 u_1^{X} \cdots u_k^{X} v_k)| = \Theta (X^k)\).
Theorem 6.3
(Removing one layer). Let \(k \geqslant 2\) and \(f : A^* \rightarrow B^*\) be computed by a
 \(\mathscr {L}\). The following are equivalent:
\(\mathscr {L}\). The following are equivalent:
-
1.
\(|f(u)| = \mathcal {O}(|u|^{k-1})\);
-
2.
\(\mathscr {L}\) is not
 ;
; -
3.
f can be computed by a
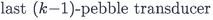 .
.
Furthermore, this property is decidable and the construction is effective.
Proof
Item 3 \(\Rightarrow \) item 1 is obvious. Item 1 \(\Rightarrow \) item 2 is lemma 6.2. Furthermore,
 can be tested by an enumeration of \(\mu (A^*)\) and A. It remains to show item 2 \(\Rightarrow \) item 3 (in an effective fashion): this is the purpose of section 6.2.
can be tested by an enumeration of \(\mu (A^*)\) and A. It remains to show item 2 \(\Rightarrow \) item 3 (in an effective fashion): this is the purpose of section 6.2.
6.2 Algorithm for removing a recursion layer
Let \(k \geqslant 2\) and \(\mathscr {U}\) be a
 that is not
that is not
 , and that computes \(f : A^* \rightarrow B^*\). We build a
, and that computes \(f : A^* \rightarrow B^*\). We build a
 \(\overline{\mathscr {U}}\) for f. Let
\(\overline{\mathscr {U}}\) for f. Let
 be the
be the
 of \(\mathscr {U}\). As before (using a
of \(\mathscr {U}\). As before (using a
 ), the
), the
 of \(\overline{\mathscr {U}}\) have access to
of \(\overline{\mathscr {U}}\) have access to
 on input \(u \in A^*\).
on input \(u \in A^*\).
Now, we describe the
 of \(\overline{\mathscr {U}}\). It has
of \(\overline{\mathscr {U}}\). It has

 for \(\mathscr {T}\) a
for \(\mathscr {T}\) a
 of \(\mathscr {U}\) and \(\rho \) a run of \(\mathscr {T}\), which are described in algorithm 1. Intuitively, these machines mimics the behavior of \(\mathscr {T}\) along the run \(\rho \) (which is not necessarily accepting) of \(\mathscr {T}\) over
of \(\mathscr {U}\) and \(\rho \) a run of \(\mathscr {T}\), which are described in algorithm 1. Intuitively, these machines mimics the behavior of \(\mathscr {T}\) along the run \(\rho \) (which is not necessarily accepting) of \(\mathscr {T}\) over
 with
with
 .
.
Since they are indexed by a run \(\rho \), it may seem that we create an infinite number of
 , but it will not be the case. Indeed, a run \(\rho \) will be represented by its first configuration \((q_1,i_1)\) and last configuration \((q_n,i_n)\). This information is sufficient to simulate exactly the two-way moves of \(\rho \), but there is still an unbounded information: the positions \(i_1\) and \(i_n\). In fact, the input will be of the form
, but it will not be the case. Indeed, a run \(\rho \) will be represented by its first configuration \((q_1,i_1)\) and last configuration \((q_n,i_n)\). This information is sufficient to simulate exactly the two-way moves of \(\rho \), but there is still an unbounded information: the positions \(i_1\) and \(i_n\). In fact, the input will be of the form
 and we shall guarantee that the \(i_1\) and \(i_n\) can be detected by the
and we shall guarantee that the \(i_1\) and \(i_n\) can be detected by the
 if i is marked. Hence the run \(\rho \) will be represented in a bounded way, independently from the input v, and so that its first and last configurations can be detected by the
if i is marked. Hence the run \(\rho \) will be represented in a bounded way, independently from the input v, and so that its first and last configurations can be detected by the
 of the
of the
 .
.
It follows from algorithm 3 that if \(\mathscr {T}\) is a
 of \(\mathscr {U}\), then for all \(v \in (A \cup \underline{A})^*\) and \(\rho \) run of \(\mathscr {T}\) on
of \(\mathscr {U}\), then for all \(v \in (A \cup \underline{A})^*\) and \(\rho \) run of \(\mathscr {T}\) on
 ,
,
 is the concatenation of the outputs produced by (the recursive calls of) \(\mathscr {T}\) along \(\rho \).
is the concatenation of the outputs produced by (the recursive calls of) \(\mathscr {T}\) along \(\rho \).
We also define a

 that is similar to
that is similar to
 , except that it ignores the mark of its input and acts as if it was in position i (as above for \(\rho \), i will be encoded by a bounded information).
, except that it ignores the mark of its input and acts as if it was in position i (as above for \(\rho \), i will be encoded by a bounded information).

\(\overline{\mathscr {U}}\) also has

 for \(\mathscr {T}\) a
for \(\mathscr {T}\) a
 of \(\mathscr {U}\), which are described in algorithm 4. Intuitively,
of \(\mathscr {U}\), which are described in algorithm 4. Intuitively,
 simulates \(\mathscr {T}\) along \(\rho \) while trying to inline some recursive calls. Whenever it is in position i and needs to call recursively \(\mathscr {L}'\) whose
simulates \(\mathscr {T}\) along \(\rho \) while trying to inline some recursive calls. Whenever it is in position i and needs to call recursively \(\mathscr {L}'\) whose
 is \(\mathscr {T}'\), it first
is \(\mathscr {T}'\), it first
 the accepting run \(\rho '\) of \(\mathscr {T}'\) on
the accepting run \(\rho '\) of \(\mathscr {T}'\) on
 , with respect to
, with respect to
 and i, as explained in definition 6.4 and depicted in fig. 8. Intuitively, this operation splits \(\rho '\) into a bounded number of runs whose positions either all
and i, as explained in definition 6.4 and depicted in fig. 8. Intuitively, this operation splits \(\rho '\) into a bounded number of runs whose positions either all
 i, or i
i, or i
 all of them, or none of these cases occur (the positions are either 0, \(|u|{+}1\) or
all of them, or none of these cases occur (the positions are either 0, \(|u|{+}1\) or
 of i).
of i).
Definition 6.4
(Slicing). Let \(u \in A^*\),
 and \(1 \leqslant i \leqslant |u|\). We let
and \(1 \leqslant i \leqslant |u|\). We let
 (resp.
(resp.
 ) be the set of positions that i
) be the set of positions that i
 (resp. that
(resp. that
 i).
i).
Let
 be a run of a
be a run of a
 \(\mathscr {T}\) on
\(\mathscr {T}\) on
 . We build by induction a sequence \(\ell _1, \dots , \ell _{N+1}\) with \(\ell _1 {:}{=}1\) and:
. We build by induction a sequence \(\ell _1, \dots , \ell _{N+1}\) with \(\ell _1 {:}{=}1\) and:
-
if \(\ell _j = n {+} 1\) then \(j {:}{=}N\) and the process ends;
-
else if
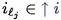 (resp.
(resp.
 , resp.
, resp.
 ), then \(\ell _{j+1}\) is the largest index such that for all \(\ell _{j} \leqslant \ell \leqslant \ell _{j+1}{-}1\),
), then \(\ell _{j+1}\) is the largest index such that for all \(\ell _{j} \leqslant \ell \leqslant \ell _{j+1}{-}1\),
 (resp.
(resp.
 , resp.
, resp.
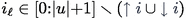 ).
).
Finally the
 of \(\rho \) ,with respect to \(\mathcal {F}\) and i, is the sequence of runs \(\rho _1, \dots , \rho _{N}\) where
of \(\rho \) ,with respect to \(\mathcal {F}\) and i, is the sequence of runs \(\rho _1, \dots , \rho _{N}\) where
 .
.
Now, let \(\rho '_1, \dots , \rho '_N\) be
 of the run \(\rho '\) of \(\mathscr {T}'\) on the input
of the run \(\rho '\) of \(\mathscr {T}'\) on the input
 . For all \(1 \leqslant j \leqslant N\), there are mainly two cases. Either the positions of \(\rho '_j\) all are in
. For all \(1 \leqslant j \leqslant N\), there are mainly two cases. Either the positions of \(\rho '_j\) all are in
 or
or
 . In this case,
. In this case,
 directly inlines
directly inlines
 within its own run (i.e. without making a recursive call). Otherwise, it makes a recursive call to
within its own run (i.e. without making a recursive call). Otherwise, it makes a recursive call to
 , except if \(\mathscr {L}'\) is a leaf of \(\mathscr {U}\) (thus \(\mathscr {L}' = \mathscr {T}'\)).
, except if \(\mathscr {L}'\) is a leaf of \(\mathscr {U}\) (thus \(\mathscr {L}' = \mathscr {T}'\)).

Finally, \(\overline{\mathscr {U}}\) is described as follows: on input \(u \in A^*\), its
 is the
is the

 , where \(\mathscr {T}\) is the
, where \(\mathscr {T}\) is the
 of \(\mathscr {U}\) and \(\rho \) is the accepting run of \(\mathscr {T}\) on
of \(\mathscr {U}\) and \(\rho \) is the accepting run of \(\mathscr {T}\) on
 (represented by the bounded information that it is both initial and final). As before, we remove the
(represented by the bounded information that it is both initial and final). As before, we remove the
 which are never called in \(\overline{\mathscr {U}}\). Observe that we have created a machine with recursion height \(k{-}1\) (because line 17 in algorithm 4 prevents from calling a k-th layer).
which are never called in \(\overline{\mathscr {U}}\). Observe that we have created a machine with recursion height \(k{-}1\) (because line 17 in algorithm 4 prevents from calling a k-th layer).
Let us justify that each
 can indeed be implemented by a
can indeed be implemented by a
 . First, let us observe that since \(\mathcal {F}\) has bounded height, the number N of
. First, let us observe that since \(\mathcal {F}\) has bounded height, the number N of
 given in line 7 of algorithm 4 is bounded. Furthermore, we claim that the first and last positions of each \(\rho '_j\) belong to a given set of bounded size, which can be detected by a
given in line 7 of algorithm 4 is bounded. Furthermore, we claim that the first and last positions of each \(\rho '_j\) belong to a given set of bounded size, which can be detected by a
 which has access to i. For the \(\rho '_j\) whose positions are in
which has access to i. For the \(\rho '_j\) whose positions are in
 , this is clear since
, this is clear since
 is bounded (because the frontier of any node is bounded). For
is bounded (because the frontier of any node is bounded). For
 we use lemma 6.5, which implies that this set is a bounded union of intervals. The last case is very similar.
we use lemma 6.5, which implies that this set is a bounded union of intervals. The last case is very similar.
Lemma 6.5
Let \(1 \leqslant i \leqslant |u|\),
 and \(\mathfrak {t}_{1}\) (resp. \(\mathfrak {t}_2\)) be its immediate left (resp. right) sibling (they exist whenever
and \(\mathfrak {t}_{1}\) (resp. \(\mathfrak {t}_2\)) be its immediate left (resp. right) sibling (they exist whenever
 , i.e. here \(\mathfrak {t}\ne \mathcal {F}\)). Then:
, i.e. here \(\mathfrak {t}\ne \mathcal {F}\)). Then:

This analysis justifies why each \(\rho '_j\) can be encoded in a bounded way. Now, we show how to implement the inlinings while using i as the current position:
-
if
 , then n is bounded (because
, then n is bounded (because
 is bounded). We can thus inline
is bounded). We can thus inline
 while staying in position i. However, when \(\mathscr {T}'\) calls some \(\mathscr {L}''\) (of
while staying in position i. However, when \(\mathscr {T}'\) calls some \(\mathscr {L}''\) (of
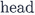 \(\mathscr {T}''\)) on position \(i_{\ell }\), we would need to call
\(\mathscr {T}''\)) on position \(i_{\ell }\), we would need to call
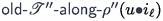 (where \(\rho ''\) is the accepting run of \(\mathscr {T}''\) along
(where \(\rho ''\) is the accepting run of \(\mathscr {T}''\) along
 ). But we cannot do this operation, since we are in position i and not in \(i_{\ell }\). The solution is that the inlined code calls
). But we cannot do this operation, since we are in position i and not in \(i_{\ell }\). The solution is that the inlined code calls
 instead, which simulates an accepting run \(\rho ''\) of \(\mathscr {T}\) on
instead, which simulates an accepting run \(\rho ''\) of \(\mathscr {T}\) on
 , even if its input is
, even if its input is
 . Note that \(i_{\ell }\) can be represented as a bounded information and recovered by a
. Note that \(i_{\ell }\) can be represented as a bounded information and recovered by a
 given
given
 as input, since i
as input, since i
 \(i_{\ell }\);
\(i_{\ell }\); -
if
 , then the nodes
, then the nodes
 are roughly below
are roughly below
 in \(\mathcal {F}\) (see fig. 5). We inline
in \(\mathcal {F}\) (see fig. 5). We inline
 , by moving along \(i_1, \dots , i_n\) as \(\rho '_j\) does. We can keep track of the height of
, by moving along \(i_1, \dots , i_n\) as \(\rho '_j\) does. We can keep track of the height of
 above the current
above the current
 (it is a bounded information). With the
(it is a bounded information). With the
 , we can detect the end of \(\rho '_j\), and go back to position i.
, we can detect the end of \(\rho '_j\), and go back to position i.
It remains to justify that \(\overline{\mathscr {U}}\) is correct. For this, we only need to show that when it reaches line 18 in algorithm 4, the output of \(\mathscr {T}'\) along \(\rho '_j\) is indeed empty. Otherwise, the conditions of lemma 6.6 would hold (since we never execute two successive recursive calls in
 positions). It provides a contradiction.
positions). It provides a contradiction.
Lemma 6.6
(Key lemma). Let \(u \in A^*\) and
 . Assume that there exists a sequence \(\mathscr {T}_1, \dots , \mathscr {T}_k\) of
. Assume that there exists a sequence \(\mathscr {T}_1, \dots , \mathscr {T}_k\) of
 of \(\mathscr {U}\) and a sequence of positions \(1 \leqslant i_1, \dots , i_k \leqslant |u|\) such that:
of \(\mathscr {U}\) and a sequence of positions \(1 \leqslant i_1, \dots , i_k \leqslant |u|\) such that:
-
\(\mathscr {T}_1\) is the
 of \(\mathscr {U}\);
of \(\mathscr {U}\); -
 and
and
 ;
; -
for all \(2 \leqslant j \leqslant k{-}1\),
 ;
; -
for all \(1 \leqslant j \leqslant k{-}1\),
 and
and
 are
are
 ;
;
Then \(\mathscr {U}\) is
 .
.
Proof
(idea). As for lemma 5.4, the key observation is that
 follows as soon as the nodes
follows as soon as the nodes
 are pairwise
are pairwise
 . Furthermore, this condition can be obtained by duplicating some nodes in \(\mathcal {F}\).
. Furthermore, this condition can be obtained by duplicating some nodes in \(\mathcal {F}\).
7 Making the two last pebbles visible
We can define a similar model to that of
 , which sees the two last calling positions instead of only the previous one. Let us name this model a
, which sees the two last calling positions instead of only the previous one. Let us name this model a
 . A very natural question is to know whether we can show an analog of theorem 3.5 for these machines.
. A very natural question is to know whether we can show an analog of theorem 3.5 for these machines.
Note that for \(k=1,2\) and 3, a
 is exactly the same as a
is exactly the same as a
 . Hence the function
. Hence the function
 of page 2 is such that
of page 2 is such that
 and can be computed by a
and can be computed by a
 , but it cannot be computed by a
, but it cannot be computed by a
 . It follows that the connection between minimal recursion height and growth of the output fails. However, this result is somehow artificial. Indeed, a
. It follows that the connection between minimal recursion height and growth of the output fails. However, this result is somehow artificial. Indeed, a
 is a degenerate case, since it can only see one last pebble. More interestingly, we show that the connection fails for arbitrary heights.
is a degenerate case, since it can only see one last pebble. More interestingly, we show that the connection fails for arbitrary heights.
Theorem 7.1
For all \(k \geqslant 2\), there exists a function \(f:A^* \rightarrow B^*\) such that \(|f(u)| = \mathcal {O}(|u|^2)\) and that can be computed by a
 , but not by a
, but not by a
 .
.
Proof
(idea). We re-use a counterexample introduced by Bojańczyk in [2] to show a similar failure result for the model of
 .
.
8 Outlook
This paper somehow settles the discussion concerning the variants of
 for which the minimal recursion height only depends on the growth of the output. As soon as two marks are visible, the combinatorics of the output also has to be taken into account, hence minimizing the recursion height in this case (e.g. for
for which the minimal recursion height only depends on the growth of the output. As soon as two marks are visible, the combinatorics of the output also has to be taken into account, hence minimizing the recursion height in this case (e.g. for
 ) seems hard with the current tools.
) seems hard with the current tools.
As observed in [13], one can extend
 by allowing the recursion height to be unbounded (in the spirit of
by allowing the recursion height to be unbounded (in the spirit of
 [9]). This model enables to produce outputs whose size grows exponentially in the size of the input. A natural question is to know whether a function computed by this model, but whose output size is polynomial, can in fact be computed with a recursion stack of bounded height (i.e. by a
[9]). This model enables to produce outputs whose size grows exponentially in the size of the input. A natural question is to know whether a function computed by this model, but whose output size is polynomial, can in fact be computed with a recursion stack of bounded height (i.e. by a
 ).
).
References
Bojańczyk, M.: Polyregular functions. arXiv preprint arXiv:1810.08760 (2018)
Bojańczyk, M.: The growth rate of polyregular functions. arXiv preprint arXiv:2212.11631 (2022)
Bojańczyk, M.: Transducers of polynomial growth. In: Proceedings of the 37th Annual ACM/IEEE Symposium on Logic in Computer Science. pp. 1–27 (2022)
Bojańczyk, M., Kiefer, S., Lhote, N.: String-to-string interpretations with polynomial-size output. In: 46th International Colloquium on Automata, Languages, and Programming, ICALP 2019 (2019)
Chytil, M.P., Jákl, V.: Serial composition of 2-way finite-state transducers and simple programs on strings. In: 4th International Colloquium on Automata, Languages, and Programming, ICALP 1977. pp. 135–147. Springer (1977)
Colcombet, T.: Green’s relations and their use in automata theory. In: International Conference on Language and Automata Theory and Applications. pp. 1–21. Springer (2011)
Dave, V., Gastin, P., Krishna, S.N.: Regular transducer expressions for regular transformations. In: Proceedings of the 33rd Annual ACM/IEEE Symposium on Logic in Computer Science. pp. 315–324. ACM (2018)
Douéneau-Tabot, G.: Pebble transducers with unary output. In: 46th International Symposium on Mathematical Foundations of Computer Science, MFCS 2021 (2021)
Douéneau-Tabot, G., Filiot, E., Gastin, P.: Register transducers are marble transducers. In: 45th International Symposium on Mathematical Foundations of Computer Science, MFCS 2020 (2020)
Douéneau-Tabot, G.: Hiding pebbles when the output alphabet is unary. In: 49th International Colloquium on Automata, Languages, and Programming, ICALP 2022 (2022)
Engelfriet, J.: Two-way pebble transducers for partial functions and their composition. Acta Informatica 52(7-8), 559–571 (2015)
Engelfriet, J., Hoogeboom, H.J.: MSO definable string transductions and two-way finite-state transducers. ACM Transactions on Computational Logic (TOCL) 2(2), 216–254 (2001)
Engelfriet, J., Hoogeboom, H.J., Samwel, B.: Xml transformation by tree-walking transducers with invisible pebbles. In: Proceedings of the twenty-sixth ACM SIGMOD-SIGACT-SIGART symposium on Principles of database systems. pp. 63–72.ACM (2007)
Gurari, E.M.: The equivalence problem for deterministic two-way sequential transducers is decidable. SIAM Journal on Computing 11(3), 448–452 (1982)
Hopcroft, J.E., Ullman, J.D.: An approach to a unified theory of automata. The Bell System Technical Journal 46(8), 1793–1829 (1967)
Kiefer, S., Nguyên, L.T.D., Pradic, C.: Revisiting the growth of polyregular functions: output languages, weighted automata and unary inputs. arXiv preprint arXiv:2301.09234 (2023)
Nguyên, L.T.D., Noûs, C., Pradic, C.: Comparison-free polyregular functions. In: 48th International Colloquium on Automata, Languages, and Programming, ICALP 2021 (2021)
Shepherdson, J.C.: The reduction of two-way automata to one-way automata. IBM Journal of Research and Development 3(2), 198–200 (1959)
Simon, I.: Factorization forests of finite height. Theor. Comput. Sci. 72(1), 65–94 (1990)
Acknowledgements
The author is grateful to Tito Nguyên for suggesting the study of the recursion height for
 .
.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Douéneau-Tabot, G. (2023). Pebble minimization: the last theorems. In: Kupferman, O., Sobocinski, P. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2023. Lecture Notes in Computer Science, vol 13992. Springer, Cham. https://doi.org/10.1007/978-3-031-30829-1_21
Download citation
DOI: https://doi.org/10.1007/978-3-031-30829-1_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-30828-4
Online ISBN: 978-3-031-30829-1
eBook Packages: Computer ScienceComputer Science (R0)






 .
.
 .
.
 .
. ;
; with same domain as
with same domain as  with input alphabet A and output B;
with input alphabet A and output B; with input A and output B; and the root label
with input A and output B; and the root label  with input A and output alphabet
with input A and output alphabet  ;
; be the accepting run of
be the accepting run of  . For all
. For all  . Then
. Then  with input alphabet
with input alphabet
 and output B;
and output B; with input A and output B; and the root label
with input A and output B; and the root label  with input
with input
 and output alphabet
and output alphabet  ;
; be the accepting run of
be the accepting run of
 on
on
 . For all
. For all  . Let
. Let
 be the morphism which erases the underlining (i.e.
be the morphism which erases the underlining (i.e.  .
. of
of  ;
;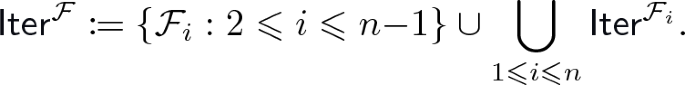
 ;
; .
.
 and a
and a
 .
.

 and that
and that



 of
of 
 in a
in a
 .
. ;
; .
. , the
, the
 inlines
inlines
 by executing the same moves and calls as
by executing the same moves and calls as  is a property that can be detected by using the
is a property that can be detected by using the
 , hence the machine only needs to remember that i was the
, hence the machine only needs to remember that i was the  (
( , we produce the output of
, we produce the output of  ,
,
 (hence the output of
(hence the output of  ). Indeed, if
). Indeed, if
 for such an
for such an
 when reaching line 12 of algorithm 2, then the conditions of lemma
when reaching line 12 of algorithm 2, then the conditions of lemma  of
of  of
of  and
and
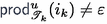 ;
; (i.e.
(i.e.
 ).
).
 of
of 
 in a
in a
 .
. ;
;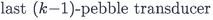 .
.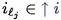 (resp.
(resp.
 , resp.
, resp.
 ), then
), then  (resp.
(resp.
 , resp.
, resp.
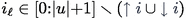 ).
).
 of a run
of a run  , then n is bounded (because
, then n is bounded (because
 is bounded). We can thus inline
is bounded). We can thus inline
 while staying in position i. However, when
while staying in position i. However, when 
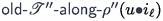 (where
(where  ). But we cannot do this operation, since we are in position i and not in
). But we cannot do this operation, since we are in position i and not in  instead, which simulates an accepting run
instead, which simulates an accepting run  , even if its input is
, even if its input is
 . Note that
. Note that  given
given
 as input, since i
as input, since i

 , then the nodes
, then the nodes
 are roughly below
are roughly below
 in
in  , by moving along
, by moving along  above the current
above the current
 (it is a bounded information). With the
(it is a bounded information). With the
 , we can detect the end of
, we can detect the end of  of
of  and
and
 ;
; ;
; and
and
 are
are
 ;
;