Abstract
We prove decidability for contextual equivalence of the \(\lambda \mu \nu \)-calculus, that is the simply-typed call-by-value \(\lambda \mu \)-calculus equipped with booleans and fresh name creation, with contexts taken in \(\lambda \mu _{\texttt{ref}}\), that is \(\lambda \mu \nu \)-calculus extended with higher-order references.
The proof exploits a labelled transition system capturing the interactions between \(\lambda \mu \nu \) programs and \(\lambda \mu _{\texttt{ref}}\) contexts. The induced bisimulation equivalence is characterized as equality of certain trees, inspired by the work of Lassen. Since these trees are computable and finite, decidability follows. Bisimulation coincides also with trace equivalence, which in turn coincides with contextual equivalence.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Dynamic allocation is central to many programming constructions. Many languages provide built-in support for dynamically-allocated resources, for example, objects in Java or references in ML. The creation of these resources is local, meaning that resources can be accessed only within their scope. They can also be passed around via function applications, in which case their scope is not static but evolves dynamically. When building semantics for such languages, one represents dynamic allocation as the creation of fresh locations, that can be seen as atoms or names.
In this paper, we study a paradigmatic language with dynamic allocation, namely the \(\nu \)-calculus, a simply-typed call-by-value \(\lambda \)-calculus with fresh atom creation and equality test of atoms, as introduced by Pitts and Stark in [24]. For instance, the \(\nu \)-calculus program \(\texttt{new}\ n \ \texttt{in}\ \lambda x.(x~=~n)\) allocates a new atom n, receives an atom x and returns the result of the comparison between x and n.
A central question while studying this language is to determine when two programs can be considered to be equivalent. The most studied approach to express behavioral equivalence between programs is contextual equivalence. Intuitively, two programs are deemed equivalent if and only if whenever they are run as part of an enclosing program called the context, it is not possible to distinguish one from the other. For instance, because the context has no way to guess the atom n, we expect the program above to be equivalent to \(\lambda x.\texttt{false}\).
Reasoning on contextual equivalence for the \(\nu \)-calculus has shown to be challenging, due to the interplay between the higher-order control flow and the scope extrusion of atoms. A variety of frameworks has been introduced to do so, based on logical relations [24], environmental bisimulations [5], and game semantics [1].
However, the question of whether this equivalence is decidable remains open since the introduction of this language 30 years ago.
In this paper, we address this question by working in an asymmetric setting, giving contexts more discriminating power than just the mere creation of atoms. Indeed, contextual equivalence depends on two languages: the language for programs, and the language for contexts interacting with these programs. We take contexts in the \(\lambda \mu _{\texttt{ref}}\)-calculus, an extension of the \(\nu \)-calculus with both higher-order references and continuations. In this setting, atoms are simply references where only the unit value can be stored. Contextual equivalence is then coarser than for the symmetric setting when the contexts are also taken in the \(\nu \)-calculus. For example, one of the standard examples of equivalence of the literature
is not an equivalence anymore, since a \(\lambda \mu _{\texttt{ref}}\) context can provide a function that stores its argument in a reference and use it to discriminate these programs.
The main result we establish in this paper is the decidability of contextual equivalence for terms of \(\nu \)-calculus with contexts in the \(\lambda \mu _{\texttt{ref}}\)-calculus. More generally, we establish this result for terms of the \(\lambda \mu \nu \)-calculus, which corresponds to terms of the \(\lambda \mu _{\texttt{ref}}\)-calculus that only use references storing the unit value.
To establish this result, we provide a Böhm-like tree representation [3, 6] for the terms of the \(\lambda \mu \nu \)-calculus. Being in call-by-value, equality of such trees coincides with Lassen’s eager normal form bisimulations [16]. Moreover, since programs in the \(\lambda \mu \nu \)-calculus are terminating, these trees, which we call Lassen trees, are finite. It is thus straightforward to check their equality. Then, we prove that Lassen trees equality is fully-abstract, that is it coincides with contextual equivalence with contexts in the \(\lambda \mu _{\texttt{ref}}\)-calculus.
Proving this full-abstraction result is done through the introduction of an operational game semantics (\(\textsf{OGS}\)) for \(\lambda \mu _{\texttt{ref}}\) by defining a Labelled Transition System (LTS) that distinguishes between internal operations, Proponent moves (originating in the program) and Opponent moves (originating in the context). Trace equivalence based on these labelled transitions is shown to coincide with the contextual equivalence of \(\lambda \mu _{\texttt{ref}}\).
The \(\textsf{OGS}\) also gives rise to a notion of bipartite bisimulation, describing a game between Proponent (the program in \(\lambda \mu _{\texttt{ref}}\)) and Opponent (a context in \(\lambda \mu _{\texttt{ref}}\)). Proponent reduces the program until it reaches a normal form, that triggers an interaction with the context. Along the game, knowledge is accumulated in configurations. When it is Opponent’s turn to play, it chooses between answering a previous function call from Proponent, or generating a new function call, to which Proponent shall answer. Among this knowledge, we accumulate the atoms that have been disclosed by the two players, so that Opponent cannot use an atom private to Proponent.
The \(\textsf{OGS}\) LTS generates infinite trees since Opponent can interrogate an arbitrary number of times each value provided by Proponent. The Lassen trees used to decide contextual equivalence are generated using a linearized variant of the \(\textsf{OGS}\) LTS, called the Prime Operational Game Semantics (\(\textsf{POGS}\)) LTS. The \(\textsf{POGS}\) LTS enforces that Opponent interrogates only once each value provided by Proponent. For this linearization to be sound, one has to guess the disclosed status of atoms as soon as they are created. This can be illustrated by considering the following example of inequivalence

Opponent must be able to interrogate at least twice each of these two programs to discriminate them. The first program would then return the same atom at each call, while the second program would return two different atoms. The Lassen tree of the first program would declare n to be disclosed when giving back the control to Opponent by providing the \(\lambda \)-abstraction, but this could not be matched by the second program, since n would not exist yet at that point of the interaction.
The main technical challenge at this point is to prove that this forecasting of the disclosure process is sound and complete. This is done by proving that the bipartite bisimilarities defined over the \(\textsf{OGS}\) LTS and the \(\textsf{POGS}\) LTS coincide. One direction is proven by lifting \(\textsf{POGS}\) bisimulations into \(\textsf{OGS}\) bisimulations via an up-to technique. The other direction is done by introducing a new limit construction of the disclosed set of atoms appearing in the \(\textsf{OGS}\) bisimulations, to transform it into a \(\textsf{POGS}\) bisimulation.
Paper outline. After introducing the \(\lambda \mu _{\texttt{ref}}\)-calculus and the \(\lambda \mu \nu \)-calculus in Section 2, we define the LTS for the \(\textsf{OGS}\) in Section 3. The induced trace equivalence coincides with contextual equivalence. We then move to Lassen trees in Section 4, and show that they yield an equivalence that coincides with bipartite bisimilarity in the \(\textsf{OGS}\) in Section 5. We discuss related work in Section 6, and present concluding remarks in Section 7. For lack of space, several technical developments are given in [9].
2 The \(\lambda \mu _{\texttt{ref}}\)-calculus and the \(\lambda \mu \nu \)-calculus
The syntax of the \(\lambda \mu _{\texttt{ref}}\)-calculus is given by the following grammar:

with \(x\in \textrm{Vars}\) (variables), \(\textsf{c}\in \textrm{Covars}\) (continution variables), \(\ell \in \textrm{Locs}\) (locations). We write \(\textsf{supp}(\texttt{M})\) for the set of locations appearing in \(\texttt{M}\), and \(\textbf{FV}(\texttt{M})\) for the free variables of \(\texttt{M}\). This language has two binders, the standard \(\lambda \)-abstraction, and the \(\mu \) binder for continuation variables \(\textsf{c},d\) [22].
A store, ranged over by \(\texttt{S}, \texttt{T}\), is a finite mapping from locations to values. \(\texttt{S}(\ell )\) stands for the value associated to \(\ell \) in \(\texttt{S}\). We use notation \(\texttt{S}\cdot [\ell \mapsto \texttt{V}]\) for the extension of \(\texttt{S}\) with a mapping for \(\ell \), which is only defined if \(\ell \) is not defined in \(\texttt{S}\). \(\texttt{S}[\ell \mapsto \texttt{V}]\) denotes the store \(\texttt{S}\) in which the value associated to \(\ell \) is updated.
The operational semantics \(\mapsto _{\textsf{op}}\) of the \(\lambda \mu _{\texttt{ref}}\)-calculus is defined over configurations, which are pairs \((\texttt{M},\texttt{S})\) formed by a term and a store. It is given by the following rules:
The typing system for terms is given by the rules in Figure 1. We chose here a typing judgement with a single typing context \(\Gamma \), so that continuation variables are given types of the shape \(\lnot \sigma \). Such negated types are also used to type evaluation contexts, as specified by the two last rules in Figure 1. While we cannot store a continuation variable \(\textsf{c}\) in a reference, we can always store its associated function \(\lambda x.[\textsf{c}]x\). Typing rules force terms of type \(\bot \) to be of the shape \([d]\texttt{M}\), following Parigot’s original presentation of the \(\lambda \mu \)-calculus [22].
We also consider a typing judgement of the shape \(\Sigma \vdash \texttt{C}: (\Gamma ;\sigma ) \,\rightsquigarrow \, (\Delta ;\tau )\), for contexts \(\texttt{C}\) that take terms \(\texttt{M}\) of type \(\Sigma ;\Gamma \vdash \texttt{M}: \sigma \) and produce terms of type \(\Sigma ;\Delta \vdash \texttt{C}[\texttt{M}] : \tau \). The typing rules defining this judgement are standard and not recalled here.
In the following, we consider the \(\lambda \mu \nu \)-calculus, the fragment of the \(\lambda \mu _{\texttt{ref}}\)-calculus that only handles references of type \(\textbf{ref}_{\texttt{Unit}}\). That is, for any reference type \(\textbf{ref}_{\sigma }\) appearing in the typing derivation, we have \(\sigma = \texttt{Unit}\).
We use \(\texttt{a},\texttt{b},\dots \) to range over locations of type \(\textbf{ref}_{\texttt{Unit}}\), also called atoms, and introduce the slightly shorter notation \(\texttt{new}\ n \ \texttt{in}\ \texttt{M}\) to stand for \(\texttt{new} \ n = () \ \texttt{in}\ \texttt{M}\) in \(\lambda \mu \nu \). The syntax for values and terms of the \(\lambda \mu \nu \)-calculus is thus:
In this setting, we see stores \(\texttt{S}\) directly as sets of atoms, all mapping to the unit value \(()\). For \(\texttt{L}\) a set of atoms. we write \(\widehat{\texttt{L}}\) for the store that maps atoms in \(\texttt{L}\) to the unit value \(()\).
We consider the following extension of the typing judgement respectively to stores \(\texttt{S}\) and value-mapping substitutions \(\gamma \):

Definition 1
A normal form \((\texttt{M},\texttt{S})\) is a configuration that is irreducible for the reduction relation \(\mapsto _{\textsf{op}}\). We write \((\texttt{M},\texttt{S})\!\Downarrow \texttt{N}\) when there exists a store \(\texttt{T}\) such that \((\texttt{M};\texttt{S}) \mapsto _{\textsf{op}}^{*} (\texttt{N};\texttt{T})\) and that \((\texttt{N};\texttt{T})\) is a normal form.
We call the types \(\texttt{Bool},\texttt{Unit}\) and \(\textbf{ref}_{\sigma }\) positive types, while \(\sigma \rightarrow \tau \) and \(\lnot \sigma \) are called negative types. By only allowing free variables of negative types, we can provide a sharp characterization of normal forms.
Theorem 2
Taking a term \(\texttt{M}\) such that \(\Sigma ;\Gamma \vdash \texttt{M}: \bot \) with \(\Gamma \) a typing context mapping variables to negative types, if \((\texttt{M},\texttt{S})\) is in normal form with respect to \(\mapsto _{\textsf{op}}\), then \(\texttt{M}\) is either a named value \([\textsf{c}]\texttt{V}\) or a neutral term \(\texttt{E}[x\texttt{V}]\).
Moreover, for any configuration \((\texttt{M},\texttt{S})\) such that \(\texttt{M}\) is in \(\lambda \mu \nu \), \(\Sigma ;\Gamma \vdash \texttt{M}: \bot \) and \(\vdash \texttt{S}:\Sigma \), there exists \(\texttt{N}\) such that \((\texttt{M},\texttt{S})\!\Downarrow \texttt{N}\).
Definition 3
Taking two terms \(\texttt{M},\texttt{N}\) such that \(\Sigma ;\Gamma \vdash \texttt{M}: \sigma \) and \(\Sigma ;\Gamma \vdash \texttt{N}: \sigma \), we say that they are contextually equivalent, written \(\Sigma ;\Gamma \vdash \texttt{M}\simeq _{ctx}\texttt{N}:\sigma \), when for all continuation variable \(\textsf{c}\) and context \(\texttt{C}\) such that \(\Sigma \vdash \texttt{C}: (\Gamma ;\sigma ) \,\rightsquigarrow \, (\textsf{c}:\lnot \texttt{Unit};\bot )\), and for all store \(\texttt{S}\) such that \(\vdash \texttt{S}:\Sigma '\), we have \((\texttt{C}[\texttt{M}],\texttt{S})\!\Downarrow [\textsf{c}]()\) if and only if \((\texttt{C}[\texttt{N}],\texttt{S})\!\Downarrow [\textsf{c}]()\).
In the definition above, we use \(\lambda \mu _{\texttt{ref}}\) contexts to observe \(\lambda \mu \nu \) terms. Such contexts can use higher-order references, and lead to divergent computations. For this reason, testing for convergence to \(()\) is enough when defining \(\simeq _{ctx}\).
3 Operational Game Semantics
We now introduce a fully-abstract trace semantics for \(\lambda \mu _{\texttt{ref}}\) programs. We follow a modular presentation, inspired by the one provided by Laird in [15], where the semantics is built from a synchronization product of three LTS:
-
the Interactive LTS \(\mathcal {L}_{\textsf{I}}\), that represents the raw interactions of programs with their environment.
-
the Typing LTS \(\mathcal {L}_{\textsf{Ty}}\), that keeps track of the polarization and types of names exchanged, to preserve well-typedness.
-
the Disclosing LTS \(\mathcal {L}_{\textsf{Di}}\), that prevents the environment from using private resources that have not been disclosed by Proponent.
3.1 Abstract values
To represent the interaction between the program and its environment, we distinguish between values that we can observe and values that we can interact with. The two players only exchange observable values, called abstract values in this paper. They are defined by the following grammar:
with \(\textsf{f}\) a function name, that is a variable used to represent functions exchanged between the two players. These correspond to the positive part of values, and are also called ultimate patterns in [17]. Like for terms, \(\textsf{supp}(\texttt{A})\) stands for the set of atoms occurring in \(\texttt{A}\). We consider the typing judgement \( \Delta \Vdash \texttt{A} : \sigma \) for abstract values, with \(\sigma \) a positive type, that is defined similarly as done for terms.
Then we introduce the abstraction relation
 that transforms a value \(\texttt{V}\) into a pair \((\texttt{A},\gamma )\) formed by an abstract value and a substitution, such that \(\texttt{A}\{ \gamma \} = \texttt{V}\):
that transforms a value \(\texttt{V}\) into a pair \((\texttt{A},\gamma )\) formed by an abstract value and a substitution, such that \(\texttt{A}\{ \gamma \} = \texttt{V}\):

3.2 Labelled Transition Systems
The two players, Opponent and Proponent, exchange moves, which are in one of six forms:
We use \(\textbf{m}\) to range over moves, and \(\textbf{p}\) (resp. \(\textbf{o}\)) to range over Proponent (resp. Opponent) moves. Initial questions are the introductory moves. In contrast with other moves, they can introduce multiple abstract values in a row, which is useful to instantiate all the variables of a typing context \(\Gamma \). They use a distinguished function name ?.
Traces \(\textbf{t}\) are sequences of moves. We write \(\overline{\textbf{m}}\) for the corresponding move with reversed polarity (input switched to output, and vice-versa). We extend this definition to switch traces, written \(\overline{\textbf{t}}\).
The three labelled transition systems we define are instances of the following definition:
Definition 4
A labelled transition system (LTS) \(\mathcal {L}\) is a triple of the form
 . \(\textrm{Confs}\) is a set of configurations \(\mathbb {C},\mathbb {D}\). \(\textrm{Actions}\) is a set of actions \(\textbf{a}\), formed by the moves \(\textbf{m}\), together with a silent action \(\textsf{op}\), corresponding to internal computations. Relation
. \(\textrm{Confs}\) is a set of configurations \(\mathbb {C},\mathbb {D}\). \(\textrm{Actions}\) is a set of actions \(\textbf{a}\), formed by the moves \(\textbf{m}\), together with a silent action \(\textsf{op}\), corresponding to internal computations. Relation
 is the labelled transition relation. We write
is the labelled transition relation. We write
 for
for
 .
.
Taking \(\mathbb {C}\) a configuration of an LTS \(\mathcal {L}\), we write \(\textbf{Tr}_{\mathcal {L}}(\mathbb {C})\) for the set of traces, as sequences of moves generated by this LTS over \(\mathbb {C}\) (so with \(\textsf{op}\) actions removed). We write \(\mathbb {C}\simeq _{\textsf{tr}}\mathbb {D}\) for the trace equivalence relation, which equates configurations \(\mathbb {C},\mathbb {D}\) when both have the same set of traces.
3.3 Interactive LTS
We consider interactive configurations \(\mathbb {I};\mathbb {J}\in \textrm{IConfs}\) which are either passive of the shape \(\langle \texttt{S};\gamma \rangle \), or active of the shape \(\langle \texttt{M};\texttt{S};\gamma \rangle \) with \(\texttt{M}\) a term, \(\texttt{S}\) a store, and \(\gamma \) a substitution. The Interactive LTS \(\mathcal {L}_{\textsf{I}}\) is then defined as the triple
 with relation
with relation
 defined in Figure 2.
defined in Figure 2.
The two rules for Proponent moves describe transitions performed by normal forms and make use of the abstraction relation. In the two rules for Opponent, the notation \(\texttt{S}\odot [\widehat{\textsf{supp}(\texttt{A})}]\) stands for \(\texttt{S}\) extended with a binding \(\texttt{a}\mapsto ()\) in the case when \(\texttt{A}=\texttt{a}\) and \(\texttt{a}\) is fresh for Proponent, and simply \(\texttt{S}\) otherwise: Proponent extends its store when a new atom is received.
3.4 Typing LTS
We consider type-context configurations \(\mathbb {S},\mathbb {T}\in \textrm{Confs}_{\textsf{Ty}}\) which are either active of the shape \(\langle \Delta _{\textsf{O}}\mid \bot ;\Delta _{\textsf{P}} \rangle \) or passive of the shape \(\langle \Delta _{\textsf{O}}\mid \Delta _{\textsf{P}} \rangle \), with \(\Delta _{\textsf{O}},\Delta _{\textsf{P}}\) two disjoint typing contexts that map variables to negative types.
The Interactive LTS \(\mathcal {L}_{\textsf{I}}\) is then defined as the triple \((\textrm{Confs}_{\textsf{Ty}},\textrm{Actions},\xrightarrow {}_{\textsf{Ty}})\) with relation \(\xrightarrow {}_{\textsf{Ty}}\) defined in Figure 3. Notice that the type of the active term is \(\bot \) since the reduction relation \(\mapsto _{\textsf{op}}\) is well-defined only on terms of this type.
Typing configurations can be used to specify interactive configurations, via the following validity judgement.
Definition 5
An interactive configuration \(\mathbb {I}\) is said to be validated by a typing configuration \(\mathbb {S}\), written \(\mathbb {I}\triangleright \mathbb {S}\), when:
-
either \(\mathbb {I}= \langle \texttt{S};\gamma \rangle \), \(\mathbb {S}= \langle \Delta _{\textsf{O}}\mid \Delta _{\textsf{P}} \rangle \), and there exists a store typing context \(\Sigma \) such that \(\Sigma ;\Delta _{\textsf{O}}\vdash \gamma : \Delta _{\textsf{P}}\) and \(\vdash \texttt{S}:\Sigma \),
-
or \(\mathbb {I}= \langle \texttt{M};\texttt{S};\gamma \rangle \), \(\mathbb {S}= \langle \Delta _{\textsf{O}}\mid \bot ;\Delta _{\textsf{P}} \rangle \), and there exists a store typing context \(\Sigma \) such that \(\Sigma ;\Delta _{\textsf{O}}\vdash \texttt{M}:\bot \), \(\Sigma ;\Delta _{\textsf{O}}\vdash \gamma : \Delta _{\textsf{P}}\) and \(\vdash \texttt{S}:\Sigma \).
3.5 Disclosing LTS
In order to enforce a non-omniscient condition on Opponent transitions, we introduce a Disclosing LTS \(\mathcal {L}_{\textsf{Di}}\triangleq (\textrm{DConfs},\textrm{Actions},\xrightarrow {}_{\textsf{Di}})\) whose configurations \(\textrm{DConfs}\) are pairs of sets of locations \(\langle \texttt{L};\textsf{D} \rangle \) with \(\textsf{D}\) a set of atoms contained in \(\texttt{L}\). The transition relation \(\xrightarrow {}_{\textsf{Di}}\) is defined in Figure 4. The condition \(\texttt{L}\cap \textsf{supp}(\textbf{o}) \subseteq \textsf{D}\) corresponds to the fact that Opponent cannot play Proponent atoms that have not been disclosed yet, i.e. not in \(\textsf{D}\).
Definition 6
An interactive configuration \(\mathbb {I}\) is said to be validated by a disclosing configuration \(\mathbb {D}= \langle \texttt{L};\textsf{D} \rangle \), written \(\mathbb {I}\triangleright \mathbb {D}\), if when writing \(\texttt{S}\) for the store component of \(\mathbb {I}\), we have \(\textrm{dom}(\texttt{S}) = \texttt{L}\).
3.6 Operational Game Semantics: LTS and Trace Equivalence
The Operational Game Semantics (OGS) LTS
 is defined over configurations \(\mathbb {G},\mathbb {H}\in \textrm{Confs}_{\textsf{ogs}}\) of the shape \((\mathbb {I},\mathbb {S},\mathbb {D})\), with \(\mathbb {I}\triangleright \mathbb {S}\) and \(\mathbb {I}\triangleright \mathbb {D}\), or over initial configurations \(\langle \Sigma ;\Gamma \vdash \texttt{M}:\sigma \rangle \) for Proponent and \(\langle \textsf{c}:\lnot \texttt{Unit} \vdash (\texttt{S};\delta ):(\Sigma ;\Gamma ) \rangle \) for Opponent. Its transition relation is defined by the following rules:
is defined over configurations \(\mathbb {G},\mathbb {H}\in \textrm{Confs}_{\textsf{ogs}}\) of the shape \((\mathbb {I},\mathbb {S},\mathbb {D})\), with \(\mathbb {I}\triangleright \mathbb {S}\) and \(\mathbb {I}\triangleright \mathbb {D}\), or over initial configurations \(\langle \Sigma ;\Gamma \vdash \texttt{M}:\sigma \rangle \) for Proponent and \(\langle \textsf{c}:\lnot \texttt{Unit} \vdash (\texttt{S};\delta ):(\Sigma ;\Gamma ) \rangle \) for Opponent. Its transition relation is defined by the following rules:

The initial question generated by \(\langle \Sigma ;\Gamma \vdash \texttt{M}:\sigma \rangle \) provides a way for Opponent to instantiate variables of \(\Gamma \) with abstract values. In this setting \(\Sigma \) only contains atoms since \(\texttt{M}\) is a term of \(\lambda \mu \nu \). The transition for \(\langle \textsf{c}:\lnot \texttt{Unit} \vdash (\texttt{S};\delta ):(\Sigma ;\Gamma ) \rangle \) represents this behavior from the point of view of Opponent. Since contexts belong to \(\lambda \mu _{\texttt{ref}}\), these initial configurations come equipped with an initial store \(\texttt{S}\) of type \(\Sigma \), but only the locations of type \(\textbf{ref}_{\texttt{Unit}}\) are considered to be disclosed, since the other ones cannot be used by Proponent. The continuation name \(\textsf{c}\) is used for Opponent to provide its final answer, which is of type \(\texttt{Unit}\), following the notion of observation used to define contextual equivalence.
We use notation
 to denote a \(\textbf{p}\) transition preceded by a possibly empty sequence of \(\textsf{op}\) transitions. Trace equivalence according to \(\mathcal {L}_\textsf{OGS}\) and contextual equivalence coincide.
to denote a \(\textbf{p}\) transition preceded by a possibly empty sequence of \(\textsf{op}\) transitions. Trace equivalence according to \(\mathcal {L}_\textsf{OGS}\) and contextual equivalence coincide.
Theorem 7
Consider two terms \(\texttt{M},\texttt{N}\) such that \(\Sigma ;\Gamma \vdash \texttt{M},\texttt{N}:\sigma \).
We have \(\langle \Sigma ;\Gamma \vdash \texttt{M}:\sigma \rangle \simeq _{\textsf{tr}}\langle \Sigma ;\Gamma \vdash \texttt{N}:\sigma \rangle \) if and only if \(\Sigma ;\Gamma \vdash \texttt{M}\simeq _{ctx}\texttt{N}:\sigma \).
Such a full-abstraction theorem was proven in [13] for RefML, that is the intuitionistic fragment of \(\lambda \mu _{\texttt{ref}}\)-calculus, without control operators. It was also proven in [10] for HOSC, a variant of the \(\lambda \mu _{\texttt{ref}}\)-calculus, with the call/cc operator, but without atom disclosure. Such a full-abstraction result being rather standard, we have chosen to present its proof in [9].
In the remainder of the paper, we focus on the \(\lambda \mu \nu \)-calculus. In particular, we only consider \(\textsf{OGS}\) configurations corresponding to \(\lambda \mu \nu \) from now on.
4 Lassen Trees for the \(\lambda \mu \nu \)-calculus
4.1 \(\textsf{POGS}\) and \(\textsf{POGS}\) bipartite bisimulation
We introduce Lassen trees for terms of the \(\lambda \mu \nu \)-calculus, as a form of linearized version of \(\mathcal {L}_{\textsf{OGS}}\), where Opponent can interrogate a name provided by Proponent only once, immediately after it has been introduced. So we consider prime interactive configurations which are either passive of the shape \(\langle \texttt{L};\gamma \rangle \), or active of the shape \(\langle \texttt{M};\texttt{L} \rangle \) with \(\texttt{M}\) a term, \(\texttt{L}\) a set of atoms, and \(\gamma \) a substitution. Compared to interactive configurations, the active configurations do not carry an environment \(\gamma \). Furthermore, we have a set of atoms rather than a full store, since this LTS is defined only for the \(\lambda \mu \nu \)-calculus and not for the whole \(\lambda \mu _{\texttt{ref}}\)-calculus.
The Prime Interactive LTS, \(\mathcal {L}_\textsf{PI}\), is then defined as
 , with
, with
 defined in Figure 5.
defined in Figure 5.
The corresponding Typing LTS is defined using the transitions given in Figure 6, which are very close in spirit to the transitions in Figure 3.
The transitions for the Disclosing LTS for \(\textsf{POGS}\) are presented on Figure 7. We compare these with the Disclosing LTS for \(\textsf{OGS}\) (Figure 4) below.
The Prime Operational Game Semantics LTS is introduced as a synchronization product, together with initial transitions, like for \(\textsf{OGS}\). More precisely, the synchronization between the interactive and typing LTSs requires that active configurations \(\langle \texttt{M};\texttt{L} \rangle \) correspond to type-contexts of the shape \(\langle \Delta _{\textsf{O}}\mid \bot \rangle \), with \(\Sigma ;\Delta _O\vdash \texttt{M}:\bot \) and \(\vdash \widehat{\texttt{L}}:\Sigma \), for some store typing context \(\Sigma \). Accordingly, for passive configurations \(\langle \texttt{L};\gamma \rangle \), we synchronize with \(\langle \Delta _{\textsf{O}}\mid \Delta _{\textsf{P}} \rangle \), and check that \(\Sigma ;\Delta _O\vdash \gamma : \Delta _P\) and \(\vdash \widehat{\texttt{L}}:\Sigma \), for some store typing context \(\Sigma \).
To synchronize with the Disclosing LTS, whose states are of the form \(\langle \texttt{L};\textsf{D} \rangle \), we simply impose that the \(\texttt{L}\) component is the same in the state of \(\mathcal {L}_\textsf{PI}\), both for active and passive configurations.
We call \(\mathcal {L}_{\textsf{POGS}}\) the LTS obtained by synchronizing \(\mathcal {L}_\textsf{PI}\), \(\mathcal {L}_{\textsf{PTy}}\) and \(\mathcal {L}_{\textsf{PDi}}\). We write \(\mathbb {P},\mathbb {Q}\in \textrm{Confs}_{\textsf{POGS}}\) the configurations of \(\mathcal {L}_{\textsf{POGS}}\). The Lassen tree of a term is then defined as the unfolding of the \(\mathcal {L}_{\textsf{POGS}}\) on the initial active configuration associated with this term.
Example 8
The Lassen trees (omitting the typing configurations) for \([\textsf{c}]\texttt{new}\ n \ \texttt{in}\ \lambda \_.n\) and \([\textsf{c}]\lambda \_.\texttt{new}\ n \ \texttt{in}\ n\) are given by:

Due to the condition \(\textsf{supp}(\textbf{p}) \subseteq \textsf{D}\) in
 , some configurations with terms in normal form do not have a corresponding Proponent transition. The dashed arrows correspond to \(\textsf{op}\) transitions that lead to such stuck configurations.
, some configurations with terms in normal form do not have a corresponding Proponent transition. The dashed arrows correspond to \(\textsf{op}\) transitions that lead to such stuck configurations.
4.2 Bipartite Bisimulations for \(\textsf{OGS}\) and \(\textsf{POGS}\)
We consider typed relations on passive and active configurations, that is, we require related configurations to have the same type. This means in particular that the environment components \(\gamma \) of the two configurations have the same domain. In addition to the typing, we also enforce that both sets of disclosed atoms are identical.
Definition 9
A bipartite bisimulation is a pair of relations \((\mathcal {R}_{Act},\mathcal {R}_{Pas})\) respectively on active and passive configurations, such that:
-
If \((\mathbb {G}_1,\mathbb {G}_2) \in \mathcal {R}_{Pas}\) then for all Opponent moves \(\textbf{o}\) and \(\mathbb {H}_1,\mathbb {H}_2\) such that
 and
and
 , we have \((\mathbb {H}_1,\mathbb {H}_2) \in \mathcal {R}_{Act}\).
, we have \((\mathbb {H}_1,\mathbb {H}_2) \in \mathcal {R}_{Act}\). -
If \((\mathbb {G}_1,\mathbb {G}_2) \in \mathcal {R}_{Act}\) then there exists a Proponent move \(\textbf{p}\) and \((\mathbb {H}_1,\mathbb {H}_2) \in \mathcal {R}_{Pas}\) such that
 and
and
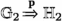 .
.
An \(\textsf{OGS}\)-bipartite bisimulation is a bipartite bisimulation defined over \(\mathcal {L}_{\textsf{OGS}}\), and a \(\textsf{POGS}\)-bipartite bisimulation is a bipartite bisimulation defined over \(\mathcal {L}_{\textsf{POGS}}\). We write \(\simeq _{\textsf{ogs}}\) and \(\simeq _{\textsf{pogs}}\) respectively for the greatest bipartite bisimulation respectively over \(\mathcal {L}_{\textsf{OGS}}\) and \(\mathcal {L}_{\textsf{POGS}}\).
The following property follows from the fact that the transition relation is deterministic (up to the choice of fresh names).
Lemma 10
\(\simeq _{\textsf{ogs}}\) coincides with trace equivalence on \(\textsf{OGS}\) configurations.
For \(\textsf{op}\) transitions, the difference between \(\textsf{OGS}\) and \(\textsf{POGS}\) shows up in the disclosing LTS: in
 , a \(\mathsf {D'}\) component can be chosen non-deterministically. This observation is related to the existential quantification in the second clause of Definition 13. Both in \(\mathcal {L}_{\textsf{OGS}}\) and \(\mathcal {L}_{\textsf{POGS}}\), there is only one possible next visible (Proponent) move. However, in \(\simeq _{\textsf{pogs}}\), the game involves choosing an appropriate set of atoms to be disclosed along
, a \(\mathsf {D'}\) component can be chosen non-deterministically. This observation is related to the existential quantification in the second clause of Definition 13. Both in \(\mathcal {L}_{\textsf{OGS}}\) and \(\mathcal {L}_{\textsf{POGS}}\), there is only one possible next visible (Proponent) move. However, in \(\simeq _{\textsf{pogs}}\), the game involves choosing an appropriate set of atoms to be disclosed along
 transitions. For instance, when constructing a \(\textsf{POGS}\) bipartite bisimulation between terms \(\texttt{new}\ n \ \texttt{in}\ \lambda \_.n\) and \(\lambda \_.\texttt{new}\ n \ \texttt{in}\ n\) from Example 8, we have two choices for the second step:
transitions. For instance, when constructing a \(\textsf{POGS}\) bipartite bisimulation between terms \(\texttt{new}\ n \ \texttt{in}\ \lambda \_.n\) and \(\lambda \_.\texttt{new}\ n \ \texttt{in}\ n\) from Example 8, we have two choices for the second step:
The latter does not satisfy the constraint on the disclosed set, since the sets are not the same in the two configurations. The former leads to a stuck configuration: \((\langle [\textsf{c}'](\lambda \_.\texttt{a})(), \{\texttt{a}\} \rangle ,\langle \{\texttt{a}\},\emptyset \rangle )\) cannot perform any Proponent move. Thus the two programs are not equivalent.
4.3 Deciding \(\simeq _{\textsf{pogs}}\)
We now study how to decide when two \(\textsf{POGS}\) configurations are bisimilar. First, trees generated by \(\mathcal {L}_{\textsf{POGS}}\) are of finite depth.
Lemma 11
Taking a \(\textsf{POGS}\) configuration \(\mathbb {G}\), any trace in \(\textbf{Tr}_{\textsf{POGS}}(\mathbb {G})\) is finite.
This lemma is proven using a biorthogonal logical predicate, following the use of biorthogonality to prove strong normalization of \(\lambda \mu \)-calculus [23], the computational metalanguage [18], and cut elimination for linear logic [8]. The proof can be found in [9].
Due to the non-determinism of atom generation in \(\mapsto _{\textsf{op}}\), of function name generation in
 , and of name picking in Opponent transitions, the trees generated by \(\mathcal {L}_{\textsf{POGS}}\) are infinitely branching. To tame this infinite branching, we see the set of moves \(\textrm{Moves}\) and the set of configurations \(\textrm{Confs}_{\textsf{POGS}}\) of \(\mathcal {L}_{\textsf{POGS}}\) as nominal sets [7] over atoms, function and continuation variables. So taking \(\pi \) a finite permutation over these sets, we write \(\pi * X\) for the action of permutation \(\pi \) over elements of nominal set X. The transition relation
, and of name picking in Opponent transitions, the trees generated by \(\mathcal {L}_{\textsf{POGS}}\) are infinitely branching. To tame this infinite branching, we see the set of moves \(\textrm{Moves}\) and the set of configurations \(\textrm{Confs}_{\textsf{POGS}}\) of \(\mathcal {L}_{\textsf{POGS}}\) as nominal sets [7] over atoms, function and continuation variables. So taking \(\pi \) a finite permutation over these sets, we write \(\pi * X\) for the action of permutation \(\pi \) over elements of nominal set X. The transition relation
 of \(\mathcal {L}_{\textsf{POGS}}\) preserves this action of permutation, i.e., it is equivariant: if
of \(\mathcal {L}_{\textsf{POGS}}\) preserves this action of permutation, i.e., it is equivariant: if
 then for all finite permutation \(\pi \), we have
then for all finite permutation \(\pi \), we have
 .
.
One can then consider a variant \(\mathcal {L}_{\textsf{DPOGS}}\) of the \(\textsf{POGS}\) LTS which uses the same set of configurations as \(\mathcal {L}_{\textsf{POGS}}\), but whose transition relation \(\xrightarrow {}_{\textsf{dpogs}}\) chooses fresh atoms and names deterministically. So \(\xrightarrow {}_{\textsf{dpogs}}\) is then deterministic on \(\textsf{op}\) and Proponent actions, and finitely branching on Opponent actions.
We remark at this point that the notion of bipartite bisimulation \(\simeq _{\textsf{pogs}}\) introduced in Definition 13 is not suited for \(\mathcal {L}_{\textsf{DPOGS}}\). Indeed, it requires equality of actions in the bisimulation game, and also that configurations related by bisimulation have the same type. So we relax the definition of \(\simeq _{\textsf{pogs}}\) and work with ternary relations, adding a finite permutation of names and atoms in order to match the actions, rather than enforcing syntactic equality.
Definition 12
A relation \(\mathcal {R}\subseteq \textrm{Confs}_{\textsf{POGS}}\times \textrm{Confs}_{\textsf{POGS}}\times \textrm{Perm}\) is said to be valid when, for all \(((\mathbb {I},\mathbb {S},\langle \_,\textsf{D} \rangle ), (\mathbb {J},\mathbb {T},\langle \_,\mathsf {D'} \rangle ),\pi ) \in \mathcal {R}\), we have \(\mathbb {T}= \pi * \mathbb {S}\) and \(\mathsf {D'}= \pi * \textsf{D}\).
Definition 13
A relaxed bipartite bisimulation is a pair of valid relations \((\mathcal {R}_{Act},\mathcal {R}_{Pas})\) respectively on active and passive configurations such that:
-
If \((\mathbb {P}_1,\mathbb {P}_2,\pi ) \in \mathcal {R}_{Pas}\) then for all Opponent moves \(\textbf{o}_1,\textbf{o}_2\), permutation \(\pi '\) extending \(\pi \), and active \(\textsf{POGS}\) configurations \(\mathbb {Q}_1,\mathbb {Q}_2\) satisfying \(\textbf{o}_2 = \pi '* \textbf{o}_1\),
 and
and
 , we have \((\mathbb {Q}_1,\mathbb {Q}_2,\pi ') \in \mathcal {R}_{Act}\).
, we have \((\mathbb {Q}_1,\mathbb {Q}_2,\pi ') \in \mathcal {R}_{Act}\). -
If \((\mathbb {P}_1,\mathbb {P}_2,\pi ) \in \mathcal {R}_{Act}\) then there exists a permutation \(\pi '\) extending \(\pi \), two Proponent moves \(\textbf{p}_1, \textbf{p}_2\) s.t. \(\textbf{p}_2 = \pi '*\textbf{p}_1\), and two passive \(\textsf{POGS}\) configurations \(\mathbb {Q}_1,\mathbb {Q}_2\) such that \((\mathbb {Q}_1,\mathbb {Q}_2,\pi ') \in \mathcal {R}_{Pas}\),
 and
and
 .
.
We write \(\simeq _{\textsf{pogs}}^{r}\) for the greatest relaxed bipartite bisimulation over \(\mathcal {L}_{\textsf{POGS}}\). From the fact that
 is equivariant, we deduce that \(\simeq _{\textsf{pogs}}^{r}\) and \(\simeq _{\textsf{ogs}}\) coincide. Since \(\mathcal {L}_{\textsf{DPOGS}}\) generates finite Lassen trees, we deduce that the bisimulation game can be decided.
is equivariant, we deduce that \(\simeq _{\textsf{pogs}}^{r}\) and \(\simeq _{\textsf{ogs}}\) coincide. Since \(\mathcal {L}_{\textsf{DPOGS}}\) generates finite Lassen trees, we deduce that the bisimulation game can be decided.
Theorem 14
Taking two \(\textsf{POGS}\) configurations \(\mathbb {P},\mathbb {Q}\), we can decide if \(\mathbb {P}\simeq _{\textsf{pogs}}\mathbb {Q}\).
4.4 Relating the Transitions in \(\textsf{OGS}\) and \(\textsf{POGS}\)
To relate the transitions in the \(\textsf{OGS}\) and in the \(\textsf{POGS}\), we need to introduce some relations and operations on \(\textsf{OGS}\) configurations.
Definition 15
Let \(\mathbb {G}= (\mathbb {I},\mathbb {S},\langle \texttt{L};\textsf{D} \rangle )\) and \(\mathbb {H}= (\mathbb {I},\mathbb {S},\langle \texttt{L};\textsf{D}' \rangle )\) be two \(\textsf{OGS}\) configurations. We write \(\mathbb {G}\subseteq _{\textsf{Di}}\mathbb {H}\) when \(\textsf{D}\subseteq \textsf{D}'\).
When \(\mathbb {G}\subseteq _{\textsf{Di}}\mathbb {H}\), the configurations only differ by their set of disclosed atoms.
Lemma 16
If \(\mathbb {G}\subseteq _{\textsf{Di}}\mathbb {H}\) and
 then
then
 and \(\mathbb {G}' \subseteq _{\textsf{Di}}\mathbb {H}'\).
and \(\mathbb {G}' \subseteq _{\textsf{Di}}\mathbb {H}'\).
Lemma 17
Let \(\mathbb {P}\) be an active prime configuration. We have the following:
-
if
 , then
, then
 ,
, -
if
 , then
, then
 .
.
In \(\textsf{POGS}\), the disclosed set increases in \(\textsf{op}\) transitions as seen above, but not in \(\textbf{p}\) transitions. In a sense, disclosing in \(\textsf{OGS}\) is done only when needed, whereas in \(\textsf{POGS}\), disclosing must be declared as soon as the atom is created. This is ensured by the additional condition \(\textsf{supp}(\textbf{p})\subseteq \textsf{D}\) in the rule for
 .
.
Lemma 18
When
 with \(\mathbb {P}\) active, we also have
with \(\mathbb {P}\) active, we also have
 .
.
However, the converse does not always hold, specifically if an atom has been declared non-disclosed but still appears in the action \(\textbf{p}\). Indeed, the transition
 is valid for \(\textsf{OGS}\), but has no counterpart in \(\textsf{POGS}\), since \(\langle \texttt{L};\emptyset \rangle \) cannot make the transition
is valid for \(\textsf{OGS}\), but has no counterpart in \(\textsf{POGS}\), since \(\langle \texttt{L};\emptyset \rangle \) cannot make the transition
 .
.
Using the following notion of limit (on \(\textsf{OGS}\) configurations), we can intuitively replace \(\textsf{D}\) by its minimal extension, preventing this phenomenon from happening.
Definition 19
Given a configuration \(\mathbb {G}=(\mathbb {I},\mathbb {S},\langle \texttt{L};\textsf{D} \rangle )\), we define its limit as:

We have that \(\mathbb {G}\subseteq _{\textsf{Di}}\textbf{lim}(\mathbb {G})\) and \(\textbf{lim}\) is idempotent. We call limit configurations those configurations that are a limit (or alternatively, that are their own limit). Being a limit configuration is preserved by moves but not necessarily by \(\textsf{op}\).
Lemma 20
Let \(\mathbb {P}\) be a limit configuration. If
 , then
, then
 .
.
For Opponent transitions, the situation is less simple since not all active \(\textsf{OGS}\) configurations are active \(\textsf{POGS}\) configurations. To circumvent that issue, we reuse the tensor product from [12]. For two \(\textsf{OGS}\) configurations where at least one is passive, we define the tensor product, written \(\otimes \), as follows:

The side conditions for the \(\texttt{L}\) and \(\textsf{D}\) components ensure that no shared atom is disclosed on one configuration but not the other.
We can then describe an active \(\textsf{OGS}\) configuration as the tensor of two \(\textsf{POGS}\) configurations (where \(\texttt{S}= \widehat{\texttt{L}})\):

Finally, we have the following property for opponent transitions:
Lemma 21
When
 , we have
, we have
 .
.
When
 , we have
, we have
 with \(\mathbb {G}= \mathbb {Q}\otimes \mathbb {P}\).
with \(\mathbb {G}= \mathbb {Q}\otimes \mathbb {P}\).
5 Relating Bisimilarities in \(\textsf{OGS}\) and \(\textsf{POGS}\)
In this section, we show that \(\simeq _{\textsf{pogs}}\) can be used to characterize \(\simeq _{\textsf{ogs}}\) for the limit configurations introduced above. We rely for that on up-to techniques for bipartite bisimulation in \(\textsf{OGS}\), which we introduce first.
5.1 Up-to techniques for \(\simeq _{\textsf{ogs}}\)
The proofs in this section use the theory of compatible functions [25, 27]. More details can be found in [9].
Definition 22 (Bipartite bisimulation up-to)
Given a function f, a bipartite bisimulation up to f is a pair \((\mathcal {R}_{Act},\mathcal {R}_{Pas})\) such that:
-
If \((\mathbb {G}_1,\mathbb {G}_2) \in \mathcal {R}_{Pas}\) then for all Opponent moves \(\textbf{o}\) and \(\mathbb {H}_1,\mathbb {H}_2\) such that
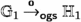 and
and
 , we have \((\mathbb {H}_1,\mathbb {H}_2) \in f(\mathcal {R}_{Act})\).
, we have \((\mathbb {H}_1,\mathbb {H}_2) \in f(\mathcal {R}_{Act})\). -
If \((\mathbb {G}_1,\mathbb {G}_2) \in \mathcal {R}_{Act}\) then there exists a Proponent move \(\textbf{p}\) and \((\mathbb {H}_1,\mathbb {H}_2) \in f(\mathcal {R}_{Pas})\) such that
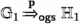 and
and
 .
.
We then define \(\texttt{hide}(\mathcal {R}_{Act}, \mathcal {R}_{Pas}) \triangleq (\subseteq _{\textsf{Di}}\mathrel {\mathcal {R}_{Act}} \supseteq _{\textsf{Di}},\; \subseteq _{\textsf{Di}}\mathrel {\mathcal {R}_{Pas}} \supseteq _{\textsf{Di}})\). Recall that we still require that \(\texttt{hide}(\mathcal {R}_{Act}, \mathcal {R}_{Pas})\) only contains pairs of configurations with the same disclosed set. The soundness of \(\texttt{hide}\) can be proved using Lemma 16.
Lemma 23
\(\texttt{hide}\) is a sound up-to technique, i.e. if \((\mathcal {R}_{Act},\mathcal {R}_{Pas})\) is a bisimulation up to \(\texttt{hide}\), then \((\mathcal {R}_{Act},\mathcal {R}_{Pas}) \subseteq \simeq _{\textsf{ogs}}\).
Given a pair of relations \((\mathcal {R}_{Act}, \mathcal {R}_{Pas})\) on active and passive \(\textsf{OGS}\) configurations respectively, we define the following functions:

Lemma 24
\(\texttt{split}(\simeq _{\textsf{ogs}}) \subseteq \simeq _{\textsf{ogs}}\).
\(\texttt{tensor}\) is not a sound up-to technique. It is nevertheless useful to reason about \(\textsf{POGS}\) bipartite bisimilar configurations; see Theorem 30 below.
5.2 Properties of the Limit (in \(\textsf{OGS}\))
Lemma 25
If \(\mathbb {G}\) is passive and
 , then there exists \(\mathbb {G}'\) such that \(\mathbb {G}\otimes \mathbb {G}' \subseteq _{\textsf{Di}}\mathbb {H}\).
, then there exists \(\mathbb {G}'\) such that \(\mathbb {G}\otimes \mathbb {G}' \subseteq _{\textsf{Di}}\mathbb {H}\).
Lemma 25 shows that transitions can only increase the substitution and the store (corresponding to the \(\mathbb {G}'\) component), and the set of disclosed atoms (represented by the use of \(\subseteq _{\textsf{Di}}\)). More precisely, \(\subseteq _{\textsf{Di}}\) is required if some atoms from \(\mathbb {G}\) are disclosed along the trace \(\textbf{t}\), in which case new ones can appear in \(\mathbb {G}'\).
Lemma 25 is language specific. It does not hold when the language allows the content of the store to be modified (like, e.g. in \(\lambda \mu _{\texttt{ref}}\)). Additionally, LTSs enforcing some local restriction on the usage of function or continuation names usually have extra components that are modified along the transitions; we return to this point in Section 7.
In a limit configuration (Definition 19), all atoms that may be disclosed at some point are disclosed. By Lemma 25, these atoms can be disclosed using a single trace.
Lemma 26
Given a passive configuration \(\mathbb {G}\), there exists a trace \(\textbf{t}\) and a configuration \(\mathbb {H}\) such that
 .
.
The limit is also useful to relate transitions in \(\textsf{OGS}\) and in \(\textsf{POGS}\) as follows.
Lemma 27
Take a \(\textsf{POGS}\) configuration \(\mathbb {P}\).
If \(\mathbb {P}\) is active and
 , then
, then
 .
.
If \(\mathbb {P}\) is passive and
 , then
, then
 .
.
All in all, we obtain that \(\simeq _{\textsf{ogs}}\) is a congruence for \(\textbf{lim}\). For \(\mathcal {R}\) a relation over configurations, we write \(\textbf{lim}(\mathcal {R})\) for the set \(\{(\textbf{lim}(\mathbb {G}),\textbf{lim}(\mathbb {H})) \mid (\mathbb {G}, \mathbb {H}) \in \mathcal {R}\}\).
Lemma 28
\(\simeq _{\textsf{ogs}}\) is closed by computing the limit: \(\textbf{lim}(\simeq _{\textsf{ogs}}){\subseteq }\simeq _{\textsf{ogs}}\).
The case for passive configurations follows immediately from Lemmas 26 and 24.
The property of the limit might make us think that the disclosure process of an atom could be decided statically, by annotating \(\texttt{new}\) syntactically. The following example shows that it is not the case:
Either n or m will be disclosed depending on the boolean b given by Opponent, but never both. So this term is indeed contextually equivalent to \(\lambda b.\texttt{new}\ n \ \texttt{in}\ \lambda \_.n\).
5.3 Correspondence Between \(\simeq _{\textsf{ogs}}\) and \(\simeq _{\textsf{pogs}}\)
Theorem 29
(From \(\simeq _{\textsf{ogs}}\) to \(\simeq _{\textsf{pogs}}\)). Consider two \(\textsf{POGS}\) configurations \(\mathbb {P}\) and \(\mathbb {Q}\). If \(\mathbb {P}\simeq _{\textsf{ogs}}\mathbb {Q}\) are both limit configurations, then \(\mathbb {P}\simeq _{\textsf{pogs}}\mathbb {Q}\).
To reason about bisimilar \(\textsf{POGS}\) configurations, we use the closure of \(\texttt{tensor}\), written \(\mathtt {\widetilde{tensor}}\). Intuitively, \(\mathtt {\widetilde{tensor}}(\mathcal {R}_{Act})\) contains the pairs \((\mathbb {G}_1 \otimes \mathbb {G}_2, \mathbb {H}_1 \otimes \mathbb {H}_2)\) with \( (\mathbb {G}_1,\mathbb {H}_1)\in \mathcal {R}_{Act}\), \((\mathbb {G}_2,\mathbb {H}_2)\in \mathtt {\widetilde{tensor}}(\mathcal {R}_{Pas})\), and \(\mathtt {\widetilde{tensor}}(\mathcal {R}_{Pas})\) contains the pairs \((\mathbb {G}_1 \otimes \mathbb {G}_2, \mathbb {H}_1 \otimes \mathbb {H}_2)\) with \( (\mathbb {G}_1,\mathbb {H}_1)\in \mathcal {R}_{Pas}\), \((\mathbb {G}_2,\mathbb {H}_2)\in \mathtt {\widetilde{tensor}}(\mathcal {R}_{Pas})\).
Theorem 30
(From \(\simeq _{\textsf{pogs}}\) to \(\simeq _{\textsf{ogs}}\)). Suppose \(\mathcal {R}\) is a \(\textsf{POGS}\) bipartite bisimulation. Then \(\mathtt {\widetilde{tensor}}(\mathcal {R})\) is a \(\textsf{OGS}\) bipartite bisimulation up-to hiding.
By Lemma 23, Theorem 30 means that if \(\mathbb {P}\simeq _{\textsf{pogs}}\mathbb {Q}\), then \(\mathbb {P}\simeq _{\textsf{ogs}}\mathbb {Q}\).
The correspondence between \(\simeq _{\textsf{ogs}}\) and \(\simeq _{\textsf{pogs}}\) is restricted to prime configurations as \(\simeq _{\textsf{pogs}}\) can only relate those. Having the additional conditions of configurations being limits is enough for our decidability result.
6 Related Work
The \(\nu \)-calculus was introduced in [24], together with logical relations to reason over contextual equivalence for this language. These logical relations use a Kripke-style definition, worlds being defined as spans of atoms to keep track of the disclosed atoms, similar to the permutation we use in our relaxed bipartite bisimulations. They capture contextual equivalence for programs of first order type, but are an incomplete technique for higher-order programs. This entails a decidability result for the first-order fragment of the \(\nu \)-calculus, since logical relations only quantify over finite objects at first-order types.
Categorical models of the \(\nu \)-calculus were provided in [29, 30], using a representation of name creation via a strong monad. Two examples of such models were given: (i) the functor category \(Set^{I}\) with I the category of finite sets and injection; (ii) the category \(\textbf{B}G\) of continuous G-sets, with G the topological group of automorphisms over \(\mathbb {N}\). None of these models are fully-abstract, since they distinguish \(\texttt{new}\ n \ \texttt{in}\ \lambda x.x= n\) from \(\lambda x.\texttt{false}\).
These models were later refined using nominal sets [7], so that types are interpreted via Fraenkel-Mostowski sets [28] or domains [14]. Both of these works are continuation models; they might be used to provide a semantics for the \(\lambda \mu \nu \)-calculus studied in this paper, a direction we wish to explore in future work. Such use of continuations was justified in [28] to provide a model for an extension of the \(\nu \)-calculus with recursion. More recently, proof-relevant logical relations were introduced to deal with recursion in the presence of name generation [4].
In [26], a model of the \(\nu \)-calculus is given in quasi-Borel spaces, showing a correspondence between random sampling and fresh name generation. This model is shown to be fully-abstract for terms of first-order types.
In [5], environmental bisimulations for the \(\nu \)-calculus are defined and shown to be fully abstract. Nevertheless, it does not seem possible to extract a decision procedure from that result, since environmental bisimulations are played over a higher-order LTS, that is, an LTS whose actions contain \(\lambda \)-terms. So this LTS is infinitely branching at higher-order types.
Eager normal-form bisimulations have been introduced by Lassen for the call-by-value \(\lambda \)-calculus [16] and \(\lambda \mu \)-calculus. In [31], a notion of bisimulation similar to \(\simeq _{\textsf{ogs}}\) is introduced and shown to be fully abstract for an untyped version of \(\lambda \mu _{\texttt{ref}}\). Compared to the standard notion of eager normal form bisimulations, the configurations in the bisimulations in [31] contain an environment similar to the environment component \(\gamma \) of the \(\textsf{OGS}\) LTS in Section 3.
In [1], a fully-abstract game model is provided for the \(\nu \)-calculus. However, this model requires an extensional collapse, that is not directly computable at higher-order type. So that model could only be used to prove the decidability of contextual equivalence for terms of first-order types. Enforcing a well-bracketed and visible behavior for Opponent in the \(\textsf{OGS}\) model, we believe that our trace model would coincide with the intentional game model of [1]. Nominal game semantics was developed for languages with nominal references and exceptions in [32]. In that setting, algorithmic presentations of game semantics make it possible to provide a classification of decidability of call-by-value languages with (bounded) integer references [19], and ground references [21]. In this setting, the undecidability of contextual equivalence originates from the use of integer references by Proponent. A detailed survey on the literature on contextual equivalence for the \(\nu \)-calculus is available in [33].
7 Conclusion
To decide the contextual equivalence between two \(\lambda \mu \nu \) typed terms \(\texttt{M}\) and \(\texttt{N}\) with contexts in the \(\lambda \mu _{\texttt{ref}}\)-calculus, we first construct the corresponding initial configurations, and we can decide by Thm. 14 if they are POGS-bisimilar. This decidability result comes from the fact that the POGS LTS generates finite trees.
Then, we prove in Thm. 29 and Thm. 30 that two initial active configurations are POGS-bisimilar iff they are OGS-bisimilar. This is possible because initial configurations are prime (they are active and \(\gamma \) is empty) and are also limit configurations (their disclosed sets contain all the atoms of the store). In Thm. 7 and Lemma 10, we prove that \(\texttt{M}\) and \(\texttt{N}\) are contextually equivalent iff the corresponding initial configurations are OGS-bisimilar, which yields decidability.
We now examine the obstacles that remain to prove the decidability of con- textual equivalence with contexts in the \(\nu \)-calculus.
First of all, in that setting, trace equivalence would not be fully-abstract anymore (Thm. 7). Indeed, without integer references, one cannot observe the sequentiality of calls and returns. So an extensional collapse would be necessary.
Another obstacle is that in the absence of higher-order references, Opponent must satisfy a condition of O-visibility [2], that corresponds to a local well-scoping discipline, for the function names it is allowed to call. Working in an intuitionistic type system, corresponding to the standard \(\lambda \)-calculus without control operators, the call-and-return discipline of the interaction between Proponent and Opponent has to be well-bracketed. These two conditions, namely O-visibility and well-bracketing, can be enforced operationally [13] in the LTS, by keeping track of part of the history of the interaction. However the reduction of \(\simeq _{\textsf{ogs}}\) to \(\simeq _{\textsf{pogs}}\) is not possible anymore in that setting. Indeed, the limit over-approximates the set of atoms that can be tested. This can be seen when comparing the programs
Assuming n is immediately disclosed makes it possible to distinguish the two programs. Because the local conditions of well-bracketing or visibility would prevent Opponent from playing some actions, Opponent could perform irreversible changes that would invalidate Lemma 25. This would make \(\simeq _{\textsf{pogs}}\) incomplete.
To handle this difficulty, we could try and use Kripke eager normal-form bisimulation [11], using a structure for worlds richer than just a set of atoms.
Finally, in absence of full ground references, that can store locations, atoms played by Opponent would also follow a local well-scoping discipline, but the discriminatory power over Player atoms would also be restricted [20]. In such a setting, the same difficulties as with well-bracketing and O-visibility would arise, and a more complex extensional collapse would be needed.
References
Samson Abramsky, Dan R. Ghica, Andrzej S. Murawski, C.-H. Luke Ong, and Ian David Bede Stark. Nominal games and full abstraction for the nu-calculus. In 19th IEEE Symposium on Logic in Computer Science (LICS 2004), 14-17 July 2004, Turku, Finland, Proceedings, pages 150–159. IEEE Computer Society, 2004.
Samson Abramsky, Kohei Honda, and Guy McCusker. A fully abstract game semantics for general references. In Thirteenth Annual IEEE Symposium on Logic in Computer Science, Indianapolis, Indiana, USA, June 21-24, 1998, pages 334–344. IEEE Computer Society, 1998.
Hendrik Pieter Barendregt. The lambda calculus - its syntax and semantics, volume 103 of Studies in logic and the foundations of mathematics. North-Holland, 1985.
Nick Benton, Martin Hofmann, and Vivek Nigam. Proof-relevant logical relations for name generation. Log. Methods Comput. Sci., 14(1), 2018.
Nick Benton and Vasileios Koutavas. A mechanized bisimulation for the nu-calculus. Higher Order and Symbolic Computation - Special Issue in Honor of Mitchell Wand, sep 2012. In Press.
Corrado Böhm. Alcune proprieta delle forme \(\beta \)-\(\eta \)-normali nel \(\lambda \)-k-calcolo. Pubblicazioni dell’Istituto per le Applicazioni del Calcolo, 696:19, 1968.
Murdoch Gabbay and Andrew M. Pitts. A new approach to abstract syntax with variable binding. Formal Aspects Comput., 13(3-5):341–363, 2002.
Jean-Yves Girard. Linear logic. Theor. Comput. Sci., 50:1–102, 1987.
Daniel Hirschkoff, Guilhem Jaber, and Enguerrand Prebet. Deciding contextual equivalence of \(\nu \)-calculus with effectful contexts (full version). https://hal.science/hal-03955303.
Guilhem Jaber and Andrzej S. Murawski. Complete trace models of state and control. In Nobuko Yoshida, editor, Programming Languages and Systems - 30th European Symposium on Programming, ESOP 2021, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2021, Luxembourg City, Luxembourg, March 27 - April 1, 2021, Proceedings, volume 12648 of Lecture Notes in Computer Science, pages 348–374. Springer, 2021.
Guilhem Jaber and Andrzej S. Murawski. Compositional relational reasoning via operational game semantics. In 36th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2021, Rome, Italy, June 29 - July 2, 2021, pages 1–13. IEEE, 2021.
Guilhem Jaber and Davide Sangiorgi. Games, mobile processes, and functions. In Florin Manea and Alex Simpson, editors, 30th EACSL Annual Conference on Computer Science Logic, CSL 2022, February 14-19, 2022, Göttingen, Germany (Virtual Conference), volume 216 of LIPIcs, pages 25:1–25:18. Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2022.
James Laird. A fully abstract trace semantics for general references. In Lars Arge, Christian Cachin, Tomasz Jurdzinski, and Andrzej Tarlecki, editors, Automata, Languages and Programming, 34th International Colloquium, ICALP 2007, Wroclaw, Poland, July 9-13, 2007, Proceedings, volume 4596 of Lecture Notes in Computer Science, pages 667–679. Springer, 2007.
James Laird. Sequentiality and the CPS semantics of fresh names. In Marcelo Fiore, editor, Proceedings of the 23rd Conference on the Mathematical Foundations of Programming Semantics, MFPS 2007, New Orleans, LA, USA, April 11-14, 2007, volume 173 of Electronic Notes in Theoretical Computer Science, pages 203–219. Elsevier, 2007.
James Laird. A Curry-style semantics of interaction: From untyped to second-order lazy \(\lambda \)\(\mu \)-calculus. In Jean Goubault-Larrecq and Barbara König, editors, Foundations of Software Science and Computation Structures - 23rd International Conference, FOSSACS 2020, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2020, Dublin, Ireland, April 25-30, 2020, Proceedings, volume 12077 of Lecture Notes in Computer Science, pages 422–441. Springer, 2020.
Søren B. Lassen. Eager normal form bisimulation. In 20th IEEE Symposium on Logic in Computer Science (LICS 2005), 26-29 June 2005, Chicago, IL, USA, Proceedings, pages 345–354. IEEE Computer Society, 2005.
Søren B. Lassen and Paul Blain Levy. Typed normal form bisimulation. In Jacques Duparc and Thomas A. Henzinger, editors, Computer Science Logic, 21st International Workshop, CSL 2007, 16th Annual Conference of the EACSL, Lausanne, Switzerland, September 11-15, 2007, Proceedings, volume 4646 of Lecture Notes in Computer Science, pages 283–297. Springer, 2007.
Sam Lindley and Ian Stark. Reducibility and tt-lifting for computation types. In Pawel Urzyczyn, editor, Typed Lambda Calculi and Applications, 7th International Conference, TLCA 2005, Nara, Japan, April 21-23, 2005, Proceedings, volume 3461 of Lecture Notes in Computer Science, pages 262–277. Springer, 2005.
Andrzej S. Murawski and Nikos Tzevelekos. Algorithmic nominal game semantics. In Gilles Barthe, editor, Programming Languages and Systems - 20th European Symposium on Programming, ESOP 2011, Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2011, Saarbrücken, Germany, March 26-April 3, 2011. Proceedings, volume 6602 of Lecture Notes in Computer Science, pages 419–438. Springer, 2011.
Andrzej S. Murawski and Nikos Tzevelekos. Full abstraction for reduced ML. Ann. Pure Appl. Log., 164(11):1118–1143, 2013.
Andrzej S. Murawski and Nikos Tzevelekos. Algorithmic games for full ground references. Formal Methods Syst. Des., 52(3):277–314, 2018.
Michel Parigot. Lambda-mu-calculus: An algorithmic interpretation of classical natural deduction. In Andrei Voronkov, editor, Logic Programming and Automated Reasoning,International Conference LPAR’92, St. Petersburg, Russia, July 15-20, 1992, Proceedings, volume 624 of Lecture Notes in Computer Science, pages 190–201. Springer, 1992.
Michel Parigot. Strong normalization for second order classical natural deduction. In Proceedings of the Eighth Annual Symposium on Logic in Computer Science (LICS ’93), Montreal, Canada, June 19-23, 1993, pages 39–46. IEEE Computer Society, 1993.
Andrew M. Pitts and Ian David Bede Stark. Observable properties of higher order functions that dynamically create local names, or what’s new? In Andrzej M. Borzyszkowski and Stefan Sokolowski, editors, Mathematical Foundations of Computer Science 1993, 18th International Symposium, MFCS’93, Gdansk, Poland, August 30 - September 3, 1993, Proceedings, volume 711 of Lecture Notes in Computer Science, pages 122–141. Springer, 1993.
D. Pous and D. Sangiorgi. Advanced Topics in Bisimulation and Coinduction (D. Sangiorgi and J. Rutten editors), chapter Enhancements of the coinductive proof method. Cambridge University Press, 2011.
Marcin Sabok, Sam Staton, Dario Stein, and Michael Wolman. Probabilistic programming semantics for name generation. Proc. ACM Program. Lang., 5(POPL):1–29, 2021.
Davide Sangiorgi. On the bisimulation proof method. Mathematical Structures in Computer Science, 8(5):447–479, 1998.
Mark R. Shinwell and Andrew M. Pitts. On a monadic semantics for freshness. Theor. Comput. Sci., 342(1):28–55, 2005.
Ian Stark. Names and Higher-Order Functions. PhD thesis, University of Cambridge, December 1994. Also available as Technical Report 363, University of Cambridge Computer Laboratory.
Ian Stark. Categorical models for local names. LISP Symb. Comput., 9(1):77–107, 1996.
Kristian Støvring and Søren B. Lassen. A complete, co-inductive syntactic theory of sequential control and state. In Jens Palsberg, editor, Semantics and Algebraic Specification, Essays Dedicated to Peter D. Mosses on the Occasion of His 60th Birthday, volume 5700 of Lecture Notes in Computer Science, pages 329–375. Springer, 2009.
Nikos Tzevelekos. Nominal Game Semantics. PhD thesis, University of Oxford, 2009.
Nikos Tzevelekos. Program equivalence with names. In Amal Ahmed, Nick Benton, Lars Birkedal, and Martin Hofmann, editors, Modelling, Controlling and Reasoning About State, 29.08. - 03.09.2010, volume 10351 of Dagstuhl Seminar Proceedings. Schloss Dagstuhl - Leibniz-Zentrum für Informatik, Germany, 2010.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Hirschkoff, D., Jaber, G., Prebet, E. (2023). Deciding Contextual Equivalence of \(\nu \)-Calculus with Effectful Contexts. In: Kupferman, O., Sobocinski, P. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2023. Lecture Notes in Computer Science, vol 13992. Springer, Cham. https://doi.org/10.1007/978-3-031-30829-1_2
Download citation
DOI: https://doi.org/10.1007/978-3-031-30829-1_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-30828-4
Online ISBN: 978-3-031-30829-1
eBook Packages: Computer ScienceComputer Science (R0)












 and
and
 , we have
, we have  and
and
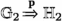 .
. and
and
 , we have
, we have  and
and
 .
. , then
, then
 ,
, , then
, then
 .
.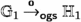 and
and
 , we have
, we have 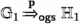 and
and
 .
.