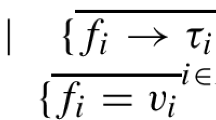Calculating Datastructures

Abstract

Where do datastructures come from? This paper explores how to systematically derive implementations of one-sided flexible arrays from a simple reference implementation. Using the dependently typed programming language Agda, each calculation constructs an isomorphic—yet more efficient—datastructure using only a handful of laws relating types and arithmetic. Although these calculations do not generally produce novel datastructures they do give insight into how certain datastructures arise and how different implementations are related.

1 Introduction

There is a rich field of program calculation, deriving a program systematically from its specification. In this paper, we explore a slightly different problem: showing how efficient datastructures can be derived from an inefficient reference implementation. In particular, we consider how to derive implementations of one-sided flexible arrays, a datastructure that offers efficient indexing without being limited to store only a fixed number of elements. Although we do not claim to invent new datastructures by means of our calculations, we can demystify the definitions of familiar datastructures, providing a constructive rationalization identifying the key design choices that are made.

In contrast to program calculation, relating a program and its specification, the calculation of datastructures requires relating two different types. As it turns out, we show how to calculate efficient implementations that are isomorphic to our reference implementation. These calculations rely exclusively on familiar laws of types and arithmetic. Indeed, we have formalised these calculations in the dependently typed programming language and proof assistant Agda. While we present our derivations in quite some detail, we occassionally will refer to the accompanying source code for a more complete account; while not provable in the current type theory underlying Agda, we will occassionally assume the axiom of functional extensionality.

After defining the interface of flexible arrays (Sect. 2), we will define the Peano natural numbers (Sect. 3), leading to a first reference implementation of flexible arrays (Sect. 4). Starting from this reference implementation, we compute an isomorphic, yet inefficient, datastructure (Sect. 5). By shifting to a more efficient (binary) number representation (Sect. 6), we can define a similar reference implementation (Sect. 7). Using this second reference implementation, we once again compute an isomorphic datastructure (Sect. 8)—but in this case several alternative choices exist (Sects. 9 & 10).

2 One-sided Flexible Arrays

Consider the following interface for one-sided flexible arrays:

An array of type stores $\textit{n}$ elements of type $\textit{elem}$, for some natural number $\textit{n}$. For the moment, we leave the type of natural numbers abstract. In what follows, we explore different implementations of arrays by varying the implementation of the natural number type.

We require flexible arrays to be isomorphic to functions from some finite set of indices to the $\textit{elem}$ type. The $\textit{lookup}$ function witnesses one direction of the isomorphism, $\textit{tabulate}$ the other.

$$\begin{aligned} lookup\,(tabulate\,f)&\equiv f \end{aligned}$$

(1a)

$$\begin{aligned} tabulate\,(lookup\,a)&\equiv a \end{aligned}$$

(1b)

In what follows, we refer to functions with a finite domain, that is functions of the form $\{i\,:\,\mathbb {N}\,\mid \, i<n\}\rightarrow \,elem$, as finite maps.

In contrast to traditional fixed-size arrays, one-sided flexible arrays can be extended at the front using the $\textit{cons}$ operation. Non-empty arrays can be shrunk with $\textit{tail}$, discarding the first element. The following properties specify the interplay of indexing and the other operations that modify the size of the array.

$$\begin{aligned} \textit{lookup}\,(\textit{cons}\,\textit{x}\,\textit{xs})\,0&\equiv \textit{x} \end{aligned}$$

(2a)

$$\begin{aligned} \textit{lookup}\,(\textit{cons}\,\textit{x}\,\textit{xs})\,(1\,{+}\,\textit{i})&\equiv \textit{lookup}\,\textit{xs}\,\textit{i} \end{aligned}$$

(2b)

$$\begin{aligned} \textit{head}\,\textit{xs}&\equiv \textit{lookup}\,\textit{xs}\,0 \end{aligned}$$

(2c)

$$\begin{aligned} \textit{lookup}\,(\textit{tail}\,\textit{xs})\,\textit{i}&\equiv \textit{lookup}\,\textit{xs}\,(1\,{+}\,\textit{i}) \end{aligned}$$

(2d)

To define any implementation of this interface, we first need to settle on the implementation of the natural number type. The most obvious choice is, of course, Peano’s representation. Once we have this in place, we can explore different implementations of the $\textit{Array}$ type.

3 Peano Numerals

To calculate an implementation of flexible arrays we proceed in two steps. First, we fix an indexing scheme by defining a type of natural numbers below some fixed, upper bound. Such an indexing scheme fixes the domain of our finite maps, $\{\textit{i}\,\mid \,\textit{i}\,{<}\,\textit{n}\}$. Next, we calculate a more efficient representation of finite maps, yielding a datastructure rather than a function. This section details the ideas underlying the first step using the simplest representation of natural numbers; in Sect. 5, we explore the second step.

3.1 Number Type

The datatype of Peano numerals describes the set of natural numbers as the least set containing $\textit{zero}$ that is closed under a $\textit{succ}$essor operation.

We use variable names such as $\textit{k}$, $\textit{m}$, and $\textit{n}$ to range over Peano numerals and use the Arabic numerals to denote $\textit{Peano}$ constants, writing $3$ rather than $\textit{succ}\,(\textit{succ}\,(\textit{succ}\,\textit{zero}))$.

The operations doubling and incrementing natural numbers, needed in Sect. 6.1, illustrate how to define functions (by induction) in Agda.¹

The underscores indicate that all three functions are written postfix.

3.2 Index Type

Having fixed the number type, we move on to define the type of valid indices in an $\textit{Array}$ of size $\textit{n}$. Here we have several alternatives, each with its own advantages and disadvantages. The most obvious transcription of $\{\textit{i}\,\mid \,\textit{i}\,{<}\,\textit{n}\}$ uses a dependent pair or $\varSigma$ type to combine a natural number and a proof that it is within bounds:

Here ${<}$ denotes the strict ordering on the naturals. While the definition is fairly straightforward, it is somewhat cumbersome to use in practice as any computation on indices involves manipulations of proofs. Before discussing alternative definitions, let us first explore some properties of the $\textit{Index}$ type.

The formulas link arithmetic on numbers to operations on types, with the number $0$ corresponding to the empty set (written $\bot$ in Agda), $1$ to a singleton set (written $\top$), addition to disjoint union (written $\uplus$), multiplication to cartesian product (written $\times$), and, finally, exponentiation to the function space. We refer to these laws as index transformations.

For example, the sum rule $\textit{Index-}{+}$ is witnessed by a mapping between indices for a pair of arrays and indices for a single array, as suggested below.

More instructively, the product rule, $\textit{Index-}{*}$, is witnessed by a mapping between indices for a two-dimensional array and indices for a one-dimensional array.

In general, there is not a single canonical witness for an index transformation. The diagram on the left above exemplifies what is known as row-major order, but there is also column-major order, shown on the right. For now, we choose to ignore these specifics. However, when we start calculating datastructures the choice of isomorphism becomes tremendously important, a point we return to in Sect. 6.2.

Remark 1 (Categorical background)

To provide some background, the type function $\textit{Index}$ is the object part of a functor from the preorder of natural numbers to the category of finite sets and total functions. (This is why the type is also known as $\textit{Fin}$ or $\textit{FinSet}$.) The action of the functor on arrows embeds $\textit{Index}\,\textit{m}$ into $\textit{Index}\,\textit{n}$, provided $m\preccurlyeq n$. In fact, the isomorphisms demonstrate that $\textit{Index}$ is simultaneously a strong monoidal functor of type $(\mathbb {N}, 0, +) \rightarrow (Set, \bot , \uplus )$ and a strong monoidal functor of type $(\mathbb {N}, 1, \cdot ) \rightarrow (Set, \top , \times )$.    $\square$

Returning to the issue of defining the $\textit{Index}$ type in Agda, we can use the isomorphisms above to determine the index set by pattern matching on the natural number $\textit{n}$.

The zero rule $\textit{Index-}0$ determines that the $\textit{Index}\,(0)$ type is uninhabited; whereas the rules for one and addition, $\textit{Index-}1$ and $\textit{Index-}{+}$, determine that $\textit{Index}\,(\textit{succ}\,\textit{n})$ contains one more element than $\textit{Index}\,\textit{n}$.

For reasons of readability, we turn the definition of $\textit{Index}$ into idiomatic Agda, replacing the type function by an inductively defined indexed datatype.

There are no constructors for $\textit{Index}\,\textit{zero}$, corresponding to the first equation of $\textit{Index}$, and two constructors for $\textit{Index}\,(\textit{succ}\,\textit{n})$, corresponding to $\textit{Index}$’s second equation. The constructor names are almost identical to those of $\textit{Peano}$. This is intentional: we want the constructors of $\textit{Index}$ to look and behave like their namesakes. The only difference is that the former carry vital type information about upper bounds. Reassuringly, all three definitions of index sets are equivalent. The straightforward, but rather technical proofs can be found in the accompanying material.

To illustrate working with indices, let us implement some index transformations that are needed later in Sect. 6.2.

The second operation combines doubling and increment. The “obvious” definition, $i\cdot 2+1= isucc(i\cdot 2+0)$ does not work, as the expression on the right-hand side has type $Index(n\cdot 2+1)$ and not $Index(n\cdot 2)$, as required. On plain naturals we can separate doubling and increment; here we need to combine the operations to be able to establish precise upper bounds. We cannot expect Agda to automatically replicate the hand-written proof:

$$\begin{aligned} i \prec n \quad \Longleftrightarrow \quad i + 1 \preccurlyeq n \quad \Longleftrightarrow \quad (i + 1) \cdot 2 \preccurlyeq n \cdot 2 \quad \Longleftrightarrow \quad i \cdot 2 + 1 \prec n \cdot 2\, . \end{aligned}$$

In general, since $\textit{Index}$ combines data and proof, index transformations require more work than their vanilla counterparts on naturals.

Now that we have a precise understanding of the domain of our finite maps, we can start calculating an implementation of the interface specified in Sect. 2.

4 Functions as Datastructures

The simplest implementation of the $\textit{Array}$ type identifies arrays and finite maps:

In this particular case, $\textit{lookup}$ and $\textit{tabulate}$ are manifest identities, rather than isomorphisms.

To complete this “implementation”, however, we still need to define the remaining operations: $\textit{nil}$, $\textit{cons}$, $\textit{head}$, and $\textit{tail}$. The empty array $\textit{nil}$ is the unique function from the empty set, defined below using an absurd pattern, written $()$. For the other functions, the specification serves as the implementation, for example, (2a) and (2b) form the definition of $\textit{cons}$, given that $\textit{lookup}$ is implemented as the identity function.

The proofs that the “implementation” satisfies the specification are consequently trivial: all the specified equivalences hold by definition.

While the “implementation” is exceptionally simple, it is also exceptionally slow: the running time of $\textit{lookup}\,\textit{xs}\,\textit{i}$ is not only determined by the index $\textit{i}$ but also by the number of operations used to build the array $\textit{xs}$. For example, even though $\textit{tail}\,(\textit{cons}\,\textit{x}\,\textit{xs})$ is extensionally equal to $\textit{xs}$, each lookup takes two additional steps as the index is first incremented by $\textit{tail}$ only to be subsequently decremented by $\textit{cons}$. In other words, the run-time behaviour of $\textit{lookup}$ is sensitive to how the array has been constructed! To avoid this problem, we turn functions into datastructures, using this “implementation” above as our starting point. Finding a suitable datastructure is the topic of the coming section.

5 Lists Also Known as Vectors

Do you remember the laws of exponents from secondary school?

$$\begin{aligned} X^0&= 1&X^1&= X&\\ X^{A + B}&= X^A \cdot X^B&X^{A \cdot B}&= \left( X^B\right) ^A \end{aligned}$$

Quite amazingly, these equalities can be re-interpreted as isomorphisms between types, where $B^A$ is the type of functions from A to B.

If we apply these isomorphisms from left to right, perhaps repeatedly, we can systematically eliminate function spaces. This process might be called defunctionalization or trieification, except that the former term is already taken.

Some background is perhaps not amiss. A trie is also known as a digital search tree. In a conventional search tree, the search path is determined on the fly by comparing a given key against the sign posts stored in the inner nodes. By contrast, in a digital search tree, the key is the search path. This idea is, of course, not limited to searching. The point of this paper is that it applies equally well to indexing: the index or position of an element within an array is a path into the datastructure that represents the array.

Remark 2 (Categorical background)

A lot more can be said about trieification: functors of the form $\textit{A}\,\rightarrow \,\textit{X}$ are contravariant in $\textit{A}$, and part of an adjoint situation, sending left adjoints (initial objects $\bot$, coproducts $\uplus$, initial algebras) to right adjoints (terminal objects $\top$, products $\times$, final coalgebras) [2, 15].    $\square$

That’s enough words for the moment, calculemus! We will now show how to derive an alternative implementation of the $\textit{Array}$ type. To trieify our type of finite maps,

we proceed by induction on the size of the array $\textit{n}$. For the derivation, we use Wim Feijen’s proof format, which features explicit justifications for the calculational steps, written between angle brackets. While the notation may be familiar, it is worth pointing out that each of our calculations is a valid Agda term, constructing the desired isomorphism. The Agda type-checker verifies that each step provides the evidence to establish the desired isomorphism. The justification for each individual step can be rather verbose: for example, the first rewrite below is justified by an isomorphism between function spaces: $dom\cong \rightarrow \cong \,cod$ applies the isomorphism $\textit{dom}$ to the domain of its function argument and $\textit{cod}$ to its codomain.

The calculation suggests a defining equation: $Array\,zero\,elem=\top$, which expresses that there is exactly one array of size $0$, namely the empty array. For non empty arrays, the calculation is almost just as straightforward.

The final isomorphism expresses that an array of size $1\,{+}\,\textit{n}$ consists of an element followed by an array of size $\textit{n}$. If we name the constructors appropriately, we obtain the familiar datatype of lists, indexed by length. This indexed type is also known as $\textit{Vector}$.

Observe that the constructors of the interface, $\textit{nil}$ and $\textit{cons}$, are now implemented by the constructors of the datatype.

If we extract the two components of the $\textit{trieify}$ isomorphism, we obtain the following definitions of $\textit{lookup}$ and $\textit{tabulate}$.

Like $\textit{trieify}$, both $\textit{lookup}$ and $\textit{tabulate}$ are defined by induction on the size. In the case of $\textit{lookup}$, the size information remains implicit as Agda is able to recreate it from the explicit argument, namely, the argument list. For $\textit{tabulate}$, no such information is available. Hence, we need to match on the implicit argument explicitly in its definition.

Unfortunately, Agda’s extraction process is only semi-automatic, so we do not trust the resulting code. The proofs that $\textit{lookup}$ and $\textit{tabulate}$ are inverses are, however, entirely straightforward and can be found in the accompanying material.

The equations for $\textit{head}$ and $\textit{tail}$ are immediate consequences of the specification.

Thanks to our reference implementation, see Sect. 4, the proof of correctness is a breeze: we simply show that the “concrete” operations on vectors are equivalent to their “specification” on finite maps. Defining a shortcut for the $\textit{lookup}$ function, , the proof obligations read as follows.

$$\begin{aligned} \llbracket nil\rrbracket&\equiv FM.nil \end{aligned}$$

(3a)

$$\begin{aligned} \llbracket cons\, x\,xs\rrbracket&\equiv FM.cons\,x\llbracket xs\rrbracket \end{aligned}$$

(3b)

$$\begin{aligned} head\,xs&\equiv FM.head\llbracket xs\rrbracket \end{aligned}$$

(3c)

$$\begin{aligned} \llbracket tail\, xs\rrbracket&\equiv FM.tail\llbracket xs\rrbracket \end{aligned}$$

(3d)

$$\begin{aligned} lookup\,xs&\equiv FM.lookup\llbracket xs\rrbracket \end{aligned}$$

(3e)

$$\begin{aligned} \llbracket tabulate\,f \rrbracket&\equiv FM.tabulate\,f \end{aligned}$$

(3f)

Here we have prefixed the operations of the reference implementation of Sect. 4 by $\textit{FM}$, short for ‘finite map’. Recalling that $\textit{FM.lookup}$ and $\textit{FM.tabulate}$ are both the identity function, Property (3e) means that $\textit{lookup}$ is indeed extensionally equal to the implementation using finite maps. Conversely, as (3f) shows, the $\textit{tabulate}$ is the right-inverse of $\textit{lookup}$, which is unique.

The vector implementation of arrays does not suffer from history-sensitivity, $\textit{tail}\,(\textit{cons}\,\textit{x}\,\textit{xs})$ is now definitionally equal to $\textit{xs}$, but thanks to the ivory tower number type, it is still too slow to be useful in practice. The cure is pretty obvious: we replace unary numbers by binary numbers—albeit with a twist.

6 Leibniz Numerals

Instead of working with Peano naturals, we could choose a different implementation of the natural number type. In this section, we will explore one possible implementation, Leibniz numbers, or binary numbers that have a unique representation of every Peano natural number.

6.1 Number Type

A Leibniz numeral is given by a sequence of digits with the most significant digit on the left. A digit is either $\texttt{1}$ or $\texttt{2}$.

Agda’s postfix syntax allows us to mimic standard notation for binary numbers: the expression $\texttt{0}b\,\texttt{1}\,\texttt{1}\,\texttt{2}\,\texttt{1}$ should be read as $(((\texttt{0}b\,\texttt{1})\,\texttt{1})\,\texttt{2})\,\texttt{1}$.

To assign a meaning to a Leibniz numeral, we map it to a Peano numeral.

For example, normalizes to 17. The meaning function makes it crystal clear that we implement a base-two positional number system, except that the digits $\texttt{1}$ and $\texttt{2}$ are used, rather than $\texttt{0}$ and $\texttt{1}$.

Thanks to this twist we avoid the problem of leading zeros: every natural number enjoys a unique representation; the Leibniz number system is non-redundant. Moreover, the meaning function establishes a one-to-one correspondence between the two number systems: $Leibniz\cong Peano$. Speaking of number conversion, the other direction of the isomorphism can be easily implemented using the “pseudo-constructors” $\textit{zero}$ and $\textit{succ}$.

The binary increment exhibits the typical recursion pattern: the least significant digit is incremented, unless it is maximal, in which case a carry is propagated to the left. Using the meaning function it is straightforward to show that the implementation is correct.

The prefix “pseudo” indicates that the operations $\textit{zero}$ and $\textit{succ}$ are not full-fledged constructors: we cannot use them in patterns on the left-hand side of definitions. To compensate for this, we additionally offer a Peano view [21, 31].

The $\textit{view}$ function itself illustrates the use of view patterns.

In a sense, $\textit{view}$ combines two functions: the test for zero and the predecessor function, again following the typical recursion pattern: the least significant digit is decremented, unless it is minimal, in which case we borrow one from the left.

The semantics of such a view is defined by a mapping into the Peano numerals. The correctness criterion asserts that $\textit{view}$ does not change the value of its argument.

Remark 3 (Agda)

You may wonder why the type $\textit{Peano-View}$ is indexed by a Leibniz numeral. Why not simply define:

In contrast to the simple, unindexed datatype above, our indexed view type keeps track of the to-be-viewed value, which turns out to be vital for correctness proofs: if $\textit{view}\,\textit{n}$ yields $\textit{as-succ}\,\textit{m}$ then we know that $\textit{n}$ definitionally equals $\textit{succ}\,\textit{m}$. The constructors of the unindexed datatype do not maintain this important piece of information, so the subsequent proofs do not go through.    $\square$

As an intermediate summary, Leibniz numerals serve as a drop-in replacement for Peano numerals: the pseudo-constructors replace $\textit{zero}$ and $\textit{succ}$ on the right-hand side of equations; the view allows us to additionally replace them in patterns on the left-hand side.

6.2 Index Type

Of course, we would like to use binary numbers for indices, as well. Therefore we need to adapt the type of positions that specifies the domain of our finite maps. The following derivation is based on the index transformations but, as we have noted in Sect. 3, there are, in general, several options for the witnesses of these transformations. In other words, we have to make some design decisions! In particular, since we use a binary, positional number system we need to inject life into the doubling isomorphism:

There are two canonical choices, one based on appending and a second one based on zipping or interleaving.

If the size is an exact power of two, halving separates the indices based on the most significant bit, whereas unzipping considers the least significant bit. (As an aside, do not be confused by the names: $\textit{append}$, $\textit{zip}$ etc. are index transformations, not operations on arrays.) Both choices are viable, however, we choose to initially focus on the first alternative and return to the second in Sect. 12, but only briefly.

Zipping maps elements of the first summand to even indices and elements of the second to odd indices.

Its inverse amounts to division by 2 with the remainder specifying the summand of the disjoint union.

Given these prerequisites the calculation of

proceeds by induction on the structure of Leibniz numerals. For the base case, there is little to do.

The calculation for the first inductive case also works without any surprises.

We plug in the definition of $\textit{Peano.Index}$, apply the doubling isomorphism based on zipping, and finally invoke the induction hypothesis. The derivation for the final case follows exactly the same pattern, except that we unfold the definition of $\textit{Peano.Index}$ twice.

As usual, we introduce names for the summands of the disjoint unions, obtaining the following index type for Leibniz numerals. Note that these indices are not the same as the $\textit{Index}$ type we saw previously, indexed by a Peano number.

A couple of remarks are in order. The index attached to the constructor names indicates the least significant digit of the upper bound. The constructors $\texttt{0}b_1$ and $\texttt{0}b_2$ say: “Operationally we are alike, both representing the zeroth index. However, we carry important type information, $\texttt{0}b_1$ lives below an odd upper bound, whereas $\texttt{0}b_2$ is below an even bound.” The definition of the index set is perhaps not quite what we expected as it amalgamates two different number systems: the by now familiar $\texttt{1}\hbox {-}\texttt{2}$ system and a variant that employs $\texttt{0}$ and $\texttt{1}$ as leading digits and $\texttt{2}$ and $\texttt{3}$ for non-leading digits.

Remark 4

As an aside, the $\texttt{2}\hbox {-}\texttt{3}$ number system is also non-redundant. In general, any binary system that uses the digits 0, ..., a in the leading position and $a+1$ and $a+2$ for the other positions, enjoys the property that every natural number has a unique representation.    $\square$

To make the semantics of these indices precise, we extract the witness for the reverse direction of the $\textit{re-index}$ing isomorphism (using $\textit{iz}$ and $\textit{is}$ as shorthands for $\textit{izero}$ and $\textit{isucc}$ on Peano indices).

Just as we saw in Sect. 3, the expressions $n\,\cdot \,2+1$ and $is\,(n\,\cdot \, 2+0)$ are quite different as they live below different upper bounds: if $j:Index \,a$, then $j \cdot 2+1 : Index(a \cdot 2)$, whereas $is(j \cdot 2+0) : Index(a \cdot 2+1)$. These types carry just enough information to avoid the infamous “index out of bounds” errors. While the definitions of $\textit{Index}$ and may seem quite bulky at first glance, they encode an essential invariant of the indices involved.

The same remark applies to the definition of $\textit{izero}$ and $\textit{isucc}$.

The successor function maps an odd number to an even number, and vice versa, correspondingly incrementing the upper bounds. Consequently, arguments and results alternate between the two number systems. This is why $isucc(i\texttt{2}_2)$ yields $(isucc\,i)\texttt{1}_1$, rather than $i\texttt{3}_2$. The recursion pattern is interesting: if the argument is below an odd bound, $\textit{isucc}$ returns immediately; a recursive call is only made for indices that live below an even upper bound. We return to this observation in Sect. 8.

Using the meaning function we can establish the correctness of $\textit{izero}$ and $\textit{isucc}$.

Both equations relate expressions of different types, for example, $\mathscr {I}\llbracket isucc\,i \rrbracket \,:\,\mathscr {N}\llbracket succ\,n \rrbracket$ whereas $is\mathscr {I}\llbracket i \rrbracket \,:\,\mathscr {N}\llbracket \,n \rrbracket +1$. Fortunately, $\textit{succ-correct}$ tells us that both types are propositionally equal.²

You may have noticed that this section replicates the structure of Sect. 6.1. It remains to define an appropriate view on Leibniz indices.

The type $\textit{Index-View}$ is implicitly parametrized by a Leibniz numeral $\textit{n}$ and explicitly parametrized by a Leibniz index of type $\textit{Index}\,(\textit{succ}\,\textit{n})$. To use this view, we still need to define a function mapping (Leibniz) indices to their corresponding $\textit{Index-View}$. To do so, we need to decide when a given index is zero, and compute the index’s predecessor when it is not. The definition of the view function merits careful study.

Recall that the Peano view combines the test for zero and the predecessor function. The same is true of $\textit{iview}$, except that arguments and results additionally alternate between the two number systems.

Finally, given the semantics of view patterns we can assert that $\textit{iview}$ does not change the value of its argument.

7 Functions as Datastructures, Revisited

To showcase the use of our new gadgets we adapt the implementation of Sect. 4 to binary indices, setting $Array\, n\,elem=Index\,n\rightarrow elem$.

As in the Peano case, “functions as datastructures” serve as our reference implementation for datastructures based on Leibniz numerals. With this specification in place, we can now try to discover a corresponding datastructure.

8 One-two Trees

Turning to the heart of the matter, let us trieify the type of finite maps based on binary indices.

The strategy should be clear: as in Sect. 5, we eliminate the type of finite maps using the laws of exponents. The base case is identical to the one for lists.

The calculation for the inductive cases follows the same rhythm—we unfold the definition of $\textit{Index}$ and apply the laws of exponents—except that we additionally invoke the induction hypothesis.

The final step in the isomorphism above expresses that an array of size $n\cdot 2+1$ consists of an element followed by two arrays of size $\textit{n}$. The isomorphism for arrays of size $n\cdot 2+2$ follows a similar pattern.

An array of size $n\cdot 2+2$ consists of two elements followed by two arrays of size $\textit{n}$. All in all, we obtain the following datatype. Its elements are called one-two trees³ for want of a better name.

As an aside, Agda like Haskell prefers curried data constructors over uncurried ones. The following equivalent definition that uses pairs shows more clearly that one-two trees are modelled after the $\texttt{1}$-$\texttt{2}$ number system,

where $A^1=A$ and $A^2=A\times A$.

Turning to the operations on one-two trees, we first extract the witnesses of the $\textit{trieify}$ isomorphism, obtaining human-readable definitions of $\textit{lookup}$ and $\textit{tabulate}$.

The implementation of $\textit{lookup}$ nicely illustrates the central idea of tries, where the index serves as a path into the tree. The least significant digit selects the node component. If the component is a sub-tree, then $\textit{lookup}$ recurses. The diagrams below visualize the indexing scheme.

A one-node corresponds to the digit  , a two-node corresponds to $\texttt{2}$. Conversely, the $\textit{tabulate}$ function computes the array corresponding to a given finite map.

For example, yields the tree depicted below.

A couple of remarks are in order. By definition, one-two trees are not only size-balanced, they are also height-balanced—the height corresponds to the length of the binary representation of the size. The binary decomposition of the size fully determines the shape of the tree; all the nodes on one level have the same “shape”; the digits determine this shape from bottom to top. In the example above, implies that the nodes on the third level (from bottom to top) are two-nodes, whereas the other nodes are one-nodes. There are $2^{3}$ nodes on the bottom level, witnessing the weight of the most significant digit.

Turning to the size-changing operations, $\textit{cons}$ is based on the binary increment. Recall that $\textit{succ}$ alternates between odd and even numbers. Accordingly, $\textit{cons}$ alternates between one- and two-nodes.

A one-node is turned into a two-node. Dually, a two-node becomes a one-node; the two surplus elements are pushed into the two sub-trees. Observe that the recursion pattern of $\textit{succ}$ dictates the recursion pattern of $\textit{cons}$, that is, whether we stop or recurse. The definition of $\textit{isucc}$ dictates the layout of the data. For example, the first component of $Node_1$ becomes the second component of $Node_2$. You may want to view a two-node as a small buffer. Consing an element to a one-node allocates the buffer; consing a further element causes the buffer to overflow.

It is also possible to derive the implementation of $\textit{cons}$ from the specification (2a)–(2b). However, as the argument is based on positions and the $\textit{Index}$ type comprises seven constructors, the calculations are rather lengthy, but wholly unsurprising, so they have been relegated to Appendix A.

Fig. 1.

One-two trees of shape $\texttt{0}b\,\texttt{1}\,\texttt{2}\,\texttt{2}$ up to $\texttt{0}b\,\texttt{1}\,\texttt{1}\,\texttt{1}\,\texttt{1}$.

Figure 1 shows a succession of one-two trees obtained by consing 4, 3, 2, 1, and 0 (in this order) to . In every second step, $\textit{cons}$ touches only the root node. However, every once in a while the entire tree is rewritten, corresponding to a cascading carry. In Fig. 1, this happens in the final step when a tree of size $\texttt{0}b\,\texttt{2}\,\texttt{2}\,\texttt{2}$ is turned into a tree of size $\texttt{0}b\,\texttt{1}\,\texttt{1}\,\texttt{1}\,\texttt{1}$.

Consequently, the worst-case running time of $\textit{cons}$ is $\varTheta (n)$. However, like the binary increment, consing shows a more favourable behaviour if a sequence of operations is taken into account: $\textit{cons}$ runs in $\varTheta (\log n)$ amortized time. This is less favourable than $\textit{succ}$, which runs in constant amortized time. The reason is simple: for each carry $\textit{succ}$ makes one recursive call, whereas $\textit{cons}$ features two calls so a carry propagation takes time proportional to the weight of the digit. We return to this point in Sect. 10.

The operations $\textit{head}$ and $\textit{tail}$ basically undo the changes of $\textit{cons}$.

As an attractive alternative to these operations we also introduce a list view, analogous to the Peano view on binary numbers.

Observe that the list view is indexed by the Peano view. The view function itself illustrates the use of view patterns.

The first and the last equation are straightforward, in particular, removing an element from a two-node yields a one-node. Following this logic, removing an element from a one-node gives a zero-node—except that our datatype does not feature this node type. Consequently, we need to borrow data from the sub-trees. To this end, a view is simultaneously placed on the size and the two sub-trees—a typical usage pattern.

The implementation of arrays using one-two trees can be shown correct with respect to our reference implementation in Sect. 7. The steps are completely analogous to the line of action in Sect. 5, but we have elided the details for reasons of space.

Remark 5 (Haskell)

It is instructive to translate the Agda code into a language such as Haskell that does not support dependent types. The datatype definition is almost the same, except that the size index is dropped.

If we represent the element of the index type by plain integers, then we need to translate the index patterns. This can be done in a fairly straightforward manner using guards and integer division.

A more sophisticated alternative is to replace each constructor of $\textit{Index}$ by a pattern synonym [27].

As the interface considered in this paper is rather narrow, there is no need to maintain the size of trees at run-time. However, if size information is needed, it can be computed on the fly,

in logarithmic time.    $\square$

9 Braun Trees

The derivation of the Leibniz index type in Sect. 6.2 and its associated trie type in Sect. 8 are entirely straightforward. Too straightforward, perhaps? This section and the next highlight the decision points and investigate alternative designs.

9.1 Index Type, Revisited

The index type for Peano numerals enjoys an appealing property: its constructors look and behave like their Peano namesakes, indicated by the isomorphisms:

$$\begin{aligned} Peano \cong \top \,\uplus \,Peano&\qquad \quad Index\,(succ\,n) \cong \,\top \,\uplus \,Index\,(n)\,. \end{aligned}$$

The same cannot be said of Leibniz indices. The indices below an even bound are based on $\texttt{2}$-$\texttt{3}$ binary numbers, rather than the $\texttt{1}$-$\texttt{2}$ system we started with.

$$\begin{aligned} Leibniz \cong \,\top \,\uplus \,Leibniz\,\uplus \,Leibniz&\quad Index\,(n\,\texttt{2})\, \cong \,\top \,\uplus \,\top \,\uplus \,Index\,(n)\uplus \,Index(n) \end{aligned}$$

Can we re-work the isomorphism on the right so that it has the same shape as the one on the left, with three constructors instead of four?

Let’s calculate, revisiting the second inductive case.

At this point, we have applied the induction hypothesis in the original derivation. An alternative is to first join the second and third summands of the disjoint union, applying the re-indexing law $\textit{Index-succ}$ backwards from right to left.

Voilà Naming the anonymous summands, we arrive at the following, alternative index type for Leibniz numerals.

The datatype features two identical sets of constructors, one for indices below an odd upper bound and a second for indices below an even upper bound.

Having changed the index type, we need to adapt the operations on indices.

If we ignore the subscripts, the first three clauses of the successor function are identical to the last three clauses. Operationally, the constructors $\texttt{1}_1$ and $\texttt{1}_2$ are treated in exactly the same way. This is precisely what we have hoped for! (At the risk of dwelling on the obvious, even though the definition of $\textit{isucc}$ seems repetitive, it is not: the proofs relating the indices to their upper bounds are quite different.)

9.2 Trie Type, Revisited

The new index type gives rise to a new trie type. We only need to adapt the trieification for the second inductive case: $n\texttt{2}$. As in the original derivation, the steps are entirely straightforward—nothing surprising here.

Using this isomorphism, we obtain a variation of the 1–2 trees we constructed previously. Once again, we have three constructors, one for each constructor of the $\textit{Leibniz}$ data type; we have added a subscript attached to the node constructors to indicate the least significant digit of the upper bound ($\texttt{1}$ or $\texttt{2}$). The pattern of computing such datastructures should now be familiar.

A moment’s reflection reveals that we have rediscovered Braun trees [4, 17]. Recall that the size of a Braun tree determines its shape: a Braun tree of odd size ($n\texttt{1}$) consists of two sub-trees of the same size; in a Braun tree of even, non-zero size ($n\texttt{2}$) the left sub-tree is one element larger. As an aside, the property that the size determines the shape is shared by all our implementations of flexible arrays. It is a consequence of the fact that the container types are based on non-redundant number systems.

Similar to one-two threes, erm, trees, Braun trees feature two constructors for non-empty trees. However, in contrast to one-two trees, indexing is the same for both constructors. This becomes apparent if we extract the witnesses from the $\textit{trieify}$ ismorphism.

We make the same observation as for the successor function: if we ignore the subscripts, the first three clauses are identical to the last three clauses. In other words, the same indexing scheme applies to both varieties of inner nodes:

The definition of $\textit{tabulate}$ is similarly repetitive.

For example, the call yields the Braun tree shown below.

Here we observe the effect of the re-indexing isomorphism based on zipping or interleaving, see Sect. 6.2. Elements at odd positions are located in the left sub-tree, elements at even, non-zero positions in the right sub-tree.

There is, however, one problem with this definition. The $Node_2$ constructor has two subtrees: one of size $\textit{n}$, the other of size $\textit{succ}\,\textit{n}$. As a result, the (implicit) Leibniz number passed implicitly to the $\textit{tabulate}$ function is not obviously decreasing: one call is passed $\textit{n}$; the other is passed $\textit{succ}\,\textit{n}$. While the latter represents a smaller natural number, it is not a structurally smaller recursive call. As a result, Agda rejects this definition as it stands. There is a reasonably straightforward argument that we can make to guarantee termination—even if the recursion is not structural, it is well-founded: each recursive call is performed on a structurally smaller Peano number. In the remainder of this section, we will ignore such termination issues.

As before, the indexing scheme determines the implementation of the size-changing operations.

Fig. 2.

Braun trees of shape $\texttt{0}b\,\texttt{1}\,\texttt{2}\,\texttt{2}$ up to $\texttt{0}b\,\texttt{1}\,\texttt{1}\,\texttt{1}\,\texttt{1}$.

Consider the definition of $\textit{cons}$. Both recursive calls of $\textit{cons}$ are applied to the right sub-tree, additionally swapping left and right subtrees. Of course! Adding an element to the front requires re-indexing: elements that were at even positions before are now located at odd positions, and vice versa. Figure 2 shows $\textit{cons}$ in action, replicating Fig. 1 for Braun trees. Observe how the lowest level is gradually populated with elements. Can you identify a pattern?

Both one-two trees and Braun trees are based on the $\texttt{1}-\texttt{2}$ number system. To illustrate how intimately the two datastructures are related, consider the effect of two consecutive $\textit{cons}$ operations:

One-two trees may be characterized as lazy Braun trees: the first $\textit{cons}$ operation is in a sense delayed with the data stored in a two-node. The next $\textit{cons}$ forces the delayed call, issuing two recursive calls. By contrast, $\textit{cons}$ for Braun trees recurses immediately, but makes only a single call. However, after two steps—swapping the sub-trees twice—the net effect is the same. The strategy, lazy or eager, determines the performance: $\textit{cons}$ for Braun trees has a worst-case running time of $\varTheta (\log n)$, whereas $\textit{cons}$ for one-two trees achieves the logarithmic time bound only in an amortized sense.

In this paper, we focus on one-sided flexible arrays. Braun trees are actually more flexible (pun intended) as they also support extension at the rear—they implement two-sided flexible arrays. Through the lens of the interface, $\textit{cons}$ and $\textit{snoc}$⁴ are perfectly symmetric. However, due to the layout of the data, their implementation for Braun trees is quite different. If an element is attached to the front, the positions, odd or even, of the original elements change: sub-trees must be swapped. By contrast, if an element is added to the rear, nothing changes: the sub-trees must stay in place. Depending on the size of the array, the position of the new element is either located in the left or in the right sub-tree, see Fig. 2. Staring at the sequence of trees, the position of the last element, the number 14, may appear slightly chaotic. Perhaps this is worth a closer look. Consider the diagram on the left below. The numbers indicate the order in which the positions on the lowest level are filled.

By contrast, the diagram on the right displays the “standard”, left-to-right ordering. Comparing the diagrams, we observe that the positions of corresponding nodes are bit-reversals of each other, for example, position $6 = (110)_2$ on the left corresponds to $3 = (011)_2$ on the right. The reason is probably clear by now: the layout of Braun trees is based on zipping (indexing LSB first), whereas the “standard” layout is based on appending (indexing MSB first).

Turning to the implementation of $\textit{snoc}$, the code is pretty straightforward since the data constructors carry the required size information: if the original size is odd, the element is added to the left sub-tree, if the size is even, it is added to the right sub-tree.

As the relative order of ${x_0}, {l}, {r}, and~{x_n}$ must not be changed, each equation is actually forced upon us! (The power of dependent types is particularly tangible if the code is developed interactively.)

The implementation of $\textit{snoc}$ shows that the cases for $Node_1$ and $Node_2$ are not necessarily equal! This has consequences when porting the code to non-dependently typed languages such as Haskell—depending on the interface explicit size information may or may not be necessary.

Remark 6 (Haskell)

Continuing the discussion of Remark 5, let us again translate Agda into Haskell code. The implementation of $\textit{snoc}$ has demonstrated that we cannot simply identify $Node_1$ and $Node_2$. For a Haskell implementation there are at least three options:

• we identify the constructors $Node_1$ and $Node_2$ but maintain explicit size information, either locally in each node or globally for the entire tree; or

• we identify the two constructors and recreate the size information on the fly—this can be done in $\varTheta (\log ^2 n)$ time [23]; or

• we faithfully copy the Agda code at the cost of some code duplication.

If we rather arbitrarily select the second option,

the implementation of $\textit{lookup}$ is short and sweet,

whereas the definition of $\textit{snoc}$ is more involved.

Unfortunately, the running time of $\textit{snoc}$ degrades to $\varTheta (\log ^2 n)$, as it is dominated by the initial call to $\textit{size}$.    $\square$

10 Random-Access Lists

Both one-two trees and Braun trees are based on the binary $\texttt{1}$-$\texttt{2}$ number system: the types are tries for (two different) index sets; the operations are based on the arithmetic operations. Alas, as already noted, the operations on sequences do not quite achieve the efficiency of their arithmetic counterparts. While the binary increment runs in constant time (in an amortized sense), consing takes logarithmic time (amortized for one-two trees and worst-case for Braun trees).

The culprit is easy to identify: the $\textit{cons}$ operation makes two recursive calls for each carry (eagerly or lazily), whereas $\textit{incr}$ makes do with only one. There are two recursive calls as we introduced two recursive sub-trees when we invoked (an instance of) the sum law during triefication, see Sect. 8:

where $A\times 2=A\uplus A$ and $A^2=A\times A$. The isomorphism states that a finite map whose domain has an even size can be represented by two maps whose domains have half the size. If you know the laws of exponents by heart, then you may realize that this is not the only option. Alternatively, we could replace the finite map by a single map that yields pairs. The formal property is a combination of the product rule also known as currying, $law-of-exponents-\times$, and the sum rule:

Building on this isomorphism the trieification of the original index set of Sect. 6.2 proceeds as follows.

A similar calculation yields $Array(n\texttt{2})elem\cong \,elem\times elem\times \,Array\,n(elem^2)$ for the second inductive case.

All in all, we obtain the following datatype, which is known as the type of binary, random-access lists.

If we wish to emphasize that our new array type is modelled after the $\texttt{1}-\texttt{2}$ system, we might prefer the following equivalent definition:

where $A^1=A$ and $A^2=A\times A$.

Two remarks are in order. First, our binary numbers are written with the most significant digit on the left. For the array types above, we have reversed the order of bits, as this corresponds to the predominant, left-to-right reading order. Second, our final implementation of arrays is a so-called nested datatype [3], where the element type changes at each level. Indeed, a random-access list can be seen as a standard list, except that it contains an element, a pair of elements, a pair of pairs of elements, and so forth. Nested datatypes are also known as non-uniform datatypes [19] or non-regular datatypes [26].

The rest is probably routine by now. As usual, we extract the witnesses of the $\textit{trieify}$ isomorphism, $\textit{lookup}$ and $\textit{tabulate}$.

The call yields the random-access list shown below.

Now the elements appear sequentially from left to right. But wait! Isn’t our indexing scheme based on interleaving rather than appending as set out in Sect. 6.2? This is probably worth a closer look. Let us define a variant of $\textit{lookup}$ that takes its two arguments in reverse order and works on the primed variants of our arrays, defined on the previous page.

If we compare the implementation of $\textit{access}$ for one-two trees

to the one for random-access lists, If we compare the implementation of $\textit{access}$ for one-two trees

we make an interesting observation. The two projection functions are composed in a different order: $access\,i\cdot \,proj_1$ versus $proj_1 \cdot access\,i$. Of course! This reflects the change in the organisation of data: we have replaced a pair of sub-trees by a sub-tree of pairs. In more detail, the k-th tree of a random-access list corresponds to the k-th level of a one-two tree. As the access order is reversed, the corresponding sequences are bit-reversal permutations of each other. Consider, for example, the lowest level: $9\;13\;11\;15\;10\;14\;12\;16$ (one-two tree) is the bit-reversal permutation of $9\;10\;11\;12\;13\;14\;15\;16$ (random-access list).

It is time to reap the harvest. Since our new datastructure is list-like, $\textit{cons}$ makes do with one recursive call.

The implementation is truly modelled after the binary increment. This entails, in particular, that $\textit{cons}$ runs in constant amortized time. Figure 3 shows $\textit{cons}$ in action, mirroring Figs. 1 and 2. The drawings nicely reflect that a $\texttt{2}$ of weight $2^k$ is equivalent to a $\texttt{1}$ of weight $2^{k+1}$, see first and third diagram.

Fig. 3.

Random-access lists of shape $\texttt{0}b\,\texttt{1}\,\texttt{2}\,\texttt{2}$ up to $\texttt{0}b\,\texttt{1}\,\texttt{1}\,\texttt{1}\,{\texttt{1}}$.

If we flip the equations for $\textit{cons}$, we obtain implementations of $\textit{head}$ and $\textit{tail}$.

Observe that we need to make the implicit size arguments explicit, so that Agda is able to distinguish between a singleton array, first equation, and an array that contains at least three elements, third equation. We leave the definition of a suitable list view as the obligatory exercise to the reader (the solution can be found in the accompanying material).

Remark 7 (Haskell)

Translating the Agda code to Haskell poses little problems as Haskell supports nested datatypes,

and the definition of recursive functions over them.

Note that the definition is not typable in a standard Hindley-Milner system as the recursive call has type $Array(elem,elem)\rightarrow (Integer\rightarrow (elem,elem))$, which is a substitution instance of the declared type. The target language must support polymorphic recursion [22]. As typability in this system is undecidable [10], Haskell requires the programmer to provide an explicit type signature.    $\square$

Random-access lists outperform one-two trees and Braun trees. But, all that glitters is not gold: unlike their rival implementations, random-access lists do not support a $\textit{snoc}$ operation, extending the end of an array. For this added flexibility, we could “symmetrize” the design. The point of departure is a slightly weird number system that features two least significant digits, one at the front and another one at the rear. Inventing some syntax, $\texttt{1}\langle \texttt{2}\langle \texttt{0}\rangle \texttt{1}\rangle \texttt{1}$, for example, represents $1 + 2 \cdot (2 + 2 \cdot 0 + 1) + 1 = 8$. If we trieify a suitable index type based on this number system, we obtain so-called finger trees [5, 16]. But that’s a story to be told elsewhere.

11 Related Work

We are, of course, not the first to observe the connection between number systems and purely functional datastructures. This observation can be traced as far back as early work by Okasaki [24] and Hinze [11, 13]. Indeed, Okasaki writes “data structures that can be cast as numerical representations are surprisingly common, but only rarely is the connection to a number system noted explicitly”. This paper tries to provide a framework for making this connection explicit.

Nor are not the first to propose such a framework. McBride’s work on ornaments describes how to embellish a data type with additional information—and even how to transport functions over one data type to work on its ornamented extension. Typical examples include showing how lists arise from decorating natural numbers with additional information; vectors arise from indexing lists with their length. Ko and Gibbons [18] have shown how these ideas can be applied to describe how binomial heaps arise as ornaments on binary numbers. Similarly, binary random-access lists can be implemented systematically in Agda by indexing with a slight variaton of the binary numbers used in this paper [29]. Instead of using the Leibniz numbers presented here, this construction uses a more traditional ‘list of bits’ to represent binary numbers. The resulting representation is no longer unique, leading to many different representations of zero—and the empty binary random access list accordingly. Without such unique a representation, the isomorphisms described in this paper do not hold. This situation is typical in data refinement [25], where isomorphisms may form too strong a requirement for certain derivations to hold.

The datastructures described in this paper are instances of so-called Napierian functors [9], more commonly know as representable functors. By design each of our datastructures is isomorphic to a functor of the form $\textit{P}\,\rightarrow \,\textit{A}$, for some (fixed) type of positions $\textit{P}$. Indeed, this is the key $\textit{lookup}$-$\textit{tabulate}$ isomorphism that we use to calculate the different datastructures throughout this paper. Gibbons’s work on Napierian functors was driven by describing APL and enforcing size invariants in multiple dimensions. Although quad trees built from binary numbers are briefly mentioned, the different datastructures that can be calculated using positions built from binary numbers remains largely unexplored.

Nor are we the first to explore type isomorphisms. DiCosmo gives an overview of the field in his survey article [7]; Hinze and James have previously shown how to adapt an equational reasoning style to type isomorphisms, using a few principles from category theory. Recent work on homotopy type theory [30], where isomorphic types are guaranteed to be equivalent, might facilitate some of the derivations done in this paper, especially when establishing that operations such as $\textit{cons}$ are respected across isomorphic implementations [20].

There is a great deal of literature on datatype generic tries [12, 14, 15]. These tries exploit the same laws of exponentiation that we have used in this paper. Typically, these tries are used for memoising computations, trading time for space, whereas this paper uses the same laws in a novel context: the derivation of datastructures. These datatype generic tries have appeared in the context of dependent types when recognising languages [1, 8] and memoising computations [28]—but their usage is novel in this context.

12 Conclusion

This paper has uncovered several well known datastructures in a new way. The key technology—tries, number representations, and type isomorphisms—have been known for decades, yet the connection between isomorphic implementations of datastructures has never been made this explicitly. In doing so, we open the door for further derivations and exploration. The traditional $\texttt{0}-\texttt{1}$ number system for binary numbers, for example, will lead to a derivation of zero-one trees, leaf-oriented Braun trees, or $\texttt{0}-\texttt{1}$ random-access lists. Providing a generic solution, however, where the shift in number representation automatically computes new datastructures, remains a subject for further work. Similarly, we have chosen to restrict ourselves to a single size dimension—an obvious question now arises how these results may be extended to handle matrices and richer nested datastructures.

A A Deriving Operations

The definition of $\textit{cons}$ for one-two trees can be systematically inferred using the abstraction function that maps one-two trees to finite maps. The types dictate that $\textit{cons}$ applied to a one-node returns a two-node, so we need to solve the equation

$$\begin{aligned} \llbracket cons\,x_0(Node_1\,x_1\,l\,r)\rrbracket&\quad \equiv \quad \llbracket \,Node_2\,x_0^{\prime }\,x_1^{\prime }\,l^{\prime }\,r^{\prime }\rrbracket \end{aligned}$$

in the unknowns $x_0^{\prime }$, $x_1^{\prime }$, $l^{\prime }$, and $r^{\prime }$. To determine the components of the two-node, we conduct a case analysis on the indices, the arguments of the finite maps. The index $i\texttt{2}_2$, for example, determines the third component, the left sub-tree. The derivation works towards a situation where we can apply the specification of $\textit{cons}$ (2b). 2b

We may conclude that $l^{\prime }\equiv l$. The other cases are equally straightforward.

The equation for two-nodes

$$\begin{aligned} \llbracket cons\,x_0(Node_2\,x_1\,x_2\,l\,r)\rrbracket&\quad \equiv \quad \llbracket \,Node_1\,x_0^{\prime }l^{\prime }r^{\prime }\rrbracket \end{aligned}$$

is more interesting to solve. Consider the index $i^{\prime }\texttt{1}_1$ that determines the second component, the left sub-tree of the one-node. We need to conduct a further case distinction on $i^{\prime }$. Otherwise, Agda is not able to figure out the predecessor of $i^{'}\texttt{1}_1$, that the equation $isucc\,i=i^{\prime }\texttt{1}_1$ uniquely determines $\textit{i}$ for a given $i^{\prime }$. For the case analysis we use a combined Peano view, on binary numbers and on binary indices, dealing with the inductive case first.

We conclude that $l^{\prime }\equiv \,cons\,x_1\,l$. Again, the calculation is straightforward, except that it is not clear why the first element of $l^{\prime }$ has to be $x_1$. The answer is simple, the sub-case $\textit{as-isucc}$ fixes the tail of the sequence, its head is determined by the base case $\textit{as-izero}$. Actually, there are two base cases, featuring almost identical calculations that only differ in the type arguments. (The “problem” can be traced back to the definition of $\textit{izero}$, which is defined by case analysis on the size index).

The derivations confirm that $l^{\prime }\equiv \,cons\,x_1\,l$.

On a final note, the steps flagged $\textit{by-definition}$ may be omitted as Agda is able to confirm the equalities automatically. But, of course, the equational proofs are targetted at human readers. An after-the-fact proof that $\textit{cons}$ is correct is actually a three-liner, plus a trivial three-liner for (2a) and a straightforward seven-liner for (2b), but would be wholly unsuitable as a derivation.