Abstract
The problem that motivates the study of ‘hypernumbers’ in the next few essays comes from the prehistory of mathematics.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
See Dickson [24, vol. 2, p. 341], where the reference is to a work of Proclus.
- 2.
The statement that \(d_{n}^{2}=2s_{n}^{2}\pm 1\) implies \(d_{n+1}^{2}=2s_{n+1}^{2}\mp 1\) can be deduced from the formula \((2s+d)^{2}+d^{2}=2s^{2}+2(s+d)^{2}\), which is Proposition 10 of Book 2 of Euclid’s Elements [39], except that Euclid had no algebraic symbolism and expressed the equation in words rather than a formula. This proposition can be proved algebraically by noting that both sides are equal to \(4s^{2}+4sd+2d^{2}\) or can be deduced from the diagram
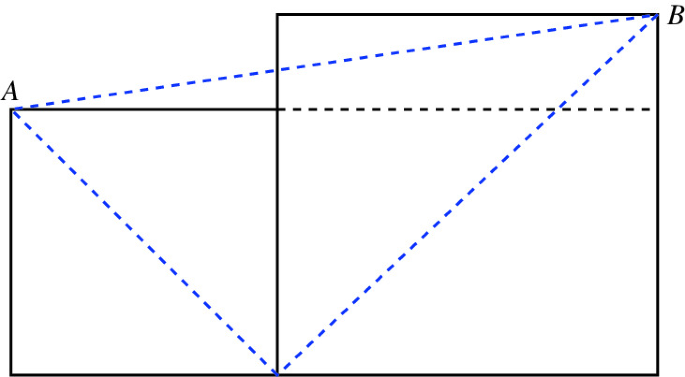
consisting of two squares, one with side s and one with side \(s+d\), resting side by side on a horizontal line with the smaller square on the left. Let A be the upper left vertex of the small square and let B be the upper right vertex of the large square. The desired identity comes from two ways of describing the square on the line segment AB. On the one hand, it is \(2s^{2}+2(s+d)^{2}\), because AB is the hypotenuse of the right triangle whose third vertex is diagonally opposite the vertices A and B in their respective squares. On the other hand, it is \((s+s+d)^{2}+d^{2}\), because AB is the hypotenuse of the right triangle whose third vertex is the point where the extension of the top side of the small square intersects the right side of the large square. Thus, \(d^{2}\ge 2s^{2}\) implies \((2s+d)^{2}\le 2(s+d)^{2}\) and \(2(s+d)^{2}-(2s+d)^{2}=d^{2}-2s^{2}\); in the same way, \(d^{2}\le 2s^{2}\) implies \((2s+d)^{2}-2(s+d)^{2}=2s^{2}-d^{2}\).
- 3.
When A is a square, the problem is to write the given B in the form \(s^{2}-t^{2}= (s-t)(s+t)\), where t is a multiple of the square root of A. Thus \(s-t=B_{1}\) and \(s+t=B_{2}\), where \(B=B_{1}B_{2}\) is one of the finite set of factorizations of B in which \(B_{1}\le B_{2}\). Since \(B_{1}+B_{2}=2s\) is even, the problem is thus to find all factorizations \(B_{1}B_{2}=B\), if any, in which \(B_{1}\le B_{2}, B_{1}\equiv B_{2}\,\textrm{mod}\, 2\), and \((B_{2}-B_{1})/2\) is a multiple of the square root of A. For each of them, \(\big (\frac{B_{1}+B_{2}}{2}\big )^2=\big (\frac{B_{1}-B_{2}}{2}\big )^2+B\) is a solution, and there are no others.
- 4.
See [18, p. 363]. The proof, using modern algebraic notation, is a simple calculation. How Brahmagupta might have proved it without algebraic notation—or how he might have known it is true—is a mystery. Certainly Euclid’s Proposition 10 of Book 2 (see note above) indicates a Greek awareness of a similar phenomenon many centuries earlier, but there is no reason to suppose that the Greeks were the first.
- 5.
See, for example, [62, p. 144]. Kronecker did not go to the extreme that I have of insisting that the multipliers all be natural numbers, so he did not need to put sums of multiples of m’s on both sides of the equation.
- 6.
The module [0] is equal only to modules of the form \([0,0, \ldots , 0]\). It is a very trivial sort of module—congruence mod it is simply equality—which for the most part will be ignored. A module in canonical form is not [0].
- 7.
If \(y^{2}=Ax^{2}\) and \(x\ne 0\), then A must be a square, as can be seen as follows: Let \([x, y]=[d]\ne [0]\). If \(y=0\), then \(A=0\) is a square. Otherwise, by Proposition 1, there are numbers \(\alpha \) and \(\beta \) for which \(\alpha x+d=\beta y\), from which it follows that \([xd]=[xd, Ax^{2}]=[xd, y^{2}]=[xd, y^{2}, \beta ^{2}y^{2}]=[xd, y^{2}, (\alpha x+d)^{2}]=[xd, y^{2}, d^{2}]= [d^{2}]\). Thus, \(xd=d^{2}, x=d, y^{2}=Ad^{2}\), and \((y/d)^{2}=A\). Or if one is willing to take the unique factorization of numbers as known, one can simply observe that some prime factor of A divides A an odd number of times, and therefore divides \(Ax^{2}\) an odd number of times, so \(Ax^{2}\) is not a square.
- 8.
This term derives from the fact that the module is in the principal class of the class group. It has always seemed to me peculiar to apply the adjective “principal” to the module itself, but the usage is universal among mathematicians.
- 9.
I have avoided Gauss’s term “reduced” because it conflicts with my term “reduction algorithm,” an algorithm for reducing a coefficient of \(\sqrt{A}\), not for reducing the module.
- 10.
The definitions imply—when use is made of the fact that if a, b and c are hypernumbers with \(c\ne 0\) then \(ac=bc\) implies \(a=b\)—that, for any nonzero hypernumber c and any module M, a congruence \(ac\equiv bc\,\textrm{mod}\, [c]M\) implies \(a\equiv b\,\textrm{mod}\, M\).
- 11.
\([1] = [1,\sqrt{A}]\), where the latter is in canonical form.
- 12.
Disquisitiones Arithmeticae [43, \(\S \S \)185, 186, 187, 195, 196, 198, 223]. The reason 79 is of interest is that it is the smallest value of A for which the class group contains a square that is not the identity—for example, \([3, 1+\sqrt{79}]^{2}\sim [9,4+\sqrt{79}] \not \sim [1]\). Perhaps Gauss’s attention was drawn to this case by the fact that it occurs in a counterexample Lagrange gave to a conjecture of Euler [66, Article 84]. Lagrange notes that the problem \(79 \cdot \square +733=\square \) has a solution (the comparison algorithm gives \([733, 476+\sqrt{79}]\sim [90,77+\sqrt{79}]\sim [1])\) but the problem \(79 \cdot \square +101=\square \) does not \(([101, 33+\sqrt{79}]\sim [45,23+\sqrt{79}]\sim [9,4+\sqrt{79}] \not \sim [1])\), contrary to a conjecture of Euler that would have implied that the answer to “Does \(A\square +B=\square \) have a solution?” might, for prime B, depend only on the class of \(B\,\textrm{mod}\, 4A\).
- 13.
Use of the “negative number” \(-1\) can be avoided by treating the values of \(\chi _{p}\) as numbers \(\textrm{mod}\, 4\), so that \(-1\equiv 3\), \((-1)^{2}\equiv 1\).
- 14.
Since \(\chi _{2}(p)=1\) for all odd primes p, it makes no difference whether \(A_{i}=2\) is included in the product in formula (1) when A is even.
- 15.
Both the English and the German translations of the Disquisitiones wrongly translate the theorems of \(\S \)236 and \(\S \)249, among others, when they use definite articles rather than indefinite ones; the original Latin of course has no articles.
- 16.
In truth, Essay 3.7 does not preserve the full generality of Gauss’s theory because it ignores forms (r, s, t) for which \(s^{2}-4rt\) is a square.
- 17.
Characteristically, Gauss does not exclude reducible forms, as is shown by the point he makes in [43, §235] of avoiding the assumption that the first coefficients of his forms are nonzero.
- 18.
By doing a good deal more algebraic work, Gauss proves Proposition 8—his “first consequence”—also in the case \(r=0\).
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Edwards, H.M. (2022). Some Quadratic Problems. In: Essays in Constructive Mathematics. Springer, Cham. https://doi.org/10.1007/978-3-030-98558-5_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-98558-5_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-98557-8
Online ISBN: 978-3-030-98558-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


