Abstract
For every univariate formula \(\chi \) (i.e., containing at most one atomic proposition) we introduce a lattice of intermediate theories: the lattice of \(\chi \)-logics. The key idea to define \(\chi \)-logics is to interpret atomic propositions as fixpoints of the formula \(\chi ^2\), which can be characterised syntactically using Ruitenburg’s theorem. We show that \(\chi \)-logics form a lattice, dually isomorphic to a special class of varieties of Heyting algebras. This approach allows us to build and describe five distinct lattices—corresponding to the possible fixpoints of univariate formulas—among which the lattice of negative variants of intermediate logics.
We would like to thank Nick Bezhanishvili for comments and discussions on this work. Also, we would like to thank the two anonymous referees for several useful remarks and suggestions. The first author was supported by the European Research Council (ERC, grant agreement number 680220). The second author was supported by Research Funds of the University of Helsinki.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
We indicate with \(\le \) the standard ordering induced by the lattice operations, that is, \(a \le b\) iff \(a \wedge _H b = a\).
- 3.
Admittedly, we are using an improper terminology (also adopted, e.g., in [7, Sec. 7]): varieties are proper classes, hence we cannot talk about the set of all varieties nor about the lattice of all varieties. A way to dispense of this problem is to instead consider a lattice consisting of equational theories, that is, sets of algebraic identities defined by a class of algebras (see, e.g., [6, Section 14] for an overview of this account). To simplify our presentation we abstract away from these issues and we maintain the terminology “lattice of varieties”.
- 4.
As a consequence of Lemma 7, in the current setting this is essentially the only case for which the map \(\boldsymbol{\chi }^2\) is not a nucleus. We can find other counterexamples if we lift the restriction of \(\chi \) being univariate.
- 5.
We are omitting the line on top of \(\boldsymbol{\delta }\) in favor of readability.
- 6.
To lighten the notation, we use the symbol \(\mathsf {Var}^{\chi }\) instead of \(\mathsf {Var}^{\chi }|_{\mathbf {IL}^{\chi }}\) for the function obtained by restricting the domain, omitting the explicit restriction of the domain. The same applies for the notation \(\mathsf {Log}^{\chi }\), used instead of \(\mathsf {Log}^{\chi }|_{\mathbf {HA}^{\chi }}\).
- 7.
We borrow this terminology from [7, Sec. 7.8]: an external characterization of a \(\chi \)-variety \(\mathcal {X}\) means a representation of \(\mathcal {X}\) by means of equations, as opposed to an internal characterizations which “does not involve identities, [...] but uses only purely algebraic tools such as various kinds of operations on algebras”.
References
Bezhanishvili, G., Holliday, W.H.: Locales, nuclei, and dragalin frames. In: Beklemishev, L., Demri, S., Máté, A. (eds.) Advances in Modal Logic, vol. 11 (2016)
Bezhanishvili, G., Holliday, W.H.: A semantic hierarchy for intuitionistic logic. Indag. Math. 30(3), 403–469 (2019)
Bezhanishvili, N., Grilletti, G., Holliday, W.H.: Algebraic and topological semantics for inquisitive logic via choice-free duality. In: Iemhoff, R., Moortgat, M., de Queiroz, R. (eds.) WoLLIC 2019. LNCS, vol. 11541, pp. 35–52. Springer, Heidelberg (2019). https://doi.org/10.1007/978-3-662-59533-6_3
Bezhanishvili, N., Grilletti, G., Quadrellaro, D.E.: An algebraic approach to inquisitive and DNA-logics. Rev. Symb. Log. 1–14 (2021). https://doi.org/10.1017/S175502032100054X
Birkhoff, G.: On the structure of abstract algebras. Math. Proc. Cambridge Philos. Soc. 31(4), 433–454 (1935)
Burris, S., Sankappanavar, H.P.: A Course in Universal Algebra. Springer, New York (1981)
Chagrov, A., Zakharyaschev, M.: Modal Logic. Oxford University Press, Oxford (1997)
Ciardelli, I.: Inquisitive semantics and intermediate logics. MSc thesis, University of Amsterdam (2009)
Ciardelli, I.: Questions in logic. Ph.D. thesis, Institute for Logic, Language and Computation, University of Amsterdam (2016)
Ciardelli, I., Groenendijk, J., Roelofsen, F.: Inquisitive Semantics. Oxford University Press, Oxford (2019)
Ciardelli, I., Roelofsen, F.: Inquisitive logic. J. Philos. Log. 40(1), 55–94 (2011)
Esakia, L.: Heyting Algebras: Duality Theory, vol. 50, 1st edn. Springer, Cham (2019)
Font, J.M.: Abstract Algebraic Logic. College Publication, London (2016)
Gabbay, D.: Semantical Investigations in Heyting’s Intuitionistic Logic, vol. 148. Springer, Dordrecht (1981). https://doi.org/10.1007/978-94-017-2977-2
Holliday, W.H.: Inquisitive intuitionistic logic. In: Olivetti, N., Verbrugge, R., Negri, S., Sandu, G. (eds.) Advances in Modal Logic, vol. 13 (2020)
Iemhoff, R., Yang, F.: Structural completeness in propositional logics of dependence. Arch. Math. Log. 55, 955–975 (2016). https://doi.org/10.1007/s00153-016-0505-8
Jankov, V.: On the relation between deducibility in intuitionistic propositional calculus and finite implicative structures. Soviet Mathematics Doklady 151, 1294–1294 (1963)
Jankov, V.: The construction of a sequence of strongly independent superintuitionistic propositional calculi. Soviet Mathematics Doklady 9, 806–807 (1968)
Kuznetsov, A.V.: Superintuitionistic logics. Mat. Issled. 10(2(36)), 150–158, 284–285 (1975). (Russian)
Miglioli, P., Moscato, U., Ornaghi, M., Quazza, S., Usberti, G.: Some results on intermediate constructive logics. Notre Dame J. Form. Log. 30(4), 543–562 (1989)
Nishimura, I.: On formulas of one variable in intuitionistic propositional calculus. J. Symb. Log. 25(4), 327–331 (1960)
Quadrellaro, D.E.: Lattices of DNA-logics and algebraic semantics of inquisitive logic. MSc thesis, University of Amsterdam (2019)
Rasiowa, H., Sikorski, R.: The Mathematics of Metamathematics. Monografie matematyczne, vol. 41, 3 edn. Polish Scientific Publications (1970)
Rieger, L.S.: On the lattice theory of Brouwerian propositional logic. Acta Facultatis Rerum Naturalium Universitatis Carolinae (Prague). Spisy Vydávané Příridorědeckou Fakultou University Karlovy, vol. 1949, no. 189 (1949)
Roelofsen, F.: Algebraic foundations for inquisitive semantics. In: van Ditmarsch, H., Lang, J., Ju, S. (eds.) LORI 2011. LNCS (LNAI), vol. 6953, pp. 233–243. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24130-7_17
Ruitenburg, W.: On the period of sequences (\(A^n(p)\)) in intuitionistic propositional calculus. J. Symb. Log. 49(3), 892–899 (1984)
Santocanale, L., Ghilardi, S.: Ruitenburg’s theorem via duality and bounded bisimulations. In: Advances in Modal Logic, Bern, Switzerland (2018)
Tarski, A.: A remark on functionally free algebras. Ann. Math. 47(1), 163–166 (1946)
Väänänen, J.: Dependence Logic: A New Approach to Independence Friendly Logic. Cambridge University Press, Cambridge (2007)
Wronski, A.: Intermediate logics and the disjunction property. Rep. Math. Log. 1, 39–51 (1973)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Proof of Lemma 7
A Proof of Lemma 7
Proof
(Proof of Lemma 7). As shown in [21, 24], the following is a presentation of all the non-constant univariate intuitiornistic formulas modulo logical equivalence:
We consider the following two properties for a univariate formula \(\phi \):
-
1.
\(\lnot \lnot \phi \equiv \top \).
-
2.
If \(\psi \) has property 1, then
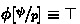 .
.
In particular, if \(\phi \) has both properties then \(\phi ^2 \equiv \top \), that is, the fix-point of \(\phi \) is \(\top \).
Firstly notice that
have both properties.


Moreover, we can show that, if \(\alpha _n\) and \(\beta _n\) have both properties, then this holds for \(\alpha _{n+1}\) and \(\beta _{n+1}\) too.


So, by induction all the formulas \(\alpha _n, \beta _n\) with \(n\ge 5\) have index at most 2 and fixpoint \(\top \). As for the remaining formulas, one can easily show their fix-points are as follows:

This concludes the proof. \(\square \)
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Grilletti, G., Quadrellaro, D.E. (2022). Lattices of Intermediate Theories via Ruitenburg’s Theorem. In: Özgün, A., Zinova, Y. (eds) Language, Logic, and Computation. TbiLLC 2019. Lecture Notes in Computer Science, vol 13206. Springer, Cham. https://doi.org/10.1007/978-3-030-98479-3_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-98479-3_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-98478-6
Online ISBN: 978-3-030-98479-3
eBook Packages: Computer ScienceComputer Science (R0)


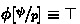 .
.