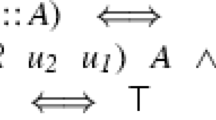Model Checking $\omega$-Regular Properties with Decoupled Search

Abstract

Decoupled search is a state space search method originally introduced in AI Planning. Similar to partial-order reduction methods, decoupled search exploits the independence of components to tackle the state explosion problem. Similar to symbolic representations, it does not construct the explicit state space, but sets of states are represented in a compact manner, exploiting component independence. Given the success of both partial-order reduction and symbolic representations when model checking liveness properties, our goal is to add decoupled search to the toolset of liveness checking methods. Specifically, we show how decoupled search can be applied to liveness verification for composed Büchi automata by adapting, and showing correct, a standard algorithm for detecting lassos (i.e., infinite accepting runs), namely nested depth-first search. We evaluate our approach using a prototype implementation.

1 Introduction

Model checking is a well-known problem in formal verification. Given a formal description of a system $\mathcal{M}$, the model checking problem is to decide whether the system satisfies a property $\phi$. In contrast to safety properties, which can only express whether there exists a finite run of the system that reaches a state with certain (bad) properties, liveness properties can express good behaviours of the system that should occur repeatedly, i.e., infinite runs in which something good happens infinitely often.

In this work, we consider a liveness verification problem that arises when composing a set $\mathcal{A}^1, \dots , \mathcal{A}^n$ of non-deterministic Büchi automata (NBA), each with its own acceptance condition. We recall that an accepting run for a single NBA is a lasso $\rho _p(\rho _c)^\omega$ with a prefix $\rho _p$ and a cycle $\rho _c$ that visits an accepting state. For the composition of a set of NBAs into an NBA we consider the following liveness property: a composed run is accepting if there is a cycle visiting a state that is accepting for all components. Such a general problem captures standard liveness verification problems related to $\omega$-regular properties. An archetypal example is automata-based LTL checking, where system components are represented as NBAs and are composed with a property monitor, represented as a Büchi automaton (often the negation of an LTL property). In this case an accepting composed run witnesses a violation of a linear-time property.

The predominant approach to address such verification problems using explicit state space search is to use nested depth-first search (NDFS) algorithms [5, 22, 32], also called double depth-first search, which perform on-the-fly checking of liveness properties while composing the NBAs. NDFS, like all state space search methods, suffers from the state explosion problem. Various methods, such as partial-order reduction [10, 19, 27, 30, 34], symbolic representations [2, 28], symmetry reduction [7, 23], or Petri-net unfolding [8, 9] have been proposed to alleviate the state explosion problem. Here, we add decoupled state space search [14], shortly decoupled search, as a new method for model checking liveness properties, complementary to the existing approaches. Indeed, as Gnad and Hoffmann [14, 15] have shown, decoupled search complements these techniques in the sense that there exist cases where it yields exponentially stronger reductions. It has also been shown that decoupled search can be fruitfully combined with partial-order reduction [16], symmetry reduction [18], and symbolic search [17].

Decoupled search has recently been introduced in AI planning [14], addressing goal reachability problems. Its applicability to model checking of safety properties has been shown in [12], where it was effectively introduced into the SPIN model checker [20]. However, the extension of decoupled search to cycle detection problems inherent to liveness model checking and NDFS algorithms has not yet been investigated. This paper addresses that investigation for the first time.

Decoupled search exploits the independence of system components, similar to partial-order reduction techniques, by not enumerating all interleavings of transitions across components. Similar to symbolic representations, decoupled search does not construct the explicit state space of the product. Instead, search nodes, called decoupled states, symbolically represent sets of states. Each decoupled state compactly represents many global states and their closure up to internal transitions of individual components. Similar to partial-order reduction or symbolic search, decoupled search can be exponentially more efficient than explicit search of the state space, as shown for reachability problems in the domains of AI planning [14] and model checking [12].

The main contribution of our paper is to extend the scope of decoupled search from safety properties, as done in [12], to liveness properties. In particular, we adapt a standard NDFS algorithm to the decoupled state representation. The resulting algorithms are able to solve the verification problem mentioned above, namely checking acceptance of composed NBAs. The main technical challenge for the correctness of our algorithms was to identify the conditions that imply existence of accepting runs in decoupled search and to show how such runs can be constructed efficiently.

We evaluate our decoupled NDFS algorithm using a prototype implementation on two showcase examples similar to the dining philosophers problem, and a set of randomly generated models. We compare to established tools, namely the SPIN model checker [20], and Petri-net unfolding with Cunf [30]. The results show that, like for safety properties, decoupled search can yield exponential advantages over state-of-the-art methods. In particular, its advantage grows with the degree to which components act independently of others, via internal transitions that do not affect other components.

The rest of the paper is structured as follows. We start in Sect. 2 by recalling the necessary background on NBAs, the verification problem we consider, and a standard NDFS algorithm typically used to solve the problem. Sections 3–5 present our contribution: Sect. 3 formalizes decoupled search in terms of composed NBAs, and shows its desired properties; Sect. 4 discusses some issues that would arise in a naïve attempt to (incorrectly) adapt it, and describes the (correct) adapted NDFS algorithm; Sect. 5 provides its correctness proof. In Sect. 6 we show our experimental evaluation, whose code and models are publicly available at [13]. Section 7 concludes the paper discussing related works and future research avenues.

2 Büchi Automata, Composition and Verification

This section recalls some basic notions of Büchi automata, their composition, the verification problem we consider in this paper for such composition, and its standard algorithmic resolution based on NDFS.

Büchi Automata and Accepting Runs. We start with the definition of non-deterministic Büchi automata (NBA).

Definition 1 (Non-deterministic Büchi Automaton)

A non-determinitic Büchi automaton $\mathcal{A}$ is a tuple $\langle S, \rightarrow , L, s_0, A \rangle$, where $S$ is a finite set of states, $L$ is a finite set of transition labels, $\rightarrow \subseteq S\times L\times S$ is a transition relation, $s_0\in S$ is an initial state, and $A\in (S\rightarrow \mathbb {B})$ is an acceptance function.

A run $\rho$ of an NBA is an infinite sequence of states $s_0, s_1, s_2, \dots \in S^\omega$ starting from the initial state. The i-th state of a run $\rho$ is denoted by $\rho [i]$ and we will use the same notation for other lists and sequences. A run $\rho$ is accepting if it traverses accepting states infinitely often. Formally, ${\tiny {\mathop {\exists }\limits ^{_\infty }}} j \in {\mathbb N}: A(s[j])$. We define a trace $\pi$ of a run $\rho = s_0, s_1, s_2, \dots \in S^\omega$ as a sequence of labels $\pi = l_0,l_1, \dots \in L^\omega$ such that $\forall _{i \in {\mathbb N}}: \langle s_i,l_i,s_{i+1} \rangle \in \rightarrow$. We will also consider finite runs $\rho \in S^n$ and finite traces $\pi \in L^n$.

As hinted in Sect. 1, the existence of accepting runs is interesting for several theoretical and practical reasons. On the theoretical side, the language of an NBA is the set of all traces $\sigma$ in $L^ \omega$ for which an accepting run exists such that $\rho [i] \xrightarrow {\sigma [i]} \rho [i+1]$ for all $i\in {\mathbb N}$. On the practical side, model checking $\omega$-regular properties, including LTL properties, can be reduced to checking the existence of accepting runs. Such runs, indeed, provide witnesses or counterexamples for the properties of interest.

Composition of NBAs. From now on we assume that the set of labels $L$ of an NBA is partitioned into a set $L_I$ of internal labels and a set $L_G$ of global labels. The notion of composition we use is based on (maximal) synchronisation on global labels, in words: in every transition involving a global label, each component having the global label in its set of labels must perform a local transition, while transitions with internal labels can be performed independently. When composing NBAs we assume w.l.o.g. that they do not share any internal label. Further, we assume that every global label is shared by at least two component NBAs. Otherwise, such labels can be made internal. We will use the following notation: for a set $\mathcal{A}^1, \dots , \mathcal{A}^n$ of NBAs, we use superscripting to denote the components of each $\mathcal{A}^i$, i.e., we assume $\mathcal{A}^i = \langle S^i, \rightarrow ^i, L^i = L_I^i \cup L_G^i, s_0^i, A^i \rangle$.

Definition 2 (Composition of NBAs)

The composition of n NBAs $\mathcal{A}^1, \dots , \mathcal{A}^n$, denoted by $\mathcal{A}^1 \parallel \dots \parallel \mathcal{A}^n$, is the NBA $\langle S, \rightarrow , L, \boldsymbol{s}_0, A \rangle$, where $S= S^1 \times \dots \times S^n$, $L= \bigcup _{i \in \{1, \dots , n\}} L^i$, $\boldsymbol{s}_0= (s_0^1, \dots , s_0^n)$, $A= \{ (s_1,\dots ,s_n) \mapsto \wedge _{i=1, \dots , n} A^i(s_i)\}$ and $\rightarrow$ is the smallest set of transitions closed under the following rules for interleaving of local transitions (1) and maximal synchronization on global labels (2):

$$ (1) \ \frac{s_i\xrightarrow {l_I}s_i' l_I \in L_I^i}{(s_1, \dots , s_i, \dots , s_n) \xrightarrow {l_I} (s_1, \dots , s_i', \dots , s_n)} $$

$$ (2) \ \frac{ \exists _{i \in \{ 1, \dots , n\}}: l_G \in L_G^i \forall _{j \in \{1, \dots , n \mid l_G \in L_G^j \}}: s_j \xrightarrow {l_G} s_j' \forall _{j \in \{1, \dots , n \mid l_G \not \in L_G^j\}}: s_j' = s_j}{(s_1, \dots , s_n) \xrightarrow {l_G} (s_1', \dots , s_n')} $$

As notation convention, we will denote component states simply by small case letters, e.g. s, and composed states $(s_1, \dots , s_n) \in S$ by $\boldsymbol{s}$, i.e., as a vector, and similarly for local runs $\rho$ (resp. traces $\pi$) and composed runs $\boldsymbol{\rho }$ (composed traces $\boldsymbol{\pi }$).

In Fig. 1 we illustrate a small example of a composition of two NBAs $\mathcal{A}^1, \mathcal{A}^2$. In the top of the figure, we show the local state space of the two components ($\mathcal{A}^1$ left, $\mathcal{A}^2$ right), where the component states are $S^1 = \{1, 2, 3\}$, $S^2 = \{A, B\}$, and the labels are defined as $L_G^1=L_G^2 = \{l^1_G, l^2_G\}$, $L_I^1 = \{l^1_I\}$, $L_I^2 = \{l^2_I\}$. A local state is accepting for $\mathcal{A}^1$, so $A^1(s) = \top$, iff $s = 2$, and similar $A^2(s) = \top$ iff $s=B$. The initial states are $s_0^1 = 1$ and $s_0^2 = A$. The transitions are as shown. In the bottom, we depict the part of the state space of the composition $\mathcal{A}^1 \parallel \mathcal{A}^2$ reachable from $\boldsymbol{s}_0= (1,A)$ as it would be generated by a standard DFS. Here, transitions via global labels synchronize the components, internal transitions are executed independently. The states crossed out would be pruned by duplicate checking, the underlined state is accepting.

Fig. 1.

Example of two NBAs, $\mathcal{A}^1$ and $\mathcal{A}^2$, and the state space of their composition $\mathcal{A}^1 \parallel \mathcal{A}^2$.

Verification Problem and Its Resolution with NDFS. The verification problem we address in this paper is the existence of accepting runs in the composed NBA $\mathcal{A}^1 \parallel \dots \parallel \mathcal{A}^n$. In words, we look for runs in $\mathcal{A}^1 \parallel \dots \parallel \mathcal{A}^n$ that infinitely often traverse states in which all component NBAs are in an accepting state. We discuss alternative acceptance conditions in Sect. 7.

Determining the existence of accepting runs in an NBA can be boiled down to the existence of so-called lassos, i.e., finite sequences of states in the NBA of the form $\boldsymbol{\rho }_p \boldsymbol{\rho }_c$ where $\boldsymbol{\rho }_p$ is the prefix of the lasso and $\boldsymbol{\rho }_c$ is the cycle of the lasso, which contains at least one accepting state and closes the cycle (i.e., $\boldsymbol{\rho }_p[\vert \boldsymbol{\rho }_p\vert - 1] = \boldsymbol{\rho }_c[|\boldsymbol{\rho }_c| - 1]$. Such a finite sequence of states represents an accepting run $\boldsymbol{\rho }_p (\boldsymbol{\rho }_c)^\omega$.

Several algorithms can be used to check the existence of lassos. The predominant family of algorithms are the variants of NDFS, originally introduced in [5]. Figure 2 shows the pseudo-code for one such variant, based on NDFS as presented in [4]. The algorithm is based on an ordinary depth-first search algorithm (DFS) that works as usual: a set V is used to record already visited states, and recursion enforces the depth-first exploration order of the state space. Moreover, a stack $Stack$ is used to keep track of the states on the current initial trace being explored. The main difference w.r.t. ordinary DFS is that a second, nested, depth-first search algorithm (NestedDFS) is invoked from accepting states on backtracking, i.e., after the recursive call to DFS. The idea is that, if this second depth-first search finds a state that is on $Stack$, then it is guaranteed that a cycle has been found, which contains at least one accepting state. That is, one finds the (un)desired lasso. The algorithm is also complete: no accepting cycle is missed.

Fig. 2.

A standard NDFS algorithm for lasso search in composed NBAs.

Fig. 3.

Example run of CheckEmptiness. The wavy arrow indicates the invocation of NestedDFS((2,  B)); the dashed arrow indicates how the cycle is closed.

In Fig. 3, we illustrate an example run of the CheckEmptiness algorithm on our example. When DFS backtracks from (2, B), NestedDFS is invoked, illustrated by the wavy arrow. NestedDFS generates the successor (2, A), which is on Stack, so a cycle is reported. We can construct an accepting run $\boldsymbol{\rho }_p(\boldsymbol{\rho }_c)^\omega$ with prefix $\boldsymbol{\rho }_p$ induced by the trace $l^1_I$ and cycle $\boldsymbol{\rho }_c$ induced by the trace $l^2_G,l^1_G,l^1_I,l^2_I$.

3 The Decoupled State Space for Composed NBAs

As previously stated, decoupled state space search was recently developed in AI planning [14], and adapted to model checking of safety properties later on [12]. It is designed to tackle the state explosion problem inherent in search problems that result from compactly represented systems with exponentially large state spaces. In AI planning, where decoupled search was originally introduced, such systems are modelled through state variables and a set of transition rules (called “actions”). The adaptation of decoupled search to reachability checking in SPIN presented in [12] devised decoupled search for automata models, but informally only. Here, we introduce decoupled search formally for NBA models. We define the decoupled state space for composed NBAs, as the result from the composition of a set of NBAs.

3.1 Decoupled Composition of NBAs

In contrast to the explicit construction of the state space, where all reachable states are generated by searching over all traces of enabled transitions, decoupled search only searches over traces of global transitions, the ones that synchronize the component NBAs. In decoupled search, a decoupled state $s^\mathcal{D}$ compactly represents a set of states closed by internal steps. This is done in terms of the sequence of global labels used to reach these states, plus a set of reached states for each component. Definition 3 formalizes this through the operation decoupled composition of NBAs, which adapts the composition operation provided in Definition 2 to decoupled state space search.

Definition 3 (Decoupled composition of NBAs)

The decoupled composition of n NBAs $\mathcal{A}^1, \dots , \mathcal{A}^n$, denoted by $\mathcal{A}^1 \parallel _\mathcal{D} \dots \parallel _\mathcal{D} \mathcal{A}^n$, is a tuple $\langle S^\mathcal{D}, {\rightarrow _\mathcal{D},} L_G, s_0^\mathcal{D}, A^\mathcal{D} \rangle$ defined as follows:

• $S^\mathcal{D}= \mathcal{P}^+(S^1) \times \dots \times \mathcal{P}^+(S^n)$, with $\mathcal{P}^+(S) := 2^S \setminus \emptyset$.

• $s_0^\mathcal{D}= \langle \mathrm {iclose}(s_0^1), \dots , \mathrm {iclose}(s_0^n) \rangle$, with $\mathrm {iclose}(s)$ being the set of states $s'$ that are reachable from s in $\mathcal{A}^i$ using only $\mathcal{A}^i$’s internal transitions $L_I^i$: $\mathrm {iclose}(s) = \{s' \mid s {\tiny \xrightarrow {l_I \in L_I^i}\negthickspace ^*} s'\}$ and $\mathrm {iclose}(S) = \bigcup _{s\in S}\mathrm {iclose}(s)$.

• $A^\mathcal{D}(s^\mathcal{D}) = \forall _{i \in \{1, \dots , n\}}: \exists s^i \in S_i: A^i(s^i)$, where $s^\mathcal{D}= \langle S_1, \dots , S_n \rangle$.

• $\rightarrow _\mathcal{D}$ is the smallest set of transitions closed under the following rule:

  $$ \frac{ l_G \in L_G \forall _{i \in \{1, \dots n\}}: S_i' = \{s_i' \mid \boldsymbol{s}\in s^\mathcal{D}: \boldsymbol{s}\xrightarrow {l_G} (s_1', \dots , s_i', \dots , s_n')\} S_i' \ne \emptyset }{s^\mathcal{D}\xrightarrow {l_G}_\mathcal{D} \langle \mathrm {iclose}(S_1'), \dots , \mathrm {iclose}(S_n') \rangle } $$

  where, abusing notation, we write $\boldsymbol{s}{\in }s^\mathcal{D}$ if $s^\mathcal{D}{=}\langle S_1, \dots , S_n \rangle$ and $\boldsymbol{s}\in S_1 \times {\dots }\times S_n$.

In the decoupled composition $\mathcal{A}^1 \parallel _\mathcal{D} \dots \parallel _\mathcal{D} \mathcal{A}^n$ a decoupled state $s^\mathcal{D}$ is defined by a tuple $\langle s^\mathcal{D}[\mathcal{A}^1], \dots , s^\mathcal{D}[\mathcal{A}^n] \rangle$, consisting of a non-empty set of component states $s^\mathcal{D}[\mathcal{A}^i]$ for each $\mathcal{A}^i$. A decoupled state represents exponentially many member states, namely all composed states $\boldsymbol{s}= (s_1, \dots , s_n)$ such that $\boldsymbol{s}\in s^\mathcal{D}[\mathcal{A}^1] \times \dots \times s^\mathcal{D}[\mathcal{A}^n]$. We will always use a superscript $\mathcal{D}$ to denote decoupled states $s^\mathcal{D}$.

We overload the subset operation $\subseteq$ for decoupled states $s^\mathcal{D}$ by doing it component-wise on the sets of reached local states, namely $s^\mathcal{D}\subseteq t^\mathcal{D}\Leftrightarrow \forall \mathcal{A}^i: s^\mathcal{D}[\mathcal{A}^i] \subseteq t^\mathcal{D}[\mathcal{A}^i]$.

During a search in the decoupled composition we define the global trace of a decoupled state $s^\mathcal{D}$, denoted $\pi ^G(s^\mathcal{D})$, as the sequence of global transitions on which $s^\mathcal{D}$ was reached from $s_0^\mathcal{D}$. For DFS, as considered in this work, this is well-defined.

In explicit state search, states that have been visited before – duplicates – are pruned to avoid repeating the search effort unnecessarily. The corresponding operation in decoupled search is dominance pruning [14]. A newly generated decoupled state $t^\mathcal{D}$ is pruned if there exists a previously seen decoupled state $s^\mathcal{D}$ that dominates $t^\mathcal{D}$, i.e., where $t^\mathcal{D}\subseteq s^\mathcal{D}$. With the correctness result given below, this is safe. One can make the representation of decoupled states, and thereby also the dominance checking, more efficient by representing the state sets $s^\mathcal{D}[\mathcal{A}^i]$ symbolically [17].

The initial decoupled state is obtained by closing each local state with internal steps ($\mathrm {iclose}$), and decoupled transitions generate decoupled states whose local states are also closed under internal steps. This maximally preserves the decomposition afforded by the decoupled representation. Namely, as we will prove in what follows, a decoupled state $s^\mathcal{D}$ compactly represents all explicit states that are reachable via traces that extend the global trace $\pi ^G(s^\mathcal{D}) = l^1_G, l^2_G, \dots , l^k_G$ with local transition labels. That is, for every component $\mathcal{A}^i$, $s^\mathcal{D}$ contains the non-empty subset of its local states $s^\mathcal{D}[\mathcal{A}^i] \subseteq S^i$ that can be reached with traces $\pi _i = l_1, l_2, \dots , l_n$ such that there exist indices $j_1< j_2< \dots < j_k$ where $l_{j_t} = \pi ^G(s^\mathcal{D})[j_t]$ for all $1 \le t \le k$. In words, after every global label on $\pi ^G(s^\mathcal{D})$, arbitrary enabled sequences of internal transitions are allowed.

We remark that the decoupled composition of a set of NBAs is always deterministic. For every pair of decoupled state $s^\mathcal{D}$ and global label $l_G$, there is a unique successor $t^\mathcal{D}$. This is easy to see, since if there is a composed state $\boldsymbol{s}$ contained in $s^\mathcal{D}$ that has multiple outgoing transitions labelled with $l_G$, all of the composed successor states are contained in $t^\mathcal{D}$. This increases the possible state space reduction compared to standard search, which needs to branch over all these successors. Note that this is different from the determinization of NBA, which comes with a blow-up [31]. The determinism is a consequence of the compact representation where all possible outcome states of a non-deterministic transition are contained in the decoupled successor state.

3.2 Correctness of Decoupled Composition

In this section we show that decoupled search, as presented here, is sound and complete w.r.t. reachability properties. We adapt the corresponding result from AI planning [14].

We require some additional notation. For a trace $\boldsymbol{\pi }$, by $\pi ^G(\boldsymbol{\pi })$ we denote the subsequence of $\boldsymbol{\pi }$ that is obtained by projecting onto the global labels $L_G$.

As previously stated, the decoupled state space captures reachability of the composed system exactly. The proof is an adaptation of previous results from AI Planning [14] to composed NBAs as considered here.

Theorem 1

A state $\boldsymbol{t}$ of a composition of NBAs $\mathcal{A}^1 \parallel \dots \parallel \mathcal{A}^n$ is reachable from a state $\boldsymbol{s}$ via a trace $\boldsymbol{\pi }$, iff there exist decoupled states $s^\mathcal{D}$, $t^\mathcal{D}$ in the decoupled composition $\mathcal{A}^1 \parallel _\mathcal{D} \dots \parallel _\mathcal{D} \mathcal{A}^n$, such that $\boldsymbol{s}\in s^\mathcal{D}$, $\boldsymbol{t}\in t^\mathcal{D}$, and $t^\mathcal{D}$ is reachable from $s^\mathcal{D}$ via $\pi ^G(\boldsymbol{\pi })$.

Proof

Let $\pi ^G(\boldsymbol{\pi }) = l^1_G, \dots , l^k_G$, and $s^\mathcal{D}_i \xrightarrow {l^{i+1}_G}_\mathcal{D} s^\mathcal{D}_{i+1}$ for all $1 \le i < k$. We prove the claim by induction over the length of $\pi ^G(\boldsymbol{\pi })$. For the base case $\vert \pi ^G(\boldsymbol{\pi })\vert = 0$, the claim trivially holds, since, by the definition of $\mathrm {iclose}()$, $s^\mathcal{D}$ contains all composed states $\boldsymbol{t}$ that are reachable from any $\boldsymbol{s}\in s^\mathcal{D}$ via only internal transitions.

Assume a decoupled state $s^\mathcal{D}_i$ is reachable from $s^\mathcal{D}$ via $l^1_G, \dots , l^i_G$. Then, by the definition of decoupled transitions and $\mathrm {iclose}()$, the state $s^\mathcal{D}_{i+1}$ contains all composed states $\boldsymbol{s}_{i+1}$ that are reachable from a state $\boldsymbol{s}_i \in s^\mathcal{D}_i$ via a trace $\pi ^{i\rightarrow i+1}$ that consists of only internal transitions and $l^{i+1}_G$. By hypothesis, we can extend the traces reaching every such $\boldsymbol{s}_i$ from a $\boldsymbol{s}\in s^\mathcal{D}$ by $\pi ^{i\rightarrow i+1}$ and obtain a trace reaching $\boldsymbol{s}_{i+1}$ from $\boldsymbol{s}$ with global sub-trace $l^1_G, \dots , l^i_G, l^{i+1}_G$.

For the other direction, if a composed state $\boldsymbol{s}_i$ is reached in a decoupled state $s^\mathcal{D}_i$ and can reach a state $\boldsymbol{s}_{i+1}$ via a trace $\pi ^{i\rightarrow i+1}$ that consists of internal labels and $l^{i+1}_G$, then there exists a decoupled transition $s^\mathcal{D}_i \xrightarrow {l^{i+1}_G}_\mathcal{D} s^\mathcal{D}_{i+1}$ and, again by the definition of decoupled transitions and $\mathrm {iclose}()$, $s^\mathcal{D}_{i+1}$ contains $\boldsymbol{s}_{i+1}$. By hypothesis $s^\mathcal{D}_i$ is reachable from $s^\mathcal{D}$, where $\boldsymbol{s}_i$ is reachable from $\boldsymbol{s}\in s^\mathcal{D}$. Thus, $s^\mathcal{D}_{i+1}$ is reachable from $s^\mathcal{D}$ via $l^1_G, \dots , l^i_G, l^{i+1}_G$.    $\square$

3.3 Relation to Other State-Space Reduction Methods

Prior work has investigated the relation of decoupled search to other state-space reduction methods in the context of AI planning [14, 15], in particular to strong stubborn sets [34], Petri-net unfolding [8, 9], and symbolic representations using BDDs [2, 28]. For all these techniques, there exist families of scaling examples where decoupled search is exponentially more efficient.

Fig. 4.

Illustration of the exponential separations to ample sets (left) and unfolding (right).

We capture this formally in terms of exponential separations. A search method X is exponentially separated from decoupled search if there exists a family of models $\{M^n{=}\mathcal{A}^1, \dots , \mathcal{A}^m \mid n \in {\mathbb N}\}$ of size polynomially related to n such that (1) the number of reachable decoupled states in $\mathcal{A}^1 \parallel _\mathcal{D} \dots \parallel _\mathcal{D} \mathcal{A}^m$ is bounded by a polynomial in n, and (2) the state space representation of $\mathcal{A}^1 \parallel \dots \parallel \mathcal{A}^m$ under X is exponential in n.

We next describe two scaling models showing that the ample sets variant of SPIN [21, 29], as a representative for partial-order reduction in explicit-state search, and Petri-net unfolding are exponentially separated from decoupled search. For symbolic search with BDDs, the reduction achieved by both methods is in general incomparable.

For ample sets, a simple model family looks as follows: there are n components, each with the same state space: two local states ${A_i,B_i}$, initial state $A_i$, two global transitions $l^{a,i}_G$, $l^{b,j}_G$, one internal transition. A component and the transitions are depicted in the left of Fig. 4 (the dashed transition is internal). The global transitions synchronize components pairwise; our argument holds for every possible such synchronization.

Under ample set pruning, no reduction is achieved (no state is pruned) because there is a global transition enabled in every state. Thus, there exists no state where only safe (i.e. internal) transitions are enabled, and the search always branches over all enabled transitions of all components. The decoupled state space, in contrast, only has a single decoupled state, where both local states are reached in each component. All decoupled successor states are dominated and will be pruned.

Similar to decoupled search, Petri-net unfolding exploits component independence by a special representation. Instead of searching over composed states and pruning transitions, the states of individual components are maintained separately.¹

A scaling model showing that unfolding is exponentially separated from decoupled search is illustrated in the right of Fig. 4. There are n components, each with the same state space with three local states $A_i, B_i, C_i$, a global label $l_G$, and transitions as shown in the figure. In a Petri net, this model is encoded with 3n places and $2^n$ transitions, one for every combination of one output place in each of the components. In the unfolding, this results in an event (the equivalent of a state) for every net transition. The decoupled state space has only two decoupled states: the initial state where $\{A_i\}$ is reached for all components, and its $l_G$-successor where $\{B_i, C_i\}$ is reached in every component.

4 NDFS for Decoupled Search

We now adapt NDFS to decoupled search. We start by discussing the deficiencies of a naïve adaptation. We will then introduce the key concepts in our fixed algorithm in Sect. 4.2, and present the algorithm itself in Sect. 4.3. We close this section by showing that the exponential separations to partial-order reduction and unfolding from Sect. 3.3 carry over to liveness checking by simple modifications of the models.

4.1 Issues with a Naïve Adaptation of NDFS

In a naïve adaptation of NDFS to decoupled search, the only thing that changes is the treatment of decoupled states, which represent sets of composed states, compared to single states in the standard variant. This leads to three mostly minor changes: (1) instead of duplicate checking we perform dominance pruning; (2) checking if a decoupled state is accepting boils down to checking if it contains an accepting member state; and (3) to see if a state $\boldsymbol{t}$ contained in a state $t^\mathcal{D}$ generated in NestedDFS is on the stack, we need to check if $t^\mathcal{D}$ has a non-empty intersection with a state on $Stack$.

As we will show next, it turns out that this naïve adaptation can miss cycles due to pruning. Revisiting a composed state in NestedDFS does actually not imply a cycle, because reaching $t^\mathcal{D}$ from $s^\mathcal{D}$ entails only that every member state of $t^\mathcal{D}$ can be reached from at least one member state of $s^\mathcal{D}$, not from all of them. The critical point is that pruning does not take into account from where states are reachable.

Consider the example in Fig. 5. The left part of the figure shows the local state space of component NBA $\mathcal{A}^1$. For simplicity, we only show a single component, which is sufficient to illustrate the issue. Here, $\mathcal{A}^1$ is defined as follows: $S^1 = \{1, 2, 3, 4\}$, $L_G^1 = \{l^1_G, l^2_G\}$, $L_I^1 = \{l^1_I, l^2_I, l^3_I\}$, $A^1(s) = \top$ iff $s \in \{2, 4\}$, and $s_0^1 = 1$. The transitions are as shown in the left of the figure. The decoupled search space generated using NDFS is depicted in the right of the figure. Pruned states are crossed out.

NestedDFS is launched (indicated by the wavy arrow) on the accepting initial state $s_0^\mathcal{D}$. Before explaining the main issue, we remark that, to ensure that a cycle through an accepting member state of $s_0^\mathcal{D}$ is found, not a cycle through a non-accepting one, we need to restrict the set of reached local states to those that are accepting, and the states internally reachable from those via $\mathrm {iclose}()$. Thus, NestedDFS starts in what we call the acceptance-restriction $s^\mathcal{D}_{0,A}$ of $s_0^\mathcal{D}$, where $s^\mathcal{D}_{0,A}[\mathcal{A}^1] = \{2, 4\}$. Now, the issue results from the fact that $s^\mathcal{D}_{0,A}$ contains two accepting member states, only one of which, namely state 2, is on a cycle. Assuming that the decoupled states are generated in order of increasing subscripts, so $s^\mathcal{D}_1$ before $s^\mathcal{D}_2$ and so on, state 2 is first reached in NestedDFS as a member state of $s^\mathcal{D}_{2,A}$, but via the transition labelled with $l^2_G$ from state 3, so the cycle cannot be closed. When generating the $l^1_G$ successor $s^\mathcal{D}_{4,A}$ of $s^\mathcal{D}_{0,A}$, its only member state 3 has already been reached in $s^\mathcal{D}_{1,A}$, so $s^\mathcal{D}_{4,A}$ is pruned and the cycle of state 2 via $l^1_G,l^2_G$ is missed. In the next Section we show how to fix this, through an extended state representation that keeps track of reachability from a set of reference states.

Fig. 5.

Counterexample showing that a naïve adaptation of the NDFS algorithm is incomplete. The (only) component NBA $\mathcal{A}^1$ is depicted on the left. The search tree on the right shows the entire reachable decoupled state space, where pruned states are crossed out; the wavy arrow depicts the invocation of NestedDFS on the acceptance restriction $s^\mathcal{D}_{0,A}$ of $s_0^\mathcal{D}$.

Another minor issue are lassos $\boldsymbol{\rho }_p(\boldsymbol{\rho }_c)^\omega$ whose cycle $\boldsymbol{\rho }_c$ is induced by internal labels only. These will not be detected, because NestedDFS only considers traces via global labels. We fix this by checking for $L_I$-cycles in every accepting decoupled state generated during DFS, to see if there exists a component that can reach such a state.

4.2 Reference-State Splits

The problem underlying the issue described in the previous section is that pruning is done regardless of the accepting states in the root node of NestedDFS. We now introduce an operation on decoupled states splitting them with respect to the set of reached local accepting states for each component. In our algorithm, this will serve to distinguish the different accepting states, and thus force dominance pruning to distinguish reachability from these. Formally, we define the restriction to accepting local states as a new transition with a global label $l^A_G$ that is a self-loop for all accepting states:

Definition 4 (Acceptance-Split Transition)

Let $\langle S^\mathcal{D}, {\rightarrow _\mathcal{D},} L, s_0^\mathcal{D}, A^\mathcal{D} \rangle$ be the decoupled composition of $\mathcal{A}^1, \dots , \mathcal{A}^n$. Let $s^\mathcal{D}$ be an accepting decoupled state, and for $1 \le i \le n$ let $\langle s^i_1, \dots , s^i_{c_i} \rangle \subseteq s^\mathcal{D}[\mathcal{A}^i]$ be the list of reached accepting states of $\mathcal{A}^i$, where for all $1 \le j \le c_i: A^i(s^i_j) = \top$. Then the acceptance-split transition $l^A_G$ in $s^\mathcal{D}$ is defined as follows:

$$\begin{aligned} \frac{ A^\mathcal{D}(s^\mathcal{D}) = \top \forall i \in \{1, \dots n\}, j \in \{1, \dots , c_i\}: s^i_j \in s^\mathcal{D}[\mathcal{A}^i] \wedge A^i(s^i_j) = \top }{s^\mathcal{D}\xrightarrow {l^A_G}_\mathcal{D} \langle \langle \mathrm {iclose}(s^1_1), \dots , \mathrm {iclose}(s^1_{c_1}) \rangle , \dots , \langle \mathrm {iclose}(s^n_1), \dots , \mathrm {iclose}(s^n_{c_n}) \rangle \rangle } \end{aligned}$$

The outcome state $s^\mathcal{D}_A$ of an acceptance-split transition is a split decoupled state. The set of reference states of $s^\mathcal{D}_A$ is $R(s^\mathcal{D}_A) := \{s \mid \exists \mathcal{A}_i : s \in s^\mathcal{D}[\mathcal{A}^i] \wedge A^i(s) = \top \}$.

In words, the operation splits up the single set of reached component states $s^\mathcal{D}[\mathcal{A}^i]$ of $\mathcal{A}^i$ into a list of state sets, where each such set $s^\mathcal{D}_A[\mathcal{A}^i]_s$ contains the states that can be reached via internal transitions from the respective accepting state $s \in s^\mathcal{D}[\mathcal{A}^i]$.

Our search algorithm will use the acceptance-split transition to generate the root node $s^\mathcal{D}_A$ of NestedDFS from an accepting state $s^\mathcal{D}$ backtracked from in DFS. Hence NestedDFS will search in the space of split decoupled states. The transitions over these behind an $s^\mathcal{D}_A$ are defined as follows:

Definition 5 (Split Transitions)

Let $\langle S^\mathcal{D}, {\rightarrow _\mathcal{D},} L, s_0^\mathcal{D}, A^\mathcal{D} \rangle$ be the decoupled composition of $\mathcal{A}^1, \dots , \mathcal{A}^n$. Let $s^\mathcal{D}$ and $t^\mathcal{D}$ be decoupled states, with a transition $s^\mathcal{D}\xrightarrow {l_G}_\mathcal{D} t^\mathcal{D}$. Let $\langle s^i_1, \dots , s^i_{c_i} \rangle \subseteq S^i$ be reference states for $\mathcal{A}^i$. Then the split transition $s^\mathcal{D}_R \xrightarrow {l_G}_\mathcal{D} t^\mathcal{D}_R$ is defined such that for every $\mathcal{A}^i$ and every $1 \le j \le c_i$ we have:

$$\begin{aligned} t^\mathcal{D}_R[\mathcal{A}^i]_{s^i_j} = {\left\{ \begin{array}{ll} \mathrm {iclose}(\{s' \in t^\mathcal{D}[\mathcal{A}^i] \mid \exists s \in s^\mathcal{D}_R[\mathcal{A}^i]_{s^i_j}: s \xrightarrow {l_G}\negthickspace ^i s'\}) &{} l_G \in L_G^i \\ s^\mathcal{D}_R[\mathcal{A}^i]_{s^i_j} &{} l_G \not \in L_G^i \end{array}\right. } \end{aligned}$$

The list of reference states for an $\mathcal{A}_i$ does not change along a trace of split transitions. Let $s^\mathcal{D}_A$ be a decoupled state generated by an acceptance-split transition $s^\mathcal{D}\xrightarrow {l^A_G}_\mathcal{D} s^\mathcal{D}_A$, then for all successor states $t^\mathcal{D}$ of $s^\mathcal{D}_A$, the set of reference states is $R(t^\mathcal{D}) = R(s^\mathcal{D}_A)$.

We extend set operations to the split representation as follows. A split decoupled state $s^\mathcal{D}_R$ dominates a split decoupled state $t^\mathcal{D}_R$, denoted $t^\mathcal{D}_R \subseteq _R s^\mathcal{D}_R$, if $R(t^\mathcal{D}_R) \subseteq R(s^\mathcal{D}_R)$ and for all components $\mathcal{A}^i$ and reference states $s \in R(t^\mathcal{D}_R) \cap S^i$ we have $t^\mathcal{D}_R[\mathcal{A}^i]_s \subseteq s^\mathcal{D}_R[\mathcal{A}^i]_s$. In contrast, state membership is defined in a global manner, across reference states. Namely, the set of local states of an $\mathcal{A}^i$ reached in a split decoupled state $s^\mathcal{D}_R$ is defined as $s^\mathcal{D}_R[\mathcal{A}^i] := \bigcup _{s \in R(s^\mathcal{D}_R) \cap S^i} s^\mathcal{D}_R[\mathcal{A}^i]_{s}$. Composed state membership is defined relative to these $s^\mathcal{D}_R[\mathcal{A}^i]$ as before.

An important property of the splitting is that it preserves reachability of member states. Concretely, for a split-transition $s^\mathcal{D}_R \xrightarrow {l_G}_\mathcal{D} t^\mathcal{D}_R$ induced by a transition $s^\mathcal{D}\xrightarrow {l_G}_\mathcal{D} t^\mathcal{D}$ for all $\mathcal{A}^i$ it holds that if $s^\mathcal{D}_R[\mathcal{A}^i] = s^\mathcal{D}[\mathcal{A}^i]$, then $t^\mathcal{D}_R[\mathcal{A}^i] = t^\mathcal{D}[\mathcal{A}^i]$.

As a notation convention, we will always denote split states $s^\mathcal{D}_R$ by a subscript R, and the direct outcome of an acceptance-split transition by $s^\mathcal{D}_A$, with a subscript $A$.

Fig. 6.

With acceptance-splitting, NestedDFS invoked on the $l^A_G$-successor $s^\mathcal{D}_{1,A}$ of $s_0^\mathcal{D}$ of the example in Fig. 5 correctly detects the cycle of state 2 induced by the trace $l^1_G,l^2_G$.

Considering our example again, Fig. 6 illustrates how, on split decoupled states, the cycle $2\xrightarrow {l^1_G} 3\xrightarrow {l^2_G} 2$ is not pruned. The state $s^\mathcal{D}_{3,R}$ is still pruned, as it contains only component states reached from state 4. In $s^\mathcal{D}_{4,R}$ and $s^\mathcal{D}_{5,R}$, the decoupled state keeps track of the traces from the origin state 2, so none of the two is pruned, since they are not dominated by any state $s^\mathcal{D}_{i, R}$ (the root node $s^\mathcal{D}_{1,A}$ of NestedDFS is not yet visited).

As indicated before, in our emptiness checking algorithm we will use split decoupled states only within NestedDFS. The seed state $s^\mathcal{D}_A$ of NestedDFS will always be the $l^A_G$-successor of an accepting state $s^\mathcal{D}$ backtracked from in DFS. Every member state of $s^\mathcal{D}_A$ is accepting, or can be reached with $L_I$-transitions from an accepting state.

4.3 Putting Things Together: Decoupled NDFS

We are now ready to describe our adaptation of the standard NDFS algorithm to decoupled compositions. The pseudo-code is shown in Fig. 7. The differences w.r.t the standard algorithm (Fig. 2) are highlighted in blue. The basic structure of the algorithm is preserved. It starts by putting the decoupled initial state $s_0^\mathcal{D}$ onto the Stack in CheckEmptiness, and launches the main DFS from it.

Fig. 7.

Adaptation of a standard NestedDFS for lasso search in decoupled compositions of NBA.

In DFS, the control flow does not change, decoupled states are generated in depth-first order by recursion, updating the stack accordingly. There are however three differences to the standard variant:

• 1. Before generating the successors, we call CheckLocalAccept on each accepting decoupled state $s^\mathcal{D}$. This detects cycles resulting from $L_I$-transitions, i.e., cycles that occur “within” a decoupled state. To this end, we check whether there exists a component $\mathcal{A}^i$ for which an accepting local state $s^i_a$ is reached that can reach itself using only internal labels $L_I^i$ (the set of such local states can be precomputed, so that the check becomes a lookup operation). We can then construct an accepting run for the composed system by appending the $L_I^i$-cycle to the sequence of states that reaches $s^i_a$ in $s^\mathcal{D}$ for $\mathcal{A}^i$. Note that it suffices if a single component moves and all other components remain in a reached accepting state.

• 2. Instead of doing duplicate checking, the algorithm performs dominance pruning, pruning a new decoupled state $t^\mathcal{D}$ if all its member states have been reached in an already visited decoupled state $r^\mathcal{D}$.

• 3. As discussed in Sect. 4.2, when we launch NestedDFS at a decoupled state $s^\mathcal{D}$, we do so on the acceptance-split $l^A_G$-successor $s^\mathcal{D}_A$ of $s^\mathcal{D}$.

NestedDFS now starts in the acceptance-split $s^\mathcal{D}_A$, and traverses split transitions as per Definition 5. On generation of a new state $t^\mathcal{D}_R$, we perform dominance pruning against the decoupled states visited during all prior calls to NestedDFS. If in an $t^\mathcal{D}_R$ for every component $\mathcal{A}^i$ there exists a reference state $s \in S^i$ that is reachable from itself, so $s \in t^\mathcal{D}[\mathcal{A}^i]_s$, then we can construct a cycle. As we will show in Theorem 4, this test is guaranteed to find all cycles that start from an accepting state $\boldsymbol{s}_A\in s^\mathcal{D}_A$.

Note that we cannot check for a non-empty intersection with states $r^\mathcal{D}$ on $Stack$, since these are not split relative to the reference states of $s^\mathcal{D}_A$. Thus, since we do not know from which local state in $r^\mathcal{D}$ the state in the intersection was reached, such a non-empty intersection would not imply a cycle. What we can do, however, is check for dominance instead, as an algorithm optimization inspired by [22]. The pseudo-code in Fig. 7 does so by checking whether $t^\mathcal{D}_R \supseteq r^\mathcal{D}$, where the $\supseteq$ relation between a split vs. non-split state is simply evaluated based on the overall sets $t^\mathcal{D}_R[\mathcal{A}^i]$ vs. $r^\mathcal{D}[\mathcal{A}^i]$ of reached components states. If this domination relation holds true, then the reachability issue mentioned in the previous section is resolved because all $\boldsymbol{t}\in r^\mathcal{D}$ are then reachable from $s^\mathcal{D}_A$ – including those $\boldsymbol{t}$ from which an accepting state $\boldsymbol{s}\in s^\mathcal{D}_A$ is reachable. Lemma 1 in the next section will spell out this argument as part of our correctness proof.

Observe that splitting a decoupled state incurs an increase in the size of the state representation, as the same local state may be reached from several reference states. More importantly, as dominance pruning is weaker on split states (which after all is the purpose of the split operation) the size of the search space may increase. As shown by the example in Fig. 5, though, there is no easy way around the splitting, since the algorithm has to be able to know from which component state the successors states are reached. Assuming a component has M accepting states, then in the worst case all local successor states that are shared between these accepting states can be visited M times across all NestedDFS invocations. Unless some of the decoupled states revisiting the same member state are pruned by dominance pruning, it can actually happen that the revisits multiply across the components, so the size of the decoupled state space in NestedDFS can potentially be exponentially larger than the standard state space. As we shall see in our experimental evaluation, typically such blow-ups do not seem to occur.

In case we want to construct a lasso, we need to store a pointer to the predecessor of each decoupled state and the label of the generating transition. With this, we can, for each component $\mathcal{A}^i$ separately, reconstruct a trace $\boldsymbol{\pi }$ of a state $\boldsymbol{t}\in t^\mathcal{D}$ reached from a state $\boldsymbol{s}\in s^\mathcal{D}$ where $\pi ^G(s^\mathcal{D}, t^\mathcal{D}) = \pi ^G(\boldsymbol{\pi })$. Here, for a decoupled state $t^\mathcal{D}$ that was reached from another decoupled state $s^\mathcal{D}$, by $\pi ^G(s^\mathcal{D}, t^\mathcal{D})$ we denote the global trace via which $t^\mathcal{D}$ was reached from $s^\mathcal{D}$. This can be done in time polynomial in the size of the component and linear in the length of $\pi ^G(s^\mathcal{D}, t^\mathcal{D})$. Since the traces for all components are synchronized via $\pi ^G(\boldsymbol{\pi })$, we add the required internal labels for each component in between every pair of global labels. We remark that, to decide if a lasso exists, we do not need to store any predecessor or generating label pointers.

We next show on an example how our algorithm works.

Fig. 8.

Illustration of the component NBAs used in Example 1.

Example 1

The model has two component NBAs $\mathcal{A}_1, \mathcal{A}_2$ illustrated in Fig. 8. It is a variant of an example from [26]. The Figure should be self-explanatory, we remark that all global transitions $l^1_G, \dots l^7_G$ induce a self loop in the only state 1 of $\mathcal{A}_2$.

CheckEmptiness starts by putting $s_0^\mathcal{D}$ onto Stack and enters DFS$(s_0^\mathcal{D})$. Let $s^\mathcal{D}_1 = \langle \{B,D\}, \{1\} \rangle$, $s^\mathcal{D}_2 = \langle \{E,F\}, \{1\} \rangle$, and $s^\mathcal{D}_3 = \langle \{D\}, \{1\} \rangle$ be the successors generated along the trace $l^1_G, l^2_G,l^3_G$ in DFS. Since $s^\mathcal{D}_3 \subseteq s^\mathcal{D}_1 \in V$, $s^\mathcal{D}_3$ is pruned and the search backtracks to $s^\mathcal{D}_1$. Say DFS selects the transition via $l^4_G$ next, generating the state $s^\mathcal{D}_4 = \langle \{C\}, \{1\} \rangle$ and its $l^5_G$-successor $s^\mathcal{D}_5=\langle \{F\}, \{1\} \rangle$. Then $s^\mathcal{D}_5$ is pruned because it is dominated by $s^\mathcal{D}_2 \in V$, and the search backtracks from $s^\mathcal{D}_4$, which is accepting.

Thus, NestedDFS$(s^\mathcal{D}_{5,A})$ is invoked, where $s^\mathcal{D}_{5,A} = \langle \langle \{C\}_C \rangle , \langle \{1\}_1 \rangle \rangle$, because C and 1 are accepting local states that become the reference states of $s^\mathcal{D}_{5,A}$. NestedDFS will follow the trace $l^5_G, l^3_G, l^6_G, l^7_G, l^7_G$, which among others generates the state $s^\mathcal{D}_{6,R} = \langle \langle \{G\}_C \rangle , \langle \{1\}_1 \rangle \rangle$ by $l^6_G$, and ends in $s^\mathcal{D}_{7,R} = \langle \langle \{G\}_C \rangle , \langle \{1\}_1 \rangle \rangle$. The latter is pruned, because it is dominated by $s^\mathcal{D}_{6,R}$, which is contained in $V'$. No cycle is reported. This is correct, because the only member state (C, 1) of $s^\mathcal{D}_{5,A}$ does not occur on a cycle.

DFS then backtracks to $s^\mathcal{D}_1 = \langle \{B,D\}, \{1\} \rangle$ and generates its remaining successor $s^\mathcal{D}_8 = \langle \{G\}, \{1\} \rangle$ via $l^6_G$. DFS further generates the $l^7_G$-successors of $s^\mathcal{D}_8$ and eventually backtracks from $s^\mathcal{D}_8$, invoking NestedDFS$(s^\mathcal{D}_{8,A})$, where $s^\mathcal{D}_{8,A} = \langle \langle \{G\}_G \rangle , \langle \{1\}_1 \rangle \rangle$.

After two transitions via $l^7_G$ the resulting state $s^\mathcal{D}_{9,R} = \langle \langle \{G\}_G \rangle , \langle \{1\}_1 \rangle \rangle$ satisfies the condition that for all components $\mathcal{A}_i$ $\exists s: s \in s^\mathcal{D}_{9,R}[\mathcal{A}^i]_s$, namely G and 1. Thus, a cycle is reported. It is induced by the trace $l^1_G, l_I, l^6_G, l^7_G, l^7_G$.

Note that no decoupled state in the second NestedDFS is pruned, since none of them is dominated by a state in $V'$ of the first NestedDFS invocation. In particular, $s^\mathcal{D}_{8,A} = \langle \{G\}_G, \{1\}_1 \rangle$ is not dominated by $s^\mathcal{D}_{6,R} = \langle \{G\}_C, \{1\}_1 \rangle$, because the reference states differ – G and 1 for $s^\mathcal{D}_{8,R}$ and C and 1 for $s^\mathcal{D}_{6,R}$.

4.4 Relation to Other State-Space Reduction Methods

The comparison to ample set pruning and Petri-net unfolding from Sect. 3.3 carries over directly to liveness checking via simple adaptations to the examples, see Fig. 9.

Fig. 9.

Illustration of the exponential separations to ample sets (left) and unfolding (right).

Theorem 2

CheckEmptiness with explicit-state search and ample sets pruning is exponentially separated from CheckEmptiness with decoupled search.

Proof (sketch). The argument from Sect. 3.3 remains valid. With the states $B_i$ accepting (see Fig. 9, left), explicit-state search with ample sets pruning in the worst case has to exhaust the entire state space. It invokes NestedDFS on the accepting state $(B_i)^n$ and, worst-case, needs to exhaust the state space again to detect the cycle. Decoupled search invokes NestedDFS on the initial state restricted to the component states $B_i$. Every successor of that state closes the cycle via an arbitrary $l^b_G$ transition. So there are only three decoupled states overall (including the acceptance-restricted initial state).    $\square$

Theorem 3

Constructing a complete unfolding prefix is exponentially separated from CheckEmptiness with decoupled search.

Proof (sketch). The component states $B_i$ are made accepting and internal transitions $B_i \rightarrow A_i$ are added to the model (see Fig. 9, right). Unfolding constructs a complete prefix as described in Sect. 3.3, plus one event for each new internal transition.² Decoupled search generates the two states as described. The second state has $\{A_i, B_i, C_i\}$ reached for all components, its successor via $l_G$ is pruned. NestedDFS is invoked on its restriction to $B_i$, in which all $A_i$ get reached via the new internal transitions. The $l_G$-successor of this state closes the cycle, so there are only four decoupled states.    $\square$

5 Decoupled NDFS Correctness

We now show the correctness of our approach. In Lemmas 1, 2, 3, we show that if our algorithm reports a cycle, then there exists an accepting run for $\mathcal{A}^1 \parallel \dots \parallel \mathcal{A}^n$. In Theorem 4, we then show that decoupled NDFS does not miss an accepting run.

We first show that the optimization of checking dominance of states in NestedDFS against states on the stack is sound, i.e., that an accepting run exists.

Lemma 1

Let $r^\mathcal{D}$ be a decoupled state on the current DFS $Stack$, and let $t^\mathcal{D}_R$ be a decoupled state generated by NestedDFS. If $t^\mathcal{D}_R \supseteq r^\mathcal{D}$, then there exists an accepting run for $\mathcal{A}^1 \parallel \dots \parallel \mathcal{A}^n$.

Proof

Let $s^\mathcal{D}$ be the accepting state that is backtracked from in DFS, i.e., the current NestedDFS was invoked on its $l^A_G$-successor $s^\mathcal{D}_A$.

From Theorem 1 we know that if $s^\mathcal{D}_2$ is reachable from $s^\mathcal{D}_1$, then for every state $\boldsymbol{s}_2 \in s^\mathcal{D}_2$ there exists a state $\boldsymbol{s}_1 \in s^\mathcal{D}_1$ such that $\boldsymbol{s}_1 \xrightarrow {\boldsymbol{\pi }} \boldsymbol{s}_2$, where $\pi ^G(\boldsymbol{\pi }) = \pi ^G(s^\mathcal{D}_1, s^\mathcal{D}_2)$.

This result also holds for decoupled states reached in NestedDFS from states in DFS. This is because the acceptance-split transition $l^A_G$ only restricts the set of reached member states of $s^\mathcal{D}$ in $s^\mathcal{D}_A$, so in particular $s^\mathcal{D}_A\subseteq s^\mathcal{D}$. Furthermore, split transitions generating states behind $s^\mathcal{D}_A$ do not affect reachability of member states of these split-decoupled states compared to their non-split counterparts.

In particular, (1) for every state $\boldsymbol{s}_2 \in s^\mathcal{D}$ there exists a state $\boldsymbol{s}_1 \in s_0^\mathcal{D}$ that reaches $\boldsymbol{s}_2$ on a trace $\boldsymbol{\pi }$ where $\pi ^G(\boldsymbol{\pi }) = \pi ^G(s_0^\mathcal{D}, s^\mathcal{D})$, which, with $s^\mathcal{D}_A\subseteq s^\mathcal{D}$ also holds for all $\boldsymbol{s}_2 \in s^\mathcal{D}_A$; and (2) for every state $\boldsymbol{t}\in t^\mathcal{D}_R$ there exists an accepting state $\boldsymbol{s}_A\in s^\mathcal{D}_A$ that reaches $\boldsymbol{t}$ on a trace $\boldsymbol{\pi }$ where $\pi ^G(\boldsymbol{\pi }) = \pi ^G(s^\mathcal{D}_A, t^\mathcal{D}_R)$.

Since $r^\mathcal{D}$ is on Stack, it holds that every $\boldsymbol{s}\in s^\mathcal{D}_A$ is reachable from a $\boldsymbol{r}\in r^\mathcal{D}$, and, with $t^\mathcal{D}_R \supseteq r^\mathcal{D}$, that every $\boldsymbol{r}\in r^\mathcal{D}$ is reachable from an accepting state $\boldsymbol{s}_A\in s^\mathcal{D}_A$.

Let $pred(s^\mathcal{D}_1, s^\mathcal{D}_2, \boldsymbol{s}_2)$ be a function that, if $s^\mathcal{D}_2$ is reachable from $s^\mathcal{D}_1$ and $\boldsymbol{s}_2 \in s^\mathcal{D}_2$, outputs a state $\boldsymbol{s}_1 \in s^\mathcal{D}_1$ that reaches $\boldsymbol{s}_2$ via a trace $\boldsymbol{\pi }$ with $\pi ^G(s^\mathcal{D}_1, s^\mathcal{D}_2) = \pi ^G(\boldsymbol{\pi })$.

Let $\boldsymbol{s}_0$ be a state reached in both $t^\mathcal{D}_R$ and $r^\mathcal{D}$, and let $\boldsymbol{s}_1 = pred(r^\mathcal{D}, t^\mathcal{D}_R, \boldsymbol{s}_0)$ be its predecessor in $r^\mathcal{D}$. If $\boldsymbol{s}_1 = \boldsymbol{s}_0$, then we are done, because there exists a lasso $\boldsymbol{s}_0, \dots , \boldsymbol{s}_0, \dots , \boldsymbol{s}_A, \dots , \boldsymbol{s}_0, \dots , \boldsymbol{s}_A$, where $\boldsymbol{s}_A$ is an accepting state traversed in $s^\mathcal{D}_A$. Such an accepting state exists because all member states of a decoupled state in NestedDFS are reachable from an accepting state in $s^\mathcal{D}_A$.

If $\boldsymbol{s}_1 \ne \boldsymbol{s}_0$, then we iterate and set $\boldsymbol{s}_i = pred(r^\mathcal{D}, t^\mathcal{D}_R, \boldsymbol{s}_{i-1})$, where such $\boldsymbol{s}_i$ exist because $r^\mathcal{D}\subseteq t^\mathcal{D}_R$. Because there are only finitely many states in $r^\mathcal{D}$, eventually we get $\boldsymbol{s}_i = \boldsymbol{s}_j$ (where $j < i$) and there exists a lasso as follows:

First, there exists a cycle $\boldsymbol{s}_i, \dots , \boldsymbol{s}_{i-1}, \dots , \boldsymbol{s}_j = \boldsymbol{s}_i$, where between every pair of states $\boldsymbol{s}_k, \boldsymbol{s}_{k-1}$ an accepting state $\boldsymbol{s}_{k,A}$ in $s^\mathcal{D}_A$ is traversed, for the same reason as before. We can obviously shift and truncate the cycle to start right after and end in $\boldsymbol{s}_{i,A}$. The prefix of the lasso is $\boldsymbol{s}_0, \dots , \boldsymbol{s}_{i,A}$.    $\square$

Lemmas 2 and 3 show the soundness of our main termination criterion, and of CheckLocalAccept.

Lemma 2

Let $t^\mathcal{D}_R$ be a split decoupled state generated in NestedDFS. If for every component $\mathcal{A}^i$ there exists a component state $s^i$ such that $s^i \in t^\mathcal{D}[\mathcal{A}^i]_{s^i}$, then there exists an accepting run for $\mathcal{A}^1 \parallel \dots \parallel \mathcal{A}^n$.

Proof

Let $s^\mathcal{D}_A$ be the acceptance-split decoupled state from which NestedDFS was started. If for every component $\mathcal{A}^i$ such an $s^i$ exists, then the state $\boldsymbol{s}= (s^1, \dots , s^n)$ is reachable in both $s^\mathcal{D}_A$ and $t^\mathcal{D}_R$. By the construction of the reached state sets $t^\mathcal{D}_R[\mathcal{A}^i]_{s^i}$, $\boldsymbol{s}$ is reachable from itself and is accepting. Hence, there exists a lasso $\boldsymbol{s}_0, \dots , \boldsymbol{s}, \dots , \boldsymbol{s}$.    $\square$

Lemma 3

Let $t^\mathcal{D}$ be an accepting decoupled state generated in DFS such that a cycle is reported by CheckLocalAccept$(t^\mathcal{D})$, then an accepting run for $\mathcal{A}^1 \parallel \dots \parallel \mathcal{A}^n$ exists.

Proof

By prerequisite, there exists an accepting member state $\boldsymbol{s}$ of $t^\mathcal{D}$. If CheckLocalAccept$(t^\mathcal{D})$ reports a cycle, then there exists a component $\mathcal{A}^i$, where an accepting state $s^i \in t^\mathcal{D}[\mathcal{A}^i]$ is reached that lies on an cycle induced by transitions labelled with $L_I^i$. Thus, we can set the local state of $\mathcal{A}^i$ in $\boldsymbol{s}$ to $s^i$, and the lasso looks as follows: $\boldsymbol{s}_0, \dots , \boldsymbol{s}, \dots , \boldsymbol{s}$, where on the cycle only $\mathcal{A}^i$ moves.    $\square$

We are now ready to prove the correctness of our decoupled NDFS algorithm.

Theorem 4

Let $\mathcal{A}^1 \parallel \dots \parallel \mathcal{A}^n$ be the composition of n NBA and let $\mathcal{A}^1 \parallel _\mathcal{D} \dots \parallel _\mathcal{D} \mathcal{A}^n$ be its decoupled composition. Then CheckEmptiness$(\mathcal{A}^1 \parallel _\mathcal{D} \dots \parallel _\mathcal{D} \mathcal{A}^n)$ reports a cycle if and only if an accepting run for $\mathcal{A}^1 \parallel \dots \parallel \mathcal{A}^n$ exists.

Proof

If CheckEmptiness reports a cycle, then by Lemmas 1, 2, and 3, which cover exactly the cases where a cycle is reported, an accepting run for $\mathcal{A}^1 \parallel \dots \parallel \mathcal{A}^n$ exists.

For the other direction, assume that $\boldsymbol{\rho }$ is an accepting run for $\mathcal{A}^1 \parallel \dots \parallel \mathcal{A}^n$. Let $\boldsymbol{s}_a$, with $0 \le a < k$, be the accepting state that starts the cycle of the lasso $\boldsymbol{\rho }_p = \boldsymbol{s}_0, \dots , \boldsymbol{s}_a$, $\boldsymbol{\rho }_c = \boldsymbol{s}_{a+1}, \dots , \boldsymbol{s}_k$, where $\boldsymbol{s}_a = \boldsymbol{s}_k$. Let $\boldsymbol{\pi } = l_1, \dots , l_k$ be the trace on which $\boldsymbol{s}_k$ is reached, i.e., for all $1 \le i < k: \langle \boldsymbol{s}_i, l_{i+1}, \boldsymbol{s}_{i+1} \rangle \in \rightarrow$.

By Theorem 1, there exists a decoupled state $s^\mathcal{D}$ reached in DFS that contains $\boldsymbol{s}_a$.

If $\boldsymbol{\pi }$ is such that for all $a < i \le k: l_i \in L_I$, i.e., the cycle $\boldsymbol{\rho }_c$ is induced only by internal labels, we next proof that CheckLocalAccept$(s^\mathcal{D})$ reports a cycle: As $\boldsymbol{s}_a$ is accepting, $s^\mathcal{D}$ is accepting, too, so unless a cycle is reported before, eventually CheckLocalAccept$(s^\mathcal{D})$ is called. If $\boldsymbol{\rho }_c$ is induced by only internal labels, then, because there cannot be any component interaction via $L_I$-transitions, there must exist a component $\mathcal{A}^i$ for which the local state $s^i$ in $\boldsymbol{s}_a$ reaches itself with only $L_I^i$-transitions. We can pick any such $\mathcal{A}^i$ and ignore transitions from $\boldsymbol{\rho }_c$ that are labelled by an element of $L_I\setminus L_I^i$, since these are not required for an accepting cycle. Consequently, CheckLocalAccept$(s^\mathcal{D})$ reports a cycle.

We next show that, if $\boldsymbol{\pi }$ contains a global label on the cycle, i.e., there exists an $i \in \{a+1, \dots , k\}$ such that $l_i \in L_G$, then, unless a cycle is reported before, NestedDFS$(s^\mathcal{D}_A)$ reports a cycle, where $s^\mathcal{D}_A$ is the $l^A_G$-successor of $s^\mathcal{D}$.

Assume for contradiction that this is not the case, i.e., no cycle has been reported before, and NestedDFS$(s^\mathcal{D}_A)$ does not report a cycle. Let NestedDFS$(s^\mathcal{D}_A)$ be the first call to NestedDFS that misses a cycle, although an $\boldsymbol{s}_a \in s^\mathcal{D}_A$ that is on a cycle exists.

If $\boldsymbol{s}_a$ is on a cycle, then by Theorem 1 there exists a decoupled state $t^\mathcal{D}$ reachable from $s^\mathcal{D}_A$ that also contains $\boldsymbol{s}_a$. The result of Theorem 1 holds in this case because, by the definition of split transitions, the splitting does not affect reachability of member states. So there exists $t^\mathcal{D}_R$ reachable from $s^\mathcal{D}_A$ that contains $\boldsymbol{s}_a$.

Denote by $\boldsymbol{\pi } _c = l_{a+1},\dots l_k$ the cycle part of $\boldsymbol{\pi }$. Because $\boldsymbol{s}_a$ is an accepting member state of $s^\mathcal{D}$, all its component states $s^i_A$ become reference states in $s^\mathcal{D}_A$. Therefore, assuming that $\pi ^G(s^\mathcal{D}_A, t^\mathcal{D}_R) = \pi ^G(\boldsymbol{\pi } _c)$, for all components we have $s^i_A\in t^\mathcal{D}_R[\mathcal{A}^i]_{s^i_A}$ and a cycle is reported. If this is not the case, then either (1) $s^\mathcal{D}$ was not reached in DFS, or (2) $t^\mathcal{D}_R$ was not reached in NestedDFS$(s^\mathcal{D}_A)$.

In case (1), there must exist a state $s^\mathcal{D}_P \supseteq s^\mathcal{D}$ that prunes $s^\mathcal{D}$. But then, $s^\mathcal{D}_P$ contains $\boldsymbol{s}_a$, too, and NestedDFS was called on its $l^A_G$-successor $s^\mathcal{D}_{P,A}$ and the cycle of $\boldsymbol{s}_a$ was missed before, in contradiction.

For (2), either (a) there exists a state $t^\mathcal{D}_{P,R} \supseteq _R t^\mathcal{D}_R$ that was reached in a prior invocation of NestedDFS on an accepting state $s^\mathcal{D}_{P,A}$, or (b) a state $t^\mathcal{D}_{P,R} \supseteq t^\mathcal{D}_R$ was reached in NestedDFS$(s^\mathcal{D}_A)$ before $t^\mathcal{D}_R$. In both cases, $t^\mathcal{D}_R$ is pruned and the cycle through $\boldsymbol{s}_a$ is missed. Case (a) can only happen if $s^\mathcal{D}_{P,A}$ contains $\boldsymbol{s}_a$, too, because the reference states of $s^\mathcal{D}_A$ need to be a subset of the ones of $s^\mathcal{D}_{P,A}$. But then, the cycle of $\boldsymbol{s}_a$ was missed before, in contradiction. For (b), if $t^\mathcal{D}_R \subseteq _R t^\mathcal{D}_{P,R}$, then for all $\mathcal{A}^i$ we have $s^i_A\in t^\mathcal{D}_{P,R}[\mathcal{A}^i]_{s^i_A}$, so the cycle would have been reported before, in contradiction.

The reachability argument in (1,2a,2b) applies recursively to all predecessors of $s^\mathcal{D}$ in DFS, and of $t^\mathcal{D}_R$ in NestedDFS$(s^\mathcal{D}_A)$, so, unless a cycle is reported before, eventually a state $s^\mathcal{D}$ is reached in DFS that contains $\boldsymbol{s}_a$, and a state $t^\mathcal{D}_R$ with $s^i_A\in t^\mathcal{D}_R[\mathcal{A}^i]_{s^i_A}$ in NestedDFS$(s^\mathcal{D}_A)$.    $\square$

Fig. 10.

Statistics on the two scaling models, where #$\mathcal{A}$ is the number of philosophers, resp. the number of NBAs, Time is runtime in seconds, #States (#S) and #E are the number of visited states, resp. generated events, and Mem (M) is the memory usage in MiB.

6 Experimental Evaluation

We implemented a prototype of the decoupled NDFS algorithm from Fig. 7. The input is specified in the Hanoi Omega-Automata format [1], describing a set of NBAs synchronized via global labels as in Definition 2. We compare our prototype to the SPIN model checker [20] (v6.5.1), and to the Cunf Petri-net unfolding tool [30] (v1.6.1). We also experimented with the symbolic model checkers NuSMV and PRISM [3, 25], but both are significantly outperformed by the other methods. We conjecture that this is because both systems are not specifically designed for asynchronous execution of processes, or LTL model checking. For SPIN, we translate each NBA to a process where NBA states are represented by state labels, internal transitions by goto statements, and global transitions by rendezvous channel operations. For the latter, SPIN only supports synchronization of two processes at a time, so we restrict the models to global transitions with exactly two components. We model acceptance for SPIN explicitly using a monitor process that gets into an accepting state if all processes are in a local accepting state. The translation for Cunf encodes NBA states as net places and transitions as net transitions into a single Petri net, ignoring the individual components. In our prototype and in SPIN, when a lasso is reported or the algorithm proved that no lasso exists within the cut-off limits, we say that the instance was solved. For Cunf, we attempt to construct a complete unfolding prefix. We consider an instance solved if the construction terminates, i.e., we do not actually check the liveness property. The experiments were performed on a cluster of Intel E5-2660 machines running at 2.20 GHz, with time (memory) cut-offs of 15 min (4 GiB). Our code and models are publicly available [13].

Fig. 11.

Left part: scatterplots with the runtime of DecNDFS on the y-axis and the one of SPIN (left column) and Cunf (right column) on the x-axis, on randomly generated models. Each point represents one instance. In the top row, we highlight different ratios of local labels with different colors/shapes, in the bottom row we highlight different numbers of components. Right part: illustrations of the ring model (top) and the fork (middle) and philosopher (bottom) NBAs of the philosophers model. Initial (accepting) states are marked by an incoming arrow (double circle).

We compare SPIN with standard options, i.e., with partial-order reduction enabled, Cunf with the cut-off rule of [10], and decoupled search (DecNDFS), using two kinds of benchmarks: (1) two scaling examples to showcase the behaviour on well-known models. One is an encoding of the dining philosophers problem, the other is a ring-shaped synchronisation topology. Both are illustrated in Fig. 11 (right). The philosophers model has 2N NBAs, N philosophers and N forks, synchronized by global transitions $l^{lF_i}_G$ and $l^{rF_i}_G$. After synchronizing with its left and right fork, a philosopher can perform an internal eat transition; after releasing the forks it can perform an internal think transition. In the ring-topology model, each component can enter a diamond-shaped region via internal transitions, followed by a synchronization with its left or right neighbor via $l^i_G$ or $l^{i+1}_G$. No accepting run exists for either model. Moreover, (2) we use a set of random automata, where for each combination of a ratio of internal transitions in $\{0\%, 20\%, \dots , 80\%\}$, i.e., the number of transitions labelled with $L_I$ divided by the total number of transitions, and a number of components in $\{2, \dots , 8\}$, we generated sets of 150 random graphs. Each component has 15 to 100 local states, out of which up to $3\%$ are accepting (at least one). We ensure that none of the instances has an internal accepting cycle to focus on more interesting cases. One could easily implement a lookup similar to CheckLocalAccept, which is necessary for DecNDFS, for the other methods, too, which then essentially simplifies the problem to basic reachability.

Fig. 12.

Number of solved instances on the random models as a function of the ratio of internal transitions (left) and the number of components #$\mathcal{A}$ (right).

In Fig. 10, we show detailed statistics for the scaling models, with increasing number of components $\#\mathcal{A}$ (Time in seconds, #States is the sum of states visited in both DFSs, #E is the number of events in the prefix, Memory in MiB). In dining philosophers, SPIN and DecNDFS show similar results. SPIN has a runtime advantage in the larger instances of roughly a factor of 2, but DecNDFS uses only a fraction of the memory. Cunf clearly outperforms both. This model is not very well suited to decoupled search. Only half of the NBAs have internal transitions, and only two each, and there are no non-deterministic transitions that DecNDFS could represent compactly. On the ring-topology model, SPIN manages to exhaust the search space for up to 9 components. Cunf and DecNDFS scale significantly higher, the number of decoupled states grows only linearly in the number of components. Cunf on the other hand does show a blow-up and runs out of memory between 50 and 75 components. This showcase example only serves to illustrate a near-to-optimal case for decoupled search reductions, which likely does not carry over in this extent to real-world models.

In Fig. 11 (left part), we show detailed runtime behaviour in terms of scatter plots with a per-instance comparison on the random models. Each point corresponds to one instance, where the x-value is the runtime of SPIN, resp. Cunf, and the y-value is the runtime of DecNDFS, so points below the diagonal indicate an advantage of DecNDFS. Different ratios of internal labels (top row) and numbers of components (bottom row) are depicted in different colors/shapes. We observe that, as expected, with a higher ratio of internal transitions, the advantage of DecNDFS increases significantly. For all ratios, DecNDFS clearly improves with a higher number of components.

In Fig. 12, for the same benchmark set we show the number of solved instances as a function of the ratio (left) and of the number of components (right). Here, we see that from around $20\%$ internal transitions, DecNDFS consistently beats both SPIN and Cunf. SPIN and Cunf also benefit from the decrease in synchronizing statements, although not as much as DecNDFS. On the right, we see that starting with 4 component NBAs (#$\mathcal{A}$), DecNDFS consistently beats SPIN and Cunf. While SPIN and Cunf show a significant decline with more components, this effect is less pronounced for DecNDFS.

7 Concluding Remarks and Future Work

We have presented an approach to adapt decoupled search, an AI planning technique to mitigate the state-space explosion, to the verification of liveness properties of composed NBAs. Specifically, we have adapted a standard on-the-fly algorithm for checking $\omega$-regular properties, nested depth-first search (NDFS), and proven its correctness. The necessary adaptations essentially pertain to the conditions that identify the existence of accepting runs, which must be handled differently given the different properties of decoupled states. Our approach extends the scope of decoupled search from safety properties, as done in [12], to liveness properties. Our experimental evaluation has shown that decoupled search can yield significant reductions in search effort across random models that consist of a set of synchronized NBAs, and simple scaling showcase examples.

We have focused on a verification problem for composed NBAs that is sufficiently general to cover significant cases like automata-based LTL model checking. We believe that our solution can be adapted to other verification problems for composed NBAs, including Büchi automata with multiple acceptance conditions such as generalized Büchi automata, and language intersection of the involved automata. Indeed, NDFS has successfully been used for emptiness checking of generalized NBA. We are confident that decoupled NDFS can be adapted to the compilation introduced by [33], where an additional “counter component” is added to keep track of the components that already have an accepting cyle during the nested DFS. Concretely, we believe that the verification problem of generalized NBA can be handled with adaptations by our approach: In the compilation by [33], the counter component increases its local state from 1 to n (assuming n components), one by one whenever component i has an accepting state. We can essentially apply the same compilation in decoupled NDFS, restricting the set of local states of $\mathcal{A}^i$ to the accepting ones when the counter is increased from i to $i+1$ by a separate acceptance-split transition $l^{A^i}_G$ for each $\mathcal{A}_i$. This ensures that a global cycle includes an accepting state for all components.

There are several interesting topics for future work, like the adaptation of optimizations proposed for basic NDFS (e.g. [22, 32]), or the combination with orthogonal state space reduction methods, as previously done in the context of AI planning for partial-order reduction [16], symmetry reduction [18], and symbolic search [17]. Having focused on NDFS [5, 22, 32] in this work, we believe that the adaptation of SCC-based algorithms is a promising line of research [6, 11], extending the scope of decoupled search further to model checking of CTL properties [24].