Counterexample-Guided Partial Bounding for Recursive Function Synthesis

Abstract

Quantifier bounding is a standard approach in inductive program synthesis in dealing with unbounded domains. In this paper, we propose one such bounding method for the synthesis of recursive functions over recursive input data types. The synthesis problem is specified by an input reference (recursive) function and a recursion skeleton. The goal is to synthesize a recursive function equivalent to the input function whose recursion strategy is specified by the recursion skeleton. In this context, we illustrate that it is possible to selectively bound a subset of the (recursively typed) parameters, each by a suitable bound. The choices are guided by counterexamples. The evaluation of our strategy on a broad set of benchmarks shows that it succeeds in efficiently synthesizing non-trivial recursive functions where standard across-the-board bounding would fail.

1 Introduction

Most computational tasks can be broken into logical units, many of which involve evaluating a function over a data collection. Recursively defined data types are broadly used to implement these collections. In functional languages, recursive functions implement computations over these recursive data types. Consider a typical scenario where a programmer has implemented a function f over a collection C by defining a recursive data type A and implementing f as a recursive function $\mathtt {foo}_A$. Later, the programmer may need a different implementation $\mathtt {foo}_B$ of f over a different data type B; perhaps B is better suited for an optimized implementation of f, or the programmer now needs an implementation of a new function g (in addition to f) over the collection C and the data type B is a much better choice than A for implementing g efficiently. Ideally, the programmer should not have to start from scratch implementing $\mathtt {foo}_B$.

In this paper, we propose a generic and efficient algorithm for synthesizing recursive functions in such contexts. Our synthesis problem is specified by the following three components: (1) a recursive reference implementation that precisely defines the functionality, (2) a high level recursion skeleton that specifies a recursion strategy (i.e. a traversal plan over the new recursive data type) for the target code, and (3) a mapping, called representation function, that converts an instance of the new data type to one of the old data type (of the reference implementation), and establishes that the two are different implementations of the same concept.

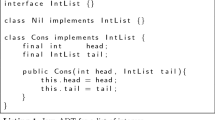
Let us illustrate our problem setup with the aid of an example. Consider the standard A-labelled binary trees, recursively defined as $T \rightarrow Nil\ |\ Node(A, T, T)$ for an arbitrary type A, and the maximum in-order prefix sum (mips)function depicted on the right. mips maintains a pair of values: sum, which keeps track of the sum of the elements it has traversed so far, and mps, which maintains the maximum value over all such sums. This reference implementation precisely defines the functional specification for a function f.

Fig. 1.

Maximum in-order prefix sum

Suppose that the programmer needs an alternative implementation that canbe efficiently parallelized, and therefore, opts for the divide-and-conquer recursion skeleton depicted on the right. The partially defined code specifies that the tree should be traversed in a manner that each subtree is processed separately, and then the results should be combined by a function join. It does not, however, specify what computation is performed; the implementation of join and the initial value for s0 are unknown. In this example, labeled binary trees are the recursive data type for both the reference implementation and the target of synthesis. In cases like this, the representation function simply becomes the identity function.

Our algorithm reduces the problem to a set of recursion-free synthesis problems, which are solved using existing synthesis tools. It synthesizes the unknown computations for join and s0, and therefore produces the divide-and-conquer implementation of mips on binary trees:

At the high level, the problem of synthesizing a new recursive function can be framed as checking the validity of formulas of the type $\exists f \forall x : \theta . \phi (f, x, \dots )$ where $\theta$ is a recursive data type (i.e. x ranges over a set of inductively defined terms), f is the target recursive function, and the ellipses stand in for all the relevant components of our specific problem statement as outlined before. Elements of type $\theta$ are unbounded in two different dimensions: the recursive structure can be of arbitrary size and each element of it belongs to an unbounded (data) domain. A straightforward way of under-approximating the unbounded specification is to bound the universal quantifier $\forall x: \theta$ in both dimensions. The synthesis problem is reformulated to synthesize the function from a bounded set of examples which are concrete bounded elements of the data type with concrete elements in them. This can be done by applying a counterexample-guided inductive synthesis (CEGIS) [34] algorithm in the straightforward way.

Alternatively, one can attempt to tackle the two dimensions independently. The quantifier $\forall x: \theta$ can be bounded in one dimension, i.e. recursive structures of bounded size can be considered, and yet the elements of these bounded structures can range over unbounded domains. More formally, the universal quantification is instantiated over a finite set of bounded-depth terms, denoted by set T, and the resulting specification becomes $\exists f. \forall \boldsymbol{a} \in D . \bigwedge _{t \in T} \phi (f, t)$ where $\boldsymbol{a}$ are the free variables of the terms in T and of non-recursive type D. This bounding reduces the original problem to a standard functional synthesis problem (over unbounded data domains) that can be discharged to one of the many known solvers, employing a variety of techniques for it. The set of terms in T can still be discovered in a counterexample guided loop in the spirit of CEGIS, and therefore this algorithm can be viewed as a symbolic CEGIS variant.

The thesis of this paper is that forcing bounds on all recursively typed variables is unnecessary and can be avoided algorithmically. A subset of variables can retain their unbounded quantification and yet the problem can be reduced to a recursion-free functional synthesis instance. Recall the mips example. The join function takes two trees, l and r, and a value a as an input. The recursion-free specification for join can retain a universal quantifier on all trees for l and limit its bounded exploration to r. In other words, one can successfully synthesize the join function from examples enumerating a few small candidate trees for r and treating h(l) (i.e. the result of the computation on l) and not l itself for the inductive enumeration of examples for synthesis. We discuss in the paper how this information can be algorithmically derived from the specific components of our synthesis problem: the reference implementation, the recursion skeleton, and the representation function.

Beyond the decision on what quantifiers should be bounded, the synthesis algorithm also needs to determine a set of terms that are used to bound these quantifiers. We propose an algorithm that discovers these bounds guided by counterexamples in a refinement-style loop. We show that this algorithm is sound, satisfies the expected weak-progress property that other CEGIS instances have, and is parsimonious in a precise sense. We have implemented this algorithm as a prototype synthesis tool Synduce and demonstrate that Synduce can efficiently synthesize recursive functions from specifications.

2 Background and Notation

The notation introduced in this section is used for formalizing the result of applying recursive functions to symbolic inputs.

Terms. We make use of a set of symbols that are partitioned into terminal symbols $\varSigma$, non-terminal symbols $\mathcal {N}$, and an infinite set of typed variables $\mathcal {V}$. There is a unique symbol $\circ _{?}$ that stands for a hole. Terms are defined by the grammar $T \rightarrow x\ |\ T\ T$ where x is a symbol, and $T\ T$ is a function application. These are the relevant classes of terms:

• Concrete terms $T(\varSigma )$ are those containing only terminal symbols. Every concrete term can be interpreted and has a concrete value.

• Symbolic terms $T(\varSigma , \mathcal {V})$ are those containing terminal symbols or variables.

• Closed terms $T(\varSigma , \mathcal {N})$ are those containing terminal or non-terminal symbols, but no variables.

• Applicative terms $T(\varSigma , \mathcal {N}, \mathcal {V})$ are those containing any symbol except the hole symbol.

• Contexts $T(\varSigma , \mathcal {N}, \mathcal {V}, \circ _{?})$ are those with at least one hole. A one-hole context $C[\ ]$ is a context with a single occurrence of $\circ _{?}$, and C[t] stands for the term formed by replacing the single hole in $C[\ ]$ with the term t.

Two terms are equal, denoted by $t =_\alpha t'$ (standard alpha conversion), iff there exists two injective substitutions $\sigma : FV(t) \rightarrow \mathcal {V}\setminus (FV(t) \cup FV(t'))$ and $\sigma ' : FV(t') \rightarrow \mathcal {V}\setminus (FV(t) \cup FV(t'))$ such that $\sigma t = \sigma ' t'$ (i.e. syntactically equal).

A symbolic term t can be expanded into a term $t'$ iff there exists a substitution $\sigma : FV(t) \rightarrow T(FV(t') \cup \varSigma )$ that substitutes the free variables of t for symbolic terms with the free variables of $t'$ such that $t' = \sigma t$. The relation $\succeq$ over symbolic terms, is a partial order defined as, $t \succeq t'$ iff t can be expanded into $t'$. A single variable is the maximal element according to this partial order and concrete terms (of any depth) are minimal elements.

Recursive Functions. This paper focuses on recursive functions $f : \tau \rightarrow D$ with terms of a recursive type ($\tau$ or $\theta$) as input, and an output of type D. These functions can be executed on concrete or symbolic input terms of type $\tau$. We assume all functions can be translated to recursion schemes as defined below:

Definition 1

([26]). A recursion scheme is a tuple $\mathcal {P}= \langle \varSigma , \mathcal {N}, \mathcal {R}, \varLambda \rangle$ where:

• $\varSigma$ is a ranked alphabet of terminals

• $\mathcal {N}$ is a finite set of typed non-terminals.

• $\mathcal {R}$ is a finite set of rewrite rules, each in one of the following shapes $(m \ge 0)$:

  (pure)	$F\ x_1\ \ldots \ x_m \rightarrow t$
  (pattern matching)	$F\ x_1\ \ldots \ x_m \ p \rightarrow t$

  where the $x_i$ are variables, p is a symbolic term, t is an applicative term in $T(\varSigma \cup \mathcal {N}\cup \{x_1, \ldots , x_n\})$, and F is a non-terminal.

• $\varLambda : \tau \rightarrow D$ is a distinguished non-terminal symbol whose defining rules are always pattern-matching rules.

We associate with each recursion scheme $\mathcal {P}$ a notion of reduction. A redex is an applicative term of the form $F\ \sigma x_1\ \ldots \ \sigma x_m\ \sigma p$ for a substitution $\sigma : \mathcal {V}\rightarrow T(\varSigma , \mathcal {N}, \mathcal {V})$ and rule $F\ x_1\ \ldots \ x_m\ p \rightarrow t$ in $\mathcal {R}$. The contractum of the redex is $\sigma t$. The one-step reduction relation $\mapsto \subseteq T(\varSigma , \mathcal {N}, \mathcal {V}) \times T(\varSigma , \mathcal {N}, \mathcal {V})$ is defined by $C[s] \mapsto C[t]$ whenever s is a redex, t is a contractum and $C[\ ]$ is a one-hole context. A recursion scheme is deterministic iff for any redex $F\ s_1\ \ldots \ s_m$ there is exactly one rule $l \rightarrow r$ (in $\mathcal {R}$) which matches that redex, i.e. there exists a substitution $\theta$ such that $F\ s_1\ \ldots \ s_m = \theta \ l$.

Given a recursion scheme $\mathcal {P}= \langle \varSigma , \mathcal {N}, \mathcal {R}, \varLambda \rangle$ and a term $s \in T(\varSigma , \mathcal {N}, \mathcal {V})$, $\mathcal {L}(\mathcal {P},s)$ denotes the language of $(\varSigma \cup \mathcal {N}\cup FV(s))$-labelled trees resulted from the maximal rewriting of the term s with the one-step reduction relation associated to $\mathcal {P}$. If $\mathcal {P}$ is deterministic, then $\mathcal {L}(\mathcal {P},s)$ is a singleton (the term s reduces to only one possible term), and $\llbracket s \rrbracket _\mathcal {P}$ denotes the unique resulting term. This notion of reduction is slightly different from the one used in [26], in that we do not require the substitution to be closed.

Symbolic Evaluation. For any function f that can be defined as a recursion scheme, the symbolic evaluation of f on input s is simply $\llbracket s \rrbracket _f$. In other words, $f(s) = \llbracket s \rrbracket _f$. In this view, recursive functions and the corresponding recursion schemes are interchangeable. For a recursion scheme $\langle \varSigma , \mathcal {N}, \mathcal {R}, \varLambda \rangle$ representing a function f and a variable x, f(x) and $\varLambda \ x$ become two different ways of referencing the same concept. In this paper, we assume that all recursion schemes to be deterministic total functions. Specifically, they terminate on all inputs; symbolic evaluation (or the equivalent reduction) of a symbolic term always terminates.

Types Notation. We use capital letters A, B, C, and D to refer to base types, which are scalar types ($\text {int}, \text {bool}, \text {char}, \ldots$) or unlabeled products of scalar types (e.g. $\text {int}\times \text {int}$). Our focus is on functions that take as input elements of recursive variant (or sum) types denoted by $\tau , \theta , \ldots$. We denote by $\kappa _1, \ldots , \kappa _n$ the constructors of a variant type $\tau$ with n variants. Each constructor is assimilated to a terminal symbol $\tau _1 \times \ldots \times \tau _k \rightarrow \tau$, where $k \ge 0$. We assume that all recursive types define finite structures, that is, one can always construct a term of type $\tau$ with a finite number of constructors and elements of base type. $x : \tau$ denotes the judgement x is of type $\tau$, and $\forall x : \tau$ denotes the universal quantification of all variables x of type $\tau$.

In this setting, where we distinguish base types and recursive types, we differentiate bounded terms, which are symbolic terms where all free variables are of base type (in $\mathcal {V}_B$), and unbounded terms where some variables can be of recursive type. An unbounded term t is a symbolic term of finite size, but there are infinitely many bounded terms that are expansions of t.

3 Formal Definition of the Synthesis Problem

The synthesis problem solved in this paper is defined by three components: a reference recursive function $f: \tau \rightarrow D$, a representation function $r: \theta \rightarrow \tau$ that maps inputs of the target function to those of f, and a recursion skeleton for the target function. All three components are formally modelled by recursion schemes (Definition 1). f and r are standard recursive functions representable by deterministic recursion schemes. The recursion scheme for the recursion skeleton $\mathcal {S}[\varXi ] : \theta \rightarrow D$ includes a special set $\varXi$ of symbols as a subset of its terminal symbols, which correspond to the unknown components for synthesis. These unknowns stand for constants or functions that have to be synthesized.

At the high level, the solution to the synthesis problem is the definition of a new recursive function. At the low level, each of the unknowns in $\varXi$ need to be given a definition. In each problem instance, it is assumed that f and $\mathcal {S}[\varXi ]$ use a common set of terminal symbols $\varSigma$ that belong to a background theory $\mathcal {T}$ (e.g. linear integer arithmetic). Formally, the solution is identified by a mapping Z from the unknowns $\varXi$ to function definitions $\lambda x_1. \ldots \lambda x_n. t$ where $n \ge 0$ and t is a symbolic term in $T(\varSigma , \{x_1, \ldots , x_n\})$ (a concrete term if $n = 0$). Let $\mathcal {S}[\varXi / Z]$ be the recursion scheme obtained by replacing the unknowns $\varXi$ by their definition in Z. Any solution Z that satisfies the following specification is a valid solution:

$$ \varPsi \equiv \forall x : \theta , \mathcal {S}[\varXi / Z](x) = (f \circ r) (x) $$

Example 1

We use a problem instance with the goal of synthesizing a recursive function on tree paths as a running example of this paper. Recall the mips function given in Fig. 1. Suppose that we want to transform it to a function on tree paths¹ as an alternative data type to labelled binary trees. For an A-labelled tree (of type Tree), $Path$ is a datatype defined by the following grammar:

$$ Path \rightarrow Top \ | \ Zip ((\top | \bot ), A, Tree , Path )$$

Intuitively, a path decomposes a tree as shown on the right. The path $Zip (\top ,a,t_a, Zip (\bot , b,t_b, Zip (\top ,c,t_c,x)))$, from the root to a leaf decomposes the tree into the subtrees $t_a$, $t_b$, and $t_c$.

The synthesis problem is specified by three recursion schemes. The recursion scheme f, on the right, models the function mips from Fig. 1. $\varLambda _f$ is the non-terminal corresponding to the main function mips and G is an auxiliary function. An additional non-terminal L is used to mirror the tuple decomposition done by the let-binding in the code of mips.

The second recursion scheme is the representation function r from paths to trees. The input path is recursively decomposed by the rewrite rules, and $Node$ is constructed recursively on the right or on the left depending on the first value contained in the $Zip$ constructor.

The last recursion scheme specifies the recursion skeleton of the target function with unknowns $s_0$, $g_l$ and $g_r$. It traverses the input path, making recursive calls ($\varLambda _S\ z$) on paths, and calling the reference function on subtrees ($\varLambda _f\ t$). The goal is then to synthesize implementations of $s_0$, $g_l$ and $g_r$ such that $\mathcal {S}[s_0,g_l,g_r]$ is equivalent to $f \circ r$.

4 Recursion-Free Approximations

A system of recursion-free equations models an approximation of the full functional specification $\varPsi$ for a recursive synthesis problem instance.

Definition 2

Given two sets of terminals $\varSigma$ and $\varXi$, a system of recursion-free equations is a finite set of constraints $\{ e_i = e_i'\}_{}$ where $e, e' \in T(\varSigma \cup \varXi , \mathcal {V}_B)$.

We denote by $\{ e_i = e_i'\}_{i \in I}$ the set of constraints of the system, and $\{x_j\}_{1 \le j \le n} \equiv \bigcup _{i \in I} FV(e_i) \cup FV(e_i')$ are the free variables in the system. The above system defines a synthesis problem where $\varSigma$ is the signature of some theory $\mathcal {T}$ and $\varXi$ is the set of unknowns to be synthesized. A solution Z to this synthesis problem is a mapping from $\varXi$ to function definitions. Z is valid iff the following formula is valid:

$$\begin{aligned} \forall x_1 : D_1. \ldots \forall x_n : D_n. \bigwedge _{i \in I} (e_i = e_i')[\varXi / Z] \end{aligned}$$

where $(e_i = e_i')[\varXi / Z]$ denotes the term in which the unknowns $\varXi$ have been replaced by their definition in Z. In the rest of the paper, we consider systems of recursion-free equations where the set of terminals $\varSigma$ and the set of unknowns $\varXi$ are fixed and the same as in the main synthesis problem of Sect. 3. We say that a system $\mathcal {E'}$ is a sound approximation of a system $\mathcal {E}$ ($\mathcal {E'} \gtrsim \mathcal {E}$) (or the synthesis problem $\varPsi$) when any solution of $\mathcal {E}$ (or $\varPsi$) is also a solution of $\mathcal {E}'$.

4.1 Partially Bounded Quantification

Consider the formal definition of the synthesis problem in Sect. 3. Bounding the quantifiers consists in expressing the problem on a finite set of bounded terms. This bounding effectively eliminates recursion; recursive calls can be inlined a bounded number of times. Yet, since the free variables of the bounded term are universally quantified over an infinite base domain, a bounded term t of type $\theta$ represents an infinite set of concrete inputs (of bounded size).

We propose a different strategy for bounding the quantifiers: we aim to instantiate the quantifier on a finite set of bounded and unbounded terms such that the resulting specification is not recursive. To start, we instantiate the universal quantifier by a finite set of arbitrary symbolic terms T. Our first approximation then becomes the set of constraints:

$$\begin{aligned} E(T) = \{ \mathcal {S}[\varXi ](t) = (f \circ r) (t) \ | t \in T \} \end{aligned}$$

(1)

The set of constraints E(T) can be seen as a synthesis problem where free variables are universally quantified and the unknowns in $\varXi$ are to be synthesized. E(T) is not guaranteed to be a system of recursion-free equations for all choices of T. For an arbitrary symbolic term t, calls to recursive functions may appear in subterms of $\mathcal {S}[\varXi ](t)$ and $(f \circ r) (t)$. Restricting T to bounded terms would yield a recursion-free system after symbolic evaluation of both sides of the equation.

This, however, is too restrictive. There may exist unbounded terms t where the equation $\mathcal {S}[\varXi ](t) = (f \circ r) (t)$ can be rewritten to an equivalent recursion-free equation. Intuitively, in an applicative term (resulting from the symbolic evaluation of a recursive function f) the simple subterms of the form f(x) where x is a variable can be eliminated by replacing f(x) with a single variable a of type D which now stands for the result of the invocation of f on any x.

Definition 3

A symbolic term t is maximally reducible (t is a MR-term) by a recursion scheme $\mathcal {P}= (\varSigma , \mathcal {N}, \mathcal {R}, \varLambda )$ iff $\llbracket t \rrbracket _{\mathcal {P}}$ is an applicative term in $T(\varSigma , \mathcal {N}, \mathcal {V})$ such that replacing all subterms of the form $(\varLambda \ x)$ (where $x \in \mathcal {V}$) by a fresh variable $x' \notin FV(t)$ yields a symbolic term.

Example 2

The term $z = Zip (\top , a, t, Top)$ where a is an integer and t is of type Tree is maximally reducible by $f \circ r$ and $\mathcal {S}[s_0,g_l,g_r]$ (cf. Example 1). First we have $r(z) = \llbracket z \rrbracket _{r} = Node (a, t, Nil)$ and $(f \circ r)(z) = G\ (L\ a\ (\varLambda _f\ t))\ Nil$. If $\varLambda _f\ t$ is replaced by $(a_1, a_2)$ (of type $\text {int}\times \text {int}$), then the term can be reduced further to $(a_1 + a, max(a_1 + a, a_2))$. For the other function, we have $\mathcal {S}[s_0,g_l,g_r](z) = g_l\ a\ (\varLambda _f\ t)\ s_0$. If $\varLambda _f\ t$ is also replaced by $(a_1, a_2)$, then the term reduces to the symbolic term $g_l\ a\ (a_1, a_2)\ s_0$. Note that z is an unbounded term, since t is a variable representing a tree of arbitrary depth.

If every term in T is maximally reducible by both $(f \circ r)$ and $\mathcal {S}[\varXi ]$, then every call to a recursive function can be eliminated in E(T). Note that this new sufficient condition for E(T) to be recursion free is strictly weaker than the condition of having the terms in T to be bounded; a maximally reducible term need not be a bounded term.

Definition 4

A set of constraints $E(T) = \{ \mathcal {S}[\varXi ](t) = (f \circ r) (t) \ | t \in T \}$ is well-formed iff every $t \in T$ is maximally reducible by $f \circ r$ and $\mathcal {S}[\varXi ]$.

A well-formed set of constraints E(T) can be transformed to a system of recursion-free equations. For each free variable $x : \theta$ in E(T), a fresh variable a : D is added and the subterms $(f \circ r)(x)$ and $\mathcal {S}[\varXi ](x)$ are replaced by a in every constraint. We call this rewriting step recursion elimination over D. Note that the calls to $f \circ r$ and $\mathcal {S}[\varXi ]$ are both replaced by the same variable, since their equivalence is part of the specification of the synthesis problem.

The transformation described above produces a recursion-free system of equations, but it does not always yield a sound abstraction, specifically when $f \circ r$ is not onto D. There may exist a solution of $\varPsi$ that is not a solution of the resulting system of equations. This can be fixed by having additional constraints (invariants) on the fresh variables. Let $Im_f : D \rightarrow \text {bool}$ a predicate such that $f \circ r$ is onto $\{c \ |\ c : D \wedge Im_f (c)\}$. Then, the abstraction is sound if the choices for a : D are limited to when $Im_f (a)$ holds.

Example 3

Recall Example 1. The maximum in-order prefix sum is not onto $\text {int}\times \text {int}$, since the second element of the pair is always a positive integer. The constraint $Im_f (x,y) = y \ge 0$ is required to make the function onto. In Example 2, $a_2$ must be a positive integer.

Definition 5

Let T be a set of maximally reducible terms by $f \circ r$ and $\mathcal {S}[\varXi ]$, and $Im_f$ a predicate such that $f \circ r$ is onto $\{c\ |\ c : D \wedge Im_f (c)\}$. We denote by $\mathcal {E}(T)$ the equation system obtained by rewriting each constraint in E(T) to a recursion free equation, through recursion elimination over $\{c\ |\ c : D \wedge Im_f (c)\}$.

In the synthesis problem defined by $\mathcal {E}(T)$, the variables introduced by recursion elimination are universally quantified over their restricted range. The exact encoding of the range restriction by $Im_f$ depends on the implementation of a synthesis oracle.

Proposition 1

Z is a solution of $\mathcal {E}(T)$ iff Z is a solution of E(T).

The proof follows from the construction of $\mathcal {E}(T)$ based on E(T). Combining this with the fact that E(T) results from bounding the universal quantifications in $\varPsi$, we can conclude that $\mathcal {E}(T)$ approximates $\varPsi$.

Theorem 1

(Sound approximation). If T is a set of maximally reducible terms by $f \circ r$ and $\mathcal {S}[\varXi ]$, $\mathcal {E}(T)$ is a sound approximation of $\varPsi$.

By construction, any solution of the functional specification $\varPsi$ is a solution of the system of equations $\mathcal {E}(T)$.

Example 4

Let $T = \{ Top, Zip(\top , a, t, Top), Zip(\bot , a, Nil, z) \}$ be a set of terms, where a : int, t : Tree and z : Path. Top is a concrete term, therefore maximally reducible. We saw in Example 2 that $Zip(\top , a, t, Top)$ is a MR-term. With a similar reasoning, one can conclude that $Zip(\bot , a, Nil, z)$ is a MR-term; note how the term differs in which subterm is unbounded depending on the first component of the Zip. Therefore, E(T) is a well-formed set of constraints and by substituting $\varLambda _f\ t$ and $\varLambda _S\ z$ for $(a_1, a_2)$ (where $a_1 : \text {int}$ and $a_2 \in \{v : \text {int}| v \ge 0\}$), we obtain the following recursion-free system of equations:

$$ \mathcal {E}(T) = \left\{ \begin{array}{rcl} 0,0 &{} = &{} s_0, \\ a_1 + a, max(a_1 + a, a_2) &{} = &{} g_l\ a\ (a_1, a_2)\ s_0 \\ a_1 + a, max(a_1 + a, a_2) &{} = &{} g_r\ a\ s_0\ (a_1, a_2) \\ \end{array}\right. $$

with free variables a : int, $a_1 : int$ and $a_2 \in \{ v : int | v \ge 0\}$.

In contrast to a canonical CEGIS setting, where the approximation is the specification projected over a finite set of concrete terms, our abstraction is over an infinite set of concrete terms represented by a finite set of symbolic terms. In the original functional specification, the equational constraint $(f \circ r)(x) = \mathcal {S}[\varXi ](x)$ ranges over all possible terms x of type $\theta$. In the abstraction $\mathcal {E}(T)$, the universally quantified variables are the free variables of the terms in the equations, which correspond to the variable symbols of scalar type used in the symbolic terms of T, modulo the introduction of fresh variables during the rewriting of the set of constraints E(T) to the system of equations $\mathcal {E}(T)$.

4.2 Refining Systems of Equations

Our approximation, the system of equations $\mathcal {E}(T)$, is parametric on a set of maximally reducible terms T. This approximation can be refined by adding terms to T, since for any two set of terms R and T such that $R \subseteq T$, $\mathcal {E}(R) \gtrsim \mathcal {E}(T)$.

The convergence of the refinement process depends on the terms added at each step. We present our refinement algorithm in the next section, but the main insights behind it, not tied to specific algorithmic choices, are captured by Propositions 2 and 3.

Proposition 2

Let T be a set of MR-terms and Z be a solution of $\mathcal {E}(T)$. Then for any term $t'$ such that there exists $t \in T$ s.t $t \succeq t'$, Z is a solution of $\mathcal {E}(T \cup \{t'\})$.

This proposition implies that if Z is a spurious solution, then a counterexample term showing that it is not a solution of $\varPsi$ is necessarily not expanded from a term in T. We also learn that T should ideally be an antichain of $\succeq$ at every refinement round, since adding expanded terms does not strengthen the approximation.

Proposition 3

Given two terms t and $t'$ such that $t \succeq t'$ (i.e. $t'$ is an expansion of t) and a set of MR-terms T such that $\forall x \in T, \lnot (x \succeq t \wedge t \succeq x)$, we have $\mathcal {E}(T \cup \{t\}) \precsim \mathcal {E}(T \cup \{t'\})$.

Adding the less expanded term (i.e. t) yields both a more general approximation and a more compact one. In other words, given a choice, always choose the least expanded term as the counterexample for refinement.

5 Synthesis Algorithm

Our synthesis algorithm computes a sequence of approximations of the functional specification $\varPsi$ from Sect. 3. Each approximation is a system of equations of the form $\mathcal {E}(T)$ (Definition 5). The approximations are incrementally refined until the synthesis solution for one is also a valid solution for the synthesis problem specified by $\varPsi$.

Fig. 2.

Approximation refinement algorithm.

Figure 2 illustrates the work flow of our algorithm. At the beginning of each iteration, a solution of the system of recursion-free equations $\mathcal {E}(T)$ is synthesized. If no solution is found, then there is no solution for the original synthesis problem, since the $\mathcal {E}(T)$ is guaranteed to be a sound approximation (Theorem 1). If a solution Z is found, then Z is verified against $\varPsi$ and if it passes, then it is returned as a solution. Otherwise, the verifier returns a counterexample term $x_C$. By Proposition 2, $x_C$ cannot be an expansion of any term in T, and new terms related to $x_C$ have to be added to T in the spirit of refinement.

The algorithm additionally keeps track of a set U of non-maximally reducible terms, which intuitively represents the set of inputs not covered by the current approximation. The sets T and U are complementary in a precise sense: $T \cup U$ is always a boundary of $\succeq$. A boundary (of a partial order) is an antichain C such that for any bounded term t, there is some c in C such that $c \succeq t$.

The counterexample $x_C$ is necessarily an expansion of some term $u_C \in U$. But since $u_C$ is by definition not maximally reducible, one cannot just remove it from U and add it to T. The Expand step takes $u_C$ as an input and produces two sets $T'$ and $U'$ to update the current sets T and U and repair the boundary before the loop restarts.

The figure on the right is a graphical representation of the boundary repair. The sets T (in blue) and U (in red) initially form a boundary. This boundary is updated by removing the term $u_C$ and adding $U'$ and $T'$ (the results of the Expand step) to form a new boundary. The fact that $T \cup U$ always forms a boundary is a required invariant of this refinement loop: (i) T, as a parameter of $\mathcal {E}(T)$, is required to be an antichain (as discussed in Sect. 4.2), and (ii) the Generalize step relies on the assumption that U is an antichain containing all the terms not yet sufficiently expanded to be in T.

We rely on existing tools/techniques for the steps Synthesize and Verify of Fig. 2. In the following, we describe the Initialize, Expand, and Generalize steps of the algorithm.

Initialization. There is a straightforward way to initialize T and U: apply the Expand component to a single variable x of type $\theta$ and take the resulting sets T of maximally reducible terms and U of non-maximally reducible terms. The Expand step is described in the next section. For Example 1, a variable x of type $Path$ is expanded to produce $T = \{Top\}$ and $U = \{ Zip (\bot , a, t, z), Zip (\top , a, t, z)\}$ with variables a, t, and z of the appropriate types.

5.1 Expand : Producing Maximally Reducible Terms

Given an input term $u_C$, Expand generates two sets $T'$ and $U'$ such that the terms

in $T'$ are maximally reducible by both $f \circ r$ and $\mathcal {S}[\varXi ]$. The computation of these terms is done by expanding the input term $u_C$ until a set of maximally reducible terms is found. The algorithm on the right illustrates the process. At each step, a term $u_0$ is picked from the set of non-maximally reducible terms $U'$. This term is expanded once, by a call to ExpandOnce (which is described later). The resulting set of terms is then partitioned into a set of maximally reducible terms $T'$ and a set of non-maximally reducible terms $U''$; the latter is used to update $U'$.

The choice of $u_0$ at the first line of the loop is important for the termination of the algorithm. There may be an infinite sequence of expansions if the $u_0$’s are adversarially chosen. There always exists a finite sequence of expansions yielding bounded terms which are by definition maximally reducible. A breadth-first exploration of all expansions is one such strategy that ensures the termination of the algorithm.

  The input of ExpandOnce is a term $u_0$ that is not maximally reducible. The following proposition characterizes $u_0$ and the reason for its non-reducibility:

Proposition 4

Let $u_0 \in T(\varSigma , \mathcal {V})$ and $g = (\varSigma , \mathcal {N}, \mathcal {R}, \varLambda )$ a recursion scheme. $u_0$ is not maximally reducible by g iff there exists a subterm of $\llbracket u_0 \rrbracket _g$ of the form $s = F\ t_1\ \ldots t_n\ x$, where $F \in \mathcal {N}$ and $F \ne \varLambda$, the terms $t_1 \ldots t_{n}$ are applicative terms, and $x \in FV(u_0)$.

The proof by cases on the subterms of $u_0$ is given in the extended version of this paper [7]. In order to take a step towards making $u_0$ maximally reducible, the variable x needs to be expanded. Expanding x into a term guarantees some rule $F\ x_1\ \ldots x_n\ p \rightarrow t \in \mathcal {R}$ can be used to reduce $u_0$ further. Such a rule is guaranteed to exist for a recursion scheme representing a total function.

Next, we define how $u_0$ is expanded at a variable x identified by Proposition 4. $u_0$ can be written as C[x] for some one-hole context $C[\ ]$. Assume the type $\beta$ of x has constructors $\kappa _1, \ldots \kappa _n$ where each $\kappa _i$ has type $\gamma _i \rightarrow \beta$. The pointwise expansion of $u_0$ at x is the set of terms $\{C[\kappa _1(x_1)], \ldots , C[\kappa _n(x_n)]\}$ where each $x_i$ is a variable (or a tuple) of variables of type $\gamma _i$.

In summary, ExpandOnce first identifies a variable x in $u_0$ (Proposition 4) that needs to be expanded and then performs the pointwise expansion of $u_0$ at x and returns the resulting set of terms.

One important feature of ExpandOnce is that terms are expanded only where needed. Proposition 4 identifies the precise location (i.e. x) where expanding is necessary and ignores locations where it is not.

Example 5

Recall Example 1. Suppose $u_0 = Zip (\top , a, t, \underline{z})$ is a (symbolic) path and an input to ExpandOnce, where a is an integer, t is of type Tree, and z is of type $Path$. $u_0$ is not maximally reducible and has to be expanded. Note that $r(u_0) = Node (a, t, \varLambda _r\ \underline{z})$ and therefore $(f \circ r)(u_0) = G\ (L\ a\ (\varLambda _f\ t))\ (\varLambda _r\ \underline{z})$. The subterm $(\varLambda _r\ \underline{z})$ blocks the reduction of the term starting with G, because $\underline{z}$ blocks the reduction of $\varLambda _r\ \underline{z}$ and therefore, $u_0$ has to be expanded at $\underline{z}$. The pointwise expansion of $u_0$ at $\underline{z}$ yields the terms $u_{1} = Zip(\top , a, t, \underline{Top})$, $u_2 = Zip (\top , a, t, \underline{ Zip (\top , a', t', z')})$, and $u_3 = Zip(\top , a, t, \underline{ Zip (\bot , a', t', z')})\}$. Note that the tree element t need not be expanded; we showed in Example 2 that $u_1$ is maximally reducible and therefore, the expansion loop stops and returns $T' = \{u_1\}$ and $U' = \{u_2, u_3\}$.

Consider the symmetric term $Zip (\bot , a, \underline{t}, z)$ acquired by replacing the $\top$ in $u_0$ with $\bot$. The expansion of this term yields $T' = Zip (\bot , a, \underline{ Nil }, z)$ and $U' = \{ Zi (\bot , a, \underline{ Node (a', l, r)}, z)\}$. Note that unlike the case for $u_0$, the tree element of the path has to be expanded and the path element need not be expanded.

5.2 Counterexample Generalization

The generalization of the counterexample $x_C$ is the unique term $u_C \in U$ such that $u_C \succeq x_C$. The term $u_C$ is guaranteed to exist because the algorithm maintains the invariant that $T \cup U$ is a boundary, and it is unique since U is always an antichain.

Example 6

After initialization, the synthesis solver attempts to find a solution for the system of equations given in Example 4. One possible solution is

$$s_0 = (0,0) g_l(a, (s_1, m_1), (s_2, m_2)) = a + s_1, max(m_1, a + s_1)$$

together with a similar solution for $g_r$. But the solution for $g_l$ is incorrect; the first component should be $a + s_1 + s_2$ (i.e. the sum of both partial sums and the label of the node). The verifier returns a counterexample of the form $x_c = Zip (\top , 1, Node (?), Zip (\top , -2, Node (?), ?))$ where the question marks stand for concrete subterms of the appropriate type. These subterms are ignored. The counterexample is generalized by selecting $u_2 = Zip(\top , a, t, Zip(\top , a', t', z'))$ (where $u_2 \succeq x_C$), the term that was stored in U after the expansion described in Example 5. This determines where the algorithm must unfold the path one more time to build a stronger approximation.

We report in Sect. 7 that Synduce succeeds in finding a solution for this example with 3 refinement rounds in 1.57 s, whereas the symbolic CEGIS (described in Sect. 1) times out after 10 min over 6 refinement rounds.

5.3 Algorithm Properties

Soundness. Under the assumption that the steps Synthesize and Verify are soundly implemented, the overall algorithm is sound. By construction, T is always a set of maximally reducible terms. Therefore, $\mathcal {E}(T)$ is a guaranteed to be a sound approximation of $\varPsi$ by Theorem 1. The soundness of the verification oracle guarantees that any returned solution is in fact a solution of the synthesis problem specified by $\varPsi$.

Weak Progress. Consider the naive algorithm that would expand T by simply adding the counterexample $x_C$ to it; $x_C$ is a maximally reducible term after all. This naive algorithm satisfies a weak progress property, namely that, the spurious solution Z from any round will not be a solution in any future round. Our algorithm does something more sophisticated and therefore it has to be argued that the same weak progress property holds. First, Expand satisfies the following property that guarantees $T \cup U$ to always be a boundary:

Proposition 5

Let t be some symbolic term and $T', U'$ be the results of the call to Expand(t). Then $T' \cup U'$ is a boundary of the set $\{ t' | t \succeq t' \}$.

Let $u_C$ be the generalization of $x_C$. Proposition 5 guarantees that Expand computes and adds all possible expansions of $u_C$ to T. This in turn implies that there always exists a term $t \succeq x_C$ in the updated set T (after the call to Expand), which rules $x_C$ out as a spurious solution in all future rounds. Note that the algorithm relies on the existence of $u_C$ in U. For this, it requires $T \cup U$ to be a boundary.

Parsimony. Finally, we can show that our algorithm is parsimonious with the selection of the terms for T in the following precise way:

Theorem 2

[Parsimony] Let us assume (T, U) is a boundary that our algorithm reaches in some round, then (T, U) is optimal in the following two senses:

• for every $t \in T \cup U$ there is no MR-term $t'$ such that $t' \succeq t$.

• there is no non-empty subset $T'$ of T and set $U'$ such that $(T \setminus T') \cup U'$ is a boundary and $\mathcal {E}(T \setminus T') \precsim \mathcal {E}(T)$.

Intuitively, all the terms in T are expanded to the extent necessary and no proper subset of T can form a boundary that maintains the same precise approximation that $T \cup U$ induces. The full proof appears in [7].

6 Implementation

Our approach is implemented in Synduce [36], a tool written in OCaml [22], and the inputs are recursive functions and datatypes written in Caml.

6.1 Verification and Synthesis Oracles

Synduce uses bounded model checking to implement Verify from Fig. 2. A bounded check for the validity of a synthesis solution Z is encoded as the validity of the formula $\wedge _{t \in T} \forall a \in FV(t). \mathcal {S}[\varXi / Z](t) = (f \circ r)(t)$ for a set of bounded terms T. Z3 [25] is used as the backend SMT solver, which produces a counterexample in the form of a term for which at least one equality constraint is invalid.

Synduce spends most of its time in the Synthesize box of Fig. 2. Since the input to Synthesize is guaranteed to be a recursion-free synthesis specification, any off-the-shelf syntax-guided synthesis (SyGuS) [4] solver that supports the standard language [29] can be used to implement Synthesize. We use CVC4 [5] for the results presented in this section.

A SyGuS problem is specified by a grammar describing the space of programs to be synthesized and a set of constraints. In this case, the grammar is generated from the type of the functions to be synthesized (the unknowns in $\varXi$), which can be inferred from the constraints where they appear. Instances of generic grammars for integers and booleans can be found in the SyGuS language specification [29], and these grammars for base types can be combined into tuples in a straightforward manner. The constraints are the equations of the system, with the addition of the predicates constraining the domain of the variables, i.e. $Im_f$ from Definition 5. Each recursion-free equation $e = e'$ is translated to a constraint of the form $\lnot (\bigwedge _{v \in FV(e) \cup FV(e')} Im_f (v))\vee e = e'$ where $Im_f(v)$ is the predicate associated to the variable v.

6.2 Baseline Method

The goal of our experimentation is to evaluate the efficiency and efficacy of the proposed partial quantifier bounding approach for synthesis of recursive programs. Since there is no available (automated) tool that solves the specific problem posed in this paper, we implemented the symbolic CEGIS technique (as outlined in Sect. 1) to serve as a baseline. To be precise, the algorithm of Fig. 2 is modified by removing the Generalize and Expand steps; the symbolic counterexample returned by the verification at each step is added directly to the set of terms instead of being generalized. The set T is also initialized as a set of bounded terms of some minimal depth, depending on the particular definition of the data type. Note that since the baseline method is counterexample-guided, it is better than the more straightforward finitization techniques, for example, manual finitization by a preset bound.

We also implemented the concrete CEGIS method (outlined in Sect. 1) to confirm that the symbolic CEGIS is the better choice. Symbolic CEGIS solves 6 more benchmarks than concrete CEGIS, and does better time-wise in the vast majority of the rest. Detailed results are given in the extended version of this paper [7].

6.3 Optimizations

We implemented a few simple, straightforward and generic (i.e. they can be incorporated in any SyGuS solver) optimizations. These aim to compensate for the brittleness of the SyGuS solvers, which can fail for very simple constraints for no good reason. Here is a brief overview of these optimizations, which are applicable to any system of equations (baseline’s and ours):

• Syntactic definitions, which are those that define an unknown function $\xi$ unequivocally in the form of $\xi (x_1, \ldots , x_n) = t$, can be identified quickly and eliminated from the synthesis task to simplify it.

• A system of equations can be split into independent subsystems by identifying an independent subsets of equations. A subset of equations is independent if it constrains a subset of the unknowns that does not appear in the rest of the set of equations. Identification of independent subsystems generates simpler subproblems.

• Instead of starting from a default initial state, we can start from a set of terms that makes for an interesting first round and consequently saves a few refinement rounds from the solution. We form a set of initial terms by using the Expand routine to expand enough terms such that each unknown appears in at least one constraint in the approximation for the first round.

These optimizations are applied to both the baseline method and our algorithm for the purpose of evaluation. The extended version of this paper [7] includes more detailed evaluation of them and experimental results illustrating their precise impact on each algorithm.

7 Evaluation

We evaluate Synduce on a broad set of benchmarks. Our benchmarks are grouped into six categories. Table 1 lists all the benchmarks, grouped accordingly. Each category, shares the same representation function and polymorphic recursion skeleton, but a different reference implementation is used to specify the synthesis problem. The recursion skeletons (and the representation functions) are polymorphic and therefore reusable. Only 9 different skeletons and 4 different representation functions were used across our 43 benchmarks. More details about the benchmarks, including the simple 9 utilized skeletons, appear in the extended version of this paper [7].

7.1 Case Studies

Changing Tree Traversals. An example of this category is the mips example used in the introduction. The reference function is a natural implementation of a function with a post- or in-order traversal of a binary tree. The target is an equivalent implementation corresponding to the divide-and-conquer tree homomorphism style recursion.

From Trees to Paths. A tree path (zipper in [24]) is a data structure used to represent a tree together with a subtree that is the focus of attention. Our running example belongs in this category. The other benchmarks in this category are from [24].

Enforcing Tail Recursion. In this category, the reference implementation is a direct-style recursion on the data structure, while the recursion skeleton specifies that an accumulator should be used to make the function tail-recursive. Tail recursive functions generally compile to more efficient code.

Combining Traversals. Suppose a collection of existing implementations computes different functions with different traversals of the same data structure. If in some larger context all of these functions need to be computed, combining them can lower the amortized cost. In this set of benchmarks, we synthesize automatically the implementation that corresponds to traversing the data structure with a single recursion strategy, combining the computations into one.

Tree Flattening. These benchmarks target the synthesis of an implementation on the more complex plane tree data structure from a reference implementation on the simpler binary tree data structure.

Parallelizing Functions on Lists. Parallelizing a function on lists can be seen as the translation of a recursive function on cons-lists to a homomorphic function on lists built with the concatenation operator. These benchmarks are from [8, 9, 23].

7.2 Experimental Results

To best of our knowledge, there are no available tools that can be directly compared against Synduce. We can transform our specification to a format that can be accepted by Leon [18]. However, the latter does not succeed in solving even the simplest of our benchmarks (e.g. sum in the list function parallelization category), likely due to the fact that the required deductive rules are missing. We comment on the rest of the available tools in Sect. 8.

Table 1. Experimental Results. Benchmarks are grouped by categories introduced in Sect. 7.1. # steps indicates the number of refinement rounds. $T_{last}$ is the elapsed time before the last call to the SyGuS solver in the last refinement step before timeout. All times are in seconds. The best time is highlighted in bold font. A ‘-’ indicates timeout (> 10 min). The “Inv” column indicates if codomain constraints were required. Experiments are run on a laptop with 16G memory and an i7-8750H 6-core CPU at 2.20 GHz running Ubuntu 19.10.

Table 1 presents the results of comparing Synduce against the baseline method. Both techniques use symbolic counterexamples, and therefore, the comparison can highlight the performance impact of our partial bounding algorithm. The most important point of comparison is the overall synthesis time. In 9 out of 43 benchmarks, the baseline method times out. In another 5 cases, it outperforms the baseline by two orders of magnitude. In the easiest of the benchmarks, i.e. when the overall synthesis time of the baseline is in tens of milliseconds, the two methods are equally good within a small margin of error. The bold number in each row highlights the fastest synthesis time.

Amongst the 9 benchmarks for which the baseline algorithm times out, 7 are cases where Synduce takes advantage of partial bounding by leaving some quantifiers unbounded. The baseline algorithm in these cases requires more terms and terms of higher complexity in the finite approximations. Two of the 9 benchmarks (post-order mps and sum + mts + mps) are cases where the set of maximally reducible terms is exactly the set of bounded terms (i.e. one cannot take advantage of partial bounding), but Synduce still outperforms the baseline because it adds smaller terms to the abstraction through generalization and produces less complex problems for the backend synthesis oracle. In summary, both counterexample generalization and the partial bounding yield big practical advantages in comparison with the baseline symbolic CEGIS algorithm.

It is noteworthy that whenever an instance is hard, the majority of the time is spent in the Synthesize step. This becomes nearly 100% of the time for the baseline algorithm whenever it times out. The weakness of the baseline method lies in the fact that the recursion-free instances generated by it are too difficult to solve by the backend solver. The timeout occurs within a few refinement rounds (at most 7) when the baseline algorithm gets stuck in the Synthesize step attempting to solve a prohibitively difficult recursion-free synthesis instance.

Across all benchmarks, our algorithm generally requires fewer refinement rounds than the baseline method. The few exceptions are the cases where the synthesis oracle gets lucky in producing a good solution when the target programs are very simple, for example in the case of the sum and product benchmarks of the flat tree category.

Finally, to isolate the precise contribution of the partial bounding idea, we evaluated the effect of each optimization on each algorithm. The applicability of a particular optimization highly depends on the particular set of constraints, which in turn depends on the specific benchmark and the algorithm (ours vs baseline) producing the constraints. Our synthesis algorithm yields more general and more succinct constraints, to which the optimizations are more often applicable. Of the 9 cases where Synduce succeeds and the baseline method times out, 7 are due to the inapplicability of these (simple) optimizations. Synduce outperforms the baseline algorithm with all optimizations turned off for both. The detailed results are given in the extended version of this paper [7].

8 Related Work

Synthesizing recursive programs is a challenging task, and several automated techniques have tackled the problem with different specifications of the problem and different approaches to the solution.

Finitization, for example by bounding the depth of unbounded inputs or the number of recursive calls or loop iterations, is a straightforward way of dealing with unboundedness in synthesis [4, 37] and verification [10]. In [32, 33], high-level synthesis techniques use domain specific knowledge to finitize input programs. Quantifier instantiation, i.e. replacing quantified terms with ground terms, is commonly used in theorem proving and verification, and has also been useful in synthesis [31]. Our proposed algorithm can be viewed in the spirit of quantifier instantiation, with the major difference that (universally) quantified terms are replaced with other (universally) quantified terms which are still over an unbounded domain, yet with fewer degrees of freedom in unboundedness.

Synthesis through Program Transformation. Our precise problem statement is inspired by the transformation system developed by Burstall and Darlington [6]. They set to automate the task of transforming an initial program specified as a set of first-order recursion equations into a more efficient program, by altering the recursive structure. Their approach is based on transformation rules and semi-automatic. They use specific rules, e.g. associativity of a data operation, to perform the transformations and such rules do not generalize well. We defer the reasoning about the operations on the data to an SMT solver, and therefore need not rely on such rules. Techniques based on program transformation have been applied to the synthesis of special classes of recursive programs before [13, 15]. For example, the work in [1] focuses on tail recursion and a lot of attention has been given to producing divide-and-conquer recursions in the way of automated parallelization [2, 8, 23].

Synthesizing Recursive Functional Programs. Inductive techniques were developed to construct recursive programs from input/output examples [35], and this approach has been extended in more recent work [16, 17]. The latter two are examples of an analytical approach to program synthesis in which programs are constructed from the analysis of examples. Other recent approaches are search-based methods. Escher [3] synthesizes recursive functions from user-provided components by interactively asking for more examples from the user. $\mathbf {\lambda ^2}$ [11] synthesizes data structure transformations from input/output examples using higher-order functions.

Tools like $\mathbf {\lambda ^2}$ and Escher can be complementary to Synduce in a more general context of recursion synthesis. The user can try to synthesize an implementation of a recursive function over a simple data type using $\mathbf {\lambda ^2}$ or Escher using input/output examples with a higher chance of success. This then serves as the reference implementation input to Synduce which can aim for a more sophisticated implementation over a more complex recursive datatype.

Myth [27], Myth2 [12] and SynQuid [28] use type information to direct the search for a program satisfying a specification. In Myth, this specification is a set of input/output examples. Myth2 generalizes this approach by treating examples as limited types. The specification for Synquid is a polymorphic refinement type, and the tool synthesizes an implementation of the given type using components provided by the user. Type-based approaches work well within the expressivity of refinement-types as specifications, but refinement types cannot express constraints for all desired synthesis tasks. Our specification is strictly stronger than both input/output examples and refinement types.

In SyntRec [14], reusable templates are used to facilitate the synthesis of algebraic data type (ADT) transformations. The reusable templates are meant to lessen the burden of the user in specifying the search space of the programs to be synthesized every time. The recursion skeletons in our framework are effectively (reusable) polymorphic recursion templates. The user can be provided with a library of common recursive datatypes with representation functions mapping between these types, and useful recursion skeletons on these datatypes. SyntRec [14] synthesizes ADT transformations from a functional specification. In contrast, our tool takes this transformation as input (the representation function) and synthesizes a function from ADT to a base type.

Leon [18], a deductive verification and synthesis framework, can synthesize recursive functions from first-order specifications with recursive predicates. In Sect. 7, we commented on a comparison of Leon against Synduce.

Higher-Order Recursion Schemes. We use recursion schemes as a model for our programs, but our contribution has very little to do with the original work introducing this model. Higher-order recursion schemes have been introduced for model checking functional programs [19,20,21, 30]. Pattern matching recursion schemes, introduced in [26], provide a model for functional programs that manipulate ADTs. We use them as an accurate description of a class of functions on ADTs and the notion of reduction associated with them as a crisp way of formulating symbolic evaluation.

9 Discussion and Future Work

We have demonstrated that partial bounding of quantifiers can be a powerful tool for the synthesis of recursive programs. Circumventing the unnecessary bounding of some quantifiers leads to simpler instances of recursion-free synthesis subtasks that can be handled by the current tools. Moreover, our counterexample generalization also yields simpler terms for bounding the quantifiers that have to be bounded. This is the result of our focus being on a class of recursive functions that perform structural recursion (i.e. recursion that deconstructs its inputs). This, together with our specific problem setup, takes the guesswork out of counterexample generalization and provides the means for a constructive counterexample generalization scheme which is demonstrably effective.

The reliance on structural recursion, therefore, limits the class of reference implementations and recursion skeletons that can define an acceptable synthesis instance in our framework. Another limitation tied to the input model is that the output of the recursive functions has to belong to the base (non-recursive) types to accommodate the reduction of the problem to one that can be solved by a backend solver. Consequently, the unknowns in a target recursion scheme have to all be functions from base types to base types.

In our problem setup, the recursion strategy (given by the recursion skeleton) is an integral part of the specification since it is used to communicate programmer intent. Expecting a complete recursion skeleton may be viewed as another limitation of our technique. For example, the mts (maximal tail sum) function can be computed as function on a list maintaining only one integer value (i.e. the current value of the maximum tail sum), yet, to implement mts in a divide-and-conquer strategy, another computation, the sum of the elements of the list, has to be performed alongside this one. It would be great if the user can ask for a divide-and-conquer recursion strategy without having to know that the additional computation of sum is required as well.

Ideally, the user should be permitted to provide an incomplete recursion skeleton which sufficiently communicates the intent and leave the recursion skeleton to be completed automatically by the synthesis procedure. This is a tricky problem. There are not only many recursion strategies to choose from, but each choice also leads to unboundedly many ways to organize the computation on data. This adds yet another dimension of unboundedness to the synthesis problem beyond the two already tackled in this paper. Note that in other recursion synthesis work such as [3, 12, 14, 28], new operations on data are not synthesized, and in contrast drawn from an existing pool of operations. Therefore, this particular problem does not apply in those contexts.

Finally, our method currently does not take into account invariants over recursive data types, e.g. an invariant that specifies that a tree is a binary search tree. Some properties of the datatypes can be encoded through the representation function, e.g. the associativity of the concatenation operator in the category of list parallelization benchmarks. Incorporating the more general invariants in future work will broaden the expressivity of the framework in handling more interesting problems.