Abstract
We study time/memory tradeoffs of function inversion: an algorithm, i.e., an inverter, equipped with an s-bit advice on a randomly chosen function \(f:[n] \mapsto [n]\) and using q oracle queries to f, tries to invert a randomly chosen output y of f, i.e., to find \(x\in f^{-1}(y)\). Much progress was done regarding adaptive function inversion—the inverter is allowed to make adaptive oracle queries. Hellman [IEEE transactions on Information Theory ’80] presented an adaptive inverter that inverts with high probability a random f. Fiat and Naor [SICOMP ’00] proved that for any s, q with \(s^3 q = n^3\) (ignoring low-order terms), an s-advice, q-query variant of Hellman’s algorithm inverts a constant fraction of the image points of any function. Yao [STOC ’90] proved a lower bound of \(sq\ge n\) for this problem. Closing the gap between the above lower and upper bounds is a long-standing open question.
Very little is known of the non-adaptive variant of the question—the inverter chooses its queries in advance. The only known upper bounds, i.e., inverters, are the trivial ones (with \(s+q= n\)), and the only lower bound is the above bound of Yao. In a recent work, Corrigan-Gibbs and Kogan [TCC ’19] partially justified the difficulty of finding lower bounds on non-adaptive inverters, showing that a lower bound on the time/memory tradeoff of non-adaptive inverters implies a lower bound on low-depth Boolean circuits. Bounds that, for a strong enough choice of parameters, are notoriously hard to prove.
We make progress on the above intriguing question, both for the adaptive and the non-adaptive case, proving the following lower bounds on restricted families of inverters:
- Linear-advice (adaptive inverter).:
-
If the advice string is a linear function of f (e.g., \(A\times f\), for some matrix A, viewing f as a vector in \([n]^n\)), then \(s+q \in \varOmega (n)\). The bound generalizes to the case where the advice string of \(f_1 + f_2\), i.e., the coordinate-wise addition of the truth tables of \(f_1\) and \(f_2\), can be computed from the description of \(f_1\) and \(f_2\) by a low communication protocol.
- Affine non-adaptive decoders.:
-
If the non-adaptive inverter has an affine decoder—it outputs a linear function, determined by the advice string and the element to invert, of the query answers—then \(s \in \varOmega (n)\) (regardless of q).
- Affine non-adaptive decision trees.:
-
If the non-adaptive inversion algorithm is a d-depth affine decision tree—it outputs the evaluation of a decision tree whose nodes compute a linear function of the answers to the queries—and \(q < cn\) for some universal \(c>0\), then \(s\in \varOmega (n/d \log n)\).
I. Haitner—Member of the Check Point Institute for Information Security.
N. Mazor et al.—Research supported by ERC starting grant 638121 and Israel Science Foundation grant 666/19.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
In the function-inversion problem, an algorithm, inverter, attempts to find a preimage for a randomly chosen \(y\in [n]\) of a random function \(f:[n] \rightarrow [n]\). The inverter is equipped with an s-bit advice on f, and may make q oracle queries to f. Since s lowerbounds the inverter space complexity and q lowerbounds the inverter time complexity, it is common to refer to the relation between s and q as the inverter’s time/memory tradeoff. The function-inversion problem is central to both theoretical and practical cryptography. On the theoretical end, the security of many systems relies on the existence of one-way functions. While the task of inverting one-way functions is very different from that of inverting random functions, understanding the latter task is critical towards developing lower bounds on the possible (black-box) implications of one-way functions, e.g., Impagliazzo and Rudich [18], Gennaro et al. [14]. But advances on this problem (at least on the positive side, i.e., inverters) are likely to find practical applications. Indeed, algorithms for function inversion are used to expose weaknesses in existing cryptosystems.
Much progress was done regarding adaptive function inversion—the inverter may choose its queries adaptively (i.e., based on answers for previous queries). Hellman [17] presented an adaptive inverter that inverts with high probability a random f. Fiat and Naor [12] proved that for any s, q with \(s^3 q = n^3\) (ignoring low-order terms), an s-advice q-query variant of Hellman’s algorithm inverts a constant fraction of the image points of any function. Yao [27] proved a lower bound of \(s\cdot q\ge n\) for this problem. Closing the gap between the above lower and upper bounds is a long-standing open question. In contrast, very little is known about the non-adaptive variant of this problem—the inverter performs all queries at once. This variant is interesting since such inverter is likely be highly parallelizable, making it significantly more tractable for real world applications. The only known upper bounds for this variant, i.e., inverters, are the trivial ones (i.e., \(s+q = n\)), and the only known lower bound is the above bound of Yao [27]. In a recent work, Corrigan-Gibbs and Kogan [9] have partially justified the difficulty of finding lower bounds on this seemingly easier to tackle problem, showing that lower bounds on non-adaptive inversion imply circuit lower bounds that, for strong enough parameters, are notoriously hard (see further details in Sect. 1.1).
1.1 Our Results
We make progress on this intriguing question, proving lower bounds on restricted families of inverters. To state our results, we use the following formalization to capture inverters with a preprocessing phase: such inverters have two parts, the preprocessing algorithm that gets as input the function to invert f and outputs an advice string a, and the decoding algorithm that takes as input the element to invert y, the advice string a, and using restricted query access to f tries to find a preimage of y. We start with describing our bound for the time/memory tradeoff of linear-advice (adaptive) inverters, and then present our lower bounds for non-adaptive inverters. In the following, fix \(n\in {\mathbb {N}}\) and let \(\mathcal {F}\) be the set of all functions from [n] to [n].
Linear-Advice Inverters. We start with a more formal description of adaptive function inverters.
Definition 1.1
(Adaptive inverters, informal). An s -advice, \(q\) -query adaptive inverter is a deterministic algorithm pair \(\mathsf {C} :=(\mathsf {C} _{\mathsf {pre}}, \mathsf {C} _{\mathsf {dec}})\), where \(\mathsf {C} _{\mathsf {pre}}:\mathcal {F}\rightarrow {\left\{ 0,1\right\} }^{s} \), and \(\mathsf {C} _{\mathsf {dec}}^{(\cdot )}:[n]\times {\left\{ 0,1\right\} }^{s} \rightarrow [n]\) is a q-query algorithm. We say that \(\mathsf {C} \) inverts \(\mathcal {F}\) with high probability if
It is common to refer to a (\(:=\mathsf {C} _{\mathsf {pre}}(f)\)) as the advice string. In linear-advice inverters, the preprocessing algorithm \(\mathsf {C} _{\mathsf {pre}}\) is restricted to output a linear function of f. That is, \(\mathsf {C} _{\mathsf {pre}}(f_1) + \mathsf {C} _{\mathsf {pre}}(f_2) = \mathsf {C} _{\mathsf {pre}}(f_1+ f_2)\), where the addition \(f_1+ f_2\) is coordinate-wise with respect to an arbitrary group over [n], and the addition \(\mathsf {C} _{\mathsf {pre}}(f_1) + \mathsf {C} _{\mathsf {pre}}(f_2)\) is over an arbitrary group that contains the image of \(\mathsf {C} _{\mathsf {pre}}\). An example of such a preprocessing algorithm is \(\mathsf {C} _{\mathsf {pre}}(f) :=A\times f\), for \(A\in \left\{ 0,1\right\} ^{s\times n}\), viewing \(f\in \mathcal {F}\) as a vector in \([n]^n\). For such inverters, we present the following bound.
Theorem 1.2
(Bound on linear-advice inverters). Assume there exists an s-advice \(q\)-query inverter with linear preprocessing that inverts \(\mathcal {F}\) with high probability. Then \(s + q\cdot \log n \in \varOmega (n)\).
We prove Theorem 1.2 via a reduction from set disjointness, a classical problem in the study of two-party communication complexity. The above result generalizes to the following bound that replaces the restriction on the decoder (e.g., linear and short output) with the ability to compute the advice string of \(f_1 + f_2\) by a low-communication protocol over the inputs \(f_1\) and \(f_2\).
Theorem 1.3
(Bound on additive-advice inverters, informal). Assume there exists a \(q\)-query inverter \(\mathsf {C} :=(\mathsf {C} _{\mathsf {pre}}, \cdot )\) and an s-bit communication two-party protocol \((\mathsf {P} _1,\mathsf {P} _2)\) such that for every \(f_1,f_2 \in \mathcal {F}\), the output of \(\mathsf {P} _1\) in \((\mathsf {P} _1(f_1),\mathsf {P} _2(f_2))\) equals with constant probability to \(\mathsf {C} _{\mathsf {pre}}(f_1 + f_2)\). Then \(s + q\cdot \log n \in \varOmega (n)\).
The above bound indeed generalizes Theorem 1.2: a preprocessing algorithm of the type required by Theorem 1.2 immediately implies a two-party party protocol of the type required by Theorem 1.3.
Non-adaptive Inverters. In the non-adaptive setting, the decoding algorithm has two phases: the query selection algorithm that chooses the queries as a function of the advice and the element to invert y, and the actual decoder that receives the answers to these queries along with the advice string and y.
Definition 1.4
(Non-adaptive inverters, informal). An s -advice, q-query non-adaptive inverter is a deterministic algorithm triplet of the form \(\mathsf {C} :=( \mathsf {C} _{\mathsf {pre}}, \mathsf {C} _\mathsf {qry}, \mathsf {C} _{\mathsf {dec}}) \), where \( \mathsf {C} _{\mathsf {pre}}:\mathcal {F}\rightarrow {\left\{ 0,1\right\} }^{s} \), \(\mathsf {C} _\mathsf {qry}:[n] \times {\left\{ 0,1\right\} }^{s} \rightarrow [n]^q\) and \(\mathsf {C} _{\mathsf {dec}}:[n] \times {\left\{ 0,1\right\} }^{s} \times [n]^q\rightarrow [n]\). We say that \(\mathsf {C} \) inverts \(\mathcal {F}\) with high probability if
Note that the query vector v is of length q, so the answer vector f(v) contains q answers. Assuming there exists a field \({\mathbb F}\) of size n (see Remark 1.7), we provide two lower bounds for such inverters.
Affine Decoders. The first bound regards inverters with affine decoders. A decoder algorithm \(\mathsf {C} _{\mathsf {dec}}\) is affine if it computes an affine function of f’s answers. That is, for every image \(y\in [n]\) and advice \(a\in \left\{ 0,1\right\} ^s\), there exists a \(q\)-sparse vector \(\alpha _y^a\in \mathbb {F} ^n\) and a field element \(\beta _y^a\in \mathbb {F} \) such that \(\mathsf {C} _{\mathsf {dec}}(y,a,f(\mathsf {C} _\mathsf {qry}(y,a)))= \langle \alpha _y^a, f \rangle + \beta _y^a\) for every \(f\in \mathcal {F}\). For this type of inverters, we present the following lower bound.
Theorem 1.5
(Bound on non-adaptive inverters with affine decoders, informal). Assume there exists an s-advice non-adaptive function inverter with an affine decoder, that inverts \(\mathcal {F}\) with high probability. Then \( s \in \varOmega (n)\).
Note that the above bound on s holds even if the inverter queries f on all inputs. While Theorem 1.5 is not very insightful for its own sake, as we cannot expect a non-adaptive inverter to have such a limiting structure, it is important since it can be generalized to affine decision trees, a much richer family of non-adaptive inverters defined below. In addition, the result should be contrasted with the question of black-box function computation, see Sect. 1.2, for which linear algorithm are optimal. Thus, Theorem 1.5 highlights the differences between these two related problems.
Affine Decision Trees. The second bound regards inverters whose decoders are affine decision trees. An affine decision tree is a decision tree whose nodes compute an affine function, over \({\mathbb F}\), of the input vector. A decoder algorithm \(\mathsf {C} _{\mathsf {dec}}\) is an affine decision tree, if for every image \(y\in [n]\), advice \(a\in \left\{ 0,1\right\} ^s\) and queries \(v = \mathsf {C} _\mathsf {qry}(y,a)\), there exists an affine decision tree \(\mathcal {T}^{y,a}\) such that \(\mathsf {C} _{\mathsf {dec}}(y,a,f(v))= \mathcal {T}^{y,a}(f)\) (i.e., the output of \(\mathcal {T}^{y,a}\) on input f) for every \(f\in \mathcal {F}\). For such inverters, we present the following bound.
Theorem 1.6
(Bounds on non-adaptive inverters with affine decision-tree decoders). Assume there exists an s-advice q-query non-adaptive function inverter with a d-depth affine decision-tree decoder, that inverts \(\mathcal {F}\) with high probability. Then the following hold:
-
\(q < c n\), for some universal constant c, \(\implies \) \(s \in \varOmega (n/d\log n)\).
-
\(q \in n^{1- \varTheta (1)}\) \(\implies \) \( s \in \varOmega ( n/d)\).
That is, we pay a factor of 1/d comparing to the affine decoder bound, and the bound on s only holds for not too large q. Affine decision trees are much stronger than affine decoders, since the choice of the affine operations it computes can be adaptively dependent on the results of previous affine operations. For example, a depth d affine decision tree can compute any function on d linear combinations of the inputs. In particular, multiplication of function values, e.g., \(f(1)\cdot f(2)\), which cannot be computed by an affine decoder, can be computed by a depth two decision tree. We note that an affine decision tree of depth q can compute any function of its q queries. Unfortunately, for \(d=q\), our bound only reproduces (up to log factors) the lower bound of Yao [27].
Remark 1.7
(Field size). In Theorems 1.5 and 1.6, the field size is assumed to be exactly n (the domain of the function to invert). Decoders over fields smaller than n are not particularly useful, since their output cannot cover all possible preimages of f. Our proof breaks down for fields of size larger than n, since we cannot use linear equations to represent the constraint that the decoder’s output must be contained in the smaller set [n].
Applications to Valiant’s Common-Bit Model. Corrigan-Gibbs and Kogan [9] showed that a lower bound on the time/memory tradeoff of strongly non-adaptive function inverters—the queries may not depend on the advice—implies a lower bound on circuit size in Valiant’s common-bit model [23, 24]. Applying the reduction of [9] with Theorem 1.6 yields the following bound: for every \(n\in {\mathbb {N}}\) for which there exists an n-size field \(\mathbb {F} \), there is an explicit function \(f:\mathbb {F} ^n\mapsto \mathbb {F} ^n\) that cannot be computed by a three-layer circuit of the following structure:
-
1.
It has \(o(\nicefrac {n}{d\log n})\) middle layer gates.
-
2.
Each output gate is connected to \(n^{1-\varTheta (1)}\) inputs gates (and to an arbitrary number of middle-layer gates).
-
3.
Each output gate computes a function which is computable by a d-depth linear decision tree in the inputs (and depends arbitrarily on the middle layer).
In fact, our bound yields that such circuits cannot even approximate f so that every output gate outputs the right value with probability larger than 1/2, over the inputs.
1.2 Additional Related Work
Adaptive Inverters
Upper Bounds. The main result in this setting is the s-advice, q-query inverter of Hellman [17], Fiat and Naor [12] that inverts a constant fraction of the image of any function, for any s, q such that \(s^3q = n^3\) (ignoring low-order terms). When used for random permutations, a variant on the same idea implies an optimum inverter with \(s\cdot q = n\). The inverter of Hellman, Fiat and Naor has found application to practical cryptanalysis, e.g., Biryukov and Shamir [5], Biryukov et al. [6], Oechslin [20].
Lower Bounds. A long line of research (Gennaro et al. [14], Dodis et al. [11], Abusalah et al. [1], Unruh [22], Coretti et al. [8], De et al. [10]) provides lower bounds for various variations on the classical setting, such as that of randomized inversion algorithms that succeed on a sub-constant fraction of functions. None of these lower bounds, however, manage to improve on Yao’s lower bound of \(s\cdot q = n\), leaving a large gap between this lower bound and Hellman, Fiat and Naor’s inverter.
Non-adaptive Inverters
Upper Bounds. In contrast with the adaptive case, it is not clear how to exploit non-adaptive queries in a non trivial way. Indeed, the only known inverters are the trivial ones (roughly, the advice is the function description, or the inverter queries the function on all inputs).
Lower Bounds. Somewhat surprisingly, the only known lower bound for non-adaptive inverters is Yao’s, mentioned above. This defies the basic intuition that this task should be easier than the adaptive case, due to the extreme limitations under which non-adaptive inverters operate. This difficulty was partially justified by the recent reduction of Corrigan-Gibbs and Kogan [9] (see Sect. 1.1) that implies that a strong enough lower bound on even strongly non-adaptive inverters, would yield a lower bound on low-depth Boolean circuits that is notoriously hard to prove.
Relation to Data Structures. The problem of function inversion with advice may also be phrased as a problem in data structures, where the advice string serves as a succinct data structure for answering questions about f. In particular, it bears strong similarity to the substring search problem using the cell-probe model [25]. This is the task of ascertaining the existence of a certain element within a large, unsorted database, using as few queries to the database and as little preprocessing as possible. Upper and lower bounds easily carry over between the two problems, a connection which was made in Corrigan-Gibbs and Kogan [9], where it was used to obtain previously unknown upper bounds on substring search.
Index Coding and Black-Box Function Computation. A syntactically related problem to function inversion is the so-called black-box function computation: an algorithm tries to compute f(x), for a randomly chosen x, using an advice of length s on f, and by querying f on q inputs other than x. Yao [26] proved that \(s\cdot q \ge n\), and presented a linear, non-adaptive algorithm that matches this lower bound.
A much-researched special case of this problem is known as the index coding problem [4], originally inspired by information distribution over networks. In this setting, a single party is in possession of a vector f, and broadcasts a short message a such that n different recipients may each recover a particular value of f, using the broadcast message and knowledge of certain other values of f, as determined by a knowledge graph. The analogy to non-adaptive black-box function computation is obvious when considering a as the advice string, and the access to various values of f as queries. While Yao’s bound on the time/memory tradeoff also holds for the index coding problem, other lower bounds, some of which consider “linear” algorithms [3, 4, 15, 16, 19], do not seem to be relevant for the function inversion problem.
Open Questions
The main challenge remains to gain a better understanding on the power of adaptive and non-adaptive function inverters. A more specific challenge is to generalize our bound on affine decoders and decision trees to affine operations over arbitrary (large) fields.
Paper Organization
A rather detailed description of our proof technique is given in Sect. 2. Basic notations, definitions and facts are given in Sect. 3, where we also prove several basic claims regarding random function inversion. The bound on linear-advice inverters is given in Sect. 4, and the bounds on non-adaptive inverters are given in Sect. 5.
2 Our Technique
In this section we provide a rather elaborate description of our proof technique. We start with the bound on linear-advice inverters in Sect. 2.1, and then in Sect. 2.2 describe the bounds for non-adaptive inverters.
2.1 Linear-Advice Inverters
Our lower bound for inverters with linear advice (and its immediate generalization to additive-advice inverters) is proved via a reduction from set disjointness, a classical problem in the study of two-party communication complexity. In the set disjointness problem, two parties, Alice and Bob, receive two subsets, \(\mathcal {X}\) and \(\mathcal {Y}\subseteq [n]\), respectively, and by communicating with each other try to determine whether \(\mathcal {X}\cap \mathcal {Y}= \emptyset \). The question is how many bits the parties have to exchange in order to output the right answer with high probability. Given an inverter with linear advice, we use it to construct a protocol that solves the set disjointness problem on all inputs in \(\mathcal {Q}:=\left\{ \mathcal {X},\mathcal {Y}\subseteq [n] :\left| \mathcal {X}\cap \mathcal {Y}\right| \le 1\right\} \) by exchanging \(s+q\cdot \log n\) bits. Razborov [21] proved that to answer with constant success probability on all input pairs in \(\mathcal {Q}\), the parties have to exchange \(\varOmega (n)\) bits. Hence, the above reduction implies the desired lower bound on the time/memory tradeoff of such inverters.
Fix a q-query s-advice inverter \(\mathsf {C} :=(\mathsf {C} _{\mathsf {pre}}, \mathsf {C} _{\mathsf {dec}})\) with linear advice, and assume for simplicity that \(\mathsf {C} \)’s success probability is one. The following observation immediately follows by definition: let \(a_f :=\mathsf {C} _{\mathsf {pre}}(f)\) and \(a_g :=\mathsf {C} _{\mathsf {pre}}(g)\) be the advice strings for some functions f and \(g\in \mathcal {F}\), respectively. The linearity of \(\mathsf {C} _{\mathsf {pre}}\) yields that \(a :=a_f+ a_g = \mathsf {C} _{\mathsf {pre}}(f +g)\). That is, a is the advice for the function \(f+ g\) (all additions are over the appropriate groups). Given this observation, we use \(\mathsf {C} \) to solve set disjointness as follows: Alice and Bob (locally) convert their input sets \(\mathcal {X}\) and \(\mathcal {Y}\) to functions  and
and  respectively, such that for any \(x\in \mathcal {X}\cap \mathcal {Y}\) it holds that
respectively, such that for any \(x\in \mathcal {X}\cap \mathcal {Y}\) it holds that  , and f(x) is uniform for \(x\notin \mathcal {X}\cap \mathcal {Y}\). Alice then sends
, and f(x) is uniform for \(x\notin \mathcal {X}\cap \mathcal {Y}\). Alice then sends  to Bob who uses it to compute
to Bob who uses it to compute  . Equipped with the advice a and the help of Alice, Bob then emulates \(\mathsf {C} _{\mathsf {dec}}(0,a)\) and finds \(x\in f^{-1}(0)\), if such exists. Since f is unlikely to map many elements outside of \(\mathcal {X}\cap \mathcal {Y}\) to 0, finding such x is highly correlated with \(\mathcal {X}\cap \mathcal {Y}\ne \emptyset \). In more details, the set disjointness protocol is defined as follows.
. Equipped with the advice a and the help of Alice, Bob then emulates \(\mathsf {C} _{\mathsf {dec}}(0,a)\) and finds \(x\in f^{-1}(0)\), if such exists. Since f is unlikely to map many elements outside of \(\mathcal {X}\cap \mathcal {Y}\) to 0, finding such x is highly correlated with \(\mathcal {X}\cap \mathcal {Y}\ne \emptyset \). In more details, the set disjointness protocol is defined as follows.
Protocol 2.1
(Set disjointness protocol  )
)
-
1.
 samples
samples 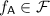 by letting
by letting 
-
2.
\(\mathsf {B} \) samples \(f_\mathsf {B} \in \mathcal {F}\) analogously, with respect to \(\mathcal {Y}\).
-
Let
 .
.
-
-
3.
 sends
sends  to \(\mathsf {B} \), and \(\mathsf {B} \) sets
to \(\mathsf {B} \), and \(\mathsf {B} \) sets  .Footnote 1
.Footnote 1
-
4.
\(\mathsf {B} \) emulates \(\mathsf {C} _{\mathsf {dec}}^f(0,a)\) while answering each query r that \(\mathsf {C} _{\mathsf {dec}}\) makes to f as follows:
-
(a)
 sends r to
sends r to
 .
. -
(b)
 sends
sends 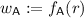 back to
back to
 .
. -
(c)
 replies
replies  to \(\mathsf {C} _{\mathsf {dec}}\) (as the value of f(r)).
to \(\mathsf {C} _{\mathsf {dec}}\) (as the value of f(r)).
-
Let x be \(\mathsf {C} _{\mathsf {dec}}\)’s answer at the end of the above emulation.
-
(a)
-
5.
The parties reject if \(x \in \mathcal {X}\cap \mathcal {Y}\) (using an additional \(\varTheta ( \log n)\) bits to find it out), and accept otherwise.
The communication complexity of \(\varPi \) is essentially \(s+q\cdot \log n\). It is also clear that the parties accept if \(\mathcal {X}\cap \mathcal {Y}=\emptyset \). For the complementary case, by construction, the intersection point of \(\mathcal {X}\cap \mathcal {Y}\) is in \(f^{-1}(0)\). Furthermore, since f(i) is a random value for all \(i\notin \mathcal {X}\cap \mathcal {Y}\), with constant probability only the intersection point is in \(f^{-1}(0)\). Therefore, the protocol is likely to answer correctly also in the case that \(\left| \mathcal {X}\cap \mathcal {Y}\right| =1\).
2.2 Non-adaptive Inverters
We focus on inverters with an affine decoder, and discuss the extension to affine decision tree decoders in Sect. 2.2. The proof follows by bounding the success probability of zero-advice inverters—the preprocessing algorithm outputs an empty string. In particular, we prove that the success probability of such inverters is at most \(2^{-\varOmega (n)}\). Thus, by a union bound over all advice strings, in order to invert \(\mathcal {F}\) with high probability, the advice string of a general (non-zero-advice) inverter has to be of length \(\varOmega (n)\).Footnote 2 Let \(\mathsf {C} :=(\mathsf {C} _\mathsf {qry},\mathsf {C} _{\mathsf {dec}})\) be a zero-advice q-query non-adaptive inverter with an affine decoder. Let F be a random element of \(\mathcal {F}\), and for \(i\in [n]\), let \(Y_i\) be a randomly and independently selected element of [n]. Let \(X_i :=\mathsf {C} _{\mathsf {dec}}(Y_i,F(\mathsf {C} _\mathsf {qry}(Y_i)))\), i.e., \(\mathsf {C} \)’s answer on challenge \(Y_i\), and let \(Z_i\) be the indicator for \(\left\{ F(X_j) = Y_j\right\} \) for all \(j\in [i]\), i.e., the event that \(\mathsf {C} \) answers the first i challenges correctly. We prove the bound by showing that for some \(m\in \varTheta (n)\) it holds that
Note that Eq. (1) bounds the probability that \(\mathsf {C} \) inverts m random elements drawn from [n] (where some of them might have no preimage at all), whereas we are interested in bounding the probability that \(\mathsf {C} \) inverts a random output of F. Yet, since F is a random function, its image covers with very high probability a constant fraction of [n], and thus Eq. (1) can be easily manipulated to derive that
Hence, in order to invert a random function with high probability, a non-zero-advice inverter has to use advice of length \(\varOmega (n)\).
We prove Eq. (1) by showing that for every \(i\in [m]\) it holds that
That is, for small enough i, the algorithm \(\mathsf {C} \) is likely to fail on inverting the i\(^{\mathrm{th}}\) challenge, even when conditioned on the successful inversion of the first \(i-1\) challenges. We note that it is easy to bound \(\Pr \left[ Z_i \mid Z_{i-1}\right] \) for zero-query inverters. The conditioning on \(Z_{i-1}\) roughly gives \(\varTheta (i)\) bits of information about F. Thus, this conditioning gives at most one bit of information about \(F^{-1}(Y_i)\), and the inverter does not have enough information to invert \(Y_i\). When moving to non-zero-queries inverters, however, the situation gets much more complicated. By making the right queries, that may depend on \(Y_{i}\), the inverter can exploit this “small” amount of information to find the preimage of \(Y_i\). This is what happens, for instance, in the adaptive inverter of Hellman [17]. Hence, for bounding \(\Pr \left[ Z_i \mid Z_{i-1}\right] \), we critically exploit the assumption that \(\mathsf {C} \) is non-adaptive and has an affine decoder. In particular, we bound \(\Pr \left[ Z_i \mid Z_{i-1}\right] \) by translating the event \(Z_{i}\) into an affine system of equations and then use a few observations about the structure of the above system to derive the desired bound. These equations will have the form \(M \times F = V\), viewing F as a random vector in \([n]^n\), for \(\mathbf{M} := \begin{pmatrix} \mathbf{M} ^{i-1} \\ \mathbf{M} ^{i} \end{pmatrix} \) and \(V := \begin{pmatrix} V^{i-1} \\ V^{i} \end{pmatrix} \), such that:
-
1.
\(\mathbf{M} ^{i-1}\) is a deterministic function of \((X_{< i},Y_{<i})\) and \(\mathbf{M} ^{i}\) is a deterministic function of \(Y_i\), letting \(X_{< i}\) stand for \((X_1,\ldots ,X_{i-1})\) and likewise for \(Y_{< i}\).
-
2.
The event \(M^{i-1}\times F' = V^{i-1}\) is the event \(\bigwedge _{j<i} \{(F'(X_j) = Y_j)\ \wedge \) \((\mathsf {C} _{\mathsf {dec}}(Y_j,F'(\mathsf {C} _\mathsf {qry}(Y_j))) = X_j)\}\), for \(F'\) being a uniform, and independent, element of \(\mathcal {F}\).
(In particular, \(M^{i-1}\times F=V^{i-1}\) implies that \(Z_{i-1}\) holds, and binds the value of \((X_{<i},Y_{<i})\) to \(V^{i-1}\).)
-
3.
The event \(M^i\times F' = V^i\) is the event \(\left\{ \mathsf {C} _{\mathsf {dec}}(Y_i,F'(\mathsf {C} _\mathsf {qry}(Y_i))) = X_i\right\} \).
(In particular, \(M^{i}\times F=V^{i }\) binds the value of \(X_i\) to \(V^i\).)
The above \(\mathbf{M} \) and V are defined as follows: assume for ease of notation that \(\mathsf {C} \) has a linear, and not affine, decoder. That is, for every \(y \in [n]\) there exists a (\(q\)-sparse) vector \(\alpha _y \in \mathbb {F} ^n\) such that \( \langle \alpha _y, F \rangle = X_y\). By definition, for every \(j < i\):
-
1.
\(\langle \alpha _{Y_j}, F \rangle = X_{j}\).
Conditioning on \(Z_{i-1}\) further implies that for every \(j < i\):
-
2.
\( F(X_j) = Y_j\).
Let \(\ell :=2i-2\), and let \(\mathbf{M} ^{i-1} \in \mathbb {F} ^{\ell \times n} \) be the (random) matrix defined by \(\mathbf{M} ^{i-1}_{2k-1} :=\alpha _{Y_k}\) and \(\mathbf{M} ^{i-1}_{2k} :=e_{X_k}\), letting \(e_j\) being the unit vector \((0^{j-1},1,0^{n-j})\). Let \(V^{i-1} \in \mathbb {F} ^{\ell } \) be the (random) vector defined by \(V^{i-1}_{2k-1} :=X_k\) and \(V^{i-1}_{2k} = Y_k\). By definition, the event \(Z_{i-1}\) is equivalent to the event \(\mathbf{M} ^{i-1} \times F = V^{i-1}\). The computation \(\mathsf {C} \) makes on input \(Y_i\) can also be described by the linear equation \(\langle \alpha _{Y_i}, F \rangle = X_i\). Let \(\mathbf{M} := \begin{pmatrix} \mathbf{M} ^{i-1} \\ \alpha _{Y_i} \end{pmatrix} \) and \(V := \begin{pmatrix} V^{i-1} \\ X_i \end{pmatrix} \). We make use of the following claims (see proofs in Sect. 3.2).
Definition 2.2
(Spanned unit vectors). For a matrix \(\mathbf{A} \in \mathbb {F} ^{a\times n}\), let  , for
, for  being the (linear) span of \(\mathbf{A} \)’s rows.
being the (linear) span of \(\mathbf{A} \)’s rows.
That is, \(\mathcal {E}(\mathbf{A} )\) is the set of indices of all unit vectors spanned by \(\mathbf{A} \). It is clear that  . The following claim states that for \(j \notin \mathcal {E}(\mathbf{A} ) \), knowing the value of \(\mathbf{A} \times F\) gives no information about \(F_j\).
. The following claim states that for \(j \notin \mathcal {E}(\mathbf{A} ) \), knowing the value of \(\mathbf{A} \times F\) gives no information about \(F_j\).
Claim 2.3
Let \(\mathbf{A} \in \mathbb {F} ^{a\times n}\) and \(v \in {\text {Im}}(\mathbf{A} )\). Then for every \(j\in [n] \setminus \mathcal {E}(\mathbf{A} )\) and \(y\in [n]\), it holds that \(\Pr _{f\leftarrow [n]^n}\left[ f_j = y \mid \mathbf{A} \times f = v\right] = 1/n\).
The second claim roughly states that by concatenating a c-row matrix to a given matrix \(\mathbf{A} \), one does not increase the spanned unit set of \(\mathbf{A} \) by more than c elements.
Claim 2.4
For every \(\mathbf{A} \in \mathbb {F} ^{\ell \times n}\) there exists an \(\ell \)-size set \(\mathcal{{S}}_A \subseteq [n]\) such that the following holds: for every \(\mathbf{B} \in \mathbb {F} ^{c\times n}\) there exists a c-size set \(\mathcal {S}_B \subseteq [n]\) such that \(\mathcal {E} \begin{pmatrix} \mathbf{A} \\ \mathbf{B} \end{pmatrix} \subseteq \mathcal{{S}}_A \cup \mathcal {S}_B\).
For bounding \(\Pr \left[ Z_i \mid Z_{i-1}\right] \) using the above observations, we write
and finish the proof by separately bounding the two terms of the above equation. Let \(H :=(X_i,Y_{\le i},\mathbf{M} ,V)\). We first note that

The first equality holds by definition of \(Z_{i-1}\), the second equality since F is independent of Y, and the last one follows by Claim 2.3. For bounding the left-hand term of Eq. (4), let \(\mathcal{{S}}\) and \(T\) be the \(\ell \)-size set and the index guaranteed by Claim 2.4 for the matrices \(\mathbf{M} ^{i-1}\) and vector \(\alpha _{Y_i}\), respectively. Compute,
The second inequality is by Claim 2.4. Since \(F(\mathcal{{S}})\) is independent of \(Y_i\), it holds that
Bounding \( \Pr \left[ Y_i = F(T) \mid Z_{i-1}\right] \) is more involved since \(T\) might depend on \(Y_i\).Footnote 3 Yet since f is a random function, a simple counting argument yields that for any (fixed and independent of f) function g:
Let \(H:=(X_{<i},Y_{<i})\), and for \(h = (x_{<i},y_{<i})\in {\text {Supp}}(H)\) compute

The first equality holds since F is independent of Y. The second inequality holds by Eq. (8), noting that under the conditioning on \(H=h\), the value of T is a deterministic function of \(Y_i\). The third inequality holds since for not too big i, \(\Pr \left[ H=h,Z_{i-1}\mid Y_{< i } = y_{<i}\right] \ge n^{-n/4}\), since this probabilistic event is essentially a system of linear equations over a randomly selected vector. Since the above holds for any h, we conclude that \( \Pr \left[ Y_i = F(T) \mid Z_{i-1}\right] \le 1/2 + o(1)\). Putting it all together, yields that \(\Pr \left[ Z_i \mid Z_{i-1}\right]< 1/n + \ell /n + 1/2 + o(1) < 3/5\), for not too large i.
Affine Decision Trees. Similarly to the affine decoder case, we prove the theorem by bounding \(\Pr \left[ Z_i \mid Z_{i-1}\right] \) for all “not too large i”. Also in this case, we bound this probability by translating the conditioning on \(Z_{i-1}\) into a system of affine equations. In particular, we would like to find proper definitions for the matrix \(\mathbf{M} = \begin{pmatrix} \mathbf{M} ^{i-1} \\ \mathbf{M} ^{i} \end{pmatrix} \) and vector \(V = \begin{pmatrix} V^{i-1} \\ V^i \end{pmatrix} \), functions of \((X_{\le i},Y_{\le i})\), such that conditions 1–3 mentioned in the affine decoder case hold.
We achieve these conditions by adding for each \(j<i\) an equation for each of the linear computations done in the decision tree that computes \(X_j\) from \(Y_j\). The price is that rather than having \(\varTheta (i)\) equations, we now have \(\varTheta (d\cdot i)\), for d being the depth of the decision tree. In order to have \(\mathbf{M} ^{i}\) a deterministic function of \(Y_i\) alone, we cannot simply make \(\mathbf{M} ^i\) reflect the d linear computations performed by the decoder, since each of these may depend on the results of previous computations, and thus depend on F. So rather, we have to add a row (i.e., an equation) for each of the q queries the decoder might use (queries that span all possible computations), which by definition also imply the dependency on q. Taking these additional rows into account yields the desired bound.
3 Preliminaries
3.1 Notation
All logarithms considered here are in base two. We use calligraphic letters to denote sets, uppercase for random variables and probabilistic events, lowercase for functions and fixed values, and bold uppercase for matrices. Let \([n] :=\left\{ 1,\ldots ,n\right\} \). Given a vector \(v\in \varSigma ^n\), let \(v_i\) denote its i\(^{\mathrm{th}}\) entry, let \(v_{< i} :=v_{1,\ldots ,i-1}\) and let \(v_{\le i} :=v_{1,\ldots ,i}\). Let \(\left( {\begin{array}{c}[n]\\ k\end{array}}\right) \) denote the set of all subsets of [n] of size k. The vector v is q-sparse if it has no more than q non-zero entries.
Functions. We naturally view functions from [n] to [m] as vectors in \([m]^n\), by letting \(f_i = f(i)\). For a finite ordered set \(\mathcal {S}:=\left\{ s_1,\ldots ,s_k\right\} \), let \(f(\mathcal {S}):=\left\{ f(s_1), f(s_2), \ldots , f(s_k)\right\} \). Let \(f^{-1}(y):=\left\{ x\in [n] :f(x)=y \right\} \) and let \({\text {Im}}(f) = \left\{ f(x):x\in [n] \right\} \). A function \(f:\mathbb {F} ^n \rightarrow \mathbb {F} \) , for a field \(\mathbb {F} \) and \(n\in {\mathbb {N}}\), is affine if there exist a vector \(v\in \mathbb {F} ^n\) and a constant \(\beta \in \mathbb {F} \) such that \(f(x)=\langle v,x \rangle + \beta \) for every \(x \in \mathbb {F} ^n\), letting \(\langle v,x \rangle :=\sum v_i \cdot x_i\) (all operations are over \(\mathbb {F} \)).
Distributions and Random Variables. The support of a distribution P over a finite set \(\mathcal {S}\) is defined by \({\text {Supp}}(P) :=\left\{ x\in \mathcal {S}: P(x)>0\right\} \). For a set \(\mathcal {S}\), let \(s\leftarrow \mathcal {S}\) denote that s is uniformly drawn from \(\mathcal {S}\). For \(\delta \in [0,1]\), let \(h(\delta ) :=-\delta \log \delta - (1-\delta )\log (1-\delta )\), i.e., the binary entropy function.
3.2 Matrices and Linear Spaces
We identify the elements of a finite field of size n with the elements of the set [n], using some arbitrary, fixed, mapping. Let \(e_i\) denote the i\(^{\mathrm{th}}\) unit vector \(e_j=(0^{j-1},1,0^{n-j})\).
For a matrix \(\mathbf{A} \in \mathbb {F} ^{a\times b}\), let \(\mathbf{A} _i\) denote the i\(^{\mathrm{th}}\) row of \(\mathbf{A} \). The span of \(\mathbf{A} \)’s rows is defined by  . Let \( {\text {Im}}(\mathbf{A} ) = \left\{ v \in \mathbb {F} ^a :\exists w\in \mathbb {F} ^b {\;\; : \;\;}\mathbf{A} \times w = v\right\} \), or equivalently, the image set of the function \(f_\mathbf{A} (w) :=\mathbf{A} \times w\). We use the following well-known fact:
. Let \( {\text {Im}}(\mathbf{A} ) = \left\{ v \in \mathbb {F} ^a :\exists w\in \mathbb {F} ^b {\;\; : \;\;}\mathbf{A} \times w = v\right\} \), or equivalently, the image set of the function \(f_\mathbf{A} (w) :=\mathbf{A} \times w\). We use the following well-known fact:
Fact 3.1
Let \(\mathbb {F} \) be a finite field of size n, let \(\mathbf{A} \in \mathbb {F} ^{a \times b}\), let \(v\in {\text {Im}}(\mathbf{A} )\), and let \(\mathcal {F}\subseteq \mathbb {F} ^b\) be the solution set of the system of equations \(\mathbf{A} \times F = v\). Then  .
.
We also make use of the following less standard notion.
Definition 3.2
(Spanned unit vectors). For a matrix \(\mathbf{A} \in \mathbb {F} ^{a\times b}\), let  .
.
That is, \(\mathcal {E}(\mathbf{A} )\) is the indices of all unit vectors spanned by \(\mathbf{A} \). It is clear that  . It is also easy to see that for any \(v\in {\text {Im}}(\mathbf{A} )\), \(\mathcal {E}(\mathbf{A} )\) holds those entries that are common to all solutions w of the system \(\mathbf{A} \times w = v\).Footnote 4 The following claim states that for \(i\notin \mathcal {E}(\mathbf{A} )\), the number of solutions w of the system \(\mathbf{A} \times w = v\) with \(w_i=y\), is the same for every y.
. It is also easy to see that for any \(v\in {\text {Im}}(\mathbf{A} )\), \(\mathcal {E}(\mathbf{A} )\) holds those entries that are common to all solutions w of the system \(\mathbf{A} \times w = v\).Footnote 4 The following claim states that for \(i\notin \mathcal {E}(\mathbf{A} )\), the number of solutions w of the system \(\mathbf{A} \times w = v\) with \(w_i=y\), is the same for every y.
Claim 3.3
Let \(\mathbb {F} \) be a finite field of size n, let \(\mathbf{A} \in \mathbb {F} ^{a\times b}\) and \(v \in {\text {Im}}(\mathbf{A} )\). Then for every \(i\in [n] \setminus \mathcal {E}(\mathbf{A} )\) and \(y\in [n]\), it holds that \(\Pr _{f\leftarrow [n]^b}\left[ f_i = y \mid \mathbf{A} \times f = v\right] = 1/n\).
Proof
Let \(\mathcal {F}_\mathbf{A ,v} :=\left\{ f\in [n]^b :\mathbf{A} \times f = v \right\} \) be the set of solutions for the equation \(\mathbf{A} \times F = v\). Since, by assumption, \(\mathbf{A} \times F=v\) has a solution, by Fact 3.1 it holds that  . Next, let \(\mathbf{A} ' := \begin{pmatrix} \mathbf{A} \\ e_i \end{pmatrix} , v' := \begin{pmatrix} v \\ y \end{pmatrix} \), and \(\mathcal {F}_\mathbf{A ,v,i,y} :=\left\{ f\in [n]^b :\mathbf{A} '\times f = v'\right\} \) (i.e., \(\mathcal {F}_\mathbf{A ,v,i,y}\) is the set of solutions for \(\mathbf{A} ' \times F = v'\)). Since, by assumption,
. Next, let \(\mathbf{A} ' := \begin{pmatrix} \mathbf{A} \\ e_i \end{pmatrix} , v' := \begin{pmatrix} v \\ y \end{pmatrix} \), and \(\mathcal {F}_\mathbf{A ,v,i,y} :=\left\{ f\in [n]^b :\mathbf{A} '\times f = v'\right\} \) (i.e., \(\mathcal {F}_\mathbf{A ,v,i,y}\) is the set of solutions for \(\mathbf{A} ' \times F = v'\)). Since, by assumption,  , it holds that \(\mathbf{A} ' \times F = v'\) has a solution and
, it holds that \(\mathbf{A} ' \times F = v'\) has a solution and  . We conclude that \(\Pr _{f\leftarrow [n]^b}\left[ f_i = y \mid \mathbf{A} \times f = v\right] = \frac{ |\mathcal {F}_\mathbf{A ,v,i,y}| }{ | \mathcal {F}_\mathbf{A ,v}| } = 1/n\).
. We conclude that \(\Pr _{f\leftarrow [n]^b}\left[ f_i = y \mid \mathbf{A} \times f = v\right] = \frac{ |\mathcal {F}_\mathbf{A ,v,i,y}| }{ | \mathcal {F}_\mathbf{A ,v}| } = 1/n\).
The following claim states that adding a small number of rows to a given matrix \(\mathbf{A} \) does not increase the set \(\mathcal {E}(\mathbf{A} )\) by much.
Claim 3.4
For every \(\mathbf{A} \in \mathbb {F} ^{\ell \times n} \) there exists an \(\ell \)-size set \(\mathcal {S}_\mathbf{A} \subseteq [n]\) such that the following holds: for any \( \mathbf{B} \in \mathbb {F} ^{ c \times n} \) there exists a \( c \)-size set \(\mathcal {S}_\mathbf{B} \subseteq [n]\) for which \(\mathcal {E} \begin{pmatrix} \mathbf{A} \\ \mathbf{B} \end{pmatrix} \subseteq \mathcal {S}_\mathbf{A} \cup \mathcal {S}_\mathbf{B} \).
Proof
Standard row operations performed on a matrix \(\mathbf{M} \) do not affect  , and thus do not affect \(\mathcal {E}(\mathbf{M} )\). Therefore, we may assume that both \(\mathbf{A} \) and \(\mathbf{B} \) are in row canonical form.Footnote 5 For a matrix \(\mathbf{M} \) in row canonical form, let \(\mathcal {L}(\mathbf{M} ) :=\{ i \in [n] :\) the i\(^{\mathrm{th}}\) column of \(\mathbf{M} \) contains a leading 1 }. Let \(\mathcal {S}_\mathbf{A} :=\mathcal {L}(\mathbf{A} )\) and note that
, and thus do not affect \(\mathcal {E}(\mathbf{M} )\). Therefore, we may assume that both \(\mathbf{A} \) and \(\mathbf{B} \) are in row canonical form.Footnote 5 For a matrix \(\mathbf{M} \) in row canonical form, let \(\mathcal {L}(\mathbf{M} ) :=\{ i \in [n] :\) the i\(^{\mathrm{th}}\) column of \(\mathbf{M} \) contains a leading 1 }. Let \(\mathcal {S}_\mathbf{A} :=\mathcal {L}(\mathbf{A} )\) and note that  . Perform Gaussian elimination on \( \begin{pmatrix} \mathbf{A} \\ \mathbf{B} \end{pmatrix} \) to yield a matrix \(\mathbf{E} \) in row canonical form, and let \(\mathcal {S}_\mathbf{E} :=\mathcal {L}(\mathbf{E} )\). Note that \(\mathcal {S}_\mathbf{A} \subseteq \mathcal {S}_\mathbf{E} \), since adding rows to a matrix may only expand the set of leading ones. Furthermore,
. Perform Gaussian elimination on \( \begin{pmatrix} \mathbf{A} \\ \mathbf{B} \end{pmatrix} \) to yield a matrix \(\mathbf{E} \) in row canonical form, and let \(\mathcal {S}_\mathbf{E} :=\mathcal {L}(\mathbf{E} )\). Note that \(\mathcal {S}_\mathbf{A} \subseteq \mathcal {S}_\mathbf{E} \), since adding rows to a matrix may only expand the set of leading ones. Furthermore,  . Clearly, \(\mathcal {E}(\mathbf{E} ) \subseteq \mathcal {S}_\mathbf{E} \), and we can write \(\mathcal {S}_\mathbf{E} = \mathcal {S}_\mathbf{A} \cup \mathcal {S}_\mathbf{B} \), for \(\mathcal {S}_\mathbf{B} :=(\mathcal {S}_\mathbf{E} \setminus \mathcal {S}_\mathbf{A} )\). Finally,
. Clearly, \(\mathcal {E}(\mathbf{E} ) \subseteq \mathcal {S}_\mathbf{E} \), and we can write \(\mathcal {S}_\mathbf{E} = \mathcal {S}_\mathbf{A} \cup \mathcal {S}_\mathbf{B} \), for \(\mathcal {S}_\mathbf{B} :=(\mathcal {S}_\mathbf{E} \setminus \mathcal {S}_\mathbf{A} )\). Finally,  , and the proof follows.
, and the proof follows.
3.3 Random Functions
Let \( {\mathcal {F}_n} \) be the set of all functions from [n] to [n]. We make the following observations.
Claim 3.5
Let \(\mathcal {S}_1,\ldots ,\mathcal {S}_n \subseteq [n]\) be \( c \)-size sets, and for \(f\in {\mathcal {F}_n} \) let \(\mathcal {K}_f:=\left\{ y\in [n] :y \in f(\mathcal {S}_y) \right\} \). Then for any \(\mu \in [0,\tfrac{1}{2}]\):
Proof
For \(\mathcal {T}:=\left\{ t_1,\ldots ,t_{\lceil \mu n\rceil } \right\} \subseteq [n]\), let \(\mathcal {F}_{\mathcal {T}} :=\left\{ f\in {\mathcal {F}_n} :\mathcal {T}\subseteq \mathcal {K}_f\right\} \). We make a rough over-counting for the size of \(\mathcal {F}_\mathcal {T}\): one can describe \(f \in \mathcal {F}_\mathcal {T}\) by choosing \(x_i \in [n]\) for each set \(\mathcal {S}_{t_i}\), and require that \(f(x_i) = t_i\) (to ensure \(t_i \in f(\mathcal {S}_{t_i})\)). There are at most \( c ^{\lceil \mu n\rceil }\) ways to perform these choices. There are no constraints on the remaining \(n-\lceil \mu n\rceil \) values of f. Therefore \(\left| \mathcal {F}_{\mathcal {T}}\right| \le c ^{\lceil \mu n\rceil } \cdot n^{n-\lceil \mu n\rceil }\). This immediately implies that \(\Pr _{f\leftarrow {\mathcal {F}_n} ,\mathcal {T}\leftarrow \left( {\begin{array}{c}[n]\\ \lceil \mu n\rceil \end{array}}\right) }\left[ \mathcal {T}\subseteq \mathcal {K}_f \right] \le \left( \frac{ c }{n}\right) ^{\lceil \mu n\rceil }\). We conclude that
The last inequality follows from Facts 3.11 and 3.10, and the fact that \(\log (1/\mu ) \ge \log (n/\lceil \mu n\rceil )\).
Claim 3.6
Let \(n\in {\mathbb {N}}\), let \(F \leftarrow \mathcal {F}_n\) and let W be an event (jointly distributed with F) of probability at least p. Let \(Y\leftarrow [n]\) be independent of F and W. Then for every \( c \)-size sets \(\mathcal {S}_1,\ldots ,\mathcal {S}_n \subseteq [n]\) and \(\gamma \in [0,\tfrac{1}{2}]\), it holds that
Proof
Let \(\mathcal {K}_f :=\left\{ y\in [n] :y \in f(\mathcal {S}_y) \right\} \). For \(\gamma \in [0,1]\), compute:

The last inequality holds since Y is independent of W and F. Since \(\Pr \left[ W\right] \ge p\), it holds that:
The second inequality is by Claim 3.5. We conclude that:
The next claim bounds the probability that a random function compresses an image set.
Claim 3.7
For any \(n\in {\mathbb {N}}\) and \(\tau , \delta \in [0,\tfrac{1}{2}]\), it holds that
\({\alpha _{ \tau , \delta }:=\Pr _{ f \leftarrow {\mathcal {F}_n} }\left[ \exists \mathcal {X}\subseteq [n]:\left| \mathcal {X}\right| \ge \tau n \wedge \left| f(\mathcal {X})\right| \le \delta n \right] \le 2^{n (h(\tau ) + h(\delta )) + \lfloor \tau n\rfloor \log \delta }}\).
Proof
Compute:
The last inequality follows from Fact 3.11, and since h is monotone in \([0,\tfrac{1}{2}]\).
The last claim states that an algorithm that inverts f(x) with good probability, is likely to return x itself.
Claim 3.8
Let \(\mathsf {C} \) be a function from \( {\mathcal {F}_n} \times [n]\) to [n] such that \(\Pr _{{\mathop {x\leftarrow [n]}\limits ^{f\leftarrow {\mathcal {F}_n} }}}\left[ \mathsf {C} (f,f(x)) \in f^{-1}(f(x))\right] \ge \alpha \). Then, \(\Pr _{{\mathop {x\leftarrow [n]}\limits ^{f\leftarrow {\mathcal {F}_n} }}}\left[ \mathsf {C} (f,f(x)) = x\right] \ge \frac{\alpha ^2}{8}\).
Proof
For \(f\in {\mathcal {F}_n} \) let \(\mathcal {P}_f(x):=f^{-1}(f(x)) \setminus \left\{ x\right\} \). We would like to provide a bound on the size of this set to ensure that x is output with high probability. Compute
We now provide a lower bound for the left-hand term. For \(d\ge 1\) compute
By linearity of expectation, \({\text {*}}{E}_{ f \leftarrow {\mathcal {F}_n} }\left[ \left| \mathcal {P}_f(x)\right| \right] = \frac{n-1}{n} < 1\). Hence by Markov’s inequality,
\(\Pr _{\begin{array}{c} f \leftarrow {\mathcal {F}_n} \\ x \leftarrow [n] \end{array} }\left[ |\mathcal {P}_f(x)| > d \right] < 1/d\). It follows that
Combining Eqs. (13) and (14) yields that
Finally, by Eqs. (12) and (15) we conclude that
Setting \(d = \frac{2}{\alpha }\) yields that \(\Pr _{\begin{array}{c} f \leftarrow {\mathcal {F}_n} \\ x \leftarrow [n] \end{array} }\left[ \mathsf {C} (f,f(x)) = x \right] \ge \frac{a^2}{4} - \frac{\alpha ^2}{8} = \frac{\alpha ^2}{8}\).
3.4 Additional Inequalities
We use the following easily-verifiable facts:
Fact 3.9
For \(x \ge 1\): \(\log x\ge 1-1/x\).
Fact 3.10
For \(\delta \le 1/2\): \(h(\delta ) \le - 2 \delta \log \delta \).
We also use the following bound:
Fact 3.11
([13]) \(\left( {\begin{array}{c}n\\ k\end{array}}\right) \le 2^{n h(\frac{k}{n})}\).
4 Linear-Advice Inverters
In this section we present lower bounds on the time/memory tradeoff of adaptive function inverters with linear advice. The extension to additive-advice inverters is given in Sect. 4.1.
To simplify notation, the following definitions and results are stated with respect to a fixed \(n\in {\mathbb {N}}\). Let \(\mathcal {F}\) be the set of all functions from [n] to [n]. All asymptotic notations (e.g., \(\varTheta \)) hide constant terms that are independent of n. We start by formally defining adaptive function inverters.
Definition 4.1
(Adaptive inverters). An s -advice, \(q\)-query adaptive inverter is a deterministic algorithm pair \(\mathsf {C} :=(\mathsf {C} _{\mathsf {pre}}, \mathsf {C} _{\mathsf {dec}})\), where \(\mathsf {C} _{\mathsf {pre}}:\mathcal {F}\rightarrow {\left\{ 0,1\right\} }^{s} \), and \(\mathsf {C} _{\mathsf {dec}}^{(\cdot )}:[n] \times {\left\{ 0,1\right\} }^{s} \rightarrow [n]\) makes up to q oracle queries. For \(f\in \mathcal {F}\) and \(y\in [n]\), let
That is, \(\mathsf {C} _{\mathsf {pre}}\) is the preprocessing algorithm that takes as input the function description and outputs a string of length s that we refer to as the advice string. The oracle-aided \(\mathsf {C} _{\mathsf {dec}}\) is the decoder algorithm that performs the actual inversion action. It receives the element to invert y and the advice string, and using q (possibly adaptive) queries to f, attempts to output a preimage of y. Finally, \(\mathsf {C} (y;f)\) is the candidate preimage the algorithms of \(\mathsf {C} \) produce for the element to invert y given the (restricted) access to f. We define adaptive inverters with linear advice as follows, recalling that we may view \(f\in \mathcal {F}\) as a vector \(\in [n]^n\).
Definition 4.2
(Linear preprocessing). A deterministic algorithm \(\mathsf {C} _{\mathsf {pre}}:\mathcal {F}\rightarrow {\left\{ 0,1\right\} }^{s} \) is linear if there exist an additive group \({\mathcal {G}}\subseteq {\left\{ 0,1\right\} }^{s} \) that contains \(\mathsf {C} _{\mathsf {pre}}(\mathcal {F})\), and an additive group \(\mathcal {K}\) of size n such that for every \(f_1,f_2 \in \mathcal {F}\) it holds that \(\mathsf {C} _{\mathsf {pre}}(f_1 +_\mathcal {K}f_2) = \mathsf {C} _{\mathsf {pre}}(f_1) +_{\mathcal {G}}\mathsf {C} _{\mathsf {pre}}(f_2)\), letting \(f_1+_\mathcal {K}f_2 :=((f_1)_1+_\mathcal {K}(f_2)_1,\dots , (f_1)_n+_\mathcal {K}(f_2)_n)\).
Below we omit the subscripts from \(+_{\mathcal {G}}\) and \( +_\mathcal {K}\) when clear from the context.
We prove the bound for inverters with linear preprocessing by presenting a reduction from the well-known set disjointness problem.
Definition 4.3
(Set disjointness). A protocol  solves set disjointness with error \(\varepsilon \) over all inputs in \(\mathcal {Q}\) \(\subseteq \left\{ (\mathcal {X},\mathcal {Y}) :\mathcal {X}, \mathcal {Y}\subseteq [\mathbb {N}] \right\} \), if for every \(({\mathcal {X}},{\mathcal {Y}})\in \mathcal {Q}\)
solves set disjointness with error \(\varepsilon \) over all inputs in \(\mathcal {Q}\) \(\subseteq \left\{ (\mathcal {X},\mathcal {Y}) :\mathcal {X}, \mathcal {Y}\subseteq [\mathbb {N}] \right\} \), if for every \(({\mathcal {X}},{\mathcal {Y}})\in \mathcal {Q}\)

for \(\delta _{{\mathcal {X}},{\mathrm {Y}}}\) being the indicator for \({\mathcal {X}}\cap {\mathcal {Y}}= \emptyset \).
Namely, except with probability \(\varepsilon \) over their private and public randomness, the two parties find out whether their input sets intersect. Set disjointness is known to require large communication over the following set of inputs.
Definition 4.4
(Communication complexity). The communication complexity of a protocol  , denoted \(CC(\varPi )\), is the maximal number of bits the parties exchange in an execution (over all possible inputs and randomness).
, denoted \(CC(\varPi )\), is the maximal number of bits the parties exchange in an execution (over all possible inputs and randomness).
Theorem 4.5
(Hardness set disjointness, Razborov [21]). Exists \(\varepsilon > 0\) such that for every protocol \(\varPi \) that solves set disjointness over all inputs in \(\mathcal {Q}:=\left\{ \mathcal {X},\mathcal {Y}\subseteq [n] :\left| \mathcal {X}\cap \mathcal {Y}\right| \le 1 \right\} \) with error \(\varepsilon \), it holds that \(CC(\varPi ) \ge \varOmega (n)\).Footnote 6
Our main result is the following reduction from set disjointness to function inversion.
Theorem 4.6
(From set disjointness to function inversion). Assume exists an s-advice, \(q\)-query linear-advice inversion algorithm with \(\Pr _{{\mathop {x\leftarrow [n]}\limits ^{f\leftarrow \mathcal {F}}}}\left[ \mathsf {C} (f(x);f) \in f^{-1}(f(x))\right] \ge \alpha \), and let \(\mathcal {Q}:=\left\{ \mathcal {X},\mathcal {Y}\subseteq [n] :\left| \mathcal {X}\cap \mathcal {Y}\right| \le 1 \right\} \). Then for every \(\varepsilon >0\) there exists a protocol that solves set disjointness with (one-sided) error \(\varepsilon \) and communication \(O\left( \frac{\log (\varepsilon )}{\log (1-\alpha ^2/8)} \cdot (s+q \log n)\right) \), on all inputs in \(\mathcal {Q}\).
Combining Theorems 4.5 and 4.6 yields the following bound on linear-advice inverters.
Corollary 4.7
(Theorem 1.2, restated). Let \(\mathsf {C} =(\mathsf {C} _{\mathsf {pre}},\mathsf {C} _{\mathsf {dec}})\) be an s-advice \(q\)-query inversion algorithm with linear preprocessing such that \(\Pr _{{\mathop {x\leftarrow [n]}\limits ^{f\leftarrow \mathcal {F}}} }\left[ \mathsf {C} (f(x);f) \in f^{-1}(f(x))\right] \ge \alpha \). Then \(s + q\log n \in \varOmega (\alpha ^2 \cdot n)\).
Proof
(Proof of Corollary 4.7). By Theorem 4.6, the existence of an s-advice, \(q\)-query linear-advice inverter \(\mathsf {C} \) with success probability \(\ge \alpha \) implies that set disjointness can be solved over \(\mathcal {Q}\), with error \(\varepsilon > 0\) and communication complexity \(O\left( \frac{\log (\varepsilon )}{\log (1-\alpha ^2/8)} \cdot (s+q \log n)\right) \). Thus, Theorem 4.5 yields that \(\frac{\log (\varepsilon )}{\log (1-\alpha ^2/8)} \cdot (s+q \log n)\in \varOmega (n)\). Since \(\frac{\log (\varepsilon )}{\log (1-\alpha ^2/8)} = \log (1/\varepsilon )\cdot \frac{1}{\log (1/(1-\alpha ^2/8))}\), and since, by Fact 3.9, it holds that \( \log (1/(1-\alpha ^2/8)) \ge \alpha ^2/8\), it follows that \(s+q\log n \in \varOmega (\alpha ^{2} \cdot n)\).
The rest of this section is devoted to proving Theorem 4.6. Fix an s-advice, \(q\)-query inverter \(\mathsf {C} =(\mathsf {C} _{\mathsf {pre}},\mathsf {C} _{\mathsf {dec}})\) with linear preprocessing. We use \(\mathsf {C} \) in Protocol 4.8 to solve set disjointness. In the protocol below we identify a vector \(v \in {\left\{ 0,1\right\} }^{n} \) with the set \(\left\{ i : v_i =1\right\} \).
Protocol 4.8
(  )
)
-
 ’s input: \(a\in {\left\{ 0,1\right\} }^{n} \).
’s input: \(a\in {\left\{ 0,1\right\} }^{n} \). -
 ’s input: \(b\in {\left\{ 0,1\right\} }^{n} \).
’s input: \(b\in {\left\{ 0,1\right\} }^{n} \). -
Public randomness: \(d \in [n]\).
-
Operation:
-
1.
 chooses \(y \leftarrow [n]\).
chooses \(y \leftarrow [n]\). -
2.
 constructs a function
constructs a function  as follows:
as follows:-
for i such that \(a_i=0\), it samples
 uniformly at random.
uniformly at random. -
for i such that \(a_i=1\), it sets
 .
.
-
-
3.
 constructs a function \(f_\mathsf {B} : [n] \rightarrow [n]\) as follows:
constructs a function \(f_\mathsf {B} : [n] \rightarrow [n]\) as follows:-
for i such that \(b_i=0\), it samples \(f_\mathsf {B} (i+d \mod n)\) uniformly at random.
-
for i such that \(b_i=1\), it sets \(f_\mathsf {B} (i + d \mod n) = y\).
-
Let
 .
.
-
-
4.
\(\mathsf {A} \) sends
 to
to  .
. -
5.
 sets
sets  .
. -
6.
 emulates \(\mathsf {C} _{\mathsf {dec}}^{f}(y,c)\): whenever \(\mathsf {C} _{\mathsf {dec}}\) sends a query r to f, algorithm
emulates \(\mathsf {C} _{\mathsf {dec}}^{f}(y,c)\): whenever \(\mathsf {C} _{\mathsf {dec}}\) sends a query r to f, algorithm 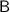 forwards it to
forwards it to  , and feeds
, and feeds 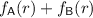 back into \(\mathsf {C} _{\mathsf {dec}}\).
back into \(\mathsf {C} _{\mathsf {dec}}\).-
Let x be \(\mathsf {C} _{\mathsf {dec}}\)’s output in the above emulation, and let \(i = x -d \mod n\).
-
-
7.
 sends \((i,b_{i})\) to
sends \((i,b_{i})\) to  . If \(a_{i}=b_{i}=1\), algorithm
. If \(a_{i}=b_{i}=1\), algorithm  outputs False and informs
outputs False and informs  .
. -
8.
Otherwise, both parties output True.
-
1.
In the following we analyze the communication complexity and success probability of \(\varPi \).
Claim 4.9
(\(\varPi \)’s communication complexity). It holds that \(CC(\varPi ) \le s + 2q(\log n + 1) + \log n + 3\).
Proof
-
1.
In Step 4, party \(\mathsf {A} \) sends
 to
to  .
. -
2.
In Step 6, the parties exchange at most \(2\log n +2\) bits for every query \(\mathsf {C} _{\mathsf {dec}}\) makes.
-
3.
In Step 7, the parties exchange at most \(\log n +3\) bits.
Thus, the total communication is bounded by \(s + 2q(\log n + 1) + \log n + 3\).
Claim 4.10
(\(\varPi \)’s success probability).
-
1.
 for every \((a,b)\in \mathcal {Q}^0 :=\left\{ \mathcal {X},\mathcal {Y}\subseteq [n] :\left| \mathcal {X}\cap \mathcal {Y}\right| = 0\right\} \).
for every \((a,b)\in \mathcal {Q}^0 :=\left\{ \mathcal {X},\mathcal {Y}\subseteq [n] :\left| \mathcal {X}\cap \mathcal {Y}\right| = 0\right\} \). -
2.
 for every \((a,b)\in \mathcal {Q}^1 :=\left\{ \mathcal {X},\mathcal {Y}\subseteq [n] :\left| \mathcal {X}\cap \mathcal {Y}\right| = 1\right\} \).
for every \((a,b)\in \mathcal {Q}^1 :=\left\{ \mathcal {X},\mathcal {Y}\subseteq [n] :\left| \mathcal {X}\cap \mathcal {Y}\right| = 1\right\} \).
Proof
By construction, it is clear that \(\varPi \) always accepts (the parties output True) on inputs \((a,b)\in \mathcal {Q}^0\). Fix \((a,b)\in \mathcal {Q}^1\), and let  and I be the values of
and I be the values of  and i respectively, in a random execution of
and i respectively, in a random execution of  . By construction,
. By construction,  for all \(j\in [n]\). For j not in the intersection, either
for all \(j\in [n]\). For j not in the intersection, either  or
or  is chosen uniformly at random by one of the parties, and therefore F(j) is uniformly distributed and independent of all other outputs. For the intersection element w, it holds that \(F(w)=y\), which is uniform, and since there is exactly one intersection, is independent from all other outputs.
is chosen uniformly at random by one of the parties, and therefore F(j) is uniformly distributed and independent of all other outputs. For the intersection element w, it holds that \(F(w)=y\), which is uniform, and since there is exactly one intersection, is independent from all other outputs.
Let \(W :=w +D \mod n\). Note that W is uniformly distributed over [n] and is independent of F. Also note that, by construction, \(Y = F(W)\). Therefore, (F, W, Y) is distributed exactly as (F, X, F(X)) for \(X\leftarrow [n]\). Hence, the assumption on \(\mathsf {C} \) yields that
and by Claim 3.8,
Therefore, both parties output False with probability at least \({\alpha ^2}/{8}\).
Proving Theorem 4.6. We now use Claims 4.9 and 4.10 to prove Theorem 4.6.
Proof
(Proof of Theorem 4.6). Let \(t= \left\lceil \frac{\log (\varepsilon )}{\log (1-\alpha ^2/8)} \right\rceil \), and consider the protocol \(\varPi ^t\), in which on input (a, b) the parties interact in protocol \(\varPi \) for t times, and accept only if they do so in all iterations. By Claims 4.9 and 4.10, the communication complexity and success probability of \(\varPi ^t\) in solving set disjointness over \(\mathcal {Q}\) match the theorem statement.
4.1 Additive-Advice Inverters
The following result generalizes Corollary 4.7 by replacing the restriction on the decoder (e.g., linear and short output) with the ability to compute the advice string of \(f_1 + f_2\) by a low-communication protocol over the inputs \(f_1\) and \(f_2\).
Theorem 4.11
(Bound on additive-advice inverters). Let \(\mathsf {C} =(\mathsf {C} _{\mathsf {pre}},\mathsf {C} _{\mathsf {dec}})\) be an \(q\)-query inversion algorithm such that \(\Pr _{{\mathop {x\leftarrow [n]}\limits ^{f\leftarrow \mathcal {F}}} }\left[ \mathsf {C} (f(x);f) \in f^{-1}(f(x))\right] \ge \alpha \). Assume exists a two-party protocol \((\mathsf {P} _1, \mathsf {P} _2)\) with communication complexity k such that for every \(f_1,f_2\in \mathcal {F}\), the output of \(\mathsf {P} _2\) in \((\mathsf {P} _1(f_1), \mathsf {P} _2(f_2))\) equals to \(\mathsf {C} _{\mathsf {pre}}(f_1+f_2)\) with probability at least \(1-\gamma \) for some \(\gamma \ge 0\), letting \(f_1+f_2\) be according to Definition 4.2. Then \({k + q\log n \in \varOmega (\alpha ^2 (1-\gamma )\cdot n)}\).
Proof
The proof follows almost the exact same lines as that of Theorem 4.6, with the following changes: first, steps 4. and 5. in Protocol 4.8 are replaced by the parties  and
and  interacting in
interacting in  , resulting in
, resulting in  outputting
outputting  (thus, transmitting a total of \(k+2q(\log n+1)+\log n + 3 \in O(k+q\log n)\) bits over the entire execution of the protocol). Second, note that due to the constant failure probability of \((\mathsf {P} _1, \mathsf {P} _2)\) in computing
(thus, transmitting a total of \(k+2q(\log n+1)+\log n + 3 \in O(k+q\log n)\) bits over the entire execution of the protocol). Second, note that due to the constant failure probability of \((\mathsf {P} _1, \mathsf {P} _2)\) in computing  , the success probability of each execution of the protocol is now lowered by a constant factor \((1-\gamma )\). This means that the rate of success when \(\mathcal {X}\cap \mathcal {Y}\ne \emptyset \) is now bounded from below by only \(\alpha ^2(1-\gamma )/8\) (rather than \(\alpha ^2/8\)). The rest of the analysis is identical to that of Theorem 4.6.
, the success probability of each execution of the protocol is now lowered by a constant factor \((1-\gamma )\). This means that the rate of success when \(\mathcal {X}\cap \mathcal {Y}\ne \emptyset \) is now bounded from below by only \(\alpha ^2(1-\gamma )/8\) (rather than \(\alpha ^2/8\)). The rest of the analysis is identical to that of Theorem 4.6.
5 Non-adaptive Inverters
In this section we present lower bounds on the time/memory tradeoff of non-adaptive function inverters. In Section 5.1, we present a bound for non-adaptive affine decoders, and in Section 5.2 we extend this bound to non-adaptive affine decision trees. To simplify notation, the following definitions and results are stated with respect to some fixed \(n\in {\mathbb {N}}\), for which there exists a finite field of size n which we denote by \(\mathbb {F} \). Let \(\mathcal {F}\) be the set of all functions from [n] to [n]. All asymptotic notations (e.g., \(\varTheta \)) hide constant terms that are independent of n. We start by formally defining non-adaptive function inverters.
Definition 5.1
(Non-adaptive inverters). An s-advice q-query non-adaptive inverter is a deterministic algorithm triplet of the form \(\mathsf {C} :=( \mathsf {C} _{\mathsf {pre}}, \mathsf {C} _\mathsf {qry}, \mathsf {C} _{\mathsf {dec}}) \), where \( \mathsf {C} _{\mathsf {pre}}:\mathcal {F}\rightarrow {\left\{ 0,1\right\} }^{s} \), \(\mathsf {C} _\mathsf {qry}:[n] \times {\left\{ 0,1\right\} }^{s} \rightarrow [n]^q\), and \(\mathsf {C} _{\mathsf {dec}}:[n] \times {\left\{ 0,1\right\} }^{s} \times [n]^q\rightarrow [n]\). For \(f\in \mathcal {F}\) and \(y\in [n]\), let
That is, \(\mathsf {C} _{\mathsf {pre}}\) is the preprocessing algorithm. It takes the function description as input and outputs a string of length s, to which we refer as the advice string. In the case that \(s=0\), we say that \(\mathsf {C} \) has zero-advice, and omit \(\mathsf {C} _{\mathsf {pre}}\) from the notation. Algorithm \(\mathsf {C} _\mathsf {qry}\) is the query selection algorithm. It chooses the queries according to the element to invert y and the advice string, and outputs q indices, to which we refer as the queries. Algorithm \(\mathsf {C} _{\mathsf {dec}}\) is the decoder algorithm that performs the actual inversion. It receives the element y, the advice string and the function’s answers to the (non-adaptive) queries selected by \(\mathsf {C} _\mathsf {qry}\) (the query indices themselves may be deduced from y and the advice), and attempts to output a preimage of y. Finally, \(\mathsf {C} (y;f)\) is the candidate preimage of y produced by the algorithms of \(\mathsf {C} \) given the (restricted) access to f.
5.1 Affine Decoders
In this section we present our bound for non-adaptive affine decoders, defined as follows:
Definition 5.2
(Affine decoder). A non-adaptive inverter \(\mathsf {C} := ( \mathsf {C} _{\mathsf {pre}}, \mathsf {C} _\mathsf {qry}, \mathsf {C} _{\mathsf {dec}}) \) has an affine decoder, if for every \(y\in [n]\) and \(a\in \left\{ 0,1\right\} ^s\) there exists a \(q\)-sparse vector \(\alpha _y^a\in {\mathbb {F}}^n\) and a field element \(\beta _y^a\in \mathbb {F} \), such that for every \(f\in \mathcal {F}\): \(\mathsf {C} _{\mathsf {dec}}(y,a,f(\mathsf {C} _\mathsf {qry}(y,a)))= \langle \alpha _y^a, f \rangle + \beta _y^a\).
The following theorem bounds the probability, over a random function f, that a non-adaptive inverter with an affine decoder inverts a random output of f with probability \(\tau \).
Theorem 5.3
Let \( \mathsf {C} = ( \mathsf {C} _{\mathsf {pre}}, \mathsf {C} _\mathsf {qry}, \mathsf {C} _{\mathsf {dec}}) \) be an s-advice non-adaptive inverter with an affine decoder and let \(\tau \in [0,1]\). Then for every \(\delta \in [0,1]\) and \(m \le n/16\), it holds that
for \(\alpha _{\tau ,\delta } :=\Pr _{f \leftarrow \mathcal {F}}\left[ \exists \tau n\text {-size set } \mathcal {X}\subset [n]:\left| f(\mathcal {X})\right| \le \delta n \right] \).
While it is not easy to see what is the best choice, per \(\tau \), of the parameters \(\delta \) and \(m\) above, the following corollary (proven in the full version) exemplifies the usability of Theorem 5.3 by considering the consequences of such a choice.
Corollary 5.4
(Theorem 1.5, restated). Let \(\mathsf {C} \) be as in Theorem 5.3, let \(\tau \ge 2 \cdot n^{-1/8}\) and assume
\(\Pr _{ f\leftarrow \mathcal {F}}\left[ \Pr _{{\mathop {y=f(x)}\limits ^{x\leftarrow [n]}} }\left[ \mathsf {C} (y;f) \in f^{-1}(y)\right] \ge \tau \right] \ge \nicefrac {1}{2}\), then \( s \in \varOmega ( \tau ^2 \cdot n)\).Footnote 7
Our key step towards proving Theorem 5.3 is showing that even when conditioned on the (unlikely) event that a zero-advice inverter successfully inverts \(i-1\) random elements, the probability the inverter successfully inverts the next element is still low. To formulate the above statement, we define the following jointly distributed random variables: let F be uniformly distributed over \(\mathcal {F}\) and let \(Y= (Y_1,...,Y_n)\) be a uniform vector over \([n]^n\). For a zero-advice inverter, we define the following random variables (jointly distributed with F and Y).
Notation 5.5
For a zero-advice inverter \(\mathsf {D} \), let \(X_i^\mathsf {D} :=\mathsf {D} (Y_i;F)\), let \(Z_i^\mathsf {D} \) be the event \(\bigwedge _{j\in [i]} \left\{ F(X_j^\mathsf {D} )=Y_j\right\} \), and let \(X^\mathsf {D} = (X_1^\mathsf {D} ,\ldots ,X_n^\mathsf {D} )\).
That is, \(X^\mathsf {D} _i\) is \(\mathsf {D} \)’s answers to the challenges \(Y_i\), and \(Z^\mathsf {D} _i\) indicates whether \(\mathsf {D} \) successfully answered each of the first i challenges. Given the above notation, our main lemma is stated as follows:
Lemma 5.6
Let \(\mathsf {D} \) be a zero-advice, non-adaptive inverter with affine decoder and let \(Z^\mathsf {D} \) be as in Notation 5.5. Then for every \(i\in [n]\) and \(\mu \in [0,\tfrac{1}{2}]\):
We prove Lemma 5.6 below, but first use it to prove Theorem 5.3.
Proving Theorem 5.3. Lemma 5.6 immediately yields a bound on the probability that \(\mathsf {D} \), a zero-advice inverter, successfully inverts the first i elements of Y. For proving Theorem 5.3, however, we need to bound the probability that \(\mathsf {D} \), and later on, an inverter with non-zero advice, finds a preimage of a random output of f. Yet, the conversion between these two measurements is rather straightforward. Hereafter we assume \(n\ge 16\), as otherwise Theorem 5.3 is trivial, as \(m = 0\).
Proof
(Proof of Theorem 5.3.). Let \( \mathsf {C} = ( \mathsf {C} _{\mathsf {pre}}, \mathsf {C} _\mathsf {qry}, \mathsf {C} _{\mathsf {dec}}) \), \(\tau \in [0,1]\), \(\delta \in [0,1]\) and m be as in the theorem statement. Fix an advice string \(a\in {\left\{ 0,1\right\} }^{s} \), and let \(\mathsf {C} ^a= (\mathsf {C} _\mathsf {qry}^a,\mathsf {C} _{\mathsf {dec}}^a)\) denote the zero-advice inverter obtained by hardcoding a as the advice of \(\mathsf {C} \) (i.e., \(\mathsf {C} _{\mathsf {pre}}^a(f)=a\) for every f). For \(j\in [n]\), let \(Z_j = Z^{\mathsf {C} ^a}_j\) and let \(\mu _j :=\max \left\{ \root 4 \of {1 / n}, \frac{4j }{ n }\right\} \). We start by showing that for every \(j \le n/16\) it holds that
Indeed, by Lemma 5.6
We write,
Since
and
we conclude that \(\Pr \left[ Z_j \mid Z_{j-1}\right] \le \frac{2j-1}{n} + \mu _j + 2^{-2\log n}\le \frac{2j}{n} + \mu _j\), proving Eq. (16).
Eq. (16) immediately yields that
We use the above to produce a bound on the number of elements that \(\mathsf {C} ^a\) successfully inverts. Let \( {\mathcal {G}}_\mathcal {Y}^a(f) :=\left\{ y \in [n] :\mathsf {C} ^a(y;f) \in f^{-1}(y)\right\} \), and compute:
Combining Eqs. (19) and (20) yields the following bound on the number of images \(\mathsf {C} ^a\) successfully inverts:
We now adapt the above bound to (the non zero-advice) \(\mathsf {C} \). Let \( {\mathcal {G}}_\mathcal {Y}(f) :=\left\{ y \in [n] :\mathsf {C} (y;f) \in f^{-1}(y)\right\} \) and let \( {\mathcal {G}}_\mathcal {X}(f) = f^{-1}( {\mathcal {G}}_\mathcal {Y}(f) )\). By Eq. (21) and a union bound,
We conclude that

The second inequality follows by the definition of \( \alpha _{\tau ,\delta }\) and Eq. (22).
Proving Lemma 5.6 In the rest of this section we prove Lemma 5.6. Fix a zero-advice non-adaptive inverter with an affine decoder \(\mathsf {D} = (\mathsf {D} _\mathsf {qry}, \mathsf {D} _{\mathsf {dec}})\), \(i \in [n]\) and \(\mu \in [0,\tfrac{1}{2}]\). Let \(X:=X^\mathsf {D} \) and, for \(j\in [n]\) let \(Z_j:=Z^\mathsf {D} _j\). We start by proving the following claim that bounds the probability in hand, assuming \(X_i\), the inverter’s answer, is coming from a small linear space. (Recall, from Definition 3.2, that  , where \(e_j\) is the j\(^{\mathrm{th}}\) unit vector in \(\mathbb {F} ^n\).)
, where \(e_j\) is the j\(^{\mathrm{th}}\) unit vector in \(\mathbb {F} ^n\).)
Claim 5.7
Let \(\mathbf{A} \in \mathbb {F} ^{\ell \times n} \), let \(v \in {\text {Im}}(\mathbf{A} )\), let \(\mathbf{B} ^1,\ldots ,\mathbf{B} ^n \in \mathbb {F} ^{t\times n}\), and, for \(y\in [n]\), let \(\mathbf{A} ^y:= \begin{pmatrix} \mathbf{A} \\ \mathbf{B} ^{y} \end{pmatrix} \). Then
Proof
By Claim 3.4 there exist an \(\ell \)-size set \(\mathcal {S}:=\mathcal{{S}}_\mathbf{A} \) and t-size sets \(\left\{ \mathcal {S}_k:=\mathcal {S}_\mathbf{B ^k}\right\} _{k\in [n]}\) such that
for every \(y\in [n]\). By Fact 3.1,

Compute,
The first inequality holds since \(\mathcal {E}(\mathbf{A} ^{Y_i}) \subseteq \mathcal {S}\cup \mathcal {S}_{Y_i}\), and the last one since \(\left| \mathcal {S}\right| \le \ell \) and \(Y_i\) is independent of F. Applying Claim 3.6 with respect to \(p :=n^{-\ell }\), \(\gamma :=\mu \), \(W :=\left\{ \mathbf{A} \times F=v\right\} \), \(Y:=Y_i\) and the sets \(\mathcal {S}_1, \ldots \mathcal {S}_n\), yields that
We conclude that \( \Pr \left[ Y_i \in F(\mathcal {E}(\mathbf{A} (Y_i))) \mid \mathbf{A} \times F= v\right] \le \frac{\ell }{n} + \mu + 2^{2\lceil \mu n\rceil \log (1/\mu ) + \lceil \mu n\rceil \log (t / n) + \ell \log n}\).
Given the above claim, we prove Lemma 5.6 as follows.
Proof
(Proof of Lemma 5.6). Since \(\mathsf {D} \) has an affine decoder, for every \(y \in [n]\) and \(X :=\mathsf {D} (y;F)\) there exist a \(q\)-sparse vector \(\alpha ^y \in \mathbb {F} ^n\) and a field element \(\beta ^y \in \mathbb {F} \) such that \( \langle \alpha ^y, F \rangle + \beta ^y = X\). Therefore, for every \(j < i\):
-
1.
\(\langle \alpha ^{Y_j}, F \rangle = - \beta ^{Y_j} + X_{j}\).
Conditioning on \(Z_{i-1}\) further implies that for every \(j < i\):
-
2.
\( F(X_j) = Y_j\).
Let \(\ell :=2i-2\), and let \(\mathbf{M} ^{i-1}\in \mathbb {F} ^{\ell \times n} \) be the (random) matrix defined, for every \(j\in [i-1]\), by \(\mathbf{M} ^{i-1}_{2j-1} :=\alpha ^{Y_j}\) and \(\mathbf{M} ^{i-1}_{2j} :=e_{X_j}\). Let \(V^{i-1}\in \mathbb {F} ^{\ell } \) be the (random) vector defined by \(V^{i-1}_{2j-1} :=-\beta ^{Y_j} + X_j\) and \(V^{i-1}_{2j} = Y_j\). By definition, conditioned on \(Z_{i-1}\) it holds that \(\mathbf{M} ^{i-1}\times F = V^{i-1}\). This incorporates in a single equation all that is known about F given \(Z_{i-1}\). To take into account the knowledge gained from the queries made while attempting to invert \(Y_i\), we combine the above with \(\alpha ^{Y_i}\) and \(\langle \alpha ^{Y_i},F \rangle \), into the matrix \(\mathbf{M} := \begin{pmatrix} \mathbf{M} ^{i-1} \\ \alpha ^{Y_i} \end{pmatrix} \) and vector \( V:= \begin{pmatrix} V^{i-1} \\ \langle \alpha ^{Y_i},F \rangle \end{pmatrix} \). By definition, \(\mathbf{M} \times F = V\). We write
and prove the lemma by separately bounding the two terms of the above equation. Let \(H :=(Y_{< i}, \mathbf{M} ^{i-1},V^{i-1})\), and note that
The first inequality holds by the definition of \(Z_i\). The second equality holds by the definition of \(Z_{i-1}\). The third equality holds since the event \(\left\{ Y_{< i}=y_{<i}, m^{i-1}\times F = v^{i-1}\right\} \) implies that \(\left\{ \mathbf{M} ^{i-1}=m^{i-1},V^{i-1}=v^{i-1}\right\} \). The last equality holds since F is independent of Y, and the last inequality follows by Claim 5.7 with respect to \(\mathbf{A} :=m^{i-1}, v :=v^{i-1} \), and \((\mathbf{B} ^1,\ldots ,\mathbf{B} ^n) :=(\alpha ^1,\ldots ,\alpha ^n)\) (viewing \(\alpha ^i\) as a matrix in \(\mathbb {F} ^{1 \times n}\)).
For bounding the right-hand term of Eq. (27), let \(H :=(X_i,Y_{\le i}, \mathbf{M} ,V)\), and compute
The second equality holds by the definition of \(Z_{i-1}\). The third equality holds since the event \(\left\{ Y_{\le i}=y_{\le i}, m\times F = v\right\} \) implies that \(\left\{ \mathbf{M} =m,V=v\right\} \), and \(X_i\) is a function of \(V\). The fourth equality holds since F is independent from Y. The last inequality follows by Claim 3.3. Combining Eqs. (27) to (29), we conclude that
5.2 Affine Decision Trees
In this section we present lower bounds for non-adaptive affine decision trees. These are formally defined as follows:
Definition 5.8
(Affine decision trees). An n-input affine decision tree over \(\mathbb {F} \) is a labeled, directed, degree \(\left| \mathbb {F} \right| \) tree \(\mathcal {T}\). Each internal node v of \(\mathcal {T}\) has label \(\alpha _v\in \mathbb {F} ^n\), each leaf \(\ell \) of \(\mathcal {T}\) has label \(o_\ell \in \mathbb {F} \), and the \(\left| \mathbb {F} \right| \) outgoing edges of every internal node are labeled by the elements of \(\mathbb {F} \). Let \(\varGamma _\mathcal {T}(v,\gamma )\) denote the (direct) child of v connected via the edge labeled by \(\gamma \). The node path \(p= (p_1,\ldots ,p_{d+1})\) of \(\mathcal {T}\) on input \(w \in \mathbb {F} ^n \) is defined by:
-
\(p_1\) is the root of \(\mathcal {T}\).
-
\(p_{i+1}=\varGamma _\mathcal {T}(p_i,\langle \alpha _{p_i},w \rangle )\).
The edge path of \(\mathcal {T}\) on w is defined by \((\langle \alpha _{p_1},w \rangle ,\cdots ,\langle \alpha _{p_{d}},w \rangle )\). Lastly, the output of \(\mathcal {T}\) on w, denoted \(\mathcal {T}(w)\), is the value of \(o_{p_{d+1}}\).
Note that the edge path determines the computation path and output. Given the above, affine decision tree decoders are defined as follows.
Definition 5.9
(Affine decision tree decoder). An inversion algorithm \(\mathsf {C} :=( \mathsf {C} _{\mathsf {pre}}, \mathsf {C} _\mathsf {qry}, \mathsf {C} _{\mathsf {dec}}) \) has a d-depth affine decision tree decoder, if for every \(y\in [n]\), \(a\in \left\{ 0,1\right\} ^s\) and \(v= \mathsf {C} _\mathsf {qry}(y,a)\), there exists an n-input, d-depth affine decision tree \(\mathcal {T}^{y,a}\) such that \(\mathsf {C} _{\mathsf {dec}}(y, a, f(v))=\mathcal {T}^{y,a}(f)\).
Note that such a decision tree may be of size \(O(n^d)\). The following theorem bounds the probability, over a random function f, that a non-adaptive inverter with an affine decision tree decoder inverts a random output of f with probability \(\tau \).
Theorem 5.10
Let \( \mathsf {C} \) be an s-advice, \((q\le n/16)\)-query, non-adaptive inverter with a d-depth affine decision tree decoder, and let \(\tau \in [0,1]\). Then for every \(\delta \in [0,1]\) and \(m \le \frac{n \log (n/q)}{4(d+1) \log n}\) it holds that
for \(\alpha _{\tau ,\delta } :=\Pr _{ f \leftarrow {\mathcal {F}_n} }\left[ \exists \tau n\text {-size set } \mathcal {X}\subset [n]:|f(\mathcal {X})| \le \delta n \right] \).
Comparing to the bound we derive on affine decoders (Theorem 5.3), we are paying above for the tree depth d, but also for the number of queries q. In particular, we essentially multiply each term of the above product by the tree depth d, and by \(\frac{\log n}{\log (n/q)}\). In addition, the theorem only holds for smaller values of m. The following corollary exemplifies the usability of Theorem 5.10 by considering the consequences of two choices of parameters.
Corollary 5.11
(Theorem 1.6, restated). Let \(\mathsf {C} \) be as in Theorem 5.10 and assume
\(\Pr _{ f\leftarrow \mathcal {F}}\left[ \Pr _{{\mathop {y=f(x)}\limits ^{x\leftarrow [n]}} }\left[ \mathsf {C} (y;f) \in f^{-1}(y)\right] \ge \tau \right] \ge \nicefrac {1}{2}\), then the following holds:
-
If \(q\le n \cdot (\nicefrac {\tau }{2})^8\), then \( s \in \varOmega ( \nicefrac {n}{d}\cdot \nicefrac {\tau ^2}{\log n})\).
-
If \(q\le n^{1-\epsilon }\), then \( s \in \varOmega (\nicefrac {n}{d} \cdot \tau ^2 \epsilon )\).
Proof
Omitted, follows by Theorem 5.10 using very similar lines to those used to derive Corollary 5.4 from Theorem 5.3.
The proof of Theorem 5.10 is omitted and can be found in the full version of this paper.
Notes
- 1.
If the inverter is only assumed to have additive advice, this step is replaced with the parties interacting in the guaranteed protocol for computing the advice for f from the descriptions of
 and
and  .
. - 2.
This first part of the proof is rather standard, cf., Akshima et al. [2].
- 3.
Indeed, this dependency between the queries to f and the value to invert is exactly what makes (efficient) inversion by adaptive inverters possible.
- 4.
That is, for every \(i\in \mathcal {E}(\mathbf{A} )\), \(w_i\) can be described as a linear combination of the entries of v, and thus \(w_i\) is fixed by v.
- 5.
(1) all zero rows are at the bottom (2) the first non-zero entry in each row is equal to 1 (known as the “leading 1”) (3) the leading 1 in each row appears strictly to the right of the leading 1 in all the rows above it (4) a column that contains a leading 1 is zero in all other entries. It is a well-known fact that a matrix can be reduced to row canonical form using Gaussian elimination, and the set of columns containing a leading 1 is unique.
- 6.
- 7.
The constant 1/2 lowerbounding the probability is arbitrary.
References
Abusalah, H., Alwen, J., Cohen, B., Khilko, D., Pietrzak, K., Reyzin, L.: Beyond hellman’s time-memory trade-offs with applications to proofs of space. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10625, pp. 357–379. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70697-9_13
Akshima, D., Cash, A., Drucker, H., Wee, et al.: Time-space tradeoffs and short collisions in merkle-damgård hash functions. In: Annual International Cryptology Conference (CRYPTO), pp. 157–186 (2020)
Alon, N., Balla, I., Gishboliner, L., Mond, A., Mousset, F.: The minrank of random graphs over arbitrary fields. Isr. J. Math. 235(1), 63–77 (2019). https://doi.org/10.1007/s11856-019-1945-8
Bar-Yossef, Z., Birk, Y., Jayram, T., Kol, T.: Index coding with side information. IEEE Trans. Inform. Theor. 57(3), 1479–1494 (2011)
Biryukov, A., Shamir, A.: Cryptanalytic time/memory/data tradeoffs for stream ciphers. In: Okamoto, T. (ed.) ASIACRYPT 2000. LNCS, vol. 1976, pp. 1–13. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44448-3_1
Biryukov, A., Shamir, A., Wagner, D.: Real time cryptanalysis of A5/1 on a PC. In: Goos, G., Hartmanis, J., van Leeuwen, J., Schneier, B. (eds.) FSE 2000. LNCS, vol. 1978, pp. 1–18. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44706-7_1
Chawin, D., Haitner, I., Mazor, N.: Lower bounds on the time/memory tradeoff of function inversion. Technical report TR20-089, Electronic Colloquium on Computational Complexity (2020)
Coretti, S., Dodis, Y., Guo, S., Steinberger, J.: Random oracles and non-uniformity. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 227–258. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_9
Corrigan-Gibbs, H., Kogan, D.: The function-inversion problem: barriers and opportunities. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019. LNCS, vol. 11891, pp. 393–421. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36030-6_16
De, A., Trevisan, L., Tulsiani, M.: Time space tradeoffs for attacks against one-way functions and PRGs. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 649–665. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_35
Dodis, Y., Guo, S., Katz, J.: Fixing cracks in the concrete: random oracles with auxiliary input, revisited. In: Coron, J., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 473–495. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_16
Fiat, A., Naor, M.: Rigorous time-space trade-offs for inverting functions. SIAM J. Comput. 29(3), 790–803 (2000)
Galvin, D.: Three tutorial lectures on entropy and counting. Technical report 1406.7872, arXiv (2014)
Gennaro, R., Gertner, Y., Katz, J., Trevisan, L.: Bounds on the efficiency of generic cryptographic constructions. SIAM J. Comput. 35(1), 217–246 (2005)
Golovnev, A., Regev, O., Weinstein, O.: The minrank of random graphs. IEEE Trans. Inform. Theor. 64(11), 6990–6995 (2018)
Haviv, I., Langberg, M.: On linear index coding for random graphs. In: 2012 IEEE International Symposium on Information Theory Proceedings, pp. 2231–2235. IEEE (2012)
Hellman, M.: A cryptanalytic time-memory trade-off. IEEE Trans. Inform. Theor. 26(4), 401–406 (1980)
Impagliazzo, R., Rudich, S.: Limits on the provable consequences of one-way permutations. In: Annual ACM Symposium on Theory of Computing (STOC), pp. 44–61 (1989)
Lubetzky, E., Stav, U.: Nonlinear index coding outperforming the linear optimum. IEEE Trans. Inform. Theor. 55(8), 3544–3551 (2009)
Oechslin, P.: Making a faster cryptanalytic time-memory trade-Off. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 617–630. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_36
Razborov, A.A.: On the distributional complexity of disjointness. Theor. Comput. Sci. 106(2), 385–390 (1992)
Unruh, D.: Random oracles and auxiliary input. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 205–223. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_12
Valiant, L.G.: Graph-theoretic arguments in low-level complexity. In: Gruska, J. (ed.) MFCS 1977. LNCS, vol. 53, pp. 162–176. Springer, Heidelberg (1977). https://doi.org/10.1007/3-540-08353-7_135
Valiant, L.G.: Why is boolean complexity theory difficult. Boolean Funct. Complex. 169, 84–94 (1992)
Yao, A.C.: Should tables be sorted? J. ACM 28(3), 615–628 (1981)
Yao, A.C.: Protocols for secure computations. In: Annual Symposium on Foundations of Computer Science (FOCS), pp. 160–164 (1982)
Yao, A.C.: Coherent functions and program checkers. In: Annual ACM Symposium on Theory of Computing (STOC), pp. 84–94 (1990)
Acknowledgements
We are thankful to Dmitry Kogan, Uri Meir and Alex Samorodnitsky for very useful discussions. We also thank the anonymous reviewers for their comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Chawin, D., Haitner, I., Mazor, N. (2020). Lower Bounds on the Time/Memory Tradeoff of Function Inversion. In: Pass, R., Pietrzak, K. (eds) Theory of Cryptography. TCC 2020. Lecture Notes in Computer Science(), vol 12552. Springer, Cham. https://doi.org/10.1007/978-3-030-64381-2_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-64381-2_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64380-5
Online ISBN: 978-3-030-64381-2
eBook Packages: Computer ScienceComputer Science (R0)





 samples
samples 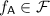 by letting
by letting 
 .
. sends
sends  to
to  .
. sends r to
sends r to
 .
. sends
sends 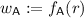 back to
back to
 .
. replies
replies  to
to  ’s input:
’s input:  ’s input:
’s input:  chooses
chooses  constructs a function
constructs a function  as follows:
as follows: uniformly at random.
uniformly at random. .
. constructs a function
constructs a function  .
. to
to  .
. sets
sets  .
. emulates
emulates  forwards it to
forwards it to  , and feeds
, and feeds 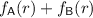 back into
back into  sends
sends  . If
. If  outputs False and informs
outputs False and informs  .
. to
to  .
. for every
for every  for every
for every  and
and  .
.