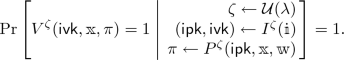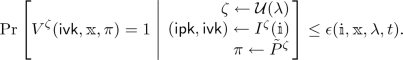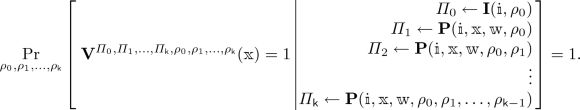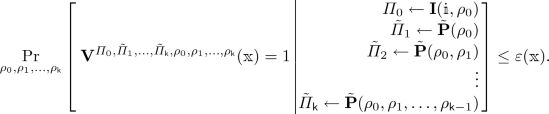Barriers for Succinct Arguments in the Random Oracle Model

Abstract

We establish barriers on the efficiency of succinct arguments in the random oracle model. We give evidence that, under standard complexity assumptions, there do not exist succinct arguments where the argument verifier makes a small number of queries to the random oracle. The new barriers follow from new insights into how probabilistic proofs play a fundamental role in constructing succinct arguments in the random oracle model.

• IOPs are necessary for succinctness. We prove that any succinct argument in the random oracle model can be transformed into a corresponding interactive oracle proof (IOP). The query complexity of the IOP is related to the succinctness of the argument.

• Algorithms for IOPs. We prove that if a language has an IOP with good soundness relative to query complexity, then it can be decided via a fast algorithm with small space complexity.

By combining these results we obtain barriers for a large class of deterministic and non-deterministic languages. For example, a succinct argument for $\mathrm {3SAT}$ with few verifier queries implies an IOP with good parameters, which in turn implies a fast algorithm for $\mathrm {3SAT}$ that contradicts the Exponential-Time Hypothesis.

We additionally present results that shed light on the necessity of several features of probabilistic proofs that are typically used to construct succinct arguments, such as holography and state restoration soundness. Our results collectively provide an explanation for “why” known constructions of succinct arguments have a certain structure.

1 Introduction

A succinct argument is a cryptographic proof system for deterministic and non-deterministic languages, whose communication complexity is “succinct” in the sense that it is sublinear in the time to decide the language (for deterministic languages) or witness size (for non-deterministic languages). In the last decade, succinct arguments have drawn the attention of researchers from multiple communities, being a fundamental cryptographic primitive that has found applications in the real world.

A central goal in the study of succinct arguments is improving their efficiency. An important complexity measure is argument size, which is the number of bits sent from the prover to the verifier. Achieving small argument size is crucial, e.g., in applications where non-interactive succinct arguments are broadcast in a peer-to-peer network and redundantly stored at every node (as in [Ben+14]). Other important complexity measures include the running time of the prover and the running time of the verifier—this latter is the complexity measure that we study in this paper.

There are applications where the running time of the verifier is the main bottleneck and call for verifiers that are extremely lightweight. These applications include obfuscating the verifier [Bon+17], or recursive constructions where an outer succinct argument proves that the verifier of an inner succinct argument has accepted [Val08, Bit+13]. In these cases, the circuit (or code) representing the verifier’s computation is used in a white-box manner and the verifier’s running time dominates the complexity of the final scheme. For instance, in the second example, the running time of the outer prover mainly depends on the running time of the inner verifier.

Our goal is to establish lower bounds on the running time of a succinct argument’s verifier.

We focus on the random oracle model. We deliberately restrict our attention to studying succinct arguments that are secure in the random oracle model (ROM). This is because the ROM is an elegant information-theoretic model within which we could hope to precisely understand the structure of arbitrary succinct arguments, and prove lower bounds on specific efficiency measures.

Moreover, the ROM supports several well-known constructions of succinct arguments that can be heuristically instantiated via lightweight cryptographic hash functions, are plausibly post-quantum secure [CMS19], and have led to realizations that are useful in practice. These constructions include the Fiat–Shamir transformation [FS86], which applies to public-coin interactive proofs (IPs); the Micali transformation [Mic00], which applies to probabilistically checkable proofs (PCPs); and the BCS transformation [BCS16], which applies to public-coin interactive oracle proofs (IOPs).

How small can verifier query complexity be? As mentioned earlier, the running time of the verifier is a crucial efficiency measure in applications of succinct arguments. While in the ROM each query is considered a constant-time operation, each query actually becomes expensive when the random oracle is heuristically instantiated via a cryptographic hash function. Each query becomes a sub-computation involving very many gates for evaluating the cryptographic hash function, which can dominate the verifier’s running time. This, for example, is the case in the recursive construction in [COS20]. In this paper, we ask: how small can the query complexity of a verifier be?

We make our question precise via the notion of bits of security. The soundness error $\mathsf {\epsilon }$ of a succinct argument in the ROM is a function of several parameters: the instance size, the output size of the random oracle, and the number of queries by the cheating prover to the random oracle. Then we say that a succinct argument provides $s$ bits of security if the soundness error $\mathsf {\epsilon }$ is at most $2^{-s}$ for every instance size up to $2^{s}$, every prover query complexity up to $2^{s}$, and when the output size of the random oracle is $\varTheta (s)$. (See Sect. 3.3 for relevant definitions.)

Known constructions of succinct arguments achieve verifier query complexities that are $\varOmega (s)$. This is true even if one were to rely on conjectured “holy grail” probabilistic proofs within these constructions. In particular, no approach is known that could achieve a verifier that makes $o(s)$ queries to the oracle (which would be very desirable).

We are interested in understanding whether small verifier query complexity is possible:

Do there exist succinct arguments with $s$ bits of security and verifier query complexity $\ll s$?

1.1 Our Contributions

In this paper we contribute new insights into the structure of succinct arguments in the ROM, which we then use to obtain evidence that the answer to the above question is negative. First we prove that IOPs are an inherent ingredient of any succinct argument in the ROM. Then we prove limitations of the obtained IOPs, thereby obtaining lower bounds on the number of queries to the random oracle by the verifier in the starting succinct argument. The limitations on IOPs that we prove are rather broad (even when applied to the case of a PCP), and may be of independent interest.

Here we remind the reader that an interactive oracle proof (IOP) [BCS16, RRR16] is a proof system that combines the notions of interactive proofs (IP) and probabilistically-checkable proofs (PCPs). Namely, it is an interactive proof where the verifier is granted oracle access to the messages sent by the prover and so can probabilistically query them. As opposed to PCPs, IOPs leverage the multiple rounds of communication, which gives them many efficiency improvements in terms of proof size and the running time of the prover. As shown in [BCS16], IOPs with suitable soundness properties can be compiled into non-interactive succinct arguments in the ROM. This, along with the concrete efficiency of IOPs, makes them a central component of many succinct arguments today.

1.1.1 IOPs are Necessary for Succinctness

We prove that IOPs are inherent to succinct arguments in the ROM in a precise sense: any succinct argument in the ROM can be generically transformed into an IOP whose query complexity depends on the “succinctness” of the argument. Namely, if the argument prover sends $\mathsf {as}$ bits to the argument verifier, then the IOP verifier makes $\mathsf {as}$ queries to proof strings sent by the IOP prover.

Moreover, and less intuitively, the IOP verifier makes $O(\mathsf {vq}\cdot \mathsf {a})$ extra queries, where $\mathsf {vq}$ is the number of queries made by the argument verifier to the random oracle and $\mathsf {a}$ is the number of adaptive rounds of queries by the (honest) argument prover to the random oracle (see Sect. 3.1 for more on adaptivity). The adaptivity parameter $\mathsf {a}$ plays a key role in our result, and it is small in all known schemes. (E.g., $\mathsf {a}=O(\log n)$ in succinct arguments obtained via the Micali transformation [Mic00].)

Theorem 1

(informal). There is an efficient transformation $\mathbb {T}$ that satisfies the following. Suppose that $\mathsf {ARG}$ is a size-$\mathsf {as}$ argument in the ROM for a language $L$ where the honest prover performs $\mathsf {pq}$ queries in $\mathsf {a}$ rounds and the verifier performs $\mathsf {vq}$ queries. Then $\mathsf {IOP}:= \mathbb {T}(\mathsf {ARG})$ is an IOP for $L$ with proof length $O(\mathsf {pq}+\mathsf {as})$ and query complexity $O(\mathsf {as}+\mathsf {vq}\cdot \mathsf {a})$. Other aspects of $\mathsf {IOP}$ (such as public coins, soundness, time and space complexities) are essentially the same as in $\mathsf {ARG}$.

Our result provides a way to construct an IOP by “reverse engineering” an arbitrary succinct argument, leading to a standalone compelling message: succinct arguments in the ROM are “hard to construct” because they must contain non-trivial information-theoretic objects. This holds regardless of the complexity of the language proved by the succinct argument. For example, IOPs are inherent even to succinct arguments for deterministic computations (where the primary efficiency goal is an argument verifier that is faster than directly deciding the language). Our necessity result is complementary to a result of Rothblum and Vadhan [RV09], which showed the necessity of PCPs for succinct arguments obtained via blackbox reductions to falsifiable assumptions (see Sect. 1.2). Their result does not apply for succinct arguments in the random oracle model.

In this paper, the necessity of IOPs for succinct arguments in the ROM is more than a compelling message. We demonstrate that the necessity of IOPs is a useful step towards establishing barriers on succinct arguments, because thanks to Theorem 1 we have reduced this problem to establishing barriers on IOPs. Our second main contribution concerns this latter task (see below).

We sketch the ideas behind Theorem 1 in Sect. 2.1; the formal statement of the theorem, which gives a precise accounting of many more parameters, is given and proved in Sect. 4.

1.1.2 From IOPs to Algorithms

We show that IOPs with good parameters (small soundness error relative to query complexity) can be translated to fast algorithms with small space complexity. This translation should be viewed as a tool to establish barriers on IOPs: if the language proved by the IOP is hard then the corresponding algorithm may (conjecturally) not exist, contradicting the existence of the IOP to begin with.

Theorem 2

(informal). Suppose that a language $L$ has a public-coin IOP with soundness error $\varepsilon$, round complexity $\mathsf {k}$, proof length $\mathsf {l}=\mathrm {poly}(n)$ over an alphabet $\varSigma$, query complexity $\mathsf {q}$, and verifier space complexity $\mathsf {vs}$. If $\varepsilon = o(2^{-\mathsf {q}\cdot \log \mathsf {l}})$ then, the language $L$ can be decided by a probabilistic algorithm that runs in time exponential in $\widetilde{O}\big (\mathsf {q}\cdot (\log |\varSigma | + \mathsf {k}) \big )$ and that runs in space $\widetilde{O}\big (\mathsf {vs}\cdot \mathsf {q}^2 \cdot (\log |\varSigma | + \mathsf {k})^2 \big )$.

We sketch the ideas behind Theorem 2 in Sect. 2.2; the formal statement is proved in Sect. 5.

Our result in fact provides a broad generalization of folklore results that impose barriers on IPs and PCPs (both are special cases of IOPs) as we discuss in Sect. 1.2. In particular, the folklore results restrict the verifier and alphabet size, while we do not. For example, Theorem 2 rules out a broader class of PCPs for the “small-query high-soundness” regime than what was previously known: under the (randomized) Exponential-Time Hypothesis (rETH),¹ if the number of queries is constant then the best possible soundness error is $1/\mathrm {poly}(n)$, as long as $\log |\varSigma | \ll n$ (otherwise a trivial PCP exists). We deduce this from the corollary obtained by setting $\mathsf {k}:= 1$ in Theorem 2.

Corollary 1

(informal). Suppose that $\mathrm {NP}$ has a PCP with perfect completeness and soundness error $\varepsilon$, and where the verifier tosses $\mathsf {r}$ random coins, makes $\mathsf {q}$ queries into a proof of length $\mathsf {l}=\mathrm {poly}(n)$ over an alphabet $\varSigma$. Under the rETH assumption, if $\widetilde{O}(\mathsf {q}\log |\varSigma |) = o(n)$, then $\varepsilon \ge 2^{-\mathsf {q}\cdot \log \mathsf {l}}$.

This yields limitations for PCPs, e.g., in the “cryptographic regime”: constant-query PCPs with negligible soundness cannot have polynomial size, even over an exponentially-large alphabet.

1.1.3 Barriers for Succinct Arguments

We now discuss our barriers for succinct arguments, which state that under standard complexity assumptions there are no succinct arguments where the verifier makes a small number of queries to the random oracle, and the honest prover has a small adaptivity parameter $\mathsf {a}$.

Suppose that $\mathrm {3SAT}$ has a succinct argument that provides $s$ bits of security and has argument size $\mathsf {as}\ll n$, where n is the number of variables in the $\mathrm {3SAT}$ formula. Suppose that the argument prover makes $\mathsf {a}$ adaptive rounds of queries to the random oracle, and the argument verifier makes $\mathsf {vq}$ queries to the random oracle. If $\mathsf {vq}\cdot \mathsf {a}\ll s$ then by Theorem 1 we get an IOP with similar efficiency parameters, and with query complexity roughly $o(s)$. Then by Theorem 2 we get an algorithm for $\mathrm {3SAT}$ that runs in time $2^{o(n)}$, contradicting the randomized Exponential Time Hypothesis.

Theorem 3

(informal). Suppose that $\mathrm {3SAT}$ has a public-coin succinct argument that provides $s$ bits of security and has argument size $\mathsf {as}\ll n$, where the prover makes $\mathsf {a}$ adaptive rounds of queries to the random oracle and the verifier makes $\mathsf {vq}$ queries to the random oracle. If $\mathsf {vq}\cdot \mathsf {a}\ll s$ then rETH is false.

The theorem applies to all constructions, but does not completely answer our motivating question because the theorem has a dependency on the adaptivity parameter $\mathsf {a}$. The question of whether this dependency can be removed remains a challenging open problem. If it turns out that it cannot be removed, then our result suggests a path to construct succinct arguments with more efficient verifiers: the standard Merkle trees (which lead to very small adaptivity) must be replaced with a deeper structure that exploits long adaptive paths of queries. This would be a very exciting development, departing from all paradigms for succinct arguments known to date!

Note that the requirement $\mathsf {as}\ll n$ is necessary as if $\mathsf {as}=n$ then a trivial argument system, where the prover sends the full satisfying assignment, has no soundness error with no random oracle calls.

We sketch how to derive our barriers in Sect. 2.3; formal statements can be found in Sect. 6, in a more general form that separately considers the case of arbitrary nondeterministic languages (of which $\mathrm {3SAT}$ is an example) and the case of arbitrary deterministic languages.

1.1.4 Additional Applications and Extensions

Our transformation from succinct arguments to IOPs (Sect. 1.1.1) leads to extensions that provide valuable insights into succinct arguments, as we discuss below.

Extension 1: preprocessing implies holography. We now consider succinct arguments in the ROM that have an additional useful feature, known as preprocessing. This means that in an offline phase one can produce a short summary for a given circuit and then, in an online phase, one may use this short summary to verify the satisfiability of the circuit with different partial assignments to its inputs.² The online phase now can be sublinear in the circuit size even for arbitrary circuits.

The BCS transformation extends to obtain preprocessing SNARGs from holographic IOPs [COS20], following a connection between preprocessing and holography introduced in [Chi+20]. Therefore, in light of Theorem 1, it is natural to ask: do all preprocessing SNARGs in the random oracle model arise from holographic IOPs? Even if SNARGs “hide” IOPs inside them (due to our result), there may be other approaches to preprocessing beyond holography, at least in principle.

We show that preprocessing does arise from holography. We extend the ideas underlying our Theorem 1 to obtain a transformation that given a preprocessing SNARG in the random oracle model outputs a holographic IOP with related complexity measures. This reverse direction strengthens the connection between preprocessing and holography established in [COS20, Chi+20].

Lemma 1

There is an efficient transformation $\mathbb {T}$ that satisfies the following. Suppose that $\mathsf {ARG}$ is a size-$\mathsf {as}$ preprocessing non-interactive argument in the ROM for an indexed relation $R$ where the honest prover performs $\mathsf {pq}$ queries in $\mathsf {a}$ rounds, the verifier performs $\mathsf {vq}$ queries, and the indexer outputs a key of size $\mathsf {ivk}$. Then $\mathsf {IOP}:= \mathbb {T}(\mathsf {ARG})$ is a holographic IOP for $R$ with proof length $O(\mathsf {pq}+\mathsf {as})$ and query complexity $O(\mathsf {ivk}+ \mathsf {as}+ \mathsf {vq}\cdot \mathsf {a})$. Other aspects of $\mathsf {IOP}$ (such as public coins, soundness, time and space complexities) are essentially the same as in $\mathsf {ARG}$.

Extension 2: on state restoration soundness. A careful reader may have noticed that our discussion so far did not touch upon a technical, yet important, aspect. Namely, observe that if we applied the transformation in Theorem 1 to a SNARG in the ROM then we would obtain a corresponding public-coin IOP. However, given what we said so far, we are not guaranteed that we can compile this IOP back into a SNARG! Indeed, the known approach for constructing SNARGs from IOPs requires the IOP to satisfy a stronger notion of soundness called state restoration soundness [BCS16]. So we should ask: does the IOP output by Theorem 1 satisfy this stronger notion?

We prove that the transformation in Theorem 1 yields an IOP with state-restoration soundness as long as the SNARG had a stronger notion of soundness that we introduce and call salted soundness. Informally, this notion allows a cheating SNARG prover to request the random oracle to re-sample the answer for a chosen query (in case the prover did not “like” the prior answer).

Lemma 2

(informal). The transformation $\mathbb {T}$ in Theorem 1 satisfies this additional property: if $\mathsf {ARG}$ is a SNARG with salted soundness error $\mathsf {\epsilon }_{\mathrm {s}}(t)$ for query budget $t$ and the prover runs in $\mathsf {a}$ adaptive rounds then $\mathsf {IOP}:= \mathbb {T}(\mathsf {ARG})$ is a public-coin IOP with state restoration soundness error $\mathsf {\epsilon }_{\mathrm {s}}(t\cdot \mathsf {m})$.

This lemma resolves the issue described above because the SNARGs constructed from (state-restoration sound) IOPs in [BCS16] do indeed satisfy the stronger notion of salted soundness (Fig. 1).

Fig. 1.

Summary of our results. The left part shows results related to “reverse engineering” succinct arguments, which derive IOPs with certain properties from succinct arguments with certain properties. The right part depicts the fact that IOPs with good enough parameters lead to algorithms that, for hard enough languages, contradict plausible complexity assumptions.

1.2 Related Work

Known limitations on IPs and PCPs. Our Theorem 2 implies that IOPs with good parameters can be translated into good algorithms. Below we summarize known facts that impose limitations on restrictions of the IOP model: interactive proofs (IPs) and probabilistically checkable proofs (PCPs).

• IPs. The following fact follows from proof techniques in [GH98] (see also [RRR16, Remark 5.1]).

Folklore 1

If a language $L$ has a public-coin IP where the communication and verifier space complexity are bounded by $c$, then $L$ can be decided by an algorithm running in space $O(c)$.

Since it is believed that $\mathrm {DTIME}[T] \not \subseteq \mathrm {SPACE}[o(T)]$, the above lemma tells us that we should not expect every language in $\mathrm {DTIME}[T]$ to have a non-trivial public-coin interactive proof.

Both Folklore 1 and our Theorem 2 lead to an algorithm with small space, and the main difference is that our theorem is a statement about IOPs rather than IPs. We note, however, that within the proof of our theorem we prove a lemma (Lemma 3) that can be viewed as a refinement of Folklore 1 as it applies even when the verifier-to-prover communication is large.

• PCPs. The following fact lower bounds a PCP’s soundness error.

Folklore 2

Suppose that $\mathrm {NP}$ has a PCP with perfect completeness and soundness error $\varepsilon$, and where the verifier tosses $\mathsf {r}$ random coins and makes $\mathsf {q}$ queries into a proof of length $\mathsf {l}$ over an alphabet $\varSigma$. Then the following holds:

• 1. $\varepsilon \ge 2^{-\mathsf {r}}$; and

• 2. Under the ETH assumption, if $\mathsf {r}= o(n)$ and $\mathsf {q}\log |\varSigma | = o(n)$ then $\varepsilon \ge 2^{-\mathsf {q}\cdot \log |\varSigma |}$.

In order to understand the implications of the above limitation, we find it helpful to recall a well-known conjecture about possible PCP constructions. The Sliding Scale Conjecture states that, for every $\varepsilon \in [1/\mathrm {poly}(n),1]$, every language in $\mathrm {NP}$ has a PCP with perfect completeness and soundness error $\varepsilon$, and where the verifier uses $O(\log n)$ random bits and makes O(1) queries into a proof over an alphabet $\varSigma$ of size $\mathrm {poly}(1/\varepsilon )$. The conjecture is tight in the sense that we cannot ask for better soundness with the same parameters.

Yet if we allow the verifier to use $\omega (\log n)$ random bits or if $\log |\varSigma |=\omega (\log n)$ then Folklore 2 does not rule out PCPs with soundness error $1/n^{\omega (1)}$. Our Corollary 1 amends this by establishing that one cannot get soundness error better than $1/\mathrm {poly}(n)$ even if the verifier uses an arbitrary number of random bits and the alphabet is arbitrarily large.

Probabilistic proofs in succinct arguments. Essentially all known constructions of succinct arguments use some form of probabilistic proof as an ingredient (possibly among other ingredients). Prior to this work, the only known formal statement seeking to explain this phenomenon is a result by Rothblum and Vadhan [RV09] stating that succinct arguments proved secure via a black-box reduction to a falsifiable assumption must “contain” a PCP. This is formalized via a transformation that, given such a succinct argument, outputs a PCP with size and query complexity related to the succinctness of the argument system (and also certain aspects of the security reduction).

Our Theorem 1 is complementary to the result in [RV09], in that we consider succinct arguments that are unconditionally secure in the random oracle model (as opposed to computationally secure in the standard model). Our techniques are also different, in that the technical challenge is to design an efficient sub-protocol to simulate a random oracle (as opposed to detecting if the adversary has “broken cryptography” by using the falsifiability of the cryptographic assumption).

2 Techniques

2.1 IOPs are Necessary for Succinctness

We describe the main ideas behind Theorem 1, which states that any succinct argument in the ROM implies an IOP with related parameters (which in particular demonstrates that IOPs are necessary for succinctness in the ROM). Let $P$ and $V$ be the prover and verifier of an arbitrary succinct argument for a language $L$ (e.g., $\mathrm {3SAT}$). We seek to “remove” the random oracle from the succinct argument by simulating it via an interactive sub-protocol and ending with an IOP for the same language $L$. We assume, without loss of generality, that $P$ and $V$ each never query the same element more than once.³

Below, we first describe a straightforward approach, then explain problems and challenges on the approach, and finally explain how we overcome the challenges to obtain our result.

A straightforward approach. We can construct an IP with a new prover $\mathbf {P}$ and a new verifier $\mathbf {V}$ that respectively simulate the argument prover $P$ and argument verifier $V$. In addition, we task the IP verifier $\mathbf {V}$ to simulate the random oracle for both $P$ and $V$, as we explain.

• Whenever the argument prover $P$ wants to query the oracle at an element x, the IP prover $\mathbf {P}$ forwards the query x to the IP verifier $\mathbf {V}$, who replies with a truly random string y that plays the role of the output of the random oracle on x.

• Whenever the argument verifier $V$ queries x, then the IP verifier $\mathbf {V}$ checks if x had appeared in the transcript as one of the queries and returns the given answer to $V$ if so, or otherwise it feeds $V$ with a truly random value.

There is a delicate, yet crucial, issue that needs to be taken care of. A cheating IP prover might query x twice (or more) to get two possible answers for the same query, which might affect the soundness of the IP (and indeed there are succinct arguments where this issue has devastating consequences on the soundness of the IP). Thus, when simulating a verifier query x, the IP verifier $\mathbf {V}$ must assert that x was not issued twice during the protocol (and otherwise reject).

The approach above perfectly removes the random oracle from the succinct argument and yields an IP with similar completeness and soundness. Henceforth we view the IP constructed above as an IOP whose verifier reads the entire transcript (queries all locations of the exchanged messages).

The problem. The problem with the IOP described above is its parameters. The argument prover $P$ might perform many queries, and in particular more than the witness size (as is the case in known constructions of succinct arguments). This dominates many parameters of the IOP, including the number of rounds, the number of bits read by the verifier, and its running time—and also yields a trivial IOP for the language. Note that proof length (the number of bits sent by $\mathbf {P}$) is fine, as we do not expect all languages in $\mathrm {NP}$ to have an IOP with small proof length, but rather only expect the IOP verifier to read a small number of locations from the prover messages.

Achieving small round complexity. We crucially exploit a parameter of the argument prover $P$ not discussed thus far, namely, its adaptivity. We say that $P$ has adaptivity $\mathsf {a}$ if it performs $\mathsf {a}$ rounds of queries to the random oracle and in each round submits a (possibly long) list of queries and receives corresponding answers. In known constructions, $\mathsf {a}$ is very small (e.g., $O(\log n)$). If $P$ has adaptivity $\mathsf {a}$, then the number of rounds in the constructed IOP can be easily reduced to $O(\mathsf {a})$, where the IOP prover $\mathbf {P}$ sends the verifier a list of queries $x_1,\ldots ,x_\mathsf {m}$, and the IOP verifier $\mathbf {V}$ replies with a list of answers $y_1,\ldots ,y_\mathsf {m}$, while applying the same logic as before. This reduces the number of rounds of the IOP, but so far has no effect on the number of queries performed by the IOP verifier $\mathbf {V}$, which remains as large as the number of queries performed by the argument prover $P$.

Perfect hash functions with locality. Our main goal now is to reduce the number of bits read by the IOP verifier $\mathbf {V}$. Consider a query x performed by the argument verifier $V$. The IOP verifier $\mathbf {V}$ needs to read the transcript to see if the query x was issued and, if so, check that it was issued only once. A simple way to find x in the transcript is to have the IOP prover $\mathbf {P}$ assist with locating x. That is, $\mathbf {P}$ points to the exact location in the transcript for where x was issued. Then $\mathbf {V}$ reads this specific location in the transcript and is assured that x was queried and at the same time reads the corresponding response y. However, how can $\mathbf {V}$ check that x was not issued twice? And how can $\mathbf {P}$ give a proof that the rest of the transcript does not contain x?

To deal with these challenges, we use perfect hash functions. These are a family of functions $\mathcal {H}= \{ h:U\rightarrow [O(m)]\}$ such that for any S of size m there exists a function $h\in \mathcal {H}$ that is one-to-one on S. Fixing such a family $\mathcal {H}$, we let the IOP prover $\mathbf {P}$ provide with each set of queries (for each round), a perfect hash function $h$ for the set $X$ of submitted queries and send an array of length O(m) such that element $x \in X$ resides in the cell at index $h(x)$. This way, instead of the IOP verifier $\mathbf {V}$ scanning (and reading) all prover messages, it suffices for $\mathbf {V}$ to read the description of h and then query the cell $h(x)$ to determine if x is in the array.

Also, the IOP verifier $\mathbf {V}$ writes the response y at the same location $h(x)$ in a dedicated array of random values, $Y[h(x)]$. This way, $\mathbf {V}$ can be convinced that x was not issued at a specific round by looking at a single cell $h(x)$ for the array given by $\mathbf {P}$ at that round. Thus, the query complexity of $\mathbf {V}$ for simulating a single query of $V$ is mainly determined by the number of rounds of the protocol, which is the rather small value $\mathsf {a}$ (the adaptivity of the honest argument prover $P$). Note that while the entire array Y is sent to the prover, the verifier needs to read only a single location from Y (we elaborate on this further below).

The locality property. Turning the above ideas into our transformation runs into several delicate issues that need to be handled to achieve soundness and good parameters. One issue is that the description of $h$ is, in fact, too large for the verifier to read in its entirety (it is larger than the set itself). However, we observe that $\mathbf {V}$ need not read the entire function description, but only the parts required for evaluating $h$ at x.

Therefore, we additionally require the perfect hash family to have a locality property where, in order to evaluate the hash function $h$ on a single element x, only a relatively small number of bits are required to be read from the description of $h$. Luckily, several known constructions have this locality property and, specifically, we use the construction of Fredman, Komlós, and Szemerédi [FKS84]. An overview of the [FKS84] construction, its locality property, and a bound on the number of bits required to read are given in Sect. 4.1.

There are additional challenges in realizing the above plan. For example, in terms of soundness, note that a cheating prover might submit a set $X$ and choose a function $h$ that is not perfect for $X$ and contains collision—this could potentially harm soundness. We deal with this and other issues on the way to proving our transformation from succinct arguments to IOPs.

The resulting IOP. This results in an IOP with the following parameters. If the prover had $\mathsf {a}$ rounds of adaptivity, then the IOP has $\mathsf {a}+1$ rounds, where the first $\mathsf {a}$ rounds are used to simulate the random oracle for the prover, and the last round is dedicated to sending the final output of the prover. The proof length of the IOP (i.e., the total communication of the protocol) is $O(\mathsf {as}+ \mathsf {pq})$ symbols where each symbol contains an output of the random oracle. Indeed, for each of the $\mathsf {pq}$ queries we an additional O(1) symbols, and for the last round we send the final argument which is $\mathsf {as}$ bits (and can be read as a single symbol).

The query complexity is $O(\mathsf {as}+\mathsf {vq}\cdot \mathsf {a})$ as for each of the $\mathsf {vq}$ queries of the prover, the verifier needs to scan all $\mathsf {a}$ rounds, and performs O(1) queries in each. Then, it reads last prover message entirely which is $\mathsf {as}$ bits (which we can view as 1 large symbol of $\mathsf {as}$ bits).

The resulting IOP has large communication of randomness from the verifier to the prover. However, the verifier, in order to decide whether to accepts, has to read only a small number of locations, and these are included in the count of the query complexity. Our definition for IOP allows the verifier to have only oracle access to its own randomness and thus the query complexity includes both locations read from the proof and from the randomness. We stress that the compiler of [BCS16] works even for this more general definition of IOP. Therefore, we do not expect to get an IOP with small verifier-to-prover communication as it could be that the succinct argument was constructed from an IOP with large communication (see Sect. 3.4 for the precise definition of IOP and a further discussion on this topic).

See Sect. 4 for further details of the proof.

2.2 Algorithms for IOPs

We describe the main ideas behind Theorem 2, which states that IOPs with good parameters can be translated to fast algorithms with small space complexity. We proceed in two steps.

• Step 1. We prove that any IOP can be simulated by an IP (interactive proof) with small prover-to-verifier communication, at the cost of a (large) completeness error that depends on how well one can guess all of the IOP verifier’s query locations (the “query entropy” of the IOP).

• Step 2. We prove a refinement of a result of Goldreich and Håstad [GH98] that states that languages with public-coin IPs with small prover-to-verifier communication can be decided via fast probabilistic algorithms with small space complexity.

We elaborate on each of these steps in turn below.

Step 1: IOP to laconic IP (Lemma 2 in Lemma 5.1). We prove that any IOP with good enough soundness relative to its query entropy can be translated to a laconic IP (an IP with small prover-to-verifier communication). Query entropy is related to the probability of guessing in advance all locations that the IOP verifier will read across the proof strings sent by the IOP prover (see Definition 5 for how query entropy is formally defined). The translation ensures that if the IOP is public coin (as indeed it is in our case) then the IP is also public coin. Moreover, at the cost of an additional completeness error, the IP verifier can be modified so that it makes a single pass on its (large) randomness tape and runs in small space. (This small-space property will be useful later on for establishing barriers on succinct arguments for deterministic languages; see Sect. 2.3.)

We construct the IP as follows. First, the IP prover guesses the locations that the IOP verifier will read. The probability of guessing all locations correctly is $2^{-\mathsf {h}}$, where $\mathsf {h}$ is the query entropy. Assuming a correct guess, the IP prover sends the description of these locations together with corresponding values. If the IOP verifier makes $\mathsf {q}$ queries across a proof of length $\mathsf {l}$ over an alphabet $\varSigma$, then the IP prover sends $\mathsf {q}\cdot \log \mathsf {l}+\mathsf {q}\cdot \log |\varSigma |$ bits. The soundness of the protocol remains the same. What changes is the completeness error, which drastically increases since guessing all locations has a small probability. However, if the soundness error is small enough and as long as there is some difference between completeness and soundness, we get a non-trivial IP. In particular, if the IOP has soundness error $\varepsilon < 2^{-\mathsf {h}}$ then the resulting IP has soundness error $\varepsilon$, completeness error $1-2^{-\mathsf {h}}$, and prover communication $\mathsf {q}\cdot \log \mathsf {l}+\mathsf {q}\cdot \log |\varSigma |$ as mentioned above.

Finally, we show that the IP can be modified (at the expense of the completeness error) to make the IP verifier perform a single pass over its randomness tape. Note that the IOP verifier might read the randomness in an arbitrary manner, which would make the IP verifier read it in a similar one. Here, we exploit the fact that the IOP verifier had only oracle access to its own random tape, and performed only a limited number of queries. We leverage this and let the IP verifier guess these locations in advance. Then, the verifier reads the randomness tape and stores only the locations it guessed. From here on, the verifier will use only the randomness stored explicitly. Assuming that it guessed correctly, it uses these locations to simulate random access for the IOP verifier. This again adds a large completeness error. However, if the soundness error is small enough, then again the resulting IP is non-trivial and, as discussed above, suffices for our purposes.

Step 2: IP to algorithm (see Lemma 3 in Lemma 5.2). Goldreich and Håstad [GH98] showed that languages with public-coin IPs with small prover-to-verifier communication can be decided via fast probabilistic algorithms. In particular, if $L$ has a public-coin IP where, for an instance of length n, the prover-to-verifier communication is bounded by $c(n)$ and the number of rounds is bounded by $\mathsf {k}(n)$ then it holds that

$$\begin{aligned} L\in \mathrm {BPTIME}\left[ 2^{O(c(n) + \mathsf {k}(n) \cdot \log \mathsf {k}(n))} \cdot \mathrm {poly}(n)\right] . \end{aligned}$$

Their result is shown only for IPs with constant completeness and soundness errors, which is not the case for the IP constructed in Step 1. We stress that the IP constructed Step 1 can be amplified via standard repetition to reach the setting of constant completeness and soundness errors, doing so would increase communication and render the IP not laconic, and hence not useful for us in this paper. Instead, we show a refinement of [GH98] that is suitable to work in the “large-error” regime of IP parameters. Details follow.

We explicitly show the dependency in the completeness and soundness errors, allowing the theorem to apply to IPs with large completeness errors (which we need). This refinement is technical, where we follow the original proof blueprint of [GH98]. We explicitly track the completeness and soundness errors rather than hiding them as constants in the Big-O notation, and adjust other parameters as a function of the completeness and soundness error values. The result is a moderately more involved formula for the running time of the final algorithm, which has these parameters in addition to the communication complexity and the number of rounds.

In particular, we get that if a language $L$ has a public-coin IP with completeness error $\alpha$, soundness error $\beta$, round complexity $\mathsf {k}$, and prover-to-verifier communication $c$, then it holds that

$$\begin{aligned} L\in \mathrm {BPTIME}\left[ 2^{O\left( c(n) + \mathsf {k}(n) \cdot \log \frac{\mathsf {k}(n)}{1-\alpha (n)-\beta (n)} \right) } \cdot \mathrm {poly}(n)\right] . \end{aligned}$$

For example, plugging in the IP obtained from Step 1, while assuming that $\varepsilon = o(2^{-\mathsf {q}\cdot \log \mathsf {l}})$ (and hiding some terms under the $\widetilde{O}$ notation) we get the expression from Theorem 2:

$$\begin{aligned} L\in \mathrm {BPTIME}\left[ 2^{\widetilde{O}\left( \mathsf {q}\cdot (\log |\varSigma | + \mathsf {k}) \right) } \right] . \end{aligned}$$

Additionally, we show that if the verifier of the IP reads its randomness in a single pass, then the same algorithm can be implemented in small space (the original implementation of [GH98] used space proportional to its running time). Looking ahead, this property is used to achieve the barrier for deterministic languages. We sketch the main idea behind the new algorithm.

The algorithm’s main goal is to compute the value of a tree $A_\mathbbm {x}$ corresponding to (an approximation of) the interaction in the IP protocol. Each node in the tree corresponds to a certain partial transcript of the IP, and computing the value of the tree suffices to decide the language. The straightforward way to compute the value is to compute the value of each node in the tree from the leaves up to the root. This would require space proportional to the size of $A_\mathbbm {x}$. Yet, in order to compute the value of the tree it would suffice to store only $\log |A_\mathbbm {x}|$ values at a time, as for any subtree it suffices to store the value of its root.

There is, however, a major issue with this approach. Namely, the space required to store even a single value of the tree is too large, as writing the location of a node in the tree includes the description of the randomness of the verifier in this partial transcript, which is too large to store explicitly. Here we exploit the fact that the verifier uses a single pass to read its randomness, and show how to compress the description of a node in the tree using the internal memory and state of the verifier, given this partial transcript. This allows us to implicitly store nodes values with small memory. Since it suffices to store only $\log |A_\mathbbm {x}|$ values at a time we get an algorithm with small memory.

This results in the following conclusion: if the space complexity of the IP verifier is $\mathsf {vs}$ when reading its randomness random tape in a single pass then

$$\begin{aligned} L\in \mathrm {SPACE}\Big [O\left( d \cdot (\mathsf {vs}+ d) \right) \Big ] , \end{aligned}$$

where $d = c(n) + \mathsf {k}(n) \cdot \log \frac{\mathsf {k}(n)}{1-\alpha (n)-\beta (n)}$. Once again, plugging in the IP obtained from Step 1, we get the other expression from Theorem 2:

$$\begin{aligned} L\in \mathrm {SPACE}\left[ \widetilde{O}\big (\mathsf {vs}\cdot \mathsf {q}^2 \cdot (\log |\varSigma | + \mathsf {k})^2 \big )\right] . \end{aligned}$$

2.3 Barriers for Succinct Arguments

Our results provide a methodology for obtaining barriers on succinct arguments for different languages, based on complexity assumptions for the language. We describe this blueprint and give two examples, one for non-deterministic languages and one for deterministic languages, and suggest that additional barriers could be achieved is a similar manner.

This methodology works as follows. Let $L$ be the language for which a barrier is desired, and suppose that one proves (or conjectures) some hardness property about the language $L$. Now assume that there exists a succinct argument for $L$ with certain efficiency parameters such as soundness, query complexity, prover adaptivity, and so on. First apply Theorem 1 to obtain an IOP with parameters related to the succinct argument, and then apply Theorem 2 to obtain an efficient algorithm for $L$. If the efficient algorithm violates the hardness of $L$, then one must conclude that the assumed succinct argument for $L$ does not exist.

Barriers for 3SAT. We apply the above methodology to obtain barriers for succinct arguments for $\mathrm {NP}$ based on the Exponential-Time Hypothesis. Suppose that $\mathrm {3SAT}$ over n variables has a succinct argument that provides $s$ bits of security and has argument size $\mathsf {as}\ll n$ (of course, if $\mathsf {as}= n$ then the scheme is trivial). Suppose also that the argument prover makes $\mathsf {a}$ adaptive rounds of queries to the random oracle, and the argument verifier makes $\mathsf {vq}$ queries to the random oracle.

We apply Theorem 1 to the argument scheme to get a related IOP. Since the argument scheme provides $s$ bits of security, then for any instance $\mathbbm {x}\le 2^{s}$ and query bound $t\le 2^{s}$ and for oracle output size $\lambda = O(s)$ we get that the resulting IOP has soundness $\varepsilon (\mathbbm {x},t,\lambda ) \le 2^{-s}$. Moreover, the verifier reads $O(\mathsf {vq}\cdot \mathsf {a})$ symbols from the transcript, the alphabet size is $|\varSigma | = 2^{\lambda }$, the number of rounds is $O(\mathsf {a})$, and the proof length is $O(\mathsf {as}+ \mathsf {pq})$, which is best to think as $\mathrm {poly}(n)$ for simplicity.

What is important to note here is that if $\mathsf {vq}\cdot \mathsf {a}\ll s$ then the query entropy of the IOP is $2^{-\mathsf {h}} = \mathsf {l}^{-\mathsf {vq}\cdot \mathsf {a}} = \omega (2^{-s})$ and thus $\varepsilon = o(2^{-\mathsf {h}})$. This means that we can apply Step 1 above to get an IP for $\mathrm {3SAT}$ where the prover-to-verifier communication is

$$\begin{aligned} c(n) = \mathsf {q}\cdot \log \mathsf {l}+ \mathsf {q}\cdot \log |\varSigma | = \mathsf {q}\cdot \log n + \mathsf {q}\cdot s= O(s^2) , \end{aligned}$$

and the difference between the completeness and soundness error is $1-\alpha (n)-\beta (n) = o(s)$. Then, using Step 2, we get a (randomized) algorithm for $\mathrm {3SAT}$ that runs in time $2^{\widetilde{O}(\mathsf {q}\cdot (\log |\varSigma | + \mathsf {k})} = 2^{o(s)} = 2^{o(n)}$, as long as $s^2 \ll n$. This contradicts the (randomized) Exponential Time Hypothesis. Note that the condition that $s^2 \ll n$ is relatively mild, as $s$ is a lower bound for the size of the argument scheme, and the main objective of a succinct argument is to have argument size much smaller than the trivial n bits of communication (sending the satisfying assignment).

The above reasoning can be generalized to any non-deterministic language in $\mathrm {NTIME}[T]$, as we work out in detail in Sect. 6.1.

Barriers for DTIME[ T]. As a second example of our methodology, we show barriers for deterministic languages. Here, we exploit the fact that the final algorithm obtained in Step 2 has small space complexity. Suppose that there is a succinct argument as above for languages in $\mathrm {DTIME}[T]$, for some time bound $T$, with argument size $\mathsf {as}\ll T$. Assume that $\mathrm {DTIME}[T] \not \subseteq \mathrm {SPACE}[o(T)]$, a rather unlikely inclusion (which is currently outside of known techniques to either prove or disprove).

As before, if $\mathsf {vq}\cdot \mathsf {a}\ll s$ then by Theorem 1 we get an IOP with similar efficiency parameters, and with query complexity $\mathsf {vq}\cdot \mathsf {a}\ll s$. Additionally, if the argument’s verifier space complexity is $\mathsf {sv}\ll T$ (which is naturally the case with a non-trivial argument scheme) then the verifier of the obtained IOP can be implemented with $O(\mathsf {sv})$ space.

Similar to the analysis we did in the non-deterministic case, here we apply Theorem 2 and get an algorithm for $L$ that runs in space

$$\begin{aligned} \widetilde{O}(\mathsf {sv}\cdot \mathsf {q}^2 \cdot (\log |\varSigma | + \mathsf {k})^2) = \widetilde{O}(s^4) = o(T) , \end{aligned}$$

as long as $s^4 \ll T$ (again, a relatively mild condition). This implies that

$$\mathrm {DTIME}[T] \subseteq \mathrm {SPACE}[o(T)],$$

which contradicts the initial conjectured hardness.

Our methodology gives meaningful barriers provided that the adaptivity of the honest prover, $\mathsf {a}$, is somewhat small, e.g., sublinear in the security parameter $s$. While this is indeed the case for all known constructions, it is not clear if a succinct argument could benefit from large adaptivity. We can thus draw the following conclusion. One possibility is that our results could be improved to eliminate the dependency on $\mathsf {a}$, for example by improving the transformation to IOP to be more efficient and contain queries from several adaptivity rounds to be in the same round of the IOP. Another possibility is that there exist succinct arguments with small verifier query complexity and large prover adaptivity. This latter possibility would be a quite surprising and exciting development, which, in particular, would depart from all paradigms for succinct arguments known to date.

2.4 Additional Results and Applications

Extension 1: preprocessing implies holography. Our Lemma 1 states that we can transform any preprocessing succinct argument into a corresponding holographic IOP. We do so by extending the transformation that underlies our Theorem 1, and below, we summarize the required changes.

Recall that in a holographic IOP there is an algorithm, known as the IOP indexer and denoted $\mathbf {I}$, that receives as input, e.g., the circuit whose satisfiability is proved and outputs an encoding of it that will be given as an oracle to the IOP verifier. Our goal here is to construct the IOP indexer by simulating the argument indexer $I$, which instead relies on the random oracle to output a short digest of the circuit for the argument verifier.

Similarly to the transformation outlined in Sect. 2.1, we need to “remove” the random oracle during the simulation. The IOP indexer uses its randomness $\rho _{0}$ to answer any oracle query performed by the argument indexer. Let $X_0$ be the set of queries performed by the argument indexer. Then, the IOP indexer finds a perfect hash function $h_0$ for $X_0$ and creates the corresponding arrays $T_0$ and $Y_0$ containing the queried elements and responded positioned according to $h_0$. Finally, the IOP indexer outputs the string $(\mathsf {ivk},h_0,T_0,Y_0)$, where $\mathsf {ivk}$ is the output of the argument indexer.

We are left to ensure that, during the transformation, any query simulated by the IOP verifier is consistent with the queries performed in the preprocessing step. The IOP prover, uses $\rho _{0}$ to simulate, in its head, the above (deterministic) process to get the same output $(\mathsf {ivk},h_0,T_0,Y_0)$, and thus can act in a consistent way to the queries in $X_0$.

The IOP verifier reads $\mathsf {ivk}$ and uses it to simulate the argument verifier. Recall that for every query x the verifier ensures that x was not issued in any previous round. Here, we modify the verify to search in the array $T_0$ in addition to the arrays in all the rounds. In this sense, the preprocessing phase acts as “round 0” of the protocol. Completeness and soundness follow in a similar manner to the original transformation.

Extension 2: on state restoration soundness. Our Lemma 2 states that the transformation in Theorem 1 yields an IOP with state-restoration soundness when applied to a SNARG that satisfies salted soundness, a stronger notion of soundness that we introduce and may be of independent interest. The motivation for this result is that in the “forward” direction we only know how to construct SNARGs from IOPs that do satisfy state-restoration soundness [BCS16], which informally means that the IOP prover cannot convince the IOP verifier with high probability even when the IOP prover is allowed to choose from multiple continuations of the interaction up to some budget. We now sketch salted soundness and the ideas behind Lemma 2.

In a succinct argument with salted soundness, the cheating argument prover is allowed to resample answers of the random oracle, in a specific way. Suppose the prover queried some element $x_1$ and got response $y_1$. If the prover wishes, it may resample $x_1$ to get a fresh new uniform response $y'_1$. This process may happen multiple times within the query budget of the algorithm. Then, the prover selects one of these answers, and proceeds to query another element $x_2$, and so on. The prover is additionally allowed to go back, and change its decision for the value of some $x_i$. However, this produces a new branch where the values for $x_j$ for $j > i$ have to be resampled. In general, at any step the prover can choose a brach from the set of all branches so far and choose to extend it. Finally, the prover outputs the argument. When the argument verifier queries an element, then it gets a response that is consistent with the branch the prover chose.

We need this security notion to get an IOP with state restoration soundness since this is precisely what a cheating IOP prover can perform within our transformation. In the state-restoration game, the cheating IOP prover can go back to a previous round and ask for new randomness from the IOP verifier. In our case, the IOP prover will get new randomness for some set of queries. Since these queries simulate a random oracle, it can get fresh randomness for a query intended for a random oracle.

Thus, we show that any cheating prover playing the state-restoration game can be transformed into a cheating prover to the salted soundness game, and yields the desired proof.

3 Definitions

3.1 Random Oracles and Oracle Algorithms

We denote by $\mathcal {U}(\lambda )$ the uniform distribution over all functions $\zeta :\{0,1\}^{*} \rightarrow \{0,1\}^\lambda$ (implicitly defined by the probabilistic algorithm that assigns, uniformly and independently at random, a $\lambda$-bit string to each new input). If $\zeta$ is sampled from $\mathcal {U}(\lambda )$, then we say that $\zeta$ is a random oracle.

In this paper, we restrict our attention to oracle algorithms that are deterministic. This is without loss of generality as we do not restrict the running of the algorithm in the random oracle model only the number of queries.

Given an oracle algorithm A and an oracle $\zeta \in \mathcal {U}(\lambda )$, $\mathsf {queries}(A,\zeta )$ is the set of oracle queries that $A^\zeta$ makes. We say that A is $t$-query if $|\mathsf {queries}(A,\zeta )| \le t$ for every $\zeta \in \mathcal {U}(\lambda )$.

Moreover, we consider complexity measures that quantify how the algorithm A makes queries: some queries may depend on prior answers while other queries do not. Letting $\zeta ^{\mathsf {m}}(x_1,\dots ,x_\mathsf {m}) := (\zeta (x_1),\dots ,\zeta (x_\mathsf {m}))$, we say that A makes queries in $\mathsf {a}$ rounds of width $\mathsf {m}$ if there exists an $\mathsf {a}$-query oracle algorithm B such that $B^{\zeta ^\mathsf {m}} \equiv A^\zeta$ for every $\zeta \in \mathcal {U}(\lambda )$. Note that $t\le \mathsf {m}\cdot \mathsf {a}$.

Finally, we consider the size of oracle queries, i.e., the number of bits used to specify the query: we say that A has queries of size $\mathsf {n}$ if for every $\zeta \in \mathcal {U}(\lambda )$ and $x \in \mathsf {queries}(A,\zeta )$ it holds that $|x| \le \mathsf {n}$.

We summarize the above via the following definition.

Definition 1

An oracle algorithm A is $(\mathsf {a},\mathsf {m},\mathsf {n})$-query if A makes queries in $\mathsf {a}$ rounds of width $\mathsf {m}$, and all queries of A have size at most $\mathsf {n}$.

3.2 Relations

We consider proof systems for binary relations and for ternary relations, as we now explain.

• A binary relation $R$ is a set of tuples $(\mathbbm {x},\mathbbm {w})$ where $\mathbbm {x}$ is the instance and $\mathbbm {w}$ the witness. The corresponding language $L=L(R)$ is the set of $\mathbbm {x}$ for which there exists $\mathbbm {w}$ such that $(\mathbbm {x},\mathbbm {w}) \in R$.

• A ternary relation $R$ is a set of tuples $(\mathbbm {i},\mathbbm {x},\mathbbm {w})$ where $\mathbbm {i}$ is the index, $\mathbbm {x}$ the instance, and $\mathbbm {w}$ the witness. The corresponding language $L=L(R)$ is the set of tuples $(\mathbbm {i},\mathbbm {x})$ for which there exists $\mathbbm {w}$ such that $(\mathbbm {i},\mathbbm {x},\mathbbm {w}) \in R$. To distinguish this case from the above case, we refer to $R$ as an indexed relation and $L$ as an indexed language.

A binary relation can be viewed as a special case of a ternary relation, where the same index has been fixed for all instances. For example, the indexed relation of satisfiable boolean circuits consists of triples where $\mathbbm {i}$ is the description of a boolean circuit, $\mathbbm {x}$ is an assignment to some of the input wires, and $\mathbbm {w}$ is an assignment to the remaining input wires that makes the circuit output 0. If we restrict this indexed relation by fixing the same circuit for all instances, we obtain a binary relation.

The proof systems that we consider for binary relations are: (a) non-interactive arguments in the random oracle model; and (b) interactive oracle proofs. The proof systems that we consider for indexed (ternary) relations are (a) preprocessing non-interactive arguments in the random oracle model; and (b) holographic interactive oracle proofs. We will define only the latter two (in Sect. 3.3 and Sect. 3.4 respectively) because the former two can be derived as special cases.

3.3 Non-interactive Arguments in the Random Oracle Model

We consider non-interactive arguments in the random oracle model, where security holds against query-bounded, yet possibly computationally-unbounded, adversaries. Recall that a non-interactive argument typically consists of a prover algorithm and a verifier algorithm that prove and validate statements for a binary relation, which represents the valid instance-witness pairs. Here we define a more general notion known as a preprocessing non-interactive argument, which works for indexed relations (see Sect. 3.2). This notion additionally involves an indexer algorithm, which receives as input an index and deterministically produces a key pair specialized for producing and validating statements relative to the given index. The usual notion of a non-interactive argument corresponds to a preprocessing non-interactive argument where the indexer algorithm is degenerate (it sets the proving key equal to the index, and similarly sets the verification key equal to the index).

Let $\mathsf {ARG}= (I, P, V)$ be a tuple of (oracle) algorithms, with $I$ deterministic. We say that $\mathsf {ARG}$ is a (preprocessing) non-interactive argument, in the random oracle model, for an indexed relation $R$ with (non-adaptive) soundness error $\mathsf {\epsilon }$ if the following holds.

• Completeness. For every $(\mathbbm {i}, \mathbbm {x}, \mathbbm {w}) \in R$ and $\lambda \in \mathbb {N}$,

  

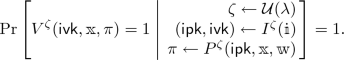
• Soundness (non-adaptive). For every $(\mathbbm {i},\mathbbm {x}) \notin L(R)$, $t$-query $\tilde{P}$, and $\lambda \in \mathbb {N}$,

  

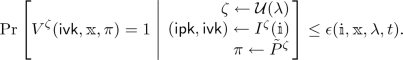
Complexity measures. We consider several complexity measures beyond soundness error. All of these complexity measures are, implicitly, functions of $(\mathbbm {i},\mathbbm {x})$ and the security parameter $\lambda$.

• sizes: proving key size $\mathsf {ipks}:= |\mathsf {ipk}|$; verification key size $\mathsf {ivks}:= |\mathsf {ivk}|$; argument size $\mathsf {as}:= |\pi |$.

• times: the indexer $I$ runs in time $\mathsf {it}$; the prover $P$ runs in time $\mathsf {pt}$; the verifier $V$ runs in time $\mathsf {vt}$.

• queries: the indexer $I$ is a $\mathsf {iq}$-query algorithm; the prover $P$ is a $(\mathsf {a},\mathsf {m},\mathsf {n})$-query algorithm (see Definition 1); the verifier $V$ is a $\mathsf {vq}$-query algorithm.

Bits of security. We are interested to discuss complexity measures, most notably argument size, also as a function of bits of security. Note, though, that we cannot directly equate “bits of security” with $- \log \mathsf {\epsilon }(\mathbbm {i},\mathbbm {x},\lambda ,t)$ because this value depends on multiple quantities that we cannot set a priori. Indeed, while we could set the output size $\lambda$ of the random oracle to be a value of our choice, we may not know which index-instance pairs $(\mathbbm {i},\mathbbm {x})$ we will consider nor a malicious prover’s query bound $t$. Thus we consider all $(\mathbbm {i},\mathbbm {x})$ and $t$ up to a large size that depends on the desired bits of security, and say that the scheme has $s$ bits of security if $- \log \mathsf {\epsilon }(\mathbbm {i},\mathbbm {x},\lambda ,t) \le s$ for all such $\mathbbm {i},\mathbbm {x},t$ and where $\lambda$ is linear in $s$. This is captured is the following definition.

Definition 2

We say that $\mathsf {ARG}$ provides $s$ bits of security if its soundness error $\mathsf {\epsilon }$ satisfies the following condition with $\lambda := c \cdot s$ for some constant $c>0$: for every index-instance pair $(\mathbbm {i},\mathbbm {x}) \notin L(R)$ and query bound $t\in \mathbb {N}$ with $\max \{|\mathbbm {i}|+|\mathbbm {x}|,t\} \le 2^{s}$ it holds that $\mathsf {\epsilon }(\mathbbm {i},\mathbbm {x},\lambda ,t) \le 2^{-s}$.

The above definition enables us to discuss any complexity measure also, and possibly exclusively, as a function of bits of security as we illustrate in the following definition.

Definition 3

We say that $\mathsf {ARG}$ has argument size $\mathsf {as}(s)$ if $\mathsf {ARG}$ provides $s$ bits of security and, moreover, $\mathsf {as}(s)$ bounds the size of an honestly-generated $\pi$ for any index-instance pair $(\mathbbm {i},\mathbbm {x}) \in L(R)$ with $|\mathbbm {i}|+|\mathbbm {x}| \le 2^{s}$ and while setting $\lambda := \varTheta (s)$.

3.4 Interactive Oracle Proofs

Interactive Oracle Proofs (IOPs) [BCS16, RRR16] are information-theoretic proof systems that combine aspects of Interactive Proofs [Bab85, GMR89] and Probabilistically Checkable Proofs [Bab+91, Fei+91, AS98, Aro+98], and also generalize the notion of Interactive PCPs [KR08]. Below we describe a generalization of public-coin IOPs that is convenient in this paper.

Recall that a $\mathsf {k}$-round public-coin IOP works as follows. For each round $i \in [\mathsf {k}]$, the prover sends a proof string $\varPi _{i}$ to the verifier; then the verifier sends a uniformly random message $\rho _{i}$ to the prover. After $\mathsf {k}$ rounds of interaction, the verifier makes some queries to the proof strings $\varPi _{1},\dots ,\varPi _{\mathsf {k}}$ sent by the prover, and then decides if to accept or to reject.

The definition that we use here generalizes the above notion in two ways.

• Holography. The proof system works for indexed relations (see Sect. 3.2), and involves an indexer algorithm that, given an index as input, samples an encoding $\varPi _{0}$ of the index; the randomness $\rho _{0}$ used by the indexer to sample the encoding $\varPi _{0}$ is public (known to prover and verifier). The verifier receives oracle access to the encoding $\varPi _{0}$, rather than explicit access to the index.

• Randomness as oracle. The verifier has oracle access to its own randomness $\rho _{1},\dots ,\rho _{\mathsf {k}}$ and to the indexer’s randomness $\rho _{0}$. This notion, which naturally arises in our results, is compatible with known compilers, as we explain in Remark 1. We will count verifier queries to the randomness $\rho _{0},\rho _{1},\dots ,\rho _{\mathsf {k}}$ separately from verifier queries to the encoding $\varPi _{0}$ and proof strings $\varPi _{1},\dots ,\varPi _{\mathsf {k}}$.

In more detail, let $\mathsf {IOP}= (\mathbf {I}, \mathbf {P},\mathbf {V})$ be a tuple where $\mathbf {I}$ is a deterministic algorithm, $\mathbf {P}$ is an interactive algorithm, and $\mathbf {V}$ is an interactive oracle algorithm. We say that $\mathsf {IOP}$ is a public-coin holographic IOP for an indexed relation $R$ with $\mathsf {k}$ rounds and soundness error $\varepsilon$ if the following holds.

• Completeness. For every $(\mathbbm {i},\mathbbm {x},\mathbbm {w}) \in R$,

  

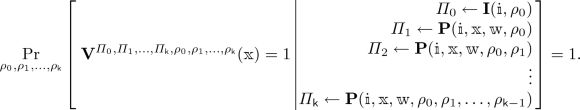
• Soundness. For every $(\mathbbm {i},\mathbbm {x}) \notin L(R)$ and unbounded malicious prover $\tilde{\mathbf {P}}$,

  

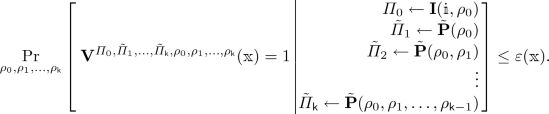
Complexity measures. We consider several complexity measures beyond soundness error. All of these complexity measures are implicitly functions of the instance $\mathbbm {x}$.

• proof length $\mathsf {l}$: the total number of bits in $\varPi _{0},\varPi _{1},\dots ,\varPi _{\mathsf {k}}$.

• proof queries $\mathsf {q}$: the number of bits read by the verifier from $\varPi _{0},\varPi _{1},\dots ,\varPi _{\mathsf {k}}$.

• randomness length $\mathsf {r}$: the total number of bits in $\rho _{0},\rho _{1},\dots ,\rho _{\mathsf {k}}$.

• randomness queries $\mathsf {q}_{\mathsf {r}}$: the total number of bits read by the verifier from $\rho _{0},\rho _{1},\dots ,\rho _{\mathsf {k}}$.

• indexer time $\mathsf {it}$: $\mathbf {I}$ runs in time $\mathsf {it}$.

• prover time $\mathsf {pt}$: $\mathbf {P}$ runs in time $\mathsf {pt}$.

• verifier time $\mathsf {vt}$: $\mathbf {V}$ runs in time $\mathsf {vt}$.

Query entropy. We additionally define a complexity measure called query entropy that, informally, captures the entropy of the query locations read by the IOP verifier in an honest execution. In particular, if the query entropy is at most $\mathsf {h}$ then the probability of predicting in advance all the locations that the verifier will read at the end of the protocol is at least $2^{-\mathsf {h}}$, where the probability is taken over the randomness of the IOP verifier and (any) randomness of the honest IOP prover.

Definition 4

Let X be a random variable. The sample-entropy of $x\in \mathsf {supp}(X)$ with respect to X is $H(x) := - \log \Pr [X=x]$. The min-entropy of X is $H_{\mathsf {min}}(X) := \min _{x\in \mathsf {supp}(X)}{H(x)}$.

Definition 5

Let $\mathsf {IOP}=(\mathbf {I}, \mathbf {P},\mathbf {V})$ be an IOP with proof length $\mathsf {l}$ for an indexed relation $R$.

• The query distribution of $\mathsf {IOP}$ for $(\mathbbm {i},\mathbbm {x},\mathbbm {w}) \in R$ is the distribution $\mathcal {D}(\mathbbm {i},\mathbbm {x},\mathbbm {w})$ over subsets $\mathcal {I}\subseteq [\mathsf {l}]$ such that the probability of $\mathcal {I}$ is the probability that the honest IOP verifier $\mathbf {V}$ reads exactly the locations in $\mathcal {I}$ in an honest execution with the IOP prover $\mathbf {P}$ for the triple $(\mathbbm {i},\mathbbm {x},\mathbbm {w})$.

• The query entropy of $\mathsf {IOP}$ for an index-instance pair $(\mathbbm {i},\mathbbm {x}) \in L(R)$ is

  $$\begin{aligned} \mathsf {h}(\mathbbm {i},\mathbbm {x}) := \max _{\mathbbm {w}\ \text { s.t. } \ (\mathbbm {i},\mathbbm {x},\mathbbm {w}) \in R} H_{\mathsf {min}}(\mathcal {D}(\mathbbm {i},\mathbbm {x},\mathbbm {w}))~. \end{aligned}$$

For any IOP with proof length $\mathsf {l}$ and query complexity $\mathsf {q}$ it holds that for any $(\mathbbm {i},\mathbbm {x},\mathbbm {w}) \in R$ the query distribution has no more entropy than the uniform distribution over subsets of size $\mathsf {q}$. Therefore it always holds that $\mathsf {h}(\mathbbm {i},\mathbbm {x}) \le \mathsf {q}(\mathbbm {i},\mathbbm {x}) \cdot \log \mathsf {l}(\mathbbm {i},\mathbbm {x})$.

Remark 1 (randomness in known compilers)

The definition of public-coin (holographic) IOP that we consider additionally grants the verifier oracle access to its own randomness, which in particular, enables the prover to receive much more randomness than allowed by the verifier’s running time. We briefly discuss why this feature is motivated by known cryptographic compilers.

First, the size of arguments produced via known cryptographic compilers does not depend on the verifier’s randomness complexity. E.g., the Micali compiler [Mic00] maps a PCP into a corresponding non-interactive argument whose size is independent of the PCP verifier’s randomness complexity; more generally, the BCS compiler [BCS16] maps a public-coin IOP into a corresponding non-interactive argument whose size is independent of the IOP verifier’s randomness complexity.

Second, the running time of the argument verifier produced by these compilers only depends on the number of queries to the randomness, but not on randomness complexity. Indeed, both in the Micali compiler and in the BCS compiler, the argument prover only needs to invoke the random oracle to answer randomness queries of the underlying PCP/IOP verifier, and in particular, does not have to materialize the unqueried randomness. This is because the random oracle, which serves as a shared randomness resource, enables the argument prover to suitably materialize all the relevant randomness without impacting the argument verifier.

4 From Succinct Arguments to Interactive Oracle Proofs

We formally re-state Theorem 1 and then prove it. The formal theorem statement is somewhat technical, as it contains the precise relationship between parameters of the succinct argument and the corresponding IOP. We advise the reader to first read the informal overview of the proof in Sect. 2.1, as it gives intuition for the relationships between the parameters.

The theorem is stated with respect to a non-interactive succinct argument, for the sake of simple presentation. The compiler naturally generalizes to succinct arguments with multiple rounds, and we describe this is Remark 2. We note that we additionally provide the query entropy of the compiled IOP (see Definition 5) as it is used later in Theorem 6.

In the theorem below, an $(\mathsf {a},\mathsf {m},\mathsf {n})$-query algorithm performs $\mathsf {a}$ rounds each containing $\mathsf {m}$ queries to a random oracle over defined over $\{0,1\}^\mathsf {n}$ (see Definition 1).

Theorem 3

(ARG $\rightarrow$ IOP). There exists a polynomial-time transformation $\mathbb {T}$ that satisfies the following. If $\mathsf {ARG}$ is a non-interactive argument in the ROM for a relation $R$ then $\mathsf {IOP}:= \mathbb {T}(\mathsf {ARG})$ is a public-coin IOP for $R$, parametrized by a security parameter $\lambda \in \mathbb {N}$, with related complexity as specified below. (All complexity measures take as input an instance $\mathbbm {x}$ and the security parameter $\lambda$.)

Moreover, the IOP prover and IOP verifier make only black-box use of the argument prover and argument verifier respectively (up to intercepting and answering their queries to the random oracle).

The rest of this section is organized as follows: in Sect. 4.1 we introduce the main tool that we use in our transformation, and in Sect. 4.2 we describe the transformation. Proofs are given in the full version of the paper.

Remark 2 (interactive arguments)

While the focus of this paper is non-interactive arguments in the random oracle model (as defined in Sect. 3.3), one could also study interactive arguments in the random oracle model. Our proof of Theorem 3 directly extends to give a result also for this more general case, with the main difference being that the round complexity of the IOP increases by the round complexity of the given argument system.

The reason why the proof directly extends is that the main technique for constructing the IOP is a sub-protocol for simulating queries to a random oracle, and this sub-protocol does not “care” if in the meantime the argument prover and argument verifier engage in a conversation. As a result, if the succinct argument has $\mathsf {k}$ rounds, then the compiled IOP has $\mathsf {k}+ \mathsf {a}$ rounds.

4.1 Tool: Perfect Hash Functions with Locality

A perfect hash function for a set S of size m in a universe $U$ is a function $h:U\rightarrow \{1,\ldots ,O(m)\}$ that is one-to-one on S. We use a seminal construction of Fredman, Komlós, and Szemerédi [FKS84], observing that it has a certain locality property that is crucial for us.

Theorem 4

(follows from [FKS84]). For any universe $U$ there exist a $\mathrm {poly}(m,\log |U|)$-time deterministic algorithm that, given as input a subset $S \subseteq U$ of size m, outputs a perfect hash function $h:U\rightarrow \{1,\ldots ,O(m)\}$ for S with $|h| = O(m \cdot \log |U|)$ bits. In fact, evaluating $h$ on a single input requires reading only $O(\log |U|)$ bits from the description of $h$, and performing $\tilde{O}(\log |U|)$ bit operations. In alternative to the deterministic algorithm, $h$ can be found in expected time $\tilde{O}(m \cdot \log |U|)$.

Proof

The FKS construction achieves a perfect hash function $h$ via two levels of hashing. The first level is a hash function $h_0 :U\rightarrow [m]$ that divides the elements of S among m bins where bin i has $b_i$ elements, with $\sum _{i=1}^{m}b_i^2 = O(m)$. The second level is a hash function $h_i :[m] \rightarrow [b_i^2]$, one for each bin $i \in [m]$, that resolves collisions inside bin i by mapping the $b_i$ elements in bin i to a range of size $b_i^2$. Hence the hash function $h$ consists of a collection of $1+m$ hash functions: one for the first level and m for the second level. Each of the $1+m$ hash functions is sampled from a family of universal hash functions (see Definition 6), which can be instantiated via the standard construction in Lemma 1 below.

Definition 6

A family $\mathcal {H}$ of hash functions mapping $U$ to [M] is universal if for any distinct $x,y \in U$ it holds that $\Pr _{h\leftarrow \mathcal {H}}[h(x) = h(y)] = 1/M$.

Lemma 1

([CW79]). Let p be a prime with $|U|< p \le \mathrm {poly}(|U|)$. The family $\mathcal {H}= \{h_{a,b} :U\rightarrow [M] \}_{a \in \mathbb {F}_{p}^{*},b \in \mathbb {F}_{p}}$ where $h_{a,b}(x) := (a \cdot x \mod p) \mod M$ is universal. Each $h_{a,b}$ has bit size $O(\log |U|)$ and can be evaluated in $\widetilde{O}(\log |U|)$ time.

The above gives us $|h_0| = O(\log |U|)$ and $|h_i| = O(\log |U|)$ for all $i \in [m]$, and in particular $|h| = O(\sum _{i=0}^{m} |h_i|) = O(m \cdot \log |U|)$.

We now discuss the locality property of the FKS construction. In order to evaluate $h$ on a single element, one needs to use only two hash functions among the $1+m$: the first level hash function $h_0$ and then the appropriate second level hash function $h_i$. Thus, to evaluate h on a single element requires reading only the relevant bits of $h_0$ and $h_i$ from the description of h, which together amount to $O(\log |U|)$ bits. The time to evaluate both $h_0$ and $h_i$ is $\widetilde{O}(\log |U|)$.

We conclude with a discussion of how to find $h$. Fredman, Komlós, and Szemerédi [FKS84] showed a $\mathrm {poly}(m,\log |U|)$-time deterministic algorithm; Alon and Naor [AN96] showed a faster deterministic algorithm, but the running time remains super-linear. Alternatively, in [FKS84], it was shown that $h$ can be found in expected time $\tilde{O}(m \cdot \log |U|)$. This follows since for a random $h_0$ it holds that $\sum _{i=1}^{m}b_i^2 = O(m)$ with high probability, and moreover, for a random $h_i$, the mapping to $[b_i^2]$ is one-to-one with high probability. Thus, in expectation, only a constant number of trials are needed to find $h_0$ and to find each $h_i$.    $\square$

4.2 The Transformation

Construction 5

(transformation $\mathbb {T}$). Let $\mathsf {ARG}= (P, V)$ be a non-interactive argument in the ROM. We construct a public-coin interactive oracle proof $\mathsf {IOP}= (\mathbf {P},\mathbf {V})$, parametrized by a choice of security parameter $\lambda \in \mathbb {N}$. The IOP prover $\mathbf {P}$ takes as input an instance $\mathbbm {x}$ and a witness $\mathbbm {w}$, and will internally simulate the argument prover $P$ on input $(\mathbbm {x},\mathbbm {w})$, answering $P$’s queries to the random oracle as described below. The IOP verifier $\mathbf {V}$ takes as input only the instance $\mathbbm {x}$, and will simulate the argument verifier $V$ on input $\mathbbm {x}$, answering $V$’s queries to the random oracle as described below.

The interactive phase of the IOP protocol proceeds as follows:

• For round $j=1,\dots ,\mathsf {a}$:

  • 1. $\mathbf {P}$ simulates $P$ to get its j-th query set $X_j=(x_1,\dots ,x_\mathsf {m})$, and finds a perfect hash function $h_j :\{0,1\}^\mathsf {n}\rightarrow [M]$ for the set $X_j$ where $M=O(\mathsf {m})$. Then, $\mathbf {P}$ creates an $M$-cell array $T_j$ such that $T_j[h_j(x_i)]=x_i$ for all $i \in [\mathsf {m}]$, and all other cells of $T_j$ are $\bot$. Finally, $\mathbf {P}$ sends $\varPi _j := (h_j,T_j)$ to $\mathbf {V}$.

  • 2. $\mathbf {V}$ samples $y_1,\dots ,y_{M} \in \{0,1\}^{\lambda }$ uniformly at random and sends $\rho _j := (y_1,\dots ,y_{M})$ to $\mathbf {P}$.

  • 3. $\mathbf {P}$ answers $P$’s query $x_i$ with the value $\rho _j[h_j(x_i)]$, for every $i \in [\mathsf {m}]$.

• $\mathbf {P}$ simulates $P$ until it outputs the non-interactive argument $\pi$; $\mathbf {P}$ sends $\varPi _{\mathsf {a}+1} := \pi$ to $\mathbf {V}$.

The query phase of the IOP protocol proceeds as follows. The IOP verifier $\mathbf {V}$ reads the non-interactive argument $\pi$ sent in the last round (the only symbol in $\varPi _{\mathsf {a}+1}$), and simulates the argument verifier $V$ on input $(\mathbbm {x},\pi )$, answering each oracle query x with an answer y that is derived as follows:

• $\mathbf {V}$ reads the necessary bits from $h_j$ (in $\varPi _j$) to evaluate $h_j(x)$;

• $\mathbf {V}$ reads $v_j := T_j[h_j(x)]$ (in $\varPi _j$) for all $j \in [\mathsf {a}]$;

• if $v_j \ne x$ for all $j \in [\mathsf {a}]$ then set y to be a random value in $\{0,1\}^{\lambda }$;

• if there exists $j \ne j'$ such that $v_j =x$ and $v_{j'} = x$ then halt and reject;

• let j be the unique value such that $v_j = x$, and set $y := \rho _j[h_j(x)]$.

If each query was answered successfully, $\mathbf {V}$ rules according to the output of $V$. (Note that, formally, the randomness used by the IOP verifier $\mathbf {V}$ to answer queries of the argument verifier $V$ that were not also asked by the argument prover $P$ should be treated as a last verifier message $\rho _{\mathsf {a}+1}$ consisting of $\mathsf {vq}$ random $\lambda$-bit strings. The IOP verifier will then “consume” this randomness as needed.)

The proof appears in the full version of the paper.

5 From Interactive Oracle Proofs to Algorithms

We formally re-state and prove Theorem 2, which states that IOPs with good parameters (small soundness error relative to soundness error or, more precisely, query entropy) can be translated to good algorithms (fast algorithms with small space complexity). We use this transformation in Sect. 6 to show that, for certain languages, if the IOP parameters are “too good” then the resulting algorithms contradict standard complexity assumptions (and therefore cannot exist).

Theorem 6 (IOP to algorithm)

Suppose that a language $L$ has a public-coin IOP with completeness error $\mathsf {c}$, soundness error $\varepsilon$, round complexity $\mathsf {k}$, proof length $\mathsf {l}$ over an alphabet $\varSigma$, query complexity $\mathsf {q}$, and query entropy $\mathsf {h}$. If then, for the language $L$ is in

$$\begin{aligned} \mathrm {BPTIME}\left[ 2^{O\left( c(n) + \mathsf {k}(n) \cdot \log \frac{\mathsf {k}(n)}{\delta (n)} \right) } \cdot \mathrm {poly}(n) \right] . \end{aligned}$$

Let the verifier space complexity be $\mathsf {vs}$, randomness length $\mathsf {r}$ (over $\varSigma$) and randomness query complexity $\mathsf {q}_{\mathsf {r}}$. If then the same algorithm can be implemented in space

$$\begin{aligned} O\left( \mathsf {vs}\cdot \left( c(n) + \mathsf {k}(n) \cdot \log \frac{\mathsf {k}(n)}{\delta '(n)} \right) ^2\right) . \end{aligned}$$

(Above it suffices to take $c$ to be the number of bits to specify the set of queries by the IOP verifier and their corresponding answers. This is useful when queries are correlated or answers are from different alphabets.)

The proof appears in the full version of the paper.

5.1 IOP to Laconic IP

The lemma below states that any IOP with good enough soundness relative to its query entropy can be translated to a laconic IP (an IP with small prover-to-verifier communication). Query entropy is the probability of guessing in advance the exact locations that the IOP verifier will read across the proof strings sent by the IOP prover; see Definition 5 for how query entropy is formally defined.

Lemma 2 (IOP to laconic IP)

Suppose that a language $L$ has an IOP with completeness error $\mathsf {c}$, soundness error $\varepsilon$, round complexity $\mathsf {k}$, proof length $\mathsf {l}$ over an alphabet $\varSigma$, query complexity $\mathsf {q}$, and query entropy $\mathsf {h}$. If $\varepsilon < (1-\mathsf {c}) \cdot 2^{-\mathsf {h}}$ then $L$ has an IP with completeness error $1-(1-\mathsf {c}) \cdot 2^{-\mathsf {h}}$, soundness error $\varepsilon$, round complexity $\mathsf {k}$, and prover-to-verifier communication $\mathsf {q}\cdot \log \mathsf {l}+\mathsf {q}\cdot \log |\varSigma |$. (More generally, communication is bounded by the number of bits to specify the set of queries by the IOP verifier and their corresponding answers.) If the IOP is public-coin then the IP is public-coin.

Moreover, the IP can be modified so that the IP verifier performs a single pass over the randomness tape, with completeness error $1-(1-\mathsf {c}) \cdot 2^{-\mathsf {h}} \cdot \mathsf {r}^{-\mathsf {q}_{\mathsf {r}}}$, and space complexity $O(\mathsf {vs}+ \mathsf {q}_{\mathsf {r}}\cdot \log \mathsf {r}+ \mathsf {q}_{\mathsf {r}}\log |\varSigma |))$ where $\mathsf {vs}$ is the space complexity of the IOP verifier.

The proof appears in the full version of the paper.

5.2 IP to Algorithm

Goldreich and Håstad [GH98] have shown that languages with public-coin IPs with small prover-to-verifier communication can be decided via fast probabilistic algorithms. Their result is shown for IPs with constant completeness and soundness errors. Below we show a refinement of their theorem, where we explicitly provide the dependency in the completeness and soundness errors, which allows supporting IPs with large completeness errors (which we need). Moreover, we note that if the IP verifier reads its randomness in a single pass, the probabilistic algorithm for deciding the language can be implemented in small space (which we also need).

Lemma 3 (IP to algorithm)

Suppose that a language $L$ has a public-coin IP with completeness error $\alpha$, soundness error $\beta$, round complexity $\mathsf {k}$, and prover-to-verifier communication $c$. Then, for $d(n) := c(n) + \mathsf {k}(n) \cdot \log \frac{\mathsf {k}(n)}{1-\alpha (n)-\beta (n)}$ the language $L$ is in

$$\begin{aligned} \mathrm {BPTIME}\left[ 2^{O\left( d \right) } \cdot \mathrm {poly}(n) \right] . \end{aligned}$$

Moreover, if the space complexity of the IP verifier is $\mathsf {vs}$ when reading its randomness random tape in a single pass then the language $L$ is in

$$\begin{aligned} \mathrm {SPACE}\left[ O\left( d \cdot (\mathsf {vs}+ d) \right) \right] . \end{aligned}$$

The proof appears in the full version of the paper.

6 Barriers for Succinct Arguments

We prove that, under plausible complexity assumptions, there do not exist succinct arguments where the argument verifier makes a small number of queries to the random oracle and the honest argument prover has a small adaptivity parameter. We separately consider that case of succinct arguments for nondeterministic languages ($\mathrm {NTIME}$) in Sect. 6.1, and the case of deterministic languages ($\mathrm {DTIME}$) in Sect. 6.2.

In both cases our approach consists of the following steps: (1) we use Theorem 3 to transform the succinct argument into a corresponding IOP; then, (2) we use Theorem 6 to transform the IOP into an algorithm with certain time and space complexity; finally, (3) we argue that, under standard complexity assumptions, such an algorithm does not exist.

6.1 The Case of Nondeterministic Languages

Theorem 7

Suppose that $\mathrm {NTIME}[T]$ has a non-interactive argument $\mathsf {ARG}$ that provides $s$ bits of security and has argument size $\mathsf {as}= o(T)$ (see Definitions 2 and 3), where the prover makes $\mathsf {a}$ adaptive rounds of $\mathsf {m}$ queries to the random oracle, and the verifier makes $\mathsf {vq}$ queries to the random oracle. If (1) $\mathsf {vq}\cdot \mathsf {a}\cdot \log (\mathsf {m}) = o(s)$; and (2) $\log n \le s\le o(T^{1/2})$, then $\mathrm {NTIME}[T(n)] \subseteq \mathrm {BPTIME}[2^{o(T(n))}]$ (an unlikely inclusion).

Remark 3 (s vs. T)

If $\mathsf {as}= \varOmega (T)$ then the trivial scheme of sending the $T$ bits of a valid witness yields a non-interactive argument (indeed, proof), and so we consider the case $\mathsf {as}= o(T)$. For technical reasons, we also need that $s= o(T^{1/2})$, a rather weak condition. Additionally, we restrict the instance size to be at most exponential in $s$, and therefore assume that $\log n \le s$.

Remark 4

(“$\mathsf {a}$” in known compilers). In the Micali transformation [Mic00], the argument prover performs $\mathsf {a}=\varTheta (\log \mathsf {l})$ rounds of queries to the random oracle (one round for each level of a Merkle tree over a PCP of size $\mathsf {l}$), whereas the argument verifier performs $\mathsf {vq}= \varTheta (\mathsf {q}\cdot \log \mathsf {l}+\mathsf {r})$ queries to the random oracle. When using known or conjectured PCPs in the Micali transformation, we get $\mathsf {vq}= \varOmega (s)$. In particular, the hypothesis $\mathsf {vq}\cdot \mathsf {a}\cdot \log (\mathsf {m}) = o(s)$ does not apply, and as expected does not lead to the inclusion stated in the theorem.

Remark 5 (interactive argument)

Similar to the way Theorem 3 is presented, to get a simple presentation, we state the above theorem for non-interactive succinct arguments. We note, however, that the theorem naturally generalizes to any public-coin succinct argument with $\mathsf {k}$ rounds (note that always $\mathsf {k}\le \mathsf {as}$), as long as $s^2 \cdot \mathsf {k}= o(T)$.

6.2 The Case of Deterministic Languages

Theorem 8

Suppose that $\mathrm {DTIME}[T]$ has a non-interactive argument $\mathsf {ARG}$ that provides $s$ bits of security and has argument size $\mathsf {as}= o(T)$ (see Definitions 2 and 3), where the prover makes $\mathsf {a}$ adaptive rounds of $\mathsf {m}$ queries to the random oracle, and the verifier makes $\mathsf {vq}$ queries to the random oracle and has space complexity $\mathsf {sv}$. If (1) $\mathsf {vq}\cdot \mathsf {a}\cdot \log (\mathsf {a}\cdot \mathsf {m}) = o(s)$; (2) $\mathsf {sv}\cdot (s^4 + \mathsf {as}^2) = o(T)$; and (3) $\log n \le s$ then $\mathrm {DTIME}[T(n)] \subseteq \mathrm {SPACE}[o(T(n))]$ (an unlikely inclusion).

The proof appears in the full version of the paper.