Abstract
We present simpler and improved constructions of 2-round protocols for secure multi-party computation (MPC) in the semi-honest setting. Our main results are new information-theoretically secure protocols for arithmetic NC1 in two settings:
- (i):
-
the plain model tolerating up to \(t < n/2\) corruptions; and
- (ii):
-
in the OLE-correlation model tolerating any number of corruptions.
Our protocols achieve adaptive security and require only black-box access to the underlying field, whereas previous results only achieve static security and require non-black-box field access. Moreover, both results extend to polynomial-size circuits with computational and adaptive security, while relying on black-box access to a pseudorandom generator. In the OLE correlation model, the extended protocols for circuits tolerate up to \(n-1\) corruptions.
Along the way, we introduce a conceptually novel framework for 2-round MPC that does not rely on the round collapsing framework underlying all of the recent advances in 2-round MPC.
H. Lin and T. Liu—Supported by NSF grants CNS-1528178, CNS-1514526, CNS-1652849 (CAREER), CNS-2026774, a Hellman Fellowship, a JP Morgan Research Award, the Defense Advanced Research Projects Agency (DARPA) and Army Research Office (ARO) under Contract No. W911NF-15-C-0236, and a subcontract No. 2017-002 through Galois. The views expressed are those of the authors and do not reflect the official policy or position of the Department of Defense, the National Science Foundation, or the U.S. Government.
H. Wee—Research supported in part by ERC Project aSCEND (H2020 639554).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Secure multi-party computation (MPC) [5, 12, 18, 23] allows a group of n mutually distrusting parties to jointly evaluate a function over their private inputs in a manner that reveals nothing beyond the output of the function. In this work, we focus on semi-honest two-round MPC protocols. The state of the art, following the recent breakthroughs in [6, 17] may be broadly classified as follows:
-
protocols for \(\mathbf{NC }^{\mathbf{1}}\) achieving information-theoretic security tolerating \(t < n/2\) adversarial parties [2];
-
protocols for polynomial-size circuits P/poly achieving computational security tolerating \(t < n/2\) adversarial parties, assuming the existence of one-way functions [1, 2];
-
protocols for polynomial-size circuits P/poly achieving computational security tolerating \(t < n\) adversarial parties, assuming the existence of oblivious transfer [6, 17].
All of these constructions follow the same high-level “round collapsing” strategy introduced in [15]. In particular, they apply garbled circuits to the circuits of parties’ algorithms of a multi-round MPC protocol, where the garbling is used to collapse the multi-round MPC protocol to a 2-round protocol.
1.1 Our Results
We present simpler and improved constructions of 2-round protocols for secure multi-party computation (MPC) in the semi-honest setting. Our main results are new information-theoretically secure protocols for arithmetic \(\mathbf{NC }^{\mathbf{1}}\) in two settings:
- (i):
-
the plain model tolerating up to \(t < n/2\) corruptions; and
- (ii):
-
in the OLE-correlation model tolerating any number of corruptions.
Two parties with an Oblivious Linear Evaluation (OLE) correlation hold respectively random elements \((a^{(1)}, b^{(1)})\) and \((a^{(2)}, b^{(2)})\) such that \(a^{(1)}a^{(2)} = b^{(1)} + b^{(2)}\) over a field.
Our protocols achieve adaptive security [10, 11] and require only black-box access to the underlying field, whereas previous results only achieve static security and require non-black-box field access. Moreover, both results extend to polynomial-size circuits with computational and adaptive security, while relying on black-box access to a pseudorandom generator. In the OLE correlation model, the extended protocols for circuits tolerate up to \(n-1\) corruptions. While the honest majority setting is a natural and well-established model, we believe that the OLE-correlation model is also very natural to study, especially for arithmetic computation: OLE correlations enable very efficient online computation, and the correlations themselve can be generated efficiently in the pre-processing phase [8, 9]. We provide a comparison of our results with the state of the art in Fig. 1 and Fig. 2.
Along the way, we introduce a conceptually novel framework for 2-round MPC that does not rely on the round collapsing framework underlying all of the recent advances in 2-round MPC staring from [15].
Our Techniques. The crux of our protocols, following [2, 19, 20], is a way to “encode” degree-3 polynomials into randomized polynomials that have degree 2 after pre-processing of local inputs and randomness – known as multi-party randomized encodings (MPREs). Following the round-collapsing framework of 2-round MPC, prior MPRE schemes garble the next-step circuits of a multi-round MPC protocol, to reduce the degree from 3 to 2.
We construct MPRE directly without using “inner” multi-round MPC. We observe that the [20] randomizing polynomials give a way to replace the multiplication between two input elements with multiplication between two random elements. With an OLE-correlation, the product of two random elements are additively shared between two parties, immediately reducing the degree to 2. In the honest majority setting, we exploit a delicate interplay between the IK02 randomized polynomials and the 2-round BGW [5] protocol for computing degree-2 polynomials (or essentially Shamir’s secret sharing scheme) to turn multiplication between two input elements into multiplication between two local random elements, again reducing the degree to 2. Our MPRE schemes and 2-round MPC protocols based on them enjoy simplicity and better efficiency.
Information-Theoretic Security vs Adaptive Security. The folklore belief is that any information theoretically secure protocol is also adaptively secure with an inefficient simulator. Therefore, to formally prove adaptive security, the technical issue is presenting an explicit efficient simulator. We systematically present and analyze efficient adaptive simulators for our protocols, taking into account different corruption schedules. The analysis benefits greatly from our simpler and modular approach.
2 Technical Overview
We present an overview of our constructions, focusing on the honest-majority 2-round MPC for arith-NC1, followed by a more detailed comparison with prior approaches.
Following [19, 20], to construct 2-round MPC for arith-NC1, it suffices to construct a 2-round protocol for the 3-party functionality \((x_1,x_2,x_3) \mapsto x_1x_2x_3\). More precisely, we need the functionality \(((x_1,s_1),(x_2,s_2),(x_3,s_3)) \mapsto x_1x_2x_3 + s_1 + s_2 + s_3\); for simplicity, we ignore the additive terms in this overview, as they are easy to handle. As with [2], the starting point of our construction is the BGW protocol for computing \(x_1x_2x_3\). In BGW and also in ABT, the parties (i) multiply Shamir shares of \(x_2,x_3\) for threshold t, (ii) perform degree reduction to obtain Shamir shares of \(x_2x_3\) for threshold t, (iii) multiply the ensuing shares by that of \(x_1\) to obtain Shamir shares of \(x_1x_2x_3\) for threshold 2t, (iv) interpolate the shares to recover \(x_1x_2x_3\). Our construction replaces steps (ii) and (iii) with a completely different gadget.
MPRE. A (n, t)-MPRE [2] for a n-party functionality \(f(\mathbf {x}_1,\ldots ,\mathbf {x}_n)\) is a randomized function \(\hat{f}(\mathbf {x}_1,\ldots ,\mathbf {x}_n;\mathbf {r}_1,\ldots ,\mathbf {r}_n)\) with the following properties:
-
(correctness). There exists an efficient decoder \(\mathsf {Dec}\) such that for all \(\mathbf {x} = (\mathbf {x}_1,\ldots ,\mathbf {x}_n), \mathbf {r} = (\mathbf {r}_1,\ldots ,\mathbf {r}_n)\),
$$\begin{aligned} \mathsf {Dec}(\hat{f}(\mathbf {x}; \mathbf {r})) = f(\mathbf {x}) \end{aligned}$$ -
(security). We say that the MPRE is (selectively) secure against up to t corruptions if there exists a simulator \(\mathsf {Sim}\) such that for any \(\mathbf {x}_1,\ldots ,\mathbf {x}_n\) and any subset \(T \subseteq [N], |T| \le t\),
$$ \mathsf {Sim}(f(\mathbf {x}_1,\ldots ,\mathbf {x}_n), \mathbf {x}_T) \approx \Bigl ( \hat{f}(\mathbf {x}_1,\ldots ,\mathbf {x}_n;\mathbf {r}_1,\ldots ,\mathbf {r}_n), \mathbf {r}_T \Bigr ) $$by distribution, where \(\mathbf {r}_1,\ldots ,\mathbf {r}_n\) on the right side are random, and \(\mathbf {x}_T \mathrel {:=}(\mathbf {x}_i : i \in T ),\mathbf {r}_T \mathrel {:=}(\mathbf {r}_i : i \in T)\).
-
(effective degree). We say that a MPRE has effective degree d if there exists functions \(h_1,\ldots ,h_n\) such that \(\hat{f}\) can be expressed as a degree d function of \(h_1(\mathbf {x}_1,\mathbf {r}_1),\ldots ,h_n(\mathbf {x}_n,\mathbf {r}_n)\). The functions \(h_i\) capture pre-computation on the local input \(\mathbf {x}_i\) and randomness \(\mathbf {r}_i\) of party \(P_i\).
In this work, we think of \(\mathbf {x}_1,\ldots ,\mathbf {x}_n,\mathbf {r}_1,\ldots ,\mathbf {r}_n\) as vectors over some field \(\mathbb {F}\). In addition, we define the following new properties:
-
We say that an MPRE is adaptively secure if the adversaries can adaptively decide which party to corrupt next, based on the encoding and/or local input and randomness of previously corrupted parties. Correspondingly, simulation is done in an “online” fashion using the output and/or inputs of already corrupted parties.
-
We extend MPRE security with leakage: Each party \(P_i\) is associated with a leakage function \(L_i\). If \(P_i\) is corrupted, the simulator will get \(L_i(\mathbf {x}_1,\dots ,\mathbf {x}_n)\) in addition to \(\mathbf {x}_i\). Unless otherwise specified, the leakage function \(L_i\) simply outputs \(\perp \).
MPRE with leakage is the key notion that captures our main gadget which uses preprocessing to reduce the degree of IK randomized polynomials from 3 to 2. This notion is also new to this work.
2.1 Our Basic Construction
Main gadget. Our main gadget is MPRE for the 4-party functionality
with the following properties:
-
(I)
it has effective degree 2;
-
(II)
tolerates any number of corruptions with leakage \(L_4((x,\mu ),a,b,\bot ) = (a,b)\).
To build this gadget, we start with the IK02 randomized encoding for \(xab + \mu \) where

As a quick warm-up, observe that we can have \(P_4\) sample all of the randomness \(w_1,w_2,w_3,w_4,w_5\). This achieves effective degree 2, but with leakage \(L_4((x,\mu ),a,b,\bot ) = (x,a,b,\mu )\). We show that by distributing the randomness more cleverly, we can reduce the leakage upon corruption of \(P_4\) to just a, b while preserving effective degree 2.
In particular, we will crucially rely on the fact that the randomized encoding contains exactly one monomial \(w_1w_5x\) of degree 3. In our MPRE,
-
\(w_2,w_3,w_4\) are shared additively, \(w_i = w_i^{(1)} + w_i^{(4)}\), between \(P_1\) and \(P_4\) (if both \(P_1\) and \(P_4\) are corrupted, then the adversary already learns all inputs \(x,a,b,\mu \));
-
\(P_4\) samples \(w_1,w_5\) and pre-computes \(w_1w_5\) so that the encoding has effective degree two.
In summary, the MPRE computes the following in effective degree 2:

To handle corruption of \(P_4\) in the analysis of the MPRE, we crucially rely on the fact that we can simulate the randomized encoding together \(w_1,w_5\) given \((xab+\mu , a, b)\). To see this, observe that given a simulated encoding \(\varPi \) and a, b, one can compute matching \(w_1=\varPi [1,1]+a\) and \(w_5 = \varPi [3,3]+b\).
MPRE for \(x_1x_2x_3\) with OLE correlations. A two-party OLE correlation over \(\mathbb {F}\) is a pair
Observe that in the IK02 randomized encoding Eq. (1), multiplication of input elements a and b is replaced with multiplication of random elements \(w_1\) and \(w_5\). If assuming OLE correlation between \(P_2,P_3\), the IK02 encoding can be computed in degree 2, without any leakage to \(P_4\) (in fact there is no need for \(P_4\) at all). This gives an effective degree 2 MPRE for computing the 3-party functionality
-
\(P_2\) and \(P_3\) hold \((w_1,b^{(1)}),(w_5,b^{(5)})\) such that \(b^{(1)} + b^{(5)} = w_1w_5\);
-
\(w_2,w_3,w_4\) are shared additively between \(P_1,P_2,P_3\).
Then the encoding computes the following in effective degree 2:

Since every degree-3 polynomial can be expanded into a sum of degree-3 monomials, we immediately obtain a degree-2 MPRE for computing general degree-3 polynomials, by computing independent MPRE for each degree-3 monomial.
Lemma 1
(MPRE for Degree-3, Honest Minority). There exists an adaptively secure MPRE for degree-3 polynomials with effective degree 2 in the OLE-correlation model, for \(t \le n\).
MPRE for \(x_1x_2x_3\) for honest majority. Next, we build a n-party MPRE with effective degree 2 for
tolerating \(t < n/2\) corruptions, as long as \(|\mathbb {F}| > n\) (without any leakage). For simplicity, we consider the setting where \(P_1\) is never corrupted. Following the overview,
-
\(P_2\) samples a random degree-t polynomial \(Q_2\) such that \(Q_2(0) = x_2\).
-
Similarly, \(P_3\) samples \(Q_3\) with \(Q_3(0) = x_3\).
-
\(P_1\) samples a random degree-\((n-1)\) polynomial Z such that \(Z(0) = 0\).
Now, consider the polynomial
Observe that Y has degree at most \(n-1\), and satisfies \(Y(0) = x_1 x_2 x_3\). Then, for each \(i=1,2,\ldots ,n\), parties \(P_1,P_2,P_3,P_i\) run the gadget MPRE to compute
The output party can recover \(Y(0) = x_1x_2x_3\) given \(Y(1),\ldots ,Y(n)\) via polynomial interpolation. In summary, the MPRE is the parallel composition of n gadget MPRE and hence have effective degree 2.
We can in fact prove security of this MPRE for up to \(t < n/2\) corruptions, as long as \(P_1\) is not corrupted. We sketc.h the security proof for the setting where the last t parties \(P_{n-t+1},\ldots ,P_n\) are corrupted:
-
We can simulate the encoding by sampling a random degree \(n-1\) polynomial Y whose constant term is \(x_1x_2x_3\), thanks to the randomization via Z;
-
To simulate the view of the last t parties, security of the gadget MPRE tells us that it suffices to simulate \(Q_2(i), Q_3(i), i=n-t+1,\ldots ,n\). By the security of Shamir’s secret sharing, these are just a collection of uniformly random field elements, and leaks no additional information to the adversary.
More generally, \(P_1\) may be corrupted, at which point \(x_1\) and the polynomial Z are revealed. To ensure privacy of \(x_2, x_3\) in this case, we need to modify the polynomial to \(Y \mathrel {:=}x_1Q_2Q_3 + Z + S\), with an additional random degree-\((n-1)\) polynomial S jointly sampled by all parties, with \(P_i\) sampling S(i) at random. To recover the output \(x_1x_2x_3\), the parties additionally compute S(0), which is a linear function over local inputs.
Since MPRE for computing degree-3 monomials gives MPRE for general degree-3 polynomials, we obtain
Lemma 2
(MPRE for Degree-3, Honest Majority). There exists an adaptively secure MPRE for degree-3 polynomials with effective degree 2 in the plain model, for \(t < n/2\).
Handling Adaptive Corruptions. All our MPRE schemes introduced so far have perfect information theoretic security. In later sections, we construct an efficient and stateful simulator for simulating the view of adaptive adversaries. In particular, the simulator \(\mathsf {Sim}\) can be decomposed into a stateful two-subroutine simulator \(({\textsf {SimO}},{\textsf {SimI}})\) in which \({\textsf {SimO}}(f(\mathbf {x}_1,\ldots ,\mathbf {x}_n))\) simulates the encoding \(\hat{f}(\mathbf {x}_1,\ldots ,\mathbf {x}_n; \mathbf {r}_1,\ldots , \mathbf {r}_n)\), and \({\textsf {SimI}}(i, \mathbf {x}_i)\) simulates \(\mathbf {r}_i\), in the order that the adaptive adversary corrupts parties.
Putting Pieces Together for \(\mathbf{NC }^{\mathbf{1}}\). Given an MPRE for computing degree-3 polynomials in a model (the OLE correlation model or in the plain model with honest majority), we can “lift” it to handle arithmetic \(\mathbf{NC }^{\mathbf{1}}\) computation in the same model, while preserving the effective degree. The IK02 randomized encoding [20] for arith-NC1 allows for transforming a function g in \(\mathbf{NC }^{\mathbf{1}}\) by a degree-3 polynomial \(\hat{g}\), such that, \(\hat{g}(\mathbf {x}_1, \cdots \mathbf {x}_n \; ; \; \mathbf {r})\) reveals only \(g(\mathbf {x}_1, \cdots , \mathbf {x}_n)\) and nothing else. This means it suffices to compute the following n-party degree-3 functionality where randomness \(\mathbf {r}\) is additively shared among all parties.
The above is an effective-degree-3 MPRE for arithmetic \(\mathbf{NC }^{\mathbf{1}}\). We further reduce the effective degree to 2, by computing the effective-degree-3 MPRE using the effective-degree-2 MPREs for degree 3 polynomials.
Lemma 3
(MPRE for Arith-NC1). There exist adaptively secure MPRE for arith-NC1 with effective degree 2 in the OLE-correlation model for any number \(t \le n\) of corruptions, and in the plain model for \(t < n/2\).
Finally, to obtain 2-round MPC for arith-NC1, we compute the effective-degree-2 MPRE using 2-round MPC for degree-2 polynomials. In the honest majority model, the BGW protocol has only 2 rounds when computing degree-2 polynomials. In the OLE correlation model, we design a very simple 2-round protocol for computing degree-2 polynomials.
Extension to Circuits. Starting from Yao’s garbled circuits, we can get a \((n-1)\)-private MPRE for P/poly with effective degree 3 that makes black-box use of a PRG G, using the techniques introduced in [4, 13]. For simplicity, consider garbling a single gate g with input wire u, v and output wire o. For each input/output wire j, each party \(P_i\) samples a pair of PRG seeds \(s^{(i)}_{j,0},s^{(i)}_{j,1}\) corresponding the wire having value 0 or 1; the two labels for wire j is then set to \(\ell _{j,b} = s^{(1)}_{j,b} \Vert \dots \Vert s^{(n)}_{j,b}\). To hide the labels of the output wire o, each party locally expands their seeds through G, and hide label \(\ell _{o,g(a,b)}\) using the XOR of PRG outputs from all parties. For instance,
where \(G_d\) for \(d =0\) or 1 outputs the first or second half of the PRG output bits respectively, and \(d, d'\) are set so that the same output bit is never reused. These table entries are further randomly permuted using mask bits \(k_{u}, k_{v}\) which are additively shared among all parties. The computed encoding is secure as long as one party remains uncorrupted. The computation makes black-box use of the PRG and has effective degree 3 after pre-processing of form:
We can then combine this with our MPRE for degree-3 polynomials with effective degree 2 (over a sufficiently large field extension of \(\mathbb {F}_2\)).
Lemma 4
(MPRE for P/poly). There exist adaptively secure MPRE for P/poly with effective degree 2 in the OLE-correlation model for any number \(t \le n-1\) of corruptions, and in the plain model for \(t < n/2\). The scheme makes black-box use of a PRG.
2-round MPC protocols for P/poly in the same models then follow.
3 Preliminaries and Definitions
For any positive integer n, define \([n] \mathrel {:=}\{1,2,\ldots ,n\}\). For any set \(S \subseteq [n]\) and vector \(\mathbf {x} = (\mathbf {x}_1,\ldots ,\mathbf {x}_n)\), where \(\mathbf {x}_i\) itself can be a vector, let \(\mathbf {x}[S]\) denote the indexed set \((\mathbf {x}_i)_{i\in S}\). Let \(\mathbb {F}\) denote a finite field, and \(\otimes \) tensor product.
3.1 MPC Protocols
Definition 1
(Functionality). An n-party functionality is a function \(f:\mathcal {X}_1\times \ldots \times \mathcal {X}_n \rightarrow \mathcal {Y}\), where \(\mathcal {X}_i\) is the i-th party’s input domain and \(\mathcal {Y}\) is the output space.
Definition 2
(MPC Protocol). An r-rounds MPC protocol \(\varPi \) for a n-party functionality f consists of n algorithms \((C_{i})_{i \in [n]}\). An execution of \(\varPi \) with inputs \(\mathbf {x} = (\mathbf {x}_1, \ldots , \mathbf {x}_n) \in \mathcal {X}_1 \times \ldots \times \mathcal {X}_n\) and security parameter \(1^\lambda \) proceeds as follows:
-
Randomness. Each party \(P_i\) samples local randomness \(\mathbf {r}_i \leftarrow \mathcal {R}_i\), where \(\mathcal {R}_i\) is the local randomness space of the \(P_i\). It initializes its state as \(\mathsf {st}^{(0)}_i = (\mathbf {x}_i,\mathbf {r}_i)\).
-
Round. \(1 \le j \le r\): Every party \(P_i\) computes \((m_{i\rightarrow 1}^{(j)},\cdots , m_{i\rightarrow n}^{(j)}) \leftarrow C_i(1^\lambda , \mathsf {st}^{(j-1)}_{i})\). For every \(i' \in [n] \setminus \{i\}\), \(P_i\) sends message \(m_{i\rightarrow i'}^{(j)}\) to party \(P_{i'}\), and receives message \(m_{i'\rightarrow i}^{(j)}\) from party \(P_{i'}\). It updates its state \(\mathsf {st}^{({j})}_i = (\mathsf {st}^{({j-1})}_i, (m_{i'\rightarrow i}^{(j)})_{i' \in [n] \setminus \{i\}})\).
-
Output: After r rounds, every party \(P_i\) computes \(\mathbf {y}_i \leftarrow C_i(1^\lambda , \mathsf {st}^{(r_i)})\), and outputs \(\mathbf {y}_i\).
Define the view of party \(P_i\) in the above execution to be \(\textsc {View}_\varPi (1^\lambda , \mathbf {x})[i] = \mathsf {st}^{(r)}_i = (\mathbf {x}_i,\mathbf {r}_i, (m_{i'\rightarrow i}^{(j)})_{i'\in [n] \setminus \{i\}, j \in [r]})\). Let \(\textsc {View}_\varPi (1^\lambda , \mathbf {x})\) denote the array of views of all parties.
We also consider MPC protocol that relies on correlated randomness. If the MPC protocol relies on correlated randomness, which is a distribution \(\mathcal {D}\) over \(\mathcal {R}'_1\times \dots \times \mathcal {R}'_n\), then in each execution of the protocol, \((\mathbf {r}_1',\dots ,\mathbf {r}'_n) \leftarrow \mathcal {D}\) is sampled by the beginning of the protocol, and each party \(P_i\) initialize its state as \(\mathsf {st}^{(0)}_i = (\mathbf {x}_i,\mathbf {r}_i,\mathbf {r}'_i)\).
Below, we suppress the appearance of the security parameter \(1^\lambda \), which is assumed implicitly.
Remark 1
We remark that the above definition considers the same output for all parties. It can be generalized to the case where each party has a different output. From a protocol design point of view, it is without loss of generality to consider a common output: To compute function f mapping \(\mathbf {x}_1, \ldots , \mathbf {x}_n\) to different outputs \(\mathbf {y}_1, \ldots , \mathbf {y}_n\), every party \(P_i\) can sample a one-time pad \(\mathbf {k}_i\) of appropriate length and jointly compute the augmented functionality mapping \((\mathbf {x}_1, \mathbf {k}_1), \ldots , (\mathbf {x}_n, \mathbf {k}_n)\) to \((\mathbf {y}_1 + \mathbf {k}_1), \ldots , (\mathbf {y}_n + \mathbf {k}_n)\), where \(\mathbf {k}_i\)’s and \(+\) should be defined appropriately for the specific functionality f. For instance, if f is a Boolean computation, \(\mathbf {k}_i\)’s should be random strings and \(+\) is XOR, and if f is an arithmetic computation over a finite field, \(\mathbf {k}_i\)’s should be random vectors and \(+\) over the field.
Definition 3
(MPC Correctness). A protocol \(\varPi \) for a functionality \(f:\mathcal {X}_1\times \ldots \times \mathcal {X}_n \rightarrow \mathcal {Y}\) is perfectly or statistically correct, if for every input tuple \(\mathbf {x} \in \mathcal {X}_1\times \ldots \times \mathcal {X}_n\) and every security parameter \(\lambda \in \mathbb {N}\), the output of every party \(P_i\) equals \(f(x_1,\ldots ,x_n)\), with probability 1 or with overwhelming probability respectively.
Definition 4
(Semi-honest Security Against Static Corruption). A protocol \(\varPi \) for a n-party functionality f is perfectly, or statistically, or computationally semi-honest secure against t-corruption, if there is a PPT simulator \(\mathsf {Sim}\), such that for every subset \(T \subseteq [n]\) of at most t parties, input tuple \(\mathbf {x}\), it holds that the real views \(\textsc {View}_\varPi (\mathbf {x})[T]\) of parties in T and the output of the simulator \(\mathsf {Sim}(T,\mathbf {x}[T], f(\mathbf {x}))\) are identically distributed, or statistically close, or computationally indistinguishable respectively.
Semi-honest Adaptive Security. In the adaptive corruption model, a semi-honest adversary is allowed to choose which party to corrupt next adaptively (up to t corruptions) depending on its current view, which includes the views of previously corrupted parties. Correspondingly, the simulator for adaptive adversaries is an interactive stateful algorithm that responds to adversary’s corruption requests with simulated views, generated from the inputs and output of corrupted parties.
Definition 5
(Semi-honest Security Against Adaptive Corruption.). A protocol \(\varPi \) for a n-party functionality f is perfectly, or statistically, or computationally semi-honest adaptively secure against t-corruption, if there is a PPT interactive and stateful simulator \(\mathsf {Sim}\), such that, for every adversary \(\mathcal {A}\) (PPT in the computational setting, computationally unbounded otherwise), input tuple \(\mathbf {x}\), the outputs of the following two experiments are identically distributed, or statistically close, or computationally indistinguishable respectively.
-
In the real world: The challenger runs an execution of \(\varPi \) on input \(\mathbf {x}\) using fresh randomness, obtaining parties’ views \(\textsc {View}_\varPi (\mathbf {x})\). The adversary \(\mathcal {A}\) adaptively and iteratively queries \({\textsf {Corrupt}}(i)\), and receives \(P_i\)’s view \(\textsc {View}_\varPi (\mathbf {x})[i]\), up to at most t corruptions. Return \(\mathcal {A}\)’s output.
-
In the simulation: Proceed identically as in the real world, except that upon \(\mathcal {A}\)’s request \({\textsf {Corrupt}}(i)\), invoke the simulator \((\widetilde{\textsc {View}}[i], \mathsf {st}) \leftarrow \mathsf {Sim}(i, \mathbf {x}_i, y, \mathsf {st})\) and sends \(\widetilde{\textsc {View}}[i]\) to \(\mathcal {A}\), where \(\mathsf {st}\) is initialized to be empty.
3.2 (Multi-party) Randomized Encoding
Definition 6
(Randomized Encoding [3, 20]). Let \(f:\mathcal {X}\rightarrow \mathcal {Y}\) be some function. The randomized encoding of f is a function  , where \(\mathcal {R}\) is the randomness space. A randomized encoding should be both correct and private.
, where \(\mathcal {R}\) is the randomness space. A randomized encoding should be both correct and private.
-
Correctness. There is a decoding function \(\mathsf {Dec}\) such that for all \(x\in \mathcal {X}, r\in \mathcal {R}\), it holds that
$$ \mathsf {Dec}(\hat{f}(x;r)) = f(x). $$ -
Privacy. There exists a efficient randomized simulation algorithm \(\mathsf {Sim}\) such that for any \(x\in \mathcal {X}\), the distribution of \(\mathsf {Sim}(f(x))\) is identical to that of \(\hat{f}(x;r)\). The privacy can be relaxed to statistical privacy (resp. computational privacy), if the \(\mathsf {Sim}(f(x))\) and \(\hat{f}(x;r)\) are statistically close (resp. computational indistinguishable).
Definition 7
(Multi-party Randomized Encoding [2]). Let \(f:\mathcal {X}_1\times \dots \times \mathcal {X}_n \rightarrow \mathcal {Y}\) be some n-party functionality. A multi-party randomized encoding (MPRE) of f consists of
-
Input space \(\mathcal {X}= \mathcal {X}_1\times \dots \times \mathcal {X}_n\) and output space \(\mathcal {Y}\);
-
Local randomness space \(\mathcal {R}_i\) for \(i\in [n]\); Correlated randomness space \(\mathcal {R}'_1\times \dots \times \mathcal {R}'_n\) together with a distribution \(\mathcal {D}\) over it;
-
Local preprocessing function
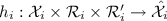 ;
; -
Encoding function
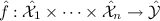 , the degree of \(\hat{f}\) is called the effective degree of this MPRE.
, the degree of \(\hat{f}\) is called the effective degree of this MPRE.
Such that for any input \((x_1,\ldots ,x_n)\), the encoding \(\hat{f}\bigl (h_1(x_1,r_1,r'_1),\dots ,h_n(x_n,r_n,r'_n)\bigr )\) represents \(y = f(x_1,\ldots ,x_n)\) in the following sense:
Correctness. There exists a decoding function  , such that for any input \((x_1,\ldots ,x_n) \in \mathcal {X}_1\times \dots \times \mathcal {X}_n\), randomness \((r_1,\dots ,r_n) \in \mathcal {R}_1\times \dots \times \mathcal {R}_n\) and correlated randomness \((r'_1,\ldots ,r'_n)\) in the support of \(\mathcal {D}\), the corresponding encodings \(\hat{y} = \hat{f}(h_1(x_1,r_1,r'_1),\dots ,h_n(x_n,r_n,r'_n))\) satisfies that \(f(x_1,\ldots ,x_n) = \mathsf {Dec}(\hat{y})\).
, such that for any input \((x_1,\ldots ,x_n) \in \mathcal {X}_1\times \dots \times \mathcal {X}_n\), randomness \((r_1,\dots ,r_n) \in \mathcal {R}_1\times \dots \times \mathcal {R}_n\) and correlated randomness \((r'_1,\ldots ,r'_n)\) in the support of \(\mathcal {D}\), the corresponding encodings \(\hat{y} = \hat{f}(h_1(x_1,r_1,r'_1),\dots ,h_n(x_n,r_n,r'_n))\) satisfies that \(f(x_1,\ldots ,x_n) = \mathsf {Dec}(\hat{y})\).
Semi-honest Adaptive t-Privacy. The MPRE is perfectly (resp. statistically or computationally) secure against t adaptive corruptions if there exists an adaptive simulator such that the following real world and ideal world are perfectly (resp. statistically or computationally) indistinguishable.
In both the real world and the ideal world, the distinguisher first chooses input \(\mathbf {x} = (x_1,\ldots ,x_n)\), and sends it to the challenger. Then the distinguisher can make queries and tries to guess which world it is.
-
In the real world: The distinguisher chooses input \(\mathbf {x} = (x_1,\ldots ,x_n)\), and sends it to the challenger. The challenger samples local randomness \(r_i\leftarrow \mathcal {R}_i\) for each \(i\in [n]\) and correlated randomness \((r'_1,\ldots ,r'_n) \leftarrow \mathcal {D}\); computes \(\hat{x}_i = h_i(x_i,r_i,r'_i)\) for \(i\in [n]\) and \(\hat{y} = \hat{f}(\hat{x}_1,\dots ,\hat{x}_n)\). In short, the challenger follows the protocol. The challenger allows the distinguisher to adaptively query the following two oracles. The later one can be queried up to t times.
-
Upon CorruptO: Output \(\hat{y}\)
-
Upon CorruptI(i): Output \(r_i, r'_i\).
-
-
In the ideal world: The distinguisher chooses input \(\mathbf {x} = (x_1,\ldots ,x_n)\), and sends it to the challenger. The challenger does nothing other than stores the input. The queries are answered by the simulator, which is a randomized stateful algorithm (SimO,SimI).
The challenger allows the distinguisher to adaptively query the following two oracles. The later one can be queried up to t times.
-
Upon CorruptO: Compute \(y=f(\mathbf {x})\) and output whatever SimO(y) outputs.
-
Upon CorruptI(i): Output what is output by SimI\(\mathrm{(}i,x_i\mathrm{)}\).
-
3.3 Composition of MPREs
If there is a MPRE for f whose encoding function is \(\hat{f}\), together with a MPRE for \(\hat{f}\) whose encoding function is  . Then Theorem 1 shows that they can be composed as a MPRE for f whose encoding function is
. Then Theorem 1 shows that they can be composed as a MPRE for f whose encoding function is  . Theorem 1 is adaptive version of Lemma 3.3 and 3.4 in [2]. Such composition is useful when
. Theorem 1 is adaptive version of Lemma 3.3 and 3.4 in [2]. Such composition is useful when  is simpler than \(\hat{f}\).
is simpler than \(\hat{f}\).
If there are MPREs for \(f_1,f_2\). W.l.o.g., assume their input domain are the same. Then Theorem 2 shows that they can be composed as a MPRE for the functionality
while preserving the complexity.
Theorem 1 (Sequential Composition)
Assume there is a perfectly (resp. statistically or computationally) adaptively t-private MPRE for functionality \(f:\mathcal {X}_1\times \dots \times \mathcal {X}_n\rightarrow \mathcal {Y}\), whose encoding function is \(\hat{f}:\hat{\mathcal {X}}_1\times \dots \times \hat{\mathcal {X}}_n\rightarrow \hat{\mathcal {Y}}\). Assume there is a perfectly (resp. statistically or computationally) adaptively t-private MPRE for \(\hat{f}\), whose encoding function is  . Then there exists a perfectly (resp. statistically or computationally) adaptively t-private MPRE for f whose encoding function is
. Then there exists a perfectly (resp. statistically or computationally) adaptively t-private MPRE for f whose encoding function is  .
.
Theorem 2 (Parallel Composition)
For each \(j\in [m]\), assume there is a perfectly (resp. statistically or computationally) adaptively t-private MPRE for functionality \(f^{(j)}:\mathcal {X}_1\times \dots \times \mathcal {X}_n\rightarrow \mathcal {Y}^{(j)}\), whose encoding function is \(\hat{f}^{(j)}:\hat{\mathcal {X}}_1^{(j)}\times \dots \times \hat{\mathcal {X}}_n^{(j)}\rightarrow \hat{\mathcal {Y}}^{(j)}\). Then there exists a perfectly (resp. statistically or computationally) adaptively t-private MPRE for f whose encoding function is \(\hat{f}\), where f concatenate the outputs of \(f^{(1)},\dots ,f^{(m)}\)
and \(\hat{f}\) is the concatenation of \(\hat{f}^{(1)},\dots ,\hat{f}^{(m)}\).
Additionally, if the MPRE for \(f^{(j)}\) has leakage \(l_i^{(j)}:\mathcal {X}_1\times \dots \times \mathcal {X}_n\rightarrow \mathcal {L}_i^{(j)}\) to \(P_i\) for \(i\in [n],j\in [m]\), then the resulting MPRE has leakage \(l_i:\mathcal {X}_1\times \dots \times \mathcal {X}_n\rightarrow \mathcal {L}_i^{(1)}\times \dots \times \mathcal {L}_i^{(m)}\),
to the i-th party.
The proof of composition theorems are defered to the full version.
4 MPRE for Degree-3 Polynomials
In this section, we build MPRE for degree-3 polynomials in two settings: (i) honest majority, and (ii) OLE correlations. Our road-map is as follows: In Sect. 4.1, we construct a 4-party gadget MPRE; in Sect. 4.2, we construct an MPRE for the 3-party functionality \(\mathsf {3MultPlus}_3\) described below, which computes a degree-3 monomial shifted by some linear terms, in the OLE-correlation model; then in Sect. 4.3, we consider the n-party version of the functionality \(\mathsf {3MultPlus}_n\) and construct an MPRE for it in the honest majority setting.

Finally, \(\mathsf {3MultPlus}\) is complete in the sense that MPRE for the \(\mathsf {3MultPlus}\) functionalities implies MPRE for general degree-3 functionalities. The proof can be found in the full version. All our MPRE have effective degree 2.
4.1 Our 4-Party Gadget MPRE with Leakage
Fix a field \(\mathbb {F}\). We begin with a MPRE with leakage for the following 4-party gadget function
For randomly sampled \(w_1,\ldots ,w_5\), [19, 20] show that \((\phi _1,\ldots ,\phi _6)\) is a randomized encoding of \(abx + \mu + \nu \), where \(\phi _1,\ldots ,\phi _6\) are defined as

[19, 20] guarantee that \(\phi _1,\ldots ,\phi _5\) are i.i.d. uniform despite the value of \((a, b, x, \mu , \nu )\). We would like to transfer this randomized encoding into an effective degree-2 MPRE with leakage.
Lemma 5
The scheme defined in Fig. 3 is an MPRE for the following 4-party gadget function
with the following properties:
-
(I)
it has effective degree 2;
-
(II)
tolerates any number of corruptions with leakage \(L_4((x,\mu ),a, b,\nu ) = (a,b)\).
Proof
The correctness is straight forward. The decoding function is the determinant of the matrix in (3), thus
For the adaptive privacy, we need to define the simulator.
-
In the real world: For input \(x, a, b, \mu , \nu \)
-
At the outset: Sample random \(w_1,w_3,w_5,w_2',w_2'',w_4',w_4''\), compute \(w_2 = w_2'+w_2''\), \(w_4 = w_4'+w_4''\), compute \((\phi _1,\ldots ,\phi _6)\) according to Eq. (3).
-
\({\textsf {CorruptO}}\): Output \(\phi _1,\ldots ,\phi _6\).
-
\({\textsf {CorruptI}}(1)\): Output \(w_3,w_2',w_4'\).
-
\({\textsf {CorruptI}}(2)\): Output \(\bot \).
-
\({\textsf {CorruptI}}(3)\): Output \(\bot \).
-
\({\textsf {CorruptI}}(4)\): Output \(w_1,w_5,w_2'',w_4''\).
-
-
In the ideal world:
-
At the Outset: Sample random \(\phi _1,\ldots ,\phi _5\),
-
Upon \({\textsf {CorruptO}}\), \({\textsf {SimO}}(y)\): Let \(\phi _6\) be the unique value that \(\det \left[ {\begin{matrix} \phi _1 &{} \phi _2 &{} \phi _6 \\ -1 &{} \phi _3 &{} \phi _4 \\ &{} -1 &{} \phi _5 \end{matrix}}\right] = y\). Output \(\phi _1,\ldots ,\phi _6\).
-
Upon \({\textsf {CorruptI}}(1)\), \({\textsf {SimI}}(1,(x,\mu ))\): Set \(w_3\) as the unique value that \(\phi _3 = x-w_3\).
If \(P_4\) is not corrupted yet, sample \(w_2',w_4'\) at random.
If \(P_4\) is already corrupted, subroutine \({\textsf {SimI}}(4,\nu ,(a,b))\) has learned a and has sampled the values of \(w_1, w_5\). Then, set \(w_2,w_4\) to satisfy \(\phi _2 = a w_3 + xw_1 - w_3w_1 -w_2\), \(\phi _4 = - w_4 + w_5 x\), and set \(w_2' = w_2 - w_2''\), \(w_4' = w_4 - w_4''\).
Output \(w_3,w_2',w_4'\).
-
Upon \({\textsf {CorruptI}}(2)\), \({\textsf {SimI}}(2,a)\): Output \(\bot \).
-
Upon \({\textsf {CorruptI}}(3)\), \({\textsf {SimI}}(3,b)\): Output \(\bot \).
-
Upon \({\textsf {CorruptI}}(4)\), \({\textsf {SimI}}(4,\nu ,(a,b))\): Set \(w_1,w_5\) to satisfy \(\phi _1 = a -w_1\), \(\phi _5 = b - w_5\).
If \(P_1\) is not corrupted yet, sample \(w_2'',w_4''\) at random.
If \(P_1\) is already corrupted, subroutine \({\textsf {SimI}}(1,(x,\mu ))\) has learned x and has sampled the value of \(w_3\). Then, set \(w_2,w_4\) to satisfy \(\phi _2 = a w_3 + xw_1 - w_3w_1 -w_2\) and \(\phi _4 = - w_4 + w_5 x\), set \(w_2'' = w_2 - w_2'\), \(w_4'' = w_4 - w_4'\).
Output \(w_1,w_5,w_2'',w_4''\).
-
To formally show that adversary cannot distinguish between the real world and the ideal world, we introduce a middle world.
-
In the middle world:
-
At the Outset: Sample random \(\phi _1,\ldots ,\phi _5\).
Let \(\phi _6\) be the unique value that \(\det \left[ {\begin{matrix} \phi _1 &{} \phi _2 &{} \phi _6 \\ -1 &{} \phi _3 &{} \phi _4 \\ &{} -1 &{} \phi _5 \end{matrix}}\right] = abx + \mu + \nu \).
Solve \(w_1,\ldots ,w_5\) from Eq. (3). Sample \(w_2',w_2''\) as additive sharing of \(w_2\), Sample \(w_4',w_4''\) as additive sharing of \(w_4\).
-
\({\textsf {CorruptO}}\): Output \(\phi _1,\ldots ,\phi _6\).
-
\({\textsf {CorruptI}}(1)\): Output \(w_3,w_2',w_4'\).
-
\({\textsf {CorruptI}}(2)\): Output \(\bot \).
-
\({\textsf {CorruptI}}(3)\): Output \(\bot \).
-
\({\textsf {CorruptI}}(4)\): Output \(w_1,w_5,w_2'',w_4''\).
-
The real world is indistinguishable from the middle world, due to the security of the randomized encoding in (3).
Comparing the ideal world with the middle world, the only difference is that the computation is deferred in the ideal world: Same as the real world, the simulator in the ideal samples random \(\phi _1,\ldots ,\phi _5\). But the simulator cannot compute \(w_1, \dots , w_5\) at the beginning as it doesn’t know \(a,b,x,\mu ,\nu \) at that moment. Instead, the simulator compute each of \(w_1, \dots , w_5\) once it has the necessary information, using exactly the method as the middle world (i.e. by solving (3)). Thus the ideal world is also indistinguishable from the middle world.
4.2 MPRE for 3-Party \(\mathsf {3MultPlus}\) Using OLE Correlation
In this section, we construct an MPRE for the three party functionality
that has effective degree 2 and tolerates any number of corruptions in the OLE-correlation model.
For randomly sampled \(w_1,\ldots ,w_5\), [19, 20] show that \((\phi _1,\ldots ,\phi _6)\) is a randomized encoding of \(x_1x_2x_3 +\alpha + \beta + \gamma \), where \(\phi _1,\ldots ,\phi _6\) are defined as

[19, 20] guarantee that \(\phi _1,\ldots ,\phi _5\) are i.i.d. uniform despite the value of \((x_1,x_2,x_3, \alpha + \beta + \gamma )\). We would like to transfer this randomized encoding into an effective degree-2 MPRE using OLE correlated randomness.
Notice that \(w_1w_5x_2\) is the only degree-3 monomial in the randomized encoding, and \(w_1,w_5\) belong to the randomness of the randomized encoding. Thus if \(w_1,w_5\) are sampled from OLE correlated randomness, monomial \(w_1w_5x_2\) can be transferred into a degree-2 term. More precisely, let \((w_1,b^{(1)},w_5,b^{(3)})\in \mathbb {F}^4\) be sampled from OLE correlation, it holds that \(w_1w_5 = b^{(1)} + b^{(3)}\). The marginal distribution of \((w_1,w_5)\) is still uniform; and \(w_1w_5x_2\) equals \((b^{(1)} + b^{(3)}) x_2\), which is a degree-2 term. Then the randomized encoding has “effective” degree 2 as it can be computed from

Lemma 6
The MPRE in Fig. 4 for the 3-party functionality \(\mathsf {3MultPlus}_3\) has effective degree 2 and tolerates any number of corruptions, in the OLE-correlation model.
Proof
The correctness is straight forward,
For the adaptive privacy, we need to define the simulator.
-
In the real world: For input \(x_1,x_2,x_3,\alpha , \beta ,\gamma \)
-
At the Outset: Sample random \(w_1,w_5, w_2^{(1)},w_2^{(2)},w_2^{(3)}, w_3^{(1)},w_3^{(2)},w_3^{(3)},w_4^{(1)},w_4^{(2)},w_4^{(3)} \in \mathbb {F}\), sample random \(b^{(1)},b^{(3)}\) that \(b^{(1)}+b^{(3)} = w_1w_5\), compute \(w_2 = \sum _{i\in [3]}w_2^{(i)}\), \(w_3 = \sum _{i\in [3]}w_3^{(i)}\), \(w_4 = \sum _{i\in [3]}w_4^{(i)}\), compute \((\phi _1,\ldots ,\phi _6)\) according to Eq. (5).
-
\({\textsf {CorruptO}}\): Output \(\phi _1,\ldots ,\phi _6\).
-
\({\textsf {CorruptI}}(1)\): Output \(w_1,b^{(1)},w_2^{(1)},w_3^{(1)},w_4^{(1)}\).
-
\({\textsf {CorruptI}}(2)\): Output \(w_2^{(2)},w_3^{(2)},w_4^{(2)}\).
-
\({\textsf {CorruptI}}(3)\): Output \(w_5,b^{(3)},w_2^{(3)},w_3^{(3)},w_4^{(3)}\).
-
-
In the ideal world:
-
At the Outset: Sample random \(\phi _1,\ldots ,\phi _5\),
-
Upon \({\textsf {CorruptO}}\), \({\textsf {SimO}}(y)\): Let \(\phi _6\) be the unique value that \(\det \left[ {\begin{matrix} \phi _1 &{} \phi _2 &{} \phi _6 \\ -1 &{} \phi _3 &{} \phi _4 \\ &{} -1 &{} \phi _5 \end{matrix}}\right] = y\). Output \(\phi _1,\ldots ,\phi _6\).
-
Upon \({\textsf {CorruptI}}(1)\), \({\textsf {SimI}}(1,(x_1,\alpha ))\): Set \(w_1\) to satisfy \(\phi _1 = x_1 -w_1\).
If \(P_3\) is not corrupted yet, sample \(b^{(1)}\) at random.
If \(P_3\) is already corrupted, subroutine \({\textsf {SimI}}(3,(x_3,\gamma ))\) has set the values of \(w_5,b^{(3)}\). Set \(b^{(1)} = w_1w_5 - b^{(3)}\).
If both \(P_2\) and \(P_3\) are corrupted, subroutines \({\textsf {SimI}}(2,(x_2,\beta ))\), \({\textsf {SimI}}(3,(x_3,\gamma ))\) have set \(w_j^{(2)},w_j^{(3)}\) for \(j\in \{2,3,4\}\). Then solve \(w_2,w_3,w_4\) from Eq. (4) and set \(w_j^{(1)} = w_j - w_j^{(2)} - w_j^{(3)}\) for \(j\in \{2,3,4\}\).
If at least one of \(P_2,P_3\) is not corrupted yet, sample \(w_2^{(1)},w_3^{(1)},w_4^{(1)} \in \mathbb {F}\).
Output \(w_1,b^{(1)},w_2^{(1)},w_3^{(1)},w_4^{(1)}\).
-
Upon \({\textsf {CorruptI}}(2)\), \({\textsf {SimI}}(2,(x_2,\beta ))\): If both \(P_1\) and \(P_3\) are corrupted, subroutines \({\textsf {SimI}}(1,(x_1,\beta ))\), \({\textsf {SimI}}(3,(x_3,\gamma ))\) have set \(w_j^{(1)},w_j^{(3)}\) for \(j\in \{2,3,4\}\). Then solve \(w_2,w_3,w_4\) from Eq. (4) and set \(w_j^{(2)} = w_j - w_j^{(1)} - w_j^{(3)}\) for \(j\in \{2,3,4\}\).
If at least one of \(P_1,P_3\) is not corrupted yet, sample \(w_2^{(2)},w_3^{(2)},w_4^{(2)} \in \mathbb {F}\).
Output \(w_2^{(2)},w_3^{(2)},w_4^{(2)}\).
-
Upon \({\textsf {CorruptI}}(3)\), \({\textsf {SimI}}(3,(x_3,\gamma ))\): Set \(w_5\) to satisfy \(\phi _5 = x_3 - w_5\).
If \(P_1\) is not corrupted yet, sample \(b^{(3)}\) at random.
If \(P_1\) is already corrupted, subroutine \({\textsf {SimI}}(1,(x_1,\alpha ))\) has set the values of \(w_1,b^{(1)}\). Set \(b^{(3)} = w_1w_5 - b^{(1)}\).
If both \(P_1\) and \(P_2\) are corrupted, subroutines \({\textsf {SimI}}(1,(x_1,\beta ))\), \({\textsf {SimI}}(2,(x_2,\gamma ))\) have set \(w_j^{(1)},w_j^{(2)}\) for \(j\in \{2,3,4\}\). Then solve \(w_2,w_3,w_4\) from Eq. (4) and set \(w_j^{(3)} = w_j - w_j^{(1)} - w_j^{(2)}\) for \(j\in \{2,3,4\}\).
If at least one of \(P_1,P_2\) is not corrupted yet, sample \(w_2^{(3)},w_3^{(3)},w_4^{(3)} \in \mathbb {F}\).
Output \(w_5,b^{(3)},w_2^{(3)},w_3^{(3)},w_4^{(3)}\).
-
To show the indistinguishability between the real world and the ideal world, we introduce a middle world.
-
In the middle world: For input \(x_1,x_2,x_3, \alpha , \beta ,\gamma \)
-
At the Outset: Sample random \(\phi _1,\ldots ,\phi _5\).
Let \(\phi _6\) be the unique value that \(\det \left[ {\begin{matrix} \phi _1 &{} \phi _2 &{} \phi _6 \\ -1 &{} \phi _3 &{} \phi _4 \\ &{} -1 &{} \phi _5 \end{matrix}}\right] = y\). Solve \(w_1,\ldots ,w_5\) from Eq. (4).
Sample random \(b^{(1)},b^{(3)}\) that \(b^{(1)}+b^{(3)} = w_1w_5\). For each of \(j\in \{2,3,4\}\), sample random \(w_j^{(1)},w_j^{(2)},w_j^{(3)}\) that \(w_j^{(1)} + w_j^{(2)} + w_j^{(3)} = w_j\).
-
\({\textsf {CorruptO}}\): Output \(\phi _1,\ldots ,\phi _6\).
-
\({\textsf {CorruptI}}(1)\): Output \(w_1,b^{(1)},w_2^{(1)},w_3^{(1)},w_4^{(1)}\).
-
\({\textsf {CorruptI}}(2)\): Output \(w_2^{(2)},w_3^{(2)},w_4^{(2)}\).
-
\({\textsf {CorruptI}}(3)\): Output \(w_5,b^{(3)},w_2^{(3)},w_3^{(3)},w_4^{(3)}\).
-
The real world is indistinguishable from the middle world, due to the security of the randomized encoding in (3).
Comparing the ideal world with the middle world, the only difference is that the computation is deferred in the ideal world: Same as the real world, the simulator in the ideal samples random \(\phi _1,\ldots ,\phi _5\). But the simulator cannot compute \(w_1, \dots , w_5\) by solving (4) at the beginning as it doesn’t know \(x_1,x_2,x_3,\alpha , \beta ,\gamma \) at that moment. Instead, the simulator compute \(w_1\) once it knows \(x_1\); compute \(w_5\) once it knows \(x_3\); and compute \(w_2,w_3,w_4\) once it knows all the inputs. Thus the ideal world is also indistinguishable from the middle world.
4.3 MPRE for n-Party \(\mathsf {3MultPlus}\) with Honest Majority
We construct an MPRE (Fig. 5) for the n-party functionality
that has effective degree 2 and tolerates minority corruptions. The construction requires \(|\mathbb {F}| > n\).
Additional Notation. Let \(\mathbb {F}\) be a field that \(|\mathbb {F}|>n\), let \(1,\ldots ,n\) denote n distinct non-zero elements in \(\mathbb {F}\). Denote by \(\mathsf {\mathcal {P}}(t, m)\) the set of degree-t polynomials P with constant term m over \(\mathbb {F}\), so that \(Q \leftarrow \mathsf {\mathcal {P}}(t,m)\) refers to sampling a random degree-t polynomial Q whose constant term is m. In addition, \(m ={\text {rec}}(t, (i_1, \sigma _1) \dots , (i_{t+1},\sigma _{t+1}))\) denotes the procedure for reconstructing the constant term from \(t+1\) points on the polynomial via interpolation. For convenience, we also denote by \(\mathsf {\mathcal {P}}(t, m)\mid (i_1, \sigma _1) \dots , (i_{s},\sigma _{s})\) the set of polynomials \(Q \in \mathsf {\mathcal {P}}(t,m)\) such that \(Q(i_1) = \sigma _1,\ldots ,Q(i_s) = \sigma _{s}\), for \(s \le t+1\).
Protocol Overview. We decompose the computation of \(x_1x_2x_3 + \alpha + \beta + \gamma \), into two parts \(x_1 x_2 x_3 + z + s\) and \(\alpha + \beta + \gamma - z - s\) where z is sampled by \(P_1\) and s is jointly sampled by all n parties. Since the second term is linear, we focus on designing an MPRE for the first part.
-
\(P_1\) samples \(z \leftarrow \mathbb {F}, Z \leftarrow \mathsf {\mathcal {P}}(n-1,z)\).
-
\(P_2\) samples \(Q_2 \leftarrow \mathsf {\mathcal {P}}(t, x_2)\) and \(P_3\) samples \(Q_3 \leftarrow \mathsf {\mathcal {P}}(t, x_3)\).
-
\(P_i\) samples \(S(i) \leftarrow \mathbb {F}\), for every \(i \in [n]\).
Let \(s = {\text {rec}}(n-1,(1,S(1)),\ldots ,(n,S(n))\).
Observe that
Here, we rely on the fact that \(2t \le n-1\). Then, for each \(i=1,2,\ldots ,n\), parties \(P_1,P_2,P_3,P_i\) can run the gadget MPRE described in Sect. 4.1 to compute Y(i)
from which the output party can reconstruct Y and the constant term \(x_1x_2x_3 + z + s\).
Security Intuition. We can prove security of this protocol for up to \(t < n/2\) corruptions. Consider two cases: If \(P_1\) is not corrupted, or corrupted. In the first case, the view of the output party consists of \(\alpha +\beta +\gamma -z - s\), and a degree \(n-1\) polynomial Y with constant term \(x_1x_2x_3+z + s\), which is random thanks to the randomization via Z. Now, suppose the adversary additional corrupts t parties, excluding \(P_1\); call this set of parties T. Then, security of the gadget MPRE tells us that the adversary also learns \(\{ Q_2(i),Q_3(i),S(i) : i \in T \}\). Suppose for now \(2,3 \notin T\). By the property of Shamir’s secret sharing, this leaks no additional information about \(x_1,x_2,x_3\) to the adversary. Now, if \(2 \in T\), then the adversary also learns \(Q_2\), but that is okay since it already learns \(x_2\); the same argument applies to \(3 \in T\).
In the second case that \(P_1\) is corrupted and adversary learns \(x_1\) and all Z(i)’s, the polynomial Y is still a random degree-\((n-1)\) polynomial with constant term \(x_1x_2x_3+z + s\) thanks to the randomization via S. If the adversary corrupts at set T of t parties, including \(P_1\), and learns \(\{ Q_2(i),Q_3(i),S(i) : i \in T \}\), Shamir’s secret sharing, again protects \(x_2,x_3\) from being leaked to the adversary.
Protocol Specification. In short, the MPRE \(\hat{F}\) for \(x_1x_2x_3 + \alpha + \beta + \gamma \) simply computes n 4-party gadget MPRE,
together with the linear term \(\alpha +\beta +\gamma + z + s\). A formal description is in Fig. 5. It is easy to see that \(\hat{F}\) has effective degree 2 since \(\hat{f}\) has effective degree \(\le 2\).
Lemma 7
The MPRE scheme in Fig. 5 for the n-party functionality \(\mathsf {3MultPlus}_n\) has effective degree 2 and satisfies t-adaptive privacy for \(t < n/2\). The construction requires \(|\mathbb {F}| > n\).
Simulator. Observe that the MPRE \(\hat{F}\) invokes the 4-party gadget MPRE \(\hat{f}\) for n times and computes a linear function \(\ell \). By the adaptive security of \(\hat{f}\) and Theorem 2, we have that the parallel composition of all n invokations of \(\hat{f}\) and the linear function \(\ell \) is an MPRE \(\hat{G}\) for the following composed functionality G:

The leakage function of \(\hat{f}\) gives the leakage function of \(\hat{G}\), which is \(L_i\) leaking \((Q_2(i), Q_3(i))\) to \(P_i\) for every i. \(\hat{G}\) is secure against \(t < n/2\) adaptive corruption. Let \(({\textsf {SimI}}_G, {\textsf {SimO}}_G)\) be its simulator. Below, we use this simulator to construct the simulator \(({\textsf {SimI}}_F, {\textsf {SimO}}_F)\) for \(\hat{F}\).
Overview. The encoding of \(\hat{F}\) consists of encoding of \(\hat{f}\) and the output of \(\ell \) with appropriate input / output. The job of \(({\textsf {SimI}}_F, {\textsf {SimO}}_F)\) is: 1) simulate the input / output of calls to \(\hat{G}\), i.e., calls to \(\hat{f}\) and \(\hat{\ell }\), and 2) invoke \(({\textsf {SimI}}_G, {\textsf {SimO}}_G)\) to simulate the encoding and local randomness of all calls to \(\hat{f}\) and \(\ell \). Task 1) requires simulating Y(i), a random n-out-of-n Shamir sharing of \(x_1x_2x_3 + z + s\) belonging to the output of encoding, all Z(i) belonging to \(P_1\), each S(i) belonging to \(P_i\), and each \(Q_2(i), Q_3(i)\) belonging to \(P_2, P_3\) respectively, and leaked to \(P_i\). Consistency between Y(i) and Z(i), S(i) is maintained by “programming” the variable that is simulated the last. This can be done as S(i) Z(i) are all marginally random and provide enough degree of freedom for programming even if all parties were corrupted. Consistency between simulating \(Q_2(i), Q_3(i)\) when \(P_2, P_3\) are corrupted and when \(P_i\) is corrupted can be maintained, thanks to the fact that at most t parties are corrupted and \(Q_2,Q_3\) have degree t with constant term \(x_2, x_3\).
Proof
(Proof of Lemma 7). We start with the formal description of the simulator.
-
Upon \({\textsf {CorruptO}}\), \({\textsf {SimO}}(y = x_1x_2x_3+\alpha +\beta +\gamma )\):
-
Sample \(\tau \leftarrow \mathbb {F}\).
-
\(\forall i\), if \(P_1, P_i\) are already corrupted, \( Y(i) = x_1 Q_2(i) Q_3(i) + Z(i) + S(i)\) is fixed.
-
Sample \( O\leftarrow \mathsf {\mathcal {P}}(n-1,\tau ) \mid (i_1, Y(i_1)),\dots , (i_s, Y(i_s))\) conditioned on the list of fixed \((i_j, Y(i_j))\)’s from previous step. (Note that \(s \le t\) points are fixed.)
Send to adversary \({\textsf {SimO}}_G(y-\tau , ( Y(i))_i)\).
-
-
Upon \({\textsf {CorruptI}}(1)\), \({\textsf {SimI}}(x_1, \alpha )\):
-
Sample \( S(1)\leftarrow \mathbb {F}\).
-
\(\forall i\), if \(P_i\) and the output party are already corrupted, find the unique Z(i) that satisfies the equation \( Y(i) = x_1 Q_2(i) Q_3(i) + Z(i) + S(i)\).
Send to adversary \({\textsf {SimI}}_G(x_1, \alpha , ( Z(i))_i, S(1))\).
-
-
Upon \({\textsf {CorruptI}}(2)\), \({\textsf {SimI}}(x_2, \beta ))\):
-
\(\forall i\), if \(P_i\) is already corrupted, \( Q_2(i)\) is already fixed.
-
Sample \(Q_2 \leftarrow \mathsf {\mathcal {P}}(t,x_2)\mid (i_1,Q_2(i_1)),\dots , (i_s,Q_2(i_s))\), conditioned on the list of fixed \((i_j, Q_2(i_j))\). (Note that this can be done as \(s \le t\) points are fixed, and \(Q_3\) has degree t.)
-
if \(P_1\) and the output party are already corrupted, find the unique S(2) that satisfies the equation \( Y(2) = x_1 Q_2(2) Q_3(2) + Z(2) + S(2)\).
Send to adversary \({\textsf {SimI}}_G(x_2, \beta , ( Q_2(i))_i, S(2))\).
-
-
Upon \({\textsf {CorruptI}}(3)\), \({\textsf {SimI}}(x_3, \gamma ))\): Same as in \({\textsf {SimI}}(x_2, \beta )\):
-
\(\forall i\), if \(P_i\) is already corrupted, \( Q_3(i)\) is already fixed.
-
Sample \(Q_3 \leftarrow \mathsf {\mathcal {P}}(t,x_3)\mid (i_1,Q_3(i_1)),\dots , (i_s,Q_3(i_s))\), conditioned on the list of fixed \((i_j, Q_3(i_j))\).
-
if \(P_1\) and the output party are already corrupted, find the unique S(3) that satisfies the equation \( Y(3) = x_1 Q_2(3) Q_3(3) + Z(3) + S(3)\).
Send to adversary \({\textsf {SimI}}_G(x_3, \gamma , ( Q_3(i))_i, S(3))\).
-
-
Upon \({\textsf {CorruptI}}(i)\), \({\textsf {SimI}}(\bot ))\) for \(i\notin \{1,2,3\}\):
-
If \(P_2\) and/or \(P_3\) is already corrupted, \( Q_2\) and/or \( Q_3\) are fixed. Otherwise, sample \( Q_2(i), Q_3(i) \leftarrow \mathbb {F}\).
-
Sample \(Q_3 \leftarrow \mathsf {\mathcal {P}}(t,x_3)\mid (i_1,Q_3(i_1)),\dots , (i_s,Q_3(i_s))\), conditioned on the list of fixed \((i_j, Q_3(i_j))\).
-
if \(P_1\) and the output party are already corrupted, find the unique S(i) that satisfies the equation \( Y(i) = x_1 Q_2(i) Q_3(i) + Z(i) + S(i)\).
Send to adversary \({\textsf {SimI}}_G( S(i), Q_2(i), Q_3(i))\).
-
Correctness of Simulation. We argue that the view of the adversary in the real world and simulation are identically distributed following from the simulation security of \(\hat{G}\) and the fact that the input/output of the invokation of \(\hat{G}\) are simulated perfectly.
Hybrid. More formally, consider the following hybrid, where input/output of the invokation of \(\hat{G}\) is generated at the beginning as in the real world, while the encoding of \(\hat{G}\) is still simulated.
-
At the Outset: With knowledge of \(x_1, x_3, x_3, \alpha , \beta , \gamma \).
-
\(\forall i\), sample \(Z(i) \leftarrow \mathbb {F}\). Let \(z = Z(0)\).
-
Sample \(Q_2 \leftarrow \mathsf {\mathcal {P}}(t, x_2)\).
-
Sample \(Q_3 \leftarrow \mathsf {\mathcal {P}}(t, x_3)\).
-
\(\forall i\), sample \(S(i) \leftarrow \mathbb {F}\). Let \(s = S(0)\).
-
\(\forall i\), compute \(Y(i) = x_1Q_2(i)Q_3(i) + Z(i) + S(i)\).
-
Compute \(\tau = x_1x_2x_3 + z + s\), and \(y= x_1x_2x_3 +\alpha +\beta +\gamma \).
-
-
Upon \({\textsf {CorruptO}}\): Send to adversary \({\textsf {SimO}}_G(y-\tau , ( Y(i))_i)\).
-
Upon \({\textsf {CorruptI}}(1)\): Send to adversary \({\textsf {SimI}}_G(x_1, \alpha , ( Z(i))_i, S(1))\).
-
Upon \({\textsf {CorruptI}}(2)\) Send to adversary \({\textsf {SimI}}_G(x_2, \beta , ( Q_2(i))_i, S(2))\).
-
Upon \({\textsf {CorruptI}}(3)\): Send to adversary \({\textsf {SimI}}_G(x_3, \gamma , ( Q_3(i))_i, S(3))\).
-
Upon \({\textsf {CorruptI}}(i)\): Send to adversary \({\textsf {SimI}}_G( S(i), Q_2(i), Q_3(i))\).
The only difference between the above hybrid and the real world is whether the encoding of \(\hat{G}\) is simulated or not, it follows from the security of \(\hat{G}\) that the views of the adversary are identically distributed. The only difference between the hybrid and the simulation is whether the input/output of the call to \(\hat{G}\) is generated at the beginning with knowledge of \(x_1, x_2, x_3, \alpha , \beta , \gamma \) or generated in a delayed fashion. Since these two ways of generation yield the same distribution, the hybrid and simulation are also identically distributed. We conclude that the real world and simulation are identically distributed.
5 MPRE for \(\mathbf{NC }^{\mathbf{1}}\) and P/poly
We lift our effective degree-2 MPRE for degree-3 functionalities constructed in the previous section, to MPRE for \(\mathbf{NC }^{\mathbf{1}}\) and P/poly. The transformation uses the former MPRE to compute degree-3 randomized encodings for \(\mathbf{NC }^{\mathbf{1}}\) [20] and for P/poly [22], and preserves the effective degree. The resulting effective-degree-2 MPRE for \(\mathbf{NC }^{\mathbf{1}}\) is information theoretically secure and tolerates any adaptive corruptions, while the resulting MPRE for P/poly is computationally secure making black box access to a PRG, and tolerates \(n-1\) adaptive corruptions.
By our sequential composition theorem (Theorem 1), it is sufficient to construct degree-3 MPRE for \(\mathbf{NC }^{\mathbf{1}}\) and for P/poly. The former is constructed in [2]. The later, a \((n-1)\)-private degree-3 MPRE for P/poly that makes black-box use of PRG, has been implicitly constructed in [13]. We will formally analyze the adaptive security of our MPRE for P/poly in the rest of the section. The adaptive security of the our MPRE for \(\mathbf{NC }^{\mathbf{1}}\) is deferred to the full version.
5.1 Computational MPRE for P/poly based on Black-box PRG
Lemma 8
The scheme in Fig. 6 is a MPRE for P/poly such that
-
the MPRE uses PRG as a black-box;
-
the MPRE is computationally secure against \(n-1\) adaptive corruptions;
-
the MPRE has effective degree 3 over boolean field.
Proof Overview. The construction is similar to Yao’s garbled circuits. Yao’s garbled circuits can be viewed as a degree-3 computational randomized encoding for P/poly.
Recall that in Yao’s garbled circuits, the construction involves many pairs of the form
so that they need to satisfy the following properties
-
\(s_j\) is uniformly random;
-
\(\hat{s}_j\) is longer than \(s_j\) and can be deterministically computed from \(s_j\);
-
if \(s_j\) is hidden, \(\hat{s}_j\) is computationally indistinguishable from uniform distribution.
PRG exactly fits the requirements. In Yao’s garbled circuits, \(s_j\) is sampled at random, and \(\hat{s}_j \mathrel {:=}G(s_j)\), where G is a PRG.
To convert Yao’s garbled circuit into a computational MPRE, the label \(s_j\) should be jointly sampled by all parties. For the MPRE to be secure, \(\hat{s}_j\) should be indistinguishable from uniform randomness as long as at least one party’s local randomness is hidden. Moreover, for the MPRE to have low effective degree, PRG should be only be used in the preprocessing phase.
A natural construction that satisfies all the requirements is
-
\(s_j \mathrel {:=}s_j^{(1)} \Vert \dots \Vert s_j^{(n)}\), where \(s_j^{(i)}\) is locally sampled by the i-th party;
-
\(\hat{s}_j \mathrel {:=}G(s_j^{(1)}) \oplus \dots \oplus G(s_j^{(n)})\).
Denote the mapping from \(s_j\) to \(\hat{s}_j\) by \(G^{\text {MP}}\), i.e.
Under the new notation, \(\hat{s}_j = G^{\text {MP}}(s_j)\).
Circuit Definition. To rigorously state our MPRE, we formalize the notations for functionality in \(\mathbf{P/poly }\). A boolean circuit is specified by a directed acyclic graph. The nodes in the graph are indexed by numbers in [m], each represents a wire in the circuit.
-
For any \(j\in [m]\), let \(x_j\) denote the wire value of the j-th wire.
-
Let \(\mathcal {J}_i\) denote the input wires of the i-th party. For each \(j\in \mathcal {J}_i\), the i-th party knows the value of \(x_j\). Let \(\mathcal {J}_\text {in} \mathrel {:=}\bigcup _i \mathcal {J}_i\) denote all the input wires.
-
Any wire other than the input wires is the output of a gate. Let \(j_1,j_2 < j\) denotes the input wires of the gate (\(j_1,j_2\) are implicit functions of j), let \(g_j:\{0,1\}\times \{0,1\}\rightarrow \{0,1\}\) be the corresponding gate function. Thus \(x_j = g_j (x_{j_1},x_{j_2})\).
-
For each wire j, let d(j) denote the fan-out of the wire.
-
Let \(\mathcal {J}_\text {out}\) denote all the output wires. Thus the circuit output consists of \(x_j\) for all \(j\in \mathcal {J}_\text {out}\).
Proof
(Proof of Lemma 8). Scheme is essentially Yao’s garbled circuit which uses \(G^{\text {MP}}\) as PRG. \(k_j\) is the permutation bit of the j-th wire. \(s_{j,0},s_{j,1}\) are the wire keys of the j-th wire. \((w_{j,0,0},w_{j,0,1},w_{j,1,0},w_{j,1,1})\) is the table associated with the j-th gate. Thus both the correctness and privacy can be proved in a similar fashion as garbled circuit.
The correctness is implied from the statement that
for all \(j\in [m]\). The statement can be proved by induction. For any \(j\in \mathcal {J}_\text {in}\), (6) is directly guaranteed by the encoding function. For any \(j\notin \mathcal {J}_\text {in}\), assume the statement holds for \(j_1,j_2\) – the two input wire of the j-th gate, then
thus \(\bar{x}_j = k_j \oplus x_j\), \(z_j = s_{j,k_j \oplus x_j } = s_{j,\bar{x}_j }\) and \(\hat{z}_j = G^{\text {MP}}(z_j) = G^{\text {MP}}(s_{j,\bar{x}_j }) = \hat{s}_{j,\bar{x}_j }\). As the consequence, for each \(j\in \mathcal {J}_\text {out}\), the decoding function will output \(\bar{x}_j \oplus k_j\), which equals the right output \(x_j\).
For adaptive privacy, the simulator in the ideal world works as the follows
-
At the Outset: Sample \(\bar{x}_j \leftarrow \{0,1\}\) for all \(j\in [m]\), sample random \(\hat{z}_j\) for all \(j\in \mathcal {J}_\text {in}\), sample random \(z_j\) and sets \(\hat{z}_j = G^{\text {MP}}(z_j)\) all \(j\notin \mathcal {J}_\text {in}\).
-
Upon \({\textsf {CorruptI}}(i)\), \({\textsf {SimI}}(i,(x_j)_{j\in \mathcal {J}_i})\): Sets \(k_j = x_j \oplus \bar{x}_j\) for all \(j \in \mathcal {J}_i\).
Sample random \(\hat{s}_{j,0}^{(i)},\hat{s}_{j,1}^{(i)}\) for all \(j\in \mathcal {J}_\text {in}\), sample random \(k_j^{(i)}\) for all \(j\notin \mathcal {J}_\text {in}\).
Set \(s_{j,\bar{x}_i}^{(i)}\) as the i-th part of \(z_{j}\) and sample random \(s_{j,\bar{x}_i\oplus 1}^{(i)}\) for all \(j\notin \mathcal {J}_\text {in}\).
Output \(\bigl (x_j,k_j\bigr )_{j\in \mathcal {J}_i},\bigl (\hat{s}_{j,0}^{(i)},\hat{s}_{j,1}^{(i)}\bigr )_{j\in \mathcal {J}_\text {in}},\bigl (k^{(i)}_j,s^{(i)}_{j,0}, s^{(i)}_{j,1}\bigr )_{j\notin \mathcal {J}_\text {in}}\).
-
Upon \({\textsf {CorruptO}}\), \({\textsf {SimO}}((x_j)_{j\in \mathcal {J}_\text {out}})\): Sets \(k_j = x_j \oplus \bar{x}_j\) for all \(j \in \mathcal {J}_\text {out}\).
For each \(j\notin \mathcal {J}_\text {in}\), the simulator sets
$$ w_{j,\bar{x}_{j_1},\bar{x}_{j_2}} = \hat{z}_{j_1}[j,\bar{x}_{j_2}] \oplus \hat{z}_{j_2}[j,\bar{x}_{j_1}] \oplus (\bar{x}_j \Vert z_{j} ), $$and samples random \(w_{j,b_1,b_2}\) for \((b_1,b_2)\ne (\bar{x}_{j_1},\bar{x}_{j_2})\).
Output \((\bar{x}_j,\hat{z}_j)_{j\in \mathcal {J}_\text {in}},(w_{j,b_1,b_2})_{j\notin \mathcal {J}_\text {in},b_1,b_2\in \{0,1\}},(k_j)_{j\in \mathcal {J}_\text {out}}\) to the adversary.
In order to show the real world and the ideal world are computationally indistinguishable from the adversary’s view, we define a sequence of \(2m+1\) hybrid worlds. In the t-th hybrid world (\(t\in \{0,\frac{1}{2},1,\frac{3}{2},\dots ,m\}\)):
-
At the Outset: The adversary decides input \((x_j)_{j\in \mathcal {J}_\text {in}}\).
Sample \(\bar{x}_j\in \{0,1\}\) for all \(j\in [m]\), sample random \(\hat{z}_j\) for all \(j\in \mathcal {J}_\text {in}\), sample random \(z_j\) and sets \(\hat{z}_j = G^{\text {MP}}(z_j)\) all \(j\notin \mathcal {J}_\text {in}\).
For all \(j\in [m]\), set \(k_j = x_j \oplus \bar{x}_j\). For all \(j\in \mathcal {J}_\text {in}\), set \(\hat{s}_{j,\bar{x}_j} = \hat{z}_j\) and sample random \(\hat{s}_{j,\bar{x}_j\oplus 1}\). For all \(j\notin \mathcal {J}_\text {in}\), set \(s_{j,\bar{x}_j} = z_j\), set \(\hat{s}_{j,\bar{x}_j} = G^{\text {MP}}(s_{j,\bar{x}_j})\), \(\hat{z}_j = G^{\text {MP}}(z_j)\), thus \(\hat{z}_j = \hat{s}_{j,\bar{x}_j}\).
set \(s_{j,\bar{x}_j} = z_j\), sample random \(s_{j,\bar{x}_j\oplus 1}\) .
For each \(j\notin \mathcal {J}_\text {in}\) that \(j\le t\), sample random \(s_{j,\bar{x}_j\oplus 1}, \hat{s}_{j,\bar{x}_j\oplus 1}\).
For each \(j\notin \mathcal {J}_\text {in}\) that \(j> t\), sample random \(s_{j,\bar{x}_j\oplus 1}\), set \(\hat{s}_{j,\bar{x}_j\oplus 1} = G^{\text {MP}}(s_{j,\bar{x}_j\oplus 1})\).
-
Upon \({\textsf {CorruptI}}(i)\): Sample random \(\hat{s}_{j,0}^{(i)},\hat{s}_{j,1}^{(i)}\) for all \(j\in \mathcal {J}_\text {in}\). Sample random \(k_j^{(i)}\) for all \(j\notin \mathcal {J}_\text {in}\). Set \(s_{j,b}^{(i)}\) as the i-th part of \(s_{j,b}\) for all \(j\notin \mathcal {J}_\text {in}\).
Send \(\bigl (x_j,k_j\bigr )_{j\in \mathcal {J}_i},\bigl (\hat{s}_{j,0}^{(i)},\hat{s}_{j,1}^{(i)}\bigr )_{j\in \mathcal {J}_\text {in}},\bigl (k^{(i)}_j,s^{(i)}_{j,0}, s^{(i)}_{j,1}\bigr )_{j\notin \mathcal {J}_\text {in}}\) to the adversary.
-
Upon \({\textsf {CorruptO}}\): For each \(j\notin \mathcal {J}_\text {in}\) that \(j\le t+\frac{1}{2}\), set
$$ w_{j,\bar{x}_{j_1},\bar{x}_{j_2}} = \hat{z}_{j_1}[j,\bar{x}_{j_2}] \oplus \hat{z}_{j_2}[j,\bar{x}_{j_1}] \oplus (\bar{x}_j \Vert z_{j} ), $$and sample random \(w_{j,b_1,b_2}\) for \((b_1,b_2)\ne (\bar{x}_{j_1},\bar{x}_{j_2})\).
For each \(j\notin \mathcal {J}_\text {in}\) that \(j> t+\frac{1}{2}\), set
$$ w_{j,b_1,b_2} = \hat{s}_{j_1,b_1}[j,b_2] \oplus \hat{s}_{j_2,b_2}[j,b_1] \oplus (k_j \oplus g_j(b_1\oplus k_{j_1},b_2\oplus k_{j_2}) \Vert s_{j,k_j \oplus g_j(b_1\oplus k_{j_1},b_2\oplus k_{j_2}) } ) $$for \(b_1,b_2\in \{0,1\}\).
The simulator sends \((\bar{x}_j,\hat{z}_j)_{j\in \mathcal {J}_\text {in}},(w_{j,b_1,b_2})_{j\notin \mathcal {J}_\text {in},b_1,b_2\in \{0,1\}},(k_j)_{j\in \mathcal {J}_\text {out}}\) to the adversary.
The ideal world is computationally indistinguishable from the real world, because 1) the real world is indistinguishable from the 0-th hybrid world; 2) the ideal world is indistinguishable from the m-th hybrid world; 3) the j-th hybrid world is computationally indistinguishable from the \((j-1)\)-th hybrid world.
The Real World is Indistinguishable from the 0-th Hybrid World as they are essentially the same. E.g. in the real world, \(k_j^{(1)},\dots ,k_j^{(n)}\) are i.i.d. random boolean, and \(k_j \mathrel {:=}k_j^{(1)} \oplus \dots \oplus k_j^{(n)}\), \(\bar{x}_j \mathrel {:=}k_j \oplus x_j\); while in the 0-th hybrid world, \(\bar{x}_j\) and \(k_j^{(i)}\) for all corrupted party i are randomly sampled, and \(k_j \mathrel {:=}\bar{x}_j \oplus x_j\). There two methods of sampling yield the same distribution.
The Ideal World is Indistinguishable from the m-th Hybrid World. Compared with the m-th hybrid world, the only difference of the ideal world is that some computation is deferred. E.g. in the m-th hybrid world, it sets \(k_j \mathrel {:=}\bar{x}_j \oplus x_j\) at the beginning; while in the ideal world, the simulator can only set \(k_j\) after \(x_j\) is given.
The the \((j-1)\)-th hybrid world. is indistinguishable from the \((j-\frac{1}{2})\)-th hybrid world. The only difference between them is how \(w_{j,0,0},w_{j,0,1},w_{j,1,0},w_{j,1,1}\) are generated.
As for \(w_{j,\bar{x}_{j_1},\bar{x}_{j_2}}\), we have

For the other three terms, \(w_{j,b_1,b_2}\) for \((b_1,b_2) \ne (\bar{x}_{j_1},\bar{x}_{j_2})\), we have

Notice that in the \((j-1)\)-th hybrid world, \(\hat{s}_{j_1,\bar{x}_{j_1}\oplus 1}\), \(\hat{s}_{j_2,\bar{x}_{j_2}\oplus 1}\) are fresh randomness that are only used to generate \(w_{j,\bar{x}_{j_1}\oplus 1,\bar{x}_{j_2}\oplus 1},w_{j,\bar{x}_{j_1},\bar{x}_{j_2}\oplus 1},w_{j,\bar{x}_{j_1}\oplus 1,\bar{x}_{j_2}}\). Thus it’s equivalent to sampling \(w_{j,b_1,b_2}\) for \((b_1,b_2) \ne (\bar{x}_{j_1},\bar{x}_{j_2})\) at random as they are already one-time padded by fresh randomness, which is exactly how they are generated in the \((j-\tfrac{1}{2})\)-th hybrid world.
The Last Piece is the Computational Indistinguishability between the j-th Hybrid World and the \((j-\tfrac{1}{2})\)-th Hybrid World. The only difference between them is how \(\hat{s}_{j,\bar{x}_{j}\oplus 1}\) is generated.
In the \((j-\tfrac{1}{2})\)-th hybrid world, \(s_{j,\bar{x}_{j}\oplus 1} = s_{j,\bar{x}_{j}\oplus 1}^{(1)} \Vert \dots \Vert s_{j,\bar{x}_{j}\oplus 1}^{(n)}\) are randomly sampled and \(\hat{s}_{j,\bar{x}_{j}\oplus 1}\) is determined by \(\hat{s}_{j,\bar{x}_{j}\oplus 1} = G^{\text {MP}}(s_{j,\bar{x}_{j}\oplus 1}) = \bigoplus _i G(s^{(i)}_{j,\bar{x}_{j}\oplus 1})\). As we are proving \((n-1)\)-privacy, the adversary cannot corrupts all parties. Let \(i^*\) denote a party currently not corrupted by the adversary. Notice that \(s^{({i^*})}_{j,\bar{x}_{j}\oplus 1}\) is only used to generate \(\hat{s}_{j,\bar{x}_{j}\oplus 1}\), thus it is computational indistinguishable if \(G(s^{(i^*)}_{j,\bar{x}_{j}\oplus 1})\) is replaced by uniform randomness. Replacing \(G(s^{({i^*})}_{j,\bar{x}_{j}\oplus 1})\) by uniform randomness is equivalent to sampling \(\hat{s}_{j,\bar{x}_{j}\oplus 1}\) at random, which is how \(\hat{s}_{j,\bar{x}_{j}\oplus 1}\) is generated in the j-th hybrid world.
6 Two-Round MPC
As what we are going to show in Lemma 9, an effective-degree-2 adaptive MPRE for functionality f and an adaptive 2-round MPC for any degree-2 functions will imply an adaptive 2-round MPC for the functionality f. In previous sections, we construct effective degree-2 MPRE for \(\mathbf{NC }^{\mathbf{1}}\) and P/poly under different settings. The last step is to construct adaptive 2-round MPC protocols for degree-2 functionalities in these settings, which are Sect. 6.1 and 6.2.
Lemma 9
Let \((\hat{f}, h_1,\ldots ,h_n)\) be a MPRE for functionality f that tolerates t adaptive corruptions. Assume there is a MPC protocol for \(\hat{f}\) that tolerates t adaptive corruptions. Then there exists a MPC protocol for f such that
-
the resulting MPC protocol has the same round and communication complexity as the MPC protocol for \(\hat{f}\);
-
the resulting MPC protocol tolerates t adaptive corruptions; the type of the simulation security (prefect, statistical or computational) align with that of the MPRE for f and MPC for \(\hat{f}\);
-
if the MPC for \(\hat{f}\) or the MPRE for f uses correlated randomness, the resulting MPC uses the same correlated randomness.
The proof is deferred to the full version.
6.1 Honest Majority and Plain Model
In the honest majority setting, the BGW [5] protocol when restricted to computing degree-2 polynomials has only two rounds. The adaptive security of BGW is proved in [14].
Lemma 10
For any degree-2 functionality f, the BGW protocol computes f in 2-round and tolerates adaptive minority corruptions.
6.2 Honest Minority and OLE Correlations
We now construct a very simple adaptively secure MPC protocol using OLE-correlation for the following \(\mathsf {2MultPlus}\) functionality, which is sufficient for computing any degree-2 polynomials.
Lemma 11
The 2-round MPC described in Figure 7 is a adaptive secure MPC protocol for the following functionality
and it tolerates an arbitrary number of corruptions.
Proof Overview. The scheme can also be explained as a randomized encoding for branching program. As \((b_1,b_2)\) is the additive secret sharing of \(a_1a_2\), the receiver essentially learns \(m_{1,1},m_{2,1}\) and \(m_{1,2} + m_{2,2}\).
As
the message received by the receiver is a randomized encoding of \(x_1x_2 + z_1 + z_2\), and \(a_1,a_2\) are the randomness of the randomness encoding. The formal proof is deferred to the full version.
References
Ananth, P., Choudhuri, A.R., Goel, A., Jain, A.: Round-optimal secure multiparty computation with honest majority. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 395–424. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_14
Applebaum, B., Brakerski, Z., Tsabary, R.: Perfect secure computation in two rounds. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11239, pp. 152–174. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_6
Applebaum, B., Ishai, Y., Kushilevitz, E.: Cryptography in NC\(^0\). SIAM J. Comput. 36(4), 845–888 (2006)
Beaver, D., Micali, S., Rogaway, P.: The round complexity of secure protocols. In: Proceedings of the 22nd Annual ACM Symposium on Theory of Computing, pp. 503–513 (1990). https://doi.org/10.1145/100216.100287
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation. In: Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali, pp. 351–371 (1988). https://doi.org/10.1145/62212.62213
Benhamouda, F., Lin, H.: k-round multiparty computation from k-round oblivious transfer via garbled interactive circuits. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 500–532. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_17
Benhamouda, F., Lin, H., Polychroniadou, A., Venkitasubramaniam, M.: Two-round adaptively secure multiparty computation from standard assumptions. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11239, pp. 175–205. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_7
Boyle, E., Couteau, G., Gilboa, N., Ishai, Y.: Compressing vector OLE. In: Lie, D., Mannan, M., Backes, M., Wang, X. (eds.) Proceedings of the ACM SIGSAC Conference on Computer and Communications Security, CCS 2018, Toronto, ON, Canada, October 15–19, 2018, pp. 896–912. ACM (2018). https://doi.org/10.1145/3243734.3243868
Boyle, E., Couteau, G., Gilboa, N., Ishai, Y., Kohl, L., Scholl, P.: Efficient pseudorandom correlation generators from ring-LPN. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020. LNCS, vol. 12171, pp. 387–416. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56880-1_14
Canetti, R.: Security and composition of multiparty cryptographic protocols. J. Cryptology 13(1), 143–202 (2000). https://doi.org/10.1007/s001459910006
Canetti, R., Feige, U., Goldreich, O., Naor, M.: Adaptively secure multi-party computation. In: Proceedings of the 28th Annual ACM Symposium on Theory of Computing, pp. 639–648. ACM (1996) https://doi.org/10.1145/237814.238015
Chaum, D., Crépeau, C., Damgård, I.: Multiparty unconditionally secure protocols. In: Proceedings of the twentieth Annual ACM Symposium on Theory of Computing, pp. 11–19. ACM (1988). https://doi.org/10.1145/62212.62214
Damgård, I., Ishai, Y.: Constant-round multiparty computation using a black-box pseudorandom generator. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 378–394. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_23
Damgård, I., Nielsen, J.B.: Adaptive versus static security in the UC model. In: Chow, S.S.M., Liu, J.K., Hui, L.C.K., Yiu, S.M. (eds.) ProvSec 2014. LNCS, vol. 8782, pp. 10–28. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-12475-9_2
Garg, S., Gentry, C., Halevi, S., Raykova, M.: Two-round secure MPC from indistinguishability obfuscation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 74–94. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_4
Garg, S., Ishai, Y., Srinivasan, A.: Two-round MPC: information-theoretic and black-box. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11239, pp. 123–151. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_5
Garg, S., Srinivasan, A.: Two-round multiparty secure computation from minimal assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 468–499. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_16
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or A completeness theorem for protocols with honest majority. In: Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali, pp. 218–229. ACM (1987). https://doi.org/10.1145/28395.28420
Ishai, Y., Kushilevitz, E.: Randomizing polynomials: a new representation with applications to round-efficient secure computation. In: Proceedings 41st Annual Symposium on Foundations of Computer Science, pp. 294–304. IEEE (2000). https://doi.org/10.1109/SFCS.2000.892118
Ishai, Y., Kushilevitz, E.: Perfect constant-round secure computation via perfect randomizing polynomials. In: Widmayer, P., Eidenbenz, S., Triguero, F., Morales, R., Conejo, R., Hennessy, M. (eds.) ICALP 2002. LNCS, vol. 2380, pp. 244–256. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45465-9_22
Ishai, Y., Mittal, M., Ostrovsky, R.: On the message complexity of secure multiparty computation. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10769, pp. 698–711. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_24
Yao, A.C.C.: Protocols for secure computations. In: 23rd Annual Symposium on Foundations of Computer Science (sfcs 1982), pp. 160–164. IEEE (1982). https://doi.org/10.1109/SFCS.1982.38
Yao, A.C.C.: How to generate and exchange secrets. In: 27th Annual Symposium on Foundations of Computer Science (sfcs 1986), pp. 162–167. IEEE (1986). https://doi.org/10.1109/SFCS.1986.25
Acknowledgements
We thank Yuval Ishai for insightful discussions. Part of this work was done while the authors were visiting the Simons Institute for the Theory of Computing.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Lin, H., Liu, T., Wee, H. (2020). Information-Theoretic 2-Round MPC Without Round Collapsing: Adaptive Security, and More. In: Pass, R., Pietrzak, K. (eds) Theory of Cryptography. TCC 2020. Lecture Notes in Computer Science(), vol 12551. Springer, Cham. https://doi.org/10.1007/978-3-030-64378-2_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-64378-2_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64377-5
Online ISBN: 978-3-030-64378-2
eBook Packages: Computer ScienceComputer Science (R0)






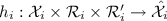 ;
;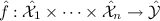 , the degree of
, the degree of 




