Equivalence Between Systems Stronger Than Resolution

Abstract

In recent years there has been an increasing interest in studying proof systems stronger than Resolution, with the aim of building more efficient SAT solvers based on them. In defining these proof systems, we try to find a balance between the power of the proof system (the size of the proofs required to refute a formula) and the difficulty of finding the proofs. Among those proof systems we can mention Circular Resolution, MaxSAT Resolution with Extensions and MaxSAT Resolution with the Dual-Rail encoding.

In this paper we study the relative power of those proof systems from a theoretical perspective. We prove that Circular Resolution and MaxSAT Resolution with extension are polynomially equivalent proof systems. This result is generalized to arbitrary sets of inference rules with proof constructions based on circular graphs or based on weighted clauses. We also prove that when we restrict the Split rule (that both systems use) to bounded size clauses, these two restricted systems are also equivalent. Finally, we show the relationship between these two restricted systems and Dual-Rail MaxSAT Resolution.

Research partially supported by the EU H2020 Research and Innovation Programme under the LOGISTAR project (Grant Agreement No. 769142), the MINECO-FEDER project TASSAT3 (TIN2016-76573-C2-2-P) and the MICINN project PROOFS (PID2019-109137GB-C21).

1 Introduction

The Satisfiability (SAT) and Maximum Satisfiability (MaxSAT) problems are central in computer science. SAT is the problem of, given a CNF formula, deciding if it has an assignment of 0/1 values that satisfy the formula. MaxSAT is the optimization version of SAT. Given a CNF formula, we want to know what is the maximum number of clauses that can be satisfied by an assignment. SAT and the decision version of MaxSAT are NP-Complete. Problems in many different areas like planning, computational biology, circuit design and verification, etc. can be solved by encoding them into SAT or MaxSAT, and then using a SAT or MaxSAT solver.

Resolution based SAT solvers can handle huge industrial formulas successfully, but on the other hand, seemingly easy tautologies like the Pigeonhole Principle require exponentially long Resolution refutations [8]. An important research direction is to implement SAT solvers based on stronger proof systems than Resolution. To be able to do that, the proof systems should not be too strong, given that the stronger a proof system is, the harder it is to find efficient algorithms to find refutations for the formulas. This is related to the notion of automatizability [2, 5].

In the last few years, a number of proof systems somewhat stronger than Resolution have been defined. Among them are MaxSAT Resolution with Extension [13], Circular Resolution [1], Dual-Rail MaxSAT [9], Weighted Dual-Rail MaxSAT [3, 14] and Sheraly-Adams proof system [7, 15]. All these systems have polynomial size proofs of formulas like the Pigeonhole Principle. Atserias and Lauria [1] showed that Circular Resolution is equivalent to the Sheraly-Adams proof system. Larrosa and Rollón [13] showed that MaxSAT Resolution with Extension can simulate Dual-Rail MaxSAT. In this paper, we show that MaxSAT Resolution with Extension is equivalent to Circular Resolution. This equivalence is parametric on the set of inference rules used by both proof systems.

Both Circular Resolution and MaxSAT Resolution with Extension use a rule called Split or Extension, where from a clause A, we can obtain both $A\vee x$ and $A\vee \lnot x$. We can add a restriction on this rule, and therefore on the proof system. If we bound the number of literals of A to be used in the split rule by k, for $k\ge 0$, we can talk about MaxSAT Resolution with k-Extension, or about k-Circular Resolution. In the present article, we also prove the equivalence of both systems, k-Circular Resolution and MaxSAT Resolution with k-Extensions, and improve the result of [13], proving that these restricted proof systems can also simulate Dual-Rail MaxSAT and Weighted Dual-Rail MaxSAT.

This paper proceeds as follows. In the preliminary Sect. 2 we introduce Circular, Weighted and Dual-Rail proofs. In Sect. 3, we prove some basic facts about these proof systems. The equivalence of Circular Resolution and MaxSAT Resolution with Extension is proved in Sect. 4. In Sect. 5, we describe a restriction of these two proof systems, show that they are equivalent, and prove that they can simulate Weighted Dual-Rail MaxSAT.

2 Preliminaries

We consider a set $x_1,\dots ,x_n$ of variables, literals of the form $x_i$ or $\lnot x_i$, clauses $A=l_1\vee \dots \vee l_r$ defined as sets of literals, and formulas defined as sets of clauses. Additionally, we also consider weighted formulas, defined as multisets of the form $\mathcal {F}=\{(A_1,u_1),\dots ,(A_r,u_r)\}$, where the $A_i$’s are clauses and the $u_i$’s are finite (positive or negative) integers. These integers $u_i$, when positive, describe the number of occurrences of the clause $A_i$. When they are negative, as we will see, they represent the obligation to prove these clauses in the future. Notice also that we do not require $A_i\ne A_j$, when $i\ne j$, thus we deal with multisets. We say that two weighted formulas are (fold-unfold) equivalent, noted $\mathcal {F}_1\approx \mathcal {F}_2$, if for any clause A, we have $\sum _{(A,u)\in \mathcal {F}_1}u=\sum _{(A,v)\in \mathcal {F}_2}v$. Notice that, contrarily to traditional Partial MaxSAT formulas, we do not use clauses with infinite weight.

An inference rule is given by a multi-set of antecedent clauses and a multi-set of consequent clauses where any truth assignment that satisfies all the antecedents, also satisfies all the consequent clauses. Notice that the MaxSAT Resolution rule was originally proposed to solve MaxSAT, and therefore, it satisfies additional properties. The rule preserves the number of unsatisfied clauses, for any assignment. Here, following the original idea of Ignatiev et al. [9], we use these MaxSAT techniques to solve SAT.

Definition 1

These are some examples of inference rules defined in the literature (with possibly different names):

where, in the MaxSAT Resolution rule, if $A=x_1\vee \dots \vee x_r$, then $\overline{A}$ denotes the set of |A| clauses $\{\lnot x_1,\ x_1\vee \lnot x_2,\ x_1\vee x_2\vee \lnot x_3,\dots ,$ $x_1\vee \dots \vee x_{r-1}\vee \lnot x_r\}$.

Notice that, in the previous definition, Symmetric Cut is a special case of Cut where $A=B$. Similarly, it is also a special case of MaxSAT Resolution where $A=B$, since $x\vee A\vee \overline{A}$ only contain tautologies that are removed. Notice that 0-Split can be generalized to the k-Split rule where Split is applied only to clauses A of length at most k. Below, we will also see that Split and Extension (defined in Sect. 3) are in essence the same inference rule.

Traditionally, fixed a set $\mathcal R$ of inference rules, a set of hypotheses $\mathcal H$ and a goal C, a proof of $\mathcal {H}\vdash C$ is a finite sequence of formulas that starts with $\mathcal H$, ends in C, and such that any other formula is one of the consequent of an inference rule in $\mathcal R$ whose antecedents are earlier in the sequence. These proofs can naturally be represented as bipartite DAGs, where nodes are either formulas or inference rules and edges denote the occurrence of a formula in the antecedents or the consequent of the rule.

In this paper we consider three distinct more complicated notions of proof, or proof systems: Circular resolution [1], MaxSAT Resolution with Extension [13], and Dual-Rail MaxSAT [9] or its generalization Weighted Dual-Rail MaxSAT [3].

All these proof systems will share the same inference rules, but they will use them in distinct ways (despite they have the same name). Thus, for instance, in the weighted context, the Cut rule will replace the premises $x\vee A$ and $\lnot x\vee B$ by the conclusion $A\vee B$. Therefore, in the weighted context, after the application of the cut, these premises are no longer available for further cuts.

All these proof systems are able to prove the Pigeonhole Principle in polynomial size. In this paper we will study the relative power of these proof systems.

2.1 Circular Proofs

First, we introduce Circular Proofs as defined by Atserias and Lauria [1]:

Definition 2 (Circular Proof)

Fixed a set of inference rules $\mathcal R$, a set of hypotheses $\mathcal H$ and a goal C, a circular proof of $\mathcal {H}\vdash C\!$ is a bipartite directed graph (I, J, E) where nodes are either inference rules ($R\in I$) or formulas¹ ($A\in J$), and edges $A\rightarrow R\in E$ denotes the occurrence of clause A in the antecedents of rule R and edges $R\rightarrow A\in E$ the occurrence of clause A in the consequent of R.

Given a flow assignment $Flow:I\rightarrow \mathbb {N}^+$ to the rules, we define the balance of the clause as:

where and are the sets of neighbours of a node.

In order to ensure soundness of a circular proof, it is required the existence of a flow assignment satisfying $Bal(A)\ge 0$, for any formula $A\in J\setminus \mathcal H$, and $Bal(C)>0$, for the goal C.

Atserias and Lauria [1] define Circular Resolution as the circular proof system where the set of inference rules is fixed to $\mathcal R=\{\textsc {Axiom},\, \textsc {Symmetric}\, \textsc {Cut}, \textsc {Split}\}$ and prove its soundness.

We will assume that the set of inference rules allows us to construct a constant size circular proof where formula A is derivable from A in one or more steps. The inference rule Axiom is included in $\mathcal {R}$ for this purpose (in the third proof of Fig. 1, $x\vee \lnot x$ is proved, which shows that Axiom rule is indeed not necessary). If A is the empty clause, we can use the Split rule or even the 0-split rule and the Cut or the Symmetric Cut rules. If A is of the form $A=x\vee A'$, we have two possibilities, as shown in Fig. 1.

Fig. 1.

Three ways to proof A from A.

The length of a proof is defined as the number of nodes of the bipartite graph.

2.2 Weighted Proofs

Second, we also introduce Weighted Proofs, following the ideas of Larrosa and Heras [12] and Bonet et al. [4, 6] for positive weights and Larrosa and Rollón [13] for positive and negative weights. The main idea is that, when we apply an inference rule, we replace the antecedents by the consequent, instead of adding the consequent to the set of proved formulas. As a consequence, formulas cannot be reused. This is similar to the definition of Read Once Resolution [10]. We use weighted formulas, i.e. multi-sets of clauses instead of sets of clauses and, or more compactly, pairs (A, u) where integer u represents the number of occurrences of clause A. This makes sense since non-reusability of clauses implies that it is not the same having one or two copies of the same clause. Allowing the use of negative weights, we can represent clauses that are not proved yet and will be proved later. Notice that these proof systems were originally designed to solve MaxSAT. Here, we use them to construct proofs of SAT problems. Hence, the original formulas are unweighted, and we only use weighted formulas in the proofs.

Definition 3 (Weighted Proof)

Fixed a set of inference rules $\mathcal R$, a set of hypotheses $\mathcal H$ and a goal C, a weighted proof of $\mathcal {H}\vdash C$ is a sequence ${\mathcal F}_1\vdash \cdots \vdash {\mathcal F}_n$ of weighted formulas such that:

• 1. $\mathcal {F}_1=\{(A,u_A)\mid A\in \mathcal {H}\}$ for some arbitrary and positive weights $u_A\ge 0$.

• 2. ${\mathcal F}_n$ contains the goal (C, u) with strictly positive weight $u>0$, and possibly other clauses, all of them with positive weight.

• 3. For every proof step ${\mathcal F}_i \vdash {\mathcal F}_{i+1}$, either

  • (a) (regular step) there exist an inference rule $A_1,\dots ,A_r\vdash B_1,\dots ,B_s\in {\mathcal R}$ and a positive weight $u>0$ such that

    $$ {\mathcal F}_{i+1}= {\mathcal F}_i \setminus \{(A_1,u),\dots ,(A_r,u)\}\cup \{(B_1,u),\dots ,(B_s,u)\} $$

    or,

  • (b) (fold-unfold step) ${\mathcal F}_{i+1}\approx {\mathcal F}_i$.

Alternatively, fold-unfold steps may be defined as the application of the Fold and Unfold rules defined as:

Notice that, in regular steps, weights are positive integers. Instead, in the Fold and Unfold rules, u and v can be negative. Clauses with weight zero are freely removed from the formula, as well as tautological clauses $x\vee \lnot x\vee A$. Notice that only one fold-unfold step is necessary between two regular steps, just to get (A, u) for every antecedent A of the next regular step, u being the weight of this next step. Moreover, only a constant-bounded number of Fold and Unfold rule applications is needed in this fold-unfold step. This motivates the definition of the length of a proof as its number of regular steps.

Larrosa and Heras [12] define MaxSAT Resolution as a method to solve MaxSAT using positive weighted proofs with the MaxSAT Resolution rule. Bonet et al. [4, 6] prove the completeness of this method for MaxSAT. The method is complete even if we restrict the hypotheses $\mathcal H$ to have weight one. Notice that the weighted proof system with the Cut rule is incomplete if we restrict hypotheses to have weight one. In other words, resolution is incomplete if we restrict hypotheses to be used only once like in Read Once Resolution [10].

Notice also that the MaxSAT resolution rule defined in [12] allows the weights of the antecedents to be different. Our version using equal weights for both antecedents is equivalent using the fold and unfold rules.

Recently, Larrosa and Rollón [13] define MaxSAT Resolution with Extension as the weighted proof system using $\mathcal {R}=\{\textsc {MaxSAT}\, \textsc {Resolution}, \textsc {Split}\}$ as inference rules. In fact, they use a rule called Extension that, as we will see below, is equivalent to the Split rule. They only explicitly mention the Fold rule, but notice that the Unfold is a special case of the Extension rule.

Traditionally, we say that formulas $F_1$ subsumes another formula $F_2$, noted $F_1\subseteq F_2$, if for every clause $A_2\in F_2$, there exists a clause $A_1\in F_1$ such that $A_1\subseteq A_2$. Instantiating a variable by true or false in a formula $F_2$ results in a formula $F_1\subseteq F_2$ subsuming it. Moreover, for most proof systems, if $F_1\subseteq F_2$ and we have a proof of $F_2$, we can easily construct a shorter proof of $F_1$. In the case of weighted proofs, we have to redefine these notions.

Definition 4 (Subsumption)

We say that a weighted formula $F_1$ subsumes another weighted formula $F_2$ if, either

• 1. $F_2=\{(B_1,v_1),\dots ,(B_s,v_s)\}$ and there is a subset $\{(A_1,u_1),\dots ,(A_r,u_r)\}\subseteq F_1$ such that $\sum _{i=1}^r u_i\ge \sum _{j=1}^s v_j$ and, for all $i=1,\dots ,r$ and $j=1,\dots ,s$, $A_i\subseteq B_j$, or

• 2. We can decompose $F_1\approx F_1'\cup F_1''$ and $F_2\approx F_2'\cup F_2''$ such that $F_1'$ subsumes $F_2'$ and $F_1''$ subsumes $F_2''$.

We say that a set of inference rules $\mathcal {R}$ is closed under subsumption if whenever $F_2\vdash _\mathcal {R} F'_2$ in one step and $F_1$ subsumes $F_2$, there exists a formula $F_1'$ such that $F_1\vdash _\mathcal {R} F_1'$ in linear² number of steps and $F_1'$ subsumes $F_2'$.

The definition of a proof system being closed under subsumption is a generalization of the definition of being closed under restrictions. If $F_1$ subsumes $F_2$, it is not necessarily true that $F_2$ under a restriction is equal to $F_1$. For instance, if $F_1=\{a,\lnot x\vee b\}$ and $F_2=\{x\vee a,\lnot x\vee b\}$, $F_1$ subsumes $F_2$, but $F_1$ is not the result of applying a restriction to $F_2$.

Notice that MaxSAT Resolution is not closed under subsumption. For example, from $F_2=\{(x\vee a,1),\ (\lnot x\vee b,1)\}$ we derive $F_2'=\{(a\vee b,1),\ (x\vee a\vee \lnot b,1),$ $(\lnot x\vee b\vee a,1)\}$. However, from $F_1=\{(a,1),\ (\lnot x\vee b,1)\}$ that subsumes $F_2$ we cannot derive any formula subsuming $F_2'$. If in addition we also use Split, from $F_1$, we can derive $F_1'=\{(a\vee b,1),$ $(a\vee \lnot b,1),\ (\lnot x\vee b,1)\}$ that subsumes $F_2'$.

Lemma 1

Weighted proofs using $\mathcal {R}=\{\textsc {MaxSAT}\, \textsc {Resolution}, \textsc {Split}\}$, $\mathcal {R}=\{\textsc {Cut}\}$ or $\mathcal {R}=\{\textsc {Split}\}$ are all closed under subsumption.

The union of rule sets closed under subsumption is closed under subsumption.

2.3 Weighted Dual-Rail Proofs

Third, we introduce the notion of Weighted Dual-Rail Proofs introduced by Bonet et al. [3] based on the notion of Dual-Rail Proofs introduced in [9]. Weighted Dual-Rail MaxSAT proofs may be seen as a special case of weighted proofs where all clause weights along the proof are positive.

The dual-rail encoding of the clauses $\mathcal {H}$ is defined as follows: Given a clause A over the variables $\{x_1,\dots ,x_n\}$, $A^{dr}$ is the clause over the variables $\{p_1,\dots ,p_n,$ $n_1,\dots ,n_n\}$ that results from replacing in A the occurrences of $x_i$ by $\lnot n_i$, and occurrences of $\lnot x_i$ by $\lnot p_i$. The semantics of $p_i$ is “variable $x_i$ is positive” and the semantics of $n_i$ is “the variable $x_i$ is negative”.

Definition 5 (Weighted Dual-Rail Proof)

Fixed a set of hypotheses $\mathcal {H}$, a weighted dual-rail proof of is a sequence $\mathcal {F}_1\vdash \cdots \vdash \mathcal {F}_m$ of positively weighted formulas over the set of variables $\{p_1,\dots ,p_n,n_1,\dots ,n_n\}$, such that:

• 1. $\mathcal {F}_1=\{(A^{dr},u_A)\mid A\in \mathcal {H}\}\cup \{(\lnot p_i\vee \lnot n_i,u_i),(p_i,v_i),(n_i,v_i)\mid i=1,\dots ,n\}$, for some arbitrary positive weights $u_A$, $u_i$ and $v_i$.

• 2. .

• 3. For every step $\mathcal {F}_i\vdash \mathcal {F}_{i+1}$, we apply the MaxSAT Resolution rule (regular step) or the fold-unfold step like in weighted proofs.

(Unweighted) Dual-Rail MaxSAT is the special case were weights $v_i$’s are equal to one. In the original definition [9], weights $u_A$’s and $u_i$ are equal to infinite. The use of infinite weights and negative weights together introduce some complications. Here, we prefer to use arbitrarily large, but finite weights, which result in an equivalent proof system.

Notice that, contrarily to generic weighted proofs, here weights are all positive. Notice also that, since weights $u_A$’s and $u_i$ are unrestricted, from clauses $\{(\lnot p_i\vee \lnot n_i,u_i),(p_i,v_i),(n_i,v_i)\}$ we can derive $\sum _{i=1}^n v_i$ copies of the empty clause plus $(p_i\vee n_i,v_i)$ for every i using the MaxSAT Resolution rule. We have to derive at least one more empty clause to prove unsatisfiability.

3 Basic Facts

In this section we prove that MaxSAT Resolution with Extension [13] may be formulated in different but equivalent ways.

First, notice that the Extension rule, defined in [13]:

does not fit to the weighted proof scheme (not all consequent formulas have the same weight in the inference rule). However, it is easy to prove that, in the construction of weighted proofs, this rule is equivalent to the Split rule:

Lemma 2

The Split and Extension rules are equivalent in weighted proof systems.

Proof

We can simulate a step of Split as:

Conversely, we can simulate a step of Extension as:

   $\blacksquare$

Second, we will prove that MaxSAT Resolution with Extension may be formulated using the Symmetric Cut rule instead of the MaxSAT Resolution rule. As we have already said, the Symmetric Cut rule is a special case of the MaxSAT Resolution rule, where $A=B$; i.e. all the clauses of the form $x\vee A\vee \lnot B$ disappear (see comments after Definition 1). Interestingly, this limited form of MaxSAT Resolution is polynomially equivalent to the normal MaxSAT Resolution in the presence of Split (or equivalently Extension).

Lemma 3

Weighted proofs using $\mathcal {R}=\{\textsc {MaxSAT}\, \textsc {Resolution, Split}\}$ are polynomially equivalent to weighted proofs using $\mathcal {R}=\{\textsc {Symmetric}\, \textsc {Cut, Split}\}$.

Proof

Symmetric Cut is a particular case of MaxSAT resolution, where $A=B$. Therefore, the equivalence is trivial in one direction.

In the opposite direction, we have to see how to simulate one step of MaxSAT resolution with a linear number of Symmetric Cut and Split steps. Let $A= a_1\vee \cdots \vee a_r$ and $B=b_1\vee \cdots \vee b_s$.

In blue we mark the clauses that are added by the last inference step.    $\blacksquare$

Notice that in the previous proof, the equivalence doesn’t follow for the subsystem where the number of literals on the formula performing the Split is bounded. So the previous argument does not show the equivalence between MaxSAT Resolution plus k-Split and Symmetric Cut plus k-Split.

Lemmas 2 and 3 allow us to conclude:

Corollary 1

MaxSAT Resolution with Extension [13] is equivalent to weighted proofs using rules $\mathcal {R}=\{\textsc {Symmetric}\, \textsc {Cut, Split}\}$.

The set $\mathcal {R}$ in Corollary 1 are precisely the rules used to define Circular Resolution [1] (except for the use of the Axiom rule that is added for a minor technical reason). This simplifies the proof of equivalence of both proof systems.

4 Equivalence of Circular Resolution and MaxSAT Resolution with Extension

In this Section we will prove a more general result: the equivalence between a proof system based on circular proofs with a set of inference rules $\mathcal R$ and a proof system based on weighted proofs using the same set of inference rules $\mathcal R$.

First we prove the more difficult direction, how we can simulate a circular proof with a weighted proof.

Lemma 4

Weighted proofs polynomially simulate Circular proofs using the same set of inference rules.

Proof

Assume we have a circular proof (I, J, E) with formula nodes J, inference nodes I, edges E, hypotheses $\mathcal {H}\subset J$ and goal $C\in J$. Without loss of generality, we assume that the hypotheses formulas do not have incoming edges: for any $A\in \mathcal {H}$, we have . Notice that removing these incoming edges in a circular proof only decreases the balance of hypotheses formulas (that are already allowed to have negative balance) and increases the balance of the origin of these edges.

Now, assign a total ordering $\mu :I\cup J\rightarrow \{1,\dots ,|I|+|J|\}$ to each node with the following restrictions: 1) hypotheses nodes $\mathcal {H}$ go before any other node, and 2) for every inference node R, the formulas it generates are placed after R in the ordering $\mu$. So, for any we have $\mu (R)<\mu (A)$. Notice that, if hypotheses nodes do not have incoming edges, there always exists such an ordering.

We construct the weighted proof $\mathcal {F}_0\vdash \mathcal {F}_{|\mathcal {H}|}\vdash \cdots \vdash \mathcal {F}_{|I|+|J|}$ defined by:

$$ \begin{array}{lll} \mathcal {F}_0 = &{} \{(A,-Bal(A))&{}\mid A\in \mathcal {H}\}\\ \mathcal {F}_m = &{} \{(A,Flow(R))&{}\mid (A\rightarrow R)\in E\wedge \mu (A)\le m< \mu (R)\}\ \cup \\ &{}\{(A,-Flow(R))&{}\mid (A\rightarrow R)\in E\wedge \mu (R)\le m< \mu (A)\}\ \cup \\ &{}\{(A,Flow(R))&{}\mid (R\rightarrow A)\in E\wedge \mu (R)\le m < \mu (A)\}\ \cup \\ &{}\{(A,Bal(A))&{}\mid A\in J\setminus \mathcal {H}\wedge \mu (A)\le m\} \end{array} $$

for any $m\in \{|\mathcal {H}|,\dots ,|I|+|J|\}$.

Notice that $\mathcal {F}_m$ only depends on the edges that connect a node smaller or equal to m with a node bigger than m. Notice also that by definition of $\mu$ we never have the situation $(R\rightarrow A)\in E\wedge \mu (A) < \mu (R)$.

Now, we will prove that this is really a weighted proof.

Since all clauses from $\mathcal {H}$ only have outgoing edges, their balance is negative, and the weights in $\mathcal {F}_0$ are positive. Since, according to $\mu$, the smallest nodes are the hypotheses, and they do not have incoming edges, we have $\mathcal {F}_{|\mathcal {H}|}=\{(A,Flow(R))\mid (A\in \mathcal {H}\wedge (A\rightarrow R)\in E\}$. Moreover, as , we can obtain $\mathcal {F}_{|\mathcal {H}|}$ from $\mathcal {F}_0$ by fold-unfold step.

For the rest of steps $\mathcal {F}_i\vdash \mathcal {F}_{i+1}$ with $i\ge |\mathcal {H}|$, we distinguish two cases according to the kind of node at position $i+1$:

• 1. For formula nodes $A\in J$, with $\mu (A)=i+1$.

  By definition of $\mu$, for any , we have $\mu (R)<\mu (A)$. For the outgoing nodes, we can decompose them into , where, for any $R\in I_1$, $\mu (R)>\mu (A)$, and for any $R\in I_2$, $\mu (R)<\mu (A)$. In $\mathcal {F}_i$, we have $(A,Flow(R))$, where , and, for every $R\in I_2$, we also have $(A,-Flow(R))$. Applying the Fold and Unfold rules, we derive the set of clauses $\{(A,Flow(R))\mid R\in I_1\}$ plus (A, m), where is the balance of A.

  

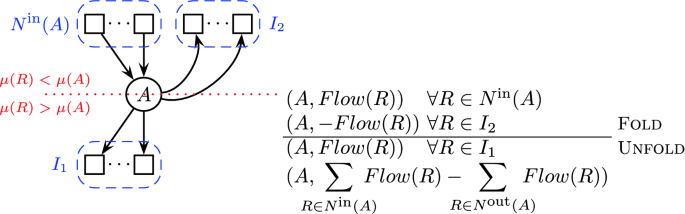
• 2. Inference nodes $R\in I$, with $\mu (R)=i+1$.

  In this case, for all consequent of R, we have $\mu (A)>\mu (R)$. However, the antecedents can be decomposed into two subsets and . In $\mathcal {F}_i$, we only have the clauses of $J_1$. In order to apply the same rule R with weights, we have to also introduce the clauses of $J_2$. This can be done applying the Unfold rule that, from the empty set of antecedents, deduces $(A,Flow(R))$ and $(A,-Flow(R))$, for any $A\in J_2$. After that, we have no problem to apply the same rule R with weight $Flow(R)$, obtaining $\mathcal {F}_{i+1}$.

  

   $\blacksquare$

Example 1

Consider the third circular proof of Fig. 1. We construct the corresponding weighted proof, as described in the proof of Lemma 4, where nodes are ordered from top to bottom according to $\mu$, and all inference nodes have the same flow:

Lemma 5

Circular proofs polynomially simulate weighted proofs using the same set of inference rules.

Proof

Assume we have a weighted proof $\mathcal {F}_1\vdash \mathcal {F}_2\vdash \dots \vdash \mathcal {F}_n$, where $\mathcal {F}_1$ are the hypotheses, and $\mathcal {F}_n$ contains the goal and the rest of clauses in $\mathcal {F}_n$ have positive weights. We will construct a circular resolution proof with three kinds of formula nodes: $J_1$ called axiom nodes, $J_2$ called auxiliary nodes (used only in the base case) and $J_3$ called normal nodes and inference nodes I such that there exist a flow assignment $Flow:I\rightarrow \mathbb {N}$ and balance $Bal:J\rightarrow \mathbb {N}$ satisfying 1) the set of axiom nodes $A\in J_1$ is the set of hypotheses in $\mathcal {F}_1$ and satisfy $Bal(A) = -\sum _{(A,c)\in \mathcal {F}_1} c$ 2) the auxiliary nodes all have positive balance and 3) for every clause (A, u) in $\mathcal {F}_n$, there exists a unique normal node $A\in J_3$ that satisfies $Bal(A) = \sum _{(A,c)\in \mathcal {F}_n} c$. The construction is by induction on n.

If $n=1$, for any hypothesis A of the weighted proof, let $u_A= \sum _{(A,u)\in \mathcal {F}_1}u$. We construct the constant-size circular proof that proves A from A with an axiom node A with balance $-u_A$, a normal node A with balance $u_A$, and the necessary auxiliary nodes. (Recall that we assume that the set of inference rules $\mathcal R$ allow us to infer A with balance $u_A$, from A with balance $-u_A$, for any clause A, using a constant-size circular proof).

Assume now, by induction hypothesis, that we have constructed a circular resolution corresponding to $\mathcal {F}_1\vdash \dots \vdash \mathcal {F}_i$. Depending on the MaxSAT resolution rule used in the step $\mathcal {F}_i\vdash \mathcal {F}_{i+1}$, we have two cases:

• 1. If the last MaxSAT inference is a Fold or Unfold, the same circular resolution proof constructed for $\mathcal {F}_1\vdash \dots \vdash \mathcal {F}_i$ works for $\mathcal {F}_1\vdash \dots \vdash \mathcal {F}_{i+1}$. Only in the special case of unfolding $\emptyset \vdash (A,u),(A,-u)$, if there is no formula node corresponding to A, we add a lonely normal node A (that will have balance zero) to ensure property 3).

• 2. If it corresponds to any other rule $R:A_1,\dots ,A_r\vdash B_1,\dots ,B_s$, we have $\mathcal {F}_i=\mathcal {F}_{i-1}\setminus \{(A_1,u),\dots ,(A_r,u)\} \cup \{(B_1,u),\dots ,(B_s,u)\}$, for some weight u. We add, to the already constructed circular resolution proof, a new inference node R with flow $Flow(R)=u$. We add edges from the formula nodes corresponding to $A_i$’s to the node R. If they do not exist, we add new normal nodes $B_j$’s. Finally, we add an edge from R to every $B_j$. The addition of these nodes has the effect of reducing the balance of $A_i$’s by u, and creating nodes $B_j$ with balance u, if they did not exist, or increasing the balance of $B_j$ in u, if it existed. By induction hypothesis, this makes property 3) hold for the new circular resolution proof and $\mathcal {F}_i$.

Notice that all clauses in $\mathcal {F}_1$ have strictly positive weight. Therefore, all axiom formula nodes in $J_1$ have negative balance and all nodes in $J_2$ positive balance. However, since clauses in $\mathcal {F}_i$, for $i\ne 1,n$ may have negative weight, balance of normal nodes in $J_3$ can also be negative during the construction of the circular resolution proof. Since all clauses in $\mathcal {F}_n$ have positive weight, at the end of the construction process, all normal nodes will have positive balance. Therefore, at the end of the process, the set of hypotheses $\mathcal {H}$ will be $J_1$.    $\blacksquare$

Corollary 2

MaxSAT Resolution with Extension and Circular Resolution are polynomially equivalent proof systems.

Proof

From Lemmas 2, 3, 4 and 5.    $\blacksquare$

5 Systems that Simulate Dual-Rail MaxSAT

In this Section, we analyze proof systems weaker than Circular Resolution and MaxSAT Resolution with Extension. We replace the Split rule by the 0-Split rule. Relaxing this rule forces us to use the non-symmetric version of the cut rules, as the following example suggests.

Example 2

Weighted proofs and circular proofs using $\{\textsc {Symmetric}\, \textsc {Cut},$ $0\text {-}\textsc {Split}\}$ are not able to prove the unsatisfiability of the following formulas

$$ F_1=\{\lnot x\vee y,\ \lnot y\vee z,\ \lnot z\vee \lnot x,\ x\vee v,\ \lnot v\vee w,\ \lnot w\vee x\} $$

$$ F_2=\{\lnot x,\ x\vee y,\ \lnot y\} $$

The previous example suggests that we cannot base a complete proof system in the Symmetric Cut rule, when we restrict the power of the Split rule. The natural question is how to compare the power of the Cut and the MaxSAT Resolution rule, when we are in the context of weighted proofs, and the rules replace the premises by the conclusions.

Example 3

Consider the formula $F_1=\{x\vee y,\ x\vee \lnot y,\ \lnot x\}$.

Assigning weight one to all the hypotheses clauses we can deduce the empty clause with weight one using MaxSAT Resolution:

In the first step of this proof, since we are working with weighted proofs, after using $x\vee y$ and $\lnot x$, these clauses disappear, and instead we obtain y and $\lnot x\vee \lnot y$.

To simulate such a step with the Cut in the replacement form, we also use $x\vee y$ and $\lnot x$, but only obtain y. In the following steps, we don’t have $\lnot x\vee \lnot y$, but we can use $\lnot x$, that subsumes it. However, we need to use clause $\lnot x$ twice (or $\lnot x$ with weight 2), one for the application of the first cut rule, and the other one to do the job of $\lnot x\vee \lnot y$. Repeating the same idea for the rest of the steps, we obtain the following proof with the Cut in the context of replacement rule with weights:

In this example, a deeper reorganization of the proof (cutting first y and then x) allows us to derive the empty clause with weights one for all the premises:

However, this is not always possible. For some unsatisfiable formulas, if we assign weight one to all the premises, we cannot obtain the empty clause using the Cut rule replacing premises by conclusions. This fact is deeply related to the incompleteness of the Read Once Resolution [10]. For instance, consider the unsatisfiable formula $\{x_1\vee x_2,\ x_3\vee x_4, \lnot x_1\vee \lnot x_3,\ \lnot x_1\vee \lnot x_4,\ \lnot x_2\vee \lnot x_3,\ \lnot x_2\vee \lnot x_4\}$ from [11]. In the context of weighted proofs, using the replacement Cut rule, we need to start with clauses with weight bigger than one in order to prove unsatisfiability. On the other hand, using MaxSAT Resolution all hypotheses may have weight one, since Bonet et al. [4, 6] prove that, for any unsatisfiable formula, we can derive the empty clause with the MaxSAT Resolution rule and weight one for all the premises.

The previous example suggests us how we can simulate a weighted proof using MaxSAT Resolution with a weighted proof using Cut, at the cost of increasing the weights of the initial clauses.

Lemma 6

Let $\mathcal {R}$ be a set of inference rules closed under subsumption.

Weighted proofs using $\{\textsc {Cut}\}\cup \mathcal {R}$ are polynomially equivalent to weighted proofs using $\{\textsc {MaxSAT}\, \textsc {Resolution}\}\cup \mathcal {R}$.

Proof

In one direction the proof is trivial, since MaxSAT Resolution has the same consequent as the Cut rule plus some additional clauses.

In the other direction, let n be the number of variables of the formula. Let $\mathcal {F}_1\vdash \dots \vdash \mathcal {F}_m$ be a weighted proof using $\{\textsc {MaxSAT}$ $\textsc {Resolution}\}\cup \mathcal {R}$. We can find an equivalent proof $\mathcal {F'}_1\vdash \dots \vdash \mathcal {F'}_{m'}$ using $\{\textsc {Cut}\}\cup \mathcal {R}$, where $m'=m\,\mathcal {O}(n)$, such that 1) $\mathcal {F'}_1= \{(A,v)\mid (A,u)\in \mathcal {F}_1 \wedge v\le k^m\,u\}$, where $k=\mathcal {O}(n)$ and 2) $\mathcal {F}'_{m'}$ subsumes $\mathcal {F}_m$.

For the base case $m=1$, it is trivial.

For the induction case $m>1$, let be the proof with MaxSAT Resolution and let $\mathcal {F'}_1\vdash \dots \vdash \mathcal {F'}_{m'}$ be the proof with Cut given by the induction hypothesis for the first m steps. There are three cases:

• 1. If the last inference step $\mathcal {F}_m\vdash \mathcal {F}_{m+1}$ is a Fold, Unfold, then the same proof already works since $\mathcal {F}'_m$ also subsumes $\mathcal {F}_{m+1}$.

• 2. If this last step applies any rule from $\mathcal {R}$, by closure under subsumption of $\mathcal {R}$, applying a linear number of rules of $\mathcal {R}$ we can construct $\mathcal {F}'_{m'}\vdash \cdots \vdash \mathcal {F}_{m'+\mathcal {O}(n)}$, where $\mathcal {F'}_{m'+\mathcal {O}(n)}$ subsumes $\mathcal {F}_{m+1}$.

• 3. If the last inference step is an application of the MaxSAT Resolution rule, let

  $$ \begin{array}{ll} \mathcal {F}_m=F\cup \{(x\vee A,u),\ (\lnot x\vee B,u)\}\hbox { and}\\ \mathcal {F}_{m+1}=F\cup \{(A\vee B,u),\ (x\vee A\vee \overline{B},u),\ (\lnot x\vee B\vee \overline{A},u)\}. \end{array} $$

  Let $r=1+\max \{|A|,|B|\}=\mathcal {O}(n)$ and let $\mathcal {F''}_1\vdash \dots \vdash \mathcal {F''}_{m'}$ the same proof as $\mathcal {F'}_1\vdash \dots \vdash \mathcal {F'}_{m'}$, where every weight has been multiplied by r. By induction hypothesis, $\mathcal {F'}_{m'}$ subsumes $\mathcal {F}_m$. Hence, $\mathcal {F''}_{m'}$ contains a clause $(A',r\,u_1)$ corresponding to $(x\vee A,u)$, where $A'\subseteq x\vee A$ and $u'\ge u$, and a clause $(B',r\,u_2)$ corresponding to $(\lnot x\vee B,u)$, where $B'\subseteq \lnot x\vee B$ and $u_2\ge u$. If $x\not \in A'$ or $\lnot x\not \in B'$, applying the Unfold rule to $\mathcal {F''}_n$ we can split these clauses into clauses subsuming $\{(A\vee B,u),\ (x\vee A\vee \overline{B},u),\ (\lnot x\vee B\vee \overline{A},u)\}$ with higher weights. Otherwise, we apply the Unfold rule to obtain r copies of $(A',u)$ and r copies of $(B',u)$, plus some useless clauses. The application of the Cut rule to one copy of $(A',u)$ and one of $(B',u)$ results in a clause that subsumes $(A\cup B,u)$. There are also at least |B| more copies of $(A',u)$ that will subsume the clauses $(x\vee A\vee \overline{B},u)$, and at least |A| more copies of $(B',u)$ that will subsume the clauses $(\lnot x\vee B\vee \overline{A},u)$.

Notice that the length of the proof is multiplied by $\mathcal {O}(n)$. The weights are multiplied by $\mathcal {O}^m(n)$, hence its logarithmic representation is multiplied by $m\,\mathcal {O}(\log n)$.    $\blacksquare$

Corollary 3

  The circular proofs system using $\{\textsc {Cut},\ \textsc {k}\text {-}\textsc {Split}\}$ is polynomially equivalent to the weighted proofs system using $\{\textsc {MaxSAT}\, \textsc {Resolution}, \ \textsc {k}\text {-}\textsc {Split}\}$.

Proof

From Lemma 6 and Lemmas 4 and 5.

In [13], it is proved that MaxSAT Resolution with Extension can simulate Dual-Rail MaxSAT. Next we prove that even using 0-Split instead of Split, it can simulate Weighted Dual-Rail, and as a consequence the weaker system Dual-Rail MaxSAT.

Theorem 1

The weighted proof system using $\mathcal {R}=\{\textsc {MaxSAT}\, \textsc {Resolution},$ $0\text {-}\textsc {Split}\}$ polynomially simulates the Weighted Dual-Rail MaxSAT proof system.

Proof

Let $\mathcal {F}_1\vdash \cdots \vdash \mathcal {F}_m$ be a proof in weighted dual-rail MaxSAT. Let $A^{rdr}$ be the reverse of the dual-rail encoding, i.e. the substitution of variable $p_i$ by $x_i$ and of $n_i$ by $\lnot x_i$. Applying this translation we get $\mathcal {F}_1^{rdr}=\{(A,u_A)\mid A\in \mathcal {H}\}\cup \{(x_i,v_i),(\lnot x_i,v_i)\mid i=1,\dots ,n\}$ and where all clauses in F have positive weight. Moreover, all steps in the proof satisfy $\mathcal {F}_{i}^{rdr}\vdash \mathcal {F}_{i+1}^{rdr}$, since all MaxSAT cuts between $p_i$ and $\lnot p_i$, or between $n_i$ and $\lnot n_i$ will become cuts of $x_i$ and $\lnot x_i$. Notice that clauses $\lnot p_i\vee \lnot n_i$ are translated back as $x_i\vee \lnot x_i$, hence tautologies and removed. Cuts in $\mathcal {F}_1\vdash \cdots \vdash \mathcal {F}_m$ with $\lnot p_i\vee \lnot n_i$, when translated back, have not any effect (they replace $p_i$ by $\lnot n_i$ or $n_i$ by $\lnot p_i$, hence $x_i$ by $x_i$), thus they are removed. We can construct then the following weighted proof using $\mathcal {R}$:

that is a valid weighted proof for .    $\blacksquare$

Corollary 4

The circular proof system using $\mathcal {R}=\{\textsc {Cut},\ 0\text {-}\textsc {Split}\}$ polynomially simulates the Weighted Dual-Rail MaxSAT proof system.

Proof

Weighted Dual-Rail MaxSAT is polynomially simulated by weighted proofs using $\{\textsc {MaxSAT}\, \textsc {Resolution},\ 0\text {-}\textsc {Split}\}$, by Theorem 1. This is simulated by weighted proofs using $\{\textsc {Cut},\ 0\text {-}\textsc {Split}\}$, by Lemma 6. And this is simulated by circular proofs using $\{\textsc {Cut},\ 0\text {-}\textsc {Split}\}$, by Lemma 4.

6 Conclusions

We have shown how circular proofs and weighted proofs (with positive and negative weights), both parametric in the set of inference rules, are equivalent proof systems. We have also shown that if Split is one of such inference rules, then it does not matter if the other rule is Cut, MaxSAT Resolution or Symmetric Cut. In all the cases, we get polynomially equivalent proof systems. This proves the equivalence of Circular Resolution [1] and MaxSAT Resolution with extensions [13].

In these formalisms, if we restrict the Split rule to clauses of length zero (as ), together with the Cut rule, we still get a strong enough proof system enable to simulate Weighted Dual-Rail MaxSAT [3, 9] and to get polynomial proofs of the pigeonhole principle.