Abstract
We address the problem of proving the satisfiability of Constrained Horn Clauses (CHCs) with Algebraic Data Types (ADTs), such as lists and trees. We propose a new technique for transforming CHCs with ADTs into CHCs where predicates are defined over basic types, such as integers and booleans, only. Thus, our technique avoids the explicit use of inductive proof rules during satisfiability proofs. The main extension over previous techniques for ADT removal is a new transformation rule, called differential replacement, which allows us to introduce auxiliary predicates corresponding to the lemmas used when making inductive proofs. We present an algorithm that applies the new rule, together with the traditional folding/unfolding rules, for the automatic removal of ADTs. We prove that if the set of the transformed clauses is satisfiable, then so is the set of the original clauses. By an experimental evaluation, we show that the use of the new rule significantly improves the effectiveness of ADT removal, and that our approach is competitive with respect to a state-of-the-art tool that extends the CVC4 solver with induction.
This work has been partially supported by GNCS-INdAM, Italy.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Constrained Horn Clauses (CHCs) constitute a fragment of the first order predicate calculus, where the Horn clause format is extended by allowing constraints on specific domains to occur in clause premises. CHCs have gained popularity as a suitable logical formalism for automatic program verification [3]. Indeed, many verification problems can be reduced to the satisfiability problem for CHCs.
Satisfiability of CHCs is a particular case of Satisfiability Modulo Theories (SMT), understood here as the general problem of determining the satisfiability of (possibly quantified) first order formulas where the interpretation of some function and predicate symbols is defined in a given constraint (or background) theory [2]. Recent advances in the field have led to the development of a number of very powerful SMT (and, in particular, CHC) solvers, which aim at solving satisfiability problems with respect to a large variety of constraint theories. Among SMT solvers, we would like to mention CVC4 [1], MathSAT [5], and Z3 [14], and among solvers with specialized engines for CHCs, we recall Eldarica [22], HSF [20], RAHFT [26], and Spacer [29].
Even if SMT algorithms for unrestricted first order formulas suffer from incompleteness limitations due to general undecidability results, most of the above mentioned tools work well in practice when acting on constraint theories, such as Booleans, Uninterpreted Function Symbols, Linear Integer or Real Arithmetic, Bit Vectors, and Arrays. However, when formulas contain universally quantified variables ranging over inductively defined algebraic data types (ADTs), such as lists and trees, then the SMT/CHC solvers often show a very poor performance, as they do not incorporate induction principles relative to the ADT in use.
To mitigate this difficulty, some SMT/CHC solvers have been enhanced by incorporating appropriate induction principles [38, 43, 44], similarly to what has been done in automated theorem provers [4]. The most creative step which is needed when extending SMT solving with induction, is the generation of the auxiliary lemmas that are required for proving the main conjecture.
An alternative approach, proposed in the context of CHCs [10], consists in transforming a given set of clauses into a new set: (i) where all ADT terms are removed (without introducing new function symbols), and (ii) whose satisfiability implies the satisfiability of the original set of clauses. This approach has the advantage of separating the concern of dealing with ADTs (at transformation time) from the concern of dealing with simpler, non-inductive constraint theories (at solving time), thus avoiding the complex interaction between inductive reasoning and constraint solving. It has been shown [10] that the transformational approach compares well with induction-based tools in the case where lemmas are not needed in the proofs. However, in some satisfiability problems, if suitable lemmas are not provided, the transformation fails to remove the ADT terms.
The main contributions of this paper are as follows.
-
(1)
We extend the transformational approach by proposing a new rule, called differential replacement, based on the introduction of suitable difference predicates, which play a role similar to that of lemmas in inductive proofs. We prove that the combined use of the fold/unfold transformation rules [17] and the differential replacement rule is sound, that is, if the transformed set of clauses is satisfiable, then the original set of clauses is satisfiable.
-
(2)
We develop a transformation algorithm that removes ADTs from CHCs by applying the fold/unfold and the differential replacement rules in a fully automated way.
-
(3)
Due to the undecidability of the satisfiability problem for CHCs, our technique for ADT removal is incomplete. Thus, we evaluate its effectiveness from an experimental point of view, and in particular we discuss the results obtained by the implementation of our technique in a tool, called AdtRem. We consider a set of CHC satisfiability problems on ADTs taken from various benchmarks which are used for evaluating inductive theorem provers. The experiments show that AdtRem is competitive with respect to Reynolds and Kuncak’s tool that augments the CVC4 solver with inductive reasoning [38].
The paper is structured as follows. In Sect. 2 we present an introductory, motivating example. In Sect. 3 we recall some basic notions about CHCs. In Sect. 4 we introduce the rules used in our transformation technique and, in particular, the novel differential replacement rule, and we show their soundness. In Sect. 5 we present a transformation algorithm that uses the transformation rules for removing ADTs from sets of CHCs. In Sect. 6 we illustrate the AdtRem tool and we present the experimental results we have obtained. Finally, in Sect. 7 we discuss the related work and make some concluding remarks.
2 A Motivating Example
Let us consider the following functional program \( Reverse \), which we write using the OCaml syntax [31]:

The functions append, rev, and len compute list concatenation, list reversal, and list length, respectively. Suppose we want to prove the following property:
Inductive theorem provers construct a proof of this property by induction on the structure of the list \(\mathtt {l}\), by assuming the knowledge of the following lemma:
The approach we follow in this paper avoids the explicit use of induction principles and also the knowledge of ad hoc lemmas. First, we consider the translation of Property (1) into a set of constrained Horn clauses [10, 43], as followsFootnote 1:

The set of clauses 1–7 is satisfiable if and only if Property (1) holds. However, state-of-the-art CHC solvers, such as Z3 or Eldarica, fail to prove the satisfiability of clauses 1–7, because those solvers do not incorporate any induction principle on lists. Moreover, some tools that extend SMT solvers with induction [38, 43] fail on this particular example because they are not able to introduce Lemma (2).
To overcome this difficulty, we apply the transformational approach based on the fold/unfold rules [10], whose objective is to transform a given set of clauses into a new set without occurrences of list variables, whose satisfiability can be checked by using CHC solvers based on the theory of Linear Integer Arithmetic only. The soundness of the transformation rules ensures that the satisfiability of the transformed clauses implies the satisfiability of the original ones. We apply the Elimination Algorithm [10] as follows. First, we introduce a new clause:

whose body is made out of the atoms of clause 1 which have at least one list variable, and whose head arguments are the integer variables of the body. By folding, from clause 1 we derive a new clause without occurrences of lists:

We proceed by eliminating lists from clause 8. By unfolding clause 8, we replace some predicate calls by their definitions and we derive the two new clauses:

We would like to fold clause 11 using clause 8, so as to derive a recursive definition of new1 without lists. Unfortunately, this folding step cannot be performed because the body of clause 11 does not contain a variant of the body of clause 8, and hence the Elimination Algorithm fails to eliminate lists in this example.
Thus, now we depart from the Elimination Algorithm and we continue our derivation by observing that the body of clause 11 contains the subconjunction ‘append(Xs,Ys,Zs), rev(Zs,Rs), len(Xs,N0), len(Ys,N1)’ of the body of clause 8. Then, in order to find a variant of the whole body of clause 8, we may replace in clause 11 the remaining subconjunction ‘append(Rs,[X],R1s), len(R1s,N21)’ by the new subconjunction ‘len(Rs,N2), diff(N2,X,N21)’, where diff is a predicate, called difference predicate, defined as follows:

From clause 11, by performing that replacement, we derive the following clause:

Now, we can fold clause 13 using clause 8 and we derive a new clause without list arguments:

At this point, we are left with the task of removing list arguments from clauses 10 and 12. As the reader may verify, this can be done by applying the Elimination Algorithm without the need of introducing additional difference predicates. By doing so, we get the following final set of clauses without list arguments:

The Eldarica CHC solver proves the satisfiability of this set of clauses by computing the following model (here we use a Prolog-like syntax):

Finally, we note that if in clause 12 we substitute the atom diff(N2,X,N21) by its model computed by Eldarica, namely the constraint ‘N21=N2+1, N2>=0’, we get exactly the CHC translation of Lemma (2). Thus, in some cases, the introduction of the difference predicates can be viewed as a way of automatically introducing the lemmas needed when performing inductive proofs.
3 Constrained Horn Clauses
Let LIA be the theory of linear integer arithmetic and Bool be the theory of boolean values. A constraint is a quantifier-free formula of \(\textit{LIA}\cup \textit{Bool}\). Let \(\mathcal C\) denote the set of all constraints. Let \(\mathcal L\) be a typed first order language with equality [16] which includes the language of \(\textit{LIA}\cup \textit{Bool}\). Let \(\textit{Pred}\) be a set of predicate symbols in \(\mathcal L\) not occurring in the language of \(\textit{LIA}\cup \textit{Bool}\).
The integer and boolean types are said to be the basic types. For reasons of simplicity we do not consider any other basic types, such as real number, arrays, and bit-vectors, which are usually supported by SMT solvers [1, 14, 22]. We assume that all non-basic types are specified by suitable data-type declarations (such as the declare-datatypes declarations adopted by SMT solvers), and are collectively called algebraic data types (ADTs).
An atom is a formula of the form \(p(t_{1},\ldots ,t_{m})\), where p is a typed predicate symbol in \(\textit{Pred}\), and \(t_{1},\ldots ,t_{m}\) are typed terms constructed out of individual variables, individual constants, and function symbols. A constrained Horn clause (or simply, a clause, or a CHC) is an implication of the form \(A\leftarrow c, B\) (for clauses we use the logic programming notation, where comma denotes conjunction). The conclusion (or head) A is either an atom or false, the premise (or body) is the conjunction of a constraint \(c\in \mathcal C\), and a (possibly empty) conjunction B of atoms. If A is an atom of the form \(p(t_{1},\ldots ,t_{n})\), the predicate p is said to be a head predicate. A clause whose head is an atom is called a definite clause, and a clause whose head is false is called a goal.
We assume that all variables in a clause are universally quantified in front, and thus we can freely rename those variables. Clause C is said to be a variant of clause D if C can be obtained from D by renaming variables and rearranging the order of the atoms in its body. Given a term t, by \({ vars}(t)\) we denote the set of all variables occurring in t. Similarly for the set of all free variables occurring in a formula. Given a formula \(\varphi \) in \({\mathcal L}\), we denote by \(\forall (\varphi )\) its universal closure.
Let \(\mathbb D\) be the usual interpretation for the symbols in \(\textit{LIA}\cup \textit{Bool}\), and let a \({\mathbb D}\)-interpretation be an interpretation of \(\mathcal L\) that, for all symbols occurring in \(\textit{LIA}\cup \textit{Bool}\), agrees with \({\mathbb D}\).
A set P of CHCs is satisfiable if it has a \({\mathbb D}\)-model and it is unsatisfiable, otherwise. Given two \({\mathbb D}\)-interpretations \(\mathbb I\) and \(\mathbb J,\) we say that \(\mathbb I\) is included in \(\mathbb J\) if for all ground atoms A, \(\mathbb I\models A\) implies \(\mathbb J\models A\). Every set P of definite clauses is satisfiable and has a least (with respect to inclusion) \({\mathbb D}\)-model, denoted M(P) [24]. Thus, if P is any set of constrained Horn clauses and Q is the set of the goals in P, then we define \(\textit{Definite}(P) \!=\! P \setminus Q\). We have that P is satisfiable if and only if \(M(\textit{Definite}(P))\models Q\).
We will often use tuples of variables as arguments of predicates and write p(X, Y), instead of \(p(X_{1},\ldots ,X_{m}, Y_{1},\ldots ,Y_{n})\), whenever the values of \(m~(\ge 0)\) and \(n~(\ge 0)\) are not relevant. Whenever the order of the variables is not relevant, we will feel free to identify tuples of distinct variables with finite sets, and we will extend to finite tuples the usual operations and relations on finite sets. Given two tuples X and Y of distinct elements, (i) their union \(X\cup Y\) is obtained by concatenating them and removing all duplicated occurrences of elements, (ii) their intersection \(X\cap Y\) is obtained by removing from X the elements which do not occur in Y, (iii) their difference \(X \!\setminus \!Y\) is obtained by removing from X the elements which occur in Y, and (iv) \(X\!\subseteq \! Y\) holds if every element of X occurs in Y. For all \(m\,\!\ge \!\,0\), \((u_{1},\ldots ,u_{m})\) = \((v_{1},\ldots ,v_{m})\) iff \(\bigwedge _{i=1}^{m}u_{i}\!=\!v_{i}\). The empty tuple () is identified with the empty set \(\emptyset \).
By A(X, Y), where X and Y are disjoint tuples of distinct variables, we denote an atom A such that \( vars (A) = X\cup Y\). Let P be a set of definite clauses. We say that the atom A(X, Y) is functional from X to Y with respect to P if
(F1) \(M(P) \models \forall X, Y, Z.\ A(X,Y) \wedge A(X,Z) ~\rightarrow ~ Y\!=\!Z\)
The reference to the set P of definite clauses is omitted, when understood from the context. Given a functional atom A(X, Y), we say that X and Y are its input and output (tuples of) variables, respectively. The atom A(X, Y) is said to be total from X to Y with respect to P if
(F2) \(M(P) \models \forall X \exists Y.\ A(X,Y)\)
If A(X, Y) is a total, functional atom from X to Y, we may write A(X; Y), instead of A(X, Y). For instance, append(Xs,Ys,Zs) is a total, functional atom from (Xs,Ys) to Zs with respect to the set of clauses 1–7 of Sect. 2.
Now we extend the above notions from atoms to conjunctions of atoms. Let F be a conjunction \(A_1(X_1;Y_1), \ldots ,A_n(X_n;Y_n)\) such that: (i) \(X\! = \!(\bigcup ^n_{i=1} X_i)\!\setminus \!(\bigcup ^n_{i=1} Y_i)\), (ii) \(Y \! = \! (\bigcup ^n_{i=1} Y_i)\), and (iii) for \(i\!=\!1,\ldots ,n,\) \(Y_i\) is disjoint from \((\bigcup ^i_{j=1} X_j) \cup (\bigcup ^{i-1}_{j=1} Y_j)\). Then, the conjunction F is said to be a total, functional conjunction from X to Y and it is also written as F(X; Y). For F(X; Y), the above properties (F1) and (F2) hold if we replace A by F. For instance, append(Xs,Ys,Zs), rev(Zs,Rs) is a total, functional conjunction from (Xs,Ys) to (Zs,Rs) with respect to the set of clauses 1–7 of Sect. 2.
4 Transformation Rules for Constrained Horn Clauses
In this section we present the rules that we propose for transforming CHCs, and in particular, for introducing difference predicates, and we prove their soundness. We refer to Sect. 2 for examples of how the rules are applied.
First, we introduce the following notion of a stratification for a set of clauses. Let \(\mathbb N\) denote the set of the natural numbers. A level mapping is a function \(\ell \!: Pred \!\rightarrow \!\mathbb {N}\). For every predicate p, the natural number \(\ell (p)\) is said to be the level of p. Level mappings are extended to atoms by stating that the level \(\ell (A)\) of an atom A is the level of its predicate symbol. A clause \( H\leftarrow c, A_{1}, \ldots , A_{n} \) is stratified with respect to \(\ell \) if, for \( i\!=\!1,\ldots ,n \), \(\ell (H)\ge \ell (A_i)\). A set P of CHCs is stratified w.r.t. \(\ell \) if all clauses in P are stratified w.r.t. \(\ell \). Clearly, for every set P of CHCs, there exists a level mapping \(\ell \) such that P is stratified w.r.t. \(\ell \) [33].
A transformation sequence from \(P_{0}\) to \(P_{n}\) is a sequence \(P_0 \Rightarrow P_1 \Rightarrow \ldots \Rightarrow P_n\) of sets of CHCs such that, for \(i\!=\!0,\ldots ,n\!-\!1,\) \(P_{i+1}\) is derived from \(P_i\), denoted \(P_{i} \Rightarrow P_{i+1}\), by applying one of the following Rules R1–R7. We assume that \(P_0\) is stratified w.r.t. a given level mapping \(\ell \).
(R1) Definition Rule. Let D be the clause \(\textit{newp}(X_1,\ldots ,X_k)\leftarrow c,A_1,\ldots ,A_n\), where: (i) newp is a predicate symbol in \(\textit{Pred}\) not occurring in the sequence \(P_0\Rightarrow P_1\Rightarrow \ldots \Rightarrow P_i\), (ii) c is a constraint, (iii) the predicate symbols of \(A_1,\ldots ,A_n\) occur in \(P_0\), and (iv) \((X_1,\ldots ,X_k)\subseteq vars (c,A_1,\ldots ,A_n)\). Then, \(P_{i+1}= P_i\cup \{D\}\). We set \(\ell (\textit{newp})=\textit{max}\,\{\ell (A_i) \mid i=1,\ldots ,n\}\).
For \(i\!=\!0,\ldots , n\), by \(\textit{Defs}_i\) we denote the set of clauses, called definitions, introduced by Rule R1 during the construction of \(P_0\Rightarrow P_1\Rightarrow \ldots \Rightarrow P_i\). Thus, \(\emptyset \!=\!\textit{Defs}_0\!\subseteq \!\textit{Defs}_1\!\subseteq \!\ldots .\) However, by using Rules R2–R7 we can replace a definition in \(P_i\), for \(i\!>\!0\), and hence it may happen that \(\textit{Defs}_{i+1}\!\not \subseteq \!P_{i+1}\).
(R2) Unfolding Rule. Let C: \(H\leftarrow c,G_L,A,G_R\) be a clause in \(P_i\), where A is an atom. Without loss of generality, we assume that \( vars (C)\cap vars (P_0)=\emptyset \). Let Cls: \(\{K_{1}\leftarrow c_{1}, B_{1},~\ldots ,~K_{m}\leftarrow c_{m}, B_{m}\}\), \(m\ge 0\), be the set of clauses in \(P_0\), such that: for \(j=1,\ldots ,m\), (1) there exists a most general unifier \(\vartheta _j\) of A and \(K_j\), and (2) the conjunction of constraints \((c, c_{j})\vartheta _j\) is satisfiable. Let \( Unf (C,A,P_0) = \{(H\leftarrow c, {c}_j,G_L, B_j, G_R) \vartheta _j \mid j=1, \ldots , m\}\). Then, by unfolding C w.r.t. A, we derive the set \( Unf (C,A,P_0)\) of clauses and we get \(P_{i+1}= (P_i\setminus \{C\}) \cup Unf (C,A,P_0)\).
When we apply Rule R2, we say that, for \(j=1, \ldots , m,\) the atoms in the conjunction \(B_j \vartheta _j\) are derived from A, and the atoms in the conjunction \((G_L, G_R) \vartheta _j\) are inherited from the corresponding atoms in the body of C.
(R3) Folding Rule. Let C: \(H\leftarrow c, G_L,Q,G_R\) be a clause in \(P_i\), and let D: \(K \leftarrow d, B\) be a clause in \(\textit{Defs}_i\). Suppose that: (i) either H is \( false \) or \(\ell (H) \ge \ell (K)\), and (ii) there exists a substitution \(\vartheta \) such that \(Q\!=\! B\vartheta \) and \(\mathbb D\models \forall (c \rightarrow d\vartheta )\). By folding \( C\) using definition \( D\), we derive clause \(E \): \( H\leftarrow c, G_L, K\vartheta , G_{R} \), and we get \( P_{i+1}= (P_{i}\setminus \{C\})\cup \{E \} \).
(R4) Clause Deletion Rule. Let C: \(H\leftarrow c,G\) be a clause in \(P_i\) such that the constraint c is unsatisfiable. Then, we get \(P_{i+1} = P_i \setminus \{C\}\).
(R5) Functionality Rule. Let C: \(H\leftarrow c, G_L,F(X;Y),F(X;Z), G_R\) be a clause in \(P_i\), where F(X; Y) is a total, functional conjunction in \( Definite (P_0)\cup Defs _i\). By functionality, from C we derive clause D: \(H\leftarrow c, Y\!=\!Z, G_L,F(X;Y),G_R\), and we get \( P_{i+1}= (P_{i}\setminus \{C\})\cup \{D \} \).
(R6) Totality Rule. Let C: \(H\leftarrow c, G_L,F(X;Y),G_R\) be a clause in \(P_i\) such that \(Y \cap vars (H\leftarrow c, G_L,G_R) = \emptyset \) and F(X; Y) is a total, functional conjunction in \( Definite (P_0)\cup Defs _i\). By totality, from C we derive clause D : \(H\leftarrow c, G_L,G_R\) and we get \( P_{i+1}= (P_{i}\setminus \{C\})\cup \{D \} \).
Since the initial set of clauses is obtained by translating a terminating functional program, the functionality and totality properties hold by construction and we do not need to prove them when we apply Rules R5 and R6.
(R7) Differential Replacement Rule. Let C: \(H\leftarrow c, G_L,F(X;Y),G_R\) be a clause in \(P_i\), and let D: \( diff (Z) \leftarrow d, F(X;Y), R(V;W)\) be a definition clause in \( Defs _i\), where: (i) F(X; Y) and R(V; W) are total, functional conjunctions with respect to \( Definite (P_0)\cup Defs _i\), (ii) \(W \cap vars (C) = \emptyset \), (iii) \(\mathbb {D}\models \forall (c\rightarrow d)\), and (iv) \(\ell (H)\!>\!\ell ( diff )\). By differential replacement, we derive E: \(H\!\leftarrow \!c, G_{\!L},R(V;\!W), diff (Z), G_{\!R}\) and we get \( P_{i+1}= (P_{i}\setminus \{C\}) \cup \{E \} \).
Rule R7 has a very general formulation that eases the proof of the Soundness Theorem, which extends to Rules R1–R7 correctness results for transformations of (constraint) logic programs [17, 18, 39, 42] (see [13] for a proof). In the transformation algorithm of Sect. 5, we will use a specific instance of Rule R7 which is sufficient for ADT removal (see, in particular, the Diff-Introduce step).
Theorem 1 (Soundness)
Let \(P_0 \Rightarrow P_1 \Rightarrow \ldots \Rightarrow P_n\) be a transformation sequence using Rules R1–R7. Suppose that the following condition holds :
- (U):
-
for \(i \!=\! 1,\ldots ,n\!-\!1\), if \(P_i \Rightarrow P_{i+1}\) by folding a clause in \(P_i\) using a definition \(D\!: H \leftarrow c,B\) in \( Defs _i\), then, for some \(j\! \in \!\{1,\ldots ,i\!-\!1,i\!+\!1,\ldots , n\!-\!1\}\), \( P_{j}\Rightarrow P_{j+1}\) by unfolding D with respect to an atom A such that \(\ell (H)=\ell (A)\).
If \(P_n\) is satisfiable, then \(P_0\) is satisfiable.
Thus, to prove the satisfiability of a set \(P_0\) of clauses, it suffices: (i) to construct a transformation sequence \(P_0 \Rightarrow \ldots \Rightarrow P_n\), and then (ii) to prove that \(P_n\) is satisfiable. Note, however, that if Rule R7 is used, it may happen that \(P_0\) is satisfiable and \(P_n\) is unsatisfiable, that is, some false counterexamples to satisfiability, so-called false positives, may be generated, as we now show.
Example 1
Let us consider the following set \(P_{1}\) of clauses derived by adding the definition clause D to the initial set \(P_{0}\!=\!\{{\mathtt{{C,1,2,3}}}\}\) of clauses:

where: (i) a(X,Y) is a total, functional atom from X to Y, (ii) r(X,W) is a total, functional atom from X to W, and (iii) D is a definition in \( Defs _{1}\). By applying Rule R7, from \(P_{1}\) we derive the set \(P_{2}\!=\!\{{\mathtt{{E,1,2,3,D}}}\}\) of clauses where:

Now we have that \(P_{0}\) is satisfiable, while \(P_{2}\) is unsatisfiable.
5 An Algorithm for ADT Removal
Now we present Algorithm \({\mathcal R}\) for eliminating ADT terms from CHCs by using the transformation rules presented in Sect. 4 and automatically introducing suitable difference predicates. If \({\mathcal R}\) terminates, it transforms a set Cls of clauses into a new set \( TransfCls \) where the arguments of all predicates have basic type. Theorem 1 guarantees that if \( TransfCls \) is satisfiable, then also Cls is satisfiable.
Algorithm \({\mathcal R}\) (see Fig. 1) removes ADT terms starting from the set \( Gs \) of goals in \( Cls \). \({\mathcal R}\) collects these goals in \( InCls \) and stores in \( Defs \) the definitions of new predicates introduced by Rule R1.
Before describing the procedures used by Algorithm \({\mathcal R}\), let us first introduce the following notions.
Given a conjunction G of atoms, \( bvars (G)\) (or \( adt{-}vars (G)\)) denotes the set of variables in G that have a basic type (or an ADT type, respectively). We say that an atom (or clause) has basic types if all its arguments (or atoms, respectively) have a basic type. An atom (or clause) has ADTs if at least one of its arguments (or atoms, respectively) has an ADT type.
Given a set (or a conjunction) S of atoms, \( SharingBlocks (S)\) denotes the partition of S with respect to the reflexive, transitive closure \(\Downarrow _S\) of the relation \(\downarrow _S\) defined as follows. Given two atoms \(A_1\) and \(A_2\) in S, \(A_1\! \downarrow _S\! A_2\) holds iff \( adt \text {-} vars (A_1) \cap adt \text {-} vars (A_2)\!\ne \! \emptyset \). The elements of the partition are called the sharing blocks of S.
A generalization of a pair \((c_1,c_2)\) of constraints is a constraint \(\alpha (c_1,c_2)\) such that \(\mathbb D \models \forall (c_1 \rightarrow \alpha (c_1,c_2))\) and \(\mathbb D \models \forall (c_2 \rightarrow \alpha (c_1,c_2))\) [19]. In particular, we consider the following generalization operator based on widening [7]. Suppose that \(c_1\) is the conjunction \((a_1,\ldots ,a_m)\) of atomic constraints, then \(\alpha (c_1,c_2)\) is defined as the conjunction of all \(a_i\)’s in \((a_1,\ldots ,a_m)\) such that \(\mathbb {D}\models \forall (c_2\! \rightarrow \! a_i)\). For any constraint c and tuple V of variables, the projection of c onto V is a constraint \(\pi (c,V)\) such that: (i) \( vars (\pi (c,V))\!\subseteq \! V\), and (ii) \(\mathbb D \models \forall (c\!\rightarrow \!\pi (c,V))\). In our implementation, \(\pi (c,V)\) is computed from \(\exists Y. c\), where \(Y\!=\! vars (c) \setminus V\), by a quantifier elimination algorithm in the theory of booleans and rational numbers. This implementation is safe in our context, and avoids relying on modular arithmetic, as is often done when eliminating quantifiers in LIA [37].
For two conjunctions \(G_1\) and \(G_2\) of atoms,  holds if \(G_1\!=\!(A_1,\ldots ,A_n)\) and there exists a subconjunction \((B_{1},\ldots , B_{n})\) of \(G_2\) (modulo reordering) such that, for \(i\!=\!1,\ldots ,n,\) \(B_i\) is an instance of \(A_i\). A conjunction G of atoms is connected if it consists of a single sharing block.
holds if \(G_1\!=\!(A_1,\ldots ,A_n)\) and there exists a subconjunction \((B_{1},\ldots , B_{n})\) of \(G_2\) (modulo reordering) such that, for \(i\!=\!1,\ldots ,n,\) \(B_i\) is an instance of \(A_i\). A conjunction G of atoms is connected if it consists of a single sharing block.
\(\scriptstyle \blacksquare \) Procedure \( Diff \text {-} Define \text {-} Fold \) (see Fig. 2). At each iteration of the body of the for loop, the \( Diff \text {-} Define \text {-} Fold \) procedure removes the ADT terms occurring in a sharing block B of the body of a clause \(C\!:\) \(H\!\leftarrow \! c, B, G'\) of \( InCls \). This is done by possibly introducing some new definitions (using Rule R1) and applying the Folding Rule R3. To allow folding, some applications of the Differential Replacement Rule R7 may be needed. We have the following four cases.
\(\bullet \) (Fold). We remove the ADT arguments occurring in B by folding C using a definition D introduced at a previous step. Indeed, the head of each definition introduced by Algorithm \({\mathcal R}\) is by construction a tuple of variables of basic type.
\(\bullet \) (Generalize). We introduce a new definition \( GenD \!:\) \( genp (V) \leftarrow \alpha (d,c), B\) whose constraint is obtained by generalizing (d, c), where d is the constraint occurring in an already available definition whose body is B. Then, we remove the ADT arguments occurring in B by folding C using \( GenD \).
\(\bullet \) (Diff-Introduce). Suppose that B partially matches the body of an available definition D: \( newp (U) \leftarrow d, B'\), that is, for some substitution \(\vartheta \), \(B=(M, F(X;Y))\), and \(B'\vartheta =(M, R(V;W))\). Then, we introduce a difference predicate through the new definition \(\widehat{D}\): \( diff (Z) \leftarrow \pi (c,X),F(X;Y),R(V;W),\) where \(Z\!=\! bvars (F(X;Y),R(V;W))\) and, by Rule R7, we replace the conjunction F(X; Y) by \((R(V;W), diff (Z))\) in the body of C, thereby deriving \(C'\). Finally, we remove the ADT arguments in B by folding \(C'\) using either D or a clause \( GenD \) whose constraint is a generalization of the pair \((d\vartheta ,c)\) of constraints.
The example of Sect. 2 allows us to illustrate this (Diff-Introduce) case. With reference to that example, clause C: \(H\!\leftarrow \! c, G\) that we want to fold is clause 11, whose body has the single sharing block B: ‘append(Xs,Ys,Zs), rev(Zs,Rs), len(Xs,N0), len(Ys,N1), append(Rs,[X],R1s), len(R1s,N21)’. Block B partially matches the body ‘append(Xs,Ys,Zs), rev(Zs,Rs), len(Xs,N0), len(Ys,N1), len(Rs,N2)’ of clause 8 of Sect. 2 which plays the role of definition D: \( newp (U)\! \leftarrow \! d, B'\) in this example. Indeed, we have that:
M= (append(Xs,Ys,Zs), rev(Zs,Rs), len(Xs,N0), len(Ys,N1)),
 , where X=(Rs,X), Y=(R1s,N21),
, where X=(Rs,X), Y=(R1s,N21),
R(V; W) = len(Rs,N2), where V= (Rs), Y= (N2).
In this example, \(\vartheta \) is the identity substitution. Morevover, the condition on the level mapping \(\ell \) required in the Diff-Define-Fold Procedure of Fig. 2 can be fulfilled by stipulating that
 and
and
 . Thus, the definition \(\widehat{D}\) to be introduced is:
. Thus, the definition \(\widehat{D}\) to be introduced is:

Indeed, we have that: (i) the projection \(\pi (c,X)\) is
 , that is, the empty conjunction, (ii) \(F(X;Y),\ R(V;W)\) is the body of clause 12, and (iii) the head variables N2, X, and N21 are the integer variables in that body. Then, by applying Rule R7, we replace in clause 11 the conjunction ‘append(Rs,[X],R1s), len(R1s,N21)’ by the new conjunction ‘len(Rs,N2), diff(N2,X,N21)’, hence deriving clause \(C'\), which is clause 13 of Sect. 2. Finally, by folding clause 13 using clause 8, we derive clause 14 of Sect. 2, which has no list arguments.
, that is, the empty conjunction, (ii) \(F(X;Y),\ R(V;W)\) is the body of clause 12, and (iii) the head variables N2, X, and N21 are the integer variables in that body. Then, by applying Rule R7, we replace in clause 11 the conjunction ‘append(Rs,[X],R1s), len(R1s,N21)’ by the new conjunction ‘len(Rs,N2), diff(N2,X,N21)’, hence deriving clause \(C'\), which is clause 13 of Sect. 2. Finally, by folding clause 13 using clause 8, we derive clause 14 of Sect. 2, which has no list arguments.
\(\bullet \) (Project). If none of the previous three cases apply, then we introduce a new definition \( ProjC \): \( newp (V) \leftarrow \pi (c,V), B,\) where \(V= bvars (B)\). Then, we remove the ADT arguments occurring in B by folding C using \( ProjC \).
The \( Diff \text {-} Define \text {-} Fold \) procedure may introduce new definitions with ADTs in their bodies, which are added to NewDefs and processed by the \( Unfold \) procedure. In order to present this procedure, we need the following notions.
The application of Rule R2 is controlled by marking some atoms in the body of a clause as unfoldable. If we unfold w.r.t. atom A clause C: \(H \!\leftarrow c, L, A, R\) the marking of the clauses in \( Unf(C,A,Ds) \) is handled as follows: the atoms derived from A are not marked as unfoldable and each atom \(A''\) inherited from an atom \(A'\) in the body of C is marked as unfoldable iff \(A'\) is marked as unfoldable.
An atom A(X; Y) in a conjunction F(V; Z) of atoms is said to be a source atom if \(X\!\subseteq \! V\). Thus, a source atom corresponds to an innermost function call in a given functional expression. For instance, in clause 1 of Sect. 2, the source atoms are append(Xs,Ys,Zs), len(Xs,N0), and len(Ys,N1). Indeed, the body of clause 1 corresponds to
 .
.
An atom A(X; Y) in the body of clause C: \(H \leftarrow c, {L}, A(X;Y), {R}\) is a head-instance w.r.t. a set Ds of clauses if, for every clause \(K\leftarrow d, B\) in Ds such that: (1) there exists a most general unifier \(\vartheta \) of A(X; Y) and K, and (2) the constraint \((c, d)\vartheta \) is satisfiable, we have that \(X\vartheta \! =\! X\). Thus, the input variables of A(X; Y) are not instantiated by unification. For instance, the atom append([X|Xs],Ys,Zs) is a head-instance, while append(Xs,Ys,Zs) is not.
In a set Cls of clauses, predicate p immediately depends on predicate q, if in Cls there is a clause of the form \(p(\ldots ) \leftarrow \ldots , q(\ldots ), \ldots \) The depends on relation is the transitive closure of the immediately depends on relation. Let \(\prec \) be a well-founded ordering on tuples of terms such that, for all terms t, u, if \(t\!\prec \! u\), then, for all substitutions \(\vartheta ,\) \(t\vartheta \!\prec \! u\vartheta \). A predicate p is descending w.r.t. \(\prec \) if, for all clauses, \(p(t;u) \leftarrow c,\, p_1(t_1;u_1),\ldots ,p_n(t_n;u_n),\) for \(i\!=\!1,\ldots ,n,\) if \(p_i\) depends on p then \(t_i\!\prec \! t\). An atom is descending if its predicate is descending. The well-founded ordering \(\prec \) we use in our implementation is based on the subterm relation and is defined as follows: \((x_1,\ldots ,x_k)\!\prec \! (y_1,\ldots ,y_m)\) if every \(x_i\) is a subterm of some \(y_j\) and there exists \(x_i\) which is a strict subterm of some \(y_j\). For instance, the predicates append, rev, and len in the example of Sect. 2 are all descending.
\(\scriptstyle \blacksquare \) Procedure Unfold (see Fig. 3) repeatedly applies Rule R2 in two phases. In Phase 1, the procedure unfolds the clauses in \( NewDefs \) w.r.t. at least one source atom. Then, in Phase 2, clauses are unfolded w.r.t. head-instance atoms. Unfolding is repeated only w.r.t descending atoms. The termination of the Unfold procedure is ensured by the fact that the unfolding w.r.t. a non-descending atom is done at most once in each phase.
\(\scriptstyle \blacksquare \) Procedure Replace simplifies some clauses by applying Rules R5 and R6 as long as possible. Replace terminates because each application of either rule decreases the number of atoms.
Thus, each execution of the Diff-Define-Fold, Unfold, and Replace procedures terminates. However, Algorithm \({\mathcal R}\) might not terminate because new predicates may be introduced by Diff-Define-Fold at each iteration of the while-do of \({\mathcal R}\). Soundness of \({\mathcal R}\) follows from soundness of the transformation rules [13].
Theorem 2
(Soundness of Algorithm \(\mathcal {R}\)). Suppose that Algorithm \({\mathcal R}\) terminates for an input set \( Cls \) of clauses, and let \( TransfCls \) be the output set of clauses. Then, every clause in \( TransfCls \) has basic types, and if \( TransfCls \) is satisfiable, then \( Cls \) is satisfiable.
Algorithm \({\mathcal R}\) is not complete, in the sense that, even if \( Cls \) is a satisfiable set of input clauses, then \({\mathcal R}\) may not terminate or, due to the use of Rule R7, it may terminate with an output set \( TransfCls \) of unsatisfiable clauses, thereby generating a false positive (see Example 1 in Sect. 4). However, due to well-known undecidability results for the satisfiability problem of CHCs, this limitation cannot be overcome, unless we restrict the class of clauses we consider. The study of such restricted classes of clauses is beyond the scope of the present paper and, instead, in the next section, we evaluate the effectiveness of Algorithm \({\mathcal R}\) from an experimental viewpoint.
6 Experimental Evaluation
In this section we present the results of some experiments we have performed for assessing the effectiveness of our transformation-based CHC solving technique. We compare our technique with the one proposed by Reynolds and Kuncak [38], which extends the SMT solver CHC4 with inductive reasoning.
Implementation. We have developed the AdtRem tool for ADT removal, which is based on an implementation of Algorithm \({\mathcal R}\) in the VeriMAP system [8].
Benchmark Suite and Experiments. Our benchmark suite consists of 169 verification problems over inductively defined data structures, such as lists, queues, heaps, and trees, which have been adapted from the benchmark suite considered by Reynolds and Kuncak [38]. These problems come from benchmarks used by various theorem provers: (i) 53 problems come from CLAM [23], (ii) 11 from HipSpec [6], (iii) 63 from IsaPlanner [15, 25], and (iv) 42 from Leon [41]. We have performed the following experiments, whose results are summarized in Table 1 Footnote 2.
(1) We have considered Reynolds and Kuncak’s dtt encoding of the verification problems, where natural numbers are represented using the built-in SMT type Int, and we have discarded: (i) problems that do not use ADTs, and (ii) problems that cannot be directly represented in Horn clause format. Since AdtRem does not support higher order functions, nor user-provided lemmas, in order to make a comparison between the two approaches on a level playing field, we have replaced higher order functions by suitable first order instances and we have removed all auxiliary lemmas from the input verification problems. We have also replaced the basic functions recursively defined over natural numbers, such as the plus and less-or-equal functions, by LIA constraints.
(2) Then, we have translated each verification problem into a set, call it P, of CHCs in the Prolog-like syntax supported by AdtRem by using a modified version of the SMT-LIB parser of the ProB system [32]. We have run Eldarica and Z3 Footnote 3, which use no induction-based mechanism for handling ADTs, to check the satisfiability of P. Rows ‘\(\mathrm {Eldarica}\)’ and ‘\(\mathrm {Z3}\)’ show the number of solved problems, that is, problems whose CHC encoding has been proved satisfiable.
(3) We have run algorithm \({\mathcal R}\) on P to produce a set T of CHCs without ADTs. Row ‘\({\mathcal R}\)’ reports the number of problems for which Algorithm \({\mathcal R}\) terminates.
(4) We have converted T into the SMT-LIB format, and then we have run Eldarica and Z3 for checking its satisfiability. Rows ‘\(\mathrm {Eldarica_{\,noADT}}\)’ and ‘\(\mathrm {Z3_{\,noADT}}\)’ report outside round parentheses the number of solved problems. There was only one false positive (that is, a satisfiable set P of clauses transformed into an unsatisfiable set T), which we have classified as an unsolved problem.
(5) In order to assess the improvements due to the use of the differential replacement rule we have applied to P a modified version, call it \(\mathcal {R}^{\circ }\), of the ADT removal algorithm \({\mathcal R}\) that does not introduce difference predicates, that is, the Diff-Introduce case of the Diff-Define-Fold Procedure of Fig. 2 is never executed. The number of problems for which \(\mathcal {R}^{\circ }\) terminates and the number of solved problems using Eldarica and Z3 are shown within round parentheses in rows ‘\({\mathcal R}\)’, ‘\(\mathrm {Eldarica_{\,noADT}}\)’, and ‘\(\mathrm {Z3_{noADT}}\)’, respectively.
(6) Finally, we have run the cvc4+ig configuration of the CVC4 solver extended with inductive reasoning [38] on the 169 problems in SMT-LIB format obtained at Step (1). Row ‘CVC4+Ind’ reports the number of solved problems.
Evaluation of Results. The results of our experiments show that ADT removal considerably increases the effectiveness of CHC solvers without inductive reasoning support. For instance, Eldarica is able to solve 15 problems out of 169, while it solves 122 problems after the removal of ADTs. When using Z3, the improvement is slightly lower, but still very considerable. Note also that, when the ADT removal terminates (129 problems out of 169), the solvers are very effective (95% successful verifications for Eldarica). The improvements specifically due to the use of the difference replacement rule are demonstrated by the increase of the number of problems for which the ADT removal algorithm terminates (from 94 to 129), and of the number of problems solved (from 94 to 122, for Eldarica).
AdtRem compares favorably to CVC4 extended with induction (compare rows ‘\(\mathrm {Eldarica_{noADT}}\)’ and ‘\(\mathrm {Z3_{noADT}}\)’ to row ‘CVC4+Ind’). Interestingly, the effectiveness of CVC4 may be increased if one extends the problem formalization with extra lemmas which may be used for proving the main conjecture. Indeed, CVC4 solves 100 problems when auxiliary lemmas are added, and 134 problems when, in addition, it runs on the dti encoding, where natural numbers are represented using both the built-in type Int and the ADT definition with the zero and successor constructors. Our results show that in most cases AdtRem needs neither those extra axioms nor that sophisticated encoding.
Finally, in Table 2 we report some problems solved by AdtRem with Eldarica that are not solved by CVC4 with induction (using any encoding and auxiliary lemmas), or vice versa. For details, see https://fmlab.unich.it/adtrem/.
7 Related Work and Conclusions
Inductive reasoning is supported, with different degrees of human intervention, by many theorem provers, such as ACL2 [27], CLAM [23], Isabelle [34], HipSpec [6], Zeno [40], and PVS [35]. The combination of inductive reasoning and SMT solving techniques has been exploited by many tools for program verification [30, 36, 38, 41, 43, 44].
Leino [30] integrates inductive reasoning into the Dafny program verifier by implementing a simple strategy that rewrites user-defined properties that may benefit from induction into proof obligation to be discharged by Z3. The advantage of this technique is that it fully decouples inductive reasoning from SMT solving. Hence, no extensions to the SMT solver are required.
In order to extend CVC4 with induction, Reynolds and Kuncak [38] also consider the rewriting of formulas that may take advantage from inductive reasoning, but this is done dynamically, during the proof search. This approach allows CVC4 to perform the rewritings lazily, whenever new formulas are generated during the proof search, and to use the partially solved conjecture, to generate lemmas that may help in the proof of the initial conjecture.
The issue of generating suitable lemmas during inductive proofs has been also addressed by Yang et al. [44] and implemented in AdtInd. In order to conjecture new lemmas, their algorithm makes use of a syntax-guided synthesis strategy driven by a grammar, which is dynamically generated from user-provided templates and the function and predicate symbols encountered during the proof search. The derived lemma conjectures are then checked by the SMT solver Z3.
In order to take full advantage of the efficiency of SMT solvers in checking satisfiability of quantifier-free formulas over LIA, ADTs, and finite sets, the Leon verification system [41] implements an SMT-based solving algorithm to check the satisfiability of formulas involving recursively defined first-order functions. The algorithm interleaves the unrolling of recursive functions and the SMT solving of the formulas generated by the unrolling. Leon can be used to prove properties of Scala programs with ADTs and integrates with the Scala compiler and the SMT solver Z3. A refined version of that algorithm, restricted to catamorphisms, has been implemented into a solver-agnostic tool, called RADA [36].
In the context of CHCs, Unno et al. [43] have proposed a proof system that combines inductive theorem proving with SMT solving. This approach uses Z3-PDR [21] to discharge proof obligations generated by the proof system, and has been applied to prove relational properties of OCaml programs.
The distinctive feature of the technique presented in this paper is that it does not make use of any explicit inductive reasoning, but it follows a transformational approach. First, the problem of verifying the validity of a universally quantified formula over ADTs is reduced to the problem of checking the satisfiability of a set of CHCs. Then, this set of CHCs is transformed with the aim of deriving a set of CHCs over basic types (i.e., integers) only, whose satisfiability implies the satisfiability of the original set. In this way, the reasoning on ADTs is separated from the reasoning on satisfiability, which can be performed by specialized engines for CHCs on basic types (e.g. Eldarica [22] and Z3-Spacer [29]). Some of the ideas presented here have been explored in [11, 12], but there neither formal results nor an automated strategy were presented.
A key success factor of our technique is the introduction of difference predicates, which can be viewed as the transformational counterpart of lemma generation. Indeed, as shown in Sect. 6, the use of difference predicates greatly increases the power of CHC solving with respect to previous techniques based on the transformational approach, which do not use difference predicates [10].
As future work, we plan to apply our transformation-based verification technique to more complex program properties, such as relational properties [9].
Notes
- 1.
In the examples, we use Prolog syntax for writing clauses, instead of the more verbose SMT-LIB syntax. The predicates
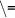 (different from), = (equal to),
(different from), = (equal to),
 (less-than),
(less-than),
 (greater-than-or-equal-to) denote constraints between integers. The last argument of a Prolog predicate stores the value of the corresponding function.
(greater-than-or-equal-to) denote constraints between integers. The last argument of a Prolog predicate stores the value of the corresponding function. - 2.
The tool and the benchmarks are available at https://fmlab.unich.it/adtrem/.
- 3.
More specifically, Eldarica v2.0.1 and Z3 v4.8.0 with the Spacer engine [28].
References
Gopalakrishnan, G., Qadeer, S. (eds.): CAV 2011. LNCS, vol. 6806. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1
Barrett, C., Tinelli, C.: Satisfiability modulo theories. In: Clarke, E., Henzinger, T., Veith, H., Bloem, R. (eds.) Handbook of Model Checking, pp. 305–343. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-10575-8_11
Bjørner, N., Gurfinkel, A., McMillan, K., Rybalchenko, A.: Horn Clause Solvers for Program Verification. In: Beklemishev, L.D., Blass, A., Dershowitz, N., Finkbeiner, B., Schulte, W. (eds.) Fields of Logic and Computation II. LNCS, vol. 9300, pp. 24–51. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-23534-9_2
Bundy, A.: The automation of proof by mathematical induction. In: Robinson, A., Voronkov, A. (eds.) Handbook of Automated Reasoning, vol. I, pp. 845–911. North Holland (2001)
Cimatti, A., Griggio, A., Schaafsma, B.J., Sebastiani, R.: The MathSAT5 SMT solver. In: Piterman, N., Smolka, S.A. (eds.) TACAS 2013. LNCS, vol. 7795, pp. 93–107. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36742-7_7
Claessen, K., Johansson, M., Rosén, D., Smallbone, N.: Automating inductive proofs using theory exploration. In: Bonacina, M.P. (ed.) CADE 2013. LNCS (LNAI), vol. 7898, pp. 392–406. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38574-2_27
Cousot, P., Halbwachs, N.: Automatic discovery of linear restraints among variables of a program. In: Proceedings of the Fifth ACM Symposium on Principles of Programming Languages, POPL 1978, pp. 84–96. ACM (1978)
De Angelis, E., Fioravanti, F., Pettorossi, A., Proietti, M.: VeriMAP: a tool for verifying programs through transformations. In: Ábrahám, E., Havelund, K. (eds.) TACAS 2014. LNCS, vol. 8413, pp. 568–574. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54862-8_47. http://www.map.uniroma2.it/VeriMAP
De Angelis, E., Fioravanti, F., Pettorossi, A., Proietti, M.: Relational verification through Horn clause transformation. In: Rival, X. (ed.) SAS 2016. LNCS, vol. 9837, pp. 147–169. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53413-7_8
De Angelis, E., Fioravanti, F., Pettorossi, A., Proietti, M.: Solving Horn clauses on inductive data types without induction. Theor. Pract. Logic Program. 18(3–4), 452–469 (2018). Special Issue on ICLP 2018
De Angelis, E., Fioravanti, F., Pettorossi, A., Proietti, M.: Lemma generation for Horn clause satisfiability: a preliminary study. In: Lisitsa, A., Nemytykh, A.P. (eds.) Proceedings Seventh International Workshop on Verification and Program Transformation, VPT@Programming 2019, EPTCS, Genova, Italy, 2nd April 2019, vol. 299, pp. 4–18 (2019)
De Angelis, E., Fioravanti, F., Pettorossi, A., Proietti, M.: Proving properties of sorting programs: a case study in Horn clause verification. In: De Angelis, E., Fedyukovich, G., Tzevelekos, N., Ulbrich, M. (eds.) Proceedings of the Sixth Workshop on Horn Clauses for Verification and Synthesis and Third Workshop on Program Equivalence and Relational Reasoning, HCVS/PERR@ETAPS 2019, EPTCS, Prague, Czech Republic, 6–7 April 2019, vol. 296, pp. 48–75 (2019)
De Angelis, E., Fioravanti, F., Pettorossi, A., Proietti, M.: Removing algebraic data types from constrained Horn clauses using difference predicates - Preliminary version. CoRR (2020). http://arXiv.org/abs/2004.07749
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Dixon, L., Fleuriot, J.: IsaPlanner: a prototype proof planner in Isabelle. In: Baader, F. (ed.) CADE 2003. LNCS (LNAI), vol. 2741, pp. 279–283. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45085-6_22
Enderton, H.: A Mathematical Introduction to Logic. Academic Press, Cambridge (1972)
Etalle, S., Gabbrielli, M.: Transformations of CLP modules. Theor. Comput. Sci. 166, 101–146 (1996)
Fioravanti, F., Pettorossi, A., Proietti, M.: Transformation rules for locally stratified constraint logic programs. In: Bruynooghe, M., Lau, K.-K. (eds.) Program Development in Computational Logic. LNCS, vol. 3049, pp. 291–339. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-25951-0_10
Fioravanti, F., Pettorossi, A., Proietti, M., Senni, V.: Generalization strategies for the verification of infinite state systems. Theor. Pract. Logic Program. 13(2), 175–199 (2013). Special Issue on the 25th Annual GULP Conference
Grebenshchikov, S., Lopes, N.P., Popeea, C., Rybalchenko, A.: Synthesizing software verifiers from proof rules. In: Proceedings of the ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2012, pp. 405–416 (2012)
Hoder, K., Bjørner, N.: Generalized property directed reachability. In: Cimatti, A., Sebastiani, R. (eds.) SAT 2012. LNCS, vol. 7317, pp. 157–171. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31612-8_13
Hojjat, H., Rümmer, P.: The ELDARICA Horn solver. In: Bjørner, N., Gurfinkel, A. (eds.) 2018 Formal Methods in Computer Aided Design, FMCAD 2018, Austin, TX, USA, 30 Oct–2 Nov 2018, pp. 1–7. IEEE (2018)
Ireland, A., Bundy, A.: Productive use of failure in inductive proof. J. Autom. Reason. 16(1), 79–111 (1996)
Jaffar, J., Maher, M.: Constraint logic programming: a survey. J. Logic Program. 19(20), 503–581 (1994)
Johansson, M., Dixon, L., Bundy, A.: Case-analysis for rippling and inductive proof. In: Kaufmann, M., Paulson, L.C. (eds.) ITP 2010. LNCS, vol. 6172, pp. 291–306. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14052-5_21
Kafle, B., Gallagher, J.P., Morales, J.F.: Rahft: a tool for verifying Horn clauses using abstract interpretation and finite tree automata. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9779, pp. 261–268. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41528-4_14
Kaufmann, M., Manolios, P., Moore, J.S.: Computer-Aided Reasoning: An Approach. Kluwer Academic Publishers, Berlin (2000)
Komuravelli, A., Gurfinkel, A., Chaki, S.: SMT-based model checking for recursive programs. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 17–34. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_2
Komuravelli, A., Gurfinkel, A., Chaki, S., Clarke, E.M.: Automatic abstraction in SMT-based unbounded software model checking. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 846–862. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_59
Leino, K.R.M.: Automating induction with an SMT solver. In: Kuncak, V., Rybalchenko, A. (eds.) VMCAI 2012. LNCS, vol. 7148, pp. 315–331. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-27940-9_21
Leroy, X., Doligez, D., Frisch, A., Garrigue, J., Rémy, D., Vouillon, J.: The OCaml system, Release 4.06. Documentation and user’s manual, Institut National de Recherche en Informatique et en Automatique, France (2017)
Leuschel, M., Butler, M.: ProB: a model checker for B. In: Araki, K., Gnesi, S., Mandrioli, D. (eds.) FME 2003. LNCS, vol. 2805, pp. 855–874. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45236-2_46
Lloyd, J.W.: Foundations of Logic Programming, 2nd edn. Springer, Berlin (1987). https://doi.org/10.1007/978-3-642-83189-8
Nipkow, T., Wenzel, M., Paulson, L.C.: Isabelle/HOL: A Proof Assistant for Higher-Order Logic. Springer, Heidelberg (2002)
Owre, S., Rushby, J.M., Shankar, N.: PVS: a prototype verification system. In: Kapur, D. (ed.) CADE 1992. LNCS, vol. 607, pp. 748–752. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-55602-8_217
Pham, T.-H., Gacek, A., Whalen, M.W.: Reasoning about algebraic data types with abstractions. J. Autom. Reason. 57(4), 281–318 (2016)
Rabin, M.O.: Decidable theories. In: Barwise, J. (ed.) Handbook of Mathematical Logic, pp. 595–629. North-Holland, Amsterdam (1977)
Reynolds, A., Kuncak, V.: Induction for SMT solvers. In: D’Souza, D., Lal, A., Larsen, K.G. (eds.) VMCAI 2015. LNCS, vol. 8931, pp. 80–98. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46081-8_5
Seki, H.: On Inductive and coinductive proofs via unfold/fold transformations. In: De Schreye, D. (ed.) LOPSTR 2009. LNCS, vol. 6037, pp. 82–96. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-12592-8_7
Sonnex, W., Drossopoulou, S., Eisenbach, S.: Zeno: an automated prover for properties of recursive data structures. In: Flanagan, C., König, B. (eds.) TACAS 2012. LNCS, vol. 7214, pp. 407–421. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28756-5_28
Suter, P., Köksal, A.S., Kuncak, V.: Satisfiability modulo recursive programs. In: Yahav, E. (ed.) SAS 2011. LNCS, vol. 6887, pp. 298–315. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-23702-7_23
Tamaki, H., Sato, T.: A generalized correctness proof of the unfold/fold logic program transformation. Technical Report 86–4, Ibaraki University, Japan (1986)
Unno, H., Torii, S., Sakamoto, H.: Automating induction for solving Horn clauses. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10427, pp. 571–591. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63390-9_30
Yang, W., Fedyukovich, G., Gupta, A.: Lemma synthesis for automating induction over algebraic data types. In: Schiex, T., de Givry, S. (eds.) CP 2019. LNCS, vol. 11802, pp. 600–617. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-30048-7_35
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
De Angelis, E., Fioravanti, F., Pettorossi, A., Proietti, M. (2020). Removing Algebraic Data Types from Constrained Horn Clauses Using Difference Predicates. In: Peltier, N., Sofronie-Stokkermans, V. (eds) Automated Reasoning. IJCAR 2020. Lecture Notes in Computer Science(), vol 12166. Springer, Cham. https://doi.org/10.1007/978-3-030-51074-9_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-51074-9_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-51073-2
Online ISBN: 978-3-030-51074-9
eBook Packages: Computer ScienceComputer Science (R0)








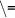 (different from),
(different from),  (less-than),
(less-than),
 (greater-than-or-equal-to) denote constraints between integers. The last argument of a Prolog predicate stores the value of the corresponding function.
(greater-than-or-equal-to) denote constraints between integers. The last argument of a Prolog predicate stores the value of the corresponding function.