Abstract
We present a practical proof search procedure for Coq based on a direct search for type inhabitants in an appropriate normal form. The procedure is more general than any of the automation tactics natively available in Coq. It aims to handle as large a part of the Calculus of Inductive Constructions as practically feasible.
For efficiency, our procedure is not complete for the entire Calculus of Inductive Constructions, but we prove completeness for a first-order fragment. Even in pure intuitionistic first-order logic, our procedure performs competitively.
We implemented the procedure in a Coq plugin and evaluated it on a collection of Coq libraries, on CompCert, and on the ILTP library of first-order intuitionistic problems. The results are promising and indicate the viablility of our approach to general automated proof search for the Calculus of Inductive Constructions.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The Curry-Howard isomorphism [39] is a correspondence between systems of formal logic and computational lambda-calculi, interpreting propositions as types and proofs as programs (typed lambda-terms). Coq [10] is an interactive proof assistant based on this correspondence. Its underlying logic is the Calculus of Inductive Constructions [10, 33, 46] – an intuitionistic dependent type theory with inductive types.
Because of the complexity and constructivity of the logic, research on automated reasoning for Coq has been sparse so far, limited mostly to specialised tactics for restricted fragments or decidable theories. The automation currently available in Coq is weaker than in proof assistants based on simpler classical foundations, like Isabelle/HOL [29].
We present a practical general fully automated proof search procedure for Coq based on a direct search for type inhabitants. We synthesise Coq terms in an appropriate normal form, using backward-chaining goal-directed search. To make this approach practical, we introduce various heuristics including hypothesis simplification, limited forward reasoning, ordered rewriting and loop checking. For efficiency, we sacrifice completeness for the entire logic of Coq, though we give a completeness proof for a first-order fragment.
We evaluated our procedure on a collection of Coq libraries (40.9% success rate), on CompCert [27] (17.1%) and on the ILTP library [36] (29.5%) of first-order intuitionistic problems. The percentages in brackets denote how many problems were solved fully automatically by the standalone tactic combined with heuristic induction. These results indicate the viability of our approach.
The procedure can be used as a standalone Coq tactic or as a reconstruction backend for CoqHammer [14] – a hammer tool [7] which invokes external automated theorem provers (ATPs) on translations of Coq problems and then reconstructs the found proofs in Coq using the information obtained from successful ATP runs. With our procedure used for reconstruction, CoqHammer achieves a 39.1% success rate on a collection of Coq libraries and 25.6% on CompCert. The reconstruction success rates (i.e. the percentage of problems solved by the ATPs that can be re-proved in Coq) are 87–97%.
1.1 Related Work
A preliminary version of a proof search procedure partly based on similar ideas was described in [14]. That procedure is less complete (not complete for the first-order fragment), slower, much more heuristic, and it performs visibly worse as a standalone tactic (see Sect. 5). It partially includes only some of the actions, restrictions and heuristic improvements described here. In particular, the construction and the unfolding actions are absent, and only special cases of the elimination and the rewriting actions are performed. See Sect. 3.
From a theoretical perspective, a complete proof search procedure for the Cube of Type Systems, which includes the pure Calculus of Constructions without inductive types, is presented in [15]. It is also based on an exhaustive search for type inhabitants. Sequent calculi suitable for proof search in Pure Type Systems are described in [22, 26].
In practice, Chlipala’s crush tactic [9] can solve many commonly occurring Coq goals. However, it is not a general proof search procedure, but an entirely heuristic tactic. In the evaluations we performed, the crush tactic performed much worse than our procedure. For Agda [30] there exists an automated prover Agsy [28] which is, however, not much stronger than Coq’s auto.
Proof search in intuitionistic first-order logic has received more attention than inhabitation in complex constructive dependent type theories. We do not attempt here to provide an overview, but only point the reader to [36] for a comparison of intuitionistic first-order ATP systems. The most promising approaches to proof search in intuitionistic first-order logic seem to be connection-based methods [6, 24, 32, 45]. Indeed, the connection-based ileanCoP [31] prover outperforms other intuitionistic ATPs by a wide margin [36].
An automated intuitionistic first-order prover is available in Coq via the firstorder tactic [11], which is based on a contraction-free sequent calculus extending the LJT system of Dyckhoff for intuitionistic propositional logic [17,18,19]. There also exists a Coq plugin for the connection-based JProver [37]. However, the plugin is not maintained and not compatible with new versions of Coq.
Coq’s type theory may be viewed as an extension of intuitionistic higher-order logic. There exist several automated provers for classical higher-order logic, like Leo [40] or Satallax [8]. Satallax can produce Coq proof terms which use the excluded middle axiom.
The approach to proof search in intuitionistic logic via inhabitation in the corresponding lambda-calculus has a long tradition. It is often an easy way to establish complexity bounds [23, 38, 42]. This approach can be traced back to Ben-Yelles [5, 23] and Wajsberg [43, 44].
One of the motivations for this work is the need for a general automated reasoning procedure in a CoqHammer [14] reconstruction backend. CoqHammer links Coq with general classical first-order ATPs, but tries to find intuitionistic proofs with no additional assumptions and to handle as much of Coq’s logic as possible. A consequence is that the reconstruction mechanism of CoqHammer cannot rely on a direct translation of proofs found by classical ATPs, in contrast to e.g. SMTCoq [2, 21] which integrates external SAT and SMT solvers into Coq.
2 Calculus of Inductive Constructions
In this section, we briefly and informally describe the Calculus of Inductive Constructions (CIC) [10, 33, 46]. For precise definitions and more background, the reader is referred to the literature. Essentially, CIC is a typed lambda calculus with dependent products \(\forall x : \tau . \sigma \) and inductive types.
An inductive type is given by its constructors, presented as, e.g.,

This declares \(\mathtt {list}\,A\) to be a type of sort \(\mathtt {Type}\) for any parameter A of sort \(\mathtt {Type}\). Above A is a parameter and \(\mathtt {Type}\rightarrow \mathtt {Type}\) is the arity of \(\mathtt {list}\). The types of constructors implicitly quantify over the parameters, i.e., the type of \(\mathtt {cons}\) above is \(\forall A : \mathtt {Type}. A \rightarrow \mathtt {list}\,A \rightarrow \mathtt {list}\,A\). In the presentation we sometimes leave the parameter A implicit.
Propositions (logical formulas) are represented by dependent types. Inductive predicates are represented by dependent inductive types, e.g., the inductive type
 defines a predicate \(\mathtt {Forall}\) on lists, parameterised by a type A and a predicate \(P : A \rightarrow \mathtt {Prop}\). Then \(\mathtt {Forall}\,A\,P\,l\) states that Px holds for every element x of l.
defines a predicate \(\mathtt {Forall}\) on lists, parameterised by a type A and a predicate \(P : A \rightarrow \mathtt {Prop}\). Then \(\mathtt {Forall}\,A\,P\,l\) states that Px holds for every element x of l.
All intuitionistic connectives may be represented using inductive types:

where \(\wedge \) and \(\vee \) are used in infix notation. All the usual introduction and elimination rules are derivable. Equality can also be defined inductively.
Below by t, u, w, \(\tau \), \(\sigma \), etc., we denote terms, by c, \(c'\), etc., we denote constructors, and by x, y, z, etc., we denote variables. We use \(\vec {t}\) for a sequence of terms \(t_1 \ldots t_n\) of an unspecified length n, and analogously for a sequence of variables \(\vec {x}\). For instance, \(t \vec {y}\) stands for \(t y_1 \ldots y_n\), where n is not important or implicit. Analogously, we use \(\lambda \vec {x} : \vec {\tau } . t\) for \(\lambda x_1 : \tau _1 . \lambda x_2 : \tau _2 . \ldots \lambda x_n : \tau _n . t\), with n implicit or unspecified. We write \(t[\vec {u}/\vec {x}]\) for \(t[u_1/x_1]\ldots [u_n/x_n]\).
The logic of Coq includes over a dozen term formers. The ones recognised by our procedure are: a sort s (e.g. Type, Set or Prop), a variable x, a constant, a constructor c, an inductive type I, an application \(t_1t_2\), an abstraction \(\lambda x : t_1 . t_2\), a dependent product \(\forall x : t_1 . t_2\) (written \(t_1 \rightarrow t_2\) if \(x \notin \mathrm {FV}(t_2)\)), and a case expression \(\mathtt {case}(t; \lambda \vec {a} : \vec {\alpha } . \lambda x : I \vec {q} \vec {a} . \tau ; \vec {x_1} : \vec {\sigma _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\sigma _k} \Rightarrow t_k)\).
In a case expression: t is the term matched on; I is an inductive type with constructors \(c_1,\ldots ,c_k\); the type of \(c_i\) is \(\forall \vec {p} : \vec {\rho } . \forall \vec {x_i} : \vec {\tau _i} . I \vec {p} \vec {u_i}\) where \(\vec {p}\) are the parameters of I; the type of t has the form \(I \vec {q} \vec {u}\) where \(\vec {q}\) are the values of the parameters; the type \(\tau [\vec {u}/\vec {a},t/x]\) is the return type, i.e., the type of the whole case expression; \(t_i\) has type \(\tau [\vec {w_i}/\vec {a},c_i \vec {q} \vec {x_i}/x]\) in \(\vec {x_i} : \vec {\sigma _i}\) where \(\vec {\sigma _i} = \vec {\tau _i}[\vec {q}/\vec {p}]\) and \(\vec {w_i} = \vec {u_i}[\vec {q}/\vec {p}]\); \(t_i[\vec {v}/\vec {x}]\) is the value of the case expression if the value of t is \(c_i \vec {q} \vec {v}\).
Note that some equality information is “forgotten” when typing the branches of a case expression. We require \(t_i\) to have type \(\tau [\vec {w_i}/\vec {a},c_i \vec {q} \vec {x_i}/x]\) in context \(\vec {x_i} : \vec {\sigma _i}\). We know that “inside” the ith branch \(t = c_i \vec {q} \vec {x_i}\) and \(\vec {u} = \vec {w_i}\), but this information cannot be used when checking the type of \(t_i\). A consequence is that permutative conversions [41, Chapter 6] are not sound for CIC and this is one reason for the incompleteness of our procedure outside the restricted first-order fragment.
Coq’s notation for case expressions is

where \(c_1,\ldots ,c_k\) are all constructors of I, and \(\_\) are the wildcard patterns matching the inductive type parameters \(\vec {q}\). For readability, we often use Coq match notation. When x (resp. \(\vec {a}\)) does not occur in \(\tau \) then we omit
 from the match. If \(\tau \) does not on either x or \(\vec {a}\), we also omit the
from the match. If \(\tau \) does not on either x or \(\vec {a}\), we also omit the
 .
.
A typing judgement has the form \(E;\varGamma \vdash t : \tau \) where E is an environment consisting of declarations of inductive types and constant definitions, \(\varGamma \) is a context - a list of variable type declarations \(x : \sigma \), and \(t,\tau \) are terms. We refer to the Coq manual [10] for a precise definition of the typing rules.
Coq’s definitional equality (conversion rule) includes \(\beta \)- and \(\iota \)-reduction:

An inductive type I is non-recursive if the types of constructors of I do not contain I except as the target. We assume the well-foundedness of the relation \(\succ \) defined by: \(I_1 \succ I_2\) iff \(I_2 \ne I_1\) occurs in the arity of \(I_1\) or the type of a constructor of \(I_1\). We write \(I \succ t\) if \(I \succ I'\) for every inductive type \(I'\) occurring in the term t.
3 The Proof Search Procedure
In this section, we describe our proof search procedure. Our approach is based on a direct search for type inhabitants in appropriate normal form [42]. For the sake of efficiency, the normal forms we consider are only a subset of possible CIC normal forms. This leads to incompleteness outside the restricted first-order fragment (see Sects. 3.6 and 4).
More precisely, the inhabitation problem is: given an environment E, a context \(\varGamma \) and a \(\varGamma \)-type \(\tau \) (i.e. \(\varGamma \vdash \tau : s\) for a sort s), find a term t such that \(E;\varGamma \vdash t : \tau \). The environment E will be kept fixed throughout the search, so we omit it from the notation.
A goal is a pair \((\varGamma ,\tau )\) with \(\tau \) a \(\varGamma \)-type, denoted \(\varGamma \vdash ? : \tau \), where \(\varGamma \) is the context and \(\tau \) is the conjecture. A solution of the goal \(\varGamma \vdash ? : \tau \) is any term t such that \(\varGamma \vdash t : \tau \).
3.1 Basic Procedure
The basic inhabitation procedure is to nondeterministically perform one of the following actions, possibly generating new subgoals to be solved recursively. If the procedure fails on one of the subgoals then the action fails. If each possible action fails then the procedure fails. The choices in the actions (e.g. of specific subgoal solutions) are nondeterministic, i.e., we consider all possible choices, each leading to a potentially different solution.
The actions implicitly determine an and-or proof search tree. We leave the exact order in which this tree is traversed unspecified, but a complete search order is to be used, e.g., breadth-first or iterative deepening depth-first.
The procedure supports five term formers in synthesised solutions: variables, constructors, applications, lambda-abstractions, case expressions. These are built with the four actions below.
-
1.
Introduction. If \(\varGamma \vdash ? : \forall x : \alpha . \beta \) then:
-
recursively search for a solution t of the subgoal \(\varGamma , x : \alpha \vdash ? : \beta \);
-
return \(\lambda x : \alpha . t\) as the solution.
-
-
2.
Application. If \(\varGamma \vdash ? : \tau \) and \(x : \forall \vec {y} : \vec {\sigma } . \rho \) is in \(\varGamma \) then:
-
for \(i=1,\ldots ,n\), recursively search for a solution \(t_i\) of the subgoal \(\varGamma \vdash ? : \sigma _i[t_1/y_1]\ldots [t_{i-1}/y_{i-1}]\);
-
if \(\rho [\vec {t}/\vec {y}] =_{\beta \iota } \tau \) then return \(x \vec {t}\) as the solution.
-
-
3.
Construction. If \(\varGamma \vdash ? : I \vec {q} \vec {w}\) with \(\vec {q}\) the parameters and \(c : \forall \vec {p} : \vec {\rho } . \forall \vec {y} : \vec {\sigma } . I \vec {p} \vec {u}\) is a constructor of I then:
-
for \(i=1,\ldots ,n\), recursively search for a solution \(t_i\) of the subgoal \(\varGamma \vdash ? : \sigma _i[\vec {q}/\vec {p}][t_1/y_1]\ldots [t_{i-1}/y_{i-1}]\);
-
if \(\vec {u}[\vec {q}/\vec {p}][\vec {t}/\vec {y}] =_{\beta \iota } \vec {w}\) then return \(c \vec {q} \vec {t}\) as the solution.
-
-
4.
Elimination. If \(\varGamma \vdash ? : \tau \), and \(x : \forall \vec {y} : \vec {\sigma } . I \vec {q} \vec {u}\) is in \(\varGamma \), and \(I : \forall \vec {p} : \vec {\rho } . \forall \vec {a} : \vec {\alpha } . s\) is in E with \(\vec {p}\) the parameters, and \(c_j : \forall \vec {p} : \vec {\rho } . \forall \vec {z_j} : \vec {\gamma _j} . I \vec {p} \vec {u_j}\) for \(j=1,\ldots ,m\) are all constructors of I, then:
-
for \(i=1,\ldots ,n\), recursively search for a solution \(t_i\) of the subgoal \(\varGamma \vdash ? : \sigma _i[t_1/y_1]\ldots [t_{i-1}/y_{i-1}]\);
-
let \(\vec {v} = \vec {u}[\vec {t}/\vec {y}]\) and \(\vec {r} = \vec {q}[\vec {t}/\vec {y}]\);
-
choose \(\tau '\) such that \(\tau '[\vec {v}/\vec {a},x\vec {t}/z] =_{\beta \iota } \tau \);
-
for \(j=1,\ldots ,m\), recursively search for a solution \(b_j\) of \(\varGamma , \vec {z_j} : \vec {\delta _j} \vdash ? : \tau '[\vec {w_j}/\vec {a},c_j\vec {r}\vec {z_j}/z]\) where \(\vec {\delta _j} = \vec {\gamma _j}[\vec {r}/\vec {p}]\) and \(\vec {w_j} = \vec {u_j}[\vec {r}/\vec {p}]\);
-
return \(\mathtt {case}(x \vec {t}; \lambda \vec {a} : \vec {\alpha } . \lambda z : I \vec {r} \vec {a} . \tau '; \vec {z_1} : \vec {\gamma _1} \Rightarrow b_1 \mid \ldots \mid \vec {z_m} : \vec {\gamma _m} \Rightarrow b_m )\) as the solution.
-
The intuition is that we search for normal inhabitants of a type. For instance, if \(\varGamma \vdash (\lambda x : \alpha . t) u : \tau \) then also \(\varGamma \vdash t[u/x] : \tau \), so it suffices to consider solutions without \(\beta \)-redexes. Assuming \(\tau \) is not a sort, it suffices to consider only variables and constructors at the head of the solution term, because \(I : \forall \vec {x} : \vec {\sigma } . s\) with s a sort for any inductive type I. This of course causes incompleteness because it may be necessary to search for inhabitants of a sort s in a subgoal.
It is straightforward to check (by inspecting the typing rules of CIC) that the described procedure is sound, i.e., any term obtained using the procedure is indeed a solution.
3.2 Search Restrictions
We now introduce some restrictions on the search procedure, i.e., on when each action may be applied. Note that this may compromise completeness, but not soundness. For a first-order fragment completeness is in fact preserved (Sect. 4).
-
Eager introduction. Perform introduction eagerly, i.e., if \(\varGamma \vdash ? : \forall x : \alpha . \beta \) then immediately perform introduction without backtracking.
This is justified by observing that we may restrict the search to solutions in \(\eta \)-long normal form. However, in general \(\eta \)-long normal forms may not exist.
-
Elimination restriction. Perform elimination only immediately after introduction or another elimination.
The intuitive justification is that in a term of the form
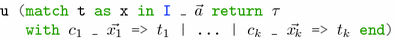 we may usually move u inside the match while preserving the type:
we may usually move u inside the match while preserving the type:
 However, this is not always possible in CIC (see Sect. 2).
However, this is not always possible in CIC (see Sect. 2). -
Eager simple elimination. Immediately after adding \(x : I \vec {q} \vec {u}\) with parameters \(\vec {q}\) into the context \(\varGamma \) (by the introduction or the elimination action), if I is a non-recursive inductive type and \(I \succ \vec {q}\), then perform elimination of x eagerly and remove the declaration of x from the context.
If \(\varGamma \vdash (\lambda x : I \vec {q} . t) : \tau \) then usually \(\varGamma \vdash (\lambda x : I \vec {q} . t') : \tau \) where \(t'\) is
 However, in general replacing a subterm \(u'\) of a term u with \(u''\) may change the type of u, even if \(u',u''\) have the same type. See Sect. 4.
However, in general replacing a subterm \(u'\) of a term u with \(u''\) may change the type of u, even if \(u',u''\) have the same type. See Sect. 4. -
Loop checking. If the same conjecture is encountered for the second time on the same proof search tree branch without performing the introduction action in the meantime, then fail.
This is justified by observing that if \(\varGamma \vdash t[u/x] : \tau \) and \(\varGamma \vdash u : \tau \), then we can just use u instead of t as the solution. In general, this restriction also causes incompleteness, for the same reason as the previous one.
It is instructive to observe how the elimination restrictions specialise to inductive definitions of logical connectives. For example, the eager simple elimination restriction for conjunction is that a goal \(\varGamma , x : \alpha \wedge \beta \vdash ? : \tau \) should be immediately replaced by \(\varGamma , x_1 : \alpha , x_2 : \beta \vdash ? : \tau \).
3.3 Heuristic Improvements
The above presentation of the proof search procedure does not yet directly lead to a practical implementation. We thus introduce “heuristic” improvements. All of them preserve soundness, but some may further compromise completeness. In fact, we believe several of the “heuristics” (e.g. most context simplifications and forward reasoning) actually do preserve completeness (under certain restrictions), but we did not attempt to rigorously prove itFootnote 1.
-
In the application action, instead of checking \(\rho [\vec {t}/\vec {y}] =_{\beta \iota } \tau \) a posteriori, use unification modulo simple heuristic equational reasoning to choose an appropriate \((x : \tau ) \in \varGamma \), possibly introducing existential metavariables to be instantiated later (like with Coq’s eapply tactic). Analogously, we use unification in the construction action.
-
In the elimination action, the choice of \(\tau '\) is done heuristically without backtracking. In practice, we use either Coq’s destruct or inversion tactic, depending on the form of the inductive type I.
-
Immediately after the introduction action, simplify the context:
-
replace \(h : \forall \vec {x} : \vec {\sigma } . \tau _1 \wedge \tau _2\) with \(h_1 : \forall \vec {x} : \vec {\sigma } . \tau _1\) and \(h_2 : \forall \vec {x} : \vec {\sigma } . \tau _2\);
-
replace \(h : \forall \vec {x} : \vec {\sigma } . \tau _1 \vee \tau _2 \rightarrow \rho \) with \(h_1 : \forall \vec {x} : \vec {\sigma } . \tau _1 \rightarrow \rho \) and \(h_2 : \forall \vec {x} : \vec {\sigma } . \tau _2 \rightarrow \rho \);
-
replace \(h : \forall \vec {x} : \vec {\sigma } . \tau _1 \wedge \tau _2 \rightarrow \rho \) with \(h' : \forall \vec {x} : \vec {\sigma } . \tau _1 \rightarrow \tau _2 \rightarrow \rho \);
-
replace \(h : \exists x : \sigma . \tau \) with \(h' : \tau \) (assuming x fresh);
-
remove some intuitionistic tautologies;
-
perform invertible forward reasoning, i.e., if \(h : \sigma \) and \(h' : \sigma \rightarrow \tau \) are in \(\varGamma \) then we replace \(h'\) with \(h'' : \tau \).
-
use Coq’s subst tactic to rewrite with equations on variables;
-
perform rewriting with some predefined lemmas from a hint database.
-
Immediately after simplifying the context as above, perform some limited forward reasoning. For instance, if h : Pa and \(h' : \forall x . P x \rightarrow \varphi \) are in \(\varGamma \), then add \(h'' : P a \rightarrow \varphi [a/x]\) to \(\varGamma \). To avoid looping, we do not use newly derived facts for further forward reasoning.
-
Elimination on terms matched in case expressions is done eagerly. In other words, if
 occurs in the conjecture or the context, with t closed, then we immediately perform the elimination action on t.
occurs in the conjecture or the context, with t closed, then we immediately perform the elimination action on t. -
After performing each action, simplify the conjecture by reducing it to (weak) normal form (using Coq’s cbn tactic) and rewriting with some predefined lemmas from a hint database.
-
We use a custom leaf solver at the leaves of the search tree. The leaf solver eagerly splits the disjunctions in the context (including quantified ones), uses Coq’s eauto with depth 2, and tries the Coq tactics congruence (congruence closure) and lia (linear arithmetic).
-
We extend the search procedure with two more actions (performed non-eagerly with backtracking):
-
1.
Unfolding. Unfold a Coq constant definition, provided some heuristic conditions on the resulting unfolding are satisfied.
-
2.
Rewriting. The order > on constants is defined to be the transitive closure of \(\{(c_1,c_2) \mid c_2 \mathrm {\ occurs\ in\ the\ definition\ of\ } c_1\}\). By \(\mathrm {lpo}_>\) we denote the lifting of > to the lexicographic path order (LPO) on terms [3, Section 5.4.2]. For the LPO lifting, we consider only terms which have obvious first-order counterparts, e.g., fxyz with f a constant corresponds to a first-order term f(x, y, z). The action is then as follows. Assume \(h : \forall \vec {x} : \vec {\sigma } . t_1 = t_2\) is in \(\varGamma \).
-
If \(\mathrm {lpo}_>(t_1,t_2)\) then rewrite with h from left to right, in the conjecture and the hypotheses, generating new subgoals and introducing existential metavariables for \(\vec {x}\) as necessary.
-
If \(\mathrm {lpo}_>(t_2,t_1)\) then rewrite with h from right to left.
-
If \(t_1,t_2\) are incomparable with \(\mathrm {lpo}_>\), then rewrite heuristically from left to right, or right to left if that fails.
For heuristic rewriting in the last point, we use the leaf solver to discharge the subgoals and we track the hypotheses to avoid unordered heuristic rewriting with the same hypothesis twice.
-
Immediately after forward reasoning, eagerly perform rewriting with those hypotheses which satisfy: (1) the target can be ordered with the lexicographic path order described above, and (2) the generated subgoals can be solved with the leaf solver.
3.4 Search Strategy
The proof search strategy is based on (bounded or iterative deepening) depth-first search. We put a bound on the cost of proof search according to one of the following two cost models.
-
Depth cost model. The depth of the search tree is bounded, with the leaf solver tactic tried at the leaves.
-
Tree cost model. The size of the entire search tree is bounded, but not the depth directly. The advantages of this approach are that (1) it allows to find deep proofs with small branching, and (2) it is easier to choose a single cost bound which performs well in many circumstances. However, this model performs slightly worse on pure first-order problems (see Sect. 5).
3.5 Soundness
Our proof search procedure, including all heuristic improvements, is sound. For the basic procedure (Sects. 3.1 and 3.2) this can be shown by straightforward induction, noting that the actions essentially directly implement CIC typing rules. For the heuristic improvements (Sect. 3.3), one could show soundness by considering the shapes of the proof terms. This is straightforward but tedious. The implementation in the Coq tactic monad guarantees soundness as only well-typed proof terms can be produced by standard Coq tactics.
3.6 Incompleteness
The inhabitation procedure presented above is not complete for the full logic of Coq. The reasons for incompleteness are as follows.
-
1.
Higher-order unification in the application action is not sufficient for completeness in the presence of impredicativity. A counterexample (from [15]) is
$$ Q : * \rightarrow *, u : \forall P : * . Q P \rightarrow P, v : Q (A \rightarrow B), w : A \vdash ? : B. $$The solution is \(u (A \rightarrow B) v w\). The target P of u unifies with B, but this does not provide the right instantiation (which is \(A \rightarrow B\)) and leaves an unsolvable subgoal ? : QB. It is worth noting, however, that this particular example can be solved thanks to limited forward reasoning (see Sect. 3.3).
-
2.
For efficiency, most variants of our tactics do not perform backtracking on instantiations of existential metavariables.
-
3.
The normal forms we implicitly search for do not suffice for completeness. One reason is that permutative conversions [41, Chapter 6] are not sound for dependent case expressions \(\mathtt {case}\) in CIC if the return type \(\tau \) depends on \(\vec {a}\) or x. We elaborate on this in the next section.
-
4.
The full logic of Coq contains more term formers than the five supported by our procedure: fix, cofix, let, ...In particular, our inhabitation procedure never performs induction over recursive inductive types, which requires fix. It does reasoning by cases, however, via the elimination action.
We believe the compromises on completeness are in practice not very severe and our procedure may reasonably be considered a general automated proof search method for CIC without fixpoints. In fact, many of the transformations on proof terms corresponding to the “restrictions” and “heuristics” above would preserve completeness in the presence of definitional proof irrelevance.
4 Normal Forms and Partial Completeness
The basic inhabitation procedure (Sects. 3.1 and 3.2) with restricted looping check is complete for a first-order fragment of CIC. We conjecture that a variant of our procedure is also complete for CIC with definitional proof irrelevance, with only non-dependent elimination, and without fixpoints. First, we describe the subset of normal forms our procedure searches for.
Permutative conversions are the two reductions below. They “move around” case expressions to expose blocked redexes.

In the second reduction rule, P stands for a list of case patterns \(\vec {y_1} : \vec {\sigma _1} \Rightarrow w_1 \mid \ldots \mid \vec {y_m} : \vec {\sigma _m} \Rightarrow w_m\). We assume \(\vec {x_i}\) do not occur in P. Similarly, \(Q,R,R',R''\) stand for the specifications of the return types, where \(Q = \lambda \vec {a} : \vec {\alpha } . \lambda x : I_1 \vec {q_1} \vec {a} . I \vec {v}\), \(R = \lambda \vec {b} : \vec {\beta } . \lambda x : I_2 \vec {q_2} \vec {b} . \tau \), \(R' = \lambda \vec {a} : \vec {\alpha } . \lambda x : I_1 \vec {q_1} \vec {a} . \tau \), \(R'' = \lambda \vec {a} : \vec {\alpha } . \lambda x : I_1 \vec {q_1} \vec {a} . \tau \).
We write \(\rightarrow _\rho \) for the union of \(\rightarrow _{\rho _1}\) and \(\rightarrow _{\rho _2}\). Note that \(\rho _1\)-reduction may create \(\beta \)-redexes, and \(\rho _2\)-reduction may create \(\iota \)-redexes.
The right-hand sides of the \(\rho \)-rules may be ill-typed if \(\sigma ,\tau \) above depend on any of \(\vec {a},\vec {b},x\), i.e., if the return type varies across the case expression branches. Moreover, even if the type of a \(\rho \)-redex subterm is preserved by a \(\rho \)-contraction, the type of the entire term might not be. For example, assume the following are provable in context \(\varGamma \): \(P : A \rightarrow s\), \(F : \forall x : A . P x\), t : A, \(t' : A\) and p : Pt. Then \(\varGamma \vdash F t : P t\) but in general \(\varGamma \not \vdash F t' : P t\) unless \(t =_{\beta \iota } t'\).
An analogous problem occurs when attempting to define \(\eta \)-long normal forms – normal forms \(\eta \)-expanded as much as possible without creating \(\beta \)-redexes. The \(\eta \)-expansion of a term t of type \(\forall x : \alpha . \beta \) is \(\lambda x : \alpha . t x\) where \(x \notin \mathrm {FV}(t)\). We do not consider \(\eta \)-expansions for inductive types. If the conversion rule does not include \(\eta \) (Coq’s does since v8.4), then \(\eta \)-expanding a subterm may change the type of the entire term. Even assuming the conversion rule does include \(\eta \), defining \(\eta \)-long forms in the presence of dependent types is not trivial if we consider \(\eta \)-expansions inside variable type annotations [16]. However, for our purposes a simpler definition by mutual induction on term structure is sufficient.
A term t is a long normal form in \(\varGamma \) (\(\varGamma \)-lnf) if:
-
\(t = \lambda x : \alpha . t'\), and \(\varGamma \vdash t : \forall x : \alpha . \beta \), and \(t'\) is a \(\varGamma \)-\((x:\alpha )\)-lnf (defined below);
-
\(t = x \vec {u}\), and \(\varGamma \vdash t : \tau \) with \(\tau \) not a product, and each \(u_i\) is a \(\varGamma \)-lnf and not a case expression;
-
\(t = c \vec {q} \vec {v}\), and \(\varGamma \vdash t : I \vec {q} \vec {w}\) with \(\vec {q}\) the parameters, and c is a constructor of I, and each \(v_i\) is a \(\varGamma \)-lnf and not a case expression;
-
\(t = \mathtt {case}(x\vec {u}; \lambda \vec {a} : \vec {\alpha } . \lambda x : I \vec {q} \vec {a} . \sigma ; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k)\), and \(\varGamma \vdash t : \tau \) with \(\tau \) not a product, and each \(u_i\) is a \(\varGamma \)-lnf and not a case expression, and each \(t_i\) is a \(\varGamma \)-\((\vec {x_i}:\vec {\tau _i})\)-lnf.
A term t is a \(\varGamma \)-\(\varDelta \)-lnf if:
-
\(\varDelta = \langle \rangle \) and t is a \(\varGamma \)-lnf;
-
\(\varDelta = x : \alpha ,\varDelta '\), and \(\alpha \) is not \(I \vec {q} \vec {u}\) for I non-recursive with \(I \succ \vec {q}\), and t is a \(\varGamma ,x:\alpha \)-\(\varDelta '\)-lnf;
-
\(\varDelta = x : I \vec {q} \vec {u},\varDelta '\), and I is non-recursive with \(I \succ \vec {q}\), and \(\vec {q}\) are the parameter values, and \(t = \mathtt {case}(x; \lambda \vec {a} : \vec {\alpha } . \lambda x : I \vec {q} \vec {a} . \tau ; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k)\), and \(\varGamma ,\varDelta \vdash t : \tau [\vec {u}/\vec {a}]\), and each \(t_i\) is a \(\varGamma \)-\(\varDelta ',\vec {x_i}:\vec {\tau _i}\)-lnf (then \(x \notin \mathrm {FV}(t_i)\)).
For the supported term formers (variables, constructors, applications, lambda-abstractions, case expressions), this definition essentially describes \(\eta \)-long \(\beta \iota \rho \)-normal forms transformed to satisfy the additional restrictions corresponding to the elimination and the eager simple elimination restrictions from Sect. 3.2.
Given an inhabitation problem \(\varGamma \vdash ? : \tau \), our procedure searches for a minimal solution in \(\varGamma \)-lnf. Solutions in \(\varGamma \)-lnf might not exist for some solvable problems. As outlined above, there are essentially two reasons: (1) with dependent elimination the return type may vary across case branches, which in particular makes permutative conversions unsound; (2) replacing a proof with a different proof of the same proposition is not sound if proofs occur in types. Point (1) may be dealt with by disallowing dependent elimination, and (2) by assuming definitional proof irrelevance. Hence, we conjecture completeness (of an appropriate variant of the procedure) for CIC with definitional proof irrelevance, with only non-dependent elimination, and without fixpoints.
Here we only prove that in a first-order fragment for every inhabited type there exists an inhabitant in \(\varGamma \)-lnf. The precise definition of the considered first-order fragment may be found in the appendix. It is essentially intuitionistic first-order logic with two predicative sorts \(\mathtt {Prop}\) and \(\mathtt {Set}\), non-dependent inductive types in \(\mathtt {Prop}\), non-dependent pattern-matching, and terms of a type in \(\mathtt {Set}\) restricted to applicative form. We use \(\vdash _\mathrm {fo}\) for the typing judgement of the first-order fragment.
For the theorem below, we consider a basic variant of our procedure (Sects. 3.1 and 3.2) which does not perform the looping check for conjectures of sort \(\mathtt {Set}\).
Theorem 1 (Completeness for a first-order fragment)
If the inhabitation problem \(\varGamma \vdash _{\mathrm {fo}} ? : \tau \) has a solution, then the inhabitation procedure will find one.
Proof (sketch)
Assume \(\varGamma \vdash _{\mathrm {fo}} t : \tau \). It suffices to show that t may be converted into a \(\varGamma \)-lnf with the same type.
First, one shows that \(\beta \iota \rho \)-reduction enjoys subject reduction and weak normalisation. The weak normalisation proof is analogous to [41, Theorem 6.1.8].
Next, one shows that \(\beta \iota \rho \)-normal forms may be expanded to \(\eta \)-long \(\beta \iota \rho \)-normal forms. Some care needs to be taken to avoid creating a \(\rho \)-redex when expanding a case expression.
Finally, one performs transformations corresponding to the elimination and the eager simple elimination restrictions. See the appendix for details.
5 Evaluation
We performed several empirical evaluations of our proof search procedure. First, on a collection of a few Coq libraries and separately on CompCert [27], we measured the effectiveness of the procedure as a standalone proof search tactic, as well as its effectiveness as a reconstruction backend for CoqHammer. We also measured the effectiveness of our procedure on pure intuitionistic first-order logic by evaluating it on the ILTP library [36] of first-order intuitionistic problems.
Our proof search procedure intends to provide general push-button automation for CIC without fixpoints, based on sound theoretical foundations. As such, it is in a category of its own, as far we know. Our evaluations in several different scenarios indicate the practical viability of our approach despite its generality. It should be noted that the tactics we compare against are not intended for full automation, but target specific small fragments of CIC or require hand-crafted hints for effective automation.
Detailed evaluation results, complete logs, Coq problem files and conversion programs are available in the online supplementary material [12]. The collection of Coq libraries and developments on which we evaluated our procedure includes: coq-ext-lib library, Hahn library, int-map (a library of maps indexed by binary integers), Coq files accompanying the first three volumes of the Software Foundations book series [1, 34, 35], a general topology library, several other projects from coq-contribs. The full list is available at [12].
The results of the standalone (left) and CoqHammer backend (right) evaluation on 4494 problems from a collection of Coq developments, and seperately the results on CompCert are presented below.

For the evaluation on CompCert, the number of problems for the CoqHammer backend evaluation is smaller because the CoqHammer translation cannot handle some Coq goals (e.g. with existential metavariables) and these were not included.
For the standalone evaluation, we first try to apply our procedure, and if it fails then we try heuristic unfolding and then try to do induction on each available hypothesis followed by the tactic. This gives a better idea of the usefulness of our procedure because the core tactic itself cannot succeed on any problems that require non-trivial induction. For comparison, an analogous combination of standard Coq tactics (or crush) with unfolding and induction is used.
For the standalone evaluation, by “sauto+i” we denote our proof search procedure, by “yelles+i” the preliminary procedure form [14], by “crush+i” a slightly improved version of the crush tactic from [9], by “coq+i” a mix of standard Coq automation tactics (including eauto, lia, congruence, firstorder). All these are combined with induction, etc., as described above.
We also performed a standalone evaluation without combining the tactics with induction or unfolding. The results are presented below. For the standalone evaluation without induction, by “coq-no-fo” we denote the same mix of standard Coq automation tactics as “coq” but not including the firstorder tactic.

The results of the standalone evaluations indicate that our procedure is useful as a standalone Coq tactic in a push-button automated proof search scenario, performing comparably or better than other tactics available for Coq.
For the evaluation of our procedure as a CoqHammer backend, we use 12 variants of our tactics (including 3 variants based on the incomplete preliminary procedure from [14]) run in parallel (i.e. a separate core assigned to each variant) for 30s (“sauto-12” row). We included the variants of the preliminary procedure form [14] to increase the diversity of the solved problems. The procedure from [14], while much more ad-hoc and heuristic, is essentially a less general version of the present one. The point of this evaluation is to show that our approach may be engineered into an effective CoqHammer reconstruction backend, and not to compare the present procedure with its limited ad-hoc variant. For comparison, we used 4 variants of combinations of standard Coq automation tactics (“coq-4” row). We show the total number and the percentage of problems solved with any of the external provers and premise selection methods employed by CoqHammer. The external provers were run for 30s each. The reconstruction success rates (“re-proved” column) are calculated separately for each prover and a range is presented.
A common property of the chosen libraries is that they use the advanced features of Coq sparingly and are written in a style where proofs are broken up into many small lemmas. Some do not use much automation, and the Software Foundations files contain many exercises with relatively simple proofs. Moreover, some of the developments modify the core hints database which is then used by the tactics. The resulting problem set is suitable for comparing proof search procedures on a restricted subset of Coq logic, but does not necessarily reflect Coq usage in modern developments. This explains the high success rate compared to CompCert. Also, CompCert uses classical logic, while our procedure tries to find only intuitionistic proofs. Hence, a lower success rate is to be expected since it is harder or impossible to re-prove some of the lemmas constructively.
The results of the evaluation on the ILTP library v1.1.2 [36] follow.
ILTP (2574 problems, 600s) | |||||||
|---|---|---|---|---|---|---|---|
tactic | proved | proved % | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 |
hprover | 662 | 25.7% | 96.3% | 52.1% | 72.7% | 43.9% | 12.9% |
tprover | 636 | 24.7% | 96.3% | 52.1% | 52.7% | 44.6% | 11.8% |
yelles | 602 | 23.4% | 79.4% | 40.1% | 52.7% | 47% | 12.2% |
sauto-3 | 760 | 29.5% | |||||
hprove10 | 565 | 22.0% | 90.8% | 40.8% | 50.9% | 38.7% | 10.3% |
firstorder | 467 | 18.1% | 95.4% | 56.3% | 58.2% | 20% | 6.7% |
ileanCoP | 934 | 36.3% | 97.7% | 95.8% | 96.4% | 95.8% | 16.8% |

We compared our procedure with firstorder [11] and with ileanCoP 1.2 [31] – a leading connection-based first-order intuitionistic theorem prover. We converted the library files to appropriate formats (Coq or ileanCoP). For ileanCoP and firstorder, the converted problem files include equality axioms (reflexivity, symmetry, transitivity, congruence). These axioms were not added for our procedure because it can already perform limited equality reasoning. We used exhaustive variants of our tactics which perform backtracking on instantiations of existential metavariables and do not perform eager simple elimination, eager or unordered rewriting. The proof search procedure is run in an iterative deepening fashion, increasing the depth or cost bound on failure. The “hprover” row shows the result for the depth cost model, “tprover” for the tree cost model, “yelles” for the preliminary procedure from [14], and “sauto-3” the combination of the results for the above three. The columns labeled with a number R show the percentage of problems with difficulty rating R for which proofs were found. The graph below the table shows how many problems were solved within a given time limit.
The firstorder tactic is generally faster than our procedure, but it finds much fewer proofs for the problems with high difficulty rating. For firstorder we did not implement iterative deepening, because the depth limit is a global parameter not changeable at the tactic language level. We set the limit to 10. To provide a fair comparison, we also evaluated our proof search procedure with the depth cost model and the depth bound fixed at 10 (“hprove10”).
In combination, the three iterative deepening variants of our procedure managed to find proofs for 80 theorems that were not proven by ileanCoP. Overall, the performance of ileanCoP is much better, but it does not produce proof terms and is restricted to pure intuitionistic first-order logic.
6 Examples
In this section, we give some examples of the use of our proof search procedure as a standalone Coq tactic. The core inhabitation procedure is implemented in the sauto tactic which uses the tree cost model and bounds the proof search by default. There are several other tactics which invoke different variants of the proof search procedure. The ssimpl tactic performs the simplifications, forward reasoning and eager actions described in Sects. 3.2 and 3.3. The implementation is available as part of a recent version of the CoqHammer tool [13, 14], and it is used as the basis of its reconstruction tactics.
Our first example is a statement about natural numbers. It can be proven by sauto without any lemmas because the natural numbers, disjunction, existential quantification and equality are all inductive types.

Note that because the proof requires inversion on nat, it cannot possibly be created by any of the standard Coq automation tactics.
Because < is defined in terms of \(\le \) which is an inductive type, sauto can prove the following lemma about lists.

The next example concerns big-step operational semantics of simple imperative programs. The commands of an imperative program are defined with an inductive type cmd. The big-step operational semantics is represented with a dependent inductive type
 , and command equivalence
, and command equivalence
 is defined in terms of
is defined in terms of
 . We skip the details of these definitions.
. We skip the details of these definitions.
Then sauto can fully automatically prove the following two lemmas. The first one states the associativity of command sequencing. The second establishes the equivalence of the while command with its one-step unfolding. On a computer with a 2.5 GHz processor, in both cases sauto finds a proof in less than 0.5 s.

Note again that both proofs require multiple inversions, and thus it is not possible to obtain them with standard Coq automation tactics.
According to Kunze [25], the following set-theoretical statement cannot be proven in reasonable time by either firstorder or JProver. The sauto tactic finds a proof in less than 0.3s. Below Seteq, Subset and In are variables of type \(U \rightarrow U \rightarrow \mathtt {Prop}\); Sum of type \(U \rightarrow U \rightarrow U\); and \(U : \mathtt {Type}\).

7 Conclusions and Future Work
We presented a practical general proof search procedure for Coq based on type inhabitation. This increases the power of out-of-the-box automation available for Coq and provides an effective reconstruction backend for CoqHammer. The empirical evaluations indicate that our approach to fully automated proof search in the Calculus of Inductive Constructions is practically viable.
For efficency reasons, the inhabitation procedure is not complete in general, but it is complete for a first-order fragment of the Calculus of Inductive Constructions. We conjecture that a variant of our procedure could be shown complete for the Calculus of Inductive Constructions with definitional proof irrelevance, with only non-dependent elimination, and without fixpoints.
We implemented the proof search procedure in OCaml and Ltac as a Coq plugin. The plugin generates values in the Coq’s tactic monad which contain callbacks to the plugin. Better efficiency would probably be achieved by directly generating Coq proof terms or sequences of basic tactics. This would, however, require much engineering work. Another disadvantage of the monadic implementation is that it limits the proof search strategy to depth-first order and precludes global caching. In the artificial intelligence literature, there are many approaches to graph and tree search [20] which might turn out to be better suited for an inhabitation procedure than the depth-first tree search.
Notes
- 1.
It is actually clear that limited forward reasoning (4th point) preserves completeness in general, because it corresponds to performing \(\beta \)-expansions on the proof term.
References
Appel, A.: Verified Functional Algorithms. Software Foundations series, volume 3. Electronic textbook (2018)
Armand, M., Faure, G., Grégoire, B., Keller, C., Théry, L., Werner, B.: A modular integration of SAT/SMT solvers to Coq through proof witnesses. In: Jouannaud, J.-P., Shao, Z. (eds.) CPP 2011. LNCS, vol. 7086, pp. 135–150. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25379-9_12
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1999)
Barendregt, H.: Lambda calculi with types. In: Handbook of Logic in Computer Science, vol. 2, pp. 118–310. Oxford University Press (1992)
Ben-Yelles, C.: Type-assignment in the lambda-calculus. Ph.D. thesis, University College Swansea (1979)
Bibel, W.: Automated Theorem Proving. Artificial Intelligence, 2nd edn. Vieweg, Wiesbaden (1987). https://doi.org/10.1007/978-3-322-90102-6
Blanchette, J., Kaliszyk, C., Paulson, L., Urban, J.: Hammering towards QED. J. Formaliz. Reason. 9(1), 101–148 (2016)
Brown, C.E.: Satallax: an automatic higher-order prover. In: Gramlich, B., Miller, D., Sattler, U. (eds.) IJCAR 2012. LNCS (LNAI), vol. 7364, pp. 111–117. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31365-3_11
Chlipala, A.: Certified Programming with Dependent Types. MIT Press, Cambridge (2013)
Coq Development Team: The Coq proof assistant, version 8.10.0 (2019). https://doi.org/10.5281/zenodo.3476303
Corbineau, P.: First-order reasoning in the calculus of inductive constructions. In: Berardi, S., Coppo, M., Damiani, F. (eds.) TYPES 2003. LNCS, vol. 3085, pp. 162–177. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24849-1_11
Czajka, Ł.: Practical proof search for Coq by type inhabitation: supplementary evaluation material. http://www.mimuw.edu.pl/~lukaszcz/sauto/index.html
Czajka, Ł., Kaliszyk, C.: CoqHammer. https://github.com/lukaszcz/coqhammer
Czajka, Ł., Kaliszyk, C.: Hammer for Coq: automation for dependent type theory. J. Autom. Reason. 61(1–4), 423–453 (2018)
Dowek, G.: A complete proof synthesis method for the cube of type systems. J. Logic Comput. 3(3), 287–315 (1993)
Dowek, G., Huet, G., Werner, B.: On the definition of the eta-long normal form in type systems of the cube. In: Informal Proceedings of the Workshop on Types for Proofs and Programs (1993)
Dyckhoff, R.: Contraction-free sequent calculi for intuitionistic logic. J. Symb. Logic 57(3), 795–807 (1992)
Dyckhoff, R.: Contraction-free sequent calculi for intuitionistic logic: a correction. J. Symb. Logic 83(4), 1680–1682 (2018)
Dyckhoff, R., Negri, S.: Admissibility of structural rules for contraction-free systems of intuitionistic logic. J. Symb. Logic 65(4), 1499–1518 (2000)
Edelkamp, S., Schrödl, S.: Heuristic Search - Theory and Applications. Academic Press, Cambridge (2012)
Ekici, B., et al.: SMTCoq: a plug-in for integrating SMT solvers into Coq. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10427, pp. 126–133. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63390-9_7
Gutiérrez, F., Ruiz, B.: Cut elimination in a class of sequent calculi for pure type systems. Electron. Notes Theor. Comput. Sci. 84, 105–116 (2003)
Hindley, J.R.: Basic Simple Type Theory, Cambridge Tracts in Theoretical Computer Science, vol. 42. Cambridge University Press, Cambridge (1997)
Kreitz, C., Otten, J.: Connection-based theorem proving in classical and non-classical logics. J. UCS 5(3), 88–112 (1999)
Kunze, F.: Towards the integration of an intuitionistic first-order prover into Coq. HaTT 2016, 30–35 (2016)
Lengrand, S., Dyckhoff, R., McKinna, J.: A focused sequent calculus framework for proof search in pure type systems. Logic. Methods Comput. Sci. 7(1) (2011)
Leroy, X.: Formal verification of a realistic compiler. Commun. ACM 52(7), 107–115 (2009)
Lindblad, F., Benke, M.: A tool for automated theorem proving in Agda. In: Filliâtre, J.-C., Paulin-Mohring, C., Werner, B. (eds.) TYPES 2004. LNCS, vol. 3839, pp. 154–169. Springer, Heidelberg (2006). https://doi.org/10.1007/11617990_10
Nipkow, T., Wenzel, M., Paulson, L.C. (eds.): Isabelle/HOL - A Proof Assistant for Higher-Order Logic. LNCS, vol. 2283. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9
Norell, U.: Towards a practical programming language based on dependent type theory. Ph.D. thesis, Chalmers University of Technology, September 2007
Otten, J.: leanCoP 2.0 and ileanCoP 1.2: high performance lean theorem proving in classical and intuitionistic logic (System Descriptions). In: Armando, A., Baumgartner, P., Dowek, G. (eds.) IJCAR 2008. LNCS (LNAI), vol. 5195, pp. 283–291. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-71070-7_23
Otten, J., Bibel, W.: Advances in connection-based automated theorem proving. In: Provably Correct Systems, pp. 211–241 (2017)
Paulin-Mohring, C.: Inductive definitions in the system Coq - rules and properties. TLCA 1993, 328–345 (1993)
Pierce, B., et al.: Programming language foundations. Software Foundations series, volume 2. Electronic textbook, May 2018
Pierce, B., et al.: Logical Foundations. Software Foundations series, volume 1, Electronic textbook, May 2018
Raths, T., Otten, J., Kreitz, C.: The ILTP problem library for intuitionistic logic. J. Autom. Reason. 38(1–3), 261–271 (2007)
Schmitt, S., Lorigo, L., Kreitz, C., Nogin, A.: JProver : integrating connection-based theorem proving into interactive proof assistants. IJCAR 2001, 421–426 (2001)
Schubert, A., Urzyczyn, P., Zdanowski, K.: On the Mints hierarchy in first-order intuitionistic logic. Logic. Methods Comput. Sci. 12(4), (2016)
Sørensen, M., Urzyczyn, P.: Lectures on the Curry-Howard Isomorphism. Elsevier, Amsterdam (2006)
Steen, A., Benzmüller, C.: The higher-order prover Leo-III. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 108–116. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_8
Troelstra, A., Schwichtenberg, H.: Basic Proof Theory. Cambridge University Press, Cambridge (1996)
Urzyczyn, P.: Inhabitation in typed lambda-calculi (a syntactic approach). In: de Groote, P., Roger Hindley, J. (eds.) TLCA 1997. LNCS, vol. 1210, pp. 373–389. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-62688-3_47
Wajsberg, M.: Untersuchungen über den Aussagenkalkül von A. Heyting. Wiadomości Matematyczne 46, 45–101 (1938)
Wajsberg, M.: On A. Heyting’s propositional calculus. In: Surma, S. (ed.) Logical Works, pp. 132–172. PAN, Warsaw (1977)
Wallen, L.: Automated Proof Search in Non-classical Logics - Efficient Matrix Proof Methods for Modal and Intuitionistic Logics. MIT Press, Cambridge (1990)
Werner, B.: Une Théorie des Constructions Inductives. Ph.D. thesis, Paris Diderot University, France (1994)
Acknowledgements
The author thanks Ping Hou for feedback on the operation of the tactics and for pointing out some bugs.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Completeness Proof for the First-Order Fragment
A Completeness Proof for the First-Order Fragment
In this appendix we prove completeness of our proof search procedure for a first-order fragment of the Calculus of Inductive Constructions. First, we precisely define the first-order fragment.
1.1 A.1 The First-Order Fragment
The system is essentially an extension of \(\lambda \)PRED from [4, Definition 5.4.5] with inductive types and higher-order functions.
A preterm is a sort \(s \in \mathcal {S}= \{*^s,*^p,\square ^s,\square ^p\}\), a variable x, a constructor c, an inductive type I, an application \(t_1t_2\), an abstraction \(\lambda x : \tau . t\), a dependent product \(\forall x : \alpha . \beta \), or a case expression \(\mathtt {case}_\tau ^{I\vec {q}}(u; \vec {x_1} : \vec {\sigma _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\sigma _k} \Rightarrow t_k)\). In a case expression, u is the term matched on, the type of u is \(I \vec {q}\) where \(\vec {q}\) are the values of the parameters, \(\tau \) is the type of the case expression and of each of the branches \(t_i\), and \(t_i[\vec {v}/\vec {x}]\) is the value of the case expression if the value of u is \(c_i \vec {q} \vec {v}\). In comparison to the full CIC, we allow only non-dependent case expressions, i.e., the return type \(\tau \) does not vary across branches. We omit the sub- and/or the superscript when clear or irrelevant.
The intuitive interpretation of the sorts is as follows. The sort \(*^p\) (also written as \(\mathtt {Prop}\)) is for propositions. First-order formulas are elements of \(*^p\). The sort \(*^s\) (also written as \(\mathtt {Set}\)) is for sets – these form a simple type structure over a collection of first-order universes. For example, when \(U : *^s\) then also \((U \rightarrow U) : *^s\). The sort \(\square ^s\) is the sort of \(*^s\). The presence of \(\square ^s\) allows to declare set variables (i.e. of sort \(*^s\)) in the context. The sort \(\square ^p\) is the sort of predicate types. We have \((\tau _1 \rightarrow \ldots \rightarrow \tau _n \rightarrow *^p) : \square ^p\) when \(\tau _i : *^s\) for \(i=1,\ldots ,n\).
An inductive declaration
declares an inductive type I with parameters \(\vec {p}\) and arity \(\forall \vec {p} : \vec {\rho } . *^p\), with n constructors \(c_1,\ldots ,c_n\) having types \(\sigma _1,\ldots ,\sigma _n\) respectively (in the context extended with \(\vec {p} : \vec {\rho }\)). We require:
-
\(\sigma _i = \forall x_i^1 : \tau _i^1 . \ldots \forall x_i^{k_i} : \tau _i^{k_i} . I \vec {p}\),
-
I does not occur in any \(\tau _i^j\).
We could allow strictly positive occurrences of I in \(\sigma _i\), non-parameter arguments to I or inductive types in \(*^s\) as well as \(*^p\). These modifications, however, would introduce some tedious technical complications. With the above definition, all inductive types are non-recursive.
The arity of a constructor \(c_i\) is \(\forall \vec {p} : \vec {\rho } . \sigma _i\), denoted \(c_i (\vec {p} : \vec {\rho }) : \sigma _i\). We assume the well-foundedness of the relation \(\succ \) defined by: \(I_1 \succ I_2\) iff \(I_2\) occurs in the arity of \(I_1\) or the arity of a constructor of \(I_1\).
An environment is a list of inductive declarations. We write \(I \in E\) if a declaration of an inductive type I occurs in the environment E. Analogously, we write \((I (\vec {p} : \vec {\rho }) : *^p) \in E\) and \((c (\vec {p} : \vec {\rho }) : \tau ) \in E\), if a declaration of I with arity \(\forall \vec {p} : \vec {\rho } . *^p\) occurs in E, or a constructor \(c (\vec {p} : \vec {\rho }) : \tau \) with arity \(\forall \vec {p} : \vec {\rho } . \tau \) occurs in a declaration in E, respectively. A context \(\varGamma \) is a list of pairs \(x:\tau \) with x a variable and \(\tau \) a term. A typing judgement has the form \(E;\varGamma \vdash t : \tau \) with \(t,\tau \) preterms. A term t is well-typed and has type \(\tau \) in the context \(\varGamma \) and environment E if \(E;\varGamma \vdash t : \tau \) may be derived using the rules from Fig. 1. We denote the empty list by \(\langle \rangle \).
The set \(\mathcal {R}= \{(*^p,*^p), (*^s,*^p), (*^s,\square ^p), (*^s,*^s)\}\) in Fig. 1 is the set of rules which determine the allowed dependent products.
The rule \((*^p,*^p)\) allows the formation of implication of two formulas:
The rule \((*^s,*^p)\) allows quantification over sets:
The rule \((*^s,\square ^p)\) allows the formation of predicates:
hence
so P is a predicate on A.
The rule \((*^s,*^s)\) allows the formation of function spaces between sets:
Note that we permit quantification over higher-order functions but the formation of lambda-abstractions is allowed only for proofs (i.e. elements of propositions) and for predicates. Elements of sets are effectively restricted to applicative form.
Note that case expressions can occur only in proofs. Hence, including \(\iota \) in the conversion rule is in fact superfluous.
In Fig. 1 we assume that the environment E is well-formed, which is defined inductively: an empty environment is well-formed, and an environment \(E, I (\vec {p} : \vec {\rho }) : *^p := c_1 : \tau _1 \mid \ldots \mid c_n : \tau _n\) (denoted E, I) is well-formed if E is and:
-
the constructors \(c_1,\ldots ,c_n\) are pairwise distinct and distinct from any constructors occurring in the declarations in E;
-
\(E; p_1 : \rho _1, \ldots , p_{j-1} : \rho _{j-1} \vdash \rho _j : \square \) with \(\square \in \{\square ^s,\square ^p\}\), for each j;
-
\(E; \vec {p} : \vec {\rho }, i : *^p \vdash \tau _j' : *^p\) for \(j=1,\ldots ,n\), where \(\tau _j'\) is \(\tau _j\) with all occurrences of \(I \vec {p}\) replaced by i.
When \(E,\varGamma \) are clear or irrelevant, we write \(\varGamma \vdash t : \tau \) or \(t : \tau \) instead of \(E;\varGamma \vdash t : \tau \). In what follows, we assume a fixed a well-formed environment E and omit it from the notation. We write \(\varGamma \vdash t : \tau : s\) if \(\varGamma \vdash t : \tau \) and \(\varGamma \vdash \tau : s\).
Standard meta-theoretical properties hold for our system, including the substitution, thinning and generation lemmas, subject reduction for \(\beta \iota \)-reduction and uniqueness of types. We will use these properties implicitly. The proofs are analogous to [4, Section 5.2] and we omit them.
The available forms of inductive types and case expressions suffice to define all intuitionistic logical connectives with their introduction and elimination rules (see Sect. 2). They do not allow for an inductive definition of equality, however.
Definition 1
-
1.
A \(\varGamma \)-proposition is a term \(\tau \) with \(\varGamma \vdash \tau : *^p\).
-
2.
A \(\varGamma \)-proof is a term t such that \(\varGamma \vdash t : \tau : *^p\) for some \(\tau \).
-
3.
A \(\varGamma \)-set is a term \(\tau \) with \(\varGamma \vdash \tau : *^s\).
-
4.
A \(\varGamma \)-element is a term t such that \(\varGamma \vdash t : \tau : *^s\) for some \(\tau \).
We often omit \(\varGamma \) and talk about propositions, proofs, sets and set elements.
1.2 A.2 Completeness Proof
The \(\beta \)-, \(\iota \)-, and \(\rho \)-reductions for our first-order system are:
In the \(\rho _2\)-reduction rule, P stands for a list of case patterns \(\vec {y_1} : \vec {\sigma _1} \Rightarrow w_1 \mid \ldots \mid \vec {y_m} : \vec {\sigma _m} \Rightarrow w_m\). We assume \(\vec {x_i}\) do not occur in P.
Because case expressions can occur only in proofs, subject reduction holds for \(\rho \)-reduction.
Lemma 1
If \(\varGamma \vdash t : \tau : *^s\) then t does not contain case expressions or lambda-abstractions.
Proof
Induction on t, using the generation lemma.
Lemma 2
If \(\varGamma \vdash \tau : \forall \vec {x} : \vec {\alpha } . s\) with \(s \in \mathcal {S}\) then:
-
1.
no \(\varGamma \)-proofs occur in \(\tau \),
-
2.
no case expressions occur in \(\tau \).
Proof
By induction on \(\tau \).
Corollary 1
If \(\varGamma \vdash t : \tau \) and t contains a case expression, then \(\varGamma \vdash \tau : *^p\).
Corollary 2
If \(\varGamma \vdash t : \varphi : *^p\) and \(\varGamma , x : \varphi \vdash u : \tau \) then \(\varGamma \vdash u[t/x] : \tau \).
Lemma 3
(Subject reduction for \(\rho \)). If \(\varGamma \vdash t : \tau \) and \(t \rightarrow _\rho t'\) then \(\varGamma \vdash t' : \tau \).
Proof
By Corollary 1, t must be a \(\varGamma \)-proof if it contains a \(\rho \)-redex.
The lemma is shown by induction on the typing derivation, analogously to [4, Theorem 5.2.15] except that where the conversion rule is used we instead appeal to Corollary 2.
Implicitly, the following theorems, lemmas and definitions depend on the typing context \(\varGamma \), which changes in the expected way when going under binders. We also implicitly consider types up to \(\beta \iota \)-equality.
Theorem 2
The \(\beta \iota \rho \)-reduction is weakly normalising on typable terms.
Proof
The proof is an adaptation of the proof of an analogous result for first-order intuitionistic natural deduction. See [41, Theorem 6.1.8].
Note that when the context is fixed, the type of each subterm is uniquely determined up to \(\beta \)-equality (the type does not contain proofs, so \(\iota \)-equality is redundant).
Set elements are in \(\beta \iota \rho \)-normal form, because they don’t contain case expressions or lambda-abstractions. Hence, the only redexes which are not proofs must occur in types and have the form \((\lambda x : \alpha . \tau ) t\) where \(\alpha : *^s\). Since each contraction of a \(\beta \)-redex of this form strictly decreases the number of lambda-abstractions (t is a set element not containing lambda-abstractions), \(\beta \)-reduction in types terminates. Moreover, redexes in types cannot be created by reducing \(\beta \iota \rho \)-redexes which are proofs, because abstraction over predicates (i.e. elements of \(\square ^p\)) is not allowed. We may thus consider only the case when all types are in \(\beta \iota \rho \)-normal form and all redexes are proofs.
The degree \(\delta (\alpha )\) of a set \(\alpha \) is 0. The degree \(\delta (\tau )\) of a proposition \(\tau \) in \(\beta \)-normal form is defined inductively.
-
If \(\tau = \forall x : \tau _1 . \tau _2\) then \(\delta (\tau ) = \delta (\tau _1) + \delta (\tau _2) + 1\).
-
If \(\tau = I\vec {q}\) with \( I (\vec {p} : \vec {\rho }) : *^p := c_1 : \forall \vec {x_1} : \vec {\tau _1} . I \vec {p} \mid \ldots \mid c_k : \forall \vec {x_k} : \vec {\tau _k} . I \vec {p} \) then \(\delta (\tau ) = \delta (\vec {\sigma _1}) + \ldots + \delta (\vec {\sigma _k}) + 1\) where \(\vec {\sigma _i}=\vec {\tau _i}[\vec {q}/\vec {p}]\) and \(\delta (\vec {\sigma _i}) = \delta (\sigma _i^1,\ldots ,\sigma _i^{m_i}) = \delta (\sigma _i^1) + \ldots + \delta (\sigma _i^{m_i})\).
-
Otherwise \(\delta (\tau ) = 0\).
Formally, this definition is by induction on the lexicographic product of the multiset extension of the well-founded order \(\succ \) on inductive types (we compare the multisets of inductive types occurring in \(\tau \)) and the size of \(\tau \).
Note that \(\delta (\tau [t/x]) = \delta (\tau )\) if \(t : *^s\) or \(t : *^p\). This is because set elements are not counted towards the degree and proofs do not occur in types.
The degree \(\delta (t)\) of a redex t is defined as follows.
-
\(\beta \)- or \(\rho _1\)-redex: \(t = t_1 t_2\) with \(t_1 : \forall x : \alpha . \tau \). Then \(\delta (t) = \delta (\forall x : \alpha . \tau )\).
-
\(\iota \)- or \(\rho _2\)-redex: \(t = \mathtt {case}_\tau ^{I\vec {q}}(u; \ldots )\). Then \(\delta (t) = \delta (I\vec {q})\).
Note that if \(t : *^p\) is a redex and \(u : *^s\) or \(u : *^p\) then \(\delta (t[u/x]) = \delta (t)\).
The case-size \(\mathrm {cs}(t)\) of a term t is defined inductively.
-
If t is not a case expression then \(\mathrm {cs}(t) = 1\).
-
If \(t = \mathtt {case}(u; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k)\) then \(\mathrm {cs}(t) = \mathrm {cs}(t_1) + \ldots + \mathrm {cs}(t_k) + 1\).
The redex-size \(\mathrm {rs}(t)\) of a redex t is defined as follows.
-
If \(t = t_1t_2\) (a \(\beta \)- or \(\rho _1\)-redex) then \(\mathrm {rs}(t) = \mathrm {cs}(t_1)\).
-
If \(t = \mathtt {case}(u;\ldots )\) (a \(\iota \)- or \(\rho _2\)-redex) then \(\mathrm {rs}(t) = \mathrm {cs}(u)\).
The argument and the targets of an application or a case expression t are defined as follows.
-
If \(t = t_1t_2\) then \(t_1\) is the target and \(t_2\) the argument.
-
If \(t = \mathtt {case}(a \vec {u}; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k)\) with a a constructor or a variable, then \(a \vec {u}\) is the argument and \(t_1,\ldots ,t_k\) are the targets.
-
If \(t = \mathtt {case}(u; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k)\) with u a case expression, then u is the target and \(t_1,\ldots ,t_k\) are the arguments.
A subterm occurrence r is to the right of a subterm occurrence \(r'\) (and \(r'\) to the left of r) if \(r'\) occurs to the right of r in the in-order traversal of the term tree where we first traverse the targets of a subterm, then visit the subterm, and then traverse its arguments. With this definition, a subterm is to the right of its targets and to the left of its arguments.
Note that the rightmost redex r of maximum degree does not occur in a target of a redex \(r'\) of maximum degree and no redex \(r''\) of maximum degree occurs in its argument (otherwise \(r',r''\) would be to the right of r).
For a \(\beta \)- or \(\rho \)-redex, the redex-size is the case-size of the target. For a \(\iota \)-redex, the redex-size is 1. Let r be the rightmost redex of maximum degree in t. Note that changing r to a case expression \(r'\) cannot increase the redex-size of a redex of maximum degree \(r''\) in t containing r. Indeed, otherwise \(r''\) would be a \(\beta \)- or \(\rho \)-redex and r would occur in its target, so \(r''\) would be to the right of r. This implies that contracting the rightmost redex r of maximum degree to \(r'\) cannot increase the redex-size of another redex of maximum degree by exposing a case expression in \(r'\). Note we have not (yet) ruled out the possibility of the contraction increasing the redex-size of a redex of maximum degree occurring inside r.
Let n be the maximum degree of a redex in t and m the sum of redex-sizes of redexes of maximum degree in t. By induction on pairs (n, m) ordered lexicographically, we show that t is weakly \(\beta \iota \rho \)-normalising.
Choose the rightmost redex r of maximum degree and contract it. This either decreases n or leaves n unchanged and decreases m.
-
If \(r = (\lambda x : \alpha . r_1) r_2 \rightarrow _\beta r_1[r_2/x]\) then no redexes of maximum degree occur in \(r_2\) (because \(r_2\) is the argument of a rightmost redex r of maximum degree). So no redexes of maximum degree get duplicated.
All redexes created by this contraction (either by exposing a possible \(\lambda \)-abstraction or case expression in \(r_1\), or by substituting \(r_2\) for x) are of smaller degree. Indeed, if e.g. \(r_2 = \mathtt {case}_{I\vec {q}}(u;\ldots )\) is substituted for x in \(\mathtt {case}^{I\vec {q}}(x;\ldots )\), then \(\alpha = I\vec {q}\) and the degree of the created \(\rho _2\)-redex is \(\delta (I\vec {q}) = \delta (\alpha ) < \delta (r)\). Other cases are similar: one notices that the degree of each redex created by substituting \(r_2\) for x is \(\delta (\alpha ) < \delta (r)\), and the degree of a redex created by exposing \(r_1[r_2/x]\) is \(\delta (\tau ) < \delta (r)\) where \(r_1 : \tau \).
We also need to show that the \(\beta \)-contraction does not increase the redex-size of another redex of maximum degree. The contraction may increase the redex-size of a redex \(r'\) in \(r_1\) by substituting \(r_2\) for x. But then \(\delta (r') = \delta (\alpha ) < \delta (r)\). As discussed before, the contraction cannot increase the redex-size of another redex of maximum degree by exposing \(r_1[r_2/x]\).
Therefore, either n decreases if r was the only redex of maximum degree, or m decreases and n does not change.
-
If \(r = \mathtt {case}_\tau ^{I\vec {q}}(c_i \vec {q} \vec {v}; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k) \rightarrow _\iota t_i[\vec {v}/\vec {x_i}]\) then no redexes of maximum degree occur in \(\vec {v}\).
Let \(v_j : \sigma _j\). Because \(\delta (\sigma _j) < \delta (I\vec {q})\), all redexes created by substituting \(\vec {v}\) for \(\vec {x_i}\) have smaller degree. If a redex is created by exposing \(t_i[\vec {v}/\vec {x_i}]\) then r occurs in t as ru or \(\mathtt {case}(r;\ldots )\). The created redex is then \(t_i[\vec {v}/\vec {x_i}] u\) or \(\mathtt {case}(t_i[\vec {v}/\vec {x_i}];\ldots )\) and has degree \(\delta (\tau )\). But ru or \(\mathtt {case}(r;\ldots )\) was a redex of degree \(\delta (\tau )\) which occurred to the right of r. This is only possible when \(\delta (\tau ) < \delta (I\vec {q})\).
By a similar argument, the \(\iota \)-contraction may increase the redex-size only of redexes of smaller degree.
-
If
$$ \begin{array}{l} r = \mathtt {case}_{\forall x : \alpha . \tau }^{I\vec {q}}(u; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k) w \rightarrow _{\rho _1} \\ \quad \quad \quad \mathtt {case}_{\tau [w/x]}^{I\vec {q}}(u; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1 w \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k w) = r' \end{array} $$then no redexes of maximum degree occur in w.
New redexes of maximum degree may be created: \(t_1 w, \ldots , t_k w\). However, the sum of the redex-sizes of these redexes is smaller than the redex-size of the contracted redex r, so m decreases.
A redex may be created by exposing \(r'\), but then the degree of this redex is \(\delta (\tau ) < \delta (r)\).
-
If
$$ \begin{array}{l} r = \mathtt {case}_\tau ^{I\vec {q}}(\mathtt {case}_{I\vec {q}}^{J\vec {p}}(u; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k); P) \rightarrow _{\rho _2} \\ \quad \quad \quad \mathtt {case}_\tau ^{J\vec {p}}(u; \vec {x_1} : \vec {\tau _1} \Rightarrow \mathtt {case}_\tau ^{I\vec {q}}(t_1; P) \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow \mathtt {case}_\tau ^{I\vec {q}}(t_k; P)) = r' \end{array} $$then no redexes of maximum degree occur in P.
New redexes of maximum degree may be created: \(\mathtt {case}_\tau ^{I\vec {q}}(t_i;P)\). The sum of the redex-sizes of these redexes is at most \(\mathrm {cs}(t_1) + \ldots + \mathrm {cs}(t_k) < \mathrm {cs}(t_1) + \ldots + \mathrm {cs}(t_k) + 1 = \mathrm {rs}(r)\).
A redex may be created by exposing \(r'\) if r occurs in ru or \(\mathtt {case}(r;\ldots )\). But then ru or \(\mathtt {case}(r;\ldots )\) was a redex to the right of r with the same degree \(\delta (\tau )\) as the created redex \(r' u\) or \(\mathtt {case}(r';\ldots )\), so the degree of the new redex must be smaller than \(\delta (I\vec {q})\).
As discussed before, the redex-size of another redex of maximum degree cannot be increased by exposing \(r'\).
Lemma 4
If t is a proof in \(\beta \iota \rho \)-normal form then one of the following holds.
-
\(t = \lambda x : \alpha . t'\) and \(t'\) is a proof in \(\beta \iota \rho \)-normal form.
-
\(t = x u_1 \ldots u_n\) and each \(u_i\) is a proof or a set element in \(\beta \iota \rho \)-normal form.
-
\(t = c \vec {q} u_1 \ldots u_n\) with \(\vec {q}\) the parameter values, and each \(u_i\) is a proof or a set element in \(\beta \iota \rho \)-normal form.
-
\(t = \mathtt {case}(x u_1 \ldots u_n; \vec {y_1} : \vec {\sigma _1} \Rightarrow w_1 \mid \ldots \mid \vec {y_m} : \vec {\sigma _m} \Rightarrow w_m)\), and each \(u_i\) is a proof or a set element in \(\beta \iota \rho \)-normal form, and each \(w_i\) is a proof in \(\beta \iota \rho \)-normal form.
Note that well-typed constructor applications \(c \vec {q} t_1 \ldots t_n\) must by definition (Fig. 1) always include all parameter values \(\vec {q}\). In other words, partial application of a constructor to only some of the parameter values is not allowed.
A set element cannot contain lambda-abstractions or case-expressions, so it is always in \(\beta \iota \rho \)-normal form.
Definition 2
The \(\eta \)-long form of a set element t is t.
The \(\eta \)-long form of a proof variable x is defined by induction on the type \(\tau : *^p\) of x in normal form: if \(\tau = \forall \vec {y} : \vec {\alpha } . \beta \) with \(\beta \) not a product, then \(\lambda \vec {y} : \vec {\alpha } . x y_1' \ldots y_n'\) where \(y_i'\) is the \(\eta \)-long form of \(y_i\). Note that the \(\eta \)-long form of x is well-defined and its type is still \(\tau \) because each \(y_i\) is either a set element (then \(y_i' = y_i)\) or a proof variable (then \(y_i\) does not occur in \(\vec {\alpha },\beta \)).
The \(\eta \)-long form of a proof t in \(\beta \iota \rho \)-normal form is defined by induction on t.
-
If \(t = \lambda x : \alpha . u\) and \(u'\) is the \(\eta \)-long form of u, then \(\lambda x : \alpha . u'\) is the \(\eta \)-long form of t.
-
If \(t = x t_1 \ldots t_k\), and \(\forall \vec {y} : {\alpha } . \tau \) is the type of t with \(\tau \) not a product, and \(t_i'\) is the \(\eta \)-long form of \(t_i\), and \(y_i'\) is the \(\eta \)-long form of (a proof variable or a set element) \(y_i\), then \(\lambda \vec {y} : \vec {\alpha } . x t_1' \ldots t_k' y_1' \ldots y_n'\) is the \(\eta \)-long form of t. For \(k=0\) this definition coincides with the definition of the \(\eta \)-long form of a proof variable.
-
If \(t = c \vec {q} t_1 \ldots t_k\), and \(\forall \vec {y} : {\alpha } . \tau \) is the type of t with \(\tau \) not a product, and \(\vec {q}\) are the parameters, and \(t_i'\) is the \(\eta \)-long form of \(t_i\), and \(y_i'\) is the \(\eta \)-long form of (a proof variable or a set element) \(y_i\), then \(\lambda \vec {y} : \vec {\alpha } . c \vec {q} t_1' \ldots t_k' y_1' \ldots y_n'\) is the \(\eta \)-long form of t.
-
If \(t = \mathtt {case}(u; \vec {y_1} : \vec {\sigma _1} \Rightarrow w_1 \mid \ldots \mid \vec {y_m} : \vec {\sigma _m} \Rightarrow w_m)\) then let \(u'\) be the \(\eta \)-long form of u and \(w_i'\) of \(w_i\). Let \(\tau = \forall \vec {z} : \vec {\alpha } . \beta \) be the type of t in normal form, with \(\beta \) not a product. Then also \(w_i' : \tau \). Thus \(w_i' = \lambda \vec {z} : \vec {\alpha } . w_i''\) because \(w_i'\) is \(\eta \)-long. We may assume none of \(\vec {z}\) occur in \(u'\). We take \(\lambda \vec {z} : \vec {\alpha } . \mathtt {case}(u'; \vec {y_1} : \vec {\sigma _1} \Rightarrow w_1'' \mid \ldots \mid \vec {y_m} : \vec {\sigma _m} \Rightarrow w_m'')\) as the \(\eta \)-long form of t.
A proof or set element t in \(\beta \iota \rho \)-normal form is \(\eta \)-long if the \(\eta \)-long form of t is t.
Note that we do not \(\eta \)-expand inductive type parameters or variable type annotations. A subterm of t is genuine if it does not occur inside an inductive type parameter or a variable type annotation in t.
Lemma 5
A proof t in \(\beta \iota \rho \)-normal form is \(\eta \)-long iff for every genuine subterm u of t such that \(u : \forall \vec {x} : \vec {\alpha } . \tau \) with \(\tau \) not a product we have \(u = \lambda \vec {x} : \vec {\alpha } . u'\).
Proof
Induction on t.
Lemma 6
The \(\eta \)-long form of a \(\beta \iota \rho \)-normal proof is \(\beta \iota \rho \)-normal and has the same type.
Proof
Induction on the definition of \(\eta \)-long form.
Definition 3
The \(\varDelta \)-case-expansion of a proof t is defined inductively.
-
The \(\langle \rangle \)-case-expansion of t is t.
-
If \(\varDelta = x : \alpha ,\varDelta '\) with \(\alpha \) not an inductive type \(I \vec {q}\) with \(I \succ \vec {q}\), then the \(\varDelta '\)-case-expansion of t is the \(\varDelta \)-case-expansion of t.
-
If \(\varDelta = x : I \vec {q},\varDelta '\) with \(I \succ \vec {q}\), and \(c_1,\ldots ,c_n\) are all constructors of I, and \(c_i \vec {q} : \forall \vec {x_i} : \vec {\tau _i} . I \vec {q}\), and \(t'\) is the \(\varDelta ',\vec {x_i}:\vec {\tau _i}\)-case-expansion of t, and \(t_i\) is the \(\iota \)-normal form of \(t'[c_i \vec {q} \vec {x_i}/x]\), then \(\mathtt {case}(x; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k)\) is the \(\varDelta \)-case-expansion of t.
The induction is on the multiset extension \(\succ _{\mathrm {mul}}\) of the bottom-extension \(\succ _\bot \) of the well-founded order \(\succ \) on inductive types. We compare the multisets \(\mathcal {M}(\varDelta )\) of inductive types of variables from \(\varDelta \), using \(\bot \) for non-inductive types, e.g.,
if \(\alpha ,\beta \) are not inductive types. In the last point of the definition, the requirement \(I \succ \vec {q}\) guarantees \(I \succ \vec {\tau _i}\), and thus \(\mathcal {M}(\varDelta ) \succ _{\mathrm {mul}} \mathcal {M}(\varDelta ',\vec {x_i}:\vec {\tau _i})\).
Lemma 7
The \(\varDelta \)-case-expansion of a proof in \(\beta \iota \rho \)-normal form is \(\beta \iota \rho \)-normal and has the same type.
Proof
By induction on the definition of \(\varDelta \)-case-expansion, using Corollary 2. Note that in the last point of the definition, taking the \(\iota \)-normal form requires reducing only the redexes created directly by substituting x with \(c_i \vec {q} \vec {x_i}\). But then because the constructor arguments are variables \(\vec {x_i}\), the \(\iota \)-contraction will result in one of the branches with some variables renamed, which cannot create new redexes if the original term was \(\beta \iota \rho \)-normal.
Definition 4
A case-context \(C[t_1,\ldots ,t_n]\) with branches \(t_1,\ldots ,t_n\) is defined inductively.
-
If t is not a case expression then it is an empty case-context with a single branch t.
-
If \(C_1[\vec {t_1}],\ldots ,C_n[\vec {t_n}]\) are case-contexts with branches \(\vec {t_1}\),...,\(\vec {t_n}\) respectively, then \(\mathtt {case}(t; \vec {x_1} \Rightarrow C_1[\vec {t_1}] \mid \ldots \mid C_n[\vec {t_n}])\) is a case-context with branches \(\vec {t_1},\ldots ,\vec {t_n}\) (i.e. the concatenation of the branch lists for \(C_1,\ldots ,C_n\)).
We write \(C[t_i]_i\) for a case-context with branches \(t_1,\ldots ,t_n\) with n unspecified.
Note that for every term there exists a unique decomposition into a case-context \(C[t_i]_i\) with branches \(t_i\). We write \(t = C[t_i]_i\) if \(C[t_i]_i\) is the case-context decomposition of t. By definition, the branches of a case-context are not case expressions.
If \(t = C[t_i]_i\) is a case-context, then by \(C[t_i']_i\) we denote the term t with branch \(t_i\) replaced by \(t_i'\) (which may now have a different case-context decomposition if \(t_i'\) is a case expression). If \(C_1[t_i]_i\) and \(C_2[u_j]_j\) are case-contexts, then \(C[w_{i,j}]_{i,j} = C_1[C_2[w_{i,j}]_j]_i\) is a case-context with branches \(w_{i,j}\) if \(w_{i,j}\) are not case expressions (and the result is well-typed).
Definition 5
The \(\epsilon \)-normal form of a set element t is t.
The\(\epsilon \)- normal form of a \(\beta \iota \rho \)-normal proof t is defined by induction on t.
-
If \(t = \lambda x : \alpha . u\), and \(u'\) is the \((x:\alpha )\)-case-expansion of the \(\epsilon \)-normal form of u, then \(\lambda x : \alpha . u'\) is the \(\epsilon \)-normal form of t.
-
If \(t = x \vec {u}\), and \(u_i'\) is the \(\epsilon \)-normal form of \(u_i\), and \(u_i' = C_i[w_{j_i}]_{j_i}\), then \(C_1[C_2[\ldots C_n[x w_{j_1} \ldots w_{j_n}]_{j_n}\ldots ]_{j_2}]_{j_1}\) is the \(\epsilon \)-normal form of t.
-
If \(t = c \vec {q} \vec {u}\) then the \(\epsilon \)-normal form of t is defined analogously to the previous point (not modifying \(\vec {q}\)).
-
If \(t = \mathtt {case}(x \vec {u}; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k)\), and \(u_i'\) is the \(\epsilon \)-normal form of \(u_i\), and \(t_i'\) is the \((\vec {x_i}:\vec {\tau _i})\)-case-expansion of the \(\epsilon \)-normal form of \(t_i\), and \(u_i' = C_i[w_{j_i}]_{j_i}\), then
$$ C_1[C_2[\ldots C_n[\mathtt {case}(x w_{j_1} \ldots w_{j_n}; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1' \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k']_{j_n}\ldots ]_{j_2}]_{j_1} $$is the \(\epsilon \)-normal form of t.
Lemma 8
The \(\epsilon \)-normal form of a \(\beta \iota \rho \)-normal proof is \(\beta \iota \rho \)-normal and has the same type.
Proof
Induction on the definition of \(\epsilon \)-normal form. We use Lemma 7 to handle case-expansions of \(\epsilon \)-normal forms in the first and the last point of the definition.
For the second point, note that if \(u_i' = C_i[w_{j_i}]_{j_i}\) with the case-context \(C_i\) non-empty, then each \(w_{j_i}\) must be a proof because it is a branch of a case expression. Hence, \(w_{j_i}\) cannot occur in the type of \(x w_{j_1} \ldots w_{j_i}\). If the case-context \(C_i\) is empty, then \(w_{j_i} = u_i'\) and either \(u_i'\) is a proof and it does not occur in the type of \(x w_{j_1} \ldots w_{j_i}\), or it is a set element and \(u_i' = u_i\). Thus each \(x w_{j_1} \ldots w_{j_n}\) has the same type as \(x \vec {u}\). It follows that \(C_1[C_2[\ldots C_n[x w_{j_1} \ldots w_{j_n}]_{j_n}\ldots ]_{j_2}]_{j_1}\) has the same type as \(x \vec {u}\). An analogous observation applies to the case-context manipulations in the last point.
We restate the definition of long normal forms from Sect. 4 specialised to the first-order fragment.
Definition 6
Any set element is in long normal form. A proof t is in long normal form (lnf) if:
-
\(t = \lambda x : \alpha . t'\), and \(t'\) is in \((x:\alpha )\)-ce-lnf (see below);
-
\(t = x \vec {u}\), and \(t : \tau \) with \(\tau \) not a product, and each \(u_i\) is in lnf and not a case expression;
-
\(t = c \vec {q} \vec {w}\), and \(t : I \vec {q}\), and each \(w_i\) is in lnf and not a case expression;
-
\(t = \mathtt {case}(x\vec {u}; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k)\), and \(t : \tau \) with \(\tau \) not a product, and each \(u_i\) is in lnf and not a case expression, and each \(t_i\) is in \((\vec {x_i}:\vec {\tau _i})\)-ce-lnf.
A proof t is in \(\varDelta \)-case-expanded long normal form (\(\varDelta \)-ce-lnf) if:
-
\(\varDelta = \langle \rangle \) and t is in lnf;
-
\(\varDelta = x : \alpha ,\varDelta '\), and \(\alpha \) is not an inductive type \(I \vec {q}\) with \(I \succ \vec {q}\), and t is in \(\varDelta '\)-ce-lnf;
-
\(\varDelta = x : I \vec {q},\varDelta '\) with \(I \succ \vec {q}\), and \(t = \mathtt {case}(x; \vec {x_1} : \vec {\tau _1} \Rightarrow t_1 \mid \ldots \mid \vec {x_k} : \vec {\tau _k} \Rightarrow t_k)\), and each \(t_i\) is in \(\varDelta ',\vec {x_i}:\vec {\tau _i}\)-ce-lnf and \(x \notin \mathrm {FV}(t_i)\).
Formally, the definition is by mutual induction on pairs (size of t, length of \(\varDelta \)) ordered lexicographically (with \(\varDelta =\langle \rangle \) for lnf).
Lemma 9
If t is in \(\varDelta \)-ce-lnf and the type of t is not a product, then t is in lnf.
Proof
Induction on the definition of \(\varDelta \)-ce-lnf.
Lemma 10
If t is in \(\varDelta \)-ce-lnf, \(x \notin \varDelta \) and \(x : I \vec {q}\), then the \(\iota \)-normal form of \(t[c_i\vec {q}\vec {y}/x]\) is in \(\varDelta \)-ce-lnf.
Proof
Induction on the definition of lnf and \(\varDelta \)-ce-lnf.
Lemma 11
If t is a proof in lnf and the type of t is not a product, then the \(\varDelta \)-case-expansion of t is in \(\varDelta \)-ce-lnf.
Proof
By induction on the definition of \(\varDelta \)-case-expansion, using Lemma 10.
Lemma 12
If \(t = C[t_i]_i\) is in lnf, then so is each \(t_i\).
Proof
Induction on the case-context C, using Lemma 9.
Lemma 13
If \(u = C[u_i]_i\) is in \(\varDelta \)-ce-lnf and all \(u_i'\) are in lnf, then \(C[u_i']_i\) is in \(\varDelta \)-ce-lnf (assuming it is well-typed).
Proof
Induction on the case-context C.
Lemma 14
The \(\epsilon \)-normal form of an \(\eta \)-long \(\beta \iota \rho \)-normal proof is in long normal form.
Proof
Induction on the definition of \(\epsilon \)-normal form, using the previous three lemmas.
Finally, we are ready to prove the completeness theorem. We consider a basic variant of our procedure (Sects. 3.1 and 3.2) which does not perform the looping check for conjectures of sort \(*^s\). With first-order restrictions on term formation, it is to be understood that the procedure performs corresponding actions only when the resulting term is well-typed, e.g., the introduction and elimination actions are not performed for conjectures of sort \(*^s\).
Theorem 3 (Completeness for the first-order fragment)
If the conjecture is a proposition or a set and the inhabitation problem has a solution, then our procedure will find one.
Proof
One checks that the procedure with the restrictions outlined above performs an exhaustive search for (minimal) inhabitants in long normal form. Note that if the conjecture is a proposition or a set, then in any subgoal the conjecture is still a proposition or a set.
By Theorem 2, Lemma 6, Lemma 8 and Lemma 14, for any solution \(t : \tau \) there exists a solution \(t' : \tau \) in long normal form. This implies completeness of our procedure without the looping check. By Corollary 2, loop checking for propositional conjectures does not compromise completeness.
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Czajka, Ł. (2020). Practical Proof Search for Coq by Type Inhabitation. In: Peltier, N., Sofronie-Stokkermans, V. (eds) Automated Reasoning. IJCAR 2020. Lecture Notes in Computer Science(), vol 12167. Springer, Cham. https://doi.org/10.1007/978-3-030-51054-1_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-51054-1_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-51053-4
Online ISBN: 978-3-030-51054-1
eBook Packages: Computer ScienceComputer Science (R0)





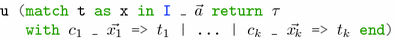 we may usually move u inside the match while preserving the type:
we may usually move u inside the match while preserving the type:
 However, this is not always possible in CIC (see Sect.
However, this is not always possible in CIC (see Sect.  However, in general replacing a subterm
However, in general replacing a subterm  occurs in the conjecture or the context, with t closed, then we immediately perform the elimination action on t.
occurs in the conjecture or the context, with t closed, then we immediately perform the elimination action on t.