Abstract
We prove Chen and Grätzer’s construction theorem for Stone algebras in Isabelle/HOL. The development requires extensive reasoning about algebraic structures in addition to reasoning in algebraic structures. We present an approach for this using classes and locales with implicit carriers. This involves using function liftings to implement some aspects of dependent types and using embeddings of algebras to inherit theorems. We also formalise a theory of filters based on partial orders.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
There is an ongoing effort of formalising results from mathematics, computer science and other disciplines using various proof assistants such as ACL2, Agda, Coq, HOL, Isabelle, Lean, Mizar, Nuprl and PVS. These systems differ in the supported logics, type systems, libraries, automation, code generation capabilities and other ways. In this paper we focus on Isabelle/HOL, which is the higher-order logic instance of the generic proof assistant Isabelle [29]. It has very good proof automation facilities, in particular through the Sledgehammer integration of automated theorem provers and SMT solvers [4, 30], but a somewhat limited type system, notably lacking dependent types.
Isabelle/HOL has a wide range of libraries that come with the system or the associated Archive of Formal Proofs at https://www.isa-afp.org/. They contain extensive theories of algebraic structures including groups, rings, lattices, Boolean algebras, Kleene algebras and many others. Algebras are frequently implemented in Isabelle/HOL using classes and locales, which offer means to package operations and axioms, arrange them in hierarchies, dynamically inherit results, and exhibit multiple instances [16, 23]. Unlike classes, locales support multiple type parameters making them useful for applications such as describing homomorphisms between different structures.
Algebraic hierarchies in Isabelle/HOL come in two flavours: one which makes the carrier sets of the algebras explicit and one which leaves them implicit. The latter assumes a universe of discourse, which all operations, axioms, definitions, theorems and proofs implicitly refer to [16]. The former adds explicit constants for carrier sets; closure properties of operations and membership in the carrier sets must be stated explicitly [2, 22].
Explicit carriers make statements more complex: theories are harder to read and to understand, and additional membership properties may create an overhead for automation [10]. It is therefore not surprising that large hierarchies of algebras have been developed with implicit carriers, which allow for convenient reasoning in algebraic structures. As development progressed over the years issues with this approach when reasoning about algebraic structures have become more apparent. For example, it is challenging to define subalgebras and to impose additional algebraic structure on a subset of an algebra. Two questions arise: to what extent can these issues be overcome while still using implicit carriers? How can hierarchies with implicit carriers be connected to hierarchies with explicit carriers while minimising redevelopment and maintenance efforts?
In the present paper we study Chen and Grätzer’s construction theorem for Stone algebras [8] with the aim of providing some answers to the first of these questions. Briefly stated, every Stone algebra S is isomorphic to a triple \((B,D,\varphi )\) comprising a Boolean algebra B, a distributive lattice D with a greatest element and a bounded lattice homomorphism \(\varphi \) from B to filters of D. Stone algebras have applications ranging from topology [21] over rough sets for representing uncertainty [31] to modelling weighted graphs for algorithm verification [14, 15]. The above theorem has not been formally proved before, is complex enough to push against some of Isabelle/HOL’s limitations, is based on algebraic structures that have been developed using implicit carriers, but requires a significant amount of reasoning about algebras that would benefit from explicit carriers.
We present a proof development of the construction theorem based on a class hierarchy of pseudo-complemented algebras with implicit carriers. The aim is to demonstrate challenges when reasoning about algebras with implicit carriers and ways to deal with them. At the same time we prepare the ground for a proof development connecting algebras with implicit carriers and explicit carriers, which we will use to study the second of the above questions in future work.
The contributions of this paper are:
-
A formal proof of Chen and Grätzer’s construction theorem for Stone algebras. This result has not been formally proved so far.
-
An Isabelle/HOL theory of filters based on partial orders. Existing theories of filters only apply to rings with a carrier and to sets of sets, respectively.
-
Examples formalised in Isabelle/HOL of inheriting universal formulas using an embedding of algebras. This technique is well known in universal algebra but has not been formalised before.
-
A function lifting technique based on universal algebra to circumvent the need for dependent types. This is a new way to get some aspects of dependent types in Isabelle/HOL.
The findings of this paper can be summarised as follows. Reasoning about algebraic structures can be carried out in Isabelle/HOL to a certain extent using implicit carriers, but would benefit from dependent types beyond. Function liftings can mitigate this problem to a certain extent, but they become complex and unnatural for more involved constructions.
In Sect. 2 we give basic definitions and state the construction theorem for Stone algebras. Section 3 discusses our theory of filters based on partial orders. The proof of the construction theorem for Stone algebras is described in Sect. 4. Sections 4.1 and 4.2 construct a triple from a Stone algebra and a Stone algebra from a triple. Sections 4.3 and 4.4 show that these constructions are mutually inverse up to isomorphism. The function lifting and embedding techniques are described in Sect. 4.2. Section 5 puts this work into context. The Isabelle/HOL theory files containing the results of this paper are available in the Archive of Formal Proofs [13].
2 Construction Theorem for Stone Algebras
This section states Chen and Grätzer’s construction theorem for Stone algebras [8] and presents the necessary algebraic structures. In particular we discuss orders, lattices, pseudocomplemented algebras, homomorphisms, filters and triples. Further details about lattices and pseudocomplemented algebras can be found, for example, in Blyth’s textbook [5].
A partial order \(\sqsubseteq \) on a set S is a reflexive, transitive and antisymmetric relation on S:

A lattice is a partially ordered set \((S,\sqsubseteq )\) where any two elements \(x, y \in S\) have a least upper bound or join \(x \sqcup y\) and a greatest lower bound or meet \(x \sqcap y\):

The operations \(\sqcup \) and \(\sqcap \) are associative, commutative, idempotent and \(\sqsubseteq \)-isotone. The absorption laws \(x \sqcup (x \sqcap y) = x = x \sqcap (x \sqcup y)\) hold. The order \(\sqsubseteq \) is connected to join and meet by \(x \sqcup y = y \mathrel {\Leftrightarrow }x \sqsubseteq y \mathrel {\Leftrightarrow }x \sqcap y = x\).
Equivalently, a lattice can be constructed from two operations \(\sqcup \) and \(\sqcap \) that are associative, commutative and satisfy the absorption laws. The relation \(\sqsubseteq \) defined by either of the connection laws \(x \sqsubseteq y \mathrel {\Leftrightarrow }x \sqcup y = y\) or \(x \sqsubseteq y \mathrel {\Leftrightarrow }x \sqcap y = x\) and the operations \(\sqcup \) and \(\sqcap \) satisfy all properties of a lattice stated above.
A lattice is bounded if it has a least element \(\bot \) and a greatest element \(\top \):

These axioms are equivalent to \(\bot \sqcup x = x = \top \sqcap x\).
A lattice is distributive if the following axioms hold:

Either of these axioms implies the other in a lattice.
A (distributive) p-algebra [5] is a bounded (distributive) lattice with a unary pseudocomplement operation  :
:

The pseudocomplement \(\overline{y}\) of an element y is the \(\sqsubseteq \)-greatest element whose meet with y is \(\bot \). An element x in a p-algebra is regular if \(\overline{\overline{x}} = x\) and dense if \(\overline{x} = \bot \). Equivalently, a p-algebra is a bounded lattice with an operation  satisfying \(\overline{\bot } = \top \) and \(\overline{\top } = \bot \) and \(x \sqcap \overline{x \sqcap y} = x \sqcap \overline{y}\).
satisfying \(\overline{\bot } = \top \) and \(\overline{\top } = \bot \) and \(x \sqcap \overline{x \sqcap y} = x \sqcap \overline{y}\).
A Stone algebra is a distributive p-algebra satisfying the following equation:

A Boolean algebra is a bounded distributive lattice with a complement  :
:

Equivalently, a Boolean algebra is a Stone algebra whose elements are all regular. An example of a Stone algebra which is not a Boolean algebra is the three-element chain \(\{ \bot , a, \top \}\) where \(\bot \sqsubseteq a \sqsubseteq \top \) and \(\overline{\bot } = \top \) and \(\overline{a} = \overline{\top } = \bot \).
A bounded-lattice homomorphism is a function \(f : A \rightarrow B\) from a bounded lattice A to a bounded lattice B preserving join, meet, the least element and the greatest element:

A subset \(X \subseteq S\) of a partially ordered set \((S,\sqsubseteq )\) is up-closed if all elements of S above any element of X are in X:

The set \(X \subseteq S\) is downward directed if any two elements of X have a lower bound in X:

A filter of S is a non-empty, downward directed, up-closed subset of S.
We give a general result about filters, which is necessary for the subsequent definition to make sense. Let D be a distributive lattice with a greatest element \(\top _D\). Then the filters of D form a bounded distributive lattice F(D) where the join of two filters X and Y is

meet is intersection, the greatest element is D, the least element is \(\{ \top _D \}\) and the lattice order is the subset order.
Following Chen and Grätzer [8], we use triple as a technical term rather than just for a collection of three components. A triple \((B,D,\varphi )\) comprises a Boolean algebra B, a distributive lattice D with a greatest element, and a bounded-lattice homomorphism \(\varphi : B \rightarrow F(D)\). Triples \((B_1,D_1,\varphi _1)\) and \((B_2,D_2,\varphi _2)\) are isomorphic if there is an isomorphism \(b : B_1 \rightarrow B_2\) of Boolean algebras \(B_1\) and \(B_2\), and an isomorphism \(d : D_1 \rightarrow D_2\) of lattices \(D_1\) and \(D_2\) with greatest elements such that \(\varphi _2(b(x)) = d'(\varphi _1(x))\), where \(d'(X) = \{ d(x) \mid x \in X \}\) applies d to all elements of X.
In this paper we formally prove the construction theorem for Stone algebras [8, 25], by which we understand the following collection of results:
-
1.
Let S be a Stone algebra. Consider the set \(B = \{ x \in S \mid \overline{\overline{x}} = x \}\) of regular elements of S, the set \(D = \{ x \in S \mid \overline{x} = \bot \}\) of dense elements of S, and the function \(\varphi : B \rightarrow 2^D\) defined by \(\varphi (x) = \{ y \in D \mid \overline{x} \sqsubseteq _S y \}\). Then \((B,D,\varphi )\) is a triple, called the triple associated with S, where B forms a subalgebra of S and D forms a subalgebra of the reduct of S to \(\sqcup \), \(\sqcap \) and \(\top \).
-
2.
Let \((B,D,\varphi )\) be a triple. Consider the set

where \({\uparrow }{z} = \{ y \in D \mid z \sqsubseteq _D y \}\) is the up-closure of z in D. Then S is a Stone algebra where
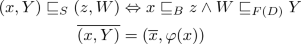
It is called the Stone algebra associated with \((B,D,\varphi )\).
-
3.
The Stone algebra associated with the triple \((B,D,\varphi )\) associated with a Stone algebra S is isomorphic to S.
-
4.
The triple associated with the Stone algebra S associated with a triple \((B,D,\varphi )\) is isomorphic to \((B,D,\varphi )\).
There are a number of construction theorems using triples for similar algebraic structures such as Heyting semilattices and pseudocomplemented distributive lattices [24, 26, 28].
3 An Isabelle/HOL Theory of Filters Based on Orders
The construction theorem for Stone algebras is based on lattices, pseudocomplemented algebras and filters. In this section, we discuss the extent to which these foundations are supported in Isabelle/HOL.
Prior to this work, Isabelle/HOL had libraries for lattices and filters, but not for pseudocomplemented algebras. We reused the available theories for lattices. Only small extensions were necessary, in particular, for directed semilattices, bounded distributive lattices and lattice homomorphisms.
The available theories for filters could not be reused as they are too specific. The theory HOL/Algebra/Ideal.thy defines ring-theoretic ideals in locales with a carrier set. In the theory HOL/Filter.thy a filter is defined as a set of sets. Filters based on orders and lattices abstract from the inner set structure; this approach is used in many texts [1, 3, 5, 9, 11]. Moreover, it is required for the construction theorem of Stone algebras, whence we implemented filters this way.
While theories were available for Boolean algebras, they did not cover pseudocomplemented algebras, which have the same signature but weaker axioms. We therefore developed a theory covering p-algebras, distributive p-algebras, Stone algebras, Heyting semilattices, Heyting algebras, Brouwer algebras and additional results for Boolean algebras. This theory has been used independently for modelling weighted graphs and verifying minimum spanning tree algorithms and has been described in this context [14, 15].
In the remainder of this section, we describe our new theory of filters in more detail. It is structured by the assumptions on the underlying order. We consider filters based on partial orders, semilattices, lattices and distributive lattices. The following is a selection of results proved in this theory:
-
1.
We generalise the ultrafilter lemma [9, Theorem 10.17] to orders with a least element. A proper filter of S is a filter of S that is different from S. An ultrafilter of S is a \(\subseteq \)-maximal proper filter of S. The ultrafilter lemma states that every proper filter of S is a subset of an ultrafilter of S. Actually, our proof does not need that \(\sqsubseteq \) is a partial order, but also works if \(\sqsubseteq \) is an arbitrary relation satisfying \(\bot \sqsubseteq x\) for some element \(\bot \) and all elements x of the algebra (defining filters as in Sect. 2 but for arbitrary \(\sqsubseteq \)). The proof uses Isabelle/HOL’s
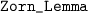 , which requires closure under union of arbitrary (possibly empty) chains of sets.
, which requires closure under union of arbitrary (possibly empty) chains of sets. -
2.
We study the lattice structure of filters. A meet-semilattice is a partially ordered set \((S,\sqsubseteq )\) where all \(x, y \in S\) have a greatest lower bound \(x \sqcap y\). A meet-semilattice is directed if any two elements have an upper bound. A meet-semilattice is bounded if it has a greatest element. The results state:
-
(a)
The set of filters where the underlying order is a directed meet-semilattice forms a lattice with a greatest element.
-
(b)
The set of filters over a bounded meet-semilattice forms a bounded lattice.
-
(c)
The set of filters over a distributive lattice with a greatest element forms a bounded distributive lattice.
-
(a)
-
3.
We connect ultrafilters and prime filters [9, Theorem 10.11]. A prime filter of S is a proper filter X of S where \(x \sqcup y \in X\) implies \(x \in X\) or \(y \in X\) for all \(x, y \in S\). The result shows that in a distributive lattice every ultrafilter is a prime filter. The lattice does not need to be bounded [9, p. 234].
-
4.
We prove a result about principal filters [12, Lemma II]. A principal filter of S is a filter X of S such that \(X = {\uparrow }{x}\) for some \(x \in S\) where \({\uparrow }{x} = \{ y \in S \mid x \sqsubseteq y \}\). The result shows that in a distributive lattice, if both join and meet of two filters are principal filters, both filters are principal filters.
4 The Construction Theorem for Stone Algebras
In this section, we describe the proof of the construction theorem for Stone algebras in Isabelle/HOL. Section 4.1 constructs the triple associated with a Stone algebra. Section 4.2 constructs the Stone algebra associated with a triple. It describes the function lifting technique for dependent types and the embedding technique, both based on universal algebra. Section 4.3 shows that the first construction followed by the second construction gives back the original Stone algebra up to isomorphism. Section 4.4 shows that the second construction followed by the first construction gives back the original triple, again up to isomorphism.
4.1 Constructing a Triple from a Stone Algebra
The first set of results concerns the construction of a triple from a Stone algebra S. Specifically, we show:
-
1.
The regular elements of S form a Boolean algebra B that is a subalgebra of S.
-
2.
The dense elements of S form a distributive lattice D with a greatest element, which is a subalgebra of the reduct of S to \(\sqcup \), \(\sqcap \) and \(\top \).
As shown in Sect. 3, it follows that the set of filters F(D) of the dense elements of S forms a bounded distributive lattice. Considering the function \(\varphi : B \rightarrow 2^D\) defined by \(\varphi (x) = \{ y \in D \mid \overline{x} \sqsubseteq _S y \}\), we show:
-
3.
\(\varphi \) maps every regular element to a filter of D.
-
4.
\(\varphi \) is a bounded-lattice homomorphism from B to F(D).
Hence \((B,D,\varphi )\) is a triple.
We have implemented Stone algebras using classes in Isabelle/HOL, situating them between lattices and Boolean algebras in the existing class hierarchy provided by HOL/Lattices.thy. Every class has a single type parameter, which represents the carrier set of an algebra and is left implicit. For every operation of an algebra there is an additional class parameter. Axioms for these operations are provided as statements assumed to hold in the context of the class but not outside. Classes can be instantiated by providing a particular type, appropriate operations and proofs of these assumptions.
Using classes to implement algebraic structures makes it easy to extend the hierarchy. For example, p-algebras are defined as a subclass of the existing class for bounded lattices, extending the latter by a unary pseudocomplement operation satisfying the appropriate axiom:

Similarly, Stone algebras are introduced as a subclass of distributive p-algebras, which are introduced as a subclass of p-algebras. On top of that, the existing class for Boolean algebras forms a subclass of the new class for Stone algebras, which is proved as follows:

Existing subclass relationships are taken into account which avoids the need to repeat proofs. For example, the axioms of bounded distributive lattices, which are necessary for Stone algebras, follow automatically since the class for Boolean algebras is a subclass of the classes for bounded lattices and distributive lattices.
Reasoning in algebraic structures and proving subclass relationships of entire algebras is well supported this way. For the Stone construction theorem, however, we need to prove that the subset of regular elements forms a Boolean algebra. This cannot be done using the subclass mechanism in a class as it implicitly refers to the entire carrier sets of the related algebras. We therefore introduce a new type corresponding to the set of regular elements. New types have to be introduced outside a class at a global level, since otherwise they could refer to class parameters making them dependent types, which are not supported by HOL:

Here ’a is a type parameter, which is constrained to being a subclass of the class for Stone algebras, and every element x of the set underlying the new type is restricted to have type ’a. New type definitions require a proof that the set they are derived from is not empty, which is discharged by the auto proof method since any Stone algebra contains \(\bot \) and \(\top \). Such a type definition automatically introduces representation and abstraction functions between the new type and the set it is derived from, and automatically derives basic theorems about these functions including their inverse relationship. We then show that this type instantiates the class for Boolean algebras:

The parentheses indicate the subclass constraint required for the type parameter, that is, the kind of algebra from which the regular elements are taken. A stronger constraint than required by the type can be provided in such an instantiation; for example, this is used to characterise the structure formed by the set of filters over various kinds of semilattice as mentioned in Sect. 3. The operations on the new type are derived from the operations on Stone algebras using the representation and abstraction functions of the type. Working with new types introduced like this often requires handling the representation and abstraction functions, which clutter definitions, statements and proofs. Some of this can be hidden using mechanisms from Isabelle/HOL’s Lifting package [18].
Similarly, we introduce a new type for the dense elements of a Stone algebra and show that it forms a distributive lattice with a greatest element. We also introduce a new type for the filters of dense elements and show that it forms a bounded distributive lattice. The proofs of these instances are simple as the operations are derived from the underlying algebras without changes. The main work is proving that filters over a distributive lattice with a greatest element form a bounded distributive lattice, which was done generally in Sect. 3.
We next construct the function \(\varphi \) mapping regular elements to sets of dense elements, where \(\Rightarrow \) is the function type constructor:

The representation functions convert elements x and y from the regular and dense types to the underlying Stone algebra, where they can be compared. The set of dense elements satisfying the given property is converted to a filter using the abstraction function of this type.
A triple consists of a Boolean algebra, a distributive lattice with a greatest element, and a structure map. The Boolean algebra and the distributive lattice are represented as HOL types with appropriate subclass constraints. Because both occur in the type of the structure map, the triple is determined simply by the structure map and its HOL type. The structure map needs to be a bounded lattice homomorphism. This information is collected in the following locale:

Unlike classes, locales support multiple type parameters such as ’a and ’b used here. Another difference is that a locale can have multiple instances for the same type. On the other hand, different instances of a class can share the same notation for an operation, which is closer to mathematical usage. It remains to show that \(\varphi \) is indeed a bounded lattice homomorphism:

The proof is cluttered with occurrences of the representation and abstraction functions for the types of regular and dense elements. The preservation of \(\sqcup \) has to be broken down into quite small steps, whereas Sledgehammer [30] is more helpful with automating the preservation of the other three operations. This is partly because the join of filters has the most complex definition, but the representation and abstraction functions cause further overhead.
Referees of this paper suggested to use the Lifting package to hide representation and abstraction functions in the definition of stone_phi and in other definitions in the following sections. The author has tried this but soon ran into problems which could not be solved during revision of the paper. One of the issues appeared to be the lack of suitable transfer rules for the composite type “’a dense filter” even though transfer rules are automatically generated for the dense and filter type constructors.
4.2 Constructing a Stone Algebra from a Triple
Next, from a triple \((B,D,\varphi )\) such that B is a Boolean algebra, D is a distributive lattice with a greatest element and \(\varphi : B \rightarrow F(D)\) is a bounded lattice homomorphism, we construct a Stone algebra S. The elements of S are pairs taken from \(B \times F(D)\) following the construction of Katriňák [25]. This set and the operations making it a Stone algebra can be defined in the locale for triples:

We need to represent the set of pairs as a type to be able to instantiate the Stone algebra class. Because the definition of this set depends on \(\varphi \), which is a parameter of the triple locale, this would require dependent types. Since Isabelle/HOL does not have dependent types, we use a function lifting instead (which is unrelated to the Lifting package). Similarly to the ‘lambda lifting’ technique in functional programming [20], our function lifting makes a conceptually local entity global by capturing its free variables as parameters. However, in our case the result is a global type not a global function.
We initially describe the process for the application at hand. Because it applies more generally we summarise the ideas at the end of this section.
We first define a type to capture the parameter \(\varphi \) of the triple locale. This parameter is the structure map that occurs in the definition of the set of pairs. The set of all structure maps is the set of all bounded lattice homomorphisms (of appropriate type):

In order to make the set a HOL type, we need to show that at least one such structure map exists. To this end we use the ultrafilter lemma shown in Sect. 3: the required bounded lattice homomorphism is essentially the characteristic map of an ultrafilter, but the latter must exist. In particular, the underlying Boolean algebra must contain at least two elements, which we guarantee by introducing a suitable subclass of the class for Boolean algebras.
We then implement the type that represents the set of pairs depending on structure maps. It uses functions from structure maps to pairs with the requirement that, for each structure map, the corresponding pair is contained in the set of pairs constructed for a triple with that structure map:

If this type could be defined in the locale triple and instantiated to Stone algebras in this locale, there would be no need for the lifting and we could work with triples directly. Since the type needs to be defined outside the triple locale at global level, we supply the type parameter (Rep_phi f) when referring to the set of pairs defined in the locale. The function lifting allows us to express the dependence on the locale parameter at the type level.
The lifted pairs form a Stone algebra, where the operations are lifted pointwise from pairs to functions:

The proofs of the Stone algebra axioms are again quite low-level as a consequence of having to deal with the function lifting in addition to various representation functions. Apart from these technical issues, at this stage the development deviates from the original statements. We are here constructing a Stone algebra of functions from structure maps to pairs, whereas the original construction yields a Stone algebra of pairs for any given structure map. However, any Stone algebra of pairs obtained for a given structure map is isomorphic to a subalgebra of the Stone algebra of functions. While this relationship cannot be expressed directly as it would again require dependent types, we can prove a special case of it.
To this end, we specialise the construction to start with the triple associated with a Stone algebra, that is, the triple obtained in Sect. 4.1. For that particular structure map stone_phi (as for any other particular structure map) the resulting type of pairs is no longer a dependent type. It is just the set of pairs obtained for the given structure map:

It could be proved directly that this type is a Stone algebra. To demonstrate how a technique of universal algebra can be realised in Isabelle/HOL, we choose a different approach: we embed the type of pairs into the lifted type. The embedding injects a pair x into a function as the value at the given structure map; this makes the embedding injective. The value of the function at any other structure map is carefully chosen to make the resulting function a Stone algebra homomorphism. We use \(\overline{\overline{x}}\), which is essentially a projection to the regular element component of x, whence the range of \(\lambda x . \overline{\overline{x}}\) has the structure of a Boolean algebra:

Again, since we reason outside the triple locale at a global level, we supply the locale parameter, in this case to both occurrences of the pseudocomplement operation triple.pairs_uminus.
We then show that stone_phi_embed is an embedding, that is, it preserves \(\sqcup \), \(\sqcap \), \(\bot \), \(\top \),  and it is injective. Hence all Stone algebra axioms can be inherited using the embedding. This is because the axioms are universal formulas, that is, first-order formulas in prenex form where all quantifiers are universal [6]. We also show that stone_phi_embed is an order-isomorphism, which allows us to inherit inequalities without transforming them to equations. It follows that the pairs form a Stone algebra:
and it is injective. Hence all Stone algebra axioms can be inherited using the embedding. This is because the axioms are universal formulas, that is, first-order formulas in prenex form where all quantifiers are universal [6]. We also show that stone_phi_embed is an order-isomorphism, which allows us to inherit inequalities without transforming them to equations. It follows that the pairs form a Stone algebra:

When proving the Stone algebra axioms, Sledgehammer automatically finds proofs using the embedding property of stone_phi_embed and the corresponding axioms of the underlying Stone algebra.
Generalising the Function-Lifting Construction. We discuss the ideas of this section as more general recipes. Mathematically speaking we wish to show that a set S depending on a parameter p forms an algebra. For instance, assume the algebra has an operation \(F : S \rightarrow S \rightarrow S\) and a relation \(R : S \rightarrow S \rightarrow \mathrm {bool}\), whose definitions may also depend on p.
In Isabelle/HOL, we have a locale L with parameter p of type A. In this locale, we define the set S of elements of type B and show S is not empty. We also define F and R and show they satisfy the axioms of the algebra. However, we cannot instantiate the class that implements the algebra. This requires a type instead of the set S and the type cannot be defined in L where it might depend on p.
We therefore simulate a dependent type outside L. Observe that for any p satisfying the assumptions of L, the locale yields a set \(S_p\); in Isabelle/HOL it is obtained by L.S p. We construct the (infinite) direct product of these sets \(\prod _p S_p\). We represent each value in this product by a function indexed with p.
Technically, we first create a type \(T'\) from the set of all possible values of the locale parameter p. This set contains the elements of type A subject to assumptions about p in L; it is not empty (or else the locale could not be instantiated). We then create the type T of functions \(f : T' \rightarrow B\) such that \(f(p) \in S_p\) for all \(p \in T'\). This is the direct product; it exists because no \(S_p\) is empty.
We show that T instantiates the algebra where F and R are lifted pointwise from S to T. Specifically, \(F_T\) f g = \(\lambda p\) . F (f p) (g p) is the lifting of F and \(R_T\) f g = \(\forall p\) . R (f p) (g p) is the lifting of R. Because the constituent sets \(S_p\) satisfy the axioms of the algebra so does their direct product T in many cases. In particular, direct products preserve universal Horn formulas [17]. Hence it suffices if all axioms are universally quantified conditional equations. This works not just for Stone algebras but for many others such as groups, rings, fields, lattices, Boolean algebras, dioids, Kleene algebras and action algebras.
We next specialise the product to a given value q for the locale parameter. That is, we create a type \(T_q\) for the set \(S_q\) and show that it instantiates the algebra. To this end, we embed \(T_q\) in T using a function \(H : T_q \rightarrow T\). Specifically, H x = \(\lambda p\) . if p = q then x else h p x, where h p is any homomorphism from \(S_q\) to \(S_p\). The latter condition for h is sufficient for H to be an embedding. While we do not give a general scheme for how to obtain h, we note that all algebras \(S_p\) are defined using the same pattern, which can help. If a suitable h is available, the axioms of the algebra can be derived for \(T_q\) via the embedding H. This works for arbitrary universal formulas, which covers even more algebras than listed above.
We explain how to derive universal formulas via embeddings using universal algebra [6]. Let X and Y be algebras with the same signature and let e be an embedding of X into Y. Let U be the universe of X. Induction over the structure of terms yields \(e(t^X\!(x_1,\dots ,x_n)) = t^Y\!(e(x_1),\dots ,e(x_n))\) for all terms t over the signature (with interpretations \(t^X,t^Y\) in X, Y) and all \(x_i \in U\). Since e is injective, \(t^X\!(x_1,\dots ,x_n) = s^X\!(x_1',\dots ,x_m') \mathrel {\Leftrightarrow }t^Y\!(e(x_1),\dots ,e(x_n)) = s^Y\!(e(x_1'),\dots ,e(x_m'))\) for all terms s, t and all \(x_i, x_j' \in U\). Consider a formula P with k free variables, which is constructed by combining such equalities between terms with propositional connectives. Induction over the structure of P yields \(P^X\!(x_1,\dots ,x_k) \mathrel {\Leftrightarrow }P^Y\!(e(x_1),\dots ,e(x_k))\) for all \(x_i \in U\). Hence, if \(\forall y_1,\dots ,y_k : P^Y\!(y_1,\dots ,y_k)\) holds, so does \(\forall x_1,\dots ,x_k : P^X\!(x_1,\dots ,x_k)\). This argument generalises from algebras to first-order structures (with relations in the signature). It does not extend to existential quantifiers as the asserted element may lie outside the range of e.
4.3 The Stone Algebra of a Triple of a Stone Algebra
Next, we show that the Stone algebra constructed in Sect. 4.2 from the triple constructed in Sect. 4.1 from a Stone algebra S is isomorphic to S. We give explicit mappings in both directions:

Without the necessary representation and abstraction functions, the first mapping is \(\lambda x . (\overline{\overline{x}}, \varphi (\overline{x}) \sqcup {\uparrow }{(x \sqcup \overline{x})})\). The second of the above mappings extracts from a pair a dense element using the following function defined in the locale triple:

The Hilbert choice construct SOME z. P(z) yields some element z that satisfies P(z). This works because the intersection of \(\varphi (x)\) with a principal filter is a principal filter, which we prove using a result shown in Sect. 3 [12, Lemma II].
We then show that sa_iso_inv and sa_iso are mutually inverse and that sa_iso is a homomorphism of Stone algebras. The proofs of these results are cluttered with representation and abstraction functions as the above definitions indicate.
4.4 The Triple of a Stone Algebra of a Triple
Finally, we show that the triple constructed in Sect. 4.1 from the Stone algebra constructed in Sect. 4.2 from a triple \((B,D,\varphi )\) is isomorphic to \((B,D,\varphi )\). This requires an isomorphism of Boolean algebras, an isomorphism of distributive lattices with a greatest element, and a commuting diagram involving the structure maps. We give explicit mappings of the Boolean algebra isomorphism and the distributive lattice isomorphism in both directions.
We first define and prove the isomorphism of Boolean algebras. Because the Stone algebra of a triple is implemented as a lifted pair, we also lift the Boolean algebra using a parameter of the same type as that used by the lifted pairs:

The resulting function type forms a Boolean algebra with operations lifted pointwise:

We can now define the mappings between the two lifted structures:

We then show that ba_iso_inv and ba_iso are mutually inverse and that ba_iso is a homomorphism of Boolean algebras.
We carry out a similar development for the isomorphism of distributive lattices with greatest elements. Again, the original distributive lattice with a greatest element needs to be lifted to match the lifted pairs. The resulting function type forms a distributive lattice with a greatest element with operations lifted pointwise. The mappings between the two lifted structures are:

The first mapping uses the following function to extract the least element of the filter of a dense pair, which turns out to be a principal filter:

We then show that dl_iso_inv and dl_iso are mutually inverse and that dl_iso preserves \(\sqcup \), \(\sqcap \) and \(\top \).
We finally show that the isomorphisms are compatible with the structure maps. This involves lifting the distributive lattice isomorphism to filters of distributive lattices as these are the targets of the structure maps. To this end, we show that the lifted isomorphism preserves filters. The compatibility of isomorphisms states that the same result is obtained in two ways by starting with a regular lifted pair p:
-
apply the Boolean algebra isomorphism to the pair; then apply a structure map f to obtain a filter of dense elements; or,
-
apply the structure map stone_phi to the pair; then apply the distributive lattice isomorphism lifted to the resulting filter.
This commutativity property is formally stated as follows:

Here g ‘ X is the union of the sets g(x) taken over all \(x \in X\).
Apart from the many representation and abstraction functions occurring in these definitions and proofs, the development again deviates from the original statements. We have to artificially lift the constituent algebras of triples – a Boolean algebra and a distributive lattice with a greatest element – to functions. This is necessary in order to establish the isomorphisms to lifted pairs, which are parameterised in \(\varphi \). The same parameter \(\varphi \) is introduced for the Boolean algebra and the distributive lattice, even though it is not needed for these, simply to get a matching cardinality for the isomorphism. This is a flow-on effect from lifting to functions in Sect. 4.2 due to the lack of dependent types there.
5 Discussion
We put this work into context by discussing a number of questions.
Are the encountered issues self-inflicted and could they have been prevented by choosing other proof assistants? Possibly; for example, some proof assistants such as Agda, Coq and Lean support dependent types. Aspects of universal algebra have been formalised in Coq [7, 32]. The present paper does not aim to find the ‘best’ system for reasoning about algebraic structures. Proof assistants differ in many dimensions; a particular choice will typically involve trade-offs. There may be various reasons (such as external requirements, existing libraries, automation support) for choosing Isabelle/HOL despite the fact it does not support dependent types. By studying a sufficiently complex example, this paper provides a data point to inform such compromises.
Are the encountered issues well known in the Isabelle community? Difficult to say. Some issues have been briefly noted [10]. We are not aware of a sufficiently complex case study exploring the limitations of reasoning about algebras with implicit carriers. Without such case studies newcomers to a community might take a very long time to appreciate the issues. This paper also provides new means to overcome some of the limitations.
Do we allow Isabelle and not the mathematics to dictate the approach? Yes and no. To formally verify any result a system has to be chosen; staying ‘close’ to the mathematics is one aspect of the trade-off mentioned above and discussed in this paper. By choosing Isabelle/HOL, its capabilities necessarily constrain the approach. The trade-off between implicit and explicit carrier sets has been discussed in the introduction. Within the setting of implicit carriers in Isabelle/HOL we tried to follow the mathematics. Of course, Isabelle’s capabilities might be extended to bring the approach closer to mathematics. Here too, this paper provides a data point to inform about what might be useful.
What concrete lessons could an Isabelle user learn? Users who wish to reason about algebraic structures can learn about the consequences of working with implicit carriers to inform their choice between them and explicit carriers. Users could find some of the techniques such as function lifting for dependent types and inheriting theorems via embeddings helpful for their work. Since the underlying universal algebra can be applied in many settings, the techniques are potentially of wider interest.
Are the experiences reported in this paper largely negative? Not in the author’s opinion. There are negative aspects and positive aspects. This paper attempts to present a balanced view to inform choices.
6 Conclusion
The proof of Chen and Grätzer’s construction theorem shows that reasoning about algebraic structures can be carried out in Isabelle/HOL using algebraic structures with implicit carrier sets. At the same time, the lack of dependent types leads to the introduction of function liftings. To remain compatible with this lifting, some other types also need to be lifted to functions even though they do not have an actual dependence. Overall this makes the constructions more complex and less related to the original proof.
An alternative way to reason about algebras is to explicitly represent their carrier sets in the corresponding classes and locales. Algebraic structures with explicit carriers are defined, for example, in the theories HOL/Algebra/*.thy. Previous work [10] briefly compares algebras with implicit and explicit carriers. It is desirable to automatically connect hierarchies of algebras with implicit and explicit carriers to ensure consistency and avoid duplication in maintenance and evolution. Isabelle/HOL’s types-to-sets framework [19, 27] offers a promising approach using local type definitions, which we will explore in future work.
The function liftings in this paper are used to work around the dependence on locale parameters. There is no claim that this gives a full-fledged implementation of dependent types. Kammüller [22] describes an approach to represent modular structures by dependent types constructed as sets in Isabelle/HOL.
References
Balbes, R., Dwinger, P.: Distributive Lattices. University of Missouri Press, Columbia (1974)
Ballarin, C.: Locales: a module system for mathematical theories. J. Autom. Reason. 52(2), 123–153 (2014)
Birkhoff, G.: Lattice Theory, Colloquium Publications, vol. XXV, 3rd edn. American Mathematical Society, Providence (1967)
Blanchette, J.C., Böhme, S., Paulson, L.C.: Extending Sledgehammer with SMT solvers. In: Bjørner, N., Sofronie-Stokkermans, V. (eds.) CADE 2011. LNCS (LNAI), vol. 6803, pp. 116–130. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22438-6_11
Blyth, T.S.: Lattices and Ordered Algebraic Structures. Springer, London (2005). https://doi.org/10.1007/b139095
Burris, S., Sankappanavar, H.P.: A Course in Universal Algebra. Springer, New York (1981)
Capretta, V.: Universal algebra in type theory. In: Bertot, Y., Dowek, G., Hirschowitz, A., Paulin, C., Théry, L. (eds.) TPHOLs 1999. LNCS, vol. 1690, pp. 131–148. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48256-3_10
Chen, C.C., Grätzer, G.: Stone lattices. I: Construction theorems. Can. J. Math. 21, 884–894 (1969)
Davey, B.A., Priestley, H.A.: Introduction to Lattices and Order, 2nd edn. Cambridge University Press, Cambridge (2002)
Foster, S., Struth, G., Weber, T.: Automated engineering of relational and algebraic methods in Isabelle/HOL. In: de Swart, H. (ed.) RAMiCS 2011. LNCS, vol. 6663, pp. 52–67. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21070-9_5
Grätzer, G.: Lattice Theory: First Concepts and Distributive Lattices. W. H. Freeman and Co., New York (1971)
Grätzer, G., Schmidt, E.T.: On ideal theory for lattices. Acta Sci. Math. 19(1–2), 82–92 (1958)
Guttmann, W.: Stone algebras. Archive of Formal Proofs (2016)
Guttmann, W.: An algebraic framework for minimum spanning tree problems. Theor. Comput. Sci. 744, 37–55 (2018)
Guttmann, W.: Verifying minimum spanning tree algorithms with Stone relation algebras. J. Log. Algebraic Methods Program. 101, 132–150 (2018)
Haftmann, F., Wenzel, M.: Constructive type classes in Isabelle. In: Altenkirch, T., McBride, C. (eds.) TYPES 2006. LNCS, vol. 4502, pp. 160–174. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74464-1_11
Horn, A.: On sentences which are true of direct unions of algebras. J. Symbol. Log. 16(1), 14–21 (1951)
Huffman, B., Kunčar, O.: Lifting and transfer: a modular design for quotients in Isabelle/HOL. In: Gonthier, G., Norrish, M. (eds.) CPP 2013. LNCS, vol. 8307, pp. 131–146. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-03545-1_9
Immler, F., Zhan, B.: Smooth manifolds and types to sets for linear algebra in Isabelle/HOL. In: Mahboubi, A., Myreen, M.O. (eds.) CPP 2019, pp. 65–77. ACM (2019)
Johnsson, T.: Lambda lifting: transforming programs to recursive equations. In: Jouannaud, J.-P. (ed.) FPCA 1985. LNCS, vol. 201, pp. 190–203. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-15975-4_37
Johnstone, P.T.: Stone Spaces. Cambridge University Press, Cambridge (1982)
Kammüller, F.: Modular structures as dependent types in Isabelle. In: Altenkirch, T., Naraschewski, W., Reus, B. (eds.) TYPES 1998. LNCS, vol. 1657, pp. 121–133. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48167-2_9
Kammüller, F., Wenzel, M., Paulson, L.C.: Locales: a sectioning concept for Isabelle. In: Bertot, Y., Dowek, G., Hirschowitz, A., Paulin, C., Théry, L. (eds.) TPHOLs 1999. LNCS, vol. 1690, pp. 149–165. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48256-3_11
Katriňák, T.: Die Kennzeichnung der distributiven pseudokomplementären Halbverbände. Journal für die reine und angewandte Mathematik 241, 160–179 (1970)
Katriňák, T.: A new proof of the construction theorem for Stone algebras. Proc. Am. Math. Soc. 40(1), 75–78 (1973)
Katriňák, T., Mederly, P.: Constructions of p-algebras. Algebra Univers. 17(1), 288–316 (1983)
Kunčar, O., Popescu, A.: From types to sets by local type definition in higher-order logic. J. Autom. Reason. 62(2), 237–260 (2018)
Nemitz, W.C.: Implicative semi-lattices. Trans. Am. Math. Soc. 117, 128–142 (1965)
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL: A Proof Assistant for Higher-Order Logic. LNCS, vol. 2283. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9
Paulson, L.C., Blanchette, J.C.: Three years of experience with Sledgehammer, a practical link between automatic and interactive theorem provers. In: Sutcliffe, G., Ternovska, E., Schulz, S. (eds.) Proceedings of the 8th International Workshop on the Implementation of Logics, pp. 3–13 (2010)
Polkowski, L.: Rough Sets: Mathematical Foundations. Springer, Heidelberg (2002). https://doi.org/10.1007/978-3-7908-1776-8
Spitters, B., van der Weegen, E.: Type classes for mathematics in type theory. Math. Struct. Comput. Sci. 21(4), 795–825 (2011)
Acknowledgement
I thank the anonymous referees for helpful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Guttmann, W. (2020). Reasoning About Algebraic Structures with Implicit Carriers in Isabelle/HOL. In: Peltier, N., Sofronie-Stokkermans, V. (eds) Automated Reasoning. IJCAR 2020. Lecture Notes in Computer Science(), vol 12167. Springer, Cham. https://doi.org/10.1007/978-3-030-51054-1_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-51054-1_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-51053-4
Online ISBN: 978-3-030-51054-1
eBook Packages: Computer ScienceComputer Science (R0)



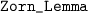 , which requires closure under union of arbitrary (possibly empty) chains of sets.
, which requires closure under union of arbitrary (possibly empty) chains of sets.