Keywords

1 Introduction

Microtubules are long protein polymers involved in a wide range of cellular activities e.g., maintaining cell stiffness/shape, intracellular transport, regulation of cell morphology and cell mechanics along with facilitation of other physiological processes [1,2,3]. Microtubules are the stiffest element in the cytoskeleton of eukaryotic cells that helps them to withstand both static and dynamic loads. Several experimental and numerical studies have been reported in the past for understanding the mechanical properties of microtubules [1, 2, 4,5,6,7]. Owing to the previously reported studies in literature, the mechanical characteristics and the basics of microtubules biomechanics are now understood reasonably well [5, 6]. However, most of the reported numerical studies on the mechanical characterization of microtubules consider only the coupling between applied stress and induced strain under the application of externally applied forces. It has also been theoretically proved that microtubules possess piezoelectric properties [8], a two-way linear coupling that results in the conversion of mechanical deformation into an applied electric field and vice-versa. The experimental basis of piezoelectric properties of microtubules is yet to come and is mainly limited due to associated intricacies in the intracellular probing of microtubules at nanoscales [9]. Importantly, such electro-mechanical integration will result in fostering many exciting applications of the biocompatible piezoelectric materials, paving a way to a new age in the field of medicine [10]. Potential applications of this promising research area in the biomedical field include minimally invasive sensors, regenerative medicine, eco-friendly energy harvesters, drug delivery, etc. [10, 11].

In what follows, a three-dimensional coupled electro-mechanical model of a microtubule has been developed including the piezoelectric effect. The main novelty of this work is in a quantitative evaluation of the effect of degradation of mechanical properties of microtubules on the electro-elastic response, based on the proposed electro-mechanical model. The motivation for studying this effect lies in the fact that the cytoskeleton of the biological cell is dynamic and the cytoskeleton mechanics can be disrupted owing to aging or pathological disease. Moreover, cytoskeleton can also be degraded, e.g., due to the application of various anti-cancer drugs used for therapeutic treatments of cancer cells [12]. Furthermore, previously reported in vitro studies indicate that the elastic modulus of cancer cells is significantly lower as compared to the healthy cells [12, 13]. Thus, in the present contribution, we focus on quantifying the effect of degradation of the microtubule, one of the most important cytoskeletal structures, on the electro-elastic response of coupled electro-mechanical model subjected to externally applied forces. Importantly, the microtubule degradation is simulated by altering the mechanical properties of the microtubule, keeping the structural features intact.

2 Coupled Electro-Mechanical Model of Microtubule

The computational domain of a microtubule modeled as an elastic hollow cylinder is presented in Sect. 2.1. The governing equations and mathematical framework adopted in the present numerical study are given in Sect. 2.2. The details of the numerical setup and necessary boundary conditions used for solving the proposed problem are provided in Sect. 2.3.

2.1 Geometrical Assumptions and Microtubule Computational Domain

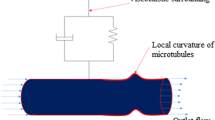
A microtubule comprising of 13 protofilaments has been modelled as a hollow cylinder having inner and outer diameters of 15 nm and 23 nm, respectively [14]. The total length of the microtubule has been considered to be 320 nm [5, 15]. Figure 1(a) presents the three-dimensional continuum-based model of a microtubule considered in the present numerical study. The material properties considered in this study can be found in Table 1 [12, 16]. Motivated by [12], mechanical degradation of microtubules have been modelled by reducing their elastic moduli (see Table 1) by 50% and 90%.

Fig. 1.
figure 1

(a) A schematic representation of the continuum-based three-dimensional model of a microtubule considered in this study and (b) Illustration of the force-time load function used in the present analysis.

Full size image
Table 1. Mechanical, piezoelectric and dielectric properties of microtubules considered in the present numerical study.
Full size table

2.2 Coupled Electro-Mechanical Model of Microtubules

The basic relationships for a linearly coupled electrical and mechanical fields are given by [17, 18]:

$$ \sigma_{ij} = c_{ijkl} \varepsilon_{kl} - e_{ijk} E_{k} , $$
(1)
$$ D_{j} = e_{jkl} \varepsilon_{kl} + \kappa_{jk} E_{k} , $$
(2)

where σij and εij are the components of elastic stress and strain tensors, respectively, Dj are the components of electric flux density vector, Ek are the components of electric field vector, cijkl are the elastic coefficients, eijk are the piezoelectric coefficients and κij is the dielectric permittivity coefficients, where subscript i, j = 1, 2, 3 and k, l = 1, 2, 3, 4, 5, 6. Further, the strain field is related to the displacement vector field by the Cauchy relationship, given by

$$ \varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right). $$
(3)

The relationship between the electric field (E) and the electric potential (ϕ) is given by

$$ E = - \nabla \cdot \phi . $$
(4)

The constitutive equations (Eqs. (1–4)) are further subjected to the equilibrium condition and Gauss’s law with the assumption of vanishing body forces and vanishing free charges:

$$ \rho \frac{{\partial^{2} u}}{{\partial t^{2} }} = \nabla \cdot \sigma , $$
(5)
$$ \nabla \cdot D = 0. $$
(6)

The elastic coefficients of microtubule obtained from its Young’s (elastic) modulus (Em) and Poisson’s ratio (ν) are given by

$$ c = \left[ \begin{aligned} \begin{array}{*{20}c} {\lambda + 2\mu } & \lambda & \lambda \\ \lambda & {\lambda + 2\mu } & \lambda \\ \lambda & \lambda & {\lambda + 2\mu } \\ \end{array} \,\,\,\,\,\,\,\,\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \hfill \\ \,\,\,\,\,\,\begin{array}{*{20}c} 0 & {\,\,\,\,\,\,\,\,\,\,\,0} & {\,\,\,\,\,\,\,\,\,\,\,\,0} \\ 0 & {\,\,\,\,\,\,\,\,\,\,\,0} & {\,\,\,\,\,\,\,\,\,\,\,\,0} \\ 0 & {\,\,\,\,\,\,\,\,\,\,\,0} & {\,\,\,\,\,\,\,\,\,\,\,\,0} \\ \end{array} \,\,\,\,\,\,\,\,\,\,\,\,\begin{array}{*{20}c} \mu & 0 & 0 \\ 0 & \mu & 0 \\ 0 & 0 & \mu \\ \end{array} \hfill \\ \end{aligned} \right], $$
(7)

where λ and µ are the Lame’s constants:

$$ \lambda = \frac{{\nu E_{m} }}{(1 + \nu )(1 - 2\nu )},\,\,\mu = \frac{{E_{m} }}{2(1 + \nu )}. $$
(8)

The present numerical study considers the piezoelectric coefficients of microtubules to be similar to that of collagen and have been adapted from [16]. Using Voigt’s notation, piezoelectric strain coefficients are given as [16]

$$ d_{ij} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ {d_{31} } & {d_{31} } & {d_{33} } \\ \end{array} \,\,\,\,\,\,\begin{array}{*{20}c} {d_{14} } & {d_{15} } & 0 \\ {d_{15} } & { - d_{14} } & 0 \\ 0 & 0 & 0 \\ \end{array} } \right], $$
(9)

where i subscript represents the direction of electric field displacement of the piezoelectric tensor and subscript j represents the associated mechanical deformation. In the present numerical study, the constitutive relations are expressed in the stress-charge form (Eqs. (1–2)), accordingly, the piezoelectric coefficients expressed in the strain-charge form (Eq. (9)) have been converted into the stress-charge form utilizing the following relation

$$ e_{ijk} = c_{jklm} d_{ilm} , $$
(10)

where \( e_{ijk} \) are the piezoelectric stress coefficients, \( c_{jklm} \) are the components of the elastic tensor given in Eq. (7) and \( d_{ilm} \) are the piezoelectric strain coefficients given in Eq. (9).

2.3 Numerical Setup and Boundary Conditions

A finite-element method (FEM) has been used for solving the coupled electro-mechanical model of microtubule presented in Fig. 1(a). A trapezoidal load function (with a loading period of 1 s), as shown in Fig. 1(b), has been used to apply the compressive force at the top surface of the microtubule. This applied force is similar to the commonly used loading-unloading paths used in nanoindentation experiments for evaluating cell biomechanics [12]. The bottom part of the microtubule has been approximated by fixed and electrically grounded boundary conditions. The initial displacement and electric potential within the computational domain have been assumed to be 0 m and 0 V, respectively. The transient electro-elastic response of the coupled model has been quantified for different values of elastic modulus of the microtubule considered in the present study. The implementation has been completed in the COMSOL Multiphysics software [19]. It’s built-in mesh generator has been used for meshing the computational domain of microtubule with heterogeneous tetrahedral mesh elements obtained after conducting a mesh convergence analysis. All the transient three-dimensional simulations have been conducted on a Dell T7400 workstation with Quad-core 2.0 GHz Intel® Xeon® processors.

3 Results and Discussion

As an initial test, the developed three-dimensional electro-mechanical model’s fidelity and integrity have been evaluated by comparing the previously reported results of zinc oxide nanowires [17] to those obtained from the current model utilizing similar geometrical details, boundary conditions and electro-mechanical parameters. Table 2 presents the comparative analysis of the maximum piezoelectric potential and displacements reported in [17] to those obtained from the current model under the application of a compressive load of 100 nN and 85 nN at the top surface of the nanowire with a fixed and electrically grounded bottom. As presented in Table 2, values of both the maximum piezoelectric potential and displacements obtained from the present model and reported in [17] are in good agreement with each other, lending confidence in the developed coupled electro-mechanical model and its extensions to microtubules, inspired by the earlier modelling of nanowire.

Table 2. Comparison of the maximum piezoelectric potential and displacements reported in the previous nanowire study [17] to that computed as a result of the present study.
Full size table

The main motive of the present numerical study was to quantify the effect of mechanical degradation of microtubules on the electro-elastic response of the coupled electro-mechanical model under the application of dynamic loads. A compressive force (whose profile has been presented in Fig. 1(b)) has been applied at the top surface of the microtubule with fixed bottom and consequently, the electro-elastic response of the microtubule has been predicted for three conditions, viz., an undegraded microtubule, a 50% degraded microtubule and a 90% degraded microtubule. Figure 2 presents the total displacement distribution at the end of 1 s of the loading period for different cases considered in the present numerical study. As depicted in Fig. 2, the maximum magnitude of the displacement at the end of the loading period (or under the application of maximum applied force) has been found to be 0.04 nm, 0.07 nm and 0.37 nm for the undegraded, 50% degraded and 90% degraded microtubules, respectively. Thus, there prevail significant variations in the induced displacements among different considered cases of the microtubule with the larger magnitudes of displacement actually induced in the highly degraded microtubule. Further, for all three cases, the maximum displacement occurs at the top surface where the external force was applied and it decreases in magnitude moving away from the top surface. It is noteworthy to mention that the concentric circles above the microtubules in Fig. 2 (and also Fig. 3) indicates the top of the undeformed microtubule.

Fig. 2.
figure 2

(Color online). Total displacement distribution (in nm) at the end of the loading period for: (a) undegraded microtubule, (b) 50% degraded microtubule, and (c) 90% degraded microtubule.

Full size image
Fig. 3.
figure 3

(Color online). Electric potential distribution (in mV) at the end of the loading period for: (a) undegraded microtubule, (b) 50% degraded microtubule, and (c) 90% degraded microtubule.

Full size image

The electric potential distribution predicted from the electro-mechanical model of microtubule under the application of dynamic load has been presented in Fig. 3 for different cases considered in this study. In Fig. 3, the maximum absolute value of electric potential has been obtained for the highly degraded microtubule, which can be attributed to a higher magnitude of the displacement induced for the microtubule with 90% degraded elastic modulus. Further, the blue side in Fig. 3 denotes the negative potential and the red side denotes the electrically ground condition. Moreover, there prevail a very negligible variation in the electric potential distribution among the undegraded and 50% degraded microtubules due to relatively smaller differences in their induced displacements.

The force-displacement curve for the three levels of mechanical degradation of the microtubules has been presented in Fig. 4. As mentioned earlier, a trapezoidal function based loading-unloading path has been used for applying force at the top surface of microtubule with a fixed bottom. It is evident from Fig. 4 that there prevail noticeable differences in the three curves representing three cases considered in the present study. The slope of the force-displacement curve is higher for the undegraded microtubule and decreases with an increase in the percentage of degradation of elastic modulus of the microtubule. In other words, the force-displacement response of microtubule subjected to externally applied load is significantly softer for the highly degraded microtubule. For example, for a displacement of about 25 pm, the corresponding forces are about 0.05 nN, 0.02 nN and 0.005 nN, respectively. Thus, the mechanical degradation of microtubule dramatically affects the force-displacement response of microtubules.

Fig. 4.
figure 4

Force-displacement response of the three-dimensional coupled electro-mechanical model of microtubule subjected to loading and unloading path for various magnitudes of mechanical degradation.

Full size image

Figure 5 presents the temporal variation of the total displacement, electric potential and volumetric strain for various magnitudes of the mechanical degradation of microtubule at a point on the top surface where the external force has been applied. As can be seen from Fig. 5(a), the displacement profile follows the same loading-unloading profile of the applied force presented in Fig. 1(b). Furthermore, significant differences have been observed in the induced displacements for different cases and it is on the higher side for the 90% degraded microtubule. Figure 5(b) presents the variation of the electrical potential (absolute value) for different magnitudes of degradation of the microtubule. Again, the profile is similar to the loading-unloading path with maximum potential obtained for the case with 90% degradation. Interestingly, there prevails a negligible variation in the distribution of electric potential for the undegraded and 50% degraded microtubules. This can be attributed to the fact that for both cases the difference in the maximum displacement value presented in Fig. 5(a) is significantly smaller as compared to the undegraded and 90% degraded microtubules which is about one order of magnitude higher.

Fig. 5.
figure 5

Temporal variation of (a) total displacement, (b) absolute value of electric potential, and (c) volumetric strain for various magnitudes of mechanical degradation of the microtubule.

Full size image

The variation of volumetric strain with respect to time for different cases of microtubule degradation has been presented in Fig. 5(c). Again, the maximum volumetric strain has been induced for the case with a 90% degraded microtubule. Thus, the results predicted from the FEM simulations of microtubules, considering our developed fully coupled electro-mechanical model, confirm that the mechanical degradation of microtubules has a pronounced effect on the electro-elastic response under dynamic loadings. The proposed model can be further extended to a more complex situation [20] by considering the complete biological cell embedded with intricate cytoskeleton and organelles for extracting more critical information of cell biomechanics subjected to different loading conditions at the cellular and sub-cellular levels. One of the major limitations of the proposed model is the consideration that microtubules behave as a linearly elastic and isotropic material, which has been motivated by [9, 12]. Future studies will be conducted to quantify the electro-elastic response of microtubules considering visco-elastic and anisotropic models.

4 Conclusion

A finite-element-based three-dimensional coupled electro-mechanical model of microtubules has been developed. A comparative analysis has been conducted for evaluating the effects of degradation of elastic moduli of microtubules on their electro-elastic response under the application of dynamic load. The obtained results demonstrate that the mechanical degradation of microtubules can significantly affect their electro-elastic response. It has been found that the 90% degraded microtubule results in one order of magnitude higher displacement and around 35% higher electric potential generation as compared to the undegraded microtubule. Accordingly, it becomes very important to account for such changes in the mechanical characteristics for more accurately quantifying the cellular biomechanics under the influence of static and dynamic forces. It is expected that the proposed model can be further extended for different applications in the quest for our better understanding of the complex behavior of cells biomechanics in general and microtubules in particular, along with designing electro-mechanical devices for medical applications.