Reduced-Cost Constrained Modeling of Microwave and Antenna Components: Recent Advances

Abstract

Electromagnetic (EM) simulation models are ubiquitous in the design of microwave and antenna components. EM analysis is reliable but CPU intensive. In particular, multiple simulations entailed by parametric optimization or uncertainty quantification may considerably slow down the design processes. In order to address this problem, it is possible to employ fast metamodels. Here, the popular solution approaches are approximation surrogates, which are versatile and easily accessible. Notwithstanding, the major issue for conventional modeling methods is the curse of dimensionality. In the case of high-frequency components, an added difficulty are highly nonlinear outputs that need to be handled. A recently reported constrained modeling attempts to broaden the applicability of approximation surrogates by confining the surrogate model setup to a small subset of the parameter space. The said region contains the parameter vectors corresponding to high-quality designs w.r.t. the considered figures of interest, which allows for a dramatic reduction of the number of training samples needed to render reliable surrogates without formally restricting the parameter ranges. This paper reviews the recent techniques employing these concepts and provides real-world illustration examples of antenna and microwave structures.

1 Introduction

Design of contemporary microwave and antenna components has been increasingly dependent on full-wave electromagnetic (EM) simulation tools. EM analysis permits reliable evaluation of arbitrary geometries and taking into account cross-couplings between system components, dielectric anisotropy, or the effects of installation fixtures and radomes. The growing involvement of EM simulation packages is especially pertinent to parameter tuning also referred to as design closure [1]. This is where the performance parameters of the structure at hand are enhanced subject to the assumed design constraints. It is most often achieved through numerical optimization, which entails significant computational expenses. Handling massive EM analyses is one of the major challenges pertaining to EM-based design processes even if local optimization is of concern. Solving tasks such as global optimization [2], uncertainty quantification or tolerance-aware design [3], may become computationally unmanageable when attempted directly at full-wave EM simulation level.

Reducing the CPU cost of EM-driven design has been the subject of extensive research. One possible option is the development of more efficient numerical algorithms, e.g., incorporation of adjoint sensitivities to speed up gradient-based procedures [4], or the employment of (local) surrogate models [5]. A notable example of the latter is space mapping [6]. Other approaches include response correction methods [7], feature-based optimization [8], or machine learning frameworks, often surrogate-assisted [9]. Another option is an overall replacement of the EM model by its faster surrogate, which permits a rapid execution of all types of simulation-based design procedures. Data-driven surrogates belong to the most popular ones due to their versatility [10]. They are constructed by approximating the data sampled from the original (here, EM) model with no physical insight required. Commonly used modeling techniques include polynomial regression [11], radial basis functions [12], kriging [13], support vector regression (SVR) [14], and polynomial chaos expansion (PCE) [15]. Available alternatives include, among others, hybridization of one of the aforementioned methods. One of these is PC kriging [16], in which polynomial chaos expansion surrogate becomes a trend function, whereas kriging interpolation is employed to account for the residuals.

Despite their merits and popularity, applicability of approximation models is limited by the curse of dimensionality. In the case of high-frequency structures, which often feature nonlinear responses, reliable data-driven surrogates can be constructed for systems described by up to four or five variables. Design utility of such models is of course questionable given the complexity of contemporary devices (both antennas and microwave). A range of methods have been developed to mitigate these problems, including high-dimensional model representation (HDMR) [17], feature-based modeling [18], orthogonal matching pursuit (OMP) [19], as well as variable-fidelity methods (Bayesian model fusion [20], co-kriging [21], or two-stage GPR [22]).

In [23], an alternative approach has been suggested, where the issue of high cost of training data acquisition is addressed by confining the surrogate model domain to a region that contains the designs that are of high quality with respect to the figures of interest relevant for the system at hand. The volume of such a region is dramatically smaller than the conventional box-constrained domain so that restricting the model validity (and, consequently, training data allocation) leads to significant computational savings. Determination of the constrained domain requires additional knowledge, normally in the form of the reference designs pre-optimized with respect to the chosen figures of interest of choice. Several variations of the constrained modeling have been reported, including rudimentary frameworks rendering surrogates that can handle a single operating condition [23], versions that allow accounting for supplementary figures of interest (e.g., substrate permittivity [24]), to techniques that permit arbitrary allocation of the reference designs [25]. The nested kriging of [26] also allows for straightforward uniform domain sampling and surrogate model optimization, which was not possible in the earlier versions.

This paper reviews the recent developments of the constrained modeling, focusing on three approaches: (i) modeling with structured reference design set [23, 24], (ii) triangulation-based modeling [25], as well as (iii) the nested kriging framework [26]. The presented methods are illustrated using real-world microwave and antenna structures, and benchmarked against conventional surrogate modeling methods. A generic formulation of the constrained modeling concept is also provided.

2 Surrogate Modeling with Domain Confinement

We start by formulating the constrained modeling concept. One of the most important components is the confined surrogate model domain. The fundamental criterion deciding upon the domain geometry is design optimality for the assumed design objectives.

2.1 Fundamental Concepts. Design Variables and Figures of Interest

Let us denote by X the parameter space for the design problem at hand. It is delimited by the lower and upper bounds on design variables l ≤ x ≤ u, where x = [x₁ … x_n]^T, l = [l₁ … l_n]^T, u = [u₁ … u_n]^T, or X = [l₁ u₁] × … × [l_n u_n]. The relevant figures of interest are f_k, k = 1, …, N. Perhaps the most representative example of a performance figure is the operating frequency (or frequencies in the case of multi-band structures) [23]. Another example is the substrate permittivity [24]. The objective space F is defined by the ranges $f_{k.\hbox{min} } \le f_{k}^{(j)} \le f_{k.\hbox{max} } ,k = 1, \ldots ,N$, i.e., F = [f_1.min f_1.max] × … × [f_N.min f_N.max]. The design goals for a given target vector f = [f₁ … f_N]^T are encoded in an objective function U(x, f). The optimum design U_f(f) w.r.t. f, is

$$ U_{f} (\varvec{f}) = \arg \mathop {\hbox{min} }\limits_{\varvec{x}} U(\varvec{x},\varvec{f}) $$

(1)

An illustration example follows: if f_k are operating frequencies of a multi-band antenna, U(·) may be defined as −min{B₁, …, B_N}, where B_j is the fractional bandwidth corresponding to f_j. Thus, minimization of U_f(f) leads to achieving the largest possible bandwidths.

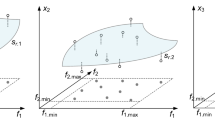
U_f(F) ⊂ X is an N-dimensional manifold (cf. Fig. 1), which determines the region of interest from the point of view of the figures f_k. It contains the designs that are of high quality w.r.t. f_k as specified by U. Hence, the surrogate constructed in the vicinity of U_f(F) is all one needs to carry out the design tasks where f_k are of concern. Focusing on U_f(F) yields considerable savings in terms of training data acquisition as compared to building the model in X. Yet, some problems arise: (i) how to identify U_f(F), (ii) how to carry out design of experiments, and, (iii) how to employ the surrogate (e.g., for parametric optimization) given geometrical complexity of the domain. Sections 3 through 5 address these issues when discussing particular realizations of the constrained modeling concept.

Fig. 1.

Basic concepts of constrained modeling: (a) the space F of figures of interest, and (b) the parameter space X. Note that the set U_f(F) constitutes an N-dimensional object (surface) in the parameter space. This set contains optimum designs for all f ∈ F. In principle, restricting the modeling process only to U_f(F) is sufficient to maintain the design utility of the surrogate [26].

2.2 Modeling Flow

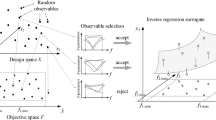
The modeling flow is shown in Fig. 2. The fundamental step of the process is a definition of the model domain. The latter is based on information acquired from a certain number of reference designs optimized for the selected values of performance figures. A particular way of utilizing this data is what distinguishes different versions of the constrained modeling frameworks.

Fig. 2.

Performance-driven modeling flow.

3 Constrained Modeling with Predefined Reference Point Allocation

The initial versions of constrained modeling framework utilized (structurally) fixed set of reference points. The advantage of this approach was simpler implementation. The downside was limited flexibility. This section describes a specific technique designed to model narrowband antennas with two figures of interest: operating frequency, and relative permittivity of the dielectric substrate [24].

3.1 Constructing the Surrogate

Here, we assume two figures of interest, specifically, the antenna operating frequency f and the relative substrate permittivity ε_r. The goal is to construct the surrogate for f_min ≤ f ≤ f_max, and ε_min ≤ ε_r ≤ ε_max. The design that is optimum for particular values of f and ε_r will be denoted as U_f(f, ε_r).

The domain of the model is a neighborhood of the surface defined using 9 reference points allocated within the discussed ranges of the operating frequency and substrate permittivity. We have $U_{f} (f^{*} ,\varepsilon_{r}^{*} )$, where f^* ∈ {f_min, f₀, f_max} and $\varepsilon_{r}^{*}$ ∈ {ε_min, ε_r0, ε_max}, cf. Fig. 3.

Fig. 3.

Graphical illustration of reference points: (a) objective space, and (b) parameter space. The domain-defining surface is marked as the dotted area between the reference points [24].

We define vectors v₁ = U_f(f_min, ε_min) − U_f(f₀, ε_r0), v₂ = U_f(f_min, ε_r0) − U_f(f₀, ε_r0), v₃ = U_f(f_min, ε_max) − U_f(f₀, ε_r0), v₄ = U_f(f₀, ε_max) − U_f(f₀, ε_r0), v₅ = U_f(f_max, ε_max) − U_f(f₀, ε_r0), v₆ = U_f(f_max, ε_r0) − U_f(f₀, ε_r0), v₇ = U_f(f_max, ε_min) − U_f(f₀, ε_r0), and v₈ = U_f(f₀, ε_min) − U_f(f₀, ε_r0), see Fig. 3(a). Let M be a manifold spanned by vectors [v₁, v₂], [v₂, v₃], …, [v₈, v₁].

$$ M = \bigcup\nolimits_{k = 1}^{8} {M_{k} } = \bigcup\nolimits_{k = 1}^{8} {\{ \varvec{y} = U_{f} (f_{0} ,\varepsilon_{r0} ) + \alpha \varvec{v}_{k} + \beta \varvec{v}_{k + 1} :\alpha ,\beta \ge 0,\;\alpha + \beta \le 1\} } $$

(2)

For consistency, v₉ = v₁. Let z be a point in the parameter space, and P_k(z) be its projection onto M_k (cf. Fig 4(b)). We have

$$ \arg \mathop {\hbox{min} }\limits_{{\bar{\alpha },\bar{\beta }}} \left\| {\varvec{z} - \left[ {U_{f} (f_{0} ,\varepsilon_{r0} ) + \bar{\alpha }\varvec{v}_{k} + \bar{\beta }\varvec{v}_{k + 1}^{\# } } \right]} \right\|^{2} $$

(3)

where $\varvec{v}_{k + 1}^{\# } = \varvec{v}_{k + 1} {-}p_{k} \varvec{v}_{k}$ with $p_{k} = v_{k}^{T} v_{k + 1} (v_{k}^{T} v_{k} )$. Thus, $\varvec{v}_{k + 1}^{\# }$ is a component of v_k+1 that is orthogonal to v_k. Consider

Fig. 4.

Auxiliary concepts for domain definition: (a) the surface of Fig. 3(b); (b) the kth surface M_k marked along with its corresponding vectors v_k and v_k+1. Also shown is an exemplary point z and its projection onto M_k [24].

$$ \left[ {\varvec{v}_{k} \;\varvec{v}_{k + 1}^{\# } } \right]\left[ {\bar{\alpha }\;\bar{\beta }} \right]^{T} = \varvec{z} - U_{f} (f_{0} ,\varepsilon_{r0} ) $$

(4)

The least-square solution to (4) (equivalent to the solution of (3)) is given as

$$ \left[ {\bar{\alpha }\;\bar{\beta }} \right]^{T} = \left( {\varvec{V}_{k}^{T} \varvec{V}_{k} } \right)^{ - 1} \varvec{V}_{k}^{T} \left( {\varvec{z} - U_{f} (f_{0} ,\varepsilon_{r0} )} \right) $$

(5)

where $\varvec{V}_{k} = \left[ {\varvec{v}_{k} \varvec{v}_{k + 1}^{\# } } \right]$. In practice, the expansion coefficients with respect to v_k and v_k+1 are of interest. These are given as $\alpha = \bar{\alpha } - p_{k} \bar{\beta },\beta = \bar{\beta }$. Note that $P_{k} (\varvec{z})$ ∈ M_k if and only if α ≥ 0, β ≥ 0, and α + β ≤ 1.

Let x_max = max{U_f(f₀, ε_r0) + v₁, …, U_f(f₀, ε_r0) + v₈} and x_min = min{U_f(f₀, ε_r0) + v₁, …, U_f(f₀, ε_r0) + v₈}; dx = x_max − x_min is the range of variation of geometry parameters within M. Using these, we can define the domain X_S by imposing the following conditions: a y ∈ X_S if

• 1. y is close to M in the sense that its orthogonal projection belongs to at least one M_k, i.e., we have $K(\varvec{y}) = \{ k \in \{ 1, \ldots ,8\} :P_{k} (\varvec{y}) \in M_{k} \} \ne \varnothing$;

• 2. $\hbox{min} \{ ||(\varvec{y} - P_{k} (\varvec{y}))//\varvec{dx}||:k \in K(\varvec{y})\} \le d_{\hbox{max} }$ (here, //stands for component-wise division); d_max is a domain thickness parameter (typically, 0.1 ≤ d_max ≤ 0.2).

Note that d_max in the second condition determines the “perpendicular” size of X_S. The size of X_S is dramatically smaller (volume-wise) than the size of the hypercube containing the reference designs. The surrogate itself is constructed using kriging interpolation of the EM model response R based on the training data allocated in X_S [24]. The design of experiments is based on random sampling within the interval [x_min, x_max] assuming uniform probability distribution. The samples allocated outside [x_min, x_max] are rejected.

3.2 Case Study: Ring Slot Antenna

The method is illustrated using a ring slot antenna of Fig. 5(a) [27], implemented on the 0.76-mm-thick substrate. The design parameters are x = [l_f l_d w_d r s s_d o g ε_r]^T; ε_r represents relative permittivity of the substrate. The feed line width w_f is computed for each ε_r to ensure 50 Ω input impedance. The EM is implemented in CST (~300,000 cells, simulation time 90 s). The goal is to construct the surrogate for the following ranged of the operating frequency and substrate permittivity: f_min = 2.5 GHz to f_max = 6.5 GHz, and ε_min = 2.0 to ε_max = 5.0. There are nine reference points generated by optimizing the antenna [28] for the pairs {f₀, ε_r} with f ∈ {2.5, 4.5, 6.5} GHz and ε_r ∈ {2.0, 3.5, 5.0}. The optimization objective is matching improvement at f₀.

Fig. 5.

Ring slot antenna: (a) geometry [27], (b) uniform versus constrained sampling for selected two-dimensional projections onto the l_f-w_d plane and the l_f-s_d plane [24].

For the sake of validation, the surrogate model was constructed using the training set of various sizes, from 100 to 1000 samples. In all cases, we used d_max = 0.2. Model validation was performed using the split-sample method with 100 test designs. The benchmark was kriging interpolation surrogate established in the original domain X = [x_min, x_max] using 1000 samples. The numerical results are gathered in Table 1, see also Fig. 6. Furthermore, Fig. 5(b) illustrates selected projections of the training data set for conventional (uniform) and proposed design of experiments. It can be observed that the accuracy improvement due to constrained sampling is considerable (by a factor of about 3.5). The constrained surrogate that exhibits the same predictive power as the corresponding conventional model can be obtained using around ten times less data samples.

Table 1. Ring slot antenna: modeling results.

Fig. 6.

Reflection characteristics of the ring-slot antenna at the selected test locations. The surrogate constructed with N = 1000 training samples: EM simulations (—), constrained surrogate (o) [24].

4 Constrained Modeling Using Domain Triangulation

In [25], a generalization of the technique presented in Sect. 3 has been proposed, which is based on triangulation of the reference designs. This technique does not only allow for arbitrary distribution of the reference points but it also has no limitations in the number of figures of interest that can be handled.

4.1 Constructing the Surrogate

The parameter and objective spaces are defined as in Sect. 2. The reference designs $\varvec{x}^{(j)} = [x_{1}^{(j)} \ldots x_{n}^{(j)} ]^{T} ,j = 1, \ldots ,p$, are optimized with respect to the figure of interest vectors $\varvec{f}^{(j)} = [f_{1}^{(j)} \ldots f_{N}^{(j)} ]^{T}$. The reference designs x^(j) are subject to Delaunay triangulation [29] to form simplexes S^(k), k = 1, …, N_S, whose vertices are S^(k) = {x^(k.1), …, x^(k.N+1)}, where x^(k.j) ∈ {x⁽¹⁾, …, x^(N)}, j = 1, …, N + 1 (cf. Fig. 7(a)).

Fig. 7.

Surrogate modeling using design reference triangulation: (a) triangulation of the reference designs (left plot) and corresponding objective vectors (right plot); (b) simplex S^(k) a, point z and its projection onto the hyper-plane H_k containing S^(k).

The model domain X_S is determined as a vicinity of the manifold M defined as

$$ M = \bigcup\limits_{k} {\{ \varvec{y} = \sum\nolimits_{j = 1}^{N + 1} {\alpha_{j} \varvec{x}^{(k.j)} :0 \le \alpha_{j} \le 1} ,\;\sum\nolimits_{j = 1}^{N + 1} {\alpha_{j} } = 1\} } $$

(6)

The region is defined using the distance from the surface M in the orthogonal complements of the subspaces containing S^(k). Given a point z, it is necessary to find the distance from it to M, which can be done by considering a projection P_k(z) onto the affine subspace H_k ⊃ S^(k). We also define the simplex anchor x⁽⁰⁾ = x^(k.1), and its spanning vectors v^(j) = x^(k.j+1) − x⁽⁰⁾, j = 1, …, N (cf. Fig. 7(b)). The projection corresponds to the expansion coefficients w.r.t. v^(j) [25]

$$ \arg \mathop {\hbox{min} }\limits_{{[\bar{\alpha }^{(1)} ,. \ldots \bar{\alpha }^{(N)} ]}} \left\| {\varvec{z} - \left[ {\varvec{x}^{(0)} + \sum\nolimits_{j = 1}^{N} {\bar{\alpha }^{(j)} } \bar{\varvec{v}}^{(j)} } \right]} \right\|^{2} $$

(7)

where the vectors $\bar{\varvec{v}}^{(j)}$ are obtained from v^(j) by orthogonalization (i.e., $\bar{\varvec{v}}^{(1)} = \varvec{v}^{(1)}$, $\bar{\varvec{v}}^{(2)} = \varvec{v}^{(2)} - a_{12} \varvec{v}^{(1)}$ where a₁₂ = v^(1)Tv⁽²⁾(v^(1)Tv⁽¹⁾, etc.). In general

$$ \bar{\varvec{V}} = \left[ {\bar{\varvec{v}}^{(1)} \;\bar{\varvec{v}}^{(2)} \;\; \ldots \;\bar{\varvec{v}}^{(N)} } \right] = \left[ {\varvec{v}^{(1)} \;\varvec{v}^{(2)} \;\; \ldots \;\varvec{v}^{(N)} } \right]\varvec{A} $$

(8)

Note that A is a triangular matrix that contains coefficients obtained from the above orthogonalization procedure. The problem (7) is equivalent to

$$ \left[ {\bar{\varvec{v}}^{(1)} \;\bar{\varvec{v}}^{(2)} \;\; \ldots \;\bar{\varvec{v}}^{(N)} } \right]\left[ \begin{aligned} \bar{\alpha }^{(1)} \\ \vdots \\ \bar{\alpha }^{(N)} \\ \end{aligned} \right] = \varvec{z} - \varvec{x}^{(0)} $$

(9)

The expansion coefficients can be found analytically as

$$ \left[ {\bar{\alpha }^{(1)} \; \ldots \;\bar{\alpha }^{(N)} } \right]^{T} = (\bar{\varvec{V}}^{T} \bar{\varvec{V}})^{ - 1} \bar{\varvec{V}}^{T} (\varvec{z} - \varvec{x}^{(0)} ) $$

(10)

The critical factor is whether P_k(z) ∈ hull(S^(k)) (hull() stands for the convex hull). For that, it is necessary to identify the expansion coefficients α^(j) of z w.r.t. {v^(j)}. The latter can be obtained as $[\alpha^{(1)} \; \ldots \;\alpha^{(N)} ]^{T} = \varvec{A}[\bar{\alpha }^{(1)} \; \ldots \;\bar{\alpha }^{(N)} ]^{T}$. It should be noted that $P_{k} (\varvec{z})$ ∈ S^(k) if

• 1. $\alpha^{(j)} \ge 0\;\;{\text{for}}\;\;j = 1, \ldots ,N,$ and

• 2. $\alpha^{(1)} + \ldots + \alpha^{(N)} \le 1$.

that is, if P_k(z) is a convex combination of the vectors v^(j).

The next step of surrogate modeling domain definition is to define $\varvec{x}_{\hbox{max} } = \hbox{max} \{ \varvec{x}^{(k)} ,\;k = 1, \ldots ,p\}$ and $\varvec{x}_{\hbox{min} } = \hbox{min} \{ \varvec{x}^{(k)} ,\;k = 1, \ldots ,p\}$. The vector $\varvec{dx} = \varvec{x}_{\hbox{max} } - \varvec{x}_{\hbox{min} }$ is an indication of the geometry parameter variability within the surface M. Using these, the surrogate model domain X_S can be defined as in [24]. More specifically, a vector y ∈ X_S if

• 1. $K(\varvec{y}) = \{ k \in \{ 1, \ldots ,N_{S} \} :P_{k} (\varvec{y}) \in S^{(k)} \} \ne \varnothing$;

• 2. $\hbox{min} \{ ||(\varvec{y} - P_{k} (\varvec{y}))//\varvec{dx}||:k \in K(\varvec{y})\} \le d_{\hbox{max} }$ (//stands for component-wise division); d_max is a user-defined parameter determining the domain thickness.

The major benefit of this definition is that X_S is considerable smaller than the original domain $X = [{\mathbf{x}}_{\hbox{min} } ,{\mathbf{x}}_{\hbox{max} } ]$ volume-wise, thus the surrogate can be constructed using a reduced training set. Notwithstanding, the domain still contains the optimum designs (with respect to the selected performance figures) so that the surrogate retains its design utility. This is demonstrated in the next section by modeling a dual-band antenna over broad ranges of both geometry and material parameters.

4.2 Verification Case: Uniplanar Dipole Antenna

For the sake of verification, let us consider a dipole antenna of Fig. 8(a) [30]. The structure is realized on Taconic RF-35 substrate of relative permittivity ε_r = 3.5 and thickness h = 0.762 mm. There are six adjustable variables x = [l₁ l₂ l₃ w₁ w₂ w₃]^T. Other parameters are fixed: l₀ = 30, w₀ = 3, s₀ = 0.15 and o = 5 are fixed (dimensions in mm). The computational model R is simulated in CST Microwave Studio (~100,000 cells; simulation time 1 min).

Fig. 8.

Uniplanar dipole antenna: (a) geometry [30], (b) allocation of the reference designs and their triangulation [25].

We aim at constructing the surrogate within the following objective space: 2.0 GHz ≤ f₁ ≤ 4.0 GHz (lower band), and 4.5 GHz ≤ f₂ ≤ 6.5 GHz (upper band). Figure 8(b) shows the allocation of the reference designs. The latter have been generated using variable-fidelity feature-based optimization [28].

Validation has been carried out by rendering the surrogates using various numbers of training samples, from 100 to 1600. In all cases, d_max = 0.05 was employed. The numerical results are gathered in Table 2. Conventional kriging metamodel is used as a benchmark. The antenna reflection characteristics according to the surrogate and EM simulation have been shown in Fig. 9.

Table 2. Modeling results and benchmarking for antenna of Fig. 8.

Fig. 9.

Reflection characteristics of the antenna of Fig. 8: electromagnetic simulations (—), triangulation-based surrogate rendered with N = 1600 training samples (o).

5 Modeling Using Nested Kriging

The nested kriging framework proposed in [26] employs two kriging metamodels. One of these models is used to establish the surrogate model domain by mapping the figure-of-interest space into the parameter space and to provide the first approximation of the region of interest. The major advantage of [26] is that design of experiments but also model optimization can be implemented in a convenient way.

5.1 Surrogate Model Construction

We use the same definitions as in Sect. 2.1 for the objective and parameter spaces. The reference designs optimized w.r.t. $\varvec{f}^{(j)} = [f_{1}^{(j)} \ldots f_{N}^{(j)} ]$ are denoted as $\varvec{x}^{(j)} = [x_{1}^{(j)} \ldots x_{n}^{(j)} ]^{T} ,j = 1, \ldots ,p$. The technique employs two kriging metamodels. The first-level one s_I(f) transforms F into the parameter space X. The model s_I is set up using the training pairs {f^(j), x^(j)}_j=1,…,p (see Fig. 10 for a graphical illustration).

Fig. 10.

The main components of the nested kriging framework: (a) reference points and the space of figures of interest F; (b) the domain defining surfaces: s_I(F), the exemplary normal vector $\varvec{v}_{1}^{(k)}$ at f^(k); the surfaces M₋ and M₊, and the domain X_S. The latter is defined as an extension of s_I(F) according to (13) [26].

The surrogate model domain X_S is defined to contain the designs that are optimum w.r.t. f_k, k = 1, …, N. The information obtained from the reference designs only permits for establishing an initial approximation of the optimum design set U_f(f). As the domain should contain the entire U_f(f) (or a vast majority of it), s_I(F) must be enlarged. This is realized by an orthogonal extension of s_I(F) towards its normal vectors. We denote by $\left\{ {\varvec{v}_{n}^{(k)} (f)} \right\},\varvec{k} = 1, \ldots ,n - N$, an orthonormal basis of vectors normal to s_I(F) at f, and define x_max = [x_max.1 … x_max.n]^T, x_min = [x_min.1 … x_min.n]^T, with $x_{\hbox{max} .k} = \hbox{max} \left\{ {x_{k}^{(j)} ,j = 1, \ldots ,p} \right\}$, and $x_{\hbox{min} .k} = \hbox{min} \left\{ {x_{k}^{(j)} ,j = 1, \ldots ,p} \right\}$. We also define x_d = x_max − x_min (parameter variations within s_I(F)). Further, extension coefficients are defined as follows:

$$ \varvec{\alpha}(\varvec{f}) = [\alpha_{1} (\varvec{f})\; \ldots \;\alpha_{n - N} (\varvec{f})]^{T} = 0.5d_{\hbox{max} } \left[ {|\varvec{x}_{d} \varvec{v}_{n}^{(1)} (\varvec{f})|\;\; \ldots \;\;|\varvec{x}_{d} \varvec{v}_{n}^{(n - N)} (\varvec{f})|} \right]^{T} $$

(11)

Similarly as for the method discussed before, d_max denotes the domain thickness. The coefficients α_k are used to delimit X_S (see also Fig. 10(b)) [26] by defining

$$ M_{ \pm } = \left\{ {\varvec{x} \in X:\varvec{x} = \varvec{s}_{I} \left( \varvec{f} \right) \pm \sum\nolimits_{k = 1}^{n - N} {\alpha_{k} (\varvec{f})\varvec{v}_{n}^{(k)} (\varvec{f})} } \right\} $$

(12)

Using (12), we get

$$ X_{S} = \left\{ {\begin{array}{*{20}c} {\varvec{x} = \varvec{s}_{I} (\varvec{f}) + \sum\nolimits_{k = 1}^{n - N} {\lambda_{k} \alpha_{k} (\varvec{f})\varvec{v}_{n}^{(k)} (\varvec{f})} :\varvec{f} \in F,} \\ { - 1 \le \lambda_{k} \le 1,\;k = 1, \ldots ,n - N} \\ \end{array} } \right\} $$

(13)

The second-level surrogate is a kriging model rendered in X_S based on $\{ \varvec{x}_{B}^{(k)} ,\varvec{R}(\varvec{x}_{B}^{(k)} )\}_{k = 1, \ldots ,NB}$, where R is the EM-simulation model of the structure of interest.

Note that the definition of X_S facilitates design of experiments which was a problem for both [23] and [25]. It is implemented using (13) and the mappings from the unit interval [0, 1]ⁿ onto X_S. Let {z^(k)}, k = 1, …, N_B, where z^(k) = [z ^(k)₁ … z ^(k)_n ]^T, denote the set of uniformly distributed data points in [0, 1]ⁿ (here, using LHS [31]). The mapping is realized in two stages. First, the function h₁.

$$ \begin{array}{*{20}c} {\varvec{y} = h_{1} ({\mathbf{z}}) = h_{1} ([z_{1} \ldots z_{n} ]^{T} )} \\ { = [f_{1.\hbox{min} } + z_{1} (f_{1.\hbox{max} } - f_{1.\hbox{min} } ) \ldots f_{N.\hbox{min} } + z_{N} (f_{N.\hbox{max} } - f_{N.\hbox{min} } )] \times [ - 1 + 2z_{N + 1} \ldots - 1 + 2z_{n} ]} \\ \end{array} $$

(14)

transforms the unit hypercube onto a F × [−1,1]^n−N (× is a Cartesian product). Subsequently, a function h₂ is defined as

$$ \varvec{x} = h_{2} (\varvec{y}) = h_{2} ([y_{1} \; \ldots \;y_{n} ]^{T} ) = \varvec{s}_{I} ([y_{1} \;\; \ldots \;\;y_{N} ]^{T} ) + \sum\nolimits_{k = 1}^{n - N} {y_{N + k} \alpha_{k} (} [y_{1} \;\; \ldots \;\;y_{N} ]^{T} )\varvec{v}_{n}^{(k)} ([y_{1} \;\; \ldots \;\;y_{N} ]^{T} ) $$

(15)

which maps F × [−1, 1]^n−N onto X_S. Hence, uniformly distributed samples x ^(k)_B in X_S are obtained as $\varvec{x}_{B}^{(k)} = H(\varvec{z}^{(k)} ) = h_{2} (h_{1} (\varvec{z}^{(k)} ))$.

The surjective mapping H also allows for implementing surrogate model optimization in its domain X_S. In particular, the optimization process can be formally carried out in the primary domain F × [−1, 1]^n−N, whereas the mapping H can be employed to perform evaluation of the structure.

5.2 Verification Case: Miniaturized Impedance Transformer

The modeling technique described in Sect. 5.1 has been validated using a miniaturized impedance matching transformer [32]. The structure is shown in Fig. 11(b). It is realized on Taconic RF-35 substrate of relative permittivity ε_r = 3.5 and thickness h = 0.762 mm. The circuit employees compact microstrip resonant cells (CMRCs) shown in Fig. 11(a).

Fig. 11.

Compact impedance transformer as verification case study for the nested kriging framework: (a) CMRC cell, (b) impedance transformer structure [32], (c) reference points [26].

The adjustable variables are x = [l_1.1 l_1.2 w_1.1 w_1.2 w_1.0 l_2.1 l_2.2 w_2.1 w_2.2 w_2.0 l_3.1 l_3.2 w_3.1 w_3.2 w_3.0]^T. The figure-of-interest space contains the operating bands [f₁ f₂] with the following ranges: 1.5 GHz ≤ f₁ ≤ 3.5 GHz, and 4.5 GHz ≤ f₂ ≤ 6.5 GHz. Here, the optimum design is understood by minimization of the maximum reflection |S₁₁| within [f₁ f₂] (which is a minimax problem). The allocation of the reference designs has been shown in Fig. 11(c).

Surrogate model validation has been carried out for various numbers of training data samples from 50 to 800. All models were generated using d_max = 0.05. The modeling error was calculated using the split-sample method with 100 random testing designs. The numerical results are shown in Table 3 (see also Fig. 12). The benchmark includes conventional kriging and RBF metamodels. It can be observed that the nested kriging framework enables two- or even three-fold reduction of the modeling error assuming the same training data set size. It should be emphasized that for this case the predictive power of all conventional surrogates is poor. The primary reason is a large number of geometry parameters and, consequently, a large volume of the conventional domain.

Table 3. Modeling results and benchmarking for impedance matching transformer.

Fig. 12.

Reflection characteristics of the circuit of Fig. 11(b): full-wave electromagnetic simulations (—), and the nested kriging surrogate rendered with N = 800 training samples (o) [26].

6 Conclusions

This paper discussed the recent developments in constrained modeling of high-frequency structures. Domain confinement permits a reduction of the computational overhead related to training data acquisition. At the same time, reliable surrogates can be rendered without formally restricting the ranges of geometry and material parameters as well as the operating conditions. There were three specific realizations of this concept discussed in the work. The main differences between these were in analytical formulation of the surrogate model domain. The simplest technique, discussed in Sect. 3, requires structured allocation of the reference designs. The second method, the triangulation-based modeling of Sect. 4, is more flexible, allows for an arbitrary placement of the reference set, and it can directly handle arbitrary number of operating conditions. The downside is a non-trivial design of experiments. The nested kriging framework is the most comprehensive: the very formulation of the model domain incorporates the means to carry out uniform design of experiments as well as optimization of the surrogate. Notwithstanding, implementation of this approach is more involved. In general, surrogate modeling with domain confinement can be considered a viable workaround dimensionality and parameter range issues, both of which are the fundamental challenges of conventional methods. At the same time, the initial computational overhead required to generate the reference points is well justified when the surrogate is reused, for example, for the purpose of dimension scaling for various operating conditions.