Data Fitting by Exponential Sums with Equal Weights

Abstract

In this paper, we introduce a Prony-type data fitting problem consisting in interpolating the table $\left\{ m, g(m)\right\} _{m=0}^M$ with $g(0)\ne 0$ in the sense of least squares by exponential sums with equal weights. We further study how to choose the parameters of the sums properly to solve the problem. Moreover, we show that the sums have some advantages in data fitting over the classical Prony exponential sums. Namely, we prove that the parameters of our sums are a priori well-controlled and thus can be found via a stable numerical framework, in contrast to those of the Prony ones. In several numerical experiments, we also compare the behaviour of both the sums and illustrate the above-mentioned advantages.

The research was financially supported by Russian Science Foundation, Agreement 19-71-10078.

1 Introduction and Main Results

Interpolation (or data fitting) of a complex-valued function $g=g(z)$, $z\in \mathbb {C}$, by a linear combination of exponents, e.g. by the Prony exponential sums

$$\begin{aligned} \mathcal {H}_K(z)=\sum _{k=1}^K \mu _k \exp (\lambda _k z),\quad \text {where } \mu _k\in \mathbb {C} \text { and }\lambda _k\in \overline{\mathbb {C}} \text { are parameters}, \end{aligned}$$

(1)

appears in many contexts in Science and Engineering, in particular, in time series analysis, physical phenomena modelling and signal processing. There exist numerous state-of-the-art analytical and numerical methods for solving the corresponding data fitting problems, see the overview in [2, 5, 7, 9,10,11,12]. One of the main challenges in the area is that the exponential data fitting is ill-conditioned in many cases [10]. Among other things, this can be connected with the behaviour of exponential sum parameters (such as $\mu _k$ and $\lambda _k$ in (1)). In particular, one can find in [6] a family of g whose corresponding parameters of (1) tend to infinity thus making the interpolation process divergent.

To address this disadvantage, we consider in this paper a modified version of the exponential sums (1) and introduce and solve the corresponding Prony-type data fitting problem. Moreover, we prove that the parameters in our exponential sums are a priori well-controlled and thus can be found via a stable numerical framework, in contrast to those in the sums (1). Let us move to the formal description of our approach.

We introduce the following Prony-type data fitting problem: numerically interpolate the table

$$\begin{aligned} \left\{ m, g(m)\right\} _{m=0}^M,\qquad g(0)\ne 0, \end{aligned}$$

(2)

by the following exponential sums with equal weights

$$\begin{aligned} H_K(z)=\frac{\mu }{K}\sum _{k=1}^K \exp (\lambda _k z), \qquad \mu \in \mathbb {C},\quad \lambda _k\in \overline{\mathbb {C}},\quad K\leqslant M. \end{aligned}$$

(3)

The fitting should be carried out by a proper choice of the parameters $\mu$ and $\{\lambda _k\}_{k=1}^K$ which depend on K, M and g. The fitting quality has to be evaluated in the sense of least squares via a numerical optimization method so that

$$\begin{aligned} \sum _{m=0}^M \left| g(m)-H_K(m)\right| ^2=\delta ^2\qquad \text {for some } \delta \geqslant 0. \end{aligned}$$

(4)

The main result of the paper in the above-mentioned settings is about the construction and the a priori control of the parameters of $H_K$ and is as follows.

Theorem 1

Given a table (2), the parameters of $H_K$ are as follows: $\mu =g(0)$ and the set $\{\lambda _k\}_{k=1}^K$ is the solution to the Newton-type moment problem

$$\begin{aligned} \sum _{m=1}^M \left| g(m)-\frac{g(0)}{K}\sum _{k=1}^K l_k^m\right| ^2=\delta ^2,\qquad \text {where}\quad l_k:=\exp (\lambda _k). \end{aligned}$$

(5)

Furthermore, if $|g(m)|\leqslant \frac{|g(0)|}{K}\, a^m$ for all $m=1,\ldots ,M$ and some $a\geqslant 1$, then¹

$$ \max _{k=1,\ldots ,K}|l_k|\leqslant \kappa a \quad \Rightarrow \quad -\infty \leqslant \mathsf{Re}\,(\lambda _k) \leqslant \ln (\kappa a),\quad \text {where } \kappa :=3+\tfrac{2K\delta }{|g(0)|}, $$

and moreover $|H_K(x)|\leqslant |g(0)|\left( \kappa a \right) ^x$ for any $x\in \mathbb {R}$.

Thus the parameters of $H_K$ are well-controlled by g in (2) and by $\delta$ in (4).

The paper is organised as follows. Section 2 provides necessary facts on and the theoretical comparison of the sums $H_K$ and $\mathcal {H}_K$. Section 3 is devoted to the proof of Theorem 1. Section 4 contains several experiments with $H_K$ and $\mathcal {H}_K$ illustrating the difference of their behaviour in numerical processes.

2 Necessary Facts on and the Comparison of $H_K$ and Classical Prony Exponential Sums

The analytical construction of (3) with $K=M$ for the table (2) was introduced in [1]. It was also shown that the problem (4) then can be solved analytically, with $\delta =0$. Moreover, if the corresponding $\mu$ and $\{\lambda _k\}_{k=1}^M$ are known precisely and determined via the so-called Newton-Prony method, then $g(z)=H_M(z)$ for $z\in \{m\}_{m=0}^{M}$. Now we briefly describe the approach from [1].

Let $L_M:=\{l_k\}_{k=1}^M$, where $l_k\in \mathbb {C}$. Consider the power sums

$$\begin{aligned} S_{m}:=S_{m}(L_M)=\sum ^M_{k=1}l^{m}_k, \qquad m=1,2,\ldots . \end{aligned}$$

(6)

One can find the set $L_M$ from the Newton moment problem

$$\begin{aligned} S_m = s_m,\quad m=1,\ldots ,M,\qquad \text {where }s_m\in \mathbb {C} \text { are given}, \end{aligned}$$

(7)

via the elementary symmetric polynomials

$$\begin{aligned} \sigma _m=\sigma _m(L_M):=\sum _{1\leqslant j_1< \ldots < j_m \leqslant M}l_{j_1}\cdots l_{j_m},\qquad m=1,\ldots ,M. \end{aligned}$$

(8)

The connection between the power sums (6) and the polynomials (8) is expressed by the well-known Newton-Girard formulas [13, Section 3.1]:

$$\begin{aligned} \sigma _1=S_1,\quad \sigma _m=\frac{(-1)^{m+1}}{m} \left( S_{m}+\sum _{j=1}^{m-1} (-1)^{j}\,S_{m-j}\sigma _j\right) ,\quad m=2,\ldots ,M. \end{aligned}$$

(9)

Moreover, $L_M$ is then the set of M roots of the unitary polynomial

$$\begin{aligned} P_M(l):=l^M-\sigma _1 l^{M-1}+\sigma _2 l^{M-2}+\ldots +(-1)^M\sigma _M. \end{aligned}$$

(10)

Consequently, given any $s_m$, one can solve (7) using (9) and (10) and the solution $L_M$ always exists and is unique. What is more, it is shown in [1] that the elements of $L_M$ are well-controlled by the table (2) under few natural assumption on g. Namely, the following result is a consequence of what is proved in [1]:

For $M\geqslant 2$, $\gamma >0$ and $a\geqslant 1$, if $|s_m|\leqslant \gamma a^m$ in (7) for $m=1,\ldots ,M$, then

$$\begin{aligned} \max _{k=1,\ldots ,K}|l_k|\leqslant \left( 1+2\gamma \right) a. \end{aligned}$$

(11)

Now we turn our attention to the Prony exponential sums (1). There exist a classical analytical Prony method for interpolating the table (2) with odd M (so that $M+1$ is even) by the sums (1) with $K=\tilde{M}:=(M+1)/2$, see e.g. [3, 6, 8, 10]. The main idea behind it is to separate calculating the parameters $\mu _k$ and $\lambda _k$. Namely, by supposing $l_k:=\exp (\lambda _k)$ and $s_m=g(m)$ one comes to the following Prony moment problem that is a weighted version of (7):

$$\begin{aligned} S^*_m = s_m,\qquad \text {where}\qquad S^*_m:=\sum _{k=1}^{\tilde{M}}\mu _kl_k^m,\qquad m=0,\ldots ,M. \end{aligned}$$

(12)

If this problem has a unique solution, then $L_{\tilde{M}}=\{l_k\}_{k=1}^{\tilde{M}}$ is the set of $\tilde{M}$ roots of the (possibly non-unitary) polynomial

$$\begin{aligned} P^*_{\tilde{M}}(l):=\sum _{m=0}^{\tilde{M}} \sigma ^*_{m} l^{m}= \left| \begin{array}{ccccc} 1 &{} l &{} l^2 &{} \ldots &{} l^{\tilde{M}}\\ s_0 &{} s_1 &{} s_2 &{} \ldots &{} s_{\tilde{M}}\\ s_1 &{} s_2 &{} s_3 &{} \ldots &{} s_{{\tilde{M}}+1}\\ \ldots &{} \ldots &{} \ldots &{} \ldots &{} \ldots \\ s_{{\tilde{M}}-1} &{} s_{\tilde{M}} &{} s_{{\tilde{M}}+1} &{} \ldots &{} s_{2{\tilde{M}}-1}\\ \end{array} \right| , \end{aligned}$$

(13)

which is an analogue of (9) and (10). Note that $\{\mu _k,\lambda _k\}_{k=1}^{\tilde{M}}$ can be uniquely determined (and thus (1) constructed) if and only if the polynomial (13) for a given set $\{s_m\}_{m=0}^M$ is exactly of degree ${\tilde{M}}$ and all its roots are pairwise distinct [6]. In general, the problem (12) can be unsolvable or have multiple solutions [6].

Let us mention that the system (12) is not only related to (1) but plays an important role in different areas of approximation theory and is closely related to Hankel matrices, Gauss quadratures, moment problems and classical Padé rational fractions (a survey can be found e.g. in [6, Section 2] or [8]).

Due to the importance of (1) and (12) in approximation theory and applied data fitting (see Introduction), multiple numerical approaches for data fitting by the sums (1) with $K\leqslant \tilde{M}$ have been proposed [2, 4, 5, 11, 12]. The fitting quality evaluation is usually performed in the sense of least squares:

$$\begin{aligned} \sum _{m=0}^M \left| g(m)-\mathcal {H}_K(m)\right| ^2\rightarrow \min . \end{aligned}$$

(14)

However, in sharp contrast to $H_K$ within (4) and (7), there are no more or less general estimates for the parameters of $\mathcal {H}_K$ similar to those in Theorem 1 and the theorems from [1], as seen from the huge bibliography on the Prony exponential sums ([2, 3, 5, 6, 8, 11, 12] and references therein). Moreover, numerical processes for finding solutions to (14) and (12) can be unstable and divergent (see [2, 6]).

To finish the comparison of $H_K$ and $\mathcal {H}_K$, let us also observe that computing (3) requires less arithmetic operations than that of (1) for each fixed z and known $\mu$, $\mu _k$ and $\lambda _k$, see [1].

3 The Proof of Theorem 1

The identity for $\mu$ follows directly from (3) and (4) for $m=0$. The optimization problem (5) is then deduced from (4) by the exchange $l_k:=\exp (\lambda _k)$.

Now let $|g(m)|\leqslant \frac{|g(0)|}{K}\, a^m$ in (2) for all $m=1,\ldots ,M$ and some ${a\geqslant 1}$. Once the solution $\{l_k\}_{k=1}^K$ to (5) and a certain $\delta$ are found by a numerical optimization method, we obtain by the triangle inequality that

$$ \left| \frac{g(0)}{K}\sum _{k=1}^K l_k^m\right| \leqslant |g(m)|+\delta \leqslant \left( \frac{|g(0)|}{K}+\delta \right) \, a^m,\quad m=1,\ldots ,K. $$

Note that m here is from 1 to K, not M. Consequently, we come to the system (7) with K unknowns and K equations:

$$ |S_m|=\left| \sum _{k=1}^K l_k^m\right| =|s_m|\leqslant \left( 1+\frac{K\delta }{|g(0)|}\right) \, a^m,\quad m=1,\ldots ,K. $$

Furthermore, by (11) we easily obtain the required inequalities for $\max _{k=1,\ldots ,K}|l_k|$ and $\mathsf{Re}\,\lambda _k$. What is more, $|H_K(x)|\leqslant \frac{|g(0)|}{K}\sum _{k=1}^K (\kappa a)^x\leqslant |g(0)| (\kappa a)^x$ for $x\in \mathbb {R}$.

Table 1. The results of experiments for different $\varepsilon$ (five digits are provided).

4 Numerical Experiments

Experiments below show the difference in the behaviour of $H_K$ and $\mathcal {H}_K$ in numerical processes and illustrate Theorem 1. In fact, one can use any suitable numerical method for finding the parameters of $H_K$ and $\mathcal {H}_K$ as the examples below are constructed to be independent of the method (see [2, 5, 11, 12] for the methods suitable for $\mathcal {H}_K$; any numerical method for non-linear least squares can be adapted for $H_K$). We produced calculations using Maple 2019 tools with 200 significant digits and same environment for both $H_K$ and $\mathcal {H}_K$, to avoid the influence of a particular method and its precision.

In order to have the same number of free parameters in the exponential sums and to establish the connection with the problems (7) and (12), we solve the data fitting problems (4) and (14) with $K=M$ and $K=(M+1)/2$, correspondingly.

We consider the following parametric table of the form (2) with $M=3$:

$$\begin{aligned} (0,1+\varepsilon ),\;(1,0+\varepsilon ),\; (2,0-\varepsilon ),\, (3,1-\varepsilon ),\qquad 0<\varepsilon \leqslant 10^{-1}. \end{aligned}$$

(15)

Note that (15) can be easily complemented to contain arbitrarily many elements. However, since the data (15) should be still fitted, the same effects will be observed for the corresponding exponential sums $H_3$ and $\mathcal {H}_2$ (see [6, Section 7]).

Fig. 1.

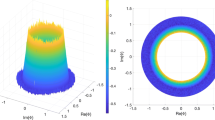
Plots of $H_3$ (blue) and $\mathcal {H}_2$ (red) for different $\varepsilon$ in the table (15) (black points): (a) $\varepsilon =10^{-1}$, (b) $\varepsilon =10^{-6}$, (c) $\varepsilon =10^{-7}$, (d) $\varepsilon =10^{-8}$ (Color figure online).

It directly follows from (13) that (15) leads to a unique solution to (12) for $0<\varepsilon \leqslant 10^{-1}$ (note that (7) always has such a solution) and therefore a proper numerical method should converge to this solution. Below we choose $\delta =10^{-10}$ in (4) and (14). Table 1 and Fig. 1 contain the results for different $\varepsilon >0$ and the extreme case $\varepsilon =0$ (this case for $\mathcal {H}_2$ was studied in [6, Section 7]).

It can be observed that for $10^{-5}\leqslant \varepsilon \leqslant 10^{-1}$ both $H_3$ and $\mathcal {H}_2$ solve the data fitting problem with good quality (see Fig. 1(a)). For $\varepsilon < 10^{-5}$, the precision of $\mathcal {H}_2$ however shrinks significantly and the data is not fitted properly, while the fitting quality of $H_3$ is still good (see Fig. 1(b), (c), (d)). This can be explained as follows.

The table (15) with $\varepsilon \rightarrow 0$ leads to an unsolvable problem (12). Thus one has a divergent numerical process for $\mathcal {H}_2$ (with $|\lambda _{1,2}|\rightarrow \infty$ and $|\mu _1|\rightarrow 0$) as $\varepsilon \rightarrow 0$. The corresponding computational errors significantly grow (200 significant digits for the parameters of $\mathcal {H}_2$ are not already enough for a reasonable precision of $\mathcal {H}_2$ itself) and this leads to the incorrect data fitting by $\mathcal {H}_2$ (especially for $m=3$) represented in Fig. 1 (b), (c), (d).

Oppositely, since the parameters of $H_3$ are well-controlled (in particular, Theorem 1 implies for the table (15) that $\mu =1+\varepsilon$, $\max _{k=1,\ldots ,3}|l_k|\leqslant 3.1(1+\varepsilon )$ and $-\infty \leqslant \mathsf{Re}\,(\lambda _k) \leqslant \varepsilon +\ln 3.1$), 200 significant digits stay enough for rather accurate calculation of $H_3$ and its representation in Fig. 1 (b), (c), (d).

5 Conclusions

In this paper, we considered the exponential sums with equal weights (3) in the context of the Prony-type problem of fitting data (the table (2)) in the sense of non-linear least squares (4). We showed how the parameters $\mu$ and $\lambda _k$ of the sums (3) should be chosen for proper data fitting. Moreover, we proved that the parameters are well-controlled by (2) and by $\delta$ in (4) (see Theorem 1) that is in sharp contrast to the case of parameters in the well-known Prony exponential sums (1). Furthermore, in several special numerical experiments, we compared the behaviour of the sums (3) and (1) and demonstrated that (3) do not produce divergent data fitting processes while (1) do in some cases.