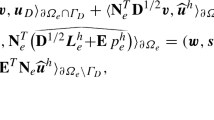Keywords

1 Introduction

The Isogeometric Analysis (IGA) [1] bridges the gap between the Computer Aided Design (CAD) and Computer Aided Engineering (CAE) communities. The idea of IGA is to apply B-spline basis functions [2] for finite element method (FEM) simulations. The ultimate goal is to perform engineering analysis directly to CAD models without expensive remeshing and recomputations. IGA has multiple applications in time-dependent simulations, including phase-field models [3, 4], phase-separation simulations with application to cancer growth simulations [5, 6], wind turbine aerodynamics [7], incompressible hyper-elasticity [8], turbulent flow simulations [9], transport of drugs in cardiovascular applications [10], or the blood flow simulations and drug transport in arteries simulations [11, 12].

The stability of a numerical method based on Petrov-Galerkin discretizations of a general weak form relies on the famous discrete inf-sup condition (see, e.g., [13]): “Babuška-Brezzi condition” (BBC) developed in years 1971–1974 at the same time by Ivo Babuśka, and Franco Brezzi [14,15,16].

Let \(\mathfrak {U}, \mathfrak {V}\) denote two Hilbert spaces. For a given variational formulation of the form:

$$\begin{aligned} \text {Find } \mathfrak {u}\in \mathfrak {U}, \text { such that } \mathfrak {b}(\mathfrak {u},\mathfrak {v})=\mathfrak {l}(\mathfrak {v}), \quad \forall \, \mathfrak {v}\in \mathfrak {V}, \end{aligned}$$
(1)

with \(\mathfrak {b}\, : \mathfrak {U}\times \mathfrak {V}\rightarrow \mathbb R\) being a bilinear form, and \(\mathfrak {l}\, : \, \mathfrak {V}\rightarrow \mathbb R\) being a linear form, the BBC condition states that the problem is stable if there exists a positive constant \(\gamma >0\), such that:

$$\begin{aligned} \sup _{\mathfrak {v}\in \mathfrak {V}, \mathfrak {v}\ne \mathbf{0}} {{| \mathfrak {b}(\mathfrak {u},\mathfrak {v})|}\over {\Vert \mathfrak {v}\Vert _\mathfrak {V}}} \ge \gamma \, \Vert \mathfrak {u}\Vert _{\mathfrak {U}}, \quad \forall \, \mathfrak {u}\in \mathfrak {U}. \end{aligned}$$
(2)

The inf-sup condition in the above form concerns the abstract formulation where we consider all the test functions from \(\mathfrak {v}\in \mathfrak {V}\) and look for solution at \(\mathfrak {u}\in \mathfrak {U}\). The above condition is satisfied also if we restrict to a conforming space of trial functions \(\mathfrak {U}_h \subset \mathfrak {U}\). This is,

$$\begin{aligned} \sup _{\mathfrak {v}\in \mathfrak {V}, \mathfrak {v}\ne \mathbf{0}} {{|\mathfrak {b}(\mathfrak {w}_h, \mathfrak {v})|} \over {\Vert \mathfrak {v}\Vert _{\mathfrak {V}}}} \ge \gamma \, \Vert \mathfrak {w}_h\Vert _{\mathfrak {U}_h}, \quad \forall \, \mathfrak {w}_h \in \mathfrak {U}_h. \end{aligned}$$
(3)

However, if we consider test functions from a finite dimensional test space \(\mathfrak {V}_h\) (not necessarily conforming), there is not guarantee that the inf-sup condition is realized on the discrete level.

There are many methods constructing test functions providing better stability of the method for a given class of problems [17,18,19,20]. In 2010 the Discontinuous Petrov-Galerkin (DPG) method was proposed, with the modern summary of the method described in [21, 22]. The key idea of the DPG method is to construct the optimal test functions “on the fly”, element by element. The DPG automatically guarantee the numerical stability of difficult computational problems, thanks to the automatic selection of the optimal basis functions. The DPG method is equivalent to the residual minimization method [21]. The DPG is a practical way to implement the residual minimization method when the computational cost of the global solution is expensive (non-linear).

There is consistent literature on residual minimization methods, especially for convection-diffusion problem [23,24,25], where it is well known that the lack of stability is the main issue to overcome. In particular, the class of DPG methods [26, 27] aim to obtain a practical approach to solve the mixed system by breaking the test spaces (at the expense of introducing a hybrid formulation).

Recently, in [28] a new stabilized finite element method based on residual minimization was introduced. The method consider first an adequate discontinuous Galerkin formulation. Then, the wanted solution is obtained by solving a residual minimization problem in terms of a dual discontinuous Galerkin norm. As in DPG methods, the method delivers a stable approximation and an error estimator to guide the adaptivity. However, its main attractive relies in that it allows to obtain a solution in a conforming sub space with the same quality of those ones obtained with the discontinuous Galerkin formulations. Last is evidenced by the authors considering standard Lagrange FEM polynomials.

In this paper, we explore the extension of [28] to IGA. We investigate the possibility of considering highly-continuous B-splines spaces as trial and broken B-spline spaces as test. We focus on the stationary Stokes problem, that requires special stabilization effort (see [29,30,31,32,33]). Due to the large range of subspaces that can be considered as trial spaces, we perform experimentations considering different setups of conforming trial spaces contained in a given broken B-spline space of degree 4. We solve the global system calling the MUMPS solver [34,35,36], and we compare the obtained results in terms of computational cost and accuracy of the obtained solution.

2 Discontinuous Galerkin Based Isogeometric Residual Minimization (DGIRM)

In this section we briefly discuss, in an abstract setting, the main idea behind the discontinuous Galerking based residual minimization method introduced in [28] in the isogeometric context.

Assume that we want to obtain an approximation \(\mathfrak {u}_h\), of the continuous problem (1), in a given discrete space \(\mathfrak {U}_h \subset \mathfrak {U}\) (eg., a highly continuous B-spline space). The residual minimization method is constructed as follows: First, a broken B-spline polynomial space \(\mathfrak {V}_h\), containing \(\mathfrak {U}_h\), is considered. Next, as starting point, is considered a discontinuous Galerkin variational formulation for problem (1) of the form:

$$\begin{aligned} \text {Find } \mathfrak {u}_h^{\mathrm {DG}} \in \mathfrak {V}_h, \text { such that } \mathfrak {b}_h(\mathfrak {u}_h^{\mathrm {DG}},\mathfrak {v}_h) = \mathfrak {l}_h(\mathfrak {v}_h), \quad \forall \, \mathfrak {v}_h\in \mathfrak {V}_h, \end{aligned}$$
(4)

the bilinear form \(\mathfrak {b}_h\) is inf-sup stable with respect to a given discrete norm \(\Vert \cdot \Vert _{\mathfrak {V}_h}\) of \(\mathfrak {V}_h\). This is, there exists a positive constant \(C_{sta}\), independent of the mesh size, such that:

$$\begin{aligned} \sup _{0 \ne \mathfrak {v}_h \in \mathfrak {V}_h} \dfrac{\mathfrak {b}_h(\mathfrak {w}_h,\mathfrak {v}_h)}{\Vert \mathfrak {v}_h\Vert _{\mathfrak {V}_h}} \ge C_{sta} \, \Vert \mathfrak {w}_h\Vert _{\mathfrak {V}_h}, \quad \forall \, \mathfrak {v}_h \in \mathfrak {V}_h. \end{aligned}$$
(5)

Finally, instead of solving the square problem (4), the wanted solution is obtained by solving the following residual minimization problem:

$$\begin{aligned} \text {Find } \mathfrak {u}_h \in \mathfrak {U}_h, \text { such that } \mathfrak {u}_h = \mathop {\mathrm {arg\,min}}\limits _{\mathfrak {w}_h \in \mathfrak {U}_h} \dfrac{1}{2}\Vert \mathfrak {l}_h - \mathfrak {B}_h \mathfrak {w}_h \Vert _{\mathfrak {V}_h'}^2, \end{aligned}$$
(6)

where \(\mathfrak {V}_h^\prime \) denotes the dual space of \(\mathfrak {V}_h\), the operator \(\mathfrak {B}_h: \mathfrak {V}_h \rightarrow \mathfrak {V}_h^\prime \) is defined as:

$$\begin{aligned} < \mathfrak {B}_h \mathfrak {w}_h,\mathfrak {v}_h>_{\mathfrak {V}^\prime _h \times \mathfrak {V}_h} := \mathfrak {b}_h\left( \mathfrak {w}_h, \mathfrak {v}_h\right) , \end{aligned}$$
(7)

and, for \(\phi \in \mathfrak {V}_h^\prime \), the dual norm \(\Vert \cdot \Vert _{\mathfrak {V}^\prime _h}\) is defined as:

$$\begin{aligned} \displaystyle \Vert \phi \Vert _{\mathfrak {V}^\prime _h} := \sup _{0 \ne \mathfrak {v}_h \in \mathfrak {V}_h} \dfrac{<\phi ,\mathfrak {v}_h>_{\mathfrak {V}_h' \times \mathfrak {V}_h}}{\Vert \mathfrak {v}_h\Vert _{\mathfrak {V}_h}}. \end{aligned}$$
(8)

Considering the Riesz operator:

$$\begin{aligned} R_{\mathfrak {V}_h} :\mathfrak {V}_h \ni v_h \rightarrow (\mathfrak {v}_h,.)_{\mathfrak {V}_h} \in \mathfrak {V}_h^\prime , \end{aligned}$$
(9)

where \((\cdot ,\cdot )_{\mathfrak {V}_h}\) denotes the inner product inducing the discrete norm \(\Vert \cdot \Vert _{\mathfrak {V}_h} = (\cdot ,\cdot )_{\mathfrak {V}_h}^{1/2}\), and defining the residual representative:

$$\begin{aligned} \mathfrak {r}_h := R_{\mathfrak {V}_h}^{-1}\left( \mathfrak {l}_h(\mathfrak {v}_h) - \mathfrak {b}_h(\mathfrak {u}_h, \mathfrak {v}_h)\right) = R_{\mathfrak {V}_h}^{-1} \mathfrak {b}_h(\mathfrak {u}_h^{\mathrm {DG}}-\mathfrak {u}_h, \mathfrak {v}_h), \end{aligned}$$
(10)

with \(R_{\mathfrak {V}_h}^{-1}\) being the inverse of the Riesz operator \(R_{\mathfrak {V}_h}\), and \(\mathfrak {u}_h^{\mathrm {DG}}\) being the solution of the DG problem (4), problem (6) can be equivalently written as the following saddle-point problem:

Find \((\mathfrak {r}_h,\mathfrak {u}_h) \in \mathfrak {V}_h \times \mathfrak {U}_h\), such that:

$$\begin{aligned} \begin{aligned} (\mathfrak {r}_h,\mathfrak {v}_h)_{\mathfrak {V}_h} + \mathfrak {b}_h(\mathfrak {u}_h,\mathfrak {v}_h)&= \mathfrak {l}_h(\mathfrak {v}_h),&\forall \, \mathfrak {v}_h \in \mathfrak {V}_h, \\ \mathfrak {b}_h(\mathfrak {w}_h,\mathfrak {r}_h)&= 0,&\forall \, \mathfrak {w}_h \in \mathfrak {U}_h. \end{aligned} \end{aligned}$$
(11)

The main attractive of the discrete saddle-point problem (11) is that it delivers automatically a stable approximation \(\mathfrak {u}_h \in \mathfrak {U}_h\) enjoying of desired properties for the solution, such as high-continuity, and a residual representation \(\mathfrak {r}_h \in \mathfrak {V}_h\) that can be used as error indicator to guide an adaptive mesh refinement. Indeed, in [28] the authors proved that, under the standard assumptions for the Discontinuous Galerkin problem (4): a) inf-sup stability (see Eq. (5)), b) boundedness and c) consistency (see [37] or [28] for definitions), problem (11) is well-posed. Additionally, it delivers an approximation \(\mathfrak {u}_h\) with the same quality, in terms of the norm \(\mathfrak {V}_h\), of the one obtained by solving problem (4). Moreover, the residual representative \(\mathfrak {r}\) is an efficient error estimator that, under an adequate saturation assumption is satisfied (see Assumptions 4 and 5 in [28]) the residual representative is also reliable.

Therefore, roughly speaking, the following two ingredients are required to perform the discontinuous Galerkin based isogeometric residual minimization:

  1. a)

    A well-posed discontinuous Galerkin formulation of the form (4), satisfying the inf-sup property (5).

  2. b)

    A conforming, in \(\mathfrak {U}\), subspace \(\mathfrak {U}_h \subset \mathfrak {V}_h\) as trial space.

3 The Stokes Problem

Let \(\varOmega \subset \mathbb {R}^2\) be a open bounded polygon with outer normal \(\mathbf{n}\), and denote by \(\partial \varOmega \) its boundary. Without loss of generality, we consider \(\varOmega = (0,1)^{{2}} \). The Stokes problem with no-slip boundary condition reads:

Find \(\mathbf {u},p\) such that:

$$\begin{aligned} \begin{array}{rll} -\varDelta \mathbf {u}+ \nabla \, p &{}=f, &{}\text { in } \varOmega ,\\ \nabla \cdot \mathbf {u}&{}=0, &{} \text { in } \varOmega ,\\ \mathbf {u}&{} = 0, &{} \text { on } \partial \varOmega , \end{array} \end{aligned}$$
(12)

where \(\mathbf {u}:=(u_1,\dots ,u_d) \, : \, \varOmega \rightarrow \mathbb {R}^{{2}}\) denotes the velocity field, \(p \, : \, \varOmega \rightarrow \mathbb {R}\) the pressure and \(f := (f_1,\dots ,f_d) \in \left[ L^2(\varOmega )\right] ^{{2}}\) a given forcing term. The solution of (12) is unique for the pressure p up to a constant, therefore, problem (12) is complemented with the following extra condition for p:

$$\begin{aligned} \int _{\varOmega } p = 0. \end{aligned}$$
(13)

3.1 Weak Variational Formulation

We consider the following Hilbert spaces: \(L^2(\varOmega ) = \{ v:\varOmega \rightarrow \mathbb R\, : \, \int _\varOmega v^2 < +\infty \}\), \(H^1(\varOmega ) = \{v \in L^2(\varOmega )\, : \, \nabla v \in [L^2(\varOmega )]^2\}\) and \(H^1_0(\varOmega ) = \{v \in H^(\varOmega ) \, : v=0 \text { on } \partial \varOmega \}\). Defining \(U := \left( H^1_0(\varOmega )\right) ^{{2}}\) as the space for the velocity field and, as consequence of condition (13), the space \(P:=L^2_0(\varOmega )\), with \(L^2_0(\varOmega )=\{p\in L^2(\varOmega ): \int _{\varOmega } p = 0\}\) for the pressure, the weak variational formulation of the strong problem (12)–(13) reads:

Find \((\mathbf {u},p)\in U \times P\), such that:

$$\begin{aligned} \begin{array}{rll} \displaystyle a(\mathbf {u},\mathbf {v})+b(\mathbf {v},p) &{}=(f,v)_{\varOmega }, &{} \forall \mathbf {v}\in U, \\ \displaystyle -b(\mathbf {u},q) &{}=0, &{} \forall q \in P, \end{array} \end{aligned}$$
(14)

where

$$\begin{aligned} \begin{aligned} a(\mathbf {u},\mathbf {v})&=\int _{\varOmega } \nabla \mathbf {u}: \nabla \mathbf {v}:= \sum _{i,j=1}^{{2}} \int _{\varOmega } \partial _j u_i \partial _j v_i, \\ b(\mathbf {v},p)&=-\int _{\varOmega } p \nabla \cdot \mathbf {v}, \end{aligned} \end{aligned}$$
(15)

and \((\cdot ,\cdot )_{\varOmega }\) denotes the inner product of \(L^2( \varOmega )\). It is well known that problem (14) is well-posed (see, eg. [37] or [13]) so we skip here the mathematical details.

3.2 An Equal-Order Discontinuous Galerkin Formulation

In this section we briefly introduce, in the isogeometric context, a discontinuous Galerkin formulation proposed by Cockburn et al. in [38] allowing to consider equal-order discontinuous spaces for the velocity and the pressure. A detailed discussion of alternative discontinuous Galerkin methods for the Stokes problem can be found in [37].

For a given mesh size h, denote by \(\varOmega _h\) a conforming isogeometric discretization of \(\varOmega \) [1]. Denote by \(F_h\) the set of all faces of \(\varOmega _h\), and by \(F_h^0 \subset F_h\) the set of internal faces. Over \(F_h\), we define \(\mathbf{n}_F\) as a predefined normal over each F being coincident with \(\mathbf{n}\) when F is a boundary face. We denote by \(h_F\) the diameter of the face being the length of the edge in 2D, and equal to \(2^{0.5*\text { length of the edge}}\) in 3D. We denote by \(S_{c1, \dots c_d}^{p_1, \dots , p_d}\) the space, defined over \(\varOmega _h\), of splines functions of degree \(p_i \ge 1\), and continuity \(c_i = -1\le p_i-1\) in the \(x_i\) coordinate. Over \(F_h\), for any function \(v_h \in S_{c1, \dots c_d}^{p_1, \dots , p_d}\), we denote by \(\left[ v_h \right] \) the jump operator, and by \(\{v_h\}\) the average operator, defined as follows:

$$\begin{aligned} \left[ v_h \right] |_F = \left\{ \begin{array}{rl} v_h^- - v_h^+ , &{} \text { if } F \in F^0_h, \\ v_h, &{} \text { if } F \in F_h \setminus F_h^0, \end{array} \right. \qquad \left\{ v_h \right\} |_F = \left\{ \begin{array}{rl} \dfrac{1}{2} (v_h^- + v_h^+) , &{} \text { if } F \in F^0_h, \\ v_h, &{} \text { if } F \in F_h \setminus F_h^0, \end{array} \right. \end{aligned}$$
(16)

with \(v_h^-\) and \(v_h^+\) denoting the left and right traces respectively, with respect to the predefined normal \(\mathbf{n}_F\). Finally, for a given \(p \ge 1\), define \(W_h := \left[ S_{-1, \dots -1}^{p, \dots , p}\right] ^{{2}}\) as the space for the discontinuous velocity, \(Q_{h} = S_{-1, \dots , -1}^{p, \dots , p}\), and \(Q_{0,h} := Q_h \cap L^2_0{(\varOmega )}\) as the space for the discontinuous pressure. The equal-order velocity and pressure discontinous Galerkin formulation reads:

Find \((\mathbf {u}_h^{\mathrm {DG}}, p_h^{\mathrm {DG}}) \in W_h \times Q_{0,h}\), such that:

$$\begin{aligned} \begin{array}{rll} \displaystyle a_h(\mathbf {u}_h^{\mathrm {DG}},\mathbf {v}_h) + b_h(\mathbf {v}_h,p_h^{\mathrm {DG}}) &{} =(f,\mathbf {v}_h)_{\varOmega },&{} \quad \forall \, \mathbf {v}_h \in W_h, \\ \displaystyle -b_h(\mathbf {u}_h^{\mathrm {DG}},q_h)+s_h(p_h^{\mathrm {DG}},q_h)&{}=0, &{} \quad \forall \, q_h \in Q_{0,h}, \end{array} \end{aligned}$$
(17)

with

$$\begin{aligned} \begin{array}{rl} a_h(\mathbf {w}_h,\mathbf {v}_h) = &{} \displaystyle \sum _{i=1,...,d} \left( \sum _{K\in \varOmega _h} \int _K \nabla w_{h,i} \cdot \nabla v_{h,i} -\sum _{F\in F_h} \int _F \{\nabla w_{h,i} \} \cdot \mathbf{n}_F [v_{h,i}] \right. \\ &{} \displaystyle \left. -{\sum _{F\in F_h} \int _F [w_{h,i} ] \cdot \{\nabla v_{h,i}\}\cdot \mathbf{n}_F }+{\sum _{F\in F_h} \int _F \frac{\eta }{h_F} [w_{h,i}] [v_{h,i}] } \right) , \end{array} \end{aligned}$$
(18)

being the discretization of the diffusive term,

$$\begin{aligned} b_h(\mathbf {v}_h,q_h)= - \sum _{K\in \varOmega _h} \int _K q_h \nabla \cdot \mathbf {v}_h+ \sum _{F\in F_h} \int _F [\mathbf {v}_h]\cdot \mathbf{n}_F \{q_h\}, \end{aligned}$$
(19)

is the discretization of the pressure-velocity coupling term, and

$$\begin{aligned} s_h(p_h,q_h)= \sum _{F\in F_h^{0}} h_F \int _F [p_h][q_h], \end{aligned}$$
(20)

an extra stabilization term allowing to consider equal-order discrete spaces. In (18), \(\eta > {\underline{\eta }}\) denotes a user-defined stabilization parameter that has to be considered large enough to guarantee the inf-sup stability (see eg.  Lemma 4.12 in [37]). Notice that, by identifying \(\mathfrak {V}_h = W_h\times Q_{0,h}\), \(\mathfrak {u}^{\mathrm {DG}}_h = (\mathbf {u}_h^{\mathrm {DG}},p_h^{\mathrm {DG}})\), and \(\mathfrak {v}_h = (\mathbf {v}_h,q_h)\), problem (17) can be equivalently written of the form (4), with \(\mathfrak {l}_h(\mathfrak {v}_h) = (f,v_h)_{\varOmega }\) and

$$\begin{aligned} \mathfrak {b}_h(\mathfrak {u}^{\mathrm {DG}}_h, \mathfrak {v}_h) := a_h(\mathbf {u}_h^{\mathrm {DG}},\mathbf {v}_h) + b_h(\mathbf {v}_h,p_h^{\mathrm {DG}})-b_h(\mathbf {u}_h^{\mathrm {DG}},q_h)+s_h(p_h^{\mathrm {DG}},q_h). \end{aligned}$$
(21)

Moreover, the bilinear form (21) satisfies the inf-sup condition (5) (see Lemma 6.13 in [37]) with the following norm:

$$\begin{aligned} \begin{aligned} |||(\mathbf {v}_h,q_h)|||^2 =&\sum _{i=1,...,d} \left( \sum _{K\in T_h} \Vert \nabla v_{h,i}\Vert ^2_{L^2(K)} + \sum _{F\in F_h} \frac{\eta }{h_F} \Vert [v_{h,i}] \Vert ^2_{L^2(F)} \right) \\&+ \Vert q_h\Vert ^2_{L^2(\varOmega )} + \sum _{F\in F_h^{0}} h_F \Vert [ q_h] \Vert ^2_{L^2(F)}. \end{aligned} \end{aligned}$$
(22)

Remark 1 (Discarding the zero-mean value restriction)

Following Remark 6.14 from [37], in practice we can ignore the zero mean-value constrain (13) in the spaces for the pressure, and call MUMPS with pivoting. Then, a zero mean-value solution can be recovered by post-processing the solution as \(p = p-\frac{1}{|\varOmega |} \int _{\varOmega }p\).

3.3 Trial Spaces for the Residual Minimization Problem

The subspace condition for the trial space give a wide range of possibilities. In this paper, we focus in the two dimensional case. For a given polynomial degree p, we denote by \(V_h = S_{-1,-1}^{p,p}\times S_{-1,-1}^{p,p}\) the test space for the velocity, and by \(Q_h = S_{-1,-1}^{p,p}\) the test space for the pressure (see Remark 1). Denoting by \(V_h \subset W_h\) the trial space for the velocity, and by \(P_h \subset Q_h\) the trial space for the pressure, we consider the following conforming couples of spaces:

  1. a)

    Raviart-Thomas type:

    \(V_h := S_{c,c-1}^{p,p-1} \times S_{c-1,c}^{p-1,p}\), \(P_h := S_{c-1,c-1}^{p-1,p-1}\), with \(p\ge 2\) and \(1 \le c \le p-1\).

  2. b)

    Second order Nédélec type:

    \(V_h := S_{c,c-1}^{p,p} \times S_{c-1,c}^{p,p}\), \(P_h := S_{c-1,c-1}^{p-1,p-1}\), with \(p\ge 2\) and \(1 \le c \le p-1\).

  3. c)

    Taylor-Hood type:

    \(V_h := S_{c,c}^{p,p} \times S_{c,c}^{p,p}\), \(P_h := S_{c,c}^{p-1,p-1}\), with \(p\ge 2\) and \(0 \le c \le p-2\).

  4. d)

    Equal-order type:

    \(V_h := S_{c,c}^{p,p} \times S_{c,c}^{p,p}\), \(P_h := S_{c,c}^{p,p}\), with \(p\ge 1\) and \(0 \le c \le p-2\).

We notice that couple of spaces a), b) and c) are stable in the classical isogeometric case (see [39]), while the couple d) is not.

4 Numerical Results

In this section, we explore the results obtained considering (as starting point) the equal-order discontinuous Galerkin formulation defined in Sect. 3.2, with \(W_h = S^{4,4}_{-1,-1} \times S^{4,4}_{-1,-1}\) and \(Q_h = S^{4,4}_{-1,-1}\) as the discontinuous spaces for the velocity and pressure respectively, and performing the discontinuous Galerkin based residual minimization method (see Sect. 2) with the several options of conforming trial spaces defined in Sect. 3.3.

4.1 A Smooth Analytical Solution

We consider the Stokes problem (12), defined over the 2D domain \(\varOmega = [0, 1]^2\), and we define the source term f in such a way that the analytical solution is given by \(\mathbf {u}= (u_1,u_2)\) and p, with (cf. [40]):

(23)

In Tables 1, 2, 3 and 4 we show the \(L^2\)-error in the approximation of the functions \(\mathbf {u}\), p and \(\mathrm {div}\, \mathbf {u}\), obtained by considering a fixed mesh of size \(20\times 20\), and the extreme allowed continuities for the Taylor-Hood type, Raviart-Thomas type, second order Nédélec type, and equal-order type trial spaces respectively. We also show the number of flops required for the resolution of the corresponding saddle-point problem (see Equation (11)). As expected, all the selected trial spaces deliver good approximations for the measured quantities. Moreover, there is no a significative difference in the approximation when considering a highly-continuous trial space, while the total number of flops is reduced in almost two orders of magnitude, when compared with its \(C^0\)-trial equivalent, and the highly-continuous equal order type trial is the one that delivers a better balance between accuracy and computational cost. Last can be also appreciated in Fig. 1, where we plot the Pareto front for the previous results (see [41]), considering the the number of floating-point operations (as performed by the MUMPS direct solver) as the vertical axis, and the numerical error measured in the \(|||(\cdot , \cdot )|||\)-norm, defined in Equation (22), as the horizontal axis.

Table 1. Taylor-Hood type trial with minimum and maximum continuity respectively.
Full size table
Table 2. Raviart-Thomas type trial with minimum and maximum continuity respectively.
Full size table
Table 3. Second-order Nédélec type trial with minimum and maximum continuity respectively.
Full size table
Table 4. Equal-order type trial with minimum and maximum continuity respectively.
Full size table
Fig. 1.
figure 1

Pareto front for different setups of trial spaces defined in Sect. 3.3. The vertical axis denotes the computational cost expressed in terms of the number of floating-point operations performed by MUMPS solver. The horizontal axis denotes the error in the \(||| (\cdot , \cdot )|||\)-norm (see (22)) for the smooth analytical problem.

Full size image
Fig. 2.
figure 2

Comparison of residual and error for different mesh dimensions, \(4\times 4\), \(8\times 8\), \(16\times 16\) and \(32\times 32\) considering as test the space \(W_h=S^{4,4}_{-1,-1}\times S^{4,4}_{-1,-1}\), \(Q_h=S^{4,4}_{-1,-1}\), and as trial the space \(V_h=S^{4,4}_{c,c}\times S^{4,4}_{c,c}\), \(P_h=S^{4,4}_{c,c}\), with \(c=0,1,2,3\) respectively (from left to the right).

Full size image
Fig. 3.
figure 3

Left panel: The formulas of the Dirichlet boudnary conditions for the velocity field. Right panel: The singularities at the pressure solution.

Full size image

Finally, in Fig. 2, we plot the error \(|||(\mathbf {u}-\mathbf {u}_h, p-p_h)|||\) (real), and the error of the residual estimation \(|||(\mathbf{r}^u_h, r^p_h)|||\) (estimated), where \(\mathbf{r}^u_h, r^p_h\) are the residual associated with the velocity and pressure respectively, obtained when considering \(V_h=S^{4,4}_{c,c}\times S^{4,4}_{c,c}\), \(P_h=S^{4,4}_{c,c}\), with \(c=0,1,2,3\) respectively, as trial spaces. As can be appreciated in the figures, increasing the continuity reduces the distance between the real and the estimated errors, implying that the error bound becomes sharper when increasing the continuity.

Table 5. Velocity \((u_1,u_2)\) and pressure p on a series of uniformly adapted meshes.
Full size table

4.2 The Lid-Cavity Flow Problem

With the spirit of exploring the behavior of the method when the solution is non-smooth, as second example we consider the well-known lid-cavity flow problem (see eg. [42]).

The problem models a plane flow of an isothermal fluid in a square lid-driven cavity of size \((0,1)^{2}\) (cf. [43]). The pressure solution in the problem exhibits two singularities at the corners, as presented on right panel in Fig. 3. For the numerical simulation, we enforce the Dirichlet boundary conditions for the velocity field in terms of a small parameter \(\varepsilon >0\), to obtain a solution with Dirichlet trace belonging to \(H^{1/2}\) (see left panel in Fig. 3). For the pressure, we fix its value at one point, which is numerically equivalent to setting the condition (13). We set a homogeneous force \( f = 0\). We consider the spaces \(W_h = S^{4,4}_{-1,-1} \times S^{4,4}_{-1,-1}\) and \(Q_h = S^{4,4}_{-1,-1}\) for as test for the velocity and pressure respectively, and the spaces \(V_h = S^{4,4}_{3,3} \times S^{4,4}_{3,3}\), \(P_h = S^{4,4}_{3,3}\) as trials for the velocity and pressure respectively, that we recall it is not stable in the classical isogeometric sense (cf. [39]). In Table 5, we plot the components of the discrete velocity field, and the discrete pressure field obtained considering several uniform meshes. As can be appreciated from the figures, also in this scenario the method delivers stable and accurate approximations, even if a highly-continuous space is chosen as trial, evidencing the performance of the method.

5 Conclusions

We investigated a Discontinuous Galerkin (DG) based residual minimization (RM) stabilization for isogeometric analysis (IGA) simulations of the stationary Stokes problem. We explore the results obtained when considering a fixed DG-type test space and several types of conforming trial spaces. The higher continuity spaces result in a lower computational effort of the solver due to the reduction of the number of degrees of freedom, without affecting significantly the approximation. Moreover, the upper error bound constant is reduced when the continuity is increased, leading to a sharper estimation of the error in terms of the analytical solution. The method is also able to capture singularities even is considering a highly-continuous trial space, as evidenced with the well-known lid-cavity flow problem in the numerical section.

As future work, we plan to extend the analysis to other kind of mixed formulations, such as the Ossen and Maxwell equations [44,45,46], as well as exploring parallelization techniques for the resolution of the saddle-point problem [47], and localized adaptive mesh refinement techniques based on the residual estimator (10). The future work will also involve incorporating of the DG method mixed with residual minimization formulation within adaptive finite element code [42, 48].