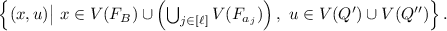Iterated Type Partitions

Abstract

This paper introduces a novel parameter, called iterated type partition, that can be computed in polynomial time and nicely places between modular-width and neighborhood diversity. We prove that the Equitable Coloring problem is W[1]-hard when parametrized by the iterated type partition. This result extends to modular-width, answering an open question on the complexity of Equitable Coloring when parametrized by modular-width. On the contrary, we show that the Equitable Coloring problem is FPT when parameterized by neighborhood diversity. Furthermore, we present a scheme for devising FPT algorithms parameterized by iterated type partition, which enables us to find optimal solutions for several graph problems. While the considered problems are already known to be FPT with respect to modular-width, the novel algorithms are both simpler and more efficient. As an example, in this paper, we give an algorithm for the Dominating Set problem that outputs an optimal set in time $O({2^t}+poly(n))$, where n and t are the size and the iterated type partition of the input graph, respectively.

1 Introduction

Some NP-hard problems can be solved by algorithms that are exponential only in the size of a parameter while they are polynomial in the size of the input. Such problems are called fixed-parameter tractable, because the problem can be solved efficiently for small values of the parameter [10, 33]. Formally, a parameterized problem with input size n and parameter ${{t}}$ is called fixed parameter tractable (FPT) if it can be solved in time $f({{t}}) \cdot n^c$, where f is a computable function only depending on ${{t}}$ and c is a constant.

An important quality of a parameter is that it is easy to compute. Unfortunately there are several parameters whose computation is an NP-hard problem. As an example computing treewidth, rankwidth, and vertex cover are all NP-hard problems but they are computable in FPT time when their respective parameters are bounded; moreover, the parameterized complexity of computing the clique-width of a graph exactly is still an open problem [11].

We start from two recently introduced parameters: modular-width [22] and neighborhood diversity [31]. Both parameters received much attention [1, 2, 5, 7, 12, 17, 18, 21, 24, 25, 29] also due to their property of being computable in polynomial time [22, 31].

As the main contribution of this paper we introduce a novel parameter called Iterated Type Partition, which nicely places between the two above parameters and allows to obtain new algorithms and hardness results.

1.1 Modular-Width

The notion of modular decomposition of graphs was introduced by Gallai in [23], as a tool to define hierarchical decompositions of graphs. It has been recently considered in [22] to define the modular-width parameter in the area of parameterized computation.

Consider graphs obtainable by an algebraic expression that uses the operations:

• 1) Creation of an isolated vertex.

• 2) Disjoint union of 2 graphs, i.e., the graph with vertex set $V (G_1 ) \cup V ( G_2 )$ and edge set $E( G_1 )\cup E( G_2 )$.

• 3) Complete join of 2 graphs, i.e., the graph with vertex set $V (G_1 ) \cup V ( G_2 )$ and edge set $E( G_1 )\cup E( G_2 )\cup \{ (v, w)\ :\ v \in V ( G_1 ),\ w\in V(G_2) \}$.

• 4) Substitution operation $G(G_1,\dots ,G_m)$ of the vertices $v_1,\dots ,v_m$ of G by the modules $G_1,\dots ,G_m$, i.e., the graph with vertex set $\bigcup _{1\le \ell \le m} V(G_\ell )$ and edge set

  $$\begin{aligned} \bigcup _{1\le \ell \le m} E(G_\ell )\cup \{(u, v)\ : \ u \in V (G_i), \ v \in V (G_j ), \ (v_i, v_j) \in E(G) \}. \end{aligned}$$

As defined in [22], the modular-width of a graph G, denoted mw(G), is the least integer m such that G can be obtained by using only the operations 1)–4) (in any number and order) and where each operation 4) has at most m modules.

1.2 Neighborhood Diversity

Given a graph $G=(V,E)$, two nodes $u,v\in V$ have the same type iff $N(v) \setminus \{u\} = N(u) \setminus \{v\}$. The neighborhood diversity of a graph G, introduced by Lampis in [31] and denoted by nd(G), is the minimum number ${{t}}$ of sets in a partition $V_1,V_2, \ldots , V_{{t}}$, of the node set V, such that all the nodes in $V_i$ have the same type, for $i\in [t]$¹.

The family $\mathcal{V}=\{V_1,V_2, \ldots , V_{{t}}\}$ is called the type partition of G.

Let $G=(V,E)$ be a graph with type partition $\mathcal{V}=\{V_1,V_2, \ldots , V_{{t}}\}$. By definition, each $V_i$ induces either a clique or an independent set in G. We treat singleton sets in the type partition as cliques. For each $V_i,V_j\in \mathcal{V}$, we get that either each node in $V_i$ is a neighbor of each node in $V_j$ or no node in $V_i$ has a neighbor in $V_j$. Hence, between each pair $V_i,V_j\in \mathcal{V}$, there is either a complete bipartite graph or no edges at all.

Starting from a graph G and its type partition $\mathcal{V}=\{V_1, \ldots , V_{{t}}\}$, we can see each element of $\mathcal{V}$ as a metavertex of a new graph H, called the type graph of G, with

• $V(H)=\{1,2,\cdots ,{{t}}\}$

• $E(H)=\{(x,y) \ | \ x \ne y \text { and for each } u\in V_x, v\in V_y \text { it holds that } (u,v)\in E(G) \}$.

We say that G is a base graph if it matches its type graph, that is, the type partition of G consists of singletons, each representing a node in V(G), and $nd(G)=|V(G)|$.

We introduce a new graph parameter, which generalizes neighborhood diversity. Given a graph G, the Iterated Type Partition of G is defined by iteratively constructing type graphs until a base graph is obtained. It is worth mentioning that our base graphs correspond to prime graphs for modular decomposition [1].

Definition 1

Given a graph $G=(V,E)$, let ${H^{(0)}}=G$ and ${H^{(i)}}$ denote the type graph of ${H^{(i-1)}}$, for $i\ge 1$. Let d be the smallest integer such that ${H^{(d)}}$ is a base graph. The iterated type partition of G, denoted by ${ itp}(G)$, is the number of nodes of ${H^{(d)}}$. The sequence of graphs ${H^{(0)}}=G, {H^{(1)}}, \cdots , {H^{(d)}}$ is called the type graph sequence of G and ${H^{(d)}}$ is denoted as the base graph of G.

An example of a graph and its type graph sequence is given in Fig. 1. For each type graph ${H^{(i)}}$ each vertex (henceforth metavertex) describes an element of the type partition of ${H^{(i-1)}}$.

Fig. 1.

A graph G with iterated type partition 5 and its corresponding type graph sequence: $G=H^{(0)},H^{(1)},H^{(2)}.$ Dashed circles group nodes having the same type.

It is well-known that determining nd(G) and the corresponding type partition, can be done in polynomial time [31]. As an immediate consequence, we have that

Theorem 1

There exists a polynomial time algorithm which, for any input graph G computes the type graphs sequence of G and, consequently, finds the value itp(G).

1.3 Relation with Other Parameters

In this section we analyze the relations between the iterated type partition parameter and some other well known parameters.

We notice that, as an iteration of neighborhood diversity, the new parameter satisfies

$$\begin{aligned} itp(G)\le nd(G). \end{aligned}$$

(1)

Actually itp(G) can be much smaller than nd(G). Indeed consider the following:

• Choose a positive integer d and a connected base graph $H^{(d)}$ having k nodes;

• For $i= d,d-1, \ldots , 1$, a new graph $H^{(i-1)}$ is obtained as follows:

  • replace each node of $H^{(i)}$, with an independent set of at least two nodes (if $d-i$ is even) or a clique of size at least two (if $d-i$ is odd).

  • for each edge of $H^{(i)}$, put a complete bipartite graph between the nodes of the graphs that replace the endpoints of the edge.

The value $nd(H^{(0)})$ is the number of nodes in $H^{(1)}$, that is at least $k 2^{d-1}$, while $itp(H^{(0)})$ is the size k of $H^{(d)}$.

We stress that iterated type partition is a “special case” of modular-width in which the modules in operation 4) can only be independent sets or cliques. Hence, it is not difficult to see that for every graph G

$$\begin{aligned} mw(G)\le itp(G). \end{aligned}$$

(2)

We know from [31] that $nd(G)\le 2^{vc(G)}+vc(G)$. Hence, by (1), we have $itp(G)\le 2^{vc(G)}+vc(G)$. Moreover, using the same arguments as in [31] is it possible to show that $cw(G)\le itp(G)+1.$ Finally, as for the neighborhood diversity we can easily show that the iterated type partition is incomparable to the treewidth by comparing the values of such parameters on a complete graph $K_n$ and a path on n nodes. A summary of the relations holding between some popular parameters is given in Fig. 2. We refer to [19] for the formal definitions of treewidth and clique-width parameters.

Fig. 2.

A summary of the relations holding among some popular parameters. In addition to the previously defined parameters, we use tw(G), cw(G) and vc(G) to denote treewidth, clique-width and minimum vertex cover of a graph G, respectively. Solid arrows denote generalization, e.g., modular-width generalizes iterated type partition. Dashed arrows denote that the generalization may exponentially increase the parameter.

1.4 Our Results and Related Work

We give both tractability and hardness results for the new parameter.

The Equitable Coloring (EQC) Problem. If the nodes of a graph G are colored with k colors such that no adjacent nodes receive the same color (i.e., properly colored) and the sizes of any two color classes differ by at most one, then G is called to be equitably k-colorable and the coloring is called an equitable k-coloring. The goal is to minimize the number of used colors. The EQC problem is a well-studied problem, which has been analyzed in terms of parameterized positive or negative results with respect to many different parameters [26].

In particular, Fellows et al. [14] have shown that EQC problem parameterized by treewidth and number of colors is W[1]-hard. A series of reductions proving that Equitable Coloring is W[1]-hard for different subclasses of chordal graphs are given in [26]: The problem is shown to be W[1]-hard if parameterized by the number of colors for block graphs and for the disjoint union of split graphs; moreover, it remains W[1]-hard for $K_{1,4}$-free interval graphs even when parameterized by treewidth, number of colors and maximum degree. In [3] an XP algorithm parameterized by treewidth is given. We notice that an XP algorithm for Equitable Coloring parametrized by iterated type partition can be obtained by using Theorem 17 in [28]. On the other side, Fiala et al. show that the Equitable Coloring problem is FPT when parameterized by the vertex cover number [16]. However, it was an open problem to establish the parameterized complexity of the Equitable Coloring problem parameterized by neighborhood diversity or modular-width. In Sect. 2 we answer to these questions by proving the following results.

Theorem 2

The Equitable Coloring problem is W[1]-hard parametrized by itp.

Recalling (2), Theorem 2 immediately gives that the Equitable Coloring Problem is W[1]-hard w.r.t. modular-width.

Corollary 1

The EQC problem is W[1]-hard parametrized by modular-width.

We also show that the Equitable Coloring W[1]-hardness drops when parameterized by the neighborhood diversity.

Theorem 3

The EQC problem is FPT when parameterized by neighborhood diversity.

FPT Algorithms w.r.t. itp. In the last section we deal with FPT algorithms with respect to iterated type partition. Some of the considered problems are already known to be FPT w.r.t modular-width. Nonetheless, we think that the new algorithms, parameterized by iterated type partition, are worthy to be considered, since they are much simpler, faster, and allow to easily determine not only the value, but also the optimal solution. As an example, we consider here the Dominating Set (DS).

Table 1 summarizes our contribution, in relation to known results. Due to space constraints, some proofs are omitted or sketched; full proofs as well as the algorithms for the Vertex Coloring (Coloring) and the Vertex Cover (VC) problems appear in the extended version of this work [6].

Table 1. The table summarizes the results known in literature for several problems parametrized by iterated type partition and related parameters. t denotes the value of the considered parameter and [*] denotes the result obtained in this paper.

2 Equitable Coloring (EQC)

In this section we prove Theorems 2 and 3.

Equitable Coloring

Instance: A graph $G=(V,E)$ and an integer k.

Question: Is it possible to color the nodes of G with exactly k colors in such a way that nodes connected by an edge receive different colors and each color class has either size $\lfloor |V|/k \rfloor$ or $\lceil |V|/k \rceil$?

2.1 Hardness

In order to prove that Equitable Coloring problem is W[1]-hard if parameterized by iterated type partition, we present a reduction from the following Bin packing problem, which has been shown to be W[1]-hard when parameterized by the number of bins [27].

• Bin-Packing

• Instance: A collection of ${{\ell }}$ items having sizes $a_1,a_2,\cdots ,a_{{{\ell }}}$, a number k of bins, and a bin capacity B.

• Question: $\exists$ a k-partition ${{P}}_1,\cdots ,{{P}}_k$ of $A=\{a_1,a_2,\cdots ,a_{{{\ell }}}\}$ such that $\sum _{a_j \in {{P}}_i} a_j = B$, $\forall \, i \in [k]$?

In general the Bin-Packing problem asks for the sum of the items of each bin to be at most B; however, the above version is equivalent to the general one (even from the parameterized point of view) as it is sufficient to add $kB-\sum _{j =1}^{{{\ell }}} a_j$ unitary items [26]. In order to describe our reduction, we introduce two useful gadgets. The first one is the flower gadget also used in [26]. Let a and k be positive integers. An (a, k)–flower ${{F_{a,k}}}$ is a graph obtained by joining $a +1$ cliques of size k to a central node y. Figure 3(a) shows the (4, 3)–flower. Formally, let $K_k^i$ be a copy of a cliques of size k, for each $i \in [a+1]$,

• $V({{F_{a,k}}})=\{y\} \cup \bigcup _{i \in [a+1]}V(K_k^i)$, and

• $E({{F_{a,k}}})= \{(y,x) \ | \ x \in \bigcup _{i \in [a+1]}V(K_k^i)\} \cup \bigcup _{i \in [a+1]}E(K_k^i).$

Fig. 3.

(a) (4, 3)–flower; (b) (3, 5, 4)–chain.

The second gadget is defined starting from three positive integers: $k, {{\ell }}$ and B. It is a sequence of independent sets $S_1, \cdots , S_k, S_{k+1}$ with $|S_i|=B$, for $i \in [k]$, and $|S_{k+1}|={{\ell }}+1$ where between each pair of consecutive sets in the sequence $S_i$, $S_{i+1}$ there is a complete bipartite graph. We call such a gadget a $(k,{{\ell }},B)$–chain ${{Q}}$. Figure 3(b) shows the (3, 5, 4)–chain. Formally,

• $V({{Q}})= \bigcup _{i \in [k+1]}S_i$, and

• $E({{Q}})= \bigcup _{i \in [k]}\{(u,v) \ | \ u \in S_i, v \in S_{i+1}\}.$

We can now describe our reduction. Let $\langle A=\{a_1,\cdots ,a_{{\ell }}\}, k, B \rangle$ be an instance of Bin-Packing. Define a graph G as follows: The set of nodes is composed by the disjoint union of two $(k,{{\ell }},B)$-chains, ${{Q'}}$ and ${{Q''}}$ plus the flowers $F_{a_1,k}, \cdots , F_{a_{{\ell }},k}, F_{B,k}$. Then join each node in the flowers to each node in the chains. In the following, whenever the number of bins k is clear by the context, we use ${{F_{a}}}$ instead of ${{F_{a,k}}}$. Formally,

• $V(G)= V({{Q'}}) \cup V({{Q''}}) \cup V({{F_{B}}}) \cup \left( \bigcup _{j \in [{{\ell }}]} V({{F_{a_j}}})\right)$, and

• $E(G) = E({{Q'}}) \cup E({{Q''}}) \cup E({{F_{B}}}) \cup \left( \bigcup _{j \in [{{\ell }}]} E({{F_{a_j}}}) \right) \cup$

  

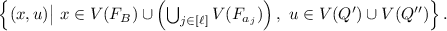
Figure 4 shows the graph G when $A=\{2,1,2,3\}$, $B=4$ and $k=3$. The number of nodes in the resulting graph G is

$$\begin{aligned} |V(G)| = |V({{Q'}})|+ |V({{Q''}})| + |V({{F_{B}}})| + \sum _{j \in [{{\ell }}]} |V({{F_{a_j}}})| = (k+3)(Bk+{{\ell }}+1). \end{aligned}$$

(3)

Fig. 4.

The type graph sequence of G when $A=\{2,1,2,3\}$, $B=4$, and $k=3$. The line connecting dashed circles indicates a complete bipartite graph between the nodes in the circles.

Lemma 1

$\langle A=\{a_1,\cdots ,a_{{\ell }}\}, k, B \rangle$ is a YES instance of Bin-Packing if and only if G is equitably $(k+3)$–colorable.

Proof

(Sketch.) We first show that, given a k-partition ${{P}}_1,\cdots ,{{P}}_k$ of A that solves the given instance of Bin-Packing, i.e., $\sum _{a_j \in {{P}}_i} a_j = B$ for each $i \in [k]$, we can construct an equitable (k+3)-coloring c of the nodes of G.

• Coloring of the nodes in ${{Q'}}$: For each $i \in [k+1]$ and $u \in S'_i$ (where $S'_i$ is the i-th set of independent nodes in the $(k,{{\ell }},B)$-chain ${{Q'}}$) assign

  $$\begin{aligned} c(u)= {\left\{ \begin{array}{ll} k+3 &{} \text{ if } \text{ i } \text{ is } \text{ odd, }\\ k+2 &{} \text{ if } \text{ i } \text{ is } \text{ even. } \end{array}\right. } \end{aligned}$$

  (4)

• Coloring of the nodes in ${{Q''}}$: For each $i \in [k+1]$ and $u \in S''_i$, (where $S''_i$ is the i-th set of independent nodes in the $(k,{{\ell }},B)$-chain ${{Q''}}$) assign

  $$\begin{aligned} c(u)= {\left\{ \begin{array}{ll} k+3 &{} \text{ if } \text{ i } \text{ is } \text{ even, }\\ k+2 &{} \text{ if } \text{ i } \text{ is } \text{ odd. } \end{array}\right. } \end{aligned}$$

  (5)

• Coloring of the nodes in ${{F_{B}}}$: Let z be the central node in ${{F_{B}}}$. Assign $c(z)=k+1$. Then, assign to each of the k nodes of the $B+1$ cliques joined to z the remaining k colors (e.g. $1,2, \cdots k$), so that the nodes of the clique have different colors.

• Coloring of the nodes in ${{F_{a_j}}}$, for $j\in [{{\ell }}]$: Let $y_j$ be the central node in ${{F_{a_j}}}$. Assign $c(y_j)=i$ if $a_j \in P_i$. Then, as before assign to each of the k nodes of the $a_j+1$ cliques joined to $y_j$ the remaining k colors, i.e., those in $\{1,2, \cdots k,k+1\}-\{i\}$, so that the nodes of the clique have different colors.

The above coloring c can be proved to be proper and such that each class of colors contains exactly $Bk +{{\ell }}+1$ nodes. By (3) this proves that c is an equitable $(k+3)$-coloring of G.

Now, let c be an equitable $(k+3)$-coloring of G. We can prove that exactly two colors among the $k+3$ are used by c to color only the nodes in the chains $Q'$ and $Q''$. Furthermore, the color used by c to color the central node of the flower ${{F_{B}}}$ is not used to color the central nodes of any other flowers ${{F_{a_1}}}, \cdots , {{F_{a_{{\ell }}}}}$. By using this result, we can prove that the k classes of colors involving the central nodes of the ${{F_{a_1}}}, \cdots , {{F_{a_{{\ell }}}}}$ induce a k-partition of A that solves our instance of Bin-Packing.    $\square$

Lemma 2

The iterated type partition ${ itp}(G)$ of G is $2k+3$.

Proof

(Sketch.) The graph G has type graph sequence ${H^{(0)}}=G, {H^{(1)}}, {H^{(2)}}, {H^{(3)}}, {H^{(4)}}$. We derive the above graphs and show that the number of nodes of the base ${H^{(4)}}$ is $2k+3$. Figure 4 shows the type graph sequence when $A=\{2,1,2,3\}$, $B=4$ and $k=3$.    $\square$

Proof

of Theorem 2. Given an instance $\langle A=\{a_1,\cdots ,a_{{\ell }}\}, k, B \rangle$ of Bin-Packing, we use the above construction to create an instance $\langle G=(V,E), { itp}(G) \rangle$ of Equitable Coloring parameterized by iterated type partition. Lemma 1 show the correctness of our reduction and Lemma 2 provides the iterated type partition of the constructed graph, showing that our new parameter ${ itp}(G)$ is linear in the original parameter k.    $\square$

2.2 Neighborhood Diversity: An FPT Algorithm

We prove here that the Equitable Coloring problem admits an FPT algorithm with respect to neighborhood diversity. W.l.o.g. we assume that the number of nodes in the input graph $G=(V,E)$ is a multiple of the number of colors k (this can be attained by adding an independent clique of $k\lceil |V|/ k \rceil - |V|$ nodes to G in such a way the answer to the equitable k-coloring question remains unchanged).

Let then $r=|V|/k$. Any equitable k-coloring of G partitions V into k classes of colors, say $C_1,\ldots ,C_k$, s.t. $C_\ell$ is an independent set of G of size $|C_\ell |=r$, for $\ell =1,\ldots , k$.

If we consider now the type partition $\{V_1, \ldots , V_{{t}}\}$ of G and the corresponding type graph $H=(V(H)=\{1,\ldots ,t\}, E(H))$, we trivially have that: Two nodes $u,v\in V$ are independent in G iff $v\in V_i$ and $u\in V_j$, with $i,j\in V(H)$, such that either i and j are independent nodes of H or $i=j$ and $V_i$ induces an independent set in G. This immediately implies that for each color class $C_\ell$ of the equitable coloring of G there exists an independent set $I_\ell =\{{\ell _1},\ldots ,{\ell _{\rho }}\}$ of H such that

$\sum _{s=1}^{\rho } |C_\ell \cap V_{\ell _s}|=r$ and

$|C_\ell \cap V_{\ell _s}|=1$ for each $s=1,\ldots ,\rho$ such that $V_{\ell _s}$ induces a clique.

Let now $\mathcal{I}$ denote the family of all independent sets in H. From the above reasoning, we have that, given any equitable k-coloring of G, we can associate to each $I\in \mathcal{I}$ an independent set of $z_I\ge 0$ colors. We can then define, for each $I\in \mathcal{I}$ and $i\in I$, an integer $z_{I,i}$ representing the number of nodes in $V_i$ that (in the coloring of G) are colored with one of the $z_I$ colors associated to I. Clearly, the value of $z_{I,i}$ is at most $z_I$ if $V_i$ induces a clique in G, but can be larger if $V_i$ induces an independent set. An equitable k-coloring of G satisfies the following conditions:

• 1. $\sum _{I\in \mathcal{I}} z_I=k$.

• 2. For each $i\in V(H)$ it holds that the sum of the values $z_{I,i}$, over all $I\in \mathcal{I}$ such that $i\in I$, is exactly $|V_i|$.

• 3. For each $I\in \mathcal{I}$ it holds that the sum over all $i\in V(H)$ of the number of nodes of $V_i$ that are colored in G with one of the $z_I$ colors associated to I is $r\cdot z_I$.

The above conditions can be expressed by the following linear program on the variables $z_I$ for each $I\in \mathcal{I}$ and $z_{I,i}$ for each $I\in \mathcal{I}$ and for each $i\in I$.

• 1. $\sum _{I\in \mathcal{I}} z_I=k$;

• 2. $\sum _{I\, :\, i\in I} z_{I,i}=|V_i|$, for each $i\in V(H)$;

• 3. $\sum _{i\in I} z_{I,i} -r\cdot z_I=0$, for each $I\in \mathcal{I}$;

• 4. $z_{I} - z_{I,i}\ge 0$ for each $I\in \mathcal{I}$ and $i\in I$ such that $V_i$ is a clique;

• 5. $z_{I,i} \ge 0$ for each $I\in \mathcal{I}$ and $i\in V(H)$.

From the above reasoning, it is clear that if the graph G admits an equitable k-coloring, then there exists an assignation of values to the variables $z_I$ and $z_{I,i}$, for each $I\in \mathcal{I}$ and $i\in I$, that satisfies the above system.

We show now that from any assignation of values to the variables $z_I$ and $z_{I,i}$ that satisfies the above system, we can obtain an equitable k-coloring of G.

• For each independent set $I\in \mathcal{I}$, such that $z_I>0$, repeat the following procedure:

  • Select a set of $z_I$ new colors, say $c^I_1, \dots , c^I_{z_I}$ (to be used only for nodes in I);

    We notice that (by 3.) the total number of nodes to be colored is $r\cdot z_I$;

  • Consider the list of colors $c^I_1,c^I_2, \dots , c^I_{z_I}, c^I_1,c^I_2, \dots , c^I_{z_I},\ldots , c^I_1,c^I_2, \dots , c^I_{z_I}$ (obtained by repeating the sequence $c^I_1,\dots , c^I_{z_I}$ r times). Assign the colors starting from the beginning of the list as follows: For each $i\in V(H)$, select $z_{I,i}$ uncolored nodes in $V_i$ (it can be done by 2.) and assign to them the next unassigned $z_{I,i}$ colors in the list.

In this way each color is used exactly r times. Moreover, since each independent set uses a separate set of colors, the total number of colors is $\sum _{I\in \mathcal{I}} z_I=k$ (crf. 1.). Furthermore, in each $V_i$ that induces a clique in G, we color $z_{I,i}\le z_{I}$ nodes (this holds by 4.). Such nodes get colors which are consecutive in the list, hence they are different. Summarizing, the desired equitable k-coloring of G has been obtained.

Finally, we evaluate the time to solve the above system. We use the well-known result that Integer Linear Programming is FPT parameterized by the number of variables.

• $\ell$-Variable Integer Linear Programming Feasibility

• Instance: A matrix $A \in Z^{m\times \ell }$ and a vector $b \in Z^m$.

• Question: Is there a vector $x \in Z^\ell$ such that $Ax \ge b$?

Proposition 1

[32] $\ell$-Variable Integer Linear Programming Feasibility can be solved in time $O(\ell ^{2.5t+o(\ell )} \cdot L)$ where L is the number of bits in the input.

Since $|V(H)|={nd}(G)$, our system uses at most $O({nd}(G) 2^{{nd}(G)})$ variables: $z_I$ for $I\in \mathcal{I}$ and $z_{I,i}$ for $I\in \mathcal{I}$ and $i\in I$. We have $O({nd}(G) 2^{{nd}(G)})$ constraints and the coefficients are upper bounded by $r=|V|/k$. Therefore, Theorem 3 holds.

3 Algorithms

In this section, we deal with FPT algorithms with respect to iterated type partition. In order to solve a problem P on an input graph G, the general algorithm scheme is:

• 1) Iterate by generating the whole type graph sequence of G.

• 2) On each graph $G'$ in the type graph sequence, a generalized version $P'$ of the original problem is defined (with $P'$ in $G'$ being equivalent to P in G).

• 3) Optimally solve $P'$ on the base graph and reconstruct the solution on the reverse type graph sequence (hence solving P in G).

If the construction of the solution for $P'$ (at step 2), can be done in polynomial time and the time to solve $P'$ on the base graph is f, then the whole algorithm needs ${O({f}+poly(n))}$ time.

Using the scheme above we are able to prove that the Dominating Set and Vertex Cover problems can be solved in time $O({2^t}+poly(n))$, while the Vertex Coloring problem is solvable in time $O({t^{2.5t+o(t)}\log n}+poly(n))$, where n and t are the size and the iterated type partition of the input graph, respectively. In the following, we present the algorithm for the Dominating Set problem. Due to space constraints the proofs for the remaining problems are given in the extended version of this paper [6].

In the following, we assume that the input graph is connected and it is not a clique. Indeed, the domination problem in disconnected graphs can be separately solved on each connected component. Moreover, in the case of a complete graph, the solution trivially consists of one vertex. Notice that the assumption of G being a non complete connected graph, implies that the base graph of G is connected and ${ itp}(G)\ge 2.$

In order to present our FPT algorithm, we consider the following generalized dominating set problem.

Definition 2

Given a graph $G=(V,E)$ (connected and not complete) and a set of nodes $Q \subseteq V$, a semi-total Dominating Set of G with respect to Q, called Q-stds of G, is a set $D\subseteq V$ such that every node in Q is adjacent to a node in D, and every other node is either a node in D or is adjacent to a node in D. The set D is called an optimal Q-stds of G, if its size is minimum among all the Q-stds of G.

Clearly, when $Q=V,$ the semi-total Dominating Set problem is the Total Domination problem [4]; if $Q=\emptyset$ it becomes the Dominating Set problem.

Lemma 3

Let $G=(V,E)$ be a graph and let $\mathcal{V}=\{V_1,\cdots , V_t\}$ be the type partition of G. Let $Q \subseteq V$. There exists an optimal Q-stds D of G such that

$$\begin{aligned} |V_x \cap D| \le 1 \qquad \text{ for } \text{ each } x\in [t]\text{. } \end{aligned}$$

(6)

Proof

Let D be an optimal Q-stds of G. Assume there exists $x\in [t]$ such that $|V_x \cap D| \ge 2$. We distinguish two cases according to $V_x$ being a clique or an independent set.

Let $V_x$ be a clique. Let u and v be two nodes in $V_x \cap D$. Let $u \not \in Q$. Since u is a neighbor of v and since u and v share the same neighborhood, we have that the set $D'=D-\{v\}$ is a Q-stds of G. Furthermore, $|D'| < |D|$ and this is not possible since D is optimal. Assume now that $u \in Q$. If there exists a neighbor w of u with $w \in V_y \cap D$, for some $y\ne x$, then as above $D'=D-\{v\}$ is a Q-stds of G and $|D'| < |D|$. If, otherwise, node u has no neighbor in D except for those in $V_x$, then we can choose any neighbor w of u with $w \in V_y \cap D$, for some $y\ne x$, and $D'=D-\{v\} \cup \{w\}$ is a Q-stds of G and $|D'| = |D|$.

Let $V_x$ be an independent set. Let u be any node in $V_x \cap D$. If there exists a neighbor w of u with $w \in V_y \cap D$, for some $y\ne x$, then the set $D'$ obtained from D removing all the nodes in $V_x$ except for u is again a Q-stds since the neighbors of nodes in $V_x$ are dominated by u and all the nodes in $V_x$ are dominated by $w\in V_y$. Furthermore, $|D'| < |D|$. Otherwise, we have that $V_x \subset D$ and for each neighbor w of u it holds $w \in V_y$, for $y\ne x$, and $w \not \in D$. Hence, the set $D'$ obtained from D removing all the nodes in $V_x$ except for u and adding to it a node $w \in V_y$, where y is such that $V_y\cap D=\emptyset$, is a Q-stds of G. Furthermore, $|D'| \le |D|$.

Repeating the above argument for each $x\in [t]$ such that $|V_x \cap D| \ge 2$, we obtain an optimal solution satisfying (6).    $\square$

The FPT algorithm Dom recursively constructs the graphs in the type graph sequence of G, until the base graph is obtained. It is initially called with Dom($G,\emptyset$). At each recursive step, the algorithm Dom(H, Q), on a graph H and a set $Q\subseteq V(H)$ of nodes that need to have a neighbor in the solution set, checks if H is a base graph or not. In case H is a base graph, then the algorithm searches by brute force the Q-stds of H and returns it. If H is not a base graph then the algorithm first constructs the type graph $H'$ and selects nodes in $V(H')$ to assemble a set $Q'$ of nodes that need to have a neighbor in the solution set, then it uses the set $D'$ of nodes in $V(H')$ returned by Dom($H',Q'$) to construct the output set $D \subseteq V(H)$. The nodes of the returned set D are chosen by selecting exactly one node from each metavertex $V_x$ having $x \in D'$. Figure 5 gives an example of the execution of Algorithm 1 on the graph G in Fig. 1.

Fig. 5.

The recursive execution of the Algorithm 1 on the graph G depicted in Fig. 1: ((a) and (b)), since the input graph is not a base graph, their type partition as well as the set $Q'$ are computed and passed to the next recursive level; (c), H is a base graph and then an optimal solution is computed exploiting a brute force approach; ((d) and (e)), an optimal solution $D=\{v_1,v_{12}\}$ is reconstructed using the solution $D'$ obtained on the reverse type graph sequence.

Lemma 4

Let H be not a base graph and let $Q \subseteq V(H)$. Let $V_1,\cdots , V_t$ be the type partition of H and let $H'$ be its type graph. If $Q'=\{ x \in V(H') \ | \ V_x \cap Q\ne \emptyset \text{ or } V_x \text{ is } \text{ an } \text{ independent } \text{ set }\}$ and $D'$ is an optimal $Q'$-stds of $H'$ then the set D returned by Dom(H, Q) is an optimal Q-stds of H.

Proof

We first prove that the set D returned by Dom(H, Q) is a Q-stds of H, then we prove its optimality. We distinguish two cases according to that a node $v \in V(H)$ is a node in Q or not. W.l.o.g. assume that $v \in V_x$, for some $x \in [t]$.

• If $v \in Q$ then $V_x \cap Q\ne \emptyset$ and by the definition of $Q'$ we have $x\in Q'$. Hence, since $D'$ is a $Q'$-stds of $H'$, there exists $y \in D'$ that is a neighbor of x in $H'$. By Algorithm 1 (see line 8) there exists a node $u_y \in V_y\cap D$. Considering that each node in $V_y$ is a neighbor of each node in $V_x$ (since $(x,y) \in E(H')$), we have that v is dominated by $u\in D$.

• Let $v \in V - Q$. We know that $D'$ is a $Q'$-stds of $H'$. Hence, if either $x \in Q'$ or $x \not \in Q' \cup D'$ we can prove, as in the previous case, that there exists $u \in D$ that dominates v. Assume now that $x \not \in Q'$ and $x \in D'$ (i.e., x can be not dominated in $H'$). By the definition of $Q'$ we have that $V_x \cap Q=\emptyset$ and $V_x$ is a clique. Hence, since by Algorithm 1 (see line 8) there exists a node $u_x \in V_x \cap D$, we have that v is a neighbor of $u_x \in D$ in the clique $V_x$.

Now, we prove that D is an optimal Q-stds of H whenever $D'$ is an optimal $Q'$-stds of $H'$. By contradiction, assume that D is not optimal and let ${\tilde{D}}$ be an optimal Q-stds of H. By Lemma 3 we can assume that, for each $x \in [t]$, at most one node in $V_x$ is a node in ${\tilde{D}}$. Let ${\tilde{D}}' = \{x \ | \ V_x \cap {\tilde{D}}\ne \emptyset \}$. We claim that ${\tilde{D}}'$ is a $Q'$-stds of $H'$. Finally, by Lemma 3 and the construction of ${\tilde{D}}'$, it is possible to prove that $|{\tilde{D}}'| < |D'|$ thus obtaining a contradiction since $D'$ is optimal.    $\square$

Theorem 4

Dom $(G,\emptyset )$ returns a minimum dominating set in time $O({2^{{ itp}(G)}}+poly(n))$.

Proof

Let ${H^{(0)}}=G, {H^{(1)}}, \cdots , {H^{(d)}}$ be the type graph sequence of G. When Dom $(G,\emptyset )$ is called, Algorithm 1 proceeds recursively, and at the i-th recursive step, for $i=0,\cdots , d$, the algorithm is called with input graph ${H^{(i)}}$ and input node set $Q_i \subseteq V({H^{(i)}})$, where $Q_i$ is constructed at line 3 of the previous step $i-1$, for $i=1,\cdots ,d$, and it is the empty set when $i=0$, i.e., $Q_0=\emptyset$. At step d, the optimal $Q_d$-stds of the base graph ${H^{(d)}}$ is established by brute force.

By Lemma 4, the set returned at the end of each recursive step i, for $i=d-1,\cdots , 0$, is the optimal $Q_i$-stds of ${H^{(i)}}$. Hence, at the end (when $i=0$) the returned set is the optimal $\emptyset$-stds of ${H^{(0)}}$, that by the definition is the minimum dominating set of G.

Considering that $|V({H^{(d)}})|={ itp}(G)$, the brute search of the solution set at step d requires time $O(2^{{ itp}(G)})$. Furthermore, since the construction of the type partition of ${H^{(i)}}$ and of its type graph can be done in polynomial time, and that both the construction of $Q_i$ and the selection of the nodes in the solution set are easily obtained in linear time, we have $O({2^{{ itp}(G)}}+poly(n))$ time.    $\square$

4 Conclusion

We introduced a novel parameter, named iterated type partition, and studied some of its properties. We show that the Equitable Coloring problem is W[1]-hard when parametrized by the iterated type partition. This result extends also to the modular-width parameter. We also prove that the hardness drops for the neighborhood diversity parameter, when the problem becomes FPT. Moreover, we presented a general strategy that enables to find FPT algorithms for several problems when parameterized by iterated type partition. The Algorithm for the Dominating Set problems has been presented, while algorithms for Vertex coloring and Vertex Cover problems appear in the extended version of the work.

It would be interesting to investigate whether the proposed strategy can be applied on other problems and if some meta-algorithm an be devised. Moreover, it would be interesting to analyze the Edge Dominating Set problem, which has been shown to be FPT with the neighborhood diversity parameter [31].