Fast Community Detection with Graph Sparsification

Abstract

A popular model for detecting community structure in large graphs is the Stochastic Block Model (SBM). The exact parameters to recover the community structure of a SBM has been well studied, and many methods have been proposed to recover a nodes’ community membership. A popular approach is to use spectral methods where the Graph Laplacian L of the given graph is created, and the Fiedler vector of the graph is found. This vector is then used to cluster nodes in the same community. While a robust method, it can be expensive to compute the Fiedler vector exactly. In this paper we examine the types of errors that can be tolerated using spectral methods while still recovering the communities. The two sources of error considered are: (i) dropping edges using different sparsification strategies; and (ii) inaccurately computing the eigenvectors. In this way, spectral clustering algorithms can be tuned to be far more efficient at detecting community structure for these community models.

1 Background and Motivation

Stochastic Block Models. Detecting communities through clustering is an important problem in a wide variety of network applications characterized by graphs [1, 3]. However, it can be difficult to study the accuracy of clustering on arbitrary graphs. To aid network analysis, generative models are frequently introduced. One popular model is the Stochastic Block Model (SBM) [2]. In this model a number of nodes n with community memberships are given, and the connectivity of vertices p and q within (and between) the communities are also specified. For a given graph with parameters G(n, p, q), we define $a=pn$, $b=qn$. It has been shown that the community structure can only be recovered when $(a-b)^2>2(a+b)$ [14]. While models of more than two communities are sometimes studied, in this paper we restrict our attention to the case where the number of communities is fixed at two. There are two reasons for this. The first is that there is more theory available to work with. The second is that in practice it is often the custom when seeking communities in a graph to recursively cluster the nodes into two groups and then continue recursively, since this approach lends itself to high performance computing [4]. A two community model is therefore relevant to real-world approaches and worthy of study. Our goal in this paper is to discuss the question of how we can recover the communities of a SBM faster, by applying graph sparsification and inaccurate eigenvector computation, without harming the accuracy of our recovery methods. Additionally, we show how we can leverage recent research on nearly linear-time solvers to capitalize on the sparser graphs we obtain.

Spectral Sparsification. A popular approach to clustering is to find the Fiedler vector of the graph Laplacian L [4]. This is faster the sparser L is. Given a matrix L, we say that matrix $\tilde{L}$ is similar iff for all x,

$$\begin{aligned} \begin{aligned}&x'Lx(1 - \epsilon ) \le x'\tilde{L}x \le x'Lx(1 + \epsilon ). \end{aligned} \end{aligned}$$

(1)

Matrices that are similar to each other by the criteria of Eq. (1) share similar eigenvectors and eigenvalues [5]. While fast methods exist for computing such similar matrices through sparsification [5], it is unclear how errors in eigenvector approximation translate into errors in the communities recovered. Answering this question is a key contribution of this paper.

Spectrum of SBM Matrices. Since we will make extensive use of the spectrum of the different matrix representations of a Stochastic Block Model (SBM), we review the known results here, and provide some new ones.

First we consider the spectrum of a two community adjacency matrix. Define $a=np$, $b=nq$, where p is the probability of a connection between nodes inside the community, and q is the probability of a connection between nodes in different communities. Then the average instance of a SBM model with these parameters can be represented in the form,

$$\begin{aligned} \begin{aligned} <\mathbf {A}>\,=\,\frac{1}{2} (a+b) \mathbf {1}\mathbf {1}^T +\frac{1}{2} ( a - b) \mathbf {u}\mathbf {u}^T \end{aligned} \end{aligned}$$

(2)

where $\mathbf {1} = (1,1,1,\dots ,1) / \sqrt{n}$ and $\mathbf {u} = (1,1\dots ,-1,-1,\dots ) / \sqrt{n}$. Any particular instance $\mathbf {A}$ of a SBM drawn from this distribution of matrices can be represented as $\mathbf {A}\,=\,<\mathbf {A}>\,+\,\mathbf {X}$, where $\mathbf {X}$ is a random Wigner matrix. Because the eigenvalues of $\mathbf {X}$ follow the famous semicircle law, the spectrum of A also follows such a distribution [14], with the exception of the two largest eigenvalues. The distribution of the bulk of the eigenvalues follows the equation,

$$\begin{aligned} \begin{aligned} \rho (z) = \frac{n}{\pi } \frac{\sqrt{2(a+b)-z^2}}{a+b}. \end{aligned} \end{aligned}$$

(3)

The radius of the bulk of the spectrum of $\mathbf {A}$ is given as below, with the center of the semi-circle being at 0.

$$\begin{aligned} \begin{aligned} r_{\mathbf {A}}=\sqrt{(}2(a+b)) \end{aligned} \end{aligned}$$

(4)

Finally we also have the two largest eigenvalues of $\mathbf {A}$ given as below.

$$\begin{aligned} \begin{aligned}&\lambda _n=\frac{1}{2} ( a + b) + 1, \lambda _{n-1} = \frac{1}{2}(a-b) + \frac{a+b}{a-b}\\ \end{aligned} \end{aligned}$$

(5)

We note that the eigenvectors of $\mathbf {A}$ are randomly distributed vectors on the unit sphere except for the top two eigenvectors. The top two eigenvectors are perturbed versions of the vectors of $<\mathbf {A}>$ [14].

We will also be interested in the spectrum and the eigenvectors of the scaled Laplacian $\mathcal {L}$ of instances of our SBM. The bulk of the spectrum of $\mathcal {L}$ is also known to follow a semi-circle distribution [11]. If we denote the average degree of the SBM as $\bar{d}$, then the distribution of the bulk of the eigenvalues follows the equation,

$$\begin{aligned} \begin{aligned} \rho (z) = \frac{2n}{\pi } \frac{\sqrt{\frac{2(a+b)}{\bar{d}^2}-z^2}}{\frac{2(a+b)}{\bar{d}^2}}. \end{aligned} \end{aligned}$$

(6)

The radius of the bulk of the spectrum are as below, with the center of the semi-circle being at 1.

$$\begin{aligned} \begin{aligned} r_{\mathcal {L}}=\frac{\sqrt{(}2(a+b))}{\bar{d}} \end{aligned} \end{aligned}$$

(7)

Avrachenkov et. al [11] states that the other non-trivial eigenvalue of $\mathcal {L}$ remains to be characterized, so we briefly show that the eigenvalues outside the semi-circle are as below and bound their deviation from this mean, since our algorithms will make use of this information.

$$\begin{aligned} \begin{aligned}&\lambda _1 = 0, \lambda _{2} = 1 - \frac{\frac{1}{2}(a-b) + \frac{a+b}{a-b}}{\bar{d}}\\ \end{aligned} \end{aligned}$$

(8)

We have $\lambda _1=0$, since $\mathcal {L}$ is a Laplacian. If $\mathbf {A}$ is a regular graph, then the value for $\lambda _{2}$ is directly computable from the eigenvalues of $\mathbf {A}$, as above. Since SMBs are close to regular, with each node having the same average degree of $a+b$, we need to show that the deviation from the mean is small and with high probability will not change the result. From Lutzeyer and Walden [16] we have that the error of applying this linear transform of the eigenvalues of A, in order to obtain the eigenvalues of $\mathcal {L}$, is $3\frac{d_{max} - d_{min}}{d_{max}+d_{min}}$. We can then use the Chernoff concentration bounds to show that this error goes to zero with high probability.

The elements of the rows of $\mathbf {A}$ are drawn from a binomial distribution, with n/2 of them with probability p, and n/2 of them with probability q. For each diagonal element of $\mathcal {L}$, we then have,

$$\begin{aligned} \begin{aligned}&\text {Pr}( |\mathcal {L}_{ii} - \bar{d} | > \sqrt{n} \sqrt{\log (n^2)} )< 2 e^{-log(n^2)}=\frac{2}{n^2}. \\ \end{aligned} \end{aligned}$$

(9)

Since we have n diagonal elements, the probability that none exceed this bound can be computed as,

$$\begin{aligned} \begin{aligned}&\lim _{n \rightarrow \infty } (1-\frac{1}{n^2})^n = 1 \end{aligned} \end{aligned}$$

(10)

The error in our approximation for $\lambda _{2}$ is then

$$\begin{aligned} \begin{aligned} 3\frac{d_{max} - d_{min}}{d_{max}+d_{min}}&= 3\frac{ \bar{d}+\sqrt{n} \sqrt{\log (n^2)} - (\bar{d}-\sqrt{n} \sqrt{\log (n^2)})}{\bar{d}+\sqrt{n} \sqrt{\log (n^2)} +\bar{d}-\sqrt{n} \sqrt{\log (n^2)} } \\&=3\frac{ 2\sqrt{n} \sqrt{\log (n^2)} }{2\bar{d}}= 3\frac{2 \sqrt{n} \sqrt{\log (n^2)} }{ n(p+q)} \\ \end{aligned} \end{aligned}$$

(11)

Taking the limit as n increases we then have,

$$\begin{aligned} \begin{aligned}&\lim _{n \rightarrow \infty } 3\frac{ 2 \sqrt{n} \sqrt{\log (n^2)} }{ n(p+q)} = 0. \\ \end{aligned} \end{aligned}$$

(12)

Finally, we state two properties of $\mathcal {L}$ that we will make use of later. We can write $\mathcal {L}=D^{-1/2}\mathbf {A}D^{-1/2}=D^{-1/2}\mathbf {X}D^{-1/2}+D^{-1/2}<\mathbf {A}>D^{-1/2}$. Recall that the eigenvectors of $\mathbf {X}$ are randomly distributed on the unit sphere. Then for any $e_i,e_j \in \mathbf {I}$

$$\begin{aligned} \begin{aligned}&E[e_iD^{-1/2}\mathbf {X}D^{-1/2}e_i ]= E[e_iD^{-1/2}\sum ^n_{j=1} \lambda _j x_jx_j'D^{-1/2}e_i] \\&E[e_iD^{-1/2}\sum ^n_{j=1} \lambda _j x_jx_j'D^{-1/2}e_i] = E[\sum _{j=1}^n \frac{1}{d_i}\lambda _i x_i x_i'= \sum _{j=1}^n \frac{1}{d_i} \lambda _i \frac{1}{n}]\\ \end{aligned} \end{aligned}$$

(13)

Alternatively, we have

$$\begin{aligned} \begin{aligned}&E[e_iD^{-1/2}\mathbf {X}D^{-1/2}e_j ]= E[e_iD^{-1/2}\sum ^n_{j=1} \lambda _j x_jx_j'D^{-1/2}e_j] \\&E[e_iD^{-1/2}\sum ^n_{j=1} \lambda _j x_jx_j'D^{-1/2}e_j] = E[\sum _{j=1}^n \frac{1}{d_i}\lambda _i x_i x_j'] = 0 \end{aligned} \end{aligned}$$

(14)

Overall Approach. We now outline our overall problem. We would like to accelerate spectral algorithms for Stochastic Block Models (SBMs) while still recovering the communities accurately. Our main approach is to analyze the impact of two different types of error on SBM algorithms. The first is ‘edge dropping’. We investigate two strategies for dropping edges which allow us to recover the communities despite, in some cases, having significantly fewer edges than the original problem. While the idea of sparsifying graphs in order to more efficiently recover communities is not new, our contribution is to determine the level of sparsification that can take place while still recovering communities.

Our second approach is to stop convergence of the eigensolver early. We analyze ‘power iteration’, and show that for many SBM instances the solver does not need to be run to convergence. We choose power iteration both because the analysis is simple, and because in conjunction with nearly linear-time solvers, and the dropping strategy previously mentioned, we can design extremely efficient algorithms. This is because power iteration based on these solvers are O(m) complexity. In some cases we can reduce the number of edges by orders of magnitude, making these solvers very attractive.

The foundation of both these methods is a careful use of the model parameters and the known results for the spectra of SBM models.

2 Methods and Technical Solutions

Sampling with Effective Resistance. The main idea is that for a given Stochastic Block Model (SBM) we know when we can recover the communities based on the parameters a, b of the model. While it is sometimes assumed that these parameters are known, Mossel et al. [7] gives Eq. (15) for recovering the parameters of an unknown SBM, where |E| is the number of edges in the graph, $k_n=\lfloor log^{1/4}(n) \rfloor$, and $X_{k_n}$ is the number of cycles of length $k_n$ in the graph. While $X_{k_n}$ is difficult to compute, Mossel et al. shows that this can be well approximated by counting the number of non-backtracking walks in the graph that can be made in O(n) time. They then obtain a linear-time algorithm for estimating a, b by showing that $a \approx \hat{d}_{n} + \hat{f}_n$, and $b \approx \hat{d}_{n} - \hat{f}_n$ where,

$$\begin{aligned} \begin{aligned}&\hat{d}_{n}= \frac{2|E|}{n}\\&\hat{f}_n = (2 k_n X_{k_n} - \hat{d}^{k_{n}})^{1/k_n}. \end{aligned} \end{aligned}$$

(15)

Once we obtain an estimate for a, b then we can estimate how much we should sparsify the graph to ensure that $(a-b)^2>2(a+b)$, while still dropping edges to obtain a much sparser matrix, for which we can obtain the Fiedler Vector much faster. We can also estimate the percentage of the nodes we will recover using the equation $\alpha ^2 =\frac{(a-b)^2-2(a-b)}{(a-b)^2}, \frac{1}{2}[1\,+\,$erf$(\sqrt{\alpha ^2/2(1-\alpha ^2)})$ [14] .

In order to understand the percentage of the edges of the graph that we should sample we need to consider what the odds are they we will sample an edge connecting two nodes inside a community, against the odds that they will sample an inter-community edge. Ideally we would only sample edges inside the communities, since this would make the communities trivial to detect. Unfortunately, it has been shown by Luxburg et al. [9, 10] that for SBM as $n \rightarrow \infty$, the effective resistance of a given edge (i, j) in the graph tends toward $\frac{1}{d_i} + \frac{1}{d_j}$. Since the degrees of the nodes in this model are O(n), the variation between effective resistances will be small, and will in any case not reflect the community structure of the graph. At this point our spectral sparsifier will be selecting edges essentially at random. While Luxburg et al. state that theoretical results suggest that the effective resistances could degenerate only for very large graphs, their experimental results show that this behaviour arises even for small communities of 1, 000 vertices.

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}(E)=2q(\frac{n}{2})^2+2p(\frac{n}{2})^2 \end{aligned}$$

(16)

$$\begin{aligned} \begin{aligned}&p_{intra} = \frac{(2p(\frac{n}{2})^2)}{{{\,\mathrm{\mathbb {E}}\,}}(E)}&q_{inter}= \frac{(2q(\frac{n}{2})^2)}{{{\,\mathrm{\mathbb {E}}\,}}(E)} \end{aligned} \end{aligned}$$

(17)

$$\begin{aligned} \begin{aligned}&\hat{p} = \frac{S p_{intra}}{2(\frac{n}{2})^{2}}&\hat{q} = \frac{S p_{inter}}{2(\frac{n}{2})^{2}} \end{aligned} \end{aligned}$$

(18)

While in some sense this is a drawback, since this result is telling us we may as well sample randomly, our algorithm can still function, and we can save the cost of computing the effective resistances. For $(a-b)^2>2(a+b)$ to hold true, there must be significantly more intra-community edges than inter-community ones. If we are sampling randomly with spectral sparsification, we should still sample more of the desired edge type, since more of this type exist and we are sampling each edge with roughly the same probability. If we have probabilities p, q, and number of nodes n, then the expected value for the number of edges is shown in Eq. (16). We can then compute the probability of sampling an intra-community or inter-community edge as in Eq. (17). If we take S samples, Eq. (18) shows the estimated $\hat{p}, \hat{q}$ for our sparsified graph. We then have $\hat{a} = \hat{p}n$, $\hat{b}=\hat{q}n$, which can be used to decide if the communities can be recovered.

Correcting Effective Resistance. While Luxburg et al. [10] show that as $n \rightarrow \infty$ the effective resistance $\mathbf {eff}_{a,b}$ for a SBM degenerates to $(1/d_i+1/d_j)$ for two nodes i, j, there are various methods known for correcting this. One of these is to multiply by the sum of the degrees. While this does not correct the issue in and of itself, since the effective resistance between every pair of nodes converges to two, the variance around two may be meaningful. Using these “scaled” effective resistances captures the community structure of a SBM, and sparsifying by these resistances can cause us to find the community structure of an SBM very quickly. These scaled effective resistances can be obtained by taking the scaled Laplacian $\mathcal {L}$ of our SBM, and applying the same algorithm that is used to estimate the effective resistance of L.

Given the constants a, b, we can calculate the average difference in scaled effective resistance between edges both inside the communities and outside. This is useful because it allows us to predict on average how much we should sample to ensure $(a-b)^2>2(a+b)$, given the increased chance of sampling inter-community edges.

Recall that $\mathbf {eff}_{a,b}=e_a\mathcal {L}^{\dagger }e_a+e_b\mathcal {L}^{\dagger }e_b-2e_a\mathcal {L}e_b$. Using our knowledge of the spectrum of $\mathcal {L}$, we can compute the average values of these terms.

$$\begin{aligned} \begin{aligned}&E[\mathcal {L}^{\dagger }_{aa}]=E[\mathcal {L}^{\dagger }_{bb}]= E[e_aD^{-1/2}\mathbf {X^{-1}}D^{-1/2}e_a]+E[e_a D^{-1/2}\mathbf {A^{-1}}D^{-1/2} e_a] \\&E[e_aD^{-1/2}\mathbf {X^{-1}}D^{-1/2}e_a]= \frac{1}{n} \sum \lambda \text { by Eq.\,(13) } \\&E[\mathcal {L}^{\dagger }_{aa}]=\frac{1}{n} \int ^{1+r_{\mathcal {L}}}_{1-r_{\mathcal {L}}} \frac{1}{z} \rho (z) dz = 1\\&E[\mathcal {L}^{\dagger }_{ab}]= E[e_aD^{1/2}X^{-1}D^{1/2}e_b] + E[e_aD^{1/2}A^{-1}D^{1/2}e_b] \\&E[e_aD^{1/2}X^{-1}D^{1/2}e_b] = 0 \text { by Eq.\,(14) so} \\&E[\mathcal {L}^{\dagger }_{ab}] = E[e_aD^{1/2}A^{-1}D^{1/2}e_b] = e_a \frac{1}{\lambda _2} \mathbf{u} {} \mathbf{u} ^Te_b\\&e_a \frac{1}{\lambda _2} \mathbf{u} {} \mathbf{u} ^Te_b = \frac{1}{\lambda _2} (-1)^x , x=0 \text { if }a,b \in G\text { and } x =1 \text { if }a,b \not \in G. \\ \end{aligned} \end{aligned}$$

(19)

We see that the effective resistance inside the group on average is $e_a\mathcal {L}^{\dagger }e_a+e_b\mathcal {L}^{\dagger }e_b-2e_a\mathcal {L}e_b=1+1-2\frac{1}{\lambda _2}$ and $e_a\mathcal {L}^{\dagger }e_a+e_b\mathcal {L}^{\dagger }e_b-2e_a\mathcal {L}e_b=1+1+2\frac{1}{\lambda _2}$ otherwise. This allows us to amend our estimates for $\hat{a}$ and $\hat{b}$. If we let $r'$ be the ratio between the effective resistance of the two links, then Eq. (21) gives the scaled $\hat{p'}$, $\hat{q'}$.

$$\begin{aligned} \begin{aligned}&p'_{intra} = \frac{p_{intra}}{p_{intra}+r'q_{intra}} \\&q'_{inter}= 1-p'_{intra}; \end{aligned} \end{aligned}$$

(20)

$$\begin{aligned} \begin{aligned}&\hat{p'} = \frac{S p'_{intra}}{2(\frac{n}{2})^{2}}&\hat{q'} = \frac{S p'_{inter}}{2(\frac{n}{2})^{2}} \end{aligned} \end{aligned}$$

(21)

We note that our method above does have a potential drawback for very small graphs. This is because we need to sample $\varTheta$(n log(n)) edges to avoid the graph being disconnected [12]. As graphs become large this should be a non-issue because we have $\lim _{n \rightarrow \infty } \frac{(pn-qn)^2-2(pn+qn)}{n log n} = \infty$, which indicates that our sampling criteria will require more edges than needed to ensure connectivity.

Computing the Eigenvector Using Inverse Power Iteration. One of the challenges of spectral methods is computing the eigenvectors needed for clustering, since this can be expensive. Given a nearly linear-time solver, one can compute the eigenvectors of a scaled graph Lapalcian in nearly time in the order of the number of elements of $\mathcal {L}$ [6], by using Inverse Power Iteration. This is attractive given our edge dropping strategy, where we may reduce the number of edges by several orders of magnitude for favourable graphs.

An additional feature is that it is possible to calculate a stopping criteria for the eigensolver that will allow us to recover the communities, even though the eigenvector has not fully converged. This is a desirable property, since full convergence can be slow. While the bound for our stopping criteria is not tight, it nevertheless is significantly faster than would otherwise be the case for full convergence.

Recall that for the power iteration we have an initial state $c_1\lambda _1 v_1+ \dots c_n \lambda _nv_n$. On average the $c_i$ terms will be of approximately the same size. We are attempting to compute the eigenvector $\mathbf {u} = (1,1\dots ,-1,-1,\dots ) / \sqrt{n}$. After each iteration of the power method we have a resultant vector which consists of the desired eigenvector $\mathbf {u}$, and some sum of the other eigenvectors. We need to compute the likely contribution from the other eigenvectors. Once these contributions are smaller than $O(\frac{1}{\sqrt{n}})$ with high probability, we can stop the iteration, because the signal from the desired eigenvector will dominate the calculation, and allow for the correct community assignment.

We need to compute the average contribution from the remaining eigenvectors at each iteration. We begin by computing the average size for each component of the other eigenvectors. Assuming all the $c_i$ are equal, we have $\lambda _2(\mathbf {u} + \sum \frac{\lambda _i}{ \lambda _2}^{k} \mathbf {v} )$. The eigenvectors $\mathbf {v}$ are randomly distributed around the unit sphere, as in Wigner matrices. We know from O’Rourke and Wang [17], that the elements of these eigenvectors are normally distributed variables, $N(0,\frac{1}{n})$.

Multiplying $N(0,\frac{1}{n})$ by $\frac{\lambda _i}{ \lambda _2}^{k}$ we have $N(0,(\frac{\lambda _n}{\lambda _2})^{2k} \frac{1}{n})$ after k iterations. We then have that each component of the sum of the eigenvectors $\mathbf {v}$ are normal variables $N(0,\varSigma (\frac{\lambda _n}{\lambda _2})^{2k} \frac{1}{n})$.

We can now use Chebyshev’s inequality to compute the probability that a component of the sum of the eigenvectors $\mathbf {v}$ is greater than $\frac{1}{\sqrt{n}}$, the size of the components of the dominant eigenvector $\mathbf {u}$ as follows,

$$\begin{aligned} \begin{aligned}&Pr(|X-E[X]| \ge a) \le \frac{Var[X]}{a^2} \\&Pr(|X| \ge \frac{1}{\sqrt{n}}) \le \frac{Var[X]}{(\frac{1}{\sqrt{n}})^2} \\&Pr(|X| \ge \frac{1}{\sqrt{n}}) \le \frac{\varSigma \frac{\lambda _n}{\lambda _2}^{2k} \frac{1}{n}}{(\frac{1}{\sqrt{n}})^2} \\&Pr(|X| \ge \frac{1}{\sqrt{n}}) \le \varSigma (\frac{\lambda _n}{\lambda _2})^{2k}. \\ \end{aligned} \end{aligned}$$

(22)

Using our knowledge of the density of the spectrum of $\mathcal {L}$, we can compute the probability in Eq. (22), for $\mathcal {L}^{\dagger }$ as follows,

$$\begin{aligned} \begin{aligned}&\varSigma (\frac{\lambda _n}{\lambda _2})^{2k} = \int ^{1+r_{\mathcal {L}}}_{1-r_{\mathcal {L}}} (\frac{\frac{1}{z}}{\lambda _2})^{2k}\rho (z) dz. \end{aligned} \end{aligned}$$

(23)

Once we know the probability of a single component of the eigenvector being greater than the $\frac{1}{\sqrt{n}}$, we can use this in a binomial distribution to calculate how many elements we are likely to incorrectly classify. We can, either stop when k is large enough to imply this is close to zero, or when the number is the same order as the error introduced by the perturbation of the main eigenvector from the addition of the random eigenvectors to $\mathbf {<A>}$, as given in [13].

Regularized Spectral Clustering. While spectral clustering is robust for matrices with high average degrees (cf.   Saade et al. [8]), for very sparse matrices that have low degree entries the technique may struggle to recover the communities when the graph approaches the theoretical limits of community detection. This issue is exacerbated by the fact that we are dropping edges, and thus may create such problematic cases. To combat this we use the method of regularized spectral clustering method given in Saade et al. [8]. Given a regularization parameter $\tau$, and the matrix $\mathbf {J}$ with constant entries $\frac{1}{n}$, the authors first define the regularized adjacency matrix $\mathbf {A}_{\tau }$ as,

$$\begin{aligned} \mathbf {A}_{\tau } = \mathbf {A} + \tau \mathbf {J} \end{aligned}$$

(24)

Similarly they define the regularized diagonal as $D_{\tau }$ as,

$$\begin{aligned} \mathbf {D}_{\tau } = \mathbf {D} + \mathbf {I}\tau \end{aligned}$$

(25)

Then the regularized scaled Laplacian is given as,

$$\begin{aligned} \mathcal {L}_{\tau } = \mathbf {D}^{-1/2}_{\tau } \mathbf {A} + \tau \mathbf {J} \mathbf {D}^{-1/2}_{\tau } \end{aligned}$$

(26)

We note that the Fiedler vector of this matrix can be computed using the power method using nearly linear-time sparse solvers. $\mathbf {D}^{-1/2}_{\tau } \mathbf {A} \mathbf {D}^{-1/2}_{\tau }$ is symmetric and diagonally dominate so we can make use of nearly linear-time solvers to compute $(\mathbf {D}^{-1/2}_{\tau } \mathbf {A} \mathbf {D}^{-1/2}_{\tau } )^{-1}x$. Then, since $\mathbf {D}^{-1/2}_{\tau } \tau \mathbf {J} \mathbf {D}^{-1/2}_{\tau }$ is a rank one matrix $\tau \mathbf {D}^{-1/2}_{\tau } j \mathbf {D}^{-1/2}_{\tau }j^T= \mathbf {D}^{-1/2}_{\tau } \tau \mathbf {J} \mathbf {D}^{-1/2}_{\tau }$, we can compute $\mathcal {L}_{\tau }^{-1}$ using the Sherman-Morrison formula which allows us to solve $\mathcal {L}_{\tau }^{-1}$ in terms of $\mathbf {D}^{-1/2}_{\tau } \mathbf {A} \mathbf {D}^{-1/2}_{\tau }$.

$$\begin{aligned} \begin{aligned}&(\mathbf {D}^{-1/2}_{\tau } \mathbf {A} \mathbf {D}^{-1/2}_{\tau })^{-1} = \mathcal {A}^{-1} , \mathbf {S} = \frac{\mathcal {A}^{-1} \mathbf {D}^{-1/2}_{\tau }j \mathbf {D}^{-1/2}_{\tau }j^T \mathcal {A}^{-1}}{1+ \mathbf {D}^{-1/2}_{\tau }j^T\mathcal {A}^{-1} \mathbf {D}^{-1/2}_{\tau }j} \rightarrow \\&\mathcal {L}_{\tau }^{-1} = (\mathbf {D}^{-1/2}_{\tau } \mathbf {A} \mathbf {D}^{-1/2}_{\tau } + \mathbf {D}^{-1/2}_{\tau }j\mathbf {D}^{-1/2}_{\tau }j^T)^{-1} = (\mathbf {D}^{-1/2}_{\tau } \mathbf {A} \mathbf {D}^{-1/2}_{\tau })^{-1} - \mathbf {S} \end{aligned} \end{aligned}$$

(27)

Using Eq. (27) we can then proceed to compute the Fielder vector using power iteration. In order to determine when to stop the power iteration we proceed in the same way as in Computing the Eigenvector Using Inverse Power Iteration by determining the spectrum $\mathcal {L}_{\tau }$. We begin by noting that $\mathcal {L}_{\tau }$ has the same spectrum as $D^{1/2}_{\tau }AD^{1/2}_{\tau }$, except that the top eigenvalue is increased by the rank one update $\mathbf {D}^{-1/2}_{\tau } \tau \mathbf {J} \mathbf {D}^{-1/2}_{\tau }$, as discussed in Ding and Zhou [15]. Since we will project out this eigenvector when performing power iteration, we then only need to consider the density function of $\mathbf {D}^{-1/2}_{\tau } \tau \mathbf {A} \mathbf {D}^{-1/2}_{\tau }$. By the same argument that we used Eq. (10), we can show that as n increases, whp this density function is given by,

$$\begin{aligned} \begin{aligned} \rho (z) = \frac{2n}{\pi } \frac{\sqrt{\frac{2(a+b)}{(\bar{d}+\tau )^2}-z^2}}{\frac{2(a+b)}{(\bar{d}+\tau )^2}} \end{aligned} \end{aligned}$$

(28)

Our Algorithm. We now present our algorithm. We first obtain (or the user provides) an estimate for the Stochastic Block Model (SBM) parameters. We then obtain the scaled effective resistances $\mathbf {eff}$ of the elements of the scaled Laplacian $\mathcal {L}$, which we then use to create a probability density function. We note that we modify the probability density function to sample the edges that have a low effective resistance over those that have a high resistance, since these are the edges that make up our community. This approach is slightly different from the standard algorithm of Spielman and Srivastava [5], which seeks to sample the highest resistance edges.

Next we compute the estimated p, q we will obtain after sparsification, using either Eq. (18) or (21), depending on our sampling strategy, and based on this we decide how much sparsification we can safely apply. After creating our new matrix, we then obtain the relevant eigenvector, depending on whether we are using the Laplacian or the Regularized Laplacian from Eq. (26).

A Comment on Complexity. While the best performance we obtained was by using the scaled effective resistance, depending on what solver is available, this may not always be the most effective strategy. This is because obtaining the scaled effective resistances using the method of Spielman and Srivastava [5], requires us to solve a number of linear systems. If a nearly linear time solver is available, this will take O(m) time, where m is the number of edges before our dropping strategy. This will dominate the cost of the computation, and we will not get significant speed-up from using power iteration, which is of order $O(m')$, where $m'$ again is the number of sparsified edges. In the case of our examples this is clearly sub-optimal, since we can reduce m several orders of magnitude and still recover the communities, even when we are dropping edges randomly. In this case it makes sense not to use the scaled effective resistance. On the other hand, in practice, we may wish to use a different eigensolver, since the code for these may be more mature. In this case, the cost of the eigensolver may dominate, especially since the cost of applicable solvers (such as Lanczos-based solvers), does not entirely depend on m. In this case the use of scaled effective resistance sampling may be more effective.

3 Empirical Evaluation

We now present some experimental results. We first examine the difference between effective-resistance and scaled-effective resistance, and how closely they follow the predicted percentage of recovery. Additionally, we investigate the time needed to compute the eigenvectors of the sparsified versus the unsparsifed matrix, and our convergence criteria for the Fiedler Vector.

Recovery of Communities. We now examine the success of our method in recovering the communities with the given sparsification. In Figs. 1a we see that using the Regularized Laplacian we can quickly recover almost all the nodes correctly, at around the sparsification level, predicted by Eqs. (18) and (21). This also highlights the impact of using the scaled effective resistance for sampling, with the method converging faster, and following the prediction of Eq. (21) more closely. We note that for both sampling methods the percent of edges we preserve is very small, of the order of $10^{-3}$ of the original graph for the Scaled Effective Resistance method.

Fig. 1.

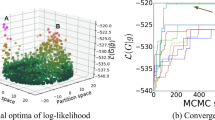
(a) Results of recovering the communities using regularization after sparsification SBM (10000, 0.5, 0.3). Shows the results for Effective resistance and Scaled Effective Resistance as well as predicted recovery. (b) Results of recovering the communities using regularization after sparsification for the political blog example. This example shows the effect of sparsification on a small graph, where there is an interval between the sparsification criteria, and the point at which the graph is connected.

In Fig. 1b, we try the real-world example of Saade et al. [8], where the authors attempt to partition two blogging communities by their political alignment. This is an interesting example because the communities are difficult to recover, requiring the use of regularization techniques, and because the graph structure is not exactly captured by the SBM model. Further this graph is quite small with only 1, 222 nodes, meaning that the graph may be disconnected, as discussed earlier in Sect. 2. Despite these difficulties, we are still able to recover the communities even after a significant amount of sparsification is applied, at the point that our criteria indicate we should be successful.

Time Saved in Eigenvector Calculation. One of the main motivations of this work is to obtain the correct community labels while spending less time computing the require eigenvectors. Since we are able to recover the communities, despite applying large amounts of sparsification, we would expect our eigensolver to converge faster. Exactly how fast depends on the solver. For the eigensolver shown in Spielman and Teng [6], built on top of their nearly linear-time solver and constructed solely to find the Fiedler vector of the Laplacian, our time to compute the eigenvector would depend on the number of elements of our graph. Since we have reduced the number of elements by multiple orders of magnitude when sampling with scaled effective-resistance we would get a multiple order of magnitude speed-up. Unfortunately, these solvers are not available for use in production code, so we do not benchmark them here.

When using the off-the-shelf solver available in Matlab to find the desired eigenvector, with our best method we achieve essentially an order of magnitude speed-up. This is because the solvers used by this method are not optimized for graphs in the way that the solver of Spielman and Teng. The observed speed-up can be seen in Table 1b.

While we do not have a nearly linear-time solver to fairly benchmark our Inverse Power method, we are able to test the number of iterations required to obtain $10^{-8}$ accuracy vs the number of iterations recommended by our stopping criteria, seen in Table 1a. In all four cases all the community nodes were recovered, even though the sparsification was of the order of $O(10^{-3})$.

Table 1. (a) Speed-up in eigensolver from sparsification for the Regularized Laplacian for SBMs (10000, 0.5, 0.3) and (10000, 0.5, 0.2) respectively, using an off the shelf solver. (b) Number of iterations of the inverse power method required to reach the stopping criteria vs number of iterations to reach $10^{-8}$ accuracy using the Scaled Laplacian for the SMB (10000, 0.5, 0.3).

4 Conclusion and Future Work

In this paper we explored the use of sparsifying by effective resistance and scaled effective resistances in order to recover sparsify SBMs, as well as effective stopping criteria for eigensolvers used for community detection. The main goal is to obtain faster solutions while still being confident in our ability to recover the communities. We have provided a method that determines the number of samples needed, depending on the type of sampling used. We found that the community structure can be recovered even when the matrix becomes very sparse. Since SBMs are a commonly studied model for clustering, this method is widely applicable. We leave several areas open for future work. While SBMs are widely studied, the model has certain intrinsic limits which prevent it from modeling certain real-world networks well. We would like to provide a similar analysis for more complex community models, in particular models which have a non-constant average degree. We could then apply our model to a larger variety of real-world graphs.