Abstract
PIE is a Prolog-embedded environment for automated reasoning on the basis of first-order logic. Its main focus is on formulas, as constituents of complex formalizations that are structured through formula macros, and as outputs of reasoning tasks such as second-order quantifier elimination and Craig interpolation. It supports a workflow based on documents that intersperse macro definitions, invocations of reasoners, and
 -formatted natural language text. Starting from various examples, the paper discusses features and application possibilities of PIE along with current limitations and issues for future research.
-formatted natural language text. Starting from various examples, the paper discusses features and application possibilities of PIE along with current limitations and issues for future research.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The prefix
 of this and related predicates should suggest
of this and related predicates should suggest
 format.
format. - 2.
Available at http://www.mettel-prover.org/scan/.
- 3.
Prover9 and Mace4 were developed between 2005 and 2010 by William McCune. Their homepage is https://www.cs.unm.edu/~mccune/prover9/.
- 4.
The standard Prolog negation operator
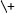 is not suited to represent classical negation as it symbolizes
is not suited to represent classical negation as it symbolizes  , non-provability.
, non-provability. - 5.
3-colorability, which is NP-complete, can be specified analogously. We consider here 2-colorability for brevity of the involved formulas.
- 6.
SWI-Prolog can be configured to permit variable names as functors, which are read in as atoms with capitalized names. The macro processor of PIE compares them to actual variable names in the macro definition.
- 7.
One color predicate can also be eliminated from an analogous specification of 3-colorability.
- 8.
In certain configurations it can also print several different interpolants.
- 9.
This is an example which involves an inference step with a constant that occurs only on the left side (\(\mathsf {a}\)) and a constant that occurs only on the right side (\(\mathsf {b}\)), which can not be handled by certain resolution-based interpolation systems. See [7, 30]. In this particular example, the order of the quantifications in the result is not relevant.
- 10.
We actually encountered right side of the implication before in Sect. 4 as the weakest sufficient condition in the macro definition of \( explanation \).
- 11.
Hypertableaux, either obtained from a hypertableau prover or obtained from a clausal tableau prover like CM by restructuring the tableau seem interesting as basis for interpolant extraction in query reformulation, as they allow to ensure that the interpolants are range restricted. Some related preliminary results are in [57].
References
Ackermann, W.: Untersuchungen über das Eliminationsproblem der mathematischen Logik. Math. Ann. 110, 390–413 (1935)
Alassaf, R., Schmidt, R.: DLS-Forgetter: an implementation of the DLS forgetting calculus for first-order logic. In: GCAI 2019. EPiC, vol. 65, pp. 127–138 (2019)
Behmann, H.: Beiträge zur Algebra der Logik, insbesondere zum Entscheidungsproblem. Math. Ann. 86(3–4), 163–229 (1922)
Benedikt, M., Kostylev, E.V., Mogavero, F., Tsamoura, E.: Reformulating queries: theory and practice. In: IJCAI 2017, pp. 837–843. ijcai.org (2017)
Benedikt, M., Leblay, J., ten Cate, B., Tsamoura, E.: Generating Plans from Proofs: The Interpolation-Based Approach to Query Reformulation. Morgan & Claypool, San Rafael (2016)
Bibel, W.: Matings in matrices. Commun. ACM 26(11), 844–852 (1983)
Bonacina, M.P., Johansson, M.: On interpolation in automated theorem proving. J. Autom. Reason. 54(1), 69–97 (2015)
Brillout, A., Kroening, D., Rümmer, P., Wahl, T.: Beyond quantifier-free interpolation in extensions of Presburger arithmetic. In: Jhala, R., Schmidt, D. (eds.) VMCAI 2011. LNCS, vol. 6538, pp. 88–102. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-18275-4_8
Brillout, A., Kroening, D., Rümmer, P., Wahl, T.: An interpolating sequent calculus for quantifier-free Presburger arithmetic. J. Autom. Reason. 47(4), 341–367 (2011)
Conradie, W.: On the strength and scope of DLS. J. Appl. Non-Classsical Logics 16(3–4), 279–296 (2006)
Craig, W.: Linear reasoning. A new form of the Herbrand-Gentzen theorem. J. Symbolic Logic 22(3), 250–268 (1957)
Craig, W.: Three uses of the Herbrand-Gentzen theorem in relating model theory and proof theory. J. Symbolic Logic 22(3), 269–285 (1957)
Delgrande, J.P.: A knowledge level account of forgetting. J. Artif. Intell. Res. 60, 1165–1213 (2017)
Doherty, P., Łukaszewicz, W., Szałas, A.: Computing circumscription revisited: a reduction algorithm. J. Autom. Reason. 18(3), 297–338 (1997)
Doherty, P., Łukaszewicz, W., Szałas, A.: Computing strongest necessary and weakest sufficient conditions of first-order formulas. In: IJCAI-01, pp. 145–151. Morgan Kaufmann (2001)
Eberhard, S., Hetzl, S., Weller, D.: Boolean unification with predicates. J. Logic Comput. 27(1), 109–128 (2017)
Engel, T.: Quantifier elimination in second-order predicate logic. Master’s thesis, Max-Planck-Institut für Informatik, Saarbrücken (1996)
Fitting, M.: First-Order Logic and Automated Theorem Proving, 2nd edn. Springer, Heidelberg (1995). https://doi.org/10.1007/978-1-4612-2360-3
Gabbay, D., Ohlbach, H.J.: Quantifier elimination in second-order predicate logic. In: KR 1992, pp. 425–435. Morgan Kaufmann (1992)
Gabbay, D.M., Schmidt, R.A., Szałas, A.: Second-Order Quantifier Elimination: Foundations, Computational Aspects and Applications. College Publications (2008)
Ghilardi, S., Lutz, C., Wolter, F.: Did I damage my ontology? A case for conservative extensions in description logics. In: KR 2006, pp. 187–197. AAAI Press (2006)
Grau, B.C., Horrocks, I., Kazakov, Y., Sattler, U.: Modular reuse of ontologies: theory and practice. J. Artif. Intell. Res. 31(1), 273–318 (2008)
Gustafsson, J.: An implementation and optimization of an algorithm for reducing formulae in second-order logic. Technical report LiTH-MAT-R-96-04, Univ. Linköping (1996)
Hoder, K., Holzer, A., Kovács, L., Voronkov, A.: Vinter: a Vampire-based tool for interpolation. In: Jhala, R., Igarashi, A. (eds.) APLAS 2012. LNCS, vol. 7705, pp. 148–156. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-35182-2_11
Hoder, K., Kovács, L., Voronkov, A.: Interpolation and symbol elimination in Vampire. In: Giesl, J., Hähnle, R. (eds.) IJCAR 2010. LNCS (LNAI), vol. 6173, pp. 188–195. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14203-1_16
Kaliszyk, C.: Efficient low-level connection tableaux. In: De Nivelle, H. (ed.) TABLEAUX 2015. LNCS (LNAI), vol. 9323, pp. 102–111. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24312-2_8
Kaliszyk, C., Urban, J.: FEMaLeCoP: fairly efficient machine learning connection prover. In: Davis, M., Fehnker, A., McIver, A., Voronkov, A. (eds.) LPAR 2015. LNCS, vol. 9450, pp. 88–96. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48899-7_7
Knuth, D.E.: Literate programming. Comput. J. 27(2), 97–111 (1984)
Koopmann, P., Schmidt, R.A.: Uniform interpolation of \(\cal{ALC}\)-ontologies using fixpoints. In: Fontaine, P., Ringeissen, C., Schmidt, R.A. (eds.) FroCoS 2013. LNCS (LNAI), vol. 8152, pp. 87–102. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40885-4_7
Kovács, L., Voronkov, A.: First-order interpolation and interpolating proof systems. In: LPAR-21, pp. 49–64. EasyChair (2017)
Letz, R.: First-order tableau methods. In: D’Agostino, M., Gabbay, D.M., Hähnle, R., Posegga, J. (eds.) Handbook of Tableau Methods, pp. 125–196. Kluwer Academic Publishers (1999)
Lin, F.: On strongest necessary and weakest sufficient conditions. Artif. Intell. 128, 143–159 (2001)
Lin, F., Reiter, R.: Forget It! In: Working Notes, AAAI Fall Symposium on Relevance, pp. 154–159 (1994)
Ludwig, M., Konev, B.: Practical uniform interpolation and forgetting for \(\cal{ALC}\) TBoxes with applications to logical difference. In: KR 2014. AAAI Press (2014)
Lutz, C., Wolter, F.: Foundations for uniform interpolation and forgetting in expressive description logics. In: IJCAI 2011, pp. 989–995. AAAI Press (2011)
Löwenheim, L.: Über Möglichkeiten im Relativkalkül. Math. Ann. 76, 447–470 (1915)
McCune, W.: Un-Skolemizing clause sets. Inf. Process. Lett. 29(5), 257–263 (1988)
McMillan, K.L.: Applications of Craig interpolants in model checking. In: Halbwachs, N., Zuck, L.D. (eds.) TACAS 2005, pp. 1–12. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31980-1_1
McMillan, K.L.: Interpolation and model checking. In: Clarke, E.M., Henzinger, T.A., Veith, H., Bloem, R. (eds.) Handbook of Model Checking, pp. 421–446. Springer, Heidelberg (2018). https://doi.org/10.1007/978-3-319-10575-8_14
Otten, J.: Restricting backtracking in connection calculi. AI Commun. 23(2–3), 159–182 (2010)
Pelzer, B., Wernhard, C.: System description: E-KRHyper. In: Pfenning, F. (ed.) CADE 2007. LNCS (LNAI), vol. 4603, pp. 508–513. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73595-3_37
Rudeanu, S.: Boolean Functions and Equations. Elsevier (1974)
Schmidt, R.A.: The Ackermann approach for modal logic, correspondence theory and second-order reduction. J. Appl. Logic 10(1), 52–74 (2012)
Schröder, E.: Vorlesungen über die Algebra der Logik. Teubner (1890–1905)
Smullyan, R.M.: First-Order Logic. Dover Publications, New York (1995). Corrected republication of the original edition by Springer-Verlag, New York (1968)
Stickel, M.E.: A Prolog technology theorem prover: implementation by an extended Prolog compiler. J. Autom. Reason. 4(4), 353–380 (1988)
Sutcliffe, G.: The TPTP problem library and associated infrastructure. From CNF to TH0, TPTP v6.4.0. J. Autom. Reason. 59(4), 483–502 (2017)
Toman, D., Weddell, G.: Fundamentals of Physical Design and Query Compilation. Morgan and Claypool, San Rafael (2011)
Wernhard, C.: Semantic knowledge partitioning. In: Alferes, J.J., Leite, J. (eds.) JELIA 2004. LNCS (LNAI), vol. 3229, pp. 552–564. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30227-8_46
Wernhard, C.: Circumscription and projection as primitives of logic programming. In: Technical Communications ICLP 2010. LIPIcs, vol. 7, pp. 202–211. Schloss Dagstuhl-Leibniz-Zentrum für Informatik (2010)
Wernhard, C.: Projection and scope-determined circumscription. J. Symbolic Comput. 47, 1089–1108 (2012)
Wernhard, C.: Abduction in logic programming as second-order quantifier elimination. In: Fontaine, P., Ringeissen, C., Schmidt, R.A. (eds.) FroCoS 2013. LNCS (LNAI), vol. 8152, pp. 103–119. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40885-4_8
Wernhard, C.: Computing with logic as operator elimination: the ToyElim system. In: Tompits, H., et al. (eds.) INAP/WLP -2011. LNCS (LNAI), vol. 7773, pp. 289–296. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-41524-1_17
Wernhard, C.: Second-order quantifier elimination on relational monadic formulas – a basic method and some less expected applications. In: De Nivelle, H. (ed.) TABLEAUX 2015. LNCS (LNAI), vol. 9323, pp. 253–269. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24312-2_18
Wernhard, C.: The PIE system for proving, interpolating and eliminating. In: PAAR 2016, pp. 125–138. CEUR-WS.org (2016)
Wernhard, C.: The Boolean solution problem from the perspective of predicate logic. In: Dixon, C., Finger, M. (eds.) FroCoS 2017. LNCS (LNAI), vol. 10483, pp. 333–350. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66167-4_19
Wernhard, C.: Craig interpolation and access interpolation with clausal first-order tableaux. ArXiv e-prints (2018). https://arxiv.org/abs/1802.04982
Wielemaker, J., Schrijvers, T., Triska, M., Lager, T.: SWI-Prolog. Theory Practice Logic Program. 12(1–2), 67–96 (2012)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Wernhard, C. (2020). Facets of the PIE Environment for Proving, Interpolating and Eliminating on the Basis of First-Order Logic. In: Hofstedt, P., Abreu, S., John, U., Kuchen, H., Seipel, D. (eds) Declarative Programming and Knowledge Management. INAP WLP WFLP 2019 2019 2019. Lecture Notes in Computer Science(), vol 12057. Springer, Cham. https://doi.org/10.1007/978-3-030-46714-2_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-46714-2_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-46713-5
Online ISBN: 978-3-030-46714-2
eBook Packages: Computer ScienceComputer Science (R0)


 of this and related predicates should suggest
of this and related predicates should suggest
 format.
format.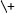 is not suited to represent classical negation as it symbolizes
is not suited to represent classical negation as it symbolizes  , non-provability.
, non-provability.