Abstract
We present the first protocols for private information retrieval that allow fast (sublinear-time) database lookups without increasing the server-side storage requirements. To achieve these efficiency goals, our protocols work in an offline/online model. In an offline phase, which takes place before the client has decided which database bit it wants to read, the client fetches a short string from the servers. In a subsequent online phase, the client can privately retrieve its desired bit of the database by making a second query to the servers. By pushing the bulk of the server-side computation into the offline phase (which is independent of the client’s query), our protocols allow the online phase to complete very quickly—in time sublinear in the size of the database. Our protocols can provide statistical security in the two-server setting and computational security in the single-server setting. Finally, we prove that, in this model, our protocols are optimal in terms of the trade-off they achieve between communication and running time.
The full version of this paper is available at https://eprint.iacr.org/2019/1075.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
A private information retrieval protocol [CGKS95, CGKS98] takes place between a client, holding an index \(i \in [n]\), and a database server, holding a string \(x = x_1 x_2 \cdots x_n \in \{0,1\}^n\). The protocol allows the client to fetch its desired bit \(x_i \in \{0,1\}\) from the database while hiding the client’s index i from the server, and using total communication that is sublinear in the database size n. A beautiful line of work, starting with that of Chor, Goldreich, Kushilevitz, and Sudan [CGKS95], constructs private information retrieval (PIR) protocols with extremely small communication complexity, either when the client can access multiple non-colluding servers holding replicas of the database [Amb97, CG97, BI01, BIKR02, Yek08, Efr12, DG16] or under computational assumptions [KO97, CMS99, KO00, GR05, OS07].
PIR is a fundamental privacy-preserving primitive: it has applications to private messaging [SCM05, AS16, ACLS18], certificate transparency [LG15], private media browsing [GCM+16], online anonymity [MOT+11, KLDF16], privacy-preserving ad targeting [Jue01], and more. In spite of the promise of PIR and the great advances in PIR protocols, there have been essentially no large-scale deployments of PIR technology to date. A primary reason is that while modern PIR protocols have very small communication requirements—as small as polylogarithmic in the database size—the computational burden they put on the server is still prohibitively expensive.
In particular, in all existing PIR schemes, the work at the servers grows linearly with the database size. That is, the servers essentially take a linear scan over the entire database to respond to each query. Beimel et al. [BIM04] proved that this limitation is in fact inherent: even in the multi-server setting, every secure PIR scheme on an n-bit database must incur \(\varOmega (n)\) total server-side work. (If the servers probe fewer than n database bits on average in responding to a client’s query, then it is likely that the client is reading one of the probed bits.)
This \(\varOmega (n)\) server-side cost is the major bottleneck for PIR schemes in theory, since all other costs in today’s PIR protocols (communication, client time, etc.) are sublinear, or even polylogarithmic, in the database size. This \(\varOmega (n)\) server-side cost is also the major bottleneck for PIR schemes in practice, as evidenced by the many heroic efforts to reduce the server-side computational cost in built PIR systems [LG15, AS16, GCM+16, TDG16, ACLS18].
In Sect. 1.4, we survey the known approaches to reducing the server-side computation in PIR-like schemes. All of these methods increase the storage requirements at the servers and the methods based on standard assumptions (i.e., not requiring obfuscation) increase the required server storage by potentially large polynomial factors. These increased storage costs present new barriers to deployment.
1.1 A New Approach: Offline/Online PIR with Sublinear Online Time
In this paper, we propose a new approach for reducing the server-side computational burden of PIR. Our idea is to push the (necessary) linear-time server-side computation into a query-independent offline phase, which allows a subsequent online phase to complete in sublinear time (Fig. 1). More precisely, we construct PIR schemes in which the client and servers interact in two phases:
-
In an offline phase, which takes place before the client has decided which bit of the database it wants to retrieve, the client fetches a one-time-use “hint” from the database servers.
-
In a subsequent online phase, which takes place after the client has decided which bit of the database it wants to retrieve, the client sends a query to the database servers. Given the servers’ answers to this query, along with the hint prefetched earlier, the client can recover its database bit of interest.
Prior work has developed PIR offline/online schemes [DIO01, BIM04, BLW17, PPY18]. In this paper, we construct the first offline/online PIR schemes that simultaneously:
-
1.
run in online time sublinear in the database size, and
-
2.
do not increase the storage requirements at the servers.
(See Sect. 1.4 and Table 1 for a comparison to prior work.) Furthermore, our schemes are based on very simple assumptions—one-way functions in the two-server setting and linearly homomorphic encryption in the single-server setting—and are concretely efficient. The remaining performance bottleneck of our schemes is that one of the servers must perform an amount of offline computation in that is linear in the database size.
Our schemes advance the state of the art in PIR by enabling two new usage models:
-
1.
Do the heavy computation in advance. Our schemes shift the heavy server-side computation out of the critical path of the client’s request. For example, we envision deployments of our PIR schemes in which the client and server execute the offline phase overnight, while the user is asleep and when computation is relatively inexpensive. In the morning, when the user wakes up and wants to, say, privately fetch an article from Wikipedia, she can run the online phase to get her article in sublinear time.
The idea of moving expensive cryptographic work into an input-independent offline phase has seen tremendous success in the setting of multiparty computation [BDOZ11, DPSZ12]. Our schemes achieve the same goal for PIR.
-
2.
Process a series of queries in sublinear amortized total time. Often, a user wants to make a series of adaptive queries to the same database (e.g., as one does when jumping from one Wikipedia article to the next). In this setting, our two-server PIR scheme allows the client to reuse a single hint, fetched in the offline phase, to make arbitrarily many adaptive online queries to the database. By reusing the hint, the amortized total server-side cost of each query—including both the costs of the offline and online phases—falls to sublinear in the database size. As far as we know, ours is the first PIR scheme that achieves sublinear amortized total time for adaptive queries without dramatically increasing the client or servers’ storage requirements.
1.2 Our Results
We give the following results for offline/online private information retrieval with sublinear online time:
Two-server PIR. We give a two server offline/online scheme with sublinear online time. Specifically, for a database consisting of n bits, the offline phase requires the client to interact with one server, which performs \(\widetilde{O}(n)\) offline computation. (The notation \(\widetilde{O}(\cdot )\) hides arbitrary polylogarithmic factors. In this section, we also elide fixed polynomials in the security parameter.) In the online phase, the client interacts with the second server, which answers the client’s query in time \(\widetilde{O}(\sqrt{n})\). We give a scheme with statistical security that has total communication \(\widetilde{O}(\sqrt{n})\). Assuming that one-way functions exist, the online communication cost falls to \(O(\log n)\).
Two-server PIR with sublinear amortized total time. We extend our two-server scheme to allow the client to reuse a single offline-phase interaction to make a series of polynomially many adaptive online-phase queries. With this scheme, the online cost of each query is still \(\widetilde{O}(\sqrt{n})\), but after q online queries, the average total computational cost—including the offline-phase computation—falls to \(\widetilde{O}(n/q + \sqrt{n})\), or sublinear in the database size.
Single-server PIR. We show how to combine a linearly homomorphic encryption scheme and a standard single-server PIR scheme to obtain a single-server offline/online PIR scheme with sublinear online time. The resulting scheme uses \(\widetilde{O}(n^{2/3})\) total communication and the server runs in online time \(\widetilde{O}(n^{2/3})\). Furthermore, neither the client nor the server performs any public-key cryptographic operations in the online phase. Under the stronger assumption that fully homomorphic encryption exists, we obtain a single-server scheme with communication and online time \(\widetilde{O}(\sqrt{n})\). One drawback is that, unlike its two-server counterpart, our single-server scheme supports only a single online query after each offline interaction, and thus we do not achieve sublinear amortized total time. The main benefit of shifting the heavy server-side computation to the offline phase remains.
A lower bound. Finally, we prove a lower bound for offline/online PIR schemes in which the servers store the database in unencoded form and keep no additional state. Specifically, we show that any scheme of this form, that uses C bits of communication in the offline phase, and that probes T bits of the database in the online phase, must satisfy \(C\cdot T\ge \widetilde{\varOmega }(n)\). This shows that in this model, as far as communication and online server time are concerned, our two-server scheme and the FHE-based single-server scheme are optimal, up to logarithmic factors.
1.3 Limitations
The primary drawback of our new PIR protocols is that they use more total communication than standard PIR schemes do. Today’s PIR schemes (with linear online server-side time) can achieve polylogarithmic communication in the computational setting [CMS99, GR05, IP07, BGI16, DGI+19] and subpolynomial communication (\(n^{O(\sqrt{\log \log n / \log n})}\)) in the two-server information-theoretic setting [DG16]. In contrast, our schemes with sublinear online time have communication \(\widetilde{\varOmega }_\lambda (\sqrt{n})\). While we show that it is possible to reduce the online-phase communication in the computational setting, our lower bound (Theorem 23) implies that any offline/online PIR scheme with online time \(\widetilde{O}(\sqrt{n})\)—such as ours—must have \(\widetilde{\varOmega }(\sqrt{n})\) total communication. This limitation is therefore inherent to PIR schemes that have sublinear online server time and in which the servers store the database in unmodified form.
In many settings, we expect that the \(\sqrt{n}\) communication cost will be acceptable. Indeed, a number of built systems using PIR [GDL+14, GCM+16, AMBFK16, ACLS18] already suffice with \(\sqrt{n}\) communication complexity, since server-side computational cost is the limiting factor. If \(\sqrt{n}\) communication is still too high, we show in Corollary 18 that it is possible to amortize the \(\sqrt{n}\) offline communication cost of our two-server scheme over polynomially many online reads, each of which requires only logarithmic communication. So, our results are still relevant to communication-sensitive settings, when having low amortized complexity is sufficient.
1.4 Related Work
Beimel, Ishai, and Malkin [BIM04] proved that the servers in any secure PIR scheme must collectively probe all n bits of the database (on average) to respond to a client’s query. We survey the existing strategies for eliminating this key performance bottleneck.
Store the database in encoded form. One ingenious way to circumvent the \(\varOmega (n)\)-server-time lower bound is to have the servers store the database in encoded form. Beimel et al. [BIM04] introduced the notion of PIR with preprocessing, in which the servers perform a one-time preprocessing of the database \(x \in \{0,1\}^n\) and store the database in encoded form \(E(x) \in \{0,1\}^N\), where E is a public encoding function and \(N \gg n\). In the two-server setting, their PIR schemes with preprocessing achieve \(n^{1/2+\epsilon }\) total communication and \(n^{1/2+\epsilon }\) server-side time, for any \(\epsilon > 0\). The downside of this approach is that the server-side encoding can be quite large. For example, to achieve \(n^{0.6}\) server-side time and communication using their two-server scheme requires the server to store an encoded database of size \(N=n^{3.2}\). Even for modest database sizes (e.g., \(n\approx 2^{20}\)), the encoded database would be much too large to materialize in practice (many petabytes). While it would be fascinating to construct improved schemes for two-server PIR with preprocessing—perhaps with encoding size \(N=10n\) and online time and communication \(n^{1/3}\)—this goal appears far out of reach.
The schemes of Beimel et al. apply only to the multi-server setting. Two recent works [BIPW17, CHR17] study doubly efficient PIR, which are in some sense single-server PIR-with-preprocessing schemes. In the designated-client model of doubly efficient PIR, the client encodes the database using a long-term secret key (hidden from the server) and stores the encoded database on the server. Under a new cryptographic assumption, the client can subsequently privately query this encoded database many times, and the server can answer the query in time sublinear in the database size. In the public-key analogue of doubly efficient PIR, a server that stores a single database encoding enables multiple mutually distrusting clients to query the database using a short public key. Boyle et al. [BIPW17] construct a public-key doubly efficient PIR scheme with sublinear query time, under a new cryptographic assumption and in a model with virtual black-box obfuscation.
Hamlin et al. [HOWW18] introduce a notion of private anonymous data access (“PANDA”) schemes, in which many clients can access an encoded database such that (1) as in standard PIR schemes, the server does not learn which bits of the database a client is reading and (2) the server can respond to a client’s request in time sublinear—even polylogarithmic—in the database size. Unlike in doubly efficient PIR schemes, the server in PANDA may store mutable state. Hamlin et al. give an instantiation of a PANDA scheme from fully homomorphic encryption [Gen09]. A limitation of the existing PANDA schemes is that they require the server storage and time to grow with the number of malicious clients interacting with the system. In our setting, in which the number of malicious clients could be unbounded, the storage and online server time of a PANDA scheme would also be unbounded.
The general framework of PIR with preprocessing is extremely promising, since preprocessing schemes can plausibly allow both polylogarithmic total communication and total work—which is impossible in the offline/online setting. That said, these preprocessing schemes necessarily increase the storage costs at the servers, by large polynomial factors in many cases. The single-server preprocessing schemes additionally rely on relatively heavy cryptographic assumptions. In contrast, in our schemes, the servers store the database x in unencoded form and keep no additional state. The trade-off is that, in our schemes, the client and servers must run the linear-server-time offline phase once per client (Sect. 4) or once per query (Sects. 3 and 5).
Use linear additional storage per query. Beimel, Ishai, and Malkin [BIM04, Section 7.2], building on earlier work of Di Crescenzo, Ishai, and Ostrovsky [DIO98, DIO01], give an alternative way to reduce the server-side online time in PIR. In their model, the client submits a request to the servers in an offline phase. The servers use this request to generate a one-time-use n-bit encoding of the n-bit database, which the servers store. In a subsequent online phase, the client can privately query the servers for a database bit and the servers use their precomputed encoding to respond in sublinear online time. The total communication and online server-side work in these schemes can be as low as \({\text {polylog}}(n)\) [Ish19]. However, the server-side storage costs can be large: for each client, the servers must store n additional bits until that client makes its online query. If m clients concurrently access the database, the storage requirements at the servers increase to mn bits. (In contrast, the schemes in our work require no extra server-side storage.)
Use linear online time. Another line of work reduces the server-side computational burden of PIR protocols by working in the offline/online model we consider. To our knowledge, all prior protocols in the offline/online model require linear online time at the servers.
Boneh, Lewi, and Wu [BLW17] show that “privately constrained PRFs” imply a two-server online/offline scheme in which only one of the servers needs to be active in the online phase. The scheme has polylogarithmic communication complexity, yet the online server’s work is linear in the database size. Subsequent work [BKM17, CC17, BTVW17] constructs such PRFs from standard lattice assumptions.
Towards reducing the server’s computation time in PIR protocols, Patel, Persiano, and Yeo [PPY18] introduce the notion of private stateful information retrieval. They give single-server schemes in which, after an offline phase, the client can privately retrieve a bit from the database while requiring the server to only perform a number of online public-key operations sublinear in the database size, along with a linear number of symmetric-key operations. The offline phase of their protocol requires the client to download a linear number of bits in the offline phase and the server must perform a linear number of total operations in the online phase. Their schemes do allow amortizing the linear-communication offline phase over multiple subsequent queries, although the online time is always linear. In contrast, our protocols have total communication and online time sublinear in the database size, even for a single query.
Demmler, Herzberg, and Schneider [DHS14] give a scheme which reduces the computational burden of each server by means of sharding the database. The combined work of all servers in their scheme is still linear.
Marginally sublinear online time. The original PIR paper [CGKS95] points out that a three-party communication protocol of Pudlák and Rödl [PR93, Theorem 3.5] yields a two-server PIR protocol. (See also the subsequent journal version [PRS97].) In particular, on an n-bit database, that protocol has total communication \(\alpha (n) = O(n \frac{\log \log n}{\log n})\), or just slightly sublinear. Closer inspection of this protocol reveals that one of the two servers can additionally be made to run in sublinear time \(\alpha (n)\), and thus this early scheme can be cast as an offline/online PIR scheme with just slightly sublinear offline communication. As far as we know, no prior work has drawn attention to this fact.
Lipmaa [Lip09] constructs a computational single-server PIR protocol with preprocessing. In its offline phase, the server encodes the database as a branching program with \((n\,+\,o(n))/\log n\) nodes, and stores the branching program, using \(n\,+\,n/{\text {polylog}}(n)\) bits. In the online phase, the server homomorphically evaluates the branching program, using a protocol of Ishai and Paskin [IP07], which requires \(O(n/\log n)\) public key operations, or slightly sublinear in the database size. (The homomorphic ciphertexts must be no shorter than the security parameter \(\lambda =\omega (\log n)\), and so, strictly speaking, the number of bit operations in the online phase is still linear. However, the running time is dominated by the public key operations.)
The complexity of these two protocols is much larger than ours but we still find it interesting to see such radically different ways to construct two-server PIR with sublinear online time.
Amortize work. It is also possible to improve the computational efficiency of PIR by having each PIR server jointly process a batch of queries. If a server can process a batch of Q queries to an n-bit database at o(Qn) cost, processing queries in a batch yields sublinear amortized time per query at the server. This general strategy is fruitful both when the batched queries originate from the same client [IKOS04, Hen16, ACLS18] and from different clients [BIM04, IKOS06, LG15].
Our multi-query scheme of Sect. 4 similarly allows the client to amortize the server’s linear-time offline computation over many queries—as in batch PIR. The difference is that our multi-query scheme allows the client to make its queries adaptively (one at a time), while batch-PIR schemes require the client to make all queries in a batch non-adaptively (all at once).
Relax the security property. One final approach to reducing the online server time in PIR is to aim for a weaker security property than standard cryptographic PIR schemes do. Toledo, Danezis, and Goldberg give PIR schemes with a differential-privacy-style notion of security and show that when some leakage of the client’s query to the server is allowed, the servers can run in sublinear online time [TDG16].
1.5 Technical Overview
To illustrate our techniques, we start by presenting a simplified version of our two-server offline/online PIR scheme with statistical security. The online phase of this protocol runs in time o(n), and the protocol’s total communication is o(n).
A toy protocol. Two servers hold a replica of the database \(x\in \{0,1\}^n\). The two phases of the protocol proceed as follows:
Offline phase. This phase takes place before the client has decided which bit it wants to read from the database.
-
The client divides the database indices \(\{1, \dots , n\}\) at random into \(\sqrt{n}\) disjoint sets \((S_1, \dots , S_{\sqrt{n}})\), each of size \(\sqrt{n}\), and sends these sets to the first server. (Sending these sets explicitly would take \(\varOmega (n \log n)\) communication, which is too much. We explain later how to reduce the communication in this step.)
-
The first server receives the sets \((S_1, \dots , S_{\sqrt{n}})\) from the client. For each such set \(S_j\), it computes the parity of the database bits indexed by the set. That is, for \(j \in \{1, \dots , \sqrt{n}\}\), the server computes the parity \(h_j \leftarrow \sum _{i \in S_j} x_i \bmod 2\). The server sends these parity bits \((h_1, \dots , h_{\sqrt{n}})\) to the client.
-
The client stores the sets \((S_1, \dots , S_{\sqrt{n}})\) and the parity bits \((h_1, \dots , h_{\sqrt{n}})\).
Online phase. This phase begins once the client has decided on the index \(i \in [n]\) of the bit it wants to read from the database.
-
The client finds the set \(S_j\) that contains its desired index i. The client then removes a single item \(i^*\) from the set \(S_j\), which it chooses as follows:
-
With probability \(1-(\sqrt{n}-1)/n\) the client chooses \(i^*\leftarrow i\).
-
With the remaining probability, the client chooses \(i^*\) randomly from the set of all other elements in \(S_j\).
The client then sends the set
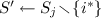 to the second server.
to the second server. -
-
Upon receiving the set \(S'\) from the client, the second server computes and sends back to the client the parity of the database bits indexed by the set: \(a\leftarrow \sum _{i\in S'}x_i\bmod {2}\). Computing the answer requires the second server to probe at most \(|S'| = O(\sqrt{n})\) bits of the database, which allows the server to run in only \(\widetilde{O}(\sqrt{n})\) time.
-
Finally, when the client receives the answer from the second server, it recovers the value of the database bit \(x_{i^*}\) by computing \(x_{i^*}\leftarrow h_j - a \bmod {2}\). Crucially, since the client has chosen \(i^*\) with a bias towards i, it recovers the value \(x_i\) of its bit of interest with high probability \(1-O(1/\sqrt{n})\). (By iterating the scheme \(\lambda \) times in parallel, the client can drive the failure probability down to at most \(2^{-\lambda }\).)
With a bit of work, it is possible to show that the set \(S'\) that the client sends to the second server is a uniformly random subset of [n] of size \(\sqrt{n}-1\). Thus, the values that both servers see are distributed independently of the index i that the client is trying to read.
The resulting scheme already achieves the main goal of interest: in the online phase, the server can respond to the client’s query in time \(O(\sqrt{n})\). However, the toy scheme also has two major shortcomings:
-
1.
The communication in the offline phase is super-linear: sending the sets \((S_1, \dots , S_{\sqrt{n}})\) to the first server requires \(\varOmega (n \log n)\) bits.
-
2.
The scheme requires \(\varTheta (n\log n)\) bits of client storage between the offline phase and the online phase.
We can address both of these challenges at once by partially derandomizing the client. In the revised scheme, in the offline phase, the client chooses a single set \(S \subseteq [n]\) of size \(\sqrt{n}\). The client also sends to the server \(\sqrt{n}\) random “shifts” \(\varDelta = \{\delta _1, \delta _2, \dots , \delta _{{\sqrt{n}}} \} \in [n]\). The client and server then use S and \(\varDelta \) to construct a collection of \(\sqrt{n}\) sets \((S_1, \dots , S_{\sqrt{n}})\) by setting, for every \(j \in \{1, \dots , \sqrt{n}\}\), \(S_j \leftarrow \{ i + \delta _j \mid i \in S\}\). The client and the server then run the rest of the toy protocol using this collection of sets. This modification increases the failure probability, since there is now some chance that the client’s desired index i will not be in any of the sets \((S_1, \dots , S_{\sqrt{n}})\). Even so, the client and servers can repeat the protocol \(O(\log n)\) times in parallel to drive down the failure probability.
This modifications reduces both the communication complexity of the offline phase and the amount of client storage and time to \(\widetilde{O}(\sqrt{n})\). With some work, we can also argue that this modification preserves security.
Improvements to the toy scheme. While the above patched two-server scheme achieves all of our efficiency goals, it leaves a few things to be desired:
-
Reducing online communication with puncturable pseudorandom sets. In the protocol sketched above, the communication in the online phase is \(\varTheta (\sqrt{n})\). Under the assumptions that one-way functions exist, we can reduce the online-phase communication to \({\text {poly}}(\lambda , \log n)\), for security parameter \(\lambda \).
To do so, we introduce a new tool, which we call a puncturable pseudorandom set (Sect. 2). Essentially, a puncturable pseudorandom set allows the client in the toy scheme above to send the server a compressed representation of the random set S, in the form of a short key k. Furthermore, the set key is “puncturable,” in that for any \(i^* \in S\), the client can produce a punctured set key \(k_{i^*}\) that is a compressed representation of
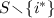 . Crucially, the punctured key \(k_{i^*}\) also hides the identity of the removed element \(i^*\).
. Crucially, the punctured key \(k_{i^*}\) also hides the identity of the removed element \(i^*\).We construct a puncturable pseudorandom set from puncturable PRFs [BW13, KPTZ13, BGI14, SW14] (Theorem 3), which have simple constructions from pseudorandom generators. The keys in our construction have size \(O(\lambda \log n)\) for sets of size \(O(\sqrt{n})\) over a universe of size n and security parameter \(\lambda \). Plugging this puncturable pseudorandom set construction into the toy scheme above reduces the communication complexity of the online phase to the length of a single punctured set key, plus the single bit answer, for \(O(\lambda \log n)\) bits total.
-
Refreshing the client’s state. The client in the toy scheme can only use the results of the (computationally expensive) offline phase to read a single bit from the database. The following modification to the toy scheme allows the client to “refresh” the bits it downloads in the offline phase, so that it can reuse these bits for many online queries (Sect. 4).
After the client makes a query for index \(i \in [n]\) using set \(S_j\), the client discards that set from its state. Now the client must somehow “refresh” its local state. Our observation is that the set \(S_j\) is a random size-\(\sqrt{n}\) subset of [n], conditioned on \(i \in S_j\). The client refreshes its state by asking the first server for the parity of a random size-\((\sqrt{n}-1)\) subset \(S'\) of [n]. Since the client already knows the value of \(x_i\), it can compute and store the parity of the database bits in the set \(S' \cup \{i\}\). (Ensuring that this refreshing process maintains security requires handling some technicalities.)
Although this construction requires the client to use independent random sets \((S_1, \dots , S_{\sqrt{n}})\), using puncturable pseudorandom sets the client can send to the offline server all of them using only \(\widetilde{O}(\sqrt{n})\) bits of communication.
-
From two servers to one. Converting the two-server offline/online PIR scheme to a single-server one is conceptually simple. Say that in the offline phase of the two-server scheme, the client sends a query q to the first server and receives an answer a. To convert it into a single-server scheme, we have the client send an encryption E(q) of its offline query to the server, and we have the server homomorphically compute and send back the encrypted answer E(a). Since the server learns nothing about the offline query q, the online phase can proceed exactly as in the two-server scheme.
With fully homomorphic encryption [Gen09], this transformation is straightforward and maintains the communication complexity of the original two-server scheme. We show in Theorem 20 that it is possible to execute these steps using the much lighter-weight tools of linearly homomorphic encryption and single-server PIR, with slightly worse communication efficiency and online time: \(\widetilde{O}(n^{2/3}) \cdot {\text {poly}}(\lambda )\), for security parameter \(\lambda \).
-
Proving optimality. Finally, we prove a lower bound on the offline communication and online time using a classic lower bound of Yao [Yao90]. In particular, we show (the full version of this work) that any offline/online PIR scheme with small offline communication and online time, and in which the servers store the database in unmodified form, implies a good solution to “Yao’s Box Problem.” We then apply a preexisting time/space lower bound against algorithms for Yao’s Box Problem to complete the lower bound (Theorem 23).
1.6 Notation
We use \(\mathbb {N}\) to denote the set of positive integers. For an integer \(n\in \mathbb {N}\), [n] denotes the set \(\{1,2,\dotsc , n\}\) and \(1^n\) denotes the all-ones binary string of length n. For \(n\in \mathbb {N}\) and \(s\in [n]\), an s-subset of [n] is a subset of size exactly s, and \(\left( {\begin{array}{c}[n]\\ s\end{array}}\right) \) denotes the set of all s-subsets of [n]. Logarithms are taken to the base 2. We ignore integrality concerns and treat expressions like \(\sqrt{n}\), \(\log n\), and m/n as integers.
The expression \({\text {poly}}(\cdot )\) refers to a fixed (unspecified) polynomial in its parameter. The notation \(\widetilde{O}(\cdot )\) hides arbitrary polylogarithmic factors, i.e., \(f(n)=\widetilde{O}(g(n))\) if \(f(n)=O(g(n))\cdot {\text {poly}}(\log n)\). The notation \(O_\lambda (\cdot )\) hides arbitrary polynomial factors in (the security parameter) \(\lambda \), i.e., \(f(n,\lambda )=O_\lambda (g(n))\) if \(f(n,\lambda ) = O(g(n)) \cdot {\text {poly}}(\lambda )\).
For a finite set S, the notation  refers to choosing x independently and uniformly at random from the set S. For a distribution \(\mathcal {D}\) over a set S, the notation
refers to choosing x independently and uniformly at random from the set S. For a distribution \(\mathcal {D}\) over a set S, the notation  refers to choosing \(x\in S\) according to distribution \(\mathcal {D}\). For \(p\in [0,1]\), the notation
refers to choosing \(x\in S\) according to distribution \(\mathcal {D}\). For \(p\in [0,1]\), the notation  refers to choosing the bit b to be ‘1’ with probability p and ‘0’ with probability \(1-p\).
refers to choosing the bit b to be ‘1’ with probability p and ‘0’ with probability \(1-p\).
We use the RAM model of computation with the size of the word logarithmic in the input length and linear in the security parameter. To avoid dependence on the specifics of the computational model, we usually specify running times up to polylogarithmic factors. Throughout this text, an efficient algorithm is a probabilistic polynomial time algorithm. Furthermore, we allow all adversaries to be non-uniform. (Though this is not fundamental, and, with appropriate modifications in the security games, the results hold also in the uniform setting.)
We say that a pseudorandom generator (PRG) or pseudorandom permutation (PRP) is \(\epsilon \)-secure if no efficient adversary can distinguish the PRG or PRP from random with advantage better than \(\epsilon (\lambda )\), on security parameter \(\lambda \).
2 Puncturable Pseudorandom Sets
In this section, we introduce a new cryptographic primitive called puncturable pseudorandom sets and give few natural constructions. Puncturable pseudorandom sets are a key component of our PIR schemes.
A puncturable pseudorandom set is very closely related to a puncturable pseudorandom function (“puncturable PRF”) [BW13, KPTZ13, BGI14, SW14, HKW15]. To explain the difference by analogy: a PRF key is a compressed representation of a function \(f: [n] \rightarrow [n]\), and a PRF key punctured at point \(x^* \in [n]\) allows its holder to evaluate f at every point in [n] except at the punctured point \(x^*\). The punctured key should reveal nothing about the value of \(f(x^*)\) to its holder. (The formal standard definition appears in the full version of this work.)
Analogously, the key for a puncturable pseudorandom set is a compressed representation of a pseudorandom set \(S \subseteq [n]\). The set key punctured at element \(x^* \in S\) allows its holder to recover all elements of S except the punctured element \(x^*\). The punctured set key reveals nothing about \(x^*\) to its holder, apart from that fact that \(x^*\) is not one of the remaining elements in S.
2.1 Definitions
Let \(s: \mathbb {N}\rightarrow \mathbb {N}\) be a function such that \(s(n)\le n\). A puncturable pseudorandom set with set size s consists of a key space \(\mathcal {K}\), a punctured-key space \({\mathcal {K}_{\mathsf {p}}}\), and a triple of algorithms:
-
\(\mathsf {Gen}(1^\lambda , n) \rightarrow {\mathsf {sk}}\), a randomized algorithm that takes as input the security parameter \(\lambda \in \mathbb {N}\), expressed in unary, and a universe size \(n \in \mathbb {N}\), expressed in binary, and outputs a set key \({\mathsf {sk}}\in \mathcal {K}\),
-
\(\mathsf {Punc}({\mathsf {sk}}, i) \rightarrow {\mathsf {sk}}_\mathsf {p}\), a deterministic algorithm that takes in a key \({\mathsf {sk}}\in \mathcal {K}\) and an element \(i\in [n]\), and outputs a punctured set key \({\mathsf {sk}}_\mathsf {p}\in {{\mathcal {K}_{\mathsf {p}}}}\), and
-
\(\mathsf {Eval}({\mathsf {sk}}) \rightarrow S\), a deterministic algorithm that takes in a key \({\mathsf {sk}}\in \mathcal {K}\cup {\mathcal {K}_{\mathsf {p}}}\) and outputs a description of a set \(S\subseteq [n]\), written as |S| strings of \(\log n\) bits in length each.
A puncturable pseudorandom set must satisfy the following notions of efficiency, correctness and security.
Efficiency. For every security parameter \(\lambda \in \mathbb {N}\) and universe size \(n \in \mathbb {N}\), the routines \(\mathsf {Gen}\), \(\mathsf {Punc}\), and \(\mathsf {Eval}\) run in time \(s(n) \cdot {\text {poly}}(\lambda , \log n)\), where s(n) is the set size.
Correctness. For every \(\lambda ,n \in \mathbb {N}\), if one samples \({\mathsf {sk}}\leftarrow \mathsf {Gen}(1^\lambda , n)\) and computes \(S \leftarrow \mathsf {Eval}({\mathsf {sk}})\), it holds, with probability 1 over the randomness of \(\mathsf {Gen}\), that
-
1.
\(S\in \left( {\begin{array}{c}[n]\\ s(n)\end{array}}\right) \), where \({\left( {\begin{array}{c}[n]\\ s(n)\end{array}}\right) }\) denotes the set of all size-s(n) subsets of [n], and
-
2.
for all \(i \in S\),
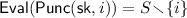 .
.
Security. Let \(\varPsi \) be a puncturable pseudorandom set with set size \(s:\mathbb {N}\rightarrow \mathbb {N}\). Let \(W_{\lambda ,n}\) be the event that adversary \(\mathcal {A}\) wins in Game 1 with respect to \(\varPsi \), with security parameter \(\lambda \) and universe size n. Then we define \(\mathcal {A}\)’s guessing advantage as:
A puncturable pseudorandom set \(\varPsi \) is computationally secure if for every \(\lambda \in \mathbb {N}\), every polynomially bounded \(n=n(\lambda )\), and every non-uniform polynomial-time adversary \(\mathcal {A}\), we have that \(\mathsf {PSAdv}[\mathcal {A},\varPsi ](\lambda ,n) \le {\text {negl}}(\lambda )\). The puncturable pseudorandom set is \(\epsilon \)-secure if that advantage is smaller than \(\epsilon (\lambda ,n)\). We say that \(\varPsi \) is perfectly secure if for every \(\lambda , n \in \mathbb {N}\) and for every (computationally unbounded) adversary \(\mathcal {A}\), we have that \(\mathsf {PSAdv}[\mathcal {A}, \varPsi ](\lambda , n) = 0\).

In the full version of this work, we show that this security property implies that the output of \(\mathsf {Eval}\) on a random key is a pseudorandom set in \({{[n]} \atopwithdelims ()s(n)}\).
Throughout this work, we often refer to puncturable pseudorandom sets as puncturable pseudorandom sets for brevity.
2.2 Constructions
Fact 2
(Perfectly secure puncturable pseudorandom set with linear-sized keys). For any function \(s: \mathbb {N}\rightarrow \mathbb {N}\) with \(s(n) \le n\), there is a perfectly secure puncturable pseudorandom set with set size s. Moreover, for universe size n, the set keys and punctured keys are both of length \((s(n)+O(1)) \log n\) bits.
Proof
The set key is the description of a set  —written as s numbers, each of \(\log n\) bits in length, along with a description of the universe size n. A punctured key is just this set of elements with the punctured element removed. \(\square \)
—written as s numbers, each of \(\log n\) bits in length, along with a description of the universe size n. A punctured key is just this set of elements with the punctured element removed. \(\square \)
Theorem 3
(puncturable pseudorandom set with short keys from puncturable PRFs). Suppose there exists an \(\epsilon _{\mathcal {F}}\)-secure puncturable PRF (we give the formal definition in the full version of this work) that, on security parameter \(\lambda \) and input-space size n, has keys of length \(\kappa (\lambda , n)\) bits and punctured keys of length \(\kappa _{\mathsf {p}}(\lambda , n)\) bits. Then, there exists an \(\epsilon \)-secure puncturable pseudorandom set with set size \(\varTheta (\sqrt{n})\) that, on security parameter \(\lambda \) and universe size n, has
-
set keys of length \(\kappa (\lambda , n) + O(\log n)\) bits and
-
punctured keys of length \(\kappa _{\mathsf {p}}(\lambda , n) + O(\log n)\) bits, and
-
\(\epsilon (\lambda , n) = {\text {poly}}(\lambda , n) \cdot (\epsilon _{\mathcal {F}} + 2^{-\lambda })\).
A puncturable pseudorandom set that proves the theorem appears in Construction 4. We prove security and correctness of the construction in the full version of this work.
Remark 4
The \(\mathsf {Gen}\) routine in Construction 4 fails with negligible probability, and therefore, as presented, the construction has imperfect correctness. We can achieve perfect correctness by having the \(\mathsf {Eval}\) and \(\mathsf {Punc}\) routines treat \({\mathsf {sk}}=\bot \) as some fixed set (e.g., the set [s]). Our security analysis accounts for this.

Instantiating Theorem 3 with the puncturable PRF [BW13, KPTZ13, BGI14] based on the tree-based PRF of Goldreich, Goldwasser, and Micali [GGM86] leads to a very efficient puncturable pseudorandom set construction from pseudorandom generators. In the full version of this work, we prove the following:
Corollary 6
Assuming that pseudorandom generators (PRGs) exist, there exists a secure puncturable pseudorandom set with set size \(\varTheta (\sqrt{n})\).
In particular, for every \(\epsilon _G\)-secure length-doubling PRG G, there exists an \(\epsilon \)-secure puncturable pseudorandom set \(\varPsi _G\) with set size \(\sqrt{n /2}\), that has, for every security parameter \(\lambda \in \mathbb {N}\) and universe size n,
-
set keys of \(\lambda + O(\log n)\) bits in length,
-
punctured keys of \(O(\lambda \log n)\) bits in length, and
-
\(\epsilon (\lambda ,n )\le {\text {poly}}(\lambda ,n)\cdot (\epsilon _G(\lambda ) + 2^{-\lambda })\).
A puncturable pseudorandom set with fast membership testing from PRPs. We say that a puncturable pseudorandom set \(\varPsi \) on universe size n has a fast membership test if there exists an algorithm \(\mathsf {InSet}\) that takes as input a set key \({\mathsf {sk}}\) and an element \(i \in [n]\), runs in time \({\text {poly}}(\lambda , \log n)\), and outputs “1” if \(i \in \varPsi .\mathsf {Eval}({\mathsf {sk}})\) and “0” otherwise. Crucially, the running time of the fast membership test must grow only with \(\log n\), rather than linearly with the set size s(n). The following is a construction of such a puncturable pseudorandom set. The proof appears in the full version of this work.
Theorem 7
Suppose there exists an \(\epsilon _P\)-secure pseudorandom permutation that, on security parameter \(\lambda \) and input-space size n, has keys of length \(\kappa (\lambda , n)\) bits. Then, there exists an \(\epsilon \)-secure puncturable pseudorandom set for any set size \(s: \mathbb {N}\rightarrow \mathbb {N}\) that, on security parameter \(\lambda \) and universe size n, has
-
set keys of length \(\kappa (\lambda , n)\) bits,
-
punctured keys of length \(s \cdot O(\log n)\) bits,
-
\(\epsilon \le {\text {poly}}(\lambda , n) \cdot \epsilon _P\), and
-
a fast membership test.
2.3 Shifting Puncturable Pseudorandom Sets
When using puncturable pseudorandom sets in this paper, we will want to equip them with two additional functionalities.
-
1.
\(\mathsf {GenWith}(1^{\lambda },n,i)\rightarrow {\mathsf {sk}}\) is an algorithm that takes in \(n\in \mathbb {N}\) and \(i \in [n]\), and outputs a uniformly random puncturable pseudorandom set key \({\mathsf {sk}}\) for a s(n)-subset of [n], subject to the constraint that \(i\in \mathsf {Eval}({\mathsf {sk}})\).
-
2.
\(\mathsf {Shift}({\mathsf {sk}}, \delta )\rightarrow {\mathsf {sk}}'\) is an algorithm that takes in a set key \({\mathsf {sk}}\in \mathcal {K}\) and an integer \(\delta \in [n]\), and outputs a set key \({\mathsf {sk}}'\) such that \(\mathsf {Eval}({\mathsf {sk}}') =\{i+\delta \,\mid \, i\in \mathsf {Eval}({\mathsf {sk}})\}\). (The addition \(i+\delta \) is done modulo n, and we identify \(0 \in \mathbb {Z}_n\) with \(n \in [n]\).)
In the full version of this work, we show how to extend any puncturable pseudorandom set to efficiently support both these functionalities by including a shift \(\varDelta \in [n]\) with every key and interpreting every element i in the base set as \((i+\varDelta ) \bmod n\) in the encompassing set. This transformation only increases the size of the puncturable set keys by an additive \(O(\log n)\) term. Therefore, we subsequently assume without a loss of generality that every puncturable set is equipped with \(\mathsf {GenWith}\) and \(\mathsf {Shift}\).
3 Two-Server PIR with Sublinear Online Time
We now formally define two-server offline/online PIR and construct such schemes that achieve sublinear online time and provide either statistical or computational security.
3.1 Definition
Informally, a two-server offline/online PIR scheme is a protocol between a client, an offline server, and an online server. Both servers have access to a database \(x \in \{0,1\}^n\). The PIR protocol proceeds in five steps:
-
1.
First, the client uses the \(\mathsf {Setup}\) algorithm to generate its own client key \(\mathsf {ck}\), along with a hint request \(q_h\). The client sends the hint request \(q_h\) to the offline server. Crucially, the client can run the \(\mathsf {Setup}\) algorithm before it has decided which bit of the database it wants to read.
-
2.
The offline server feeds the hint request \(q_h\) and the database \(x \in \{0,1\}^n\) into the \(\mathsf {Hint}\) algorithm, which generates a hint \(h\) that the offline server returns to the client.
-
3.
Once the client has decided on the index \(i \in [n]\) of the bit it wants to read from the database, it feeds its key \(\mathsf {ck}\) and index i into the \(\mathsf {Query}\) algorithm, which produces a query q. The client sends this query to the online server.
-
4.
The online server feeds the client’s query q into the \(\mathsf {Answer}\) algorithm that is further given access to the database. (The focus is on schemes in which the \(\mathsf {Answer}\) algorithm probes o(n) bits of the database and run in time o(n).) The online server then returns the answer \(a\) to the client.
-
5.
The client feeds the hint \(h\) and the answer \(a\) into algorithm \(\mathsf {Reconstruct}\), which outputs the i-th bit of the database.
A secure offline/online PIR scheme should guarantee that neither server independently learns anything (in either a statistical or computational sense) about the client’s private index i.
Definition 8
(Offline/online PIR). An offline/online PIR scheme is a tuple \(\varPi =(\mathsf {Setup},\mathsf {Hint},\mathsf {Query},\mathsf {Answer},\mathsf {Reconstruct})\) of five efficient algorithms:
-
\(\mathsf {Setup}(1^{\lambda },n) \rightarrow (\mathsf {ck}, q_h)\), a randomized algorithm that takes in security parameter \(\lambda \) and database length n and outputs a client key \(\mathsf {ck}\) and a hint request \(q_h\).
-
\(\mathsf {Hint}(x, q_h) \rightarrow h\), a deterministic algorithm that takes in a database \(x\in \{0,1\}^n\) and a hint request \(q_h\) and outputs a hint \(h\),
-
\(\mathsf {Query}(\mathsf {ck}, i) \rightarrow q\), a randomized algorithm that takes in the client’s key \(\mathsf {ck}\) and an index \(i\in [n]\), and outputs a query \(q\),
-
\(\mathsf {Answer}^x(q) \rightarrow a\), a deterministic algorithm that takes as input a query \(q\) and gets access to an oracle that:
-
takes as input an index \(j \in [n]\), and
-
returns the j-th bit of the database \(x_j \in \{0,1\}\),
outputs an answer string \(a\), and
-
-
\(\mathsf {Reconstruct}(h, a) \rightarrow x_i\), a deterministic algorithm that takes as a hint \(h\) and an answer \(a\), and outputs a bit \(x_i\).
Furthermore, the scheme \(\varPi \) must satisfy the following properties:
Correctness. For every \(\lambda ,n\in \mathbb {N}\), \(x\in \{0,1\}^n\), and \(i \in [n]\), we require that
where the probability is taken over any randomness used by the algorithms.
Security. For \(\lambda ,n\in \mathbb {N}\), and \(i, j\in [n]\), define the distribution
and for an adversary \(\mathcal {A}\), define the adversary’s advantage as
Scheme \(\varPi \) is computationally secure if for every polynomially bounded function \(n(\lambda )\) and every efficient adversary \(\mathcal {A}\), the quantity \(\mathsf {PIRadv}[\mathcal {A},\varPi ](\lambda ,n(\lambda ))\) is a negligible function of \(\lambda \). In particular, we say it is \(\epsilon \)-secure if this advantage is at most \(\epsilon (\lambda ,n)\). The scheme is statistically secure if the same holds true even for computationally unbounded adversaries.
Remark 9
(Online running time). In Definition 8, the online server’s answer algorithm \(\mathsf {Answer}\) gets oracle access to the bits of the database \(x\). We do so to emphasize that, for all of the PIR schemes described in this paper, the online server runs in time sublinear in the database size n, and can thus reply to the client’s query after probing only o(n) bits of the database. In practice, the online server could implement each oracle call using a lookup to the database in \(\widetilde{O}(1)\) time, in a reasonable model of computation (e.g., the RAM model).
Remark 10
(Information-theoretic PIR as offline/online PIR). It turns out that any two-server PIR scheme with perfect information-theoretic security can be cast as an offline/online PIR scheme. To see why: in a two-server perfectly secure PIR, the distribution over query strings that the client sends to each server is independent of the database bit that the client wants to read. (If not, the scheme cannot possibly be perfectly secure.) Thus, the client can query one of the two servers server before it knows which database bit it wants to read.
However, in all existing two-server perfectly secure PIR schemes, both servers run in time \(\varOmega (n)\) on databases of size n. Therefore, viewing any standard two-server PIR scheme as an offline/online scheme yields a two-server offline/online PIR scheme in which the online running time is \(\varOmega (n)\). In contrast, we construct offline/online PIR schemes in which the online server runs in time o(n).
3.2 New Constructions
The following theorem, which we prove at the end of this subsection, captures our main result on two-server offline/online PIR. It shows that it is possible to simultaneously achieve sublinear total communication and sublinear online time:
Theorem 11
(Two-server statistically secure offline/online PIR). There exists a statistically secure two-server offline/online PIR scheme, such that on every n-bit database and every security parameter \(\lambda \in \mathbb {N}\):
-
the offline phase uses \(O(\lambda \sqrt{n}\log ^2 n)\) bits of communication,
-
the offline server runs in time \(\widetilde{O}_\lambda (n)\),
-
the online phase uses \(O(\lambda \sqrt{n}\log n)\) bits of communication,
-
the online server runs in time \(\widetilde{O}_\lambda (\sqrt{n})\), and
-
the client uses time and memory \(\widetilde{O}_\lambda (\sqrt{n})\).
Moreover, the security advantage of any adversary is at most \({\text {poly}}(\lambda , n) \cdot 2^{-\lambda }\).
Remark 12
(Concrete efficiency). For simplicity, we give the running times of the routines in our schemes up to \({\text {poly}}(\lambda , \log n)\)-factors. It is possible to make these hidden factors as small as \(O(\lambda \log n)\).
Remark 13
(Trading communication for online time). By adjusting the parameters of the construction, it is possible to generalize Theorem 11 to give a two-server offline/online PIR scheme in which, for any function \(C:\mathbb {N}\rightarrow \mathbb {N}\) with \(C(n) \le n/2\), the offline phases uses C(n) bits of communication, and the online server runs in time \(\widetilde{O}(n / C(n))\). This adjustment requires the client and preprocessing server to have access to a sequence of common random bits, or, in the computational setting, assuming the existence of pseudorandom generators.
In the full version of this work we discuss additional issues such as support of databases with longer rows, further reducing the client’s online time via a connection to the 3-SUM problem, and implications of Theorem 11 for random self-reductions.
The following theorem, which we prove at the end of this subsection, shows that, if we settle for only computational—rather than statistical—security, we can decrease the online communication cost of the PIR scheme of Theorem 11 from \(O_\lambda (\sqrt{n}\log n)\) to \(O_\lambda (\log n)\) without degrading any other efficiency metrics. It also allows us to slightly decrease the offline communication cost.
Theorem 14
(Two-server computational offline/online PIR). Assuming the existence of pseudorandom generators, there exists a two-server offline/online PIR scheme \(\varPsi \) that satisfies the efficiency criteria of Theorem 11, except that
-
the communication cost of the offline phase decreases to \(O(\lambda \sqrt{n} \log n)\),
-
the communication cost of the online phase decreases to \(O(\lambda ^2\log n)\), and
-
if the underlying PRG is \(\epsilon _G\)-secure, the PIR scheme is \(\epsilon \)-secure for \(\epsilon (\lambda ,n)={\text {poly}}(\lambda ,n)\cdot (\epsilon _G(\lambda , n) + 2^{-\lambda })\).
The main building block we use to construct two-server PIR schemes with low communication complexity and low online server time is puncturable pseudorandom sets with small keys. We give the construction in the next subsection, and prove the following lemma about the construction in the full version of this work.
Lemma 15
Let \(s:\mathbb {N}\rightarrow \mathbb {N}\) be any function such that \(s(n) \le n/2\). Let \(\varPsi \) be an \(\epsilon _\varPsi \)-secure puncturable pseudorandom set with set size s, key size \(\kappa \), and punctured key size \(\kappa _{\mathsf {p}}\). Then there exists a two-server \(\epsilon \)-secure offline/online PIR scheme \(\varPi _\varPsi \), such that on security parameter \(\lambda \) and every n-bit database, in the offline phase:
-
the client sends \(\lambda \kappa + (\lambda n/s(n))\log ^2n\) bits to the server,
-
the offline server runs in time \(n\cdot {\text {poly}}(\lambda , \log n)\),
-
the offline server’s answer is \(O((\lambda n/s(n))\log n)\) bits in length.
In the online phase:
-
the client sends \(\lambda \kappa _{\mathsf {p}}\) bits to the server,
-
the online server runs in time \(s(n) \cdot {\text {poly}}(\lambda , \log n)\), and
-
the online server’s answer consists of \(\lambda \) bits.
Furthermore,
-
the client runs in time \((s(n) + n/s(n))\cdot {\text {poly}}(\lambda ,\log n)\) and stores \(O(\lambda \kappa + (\lambda n/s(n))\log ^2 n)\) bits between the offline and online phases, and
-
the advantage \(\epsilon (\lambda ,n) \le {\text {poly}}(\lambda , n)\cdot \left( \epsilon _\varPsi (\lambda ,n) + 2^{-\lambda }\right) \).
Theorem 11 follows by instantiating Lemma 15 with the information-theoretic puncturable pseudorandom set construction of Fact 2, which has keys and puncturable keys of length at most \((s+O(1))\log n\), and by setting \(s=\sqrt{n}\).
Theorem 14 follows by instantiating Lemma 15 with the puncturable pseudorandom set of Corollary 6, which has keys of length \(O(\lambda )\) and punctured keys of length \(O(\lambda \log n)\), and setting \(s=\sqrt{n}\). Additionally we reduce the offline communication from \(O(\lambda \sqrt{n} \log ^2n)\) to \(O(\lambda \sqrt{n} \log n)\) by replacing the random shifts used in Construction 16 with pseudorandom ones, generated from one seed of length \(\lambda \).

3.3 Construction of PIR from Puncturable Pseudorandom Sets
We first present an overview of the construction. The formal specification appears in the full version of this work, and the full analysis appears there as well.
The PIR scheme makes use of a puncturable pseudorandom set \(\varPsi = (\mathsf {Gen}, \mathsf {Punc},\mathsf {Eval})\) with set size s(n) extended by routines \((\mathsf {Shift}, \mathsf {GenWith})\). We denote  and assume without loss of generality that \(s \ge \log n\), as otherwise, a scheme in which the offline server sends the entire database to the client trivially satisfies the lemma. We also define
and assume without loss of generality that \(s \ge \log n\), as otherwise, a scheme in which the offline server sends the entire database to the client trivially satisfies the lemma. We also define  . The PIR scheme operates in two phases, in each of which the client interacts with one of the two servers:
. The PIR scheme operates in two phases, in each of which the client interacts with one of the two servers:
Offline phase
-
1.
The client samples a random set key \({\mathsf {sk}}\leftarrow \mathsf {Gen}(1^\lambda , n)\) for universe size n and set of size s. It also samples m random shifts \(\delta _1,\dotsc ,\delta _m\in [n]\). The client sends the set key and the shifts to the offline server.
-
2.
Upon receiving the set key \({\mathsf {sk}}\) and the random shifts \(\delta _1,\dotsc ,\delta _m\) from the client, the offline server expands the set key to get the set \(S \leftarrow \mathsf {Eval}({\mathsf {sk}}) \subseteq [n]\). Each shift \(\delta _j\in [n]\) defines a “shifted” set \(S_j\leftarrow \{x+\delta _j \bmod {n} \mid x\in S \}\) (when adding elements in [n], we identify it with \(\mathbb {Z}_n\)). For each shift \(\delta _j\), the offline server computes the parity of the bits pointed by the shifted set \(S_j\), i.e., sets \(h_j \mathrel {\mathop :}=\sum _{i \in S_j} x_i \bmod 2\). These bits constitute the hint \(h=(h_1, \dots , h_m) \in \{0,1\}^m\), which the server sends to the client.
Online phase. The client takes as input an index \(i_{\mathsf {pir}}\in [n]\) of the database it wants to query. The client has its set key \({\mathsf {sk}}\) and the shifts vector \(\delta \) from the offline phase and the hint \(h \in \{0,1\}^m\) from the offline server.
-
1.
The client expands the set key \({\mathsf {sk}}\) into the set \(S \leftarrow \mathsf {Eval}({\mathsf {sk}})\). It then searches for a value \(j \in [m]\) such that \(i_{\mathsf {pir}}+ \delta _j \in S\). (The client can execute this search in \(O(m + n)\) time using a hash table.)
-
If such a shift \(\delta _j\) exists, the client computes the corresponding shifted set key \({\mathsf {sk}}_q \leftarrow \mathsf {Shift}({\mathsf {sk}}, \delta _j)\), so that \(i_{\mathsf {pir}}\) falls into the set \(\mathsf {Eval}({\mathsf {sk}}_q)\).
-
If such an index does not exist, the client samples an element
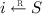 and computes the shifted set \({\mathsf {sk}}_q \leftarrow \mathsf {Shift}({\mathsf {sk}}, i_{\mathsf {pir}}- i')\).
and computes the shifted set \({\mathsf {sk}}_q \leftarrow \mathsf {Shift}({\mathsf {sk}}, i_{\mathsf {pir}}- i')\).
Either way, we refer to the chosen set key as \({\mathsf {sk}}_q\) and it holds \(i_{\mathsf {pir}}\in \mathsf {Eval}({\mathsf {sk}}_q)\).
-
-
2.
The client samples a bit
 and then chooses an element \(i_{\mathsf {punc}}\) at which to puncture its set key \({\mathsf {sk}}_q\).
and then chooses an element \(i_{\mathsf {punc}}\) at which to puncture its set key \({\mathsf {sk}}_q\).-
If \(b=0\), the client punctures the key \({\mathsf {sk}}_q\) at the point: \(i_{\mathsf {punc}}\leftarrow i_{\mathsf {pir}}\).
-
If \(b=1\), the client punctures the key \({\mathsf {sk}}_q\) at a random point:
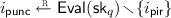 .
.
The client sends the punctured key
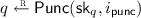 to the online server. (In the proof, we show that this punctured key computationally hides the index \(i_{\mathsf {pir}}\) of the bit that the client wants to fetch from the database.)
to the online server. (In the proof, we show that this punctured key computationally hides the index \(i_{\mathsf {pir}}\) of the bit that the client wants to fetch from the database.) -
-
3.
The online server computes the punctured set \(S^* \leftarrow \mathsf {Eval}(q)\subseteq [n]\) and views this set as \(s-1\) pointers to bits in the database \(x \in \{0,1\}^n\). The online server computes the parity of these \(s-1\) bits: \(a\leftarrow \sum _{i \in S^*} x_i \bmod 2\). The online server then returns this parity to the client. Notice that the online server only needs to probe \(s-1\) bits of the database and can run in time \(s \cdot {\text {poly}}(\lambda , \log n)\).
-
4.
If, in Step 2, the client’s random bit \(b=0\), the client can recover the bit at position \(i_{\mathsf {pir}}\) in the database from the hint \(h\) and the answer \(a\) by computing
 .
.
Note that the scheme fails if either \(i_{\mathsf {punc}}\ne i_{\mathsf {pir}}\) or \(i_{\mathsf {pir}}\notin \cup _{j\in [m]} S_j\). The probability of the former is \((s-1)/n\) and, by setting \(m\approx n\log n/s\), we can drive down the probability of the latter to be approximately 1/n. By running \(O(\lambda )\) instances of the scheme in parallel, using independent randomness for each instance, we can drive the overall failure probability to be negligible in \(\lambda \).
It is now possible to transform the PIR scheme into one with perfect correctness, at the expense of a negligible security loss. To do so, if the client detects an error (which happens with only a negligible probability), it simply reads its desired bit from the database using a non-private lookup. (Achieving perfect correctness and security is also possible, at the cost of having an offline phase that runs in expected polynomial time.)
4 Two-Server PIR with Sublinear Amortized Time
One shortcoming of the PIR scheme of the previous section is that every execution of its offline phase supports only one subsequent query. To perform each additional query, the client and the server must rerun the offline phase. Therefore, although the online query-processing time is sublinear, the overall cost of each query, including that of the offline phase, remains linear.
We now extend the scheme of the previous section such that a single execution of the offline phase enables the client to subsequently query the database polynomially many times, without ever having to rerun the offline phase. The extended scheme is nearly as efficient as the basic, single-query scheme. The only loss in efficiency is the online communication, which increases to \(\widetilde{O}(n^{1/2})\). We stress that the client can choose the retrieved indices adaptively, and so our scheme does not rely on jointly processing a batch of queries.
Our security definition, given in the full version of this work, accounts for an active (fully malicious) adversary that controls either of the two servers, and can adaptively choose the database indices that the client queries. Here, we give our main result:
Theorem 17
(Two-server multi-query offline/online PIR). Assuming the existence of pseudorandom permutations, there exists a two-server multi-query offline/online PIR scheme, such that on every n-bit database and every security parameter \(\lambda \in \mathbb {N}\), in the offline phase:
-
the offline server runs in time \(\widetilde{O}_\lambda (n)\),
-
the total communication is \(O(\lambda \sqrt{n} \log n)\) bits,
and in the online phase:
-
the online server runs in time \(\widetilde{O}_\lambda (\sqrt{n})\),
-
the total communication is \(O(\lambda \sqrt{n} \log n)\) bits, and
-
if the underlying PRP is \(\epsilon _P\)-secure, the PIR scheme is \(\epsilon \)-secure for \(\epsilon (\lambda , n) \le {\text {poly}}(\lambda ,n) \cdot (\epsilon _P(\lambda , n) + 2^{-\lambda })\).
Furthermore, the client uses offline time, storage, and online time \(\widetilde{O}_\lambda (n^{1/2})\).
In the full version of this work, we give the construction that fully specifies the scheme that proves Theorem 17. The full analysis appears in the full version of this work, where we also prove the following corollary:
Corollary 18
(Reducing communication). Assuming the existence of pseudorandom generators, there exists a scheme as in Theorem 17, albeit
-
the client offline time increases to \(\widetilde{O}_\lambda (n)\),
-
the client storage and online time increases to \(\widetilde{O}_\lambda (n^{5/6})\), and
-
the total online communication decreases to \(O(\lambda ^2 \log n)\).
Remark 19
As in Sect. 3, it is possible to achieve statistical security, by replacing the computationally secure puncturable pseudorandom set in the proof of Theorem 17, with a perfectly secure one and applying a standard “balancing” technique [CGKS95, Section 4.3] to get a scheme with online work and communication \(\widetilde{O}_\lambda (n^{2/3})\).
4.1 Sketch of the Construction
We sketch the construction here, but refer to In the full version of this work for the details.
Our starting point is the single-query scheme of Sect. 3. There, the hint consists of a list of \(m = \sqrt{n} \log n\) random sets \(S_1, \dots , S_m \subseteq [n]\), each of size roughly \(\sqrt{n}\), represented by m puncturable pseudorandom set keys, along with the parity of the database bits in each set. In the online phase, to read the ith database bit, the client finds a set \(S_j \in \{S_1, \dots , S_m\}\) such that \(i \in S_j\) and with good probability sends to the right server the set  . Once the client has used the set \(S_j\) to make a query, the client cannot use \(S_j\) again. If the client used \(S_j\) to query for another index \(i'\), the right server would, with good probability, see
. Once the client has used the set \(S_j\) to make a query, the client cannot use \(S_j\) again. If the client used \(S_j\) to query for another index \(i'\), the right server would, with good probability, see  . Taking the difference of these sets would reveal the secret indices \(\{i,i'\}\) to the right server, breaking security.
. Taking the difference of these sets would reveal the secret indices \(\{i,i'\}\) to the right server, breaking security.
The key to supporting multiple queries with only one execution of the offline phase is to have the client “refresh” its hint every time it queries the database. We refer to the two servers as “left” and “right”. The left server provides the hint to the client in the offline phase, and later helps the client to refresh that hint after each subsequent read operation. The right server answers the queries that allow the client to reconstruct the database bits it is attempting to read (as in our constructions of Sect. 3).
The online-phase interaction with the right server proceeds exactly as in the single-query scheme: the client sends a punctured set to the right server and recovers the bit \(x_i\). However, the client in the multi-query scheme must somehow replace the set \(S_j\) (and the corresponding parity bit) with a fresh random set \(S_{\mathsf {new}}\). To make this work, we must answer two questions: (i) How does the client sample the set \(S_{\mathsf {new}}\)? and (ii) How does the client fetch the corresponding parity bit \(\sum _{i \in S_{\mathsf {new}}} x_i \bmod 2\)?
First, for correctness and privacy to hold for future queries, the client must sample the replacement set \(S_{\mathsf {new}}\) in a way that preserves the joint distribution of the sets \(S_1, \dots , S_m\). Notice that sampling a fresh random set \(S_{\mathsf {new}}\) of the proper size will not work, since it distorts the joint distribution of the sets. In particular, replacing a set \(S_j\) that contains i with a fresh random set causes the expected number of sets in \(S_1, \dots , S_m\) containing i to decrease. What does work is to have the client sample a fresh random set \(S_{\mathsf {new}}\) subject to the constraint that it contains the index i that the client just read. This is possible since, as described in Sect. 2.3, punctured sets support biased sampling.
Second, the client needs to construct the correct parity bit \(h_{\textsf {new}}=\sum _{i\in S_{\mathsf {new}}}x_i \bmod 2\) for the new set \(S_{\mathsf {new}}\). The client obtains the new parity bit by (1) puncturing the set \(S_{\mathsf {new}}\) at element i and (2) querying the left server on the punctured set. The left server then replies with the parity of the bits in the punctured set  . At this point the client can recover the parity of the new set \(S_{\mathsf {new}}\) by adding the reply from the left server and the value \(x_i\), which it reconstructs, as in the single-query case, using the reply from the right server.
. At this point the client can recover the parity of the new set \(S_{\mathsf {new}}\) by adding the reply from the left server and the value \(x_i\), which it reconstructs, as in the single-query case, using the reply from the right server.
The final complication is that, as in Sect. 5, in order for the punctured set to look random, the client occasionally needs to send to the servers a set punctured at the retrieved index i. In this case, the read operation fails. When this happens, the client sends a punctured version of the new set \(S_{\mathsf {new}}\) to both servers, the client leaves its hint state unchanged, and the read operations fails.
As in Sect. 5, by running \(\lambda \) instances of the scheme in parallel we can drive the overall failure probability to be negligible in \(\lambda \). We can then trade the failure probability for a negligible security loss and get a perfectly correct scheme.
5 Single-Server PIR with Sublinear Online Time
In this section, we introduce single-server offline/online PIR. The syntax and correctness properties of a single-server offline/online PIR scheme, formally defined in the full version of this work, are exactly as in Definition 8. The key difference is that, in the single-server setting, the client interacts with the same server in both the offline phase and the online phase. Still the server should learn nothing about the database index the client wants to retrieve.
Unlike in the two-server setting, where we can achieve statistical security, in the single-server setting, we must rely on computational assumptions [CGKS95]. Since non-trivial single-server PIR implies oblivious transfer [DMO00], our assumptions must imply public-key cryptography.
Our single-server schemes shift all of the expensive work of responding to the client’s PIR query—the linear-time scan over the database and the public-key operations—into the offline phase. The server can then respond to the client’s query in the online phase much more quickly, with
-
no public-key cryptographic operations and
-
server time sublinear in the size of the database.
Our main construction (Theorem 20) achieves \(\widetilde{O}_\lambda (n^{2/3})\) communication and online time and \(\widetilde{O}_\lambda (n)\) server computational time in the offline phase, using linearly homomorphic encryption and standard single-server PIR. We also sketch an asymptotically superior construction (Theorem 22) that achieves \(\widetilde{O}_\lambda (n^{1/2})\) communication and online time, at the cost of using fully homomorphic encryption [Gen09]. Our lower bound of Sect. 6 proves the optimality of this latter scheme, up to log factors, with respect to the trade-off between offline communication and online time, given the restriction that the server must store the database in unencoded from and use no extra storage.
A drawback of our single-server PIR schemes is that they have polynomial communication \(\varOmega (n^{1/2})\), which is higher than the \({\text {polylog}}(n)\) communication of state-of-the-art standard single-server PIR schemes [CMS99]. That said, in some applications, the benefits of sublinear online time and no public-key cryptography in the online phase may outweigh the costs.
The main result of this section is:
Theorem 20
(Single-server offline/online PIR). Suppose there exist:
-
a linearly homomorphic encryption scheme (as defined in the full version of this work) with ciphertext space \(\mathbb {G}\) and
-
single-server PIR with communication cost \({\text {poly}}(\lambda , \log n)\) and server computation time \(\widetilde{O}_\lambda (n)\) (for every database size n and security parameter \(\lambda \in \mathbb {N}\)).
Then, there exists a single-server offline/online PIR scheme, that makes black-box use of the group \(\mathbb {G}\), such that for every security parameter \(\lambda \in \mathbb {N}\) and n-bit database, it uses
-
in the offline phase: \(\widetilde{O}_\lambda (n^{2/3})\) bits of communication and \(\widetilde{O}_\lambda (n)\) operations in \(\mathbb {G}\), and
-
in the online phase: \(\widetilde{O}_\lambda (n^{1/3})\) bits of communication, \(\widetilde{O}_\lambda (n^{2/3})\) time, and no operations in \(\mathbb {G}\).
Moreover, the client uses time and memory \(\widetilde{O}_\lambda (n^{2/3})\).
We prove Theorem 20 in the full version of this work.
Remark 21
(A much simpler scheme). In the full version of this work, we give a very simple—and likely easy-to-implement—single-server offline/online scheme that requires only linearly homomorphic encryption and has \(O(\sqrt{n})\) total communication, online time, and client storage. The scheme uses no public-key cryptographic operations in the online phase, and its simplicity makes it potentially attractive for practical applications. The downside is that its online phase requires a linear number of bit operations (but no public-key operations).
Patel, Persiano, and Yeo [PPY18] give an offline/online scheme with linear communication and linear online server time (but a sublinear number of online public-key operations) while this simple scheme has sublinear communication and no public-key operations in the online phase. In contrast, the client in their scheme can use a single offline phase for many online operations, while our single-server scheme requires an offline phase before each online query.
Improving efficiency with higher-order homomorphisms
If we use a homomorphic encryption scheme that supports degree-two [BGN05] or higher-degree homomorphic computation, we can build offline/online PIR schemes that provide even better communication efficiency. For example, given a fully homomorphic encryption scheme [Gen09] (FHE), we can use the idea of Theorem 20 with the two-server PIR scheme of Construction 16 to obtain:
Theorem 22
(Informal). Assume fully homomorphic encryption exists. Then, for all security parameters \(\lambda \in \mathbb {N}\), there is a single-server offline/online PIR scheme on n-bit databases that uses \(\widetilde{O}_\lambda (\sqrt{n})\) bits of communication and \(\widetilde{O}_\lambda (\sqrt{n})\) server-side time in the online phase.
The observation is that, in the two-server setting (Construction 16), the client only sends the server a PRG seed. By using FHE, the client in the single-server setting could send the server an encryption of that seed, and the server could homomorphically evaluate the offline server’s algorithm on the encrypted seed. The online phase remains the same. In the full version of this work, we discuss possible routes towards obtaining a similarly efficient scheme under weaker assumptions.
6 Lower Bound for PIR with Sublinear Online Time
In this section, we prove that the offline/online PIR schemes we construct in Sect. 3 achieve the optimal trade-off, up to log factors, between
-
the number of bits C that the client downloads in the offline phase and
-
the running time T of the server in the online phase.
Specifically, we show that any offline/online PIR scheme, in which the servers store the database in its unmodified form and use no additional storage, and that succeeds with constant probability on a database of size n, must have \((C+1)(T+1) = \widetilde{\varOmega }(n)\).
The fact that we are able to obtain a polynomial lower bound on the communication complexity of offline/online PIR schemes may be somewhat surprising, as it has been notoriously difficult to obtain communication lower bounds for standard two-server PIR, in which the servers’ running time is unbounded. In particular, in the information-theoretic setting, the best communication lower bound for two-server PIR stands at \(C \ge (5 - o(1)) \cdot \log _2 n\) bits. In contrast, for two-server PIR schemes in which one of the servers is restricted to run in time \(T \le \sqrt{n}\), we obtain a polynomial communication lower bound of \(C \ge \widetilde{\varOmega }(\sqrt{n})\).
Our lower bound holds even against offline/online PIR schemes that provide only computational security, as well as against single-server offline/online PIR schemes. Our PIR schemes of Section 3 achieve this bound, up to logarithmic factors, as does the single-server scheme of Theorem 22.
Theorem 23
Consider a computationally secure offline/online PIR scheme such that, on security parameter \(\lambda \in \mathbb {N}\) and database size \(n\in \mathbb {N}\),
-
the client downloads C bits in the offline phase,
-
the online server stores the database in its original form and probes T bits of the database in the course of processing the client’s query, and
-
the client recovers its desired bit with probability at least \(\epsilon \), over the choice of its randomness.
Then, for polynomially bounded \(n=n(\lambda )\), it holds that
and in particular for \(\epsilon \ge 1/2 + \varOmega (1)\) and large enough \(\lambda \) it holds that
We prove Theorem 23 by showing that an offline/online PIR scheme implies a solution for a computational task called “Yao’s Box Problem.” Using a preexisting lower bound for the Box Problem immediately gives a communication-time lower bound on offline/online PIR schemes. The details appear in the full version of this work.
Remark 24
The lower bound of Theorem 23 does not preclude schemes that achieve better communication and lower bound by virtue of having the servers store some form of encoding of the database. We discuss schemes of this form [DIO01, BIM04] in Sect. 1.4. In particular, constructing PIR schemes with preprocessing [BIM04] that beat the above lower bound (in terms of their communication and online time) seems like an interesting open problem.
7 Open Questions
This work leaves open a number of questions:
-
Is it possible to construct offline/online PIR schemes in which the client runs in total time o(n), stores o(n) bits, and has online running time \({\text {polylog}}(n)\)?
-
Does Theorem 22 follow from an assumption weaker than FHE?
-
Can we construct a multi-query scheme (Sect. 4) with only one server?
-
In the full version of this work, we show how to view our PIR construction via a new abstraction that we call sparse distributed point functions (“sparse DPFs”), inspired by the standard notion of DPFs [GI14]. Are there even simpler constructions of sparse DPFs than the ones implied by our PIR schemes?
References
Angel, S., Chen, H., Laine, K., Setty, S.T.V.: PIR with compressed queries and amortized query processing. In: S&P (2018)
Ambainis, A.: Upper bound on the communication complexity of private information retrieval. In: Degano, P., Gorrieri, R., Marchetti-Spaccamela, A. (eds.) ICALP 1997. LNCS, vol. 1256, pp. 401–407. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63165-8_196
Aguilar-Melchor, C., Barrier, J., Fousse, L., Killijian, M.-O.: XPIR: private information retrieval for everyone. In: PETS 2016, no. 2, pp. 155–174 (2016)
Angel, S., Setty, S.: Unobservable communication over fully untrusted infrastructure. In: SOSP 2016 (2016)
Bendlin, R., Damgård, I., Orlandi, C., Zakarias, S.: Semi-homomorphic encryption and multiparty computation. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 169–188. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_11
Boyle, E., Goldwasser, S., Ivan, I.: Functional signatures and pseudorandom functions. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 501–519. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_29
Boyle, E., Gilboa, N., Ishai, Y.: Function secret sharing: improvements and extensions. In: CCS 2016 (2016)
Boneh, D., Goh, E.-J., Nissim, K.: Evaluating 2-DNF formulas on ciphertexts. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 325–341. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_18
Beimel, A., Ishai, Y.: Information-theoretic private information retrieval: a unified construction. In: Orejas, F., Spirakis, P.G., van Leeuwen, J. (eds.) ICALP 2001. LNCS, vol. 2076, pp. 912–926. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-48224-5_74
Beimel, A., Ishai, Y., Kushilevitz, E., Raymond, J.: Breaking the \({O (n^{1/(2k-1)})}\) barrier for information-theoretic private information retrieval. In: FOCS 2002 (2002)
Beimel, A., Ishai, Y., Malkin, T.: Reducing the servers’ computation in private information retrieval: PIR with preprocessing. J. Cryptol. 17(2), 125–151 (2004)
Boyle, E., Ishai, Y., Pass, R., Wootters, M.: Can we access a database both locally and privately? In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10678, pp. 662–693. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_22
Boneh, D., Kim, S., Montgomery, H.: Private puncturable PRFs from standard lattice assumptions. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 415–445. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_15
Boneh, D., Lewi, K., Wu, D.J.: Constraining pseudorandom functions privately. In: Fehr, S. (ed.) PKC 2017. LNCS, vol. 10175, pp. 494–524. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54388-7_17
Brakerski, Z., Tsabary, R., Vaikuntanathan, V., Wee, H.: Private constrained PRFs (and more) from LWE. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 264–302. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_10
Boneh, D., Waters, B.: Constrained pseudorandom functions and their applications. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 280–300. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_15
Canetti, R., Chen, Y.: Constraint-hiding constrained PRFs for NC\(^1\) from LWE. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 446–476. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_16
Chor, B., Gilboa, N.: Computationally private information retrieval. In: STOC 1997 (1997)
Chor, B., Goldreich, O., Kushilevitz, E., Sudan, M.: Private information retrieval. In: FOCS 1995 (1995)
Chor, B., Goldreich, O., Kushilevitz, E., Sudan, M.: Private information retrieval. J. ACM 45(6), 965–982 (1998)
Canetti, R., Holmgren, J., Richelson, S.: Towards doubly efficient private information retrieval. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10678, pp. 694–726. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_23
Cachin, C., Micali, S., Stadler, M.: Computationally private information retrieval with polylogarithmic communication. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 402–414. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_28
Dvir, Z., Gopi, S.: 2-server PIR with subpolynomial communication. J. ACM 63(4), 39:1–39:15 (2016)
Döttling, N., Garg, S., Ishai, Y., Malavolta, G., Mour, T., Ostrovsky, R.: Trapdoor hash functions and their applications. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 3–32. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_1
Demmler, D., Herzberg, A., Schneider, T.: RAID-PIR: practical multi-server PIR. In: CCSW 2014 (2014)
Di Crescenzo, G., Ishai, Y., Ostrovsky, R.: Universal service-providers for database private information retrieval. In: PODC (1998)
Di Crescenzo, G., Ishai, Y., Ostrovsky, R.: Universal service-providers for private information retrieval. J. Cryptol. 14(1), 37–74 (2001)
Di Crescenzo, G., Malkin, T., Ostrovsky, R.: Single database private information retrieval implies oblivious transfer. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 122–138. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_10
Damgård, I., Pastro, V., Smart, N., Zakarias, S.: Multiparty computation from somewhat homomorphic encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 643–662. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_38
Efremenko, K.: 3-query locally decodable codes of subexponential length. SIAM J. Comput. 41(6), 1694–1703 (2012)
Gupta, T., Crooks, N., Mulhern, W., Setty, S., Alvisi, L., Walfish, M.: Scalable and private media consumption with Popcorn. In: NSDI 2016 (2016)
Goldberg, I., Devet, C., Lueks, W., Yang, A., Hendry, P., Henry, R.: Percy++, version 1.0 (2014). http://percy.sourceforge.net/
Gentry, C.: A fully homomorphic encryption scheme. Ph.D. thesis, Stanford University (2009)
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33(4), 792–807 (1986)
Gilboa, N., Ishai, Y.: Distributed point functions and their applications. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 640–658. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_35
Gentry, C., Ramzan, Z.: Single-database private information retrieval with constant communication rate. In: Caires, L., Italiano, G.F., Monteiro, L., Palamidessi, C., Yung, M. (eds.) ICALP 2005. LNCS, vol. 3580, pp. 803–815. Springer, Heidelberg (2005). https://doi.org/10.1007/11523468_65
Henry, R.: Polynomial batch codes for efficient IT-PIR. In: PoPETs 2016, no. 4, pp. 202–218 (2016)
Hohenberger, S., Koppula, V., Waters, B.: Adaptively secure puncturable pseudorandom functions in the standard model. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 79–102. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_4
Hamlin, A., Ostrovsky, R., Weiss, M., Wichs, D.: Private anonymous data access. Cryptology ePrint Archive, Report 2018/363 (2018)
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Sahai, A.: Batch codes and their applications. In: STOC 2004 (2004)
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Sahai, A.: Cryptography from anonymity. In: FOCS 2006 (2006)
Ishai, Y., Paskin, A.: Evaluating branching programs on encrypted data. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 575–594. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_31
Ishai, Y.: Private communication (2019)
Juels, A.: Targeted advertising... and privacy too. In: Naccache, D. (ed.) CT-RSA 2001. LNCS, vol. 2020, pp. 408–424. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45353-9_30
Kwon, A., Lazar, D., Devadas, S., Ford, B.: Riffle: efficient communication system with strong anonymity. In: PoPETs 2016, no. 2, pp. 115–134 (2016)
Kushilevitz, E., Ostrovsky, R.: Replication is not needed: single database, computationally-private information retrieval. In: FOCS 1997 (1997)
Kushilevitz, E., Ostrovsky, R.: One-way trapdoor permutations are sufficient for non-trivial single-server private information retrieval. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 104–121. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_9
Kiayias, A., Papadopoulos, S., Triandopoulos, N., Zacharias, T.: Delegatable pseudorandom functions and applications. In: CCS 2013 (2013)
Lueks, W., Goldberg, I.: Sublinear scaling for multi-client private information retrieval. In: Böhme, R., Okamoto, T. (eds.) FC 2015. LNCS, vol. 8975, pp. 168–186. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47854-7_10
Lipmaa, H.: An oblivious transfer protocol with log-squared communication. In: Zhou, J., Lopez, J., Deng, R.H., Bao, F. (eds.) ISC 2005. LNCS, vol. 3650, pp. 314–328. Springer, Heidelberg (2005). https://doi.org/10.1007/11556992_23
Lipmaa, H.: First CPIR protocol with data-dependent computation. In: Lee, D., Hong, S. (eds.) ICISC 2009. LNCS, vol. 5984, pp. 193–210. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14423-3_14
Mittal, P., Olumofin, F.G., Troncoso, C., Borisov, N., Goldberg, I.: PIR-Tor: scalable anonymous communication using private information retrieval. In: USENIX Security 2011 (2011)
Ostrovsky, R., Skeith, W.E.: A survey of single-database private information retrieval: techniques and applications. In: Okamoto, T., Wang, X. (eds.) PKC 2007. LNCS, vol. 4450, pp. 393–411. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71677-8_26
Patel, S., Persiano, G., Yeo, K.: Private stateful information retrieval. In: CCS 2018 (2018)
Pudlák, P., Rödl, V.: Modified ranks of tensors and the size of circuits. In: STOC 1993 (1993)
Pudlák, P., Rödl, V., Sgall, J.: Boolean circuits, tensor ranks, and communication complexity. SIAM J. Comput. 26(3), 605–633 (1997)
Sassaman, L., Cohen, B., Mathewson, N.: The Pynchon Gate: a secure method of pseudonymous mail retrieval. In: WPES 2005 (2005)
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: STOC 2014 (2014)
Toledo, R.R., Danezis, G., Goldberg, I.: Lower-cost \(\epsilon \)-private information retrieval. In: PoPETs 2016, no. 4, pp. 184–201 (2016)
Yao, A.C.-C.: Coherent functions and program checkers. In: STOC 1990 (1990)
Yekhanin, S.: Towards 3-query locally decodable codes of subexponential length. J. ACM 55(1), 1:1–1:16 (2008)
Acknowledgements
We gratefully acknowledge Dan Boneh for his advice on technical questions and for supporting our work on this project from the beginning. We thank Yuval Ishai for answering our questions about PIR, Sam Kim and David Wu for feedback on early versions of this work, and Helger Lipmaa for kindly pointing us to related work. Finally, we would like to thank the anonymous Eurocrypt reviewers for their many constructive comments. This work was supported by CISPA, DARPA, NSF, ONR, and the Simons Foundation.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Corrigan-Gibbs, H., Kogan, D. (2020). Private Information Retrieval with Sublinear Online Time. In: Canteaut, A., Ishai, Y. (eds) Advances in Cryptology – EUROCRYPT 2020. EUROCRYPT 2020. Lecture Notes in Computer Science(), vol 12105. Springer, Cham. https://doi.org/10.1007/978-3-030-45721-1_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-45721-1_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-45720-4
Online ISBN: 978-3-030-45721-1
eBook Packages: Computer ScienceComputer Science (R0)






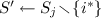 to the second server.
to the second server.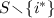 . Crucially, the punctured key
. Crucially, the punctured key 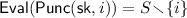 .
.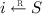 and computes the shifted set
and computes the shifted set  and then chooses an element
and then chooses an element 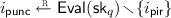 .
.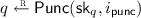 to the online server. (In the proof, we show that this punctured key computationally hides the index
to the online server. (In the proof, we show that this punctured key computationally hides the index  .
.