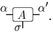Skip to main content
SpringerLink
Log in

Affleck–Kennedy–Lieb–Tasaki Model

  • Chapter
  • First Online:
Physics and Mathematics of Quantum Many-Body Systems

Part of the book series: Graduate Texts in Physics ((GTP))

  • 3968 Accesses

Abstract

In 1987, Affleck, Kennedy, Lieb, and Tasaki proposed a one-dimensional \(S=1\) antiferromagnetic quantum spin model, now called the AKLT model, whose ground state can be written down explicitly. It was shown that the energy spectrum of the model has a finite gap above the ground state energy, and the ground state correlation function decays exponentially [4, 5]. These results agree with Haldane’s conclusion for the integer spin antiferromagnetic Heisenberg chain. But note that this does not prove the Haldane “conjecture” since the model is different from the Heisenberg model. Nevertheless this work proves that there exists an \(S=1\) chain that has a unique disordered ground state with a gap, and hence provides a strong support to Haldane’s conclusion. It also provides a starting point of further studies of various phenomena and concepts related to the Haldane gap, as we shall see in Chap. 8. Now it is commonly believed that the AKLT model is (in some sense) at the “center” of the Haldane phase. In Sect. 7.1 we give a detailed discussion of the main results about the AKLT model. In Sect. 7.2 we study some unexpected features of the model, which will turn out to be essential for the study of Haldane phenomena. In Sect. 7.3 we discuss extensions and closely related models.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 89.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Hardcover Book
USD 119.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    From (2.2.19), we see that \(\hat{\varvec{S}}_x\cdot \hat{\varvec{S}}_{x+1}\) takes two eigenvalues, \(-3/4\) and 1/4. The identity then follows.

  2. 2.

    Some exact excited states were obtained in [9, 64, 65]. Unlike in integrable models, it is not possible to obtain general excited states.

  3. 3.

    From numerical works, the energy gap of the AKLT model for large L is estimated to be about 0.7. See, e.g., [32, 34].

  4. 4.

    See footnote 4 in p. 156.

  5. 5.

    In actual magnetic materials, a spin \(S=1\) comes from two \(S=1/2\)’s (of electrons) coupled by Hund’s rule. But this mathematical construction is valid irrespective of the origin of the spin \(S=1\).

  6. 6.

    Proof Because of the SU(2) invariance, it suffices to show that \(\hat{S}^{(3)}{\mathscr {S}}={\mathscr {S}}(\hat{S}^{(3)}_\mathrm{L}+\hat{S}^{(3)}_\mathrm{R})\). This is easily verified by operating the both sides to \(|\psi ^\sigma _\mathrm{L}\rangle |\psi ^{\sigma '}_\mathrm{R}\rangle \).

  7. 7.

    We believe that the term “valence-bond solid state” was first used in [4] to mean the specific class of states, which includes (7.1.12), introduced in [4, 5]. But recently it is also common to call a simple tensor product of valence bonds the VBS state. See footnote 10 below. The state (7.1.12) is also known as the AKLT state.

  8. 8.

    This construction has been implemented in an optical experiment, and the “photonic VBS state” was generated [40]. The experiment is motivated by measurement based quantum computation with the VBS state [17, 60, 63].

  9. 9.

    When L is odd, one can use the state which almost is the Néel state, with one extra 0. The argument is then essentially the same.

  10. 10.

    Here “dimer”, as opposed to “monomer”, stands for a pair of neighboring sites. The product state of singlet pairs which cover the whole lattice site is called the dimer state (or, more precisely, the dimer covering state). It is sometimes called the VBS (valence-bond solid) state. See footnote 7 above.

  11. 11.

    This should be obvious. To be rigorous, we are using Lemma A.10 in p. 469.

  12. 12.

    This is guaranteed since the ring of polynomials (with complex coefficients) is in a unique factorization domain [89].

  13. 13.

    See [7, 35, 47,48,49,50] for refinements and extensions of Knabe’s method, e.g., to systems with open boundaries or in higher dimensions. A related but different method for proving the existence of a finite gap in higher dimensional models is employed in [1, 71, 72]. See Sect. 7.3.2.

  14. 14.

    The ground states are degenerate. See Sect. 7.2.3.

  15. 15.

    Exactly as in Problem 2.5.c (p. 39), one can show that \(\langle \varPhi _\mathrm{VBS}|(\hat{S}^{(3)}_x)^2|\varPhi _\mathrm{VBS}\rangle =2/3\). This means that the average densities of \(+\), −, and 0 are all equal to 1/3. See also Problem 7.2.2.c (p. 200).

  16. 16.

    The term “quantum spin liquid” is used to indicate a variety of spin systems which exhibit liquid-like behavior. See, e.g., the review articles [59, 76].

  17. 17.

    This corresponds to the definition (3.4.6) of long-range order, which is expected to be equivalent to the definition (3.4.3) used throughout Part I. To be rigorous the existence of the limits in (7.2.4) and (7.2.7) are note proved in general.

  18. 18.

    Here the existence of the limits in (7.2.7) can be proved.

  19. 19.

    The reader anxious to study another exotic property of the AKLT model may skip this subsection and jump to Sect. 7.2.3 (and come back here when necessary).

  20. 20.

    The structure essentially equivalent to matrix product states was already known in the context of classical statistical mechanics. The work by Baxter [13] is an early example.

  21. 21.

    In the original works [26,27,28], matrix product states were called finitely correlated states. The term matrix product states was introduced later in [43]. See also [82, 83], where the representation was rediscovered and put into a slightly different context.

  22. 22.

    The general construction of matrix product states given in [28] has two parents: the AKLT model and Accardi’s proposal for the construction of quantum Markov chains [2, 3]. The relationship between the two is clarified in [66]. Note, however, that there are several definitions of quantum Markov chains that continue to be used in parallel. For example, in the quantum information community a common definition is given in terms of the case of equality in the strong subadditivity property of entropy [38].

  23. 23.

    The derivation is by no means the unique or the most convenient way to derive the matrix product representation of the VBS state. See Sect. 4.1.5 of [77] for a simple derivation which starts from the expression (7.1.11) of the pre-VBS state (which is (84) of [77]), and [80] for a derivation based on the Schwinger boson representation of [10].

  24. 24.

    The spin configuration \(\varvec{\sigma }=(0,\ldots ,0)\) is the only exception. It is generated both by \((1,\ldots ,1)\) and \((2,\ldots ,2)\).

  25. 25.

    These states satisfy \(\hat{S}^{(\alpha )}|p^{(\alpha )}\rangle =0\) and \(\exp [-i(\pi /2)\hat{S}^{(\alpha )}]\,|p^{(\beta )}\rangle =\sum _{\gamma =1,2,3}\varepsilon _{\alpha \beta \gamma }\,|p^{(\gamma )}\rangle \) for any \(\alpha ,\beta ,\gamma =1,2,3\), where \(\varepsilon _{\alpha \beta \gamma }\) is the Levi-Civita symbol (see (A.3.1)).

  26. 26.

    It is natural to represent (in general) \((A^\sigma _{\alpha ,\alpha '})^*\) as

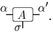
  27. 27.

    In (7.2.27), (7.2.28), and (7.2.29), we used a notation that is valid when the operator \(\hat{S}^{(3)}\) is replaced by an arbitrary local operator. The double sum in the second expression of (7.2.29) is not necessary if we are interested only in \(\hat{S}^{(3)}\).

  28. 28.

    Suppose we start from the vector \((0,1,0)^\mathrm{t}\). Multiplying it by \(\mathsf {A}^\downarrow \), we get \((0,0,1)^\mathrm{t}\). Since further multiplication by \(\mathsf {A}^\downarrow \) only yields zero, we multiply the result by \(\mathsf {A}^\uparrow \) to get \((0,1/\sqrt{2},0)^\mathrm{t}\). Note that the vector is now proportional to the initial one. Going back to the initial vector \((0,1,0)^\mathrm{t}\), we can also multiply it by \(\mathsf {A}^\uparrow \) to get \((-1,0,0)^\mathrm{t}\), and then by \(\mathsf {A}^\downarrow \) to get \((0,-1/\sqrt{2},0)^\mathrm{t}\). In this way we have formed a singlet pair \(\{|\!\uparrow \rangle |\!\downarrow \rangle -|\!\downarrow \rangle |\!\uparrow \rangle \}/\sqrt{2}\).

  29. 29.

    See [28, 70]. For mathematical details see also Sect. 6.3 of [90].

  30. 30.

    The eigenvector corresponding to \(\lambda \) is \(\delta _{\alpha ',\beta '}\) since \(\sum _{\alpha ',\beta '}(\tilde{\mathsf {A}})_{\alpha ,\beta ;\alpha ',\beta '}\,\delta _{\alpha ',\beta '} =\sum _{\alpha ',\sigma }(A^\sigma _{\alpha ,\alpha '})^*\,A^\sigma _{\beta ,\alpha '} =\sum _\sigma (\mathsf {A}^\sigma (\mathsf {A}^\sigma )^\dagger )_{\beta ,\alpha }=\lambda \,\delta _{\alpha ,\beta }\).

  31. 31.

    The condition (7.2.41) is valid with \(\lambda =3/4\). The four matrices \(\mathsf {A}^0\mathsf {A}^+\), \(\mathsf {A}^0\mathsf {A}^-\), \(\mathsf {A}^+\mathsf {A}^-\), and \(\mathsf {A}^-\mathsf {A}^+\) are enough to span the whole \(2\times 2\) matrices; the condition (i) is verified with \(\ell _0=2\).

  32. 32.

    The condition (7.2.41) is valid with \(\lambda =1\). But we find, with the aid of a computer, that the transfer matrix \(\tilde{\mathsf {A}}\) has eigenvalues \(\pm 1\).

  33. 33.

    To be precise, let \(\rho [\cdot ]\) be an arbitrary translation invariant state on the infinite chain. (See Appendix A.7 for the notation.) Then one can take a sequence \(\rho _j[\cdot ]\) with \(j=1,2,\ldots \) of matrix product states on the infinite chain such that \(\lim _{j\uparrow \infty }\rho _j[\hat{A}]=\rho [\hat{A}]\) for each \(\hat{A}\in \mathfrak {A}_\mathrm{loc}\).

  34. 34.

    A general construction (which may not give the simplest parent Hamiltonian) is as follows. Take the open chain \(\{x,\ldots ,x+\ell _0\}\) with \(\ell _0+1\) sites, where \(\ell _0\) is the constant determined in Theorem 7.5, and consider the corresponding matrix product states (7.2.45) with all possible boundary terms. Let \(\hat{P}_x\) be the projection onto the space spanned by all these matrix product states. Then \(\hat{H}=-\sum _x\hat{P}_x\) gives a desired parent Hamiltonian.

  35. 35.

    See footnote 4 in p. 156.

  36. 36.

    It may be useful to know that our \(\tilde{\mathsf {A}}\) and \(\tilde{\mathsf {B}}\) become \(\mathbb {E}_\mathbbm {1}\) and \(\mathbb {E}_{\hat{S}^{(3)}}\), respectively, in [28].

  37. 37.

    We learned this from Hosho Katsura. See [48] for recent refinements of the method.

  38. 38.

    Examine the representation (7.2.1), and see what type of spin configurations one gets for each state.

  39. 39.

    One can of course write down a formula corresponding to (7.3.1), exactly as we did in (7.1.12) for the \(S=1\) chain.

  40. 40.

    More generally (7.3.2) is expressed in terms of a polynomial including \((\hat{\varvec{S}}_x\cdot \hat{\varvec{S}}_{x+1})^4\).

  41. 41.

    For simplicity we only discuss VBS states were each bond of the lattice carries one valence bond. Clearly one can define more general VBS states with multiple valence bonds on each lattice bond as in (7.3.1).

  42. 42.

    We assume that the boundary conditions are chosen so that the lattice is bipartite.

  43. 43.

    Note that our uniqueness theorem is limited to translation invariant states. We still do not have a stronger uniqueness theorem comparable to Theorem 7.2 in p. 179.

  44. 44.

    It was demonstrated in [12, 21, 22] that whether a given quantum spin system has a gap or not (in the infinite volume) can be an undecidable problem. Although these results are highly nontrivial and deep, the difficulty related to the gap in the hexagonal lattice AKLT model has nothing to do with the undecidability. (And the existence of a gap was finally (almost) decided. See below.) 

  45. 45.

    First part of the work is fully rigorous, but the second part is numerical. Therefore the lower bound for the energy gap, although being reliable and conclusive, is not yet mathematically rigorous.

  46. 46.

    Again the first part is rigorous and the second part is numerical. But this work is closer to (or may be regarded as) a computer-aided proof since only the Lanczos method is used in the numerical part.

  47. 47.

    One might wonder if the two-dimensional VBS state exhibits exotic properties similar to those of its one-dimensional counterpart. It is obvious from the construction that the state defined on a finite lattice with open boundary is accompanied by edge spins that live on boundary sites. On the other hand it is likely that the state does not have a simple hidden order as in the one-dimensional VBS state. This observation is consistent with the modern picture that the two dimensional VBS state has only weak SPT (symmetry protected topological) order. See the end of Sect. 8.3.4.

  48. 48.

    If all sites are identical the tensor is simply \(A^{\sigma }_{(\alpha _{x,y})_{y\in {\mathscr {N}}(x)}}\).

  49. 49.

    See [11] for experimental realizations of the Briegel–Raussendorf state.

  50. 50.

    In the original paper by Briegel and Raussendorf [19], the term “cluster state” was introduced primarily to indicate the state (7.3.29) defined on a connected percolation cluster. See also [18].

  51. 51.

    In Sects. 8.2.3 and 8.3.2, in connection with the notion of symmetry protected topological (SPT) phase, we argue that the invariance under the \(\mathbb {Z}_2\times \mathbb {Z}_2\) transformation is an essential property of the VBS state and the AKLT model. The state (7.3.16) and the corresponding Hamiltonian (7.3.21) also have \(\mathbb {Z}_2\times \mathbb {Z}_2\) symmetry. More precisely, when L is even, the Hamiltonian (7.3.21) commutes with both \(\hat{U}_\mathrm{odd}:=\prod _{\ell =1}^{L/2}\hat{\sigma }^{(1)}_{2\ell -1}\) and \(\hat{U}_\mathrm{even}:=\prod _{\ell =1}^{L/2}\hat{\sigma }^{(1)}_{2\ell }\). For the aspect of the Briegel–Raussendorf as a state in a nontrivial symmetry protected topological phase, see, e.g., [78].

  52. 52.

    Let us start from the vector \((1,0)^\mathrm{t}\). The vector does not change when we multiply it (repeatedly) by \(\mathsf {A}^\uparrow \). When we multiply \((1,0)^\mathrm{t}\) by \(\mathsf {A}^\downarrow \), it changes to \((0,1)^\mathrm{t}\), passing information to the left that there is a \(\downarrow \). A multiplication of \((0,1)^\mathrm{t}\) by \(\mathsf {A}^\uparrow \) simply reverts it to \((1,0)^\mathrm{t}\). But when we multiply \((0,1)^\mathrm{t}\) by \(\mathsf {A}^\downarrow \), we get \((0,-1)^\mathrm{t}\) which contains the desired phase factor (and still the information that there is a \(\downarrow \) is passed to the left).

  53. 53.

    Note that our usage of the term cluster is very much different from that in the original paper by Briegel and Raussendorf [19].

  54. 54.

    We find that the names “graph state” and “hyper graph state” are too general and do not characterize the particular states (7.3.29) or (7.3.33) very well. Since these states are characterized by the quantum mechanical phase associated with each cluster, we feel that the name “cluster-phase state” is somewhat more appropriate. In this terminology one may specify the type of cluster by talking about the bond-phase state, the triangle-phase state, or the plaquette-phase state. The  bond-phase state is of course the Briegel–Raussendorf state (7.3.29). (It is unfortunate that the term “cluster phase” (without hyphen) is used, e.g., in [74] to mean a symmetry protected topological phase that includes the cluster state.)

  55. 55.

    The state is called the triangle-phase state in the terminology proposed in footnote 54.

References

  1. H. Abdul-Rahman, M. Lemm, A. Lucia, B. Nachtergaele, A. Young, A class of two-dimensional AKLT models with a gap (2019), arXiv:1901.09297

  2. L. Accardi, Topics in quantum probability. Phys. Rep. 77, 169–192 (1981)

    Article  ADS  MathSciNet  Google Scholar 

  3. L. Accardi, A. Frigerio, Markovian cocycles. Proc. R. Ir. Acad. 83A(2), 251–263 (1983)

    MathSciNet  MATH  Google Scholar 

  4. I. Affleck, T. Kennedy, E.H. Lieb, H. Tasaki, Rigorous results on valence-bond ground states in antiferromagnets. Phys. Rev. Lett. 59, 799 (1987)

    Article  ADS  Google Scholar 

  5. I. Affleck, T. Kennedy, E.H. Lieb, H. Tasaki, Valence bond ground states in isotropic quantum antiferromagnets. Commun. Math. Phys. 115, 477–528 (1988), https://projecteuclid.org/euclid.cmp/1104161001

  6. M. Aizenman, H. Duminil-Copin, S. Warzel, Dimerization and Néel order in different quantum spin chains through a shared loop representation, preprint (2020), arxiv:2002.02543

  7. A. Anshu, Improved local spectral gap thresholds for lattices of finite dimension (2019), arXiv:1909.01516v1

  8. I. Arad, Z. Landau, U. Vazirani, T. Vidick, Rigorous RG algorithms and area laws for low energy eigenstates in 1D. Commun. Math. Phys. 356, 65–105 (2017), arXiv:1602.08828

  9. D.P. Arovas, Two exact excited states for the \(S = 1\) AKLT chain. Phys. Lett. A 137, 431–433 (1989)

    Article  ADS  Google Scholar 

  10. D.P. Arovas, A. Auerbach, F.D.M. Haldane, Extended Heisenberg models of antiferromagnetism: analogies to the fractional quantum Hall effect. Phys. Rev. Lett. 60, 531 (1988)

    Article  ADS  MathSciNet  Google Scholar 

  11. W. Asavanant, Y. Shiozawa, S. Yokoyama, B. Charoensombutamon, H. Emura, R.N. Alexander, S. Takeda, J. Yoshikawa, N.C. Menicucci, H. Yonezawa, A. Furusawa, Generation of time-domain-multiplexed two-dimensional cluster state. Science 366, 373–376 (2019), arXiv:1903.03918

  12. J. Bausch, T. Cubitt, A. Lucia, D. Perez-Garcia, Undecidability of the spectral gap in one dimension (2018), arXiv:1810.01858

  13. R.J. Baxter, Dimers on a rectangular lattice. J. Math. Phys. 9, 650 (1968)

    Article  ADS  Google Scholar 

  14. O. Bratteli, P. Jorgensen, Endomorphisms of \(B(H)\) II. Finitely correlated states on \(O_n\). J. Funct. Anal. 145, 323–373 (1997)

    Google Scholar 

  15. O. Bratteli P. Jorgensen, A. Kishimoto, R.F. Werner, Pure states on \(\cal{O}_d\). J. Oper. Theory 43, 97–143 (2000)

    Google Scholar 

  16. O. Bratteli, P. Jorgensen, G. Price, Endomorphisms of \(B(\cal{H})\): quantization, nonlinear partial differential equations, and operator algebra, in Proceedings of Symposia in Pure Mathematics, vol. 59 (1996), pp. 93–138, https://www.duo.uio.no/handle/10852/43152

  17. G.K. Brennen, A. Miyake, Measurement-based quantum computer in the gapped ground state of a two-body hamiltonian. Phys. Rev. Lett. 101, 010502 (2008), arXiv:0803.1478

  18. H.J. Briegel, Cluster states, in Compendium of Quantum Physics, ed. by D. Greenberger, K. Hentschel, F. Weinert (Springer, Berlin, 2009), https://link.springer.com/chapter/10.1007/978-3-540-70626-7_30

  19. H.J. Briegel, R. Raussendorf, Persistent entanglement in arrays of interacting particles. Phys. Rev. Lett. 86, 910 (2001), arXiv:quant-ph/0004051

  20. W.J. Caspers, K.M. Emmett, W. Magnus, The Majumdar-Ghosh chain. Twofold ground state and elementary excitations. J. Phys. A: Math. Gen. 17, 2687 (1984)

    Google Scholar 

  21. T.B. Cubitt, D. Perez-Garcia, M.M. Wolf, Undecidability of the spectral gap. Nature 528, 207–211 (2015), arXiv:1502.04135

  22. T.B. Cubitt, D. Perez-Garcia, M.M. Wolf, Undecidability of the spectral gap (full version) (2015), arXiv:1502.04573

  23. M. den Nijs, K. Rommelse, Preroughening transitions in crystal surfaces and valence-bond phases in quantum spin chains. Phys. Rev. B 40, 4709 (1989)

    Article  ADS  Google Scholar 

  24. F.J. Dyson, E.H. Lieb, B. Simon, Phase transitions in quantum spin systems with isotropic and nonisotropic interactions. J. Stat. Phys. 18, 335–382 (1978)

    Article  ADS  MathSciNet  Google Scholar 

  25. D.V. Else, I. Schwarz, S.D. Bartlett, A.C. Doherty, Symmetry-protected phases for measurement-based quantum computation. Phys. Rev. Lett. 108, 240505 (2012), arXiv:1201.4877

  26. M. Fannes, B. Nachtergaele, R.F. Werner, Exact antiferromagnetic ground states of quantum spin chains. Europhys. Lett. 10, 633–637 (1989)

    Article  ADS  Google Scholar 

  27. M. Fannes, B. Nachtergaele, R.F. Werner, Valence bond states on quantum spin chains as ground states with spectral gap. J. Phys. A Math. Gen. 24, L185–190 (1991)

    Google Scholar 

  28. M. Fannes, B. Nachtergaele, R.F. Werner, Finitely correlated states on quantum spin chains. Commun. Math. Phys. 144, 443–490 (1992), https://projecteuclid.org/euclid.cmp/1104249404

  29. M. Fannes, B. Nachtergaele, R.F. Werner, Ground states of VBS models on Cayley trees. J. Stat. Phys. 66, 939–973 (1992)

    Article  ADS  MathSciNet  Google Scholar 

  30. M. Fannes, B. Nachtergaele, R.F. Werner, Abundance of translation invariant pure states on quantum spin chains. Lett. Math. Phys. 25, 249–258 (1992)

    Article  ADS  MathSciNet  Google Scholar 

  31. M. Fannes, B. Nachtergaele, R.F. Werner, Finitely correlated pure states. J. Funct. Anal. 120, 511–534 (1994), ftp://ace2.ma.utexas.edu/pub/mp_arc/converted/92/92-132.ps.gz

  32. G. Fáth, J. Sólyom, Solitonic excitations in the Haldane phase of an \(S=1\) chain. J. Phys.: Condens. Matter 5, 8983 (1993), arXiv:cond-mat/9309011

  33. E. Fradkin, Field Theories of Condensed Matter Physics (Cambridge University Press, Cambridge, 2013)

    Google Scholar 

  34. A. Garcia-Saez, A. Murg, T.-C. Wei, Spectral gaps of Affleck-Kennedy-Lieb-Tasaki hamiltonians using tensor network methods. Phys. Rev. B 88, 245118 (2013), arXiv:1308.3631

  35. D. Gosset, E. Mozgunov, Local gap threshold for frustration-free spin systems. J. Math. Phys. 57, 091901 (2016), arXiv:1512.00088

  36. D. Gross, Computational power of quantum many-body states and some results on discrete phase spaces, Ph.D. thesis, London University (2008), http://www.thp.uni-koeln.de/gross/files/diss.pdf

  37. D. Gross, J. Eisert, Quantum computational webs. Phys. Rev. A 82, 040303(R) (2010), arXiv:0810.2542

  38. P. Hayden, R. Jozsa, D. Petz, A. Winter, Structure of states which satisfy strong subadditivity of quantum entropy with equality. Commun. Math. Phys. 246, 359–374 (2004), arXiv:quant-ph/0304007

  39. M. Hein, W. Dür, J. Eisert, R. Raussendorf, M. Van den Nest, H.-J. Briegel, Entanglement in graph states and its applications, in Proceedings of the International School of Physics “Enrico Fermi” on “Quantum Computers, Algorithms and Chaos, Varenna, Italy (2005), arXiv:quant-ph/0602096

  40. R. Kaltenbaek, J. Lavoie, B. Zeng, S.D. Bartlett, K.J. Resch, Optical one-way quantum computing with a simulated valence-bond solid. Nat. Phys. 6, 850–854 (2010), https://www.nature.com/articles/nphys1777

  41. T. Kennedy, E.H. Lieb, H. Tasaki, A two-dimensional isotropic quantum antiferromagnet with unique disordered ground state. J. Stat. Phys. 53, 383–415 (1988)

    Article  ADS  MathSciNet  Google Scholar 

  42. T. Kennedy, H. Tasaki, Hidden symmetry breaking and the Haldane phase in \(S= 1\) quantum spin chains. Commun. Math. Phys. 147, 431–484 (1992), https://projecteuclid.org/euclid.cmp/1104250747

  43. A. Klümper, A. Schadschneider, J. Zittartz, Matrix product ground states for one-dimensional spin-1 quantum antiferromagnets. Europhys. Lett. 24, 293 (1993)

    Article  ADS  Google Scholar 

  44. S. Knabe, Energy gaps and elementary excitations for certain VBS-quantum antiferromagnets. J. Stat. Phys. 52, 627–638 (1988)

    Article  ADS  MathSciNet  Google Scholar 

  45. M. Koch-Janusz, D.I. Khomskii, E. Sela, Affleck-Kennedy-Lieb-Tasaki state on a honeycomb lattice from \(t_{2g}\) orbitals.  Phys. Rev. Lett. 114, 247204 (2015), arXiv:1501.03512

  46. A. Laeuchli, G. Schmid, S. Trebst, Spin nematic correlations in bilinear-biquadratic \(S=1\)  spin chains, Phys. Rev. B 74, 144426 (2006), arXiv:cond-mat/0607173

  47. M. Lemm, Finite-size criteria for spectral gaps in  \(D\)-dimensional quantum spin systems, (2019), arXiv:1902.07141

  48. M. Lemm, E. Mozgunov, Spectral gaps of frustration-free spin systems with boundary (2018), arXiv:1801.08915

  49. M. Lemm, A. Sandvik, L. Wang, Existence of a spectral gap in the AKLT model on the hexagonal lattice (2019), arXiv:1910.11810

  50. M. Lemm, A. Sandvik, S. Yang, The AKLT model on a hexagonal chain is gapped. J. Stat. Phys. (2019), arXiv:1904.01043

  51. C.K. Majumdar, Antiferromagnetic model with known ground state. J. Phys. C 3, 911–915 (1970)

    Article  ADS  Google Scholar 

  52. C.K. Majumdar, D.K. Ghosh, On next nearest-neighbor interaction in linear chain. I, II. J. Math. Phys. 10, 1388–1402 (1969)

    Google Scholar 

  53. T. Matsui, Translational symmetry breaking and soliton sectors for massive quantum spin models in \(1+1\) dimensions. Commun. Math. Phys. 189, 127–144 (1997)

    Article  ADS  MathSciNet  Google Scholar 

  54. T. Matsui, The split property and the symmetry breaking of the quantum spin chain. Commun. Math. Phys. 218, 393–416 (2001)

    Article  ADS  MathSciNet  Google Scholar 

  55. T. Matsui, Boundedness of entanglement entropy and split property of quantum spin chains. Rev. Math. Phys. 1350017 (2013), arXiv:1109.5778

  56. T. Matsui, A characterization of finitely correlated pure states. Infin. Dimens. Anal. Q. Probab. 1, 647–661 (1998)

    Article  Google Scholar 

  57. S. Michalakis, J.P. Zwolak, Stability of frustration-free hamiltonians. Commun. Math. Phys. 322, 277–302 (2013), arXiv:1109.1588

  58. J. Miller, A. Miyake, Hierarchy of universal entanglement in 2D measurement-based quantum computation. npj Q. Inf. 2, 16036 (2016), https://www.nature.com/articles/npjqi201636

  59. G. Misguich, Quantum spin liquids, Lectures Given at the Les Houches Summer School on Exact Methods in Low-dimensional Statistical Physics and Quantum Computing (2008), arXiv:0809.2257

  60. A. Miyake, Quantum computation on the edge of a symmetry-protected topological order, Phys. Rev. Lett. 105, 040501 (2010), arXiv:1003.4662

  61. A. Miyake, Quantum computational capability of a 2D valence bond solid phase. Ann. Phys. 326, 1656–1671 (2011), arXiv:1009.3491

  62. A. Molnar, Y. Ge, N. Schuch, J.I. Cirac, A generalization of the injectivity condition for Projected entangled pair states (2017), arXiv:1706.07329

  63. T. Morimae, V. Dunjko, E. Kashefi, Ground state blind quantum computation on AKLT state. Q. Inf. Comput. 15, 0200–0234 (2015), arXiv:1009.3486

  64. S. Moudgalya, S. Rachel, B.A. Bernevig, N. Regnault, Exact excited states of non-integrable models. Phys. Rev. B 98, 235155 (2018), arXiv:1708.05021

  65. S. Moudgalya, N. Regnault, B.A. Bernevig, Entanglement of exact excited states of AKLT models: exact results, many-body scars and the violation of strong ETH. Phys. Rev. B 98, 235156 (2018), arXiv:1806.09624

  66. B. Nachtergaele, Working with quantum Markov states and their classical analogues, in Quantum Probability and Applications V, Lecture Notes in Mathematics, vol. 1442, ed. by L. Accardi, W. von Waldenfelds (Springer, Berlin, 1990), pp. 267–285, https://link.springer.com/chapter/10.1007

  67. B. Nachtergaele, The spectral gap for some spin chains with discrete symmetry breaking. Commun. Math. Phys. 175, 565–606 (1996), https://projecteuclid.org/euclid.cmp/1104276093

  68. E.J. Neves, J.F. Perez, Long range order in the ground state of two-dimensional antiferromagnets. Phys. Lett. 114A, 331–333 (1986)

    Article  ADS  Google Scholar 

  69. K. Nomura, Onset of incommensurability in quantum spin chains. J. Phys. Soc. Jpn. 72, 476–478 (2003), arXiv:cond-mat/0210143

  70. D. Perez-Garcia, F. Verstraete, M.M. Wolf, J.I. Cirac, Matrix product state representations. Q. Inf. Comput. 7, 401 (2007), arXiv:quant-ph/0608197

  71. N. Pomata, T.-C. Wei, AKLT models on decorated square lattices are gapped. Phys. Rev. B 100, 094429 (2019), arXiv:1905.01275

  72. N. Pomata, T.-C. Wei, Demonstrating the AKLT spectral gap on 2D degree-3 lattices (2019), arXiv:1911.01410

  73. R. Raussendorf, H.-J. Briegel, A one-way quantum computer. Phys. Rev. Lett. 86, 5188 (2001), arXiv:quant-ph/0010033

  74. R. Raussendorf, C. Okay, D.-S. Wang, D.T. Stephen, H. Poulsen-Nautrup, A computationally universal phase of quantum matter. Phys. Rev. Lett. 122, 090501 (2019), arXiv:1803.00095

  75. M. Rossi, M. Hube, D. Bruß, C. Macchiavello, Quantum hypergraph states. New J. Phys. 15, 113022 (2013), http://iopscience.iop.org/article/10.1088/1367-2630/15/11/113022/meta

  76. L. Savary, L. Balents, Quantum spin liquids. Rep. Prog. Phys. 80, 016502 (2017), arXiv:1601.03742

  77. U. Schollwöck, The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 326, 96 (2011), arXiv:1008.3477

  78. W. Son, L. Amico, V. Vedral, Topological order in 1D Cluster state protected by symmetry. Q. Inf. Process. 11, 1961–1968 (2012), arXiv:1111.7173

  79. W. Spitzer, S. Starr, Improved bounds on the spectral gap above frustration-free ground states of quantum spin chains. Lett. Math. Phys. 63, 65–177 (2003), arXiv:math-ph/0212029

  80. K. Totsuka, M. Suzuki, Matrix formalism for the VBS-type models and hidden order. J. Phys.: Condens. Matter 7, 1639–1662 (1995)

    Google Scholar 

  81. P.M. van den Broeck, Exact value of the ground state energy of the linear antiferromagnetic Heisenberg chain with nearest and next-nearest neighbour interactions. Phys. Lett. A 77, 261–262 (1980)

    Article  ADS  MathSciNet  Google Scholar 

  82. G. Vidal, Efficient classical simulation of slightly entangled quantum computations. Phys. Rev. Lett. 91, 147902 (2003), arXiv:quant-ph/0301063

  83. G. Vidal, Efficient simulation of one-dimensional quantum many-body systems. Phys. Rev. Lett. 93, 040502 (2004), arXiv:quant-ph/0310089

  84. T.-C. Wei, Quantum spin models for measurement-based quantum computation. Adv. Phys.: X 1, 1461026 (2018), https://www.tandfonline.com/doi/full/10.1080/23746149.2018.1461026

  85. T.-C. Wei, I. Affleck, R. Raussendorf, Affleck-Kennedy-Lieb-Tasaki state on a honeycomb lattice is a universal quantum computational resource. Phys. Rev. Lett. 106, 070501 (2011), arXiv:1102.5064

  86. T.-C. Wei, I. Affleck, R. Raussendorf, The 2D AKLT state on the honeycomb lattice is a universal resource for quantum computation. Phys. Rev. A 86, 032328 (2012), arXiv:1009.2840

  87. X.-G. Wen, Quantum Field Theory of Many-Body Systems: From the Origin of Sound to an Origin of Light and Electrons (Oxford University Press, Oxford, 2007)

    Google Scholar 

  88. H. Weyl, The Theory of Groups and Quantum Mechanics (Dover Publication, Dover, 2014)

    Google Scholar 

  89. Wikipedia, Unique factorization domain, https://en.wikipedia.org/wiki/Unique_factorization_domain

  90. M.M. Wolf, Quantum Channels & Operations Guided Tour, Unpublished lecture note (2012), https://www-m5.ma.tum.de/foswiki/pub/M5/Allgemeines/MichaelWolf/QChannelLecture.pdf

  91. D.A. Yarotsky, Ground states in relatively bounded quantum perturbations of classical lattice systems. Commun. Math. Phys. 261, 799–819 (2006), arXiv:math-ph/0412040

  92. B. Yoshida, Topological phases with generalized global symmetries. Phys. Rev. B 93, 155131 (2016), arXiv:1508.03468

  93. B. Zeng, X. Chen, D.-L. Zhou, X.-G. Wen, Quantum Information Meets Quantum Matter: From Quantum Entanglement to Topological Phase in Many-Body Systems, Quantum Science and Technology (Springer, Berlin, 2019), arXiv:1508.02595

Download references

Author information

Authors and Affiliations

  1. Gakushuin University, Tokyo, Japan

    Hal Tasaki

Authors
  1. Hal Tasaki
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hal Tasaki .

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Switzerland AG

About this chapter

Check for updates. Verify currency and authenticity via CrossMark

Cite this chapter

Tasaki, H. (2020). Affleck–Kennedy–Lieb–Tasaki Model. In: Physics and Mathematics of Quantum Many-Body Systems. Graduate Texts in Physics. Springer, Cham. https://doi.org/10.1007/978-3-030-41265-4_7

Download citation

Publish with us

Policies and ethics

Search

Navigation