Abstract
Building a static analyser for a real language involves modeling of large domains capturing the many available data types. To scale domain design and support efficient development of project-specific analyzers, it is desirable to be able to build, extend, and change abstractions in a systematic and modular fashion. We present a framework for modular design of abstract domains for recursive types and higher-order functions, based on the theory of solving recursive domain equations. We show how to relate computable abstract domains to our framework, and illustrate the potential of the construction by modularizing a monolithic domain for regular tree grammars. A prototype implementation in the dependently typed functional language Agda shows how the theoretical solution can be used in practice to construct static analysers.
Authors ordered alphabetically.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
The construction would not work if we used final coalgebras.
- 2.
We have flattened the tuple in the first argument, to improve presentation.
- 3.
- 4.
In
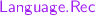 and
and
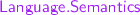 modules.
modules. - 5.
In
 and
and
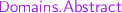 modules respectively.
modules respectively.
References
Abbott, M.G., Altenkirch, T., Ghani, N.: Containers: constructing strictly positive types. Theoret. Comput. Sci. 342(1), 3–27 (2005)
Abramsky, S., Jung, A.: Domain theory. In: Abramsky, S., Gabbay, D.M., Maibaum, T.S.E. (eds.) Handbook of Logic in Computer Science, vol. 3, pp. 1–168. Clarendon Press, Oxford (1994)
Aiken, A., Murphy, B.R.: Implementing regular tree expressions. In: Hughes, J. (ed.) FPCA 1991. LNCS, vol. 523, pp. 427–447. Springer, Heidelberg (1991). https://doi.org/10.1007/3540543961_21
Awodey, S.: Category Theory. Oxford University Press, Oxford (2011)
Benton, P.N.: Strictness properties of lazy algebraic datatypes. In: Cousot, P., Falaschi, M., Filé, G., Rauzy, A. (eds.) WSA 1993. LNCS, vol. 724, pp. 206–217. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-57264-3_42
Bodin, M., Gardner, P., Jensen, T., Schmitt, A.: Skeletal semantics and their interpretations. PACMPL 3(POPL), 44:1–44:31 (2019)
Chang, B.E., Rival, X.: Relational inductive shape analysis. In: Necula, G.C., Wadler, P. (eds.) POPL 2008, pp. 247–260. ACM (2008)
Chang, B.-Y.E., Rival, X., Necula, G.C.: Shape analysis with structural invariant checkers. In: Nielson, H.R., Filé, G. (eds.) SAS 2007. LNCS, vol. 4634, pp. 384–401. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74061-2_24
Cousot, P.: The calculational design of a generic abstract interpreter. In: Broy, M., Steinbrüggen, R. (eds.) Calculational System Design. NATO ASI Series F. IOS Press, Amsterdam (1999)
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: Graham, R.M., Harrison, M.A., Sethi, R. (eds.) POPL 1977, pp. 238–252. ACM (1977)
Cousot, P., Cousot, R.: Invited talk: higher order abstract interpretation (and application to comportment analysis generalizing strictness, termination, projection, and PER analysis. In: Bal, H.E. (ed.) Proceedings of the IEEE Computer Society 1994 International Conference on Computer Languages, Toulouse, France, 16–19 May 1994, pp. 95–112. IEEE Computer Society (1994)
Cousot, P., Cousot, R.: Formal language, grammar and set-constraint-based program analysis by abstract interpretation. In: FPCA 1995, pp. 170–181. ACM (1995)
Cousot, P., Cousot, R.: Modular static program analysis. In: Horspool, R.N. (ed.) CC 2002. LNCS, vol. 2304, pp. 159–179. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45937-5_13
Darais, D., Labich, N., Nguyen, P.C., Horn, D.V.: Abstracting definitional interpreters (functional pearl). PACMPL 1(ICFP), 12:1–12:25 (2017)
Jensen, T.P.: Disjunctive program analysis for algebraic data types. ACM Trans. Program. Lang. Syst. 19(5), 751–803 (1997)
Journault, M., Miné, A., Ouadjaout, A.: Modular static analysis of string manipulations in C programs. In: Podelski, A. (ed.) SAS 2018. LNCS, vol. 11002, pp. 243–262. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-99725-4_16
Keidel, S., Poulsen, C.B., Erdweg, S.: Compositional soundness proofs of abstract interpreters. PACMPL 2(ICFP), 72:1–72:26 (2018)
Midtgaard, J., Jensen, T.: A calculational approach to control-flow analysis by abstract interpretation. In: Alpuente, M., Vidal, G. (eds.) SAS 2008. LNCS, vol. 5079, pp. 347–362. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-69166-2_23
Nielson, F., Nielson, H.R.: The tensor product in wadler’s analysis of lists. Sci. Comput. Program. 22(3), 327–354 (1994)
Nielson, F., Nielson, H.R., Hankin, C.: Principles of Program Analysis. Springer, Heidelberg (1999). https://doi.org/10.1007/978-3-662-03811-6
Norell, U.: Dependently typed programming in agda. In: Koopman, P., Plasmeijer, R., Swierstra, D. (eds.) AFP 2008. LNCS, vol. 5832, pp. 230–266. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04652-0_5
Rival, X., Toubhans, A., Chang, B.-Y.E.: Construction of abstract domains for heterogeneous properties (position paper). In: Margaria, T., Steffen, B. (eds.) ISoLA 2014. LNCS, vol. 8803, pp. 489–492. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45231-8_40
Streicher, T.: Domain-Theoretic Foundations of Functional Programming. World Scientific Publishing Company, Singapore (2006)
Tarski, A.: A lattice-theoretical fixpoint theorem and its applications. Pac. J. Math. 5(2), 285–309 (1955)
Toubhans, A., Chang, B.-Y.E., Rival, X.: Reduced product combination of abstract domains for shapes. In: Giacobazzi, R., Berdine, J., Mastroeni, I. (eds.) VMCAI 2013. LNCS, vol. 7737, pp. 375–395. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-35873-9_23
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
A Proofs
A Proofs
Theorem 1
If \(\rho _1 \subseteq \rho _2\) then \([\![e ]\!]\rho _1 \subseteq [\![e ]\!]\rho _2\)
Proof
Most cases follow straightforwardly by induction over the syntax of terms e and functoriality of the powerset lifting \(\mathscr {P}\). We will consider the interesting cases below:
-
Case \(e = x\): follows by monotonicity of premise.
-
Case
 : follows by monotonicity of extension and induction hypothesis.
: follows by monotonicity of extension and induction hypothesis. -
Case
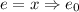 : follows by monotonicity of extension and induction hypothesis.
: follows by monotonicity of extension and induction hypothesis. -
Case \(e = \textsf {fix } \; x. e_0\): follows by monotonicity of extension, induction hypothesis and the fact that the intersection of a set of monotone functions is itself a set of monotone functions.
Proposition 1
Let E be a set and \({E^{\sharp }}\) a complete lattice. There is a bijective correspondence between maps  and Galois connections
and Galois connections  . The correspondence maps a Galois connection to \(\upalpha ^{{1}{}}_{}\) defined as \(\upalpha ^{{1}{}}_{} (x) = \upalpha _{}(\{x\})\) and a map \(\upalpha ^{{1}{}}_{}\) to the Galois connection:
. The correspondence maps a Galois connection to \(\upalpha ^{{1}{}}_{}\) defined as \(\upalpha ^{{1}{}}_{} (x) = \upalpha _{}(\{x\})\) and a map \(\upalpha ^{{1}{}}_{}\) to the Galois connection:

The correspondence can be summarized in the following diagram.

Proof
Theorem 3
Suppose the abstract interpretation of recursive types

satisfies the equations
If  then \([\![t ]\!] \subseteq \upgamma ([\![t ]\!]^{\sharp })\), or equivalently \(\upalpha ([\![t ]\!]) \sqsubseteq [\![t ]\!]^{\sharp }\)
then \([\![t ]\!] \subseteq \upgamma ([\![t ]\!]^{\sharp })\), or equivalently \(\upalpha ([\![t ]\!]) \sqsubseteq [\![t ]\!]^{\sharp }\)
Theorem 3 is proved by induction on typing judgements, and must therefore be extended to open terms. This is done in the following lemma, which uses an extension of the maps \(\upgamma \) and \(\upalpha \) to contexts defined in the obvious (pointwise) way.
Lemma 1
Suppose  , and that \(\rho \in [\![\varGamma ]\!]\) and \(\rho ^{\sharp } \in [\![\varGamma ]\!]^{\sharp }\), are such that \(\rho \subseteq \upgamma (\rho ^{\sharp })\). If the conditions on the abstract interpretation of recursive types of Theorem 3 are satisfied, then \([\![t ]\!]\rho \subseteq \upgamma ([\![t ]\!]^{\sharp }\rho ^{\sharp })\) or, equivalently, \(\upalpha ([\![t ]\!]\rho ) \subseteq [\![t ]\!]^{\sharp }\rho ^{\sharp }\)
, and that \(\rho \in [\![\varGamma ]\!]\) and \(\rho ^{\sharp } \in [\![\varGamma ]\!]^{\sharp }\), are such that \(\rho \subseteq \upgamma (\rho ^{\sharp })\). If the conditions on the abstract interpretation of recursive types of Theorem 3 are satisfied, then \([\![t ]\!]\rho \subseteq \upgamma ([\![t ]\!]^{\sharp }\rho ^{\sharp })\) or, equivalently, \(\upalpha ([\![t ]\!]\rho ) \subseteq [\![t ]\!]^{\sharp }\rho ^{\sharp }\)
Theorem 3 obviously follows from this as a special case. Before proving Lemma 1 we need a few lemmas.
Lemma 2
If B is an open type and A a closed one, then  and
and 
Proof
Easy induction on B, which we omit.
Lemma 3
For any open type B and closed type A the following equality holds

In diagram style, this is

Proof
Induction on B. The cases of integers and unit type are trivial. In the case of a type variable X, we get

In the case of a product type we get

using the induction hypothesis in the third equality. The case for sum types is somewhat similar, except here we must branch over the input being an injection on the left or right. In the first case we get

again using the induction hypothesis in the third equality. The case of the input being an injection on the right is similar.
The final case is that of functions:  . If \(f : {[\![A_1 ]\!] \rightarrow [\![B_1 ]\!]([\![A ]\!]^\sharp )}\) then
. If \(f : {[\![A_1 ]\!] \rightarrow [\![B_1 ]\!]([\![A ]\!]^\sharp )}\) then

By the induction hypothesis

which implies

since either side of this equation is the unique extension of the corresponding sides of the equation above to continuous maps. Thus, we get

proving the case and concluding the proof.
Lemma 4
If B is an open type, then the following diagram commutes

Proof
It suffices to show that  since the two compositions in the diagram are the unique extensions of the two sides of this equation to continuous maps. By definition of \(\upalpha ^{{1}{}}_{\mu X.B} \) we get
since the two compositions in the diagram are the unique extensions of the two sides of this equation to continuous maps. By definition of \(\upalpha ^{{1}{}}_{\mu X.B} \) we get
By Lemma 3 the right hand side of this is equal to  which concludes the proof.
which concludes the proof.
We can now prove Lemma 1.
Proof (Lemma 1). By induction on typing derivation:
-
Case \(t = x\) trivial
-
Case \(t = \textsf {fix } \; \lambda x. s. \): By IH we get:
$$\begin{aligned}{}[\![s ]\!]\rho [x \mapsto \upgamma ([\![t ]\!]^{\sharp }\rho ^{\sharp })]&\subseteq \upgamma ([\![s ]\!]^{\sharp }\rho ^{\sharp }[x \mapsto [\![t ]\!]^{\sharp }\rho ^{\sharp }]) \\&= \upgamma ([\![t ]\!]^{\sharp }\rho ^{\sharp }) \end{aligned}$$So \(\upgamma ([\![t ]\!]^{\sharp }\rho ^{\sharp })\) is a post-fixpoint of \(\lambda a. [\![s ]\!]\rho [x \mapsto a]\) and so greater than the greatest lower bound of these (\([\![t ]\!]\rho = \bigcap \{ a \mid [\![s ]\!]\rho [x \mapsto a] \subseteq a \}\)).
-
Case \(t = s \; u\): Recall that
 is defined as: $$ \upalpha (F) = \bigsqcup _{f \in F} \upalpha _{B} \circ \mathscr {P}(f) \circ \upgamma _{A} $$
is defined as: $$ \upalpha (F) = \bigsqcup _{f \in F} \upalpha _{B} \circ \mathscr {P}(f) \circ \upgamma _{A} $$Then

-
Case
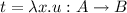 We must show that for all \(f \in [\![\lambda x. u ]\!]\rho \) it holds that $$\upalpha \circ \mathscr {P}(f) \circ \upgamma \sqsubseteq [\![\lambda x. u ]\!]^{\sharp }\rho ^{\sharp }$$
We must show that for all \(f \in [\![\lambda x. u ]\!]\rho \) it holds that $$\upalpha \circ \mathscr {P}(f) \circ \upgamma \sqsubseteq [\![\lambda x. u ]\!]^{\sharp }\rho ^{\sharp }$$or equivalently
$$\begin{aligned} \mathscr {P}(f) \circ \upgamma \sqsubseteq \upgamma \circ [\![\lambda x. u ]\!]^{\sharp }\rho ^{\sharp } \end{aligned}$$(1)We know by IH that for all \(a^{\sharp }\) it holds
$$\begin{aligned}{}[\![u ]\!]\rho [x \mapsto \upgamma (a^{\sharp })]&\subseteq \upgamma ([\![u ]\!]^{\sharp }\rho ^{\sharp }[x \mapsto \upalpha (\upgamma (a^{\sharp }))]) \end{aligned}$$(2)$$\begin{aligned}&\subseteq \upgamma ([\![u ]\!]^{\sharp }\rho ^{\sharp }[x \mapsto a^{\sharp }]) \end{aligned}$$(3)To show Eq. (1) we must show that for all \(a \in \upgamma (a^{\sharp })\) it holds:
$$\begin{aligned} f(a)&\in \upgamma (([\![\lambda x. u ]\!]^{\sharp }\rho ^{\sharp })a^{\sharp }) \\&= \upgamma ([\![u ]\!]^{\sharp }\rho ^{\sharp }[x \mapsto a^{\sharp }]) \end{aligned}$$The assumption \(f \in [\![\lambda x. u ]\!]\rho \) means precisely that \(f(a) \in [\![u ]\!]\rho [x \mapsto \{a\}] \subseteq [\![u ]\!]\rho [x \mapsto \upgamma (a^{\sharp })]\) (by monotonicity), so by Eq. (3) we conclude.
-
Case \(t = \textsf {fold } \; u : \mu X. A\), The case is proved as follows
$$\begin{aligned} \upalpha ([\![\textsf {fold } \; u ]\!]\rho )&= \upalpha (\mathscr {P}(\textsf {fold })([\![u ]\!]\rho )) \\&= \textsf {fold }^{\sharp }(\upalpha ([\![u ]\!]\rho )) \\&\sqsubseteq \textsf {fold }^{\sharp }([\![u ]\!]^{\sharp }\rho ^{\sharp }) \\&= [\![\textsf {fold } \; u ]\!]^{\sharp }\rho ^{\sharp } \end{aligned}$$using Lemma 4 for the second equality.
-
Case
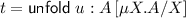 First note that $$ \upalpha \circ \mathscr {P}(\textsf {unfold }) \sqsubseteq \textsf {unfold }^{\sharp } \circ \upalpha $$
First note that $$ \upalpha \circ \mathscr {P}(\textsf {unfold }) \sqsubseteq \textsf {unfold }^{\sharp } \circ \upalpha $$since
$$\begin{aligned} \upalpha \circ \mathscr {P}(\textsf {unfold })&\sqsubseteq \textsf {unfold }^{\sharp }\circ \textsf {fold }^{\sharp }\circ \upalpha \circ \mathscr {P}(\textsf {unfold }) \\&= \textsf {unfold }^{\sharp }\circ \upalpha \circ \mathscr {P}(\textsf {fold }\circ \textsf {unfold }) \\&= \textsf {unfold }^{\sharp }\circ \upalpha \end{aligned}$$and so
$$\begin{aligned} \upalpha ([\![\textsf {unfold } \; u ]\!]\rho )&= \upalpha (\mathscr {P}(\textsf {unfold })([\![u ]\!]\rho )) \\&\sqsubseteq \textsf {unfold }^{\sharp }(\upalpha ([\![u ]\!]\rho )) \\&\sqsubseteq \textsf {unfold }^{\sharp }([\![u ]\!]^{\sharp }\rho ^{\sharp }) \text { by IH} \\&= [\![\textsf {unfold } \; u ]\!]^{\sharp }\rho ^{\sharp } \end{aligned}$$
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Al-Sibahi, A.S., Jensen, T., Møgelberg, R.E., Wąsowski, A. (2020). Galois Connections for Recursive Types. In: Di Pierro, A., Malacaria, P., Nagarajan, R. (eds) From Lambda Calculus to Cybersecurity Through Program Analysis. Lecture Notes in Computer Science(), vol 12065. Springer, Cham. https://doi.org/10.1007/978-3-030-41103-9_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-41103-9_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-41102-2
Online ISBN: 978-3-030-41103-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


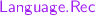 and
and
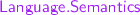 modules.
modules. and
and
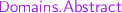 modules respectively.
modules respectively. : follows by monotonicity of extension and induction hypothesis.
: follows by monotonicity of extension and induction hypothesis.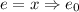 : follows by monotonicity of extension and induction hypothesis.
: follows by monotonicity of extension and induction hypothesis. is defined as:
is defined as: 
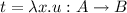 We must show that for all
We must show that for all 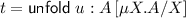 First note that
First note that