A Compact Filter Regularization Method for Solving Sideways Heat Equation

Abstract

In this paper, the stable approximate solution of the sideways heat equation is numerically investigated. The problem is severely ill-posed because if the solution exists, it does not depend continuously on the data. We introduce the compact filter regularization as a new, simple and convenient regularization method. Furthermore, the numerical implementation of the method is discussed. The numerical example shows that the proposed method is efficient and feasible.

1 Introduction

The sideways heat equation (SHE) often occurs in many industrial and engineering applications. The sideways heat equation is a model of a situation where one wishes to find out the surface temperature, but the surface itself is inaccessible for measurement [1]. Practically, the data available to us is measured data as it is based on the observations. This kind of problem is severely ill-posed since any small disruption in the observed data may lead to a drastic change in the solution. The ill-posed problems are susceptible to measurement and computational error, due to which the numerical recovery of the temperature is a tough task. Moreover, any existing numerical methods for classical PDEs cannot be directly applied to ill-posed problems to obtain a stable solution.

To overcome such difficulties, some special regularization methods [2, 3] are required for stabilizing computations. Such as, Tikhonov method [4], quasi-reversibility method [5, 6], optimal filtering method [7], wavelet and wavelet-Galerkin method [8], wavelet and Fourier method  [9], wavelet and spectral regularization method [10, 11], and so on.

A set of high order compact explicit filtering scheme is discussed in [12] to filter the high-frequency phenomena. Generally, if we use any regularization by filtering approach, the filtering is done in the Fourier space. Compact filter regularization (CFR) is a very simple and efficient method since filtering is done in the physical domain rather than other domain. The contribution of our paper can be seen as follows:

• In this paper, the key objective is to apply the compact filter as a regularization method to obtain a stable solution of SHE.

• Compact filters are a smooth filter which is preferred as compared to sharp filter.

• We do not have to go back and forth each time between physical and other domain, unlike other filtering methods.

• The proposed method is easy to implement and more efficient as all the computations are done in the physical domain only.

• A numerical example is discussed and compared with the Fourier method in terms of CPU time.

2 Problem Formulation

In a one-dimensional setting, the ill-posed problem for the heat equation in the bounded domain can be modeled as the following problem:

$$\begin{aligned} \begin{aligned} u_{t}&= \nu u_{xx} ,\; \; x \in (0,L), ~~ t \in [0,2\pi ], \\ u(x,0)&= 0 , \; \; \; \;\;\;\; x \in (0,L), \\ u(L,t)&= \phi (t) , \; \; \; t \in [0,2\pi ],\; \; \; u|_{x\rightarrow \infty }\; \text {bounded} , \end{aligned} \end{aligned}$$

(1)

where the constant $L>0$ and $\nu$ is thermal conductivity. The aim is to determine the distribution of surface temperature for $x \in (0,L)$ for the given Cauchy data $u(L,t)=\phi (t)$. It is assumed that the function $\phi (.),\; u(x,.)$ and other functions which will appear in the paper vanish for $t<0$. This problem is referred to as the sideways heat equation. Physically, the data $\phi$ can only be measured, which results in some measurement errors. The exact data $\phi$ and measured data $\phi ^{\delta }$ satisfy $\Vert \phi -\phi ^{\delta }\Vert _2\le \delta$, where $\Vert .\Vert _2$ denotes the $L_2$-norm in $[0,2\pi ]$ and $\delta >0$ stand for the noise level.

The ill-posedness of the problem can be identified if we solve them in the Fourier domain. Let the exact solution u for the problem (1) can be represented in the Fourier expansion as

$$\begin{aligned} u(x,t)=\displaystyle \sum _{k=-\infty }^{\infty }u_k(x)e^{ikt}, \end{aligned}$$

(2)

where

$$\begin{aligned} u_{k}=\,{<}u(x,t),e^{-ikt}{>}\,=\frac{1}{2\pi }\int _{0}^{2\pi }u(x,t)e^{-ikt}dt, \end{aligned}$$

(3)

and $<.,.>$ is the inner product in $L_2(0,2\pi )$. The solution of the problem (1) in the frequency domain is

$$\begin{aligned} u_{k}(x)=e^{(L-x)\nu \sqrt{ik}}\phi _{k}, \end{aligned}$$

(4)

or, equivalently,

$$\begin{aligned} u(x,t)=\displaystyle \sum _{k=-\infty }^{\infty }e^{(L-x)\nu \sqrt{ik}}\phi _{k}e^{ikt}, \end{aligned}$$

(5)

where the principle value of $\sqrt{ik}$ is given by

$$\begin{aligned} \sqrt{ik}=\left\{ \begin{array}{ll} (1+i)\sqrt{\frac{|k|}{2}}, &{} k\ge 0\\ (1-i)\sqrt{\frac{|k|}{2}}, &{} k< 0 \end{array} \right. . \end{aligned}$$

(6)

We note that $e^{\sqrt{ik}}$ tends to infinity as k tends to infinity since the real part of $\sqrt{ik}$ is positive. For our solution $u_{k}(x)$ to be in $L_2(\mathbb {R})$, (4) implies that the exact data $\phi _{k}$ must decay rapidly as $k \rightarrow \infty$. Practically, we have measured data $\phi _{k}^{\delta }$ instead of $\phi _{k}$, for which such decay is not attainable in the Fourier domain. To deal with this problem, we must use some regularization methods to filter away the high frequencies.

3 Compact Filter Regularization

High order compact filtering [12] is an explicit spatial filtering technique which filters the high unwanted wavenumber in the spatial domain. Filters are either smooth filter (obtained from the sharp filter by smoothing the sharp vertical edge at a cut off wavenumber) or sharp filter (whose value is either zero or one depending on whether the wavenumber modes are greater or below than some cutoff wavenumber). Compact filters are smooth filters rather than the sharp filter. If $y_{f}(t)$ denotes the filtered value of function y(t) for $t \in (0,T)$, then general high order compact filter for the interior domain is expressed as

$$\begin{aligned} \begin{aligned} \beta y_{f}(t-2\tau )&+\alpha y_{f}(t-\tau )+y_{f}(t)+\alpha y_{f}(t+\tau )+\beta y_{f}(t+2\tau ) = ay(t)+\frac{b}{2}(y(t+\tau )\\&+y(t-\tau ))+\frac{c}{2}(y(t+2\tau )+y(t-2\tau ))+\frac{d}{2}(y(t+3\tau )+y(t-3\tau )), \end{aligned} \end{aligned}$$

(7)

where $\tau$ is the step length. Through Fourier analysis, the transfer function $F_{\alpha }(\omega )$ corresponding to the (7) is given by

$$\begin{aligned} F_{\alpha }(\omega )=\frac{a+b\cos (\omega )+c\cos (2\omega )+d\cos (3\omega )}{1+2\alpha \cos (\omega )+2 \beta \cos (2\omega )}. \end{aligned}$$

(8)

Here, $\omega =2\pi k\tau /T$ is the modified wavenumber and its value lies in $(0,\pi )$. For the filters, the necessary criteria required is to eliminate all the phenomena arising at wavenumber $\omega =\pi$, i.e., $F_{\alpha }(\pi )=0$. For different formal accuracy, the coefficients in (7) are obtained by matching the coefficients of Taylor series of various order along with the required condition for the transfer function $F_{\alpha }(\pi )=0$. Here we use a fourth-order compact filter which can be obtained by solving the following set of coefficients

$$\begin{aligned} a=\frac{1}{8}(5+6\alpha ), \; b=\frac{1}{2}(1+2\alpha ), \;c=-\frac{1}{8}(1-2\alpha ), \end{aligned}$$

(9)

with $\beta =0, d=0$ (tridiagonal scheme). Putting the values of a, b and c from (9) to (8), we obtain

$$\begin{aligned} F_{\alpha }(\omega )= \frac{(5+6\alpha )+(4+8\alpha )\cos (\omega )-(1-2\alpha )\cos (2\omega )}{8(1+2\alpha \cos (\omega ))}. \end{aligned}$$

(10)

The coefficients a, b, and c are given in terms of single variable $\alpha$, which is called the control variable. The range of $\alpha$ usually varies from 0 to 0.5. Values of $\alpha$ close to 0.5 correspond to filtering of only high wavenumber modes.

The interior compact filters given in (7) cannot be utilized for non-periodic boundary points due to relatively large symmetric stencils. Hence, for boundary filters, a one-sided fourth-order compact filter is used which is explicitly given as

$$\begin{aligned} \begin{aligned} y_{f}(0)&= \frac{15}{16}y(0)+\frac{1}{16}\left( 4y(\tau )-6y(2\tau )+4y(3\tau )-y(4\tau )\right) \!,\\ y_{f}(\tau )&= \frac{3}{4}y(\tau )+\frac{1}{16}\left( y(0)+6y(2\tau )-4y(3\tau )+y(4\tau )\right) \!, \end{aligned} \end{aligned}$$

(11)

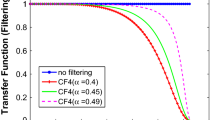
with exact filtering of wavenumber $\omega =\pi$. The similar expression can be written for $y_{f}(T-\tau )$ and $y_{f}(T)$. We use (11) for boundary point and (7) for any interior value of t to obtain filtered function $y_{f}(t)$ from the function y(t). The plot of filtering transfer function $F_\alpha (\omega )$ (given in (10)) versus wavenumber $\omega$ for different values of $\alpha$ is shown in Fig. 1.

Fig. 1.

Transfer function $F_\alpha (\omega )$ versus wavenumber $\omega$ for no filtering and fourth-order compact filtering with $\alpha =0.4$, 0.45 and 0.49.

From Fig. 1, we can see that as we reduce the value of $\alpha$ from 0.5, not only high wavenumber mode, but a wide range of wavenumber spectrum is also filtered. It is also clear from the figure that $F_\alpha (\pi ) =0$ for all $\alpha$.

The compact filter regularized solution for problem (1) with measured data $\phi ^{\delta }(.)$ can be presented as

$$\begin{aligned} u_f^{\delta }(x,t)=\displaystyle \sum _{k=-M}^{M}e^{(L-x)\nu \sqrt{ik}}F_{\alpha }(\omega )\phi _{k}^{\delta }e^{ikt}, \end{aligned}$$

(12)

where $\omega =k\tau$ as $t \in [0,2\pi ]$. The step length $\tau$ plays the role of regularization parameter and M is taken as $M=[\frac{\pi }{\tau }]$ where [.] denoted the greatest integer part of a real number.

4 Numerical Implementation of CFR Method

To obtain the stable numerical solution, we will use the method of lines to solve the Cauchy problem. Let $t_n$ be the coordinate of the node after time discretization with n denotes the indices for discrete time. Consider the equidistant grid $0=t_1<t_2< \dotsc <t_{N+1}=2\pi$ where $1 \le n\le N+1$ and $N =\frac{2\pi }{\tau }$ with $M=N/2$. The block operator equation of the discretized problem (1) using compact filter with $L=1$ can be rewritten as

$$\begin{aligned} \begin{aligned} \begin{bmatrix} U_f(x) \\ \nu U_{f,x}(x) \end{bmatrix}_x&=\begin{bmatrix} 0 &{} \nu ^{-1}I \\ D &{} 0 \end{bmatrix} \begin{bmatrix} U_f(x) \\ \nu U_{f,x}(x) \end{bmatrix}\!, \quad x \in (0,1),\\ \begin{bmatrix} U_f(1) \\ U_{f,x}(1) \end{bmatrix}&= [\phi _f^{\delta ,1}, \dotsc \phi _f^{\delta ,N+1},\rho _f^{\delta ,1},\dotsc ,\rho _f^{\delta ,N+1}]^T\\ u_{f}(x,t_1)&\approx u_f^1=0,\quad x \in (0,1), \end{aligned} \end{aligned}$$

(13)

where D is the time discretization matrix, and $U_f(x)$ is the vector containing the values $u_f^n$. We will use (7) at a given discrete node $t_n$ to obtain the filtered value $u_f^n$ of u. The vectors $U_f(x)$, $U_f(1)$ and $U_{f,x}(1)$ are represented as

$$U_f(x)=[u_f^1,u_f^2 \dotsc u_f^{N}, u_f^{N+1}]^T,$$

$$U_f(1)=[\phi _f^{\delta ,1},\phi _f^{\delta ,2} \dotsc \phi _f^{\delta ,N}, \phi _f^{\delta ,N+1}]^T,\quad U_{f,x}(1)=[\rho _f^{\delta ,1},\rho _f^{\delta ,2} \dotsc \rho _f^{\delta ,N}, \rho _f^{\delta ,N+1}]^T.$$

The problem defined by (13) is considered as method of lines.

The time discretization matrix D is obtained using central difference approximation, i.e.,

$$\begin{aligned} D_n=\frac{u_f^{n+1}-u_f^{n-1}}{2\tau }, \quad 2\le n \le N, \end{aligned}$$

(14)

where, as before, $\tau$ is the time step length. At $n=N+1$, we use linear extrapolation, i.e.,

$$\begin{aligned} \begin{aligned} D_{N+1}=D_N+(D_N-D_{N-1}) =\frac{1}{2\tau }(1 \quad -2 \quad -1 \quad 2) \begin{bmatrix} u_f^{N-2}\\ u_f^{N-1}\\ u_f^{N}\\ u_f^{N+1} \end{bmatrix}\!. \end{aligned} \end{aligned}$$

Finally, to obtain the stable numerical solution of sideways heat equation using a compact filter regularization method, the necessary steps of the algorithm are given as follows:

4.1 Numerical Experiment

In this section, we present a numerical example of the sideways heat equation to illustrate the stability and effectiveness of our proposed compact filter regularization method. The method of lines is used to solve the discretized version of the sideways heat equation as given by (13) for numerical experiments. Central difference approximation is used for time derivative, and then the Runge-Kutta-Fehlberg method (ode45 in Matlab) is applied to perform the space marching. In all the experiments, the required accuracy in the R-K method was $10^{-4}$.

To obtain the noisy data $\phi ^{\delta }(t)$ and $\rho ^{\delta }(t)$, we introduce some random noise $\eta$, i.e., $\phi ^{\delta }(t)=\phi (t)+\eta ,\quad \rho ^{\delta }(t)=\rho (t)+\eta$, where $\eta =\delta \times \text{ rand(t) }\times ||.||_{\infty }$,  rand(t) is the random vector obtained using MATLAB function ‘rand’ and $\delta$ is the noise level of the measured data. For comparing the numerical and exact solution, relative error at fixed x is computed as

$$e_{2}(u)=\frac{||u_f^{\delta }(x,.)-u(x,.)||_{2}}{||u(x,.)||_{2}},$$

where $u_f^{\delta }(x,.)$ stands for the numerical regularized solution with noisy data and u(x, .) stands for exact solution of the problem considered.

Example.It is easy to verify that $u(x,t)=\left\{ \begin{array}{ll} \frac{x+1}{t^{3/2}}\exp {\left( -\frac{(x+1)^2}{4t}\right) }, &{} t \in (0,2\pi ),\\ 0, &{} t\le 0, \end{array} \right.$ is the exact solution of the problem (1) with data

$$ \phi (t)=\left\{ \begin{array}{ll} \frac{2}{t^{3/2}}\exp {\left( -\frac{1}{t}\right) }, &{} t \in (0,2\pi ).\\ 0, &{} t\le 0, \end{array} \right. $$

with $u(x,0)=0$. The exact solution at $x=0$ is $h(t):=u(0,t)= t^{-3/2}\exp {\left( -\frac{1}{4t}\right) }.$

To obtain the numerical results, the noise level is fixed at $10^{-3}$, and the constant coefficient of the differential operator is set at $\nu =1$. We choose $N=\frac{2\pi }{\tau }$ and corresponding $M=N/2$ for ML solution. The step size for x is taken as 1/128. The exact and regularized solution for different x is computed using the method of lines and shown in Fig. 2. From the figure, we find that the computed results using our proposed regularization method is stable and effective. In Table 1, the relative error at different x for two noise level $\delta$ is displayed from which we can observe that the computed regularized solution are better for large x. Furthermore, it can also be seen that the regularized solution becomes worse as we increase the noise level $\delta$, which is obvious. To compare our proposed method in terms of CPU time, we have solved our problem using the Fourier method [9] where filtering is done in the Fourier domain with $k=M$. The CPU time for both the method is given in Table 2 from which it is clear that proposed method is more efficient.

Fig. 2.

Plot of exact and regularized solution with $\delta =10^{-3}$.

Table 1. Relative error for test problem 1 with noise level $\delta _1=10^{-3}$, $\delta _2=10^{-2}$.

Table 2. Comparison of CPU time for test problem 1 with proposed method and Fourier method [9].

5 Conclusion

In this paper, the sideways heat equation is solved by the compact filter regularization method. The numerical experiment is done to obtain a stable solution of the SHE. We conclude that the numerical implementation of the proposed method is simple and efficient. Numerical results are presented and compared with the existing one to demonstrate that the proposed method is effective and works well. In the future, we would like to extend the proposed method for the solution of two-dimensional SHE and also some other non-linear ill-posed problems.