Abstract
Let U be an arbitrary non-empty (distributive) set of objects (a so-called universe of discourse). Let \(\sqsubset \) be the extension of the relational concept being a part with respect to U. It is a binary relation in U which strictly partially orders the universe.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
For more on the concepts of a partial order and a strict partial order, see Appendices A.3, B.1 and B.2.
- 2.
On the subject of quasi-orders, see Appendices A.3 and B.9.
- 3.
In the diagram of Model 2.1 occur the names of conditions which will only be introduced later. This model will, however, also be used for those conditions. The same will be true of other models we will meet.
- 4.
We shall always proceed in this way when the class \({\mathbf {\mathsf{{POS}}}}\) is our object of interest.
- 5.
The very same concept is found under the names of ‘discreteness’ and ‘disjointness’ in (Leonard and Goodman 1940, p. 46) and (Simons 1987, p. 28), respectively. The symbol used here is modelled on the symbol used in (Simons 1987). In (Leonard and Goodman 1940), the symbol ‘\(\urcorner \llcorner \)’ is used. The terms ‘discreteness’ and ‘disjointness’ are, however, inaccurate, because it is possible to give an interpretation of mereology in point-free geometry, in which two objects are exterior to one another yet “touch”.
- 6.
- 7.
Degenerate structures are of no interest to us, although all the conditions mentioned also hold in such structures if we accept that their single element is an atom.
- 8.
- 9.
Obviously, it can only be the zero in degenerate structures.
- 10.
In (Simons 1987) sentence (\(\mathrm {ext}_{\scriptscriptstyle \sqsubset }\mathrm {+}\)) is called the Proper Parts Principle. In Simons’ terminology ‘proper part’ corresponds to what we understand here by ‘part’.
- 11.
- 12.
Simons (1987, p. 29) gives another proof of this result.
- 13.
Recall that the simpler Model 2.3 from the class \({_{{\mathbf {\mathsf{{s}}}}}}{{\mathbf {\mathsf{{POS}}}}}\) suffices to show that (\(\mathrm {SSP}\)) does not follow from (\(\mathrm {ext}_{\scriptscriptstyle \bigcirc }\)). Obviously, another model simpler than Model 2.4 would likewise suffice to show that, in the class \({_{{\mathbf {\mathsf{{s}}}}}}{{\mathbf {\mathsf{{POS}}}}}\), condition (\(\mathrm {SSP}\)) does not follow from (\(\mathrm {ext}_{\scriptscriptstyle \sqsubset }\mathrm {+}\)).
- 14.
The simpler Model 2.1 from \({_{{\mathbf {\mathsf{{s}}}}}}{{\mathbf {\mathsf{{POS}}}}}\) suffices to show that (\(\mathrm {WSP}\)) does not follow from (\(\mathrm {ext}_{\scriptscriptstyle \sqsubset }\mathrm {+}\)).
- 15.
Here, the symbols ‘\(\sqsubset \)’, ‘\(\sqsubseteq \)’, ‘
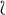 ’, ‘\(\bigcirc \)’ and ‘\((\!\!)\)’ play a double role: as two-place predicates and the names of binary relations (more precisely: variable or binary relations). Obviously, it would be possible to have different symbols for the predicates and the names of relations.
’, ‘\(\bigcirc \)’ and ‘\((\!\!)\)’ play a double role: as two-place predicates and the names of binary relations (more precisely: variable or binary relations). Obviously, it would be possible to have different symbols for the predicates and the names of relations. - 16.
It needn’t be a new class of structures. A given class may simply have various different names (through the addition of different names of conditions).
- 17.
With reference to Sect. 2.1.2, let us recall that (\(\mathrm {r}_{\scriptscriptstyle \sqsubseteq }\)) is a direct consequence of definition (\(\mathrm {df}\,\sqsubseteq \)) and the reflexivity of identity. Therefore, in our theory we can have condition (\(\mathrm {r}_{\scriptscriptstyle \sqsubseteq }\)) without any additional assumptions. This holds for all the sentences in this lemma.
- 18.
The proven sentence says that in the class \({_{{\mathbf {\mathsf{{s}}}}}}{{\mathbf {\mathsf{{POS}}}}}\) (resp. \({\mathbf {\mathsf{{QOS}}}}\)) the relation \(\mathrel {\mathsf {sum}}\) is included in the relation \(\mathrel {\mathsf {fu}}\) satisfying the following condition: \(x\mathrel {\mathsf {fu}}S\) iff \(\mathsf {O}(x)=\bigcup \mathsf {O}[S]\). The relation \(\mathrel {\mathsf {fu}}\) is another explication of the concept of being a collective set. In Sect. 2.12 of this chapter we will show that in the class \({_{{\mathbf {\mathsf{{s}}}}}}{{\mathbf {\mathsf{{PPOS}}}}}\) we obtain \(\mathord {\mathrel {\mathsf {sum}}}=\mathord {\mathrel {\mathsf {fu}}}\).
- 19.
Henceforth, we will omit ‘and from our definitions’ from statements of entailments.
- 20.
Obviously, to reject (\(\mathrm {S}_{\scriptscriptstyle \mathrel {\mathsf {sum}}}\)), (\(\mathrm {U}_{\scriptscriptstyle \mathrel {\mathsf {sum}}}\)) and (\(\mathrm {M}_{\scriptscriptstyle \mathrel {\mathsf {sum}}}\)) in the class \({_{{\mathbf {\mathsf{{s}}}}}}{{\mathbf {\mathsf{{POS}}}}}\), Model 2.1 suffices. To see this, \(1\not \sqsubseteq 0\) and thanks to (2.6.5) and (2.6.7): \(0\mathrel {\mathsf {sum}}\{0\}\) and \(1\mathrel {\mathsf {sum}}\{0\}\).
- 21.
In (Leonard and Goodman 1940), the relation \(\mathrel {\mathsf {fu}}\) is also called the relation of sum-individual.
- 22.
- 23.
Similar to how the empty set \(\varnothing \) is disjoint from every other set, including itself.
References
Casati, R., & Varzi, A. C. (1999). Parts and places. Cambridge: The MIT Press.
Chisholm, R. M. (1992/93). Spatial continuity and the theory of part and whole. A Brentano study. Brentano Studien, 4, 11–23.
Leonard, H. S., & Goodman, N. (1940). The calculus of individuals and its uses. Journal of Symbolic Logic, 5(2), 45–55. http://dx.doi.org/10.2307/2266169
Leśniewski, S. (1931). O podstawach matematyki (On the foundations of mathematics). Przegląd Filozoficzny, 34, 142–170.
Libardi, M. (1990). Teorie delle parti e dell’intero. Mereolologie estensionali (Theories of parts and the whole. Extensional mereologies). Vol. II of Quaderni, Aprile–Dicembre.
Pietruszczak, A. (2000). Metamereologia (Metamereology). Toruń: The Nicolaus Copernicus Univesity Press. English version (2018): Metamereology. Toruń: The Nicolaus Copernicus Univesity Scientific Publishing House. https://doi.org/10.12775/3961-4
Pietruszczak, A. (2018). Metamereology. Toruń: The Nicolaus Copernicus Univesity Scientific Publishing House. English version of (Pietruszczak, 2000). https://doi.org/10.12775/3961-4
Simons, P. (1987). Parts. A study in ontology. Oxford: Oxford University Press. http://dx.doi.org/10.1093/acprof:oso/9780199241460.001.0001
Tarski, A. (1929). Les fondements de la géométrie des corps (Foundations of the geometry of solids). Księga Pamiątkowa Pierwszego Zjazdu Mate (pp. 29–30).
Tarski, A. (1956). Fundations of the geometry of solids. In J. H. Woodger (Ed.), Logic, semantics, metamathematics. Papers from 1923 to 1938 (pp. 24–29). Oxford: Oxford University Press. English version of (Tarski, 1929).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Pietruszczak, A. (2020). “Existentially Neutral” Theories of Parts. In: Foundations of the Theory of Parthood. Trends in Logic, vol 54. Springer, Cham. https://doi.org/10.1007/978-3-030-36533-2_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-36533-2_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-36532-5
Online ISBN: 978-3-030-36533-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


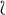 ’, ‘
’, ‘