Abstract
The complexity of collision-resistant hash functions has been long studied in the theory of cryptography. While we often think about them as a Minicrypt primitive, black-box separations demonstrate that constructions from one-way functions are unlikely. Indeed, theoretical constructions of collision-resistant hash functions are based on rather structured assumptions.
We make two contributions to this study:
-
1.
A New Separation: We show that collision-resistant hashing does not imply hard problems in the class Statistical Zero Knowledge in a black-box way.
-
2.
New Proofs: We show new proofs for the results of Simon, ruling out black-box reductions of collision-resistant hashing to one-way permutations, and of Asharov and Segev, ruling out black-box reductions to indistinguishability obfuscation. The new proofs are quite different from the previous ones and are based on simple coupling arguments.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Collision-resistant hash functions (CRHFs) are perhaps one of the most studied and widely used cryptographic primitives. Their applications range from basic ones like “hash-and-sign” [Dam87, Mer89] and statistically hiding commitments [DPP93, HM96] to more advanced ones like verifiable delegation of data and computation [Kil92, BEG+94] and hardness results in complexity theory [MP91, KNY17].
Constructions. Collision resistance is trivially satisfied by random oracles and in common practice, to achieve it, we heuristically rely on unstructured hash functions like SHA. Accordingly, we often think of CRHFs as a creature of Minicrypt, the realm of symmetric key cryptography [Imp95]. However, when considering theoretical constructions with formal reductions, collision resistance is only known based on problems with some algebraic structure, like Factoring, Discrete Log, and different short vector and bounded distance decoding problems (in lattices or in binary codes) [Dam87, GGH96, PR06, LM06, AHI+17, YZW+17, BLVW19]. Generic constructions are known from claw-free permutations [Dam87, Rus95], homomorphic primitives [OK91, IKO05], and private information retrieval [IKO05], which likewise are only known from similar structured assumptions. An exception is a recent work by Holmgren and Lombardi [HL18] which constructs CRHFs from a new assumption called one-way product functions. These are functions where efficient adversaries succeed in inverting two random images with probability at most \(2^{-n-\omega (\log n)}\). Indeed, this assumption does not explicitly require any sort algebraic structure.
Understanding the Complexity of CRHFs. In light of the above, it is natural to study what are the minimal assumptions under which CRHFs can be constructed, and whether they require any sort of special structure. Here Simon [Sim98] provided an explanation for our failure to base CRHFs on basic Minicrypt primitives like one-way functions or one-way permutations. He showed that there are no black-box reductions of CRHFs to these primitives. In fact, Asharov and Segev [AS15] demonstrated that the difficulty in constructing CRHFs from general assumptions runs far deeper. They showed that CRHFs cannot be black-box reduced even to indistinguishability obfuscation (and one-way permutations), and accordingly not to anyone of the many primitives it implies, like public key encryption, oblivious transfer, or functional encryption.
CRHFs and SZK. An aspect common to many CRHF constructions is that they rely on assumptions that imply hardness in the class \({\mathsf {SZK}}\). Introduced by Goldwasser, Micali and Rackoff [GMR85], \({\mathsf {SZK}}\) is the class of promise problems with statistical zero-knowledge proofs. Indeed, \({\mathsf {SZK}}\) hardness is known to follow from various algebraic problems that lead to CRHFs, such as Discrete Logarithms [GK93], Quadratic Residuosity [GMR85], and Lattice Problems [GG98, MV03], as well as from generic primitives that lead to CRHFs such as homomorphic encryption [BL13], lossy functions [PVW08], and computational private information retrieval [LV16].
The formal relation between \({\mathsf {SZK}}\) and CRHFs is still not well understood. As possible evidence that \({\mathsf {SZK}}\) hardness may be sufficient to obtain collision resistance, Komargodski and Yogev [KY18] show that average-case hardness in \({\mathsf {SZK}}\) implies a relaxations of CRHFs known as distributional CRHFs. Applebaum and Raykov [AR16] show that CRHFs are implied by average-case hardness in a subclass of \({\mathsf {SZK}}\) of problems that have a perfect randomized encoding. Berman et al. [BDRV18] showed that average-case hardness of a variant of entropy approximation, a complete problem for the class of Non-Interactive SZK (\(\mathsf {NISZK}\)), suffices to construct yet a different relaxation known as multi-collision resistance.
Is hardness in \({\mathsf {SZK}}\) necessary for CRHFs? Our perception of CRHFs as a Minicrypt primitive, as well as the result by Holmgren and Lombardi mentioned above, suggest that this should not be the case. However, we do not know how to prove this. Meaningfully formalizing a statement of the form “CRHFs do not require \({\mathsf {SZK}}\) hardness” requires care—it is commonly believed that \({\mathsf {SZK}}\) does contain hard problems, and if this is the case then formally, CRHFs (or any other assumption for that matter) imply hardness in \({\mathsf {SZK}}\). To capture this statement we again resort to the methodology of black-box separations; that is, we aim to prove that hard problems in \({\mathsf {SZK}}\) cannot be obtained from CRHFs in a black-box way.
Recent work by Bitansky, Degwekar, and Vaikuntanathan [BDV17] showed that a host of primitives, essentially, all primitives known to follow from IO, do not lead to hard problems in \({\mathsf {SZK}}\) through black-box reductions. Their separation, however, does not imply a separation from CRHFs; indeed, CRHFs are not known to follow from IO, and in fact according to Asharov and Segev [AS15], cannot in a black-box way.
1.1 This Work
In this work, we close the above gap, proving that CRHFs do not imply hardness in \({\mathsf {SZK}}\) through black-box reductions.
Theorem 1.1
There are no fully black-box reductions of any (even worst-case) hard problem in \({\mathsf {SZK}}\) to CRHFs.
Here by fully black box we mean reductions where both the construction and the security proof are black box in the CRHF and the attacker, respectively. This is the common type of reductions used in cryptography. We refer the reader to the technical overview in Sect. 2 for more details.
New Proofs of Simon and Asharov and Segev. Our second contribution is new proofs for the results of Simon [Sim98], ruling out fully black-box reductions of CRHFs to OWPs,Footnote 1 and of Asharov and Segev [AS15], ruling out black-box reductions of CRHFs to OWPs and IO. The new proofs draw from ideas used in [BDV17]. They are based mostly on simple coupling arguments and are quite different from the original proofs.
1.2 More Related Work on Black-Box Separations
Following the seminal work of Impagliazzo and Rudich [IR89], black-box separations in cryptography have been thoroughly studied (see, e.g., [Rud88, KST99, GKM+00, GT00, GMR01, BT03, RTV04, HR04, GGKT05, Pas06, GMM07, BM09, HH09, BKSY11, DLMM11, KSS11, GKLM12, DHT12, Fis12, BBF13, Pas13, BB15, GHMM18]). Most of this study has been devoted to establishing separations between different cryptographic primitives and some of it to putting limitations on basing cryptographic primitives on \({\mathsf {NP}}\)-hardness [GG98, AGGM06, MX10, BL13, BB15, LV16].
Perhaps most relevant to our works are the works of Simon [Sim98], Asharov and Segev [AS15] and [BDV17] mentioned above, as well as the work by Haitner et al. [HHRS15] who gave an alternative proof for the Simon result (and extended it to the case of statistically-hiding commitments of low round complexity).
We also note that [KNY18] claim to show that distributional CRHFs cannot be reduced to multi-collision resistant hash functions in a black box way, which given the black-box construction of distributional CRHFs from \({\mathsf {SZK}}\) hardness [KY18], would imply that \({\mathsf {SZK}}\) hardness cannot be obtained from multi-collision resistance in a black box way. However, for the time being there seems to be a gap in the proof of this claim [Per].
2 Techniques
We now give an overview of the techniques behind our results.
Ruling Out Black-Box Reductions. Most constructions in cryptography are fully black-box [RTV04], in the sense that both the construction and (security) reduction are black box. In a bit more detail, a fully black-box construction of a primitive \(\mathcal {P}'\) from another primitive \(\mathcal {P}\) consists of two algorithms: a construction \(\mathsf {C}\) and a reduction \( \mathsf {R}\). The construction \(\mathsf {C}^{\mathcal {P}}\) implements \(\mathcal {P}'\) for any valid oracle \(\mathcal {P}\). The reduction \(\mathsf {R}^{\mathsf {A}, \mathcal {P}}\), given oracle-access to any adversary \(\mathsf {A}\) that breaks \(\mathsf {C}^{\mathcal {P}}\), breaks the underlying \(\mathcal {P}\). Hence, breaking the instantiation \(\mathsf {C}^{\mathcal {P}}\) of \(\mathcal {P}'\) is at least as hard as breaking \(\mathcal {P}\) itself.
A common methodology to rule out fully black black-box constructions of a primitive \(\mathcal {P}'\) from primitive \(\mathcal {P}\) (see e.g., [Sim98, HR04, HHRS15]), is to demonstrate oracles \((\varGamma ,\mathsf {A})\) such that:
-
relative to \(\varGamma \), there exists a construction \(\mathsf {C}^\varGamma \) realizing \(\mathcal {P}\) that is secure in the presence of \(\mathsf {A}\),
-
but any construction \(\mathsf {C}'^\varGamma \) realizing \(\mathcal {P}'\) can be broken in the presence of \(\mathsf {A}\).
Indeed, if such oracles \((\varGamma ,\mathsf {A})\) exist, then no efficient reduction will be able to use (as a black-box) the attacker \(\mathsf {A}\) against \(\mathcal {P}'\) to break \(\mathcal {P}\) (as the construction of \(\mathcal {P}\) is secure in the presence of \(\mathsf {A}\)).
We now move on to explain how each of our results is shown in this framework.
2.1 Collision Resistance When SZK Is Easy
Our starting point is the work by [BDV17] who showed oracles relative to which Indistinguishability Obfuscation (IO) and One-Way Permutations (OWPs) exist and yet \({\mathsf {SZK}}\) is easy. We next recall their approach and explain why it falls short of separating CRHFs from \({\mathsf {SZK}}\). We then explain the approach that we take in order to bridge this gap.
Black-box Constructions of SZK Problems. The [BDV17] modeling of problems in \({\mathsf {SZK}}\) follows the characterization of \({\mathsf {SZK}}\) by Sahai and Vadhan [SV03] through its complete Statistical Difference Problem (SDP). SDP is a promise problem, where given circuit samplers \((C_0, C_1)\), the task is to determine if the statistical distance between their respective output distributions is large (\({>}2/3\)) or small (\({<}1/3\)). Accordingly, we can model a black-box construction of a statistical distance problem \(\mathrm {SDP}^{\varPsi }\), relative to an oracle \(\varPsi \), defined by
Jumping ahead, our eventual goal will be construct an oracle \(\varGamma = (\varPsi ,\mathsf {A})\) such that \(\mathrm {SDP}^{\varPsi }\) is easy in the presence of \(\mathsf {A}\), and yet \(\varPsi \) can be used to securely realize a CRHF, in the presence of \(\mathsf {A}\). Here we naturally choose \(\varPsi \) to be a random shrinking function f, and for the \({\mathsf {SZK}}\) breaker \(\mathsf {A}\) adopt the oracle \(\mathsf {SDO}^f\) from [BDV17]. \(\mathsf {SDO}^f\) is a randomized oracle that takes as input a pair of oracle-aided circuits \((C_0^{(\cdot )}, C_1^{(\cdot )})\), computes the statistical distance \(s = \mathrm {SD}(C_0^f, C_1^f)\), samples a random value \(t\leftarrow (1/3, 2/3)\), and outputs:
This oracle is clearly sufficient to break (or rather, decide) \(\mathrm {SDP}^f\). The challenge is in showing that CRHFs exist in the presence of the oracle \(\mathsf {SDO}^f\), which may make exponentially many queries to f when computing the statistical distance.
One-Way Permutations in the Presence of \(\mathsf {SDO}\). Toward proving the existence of CRHFs in the presence of \(\mathsf {SDO}\), we first recall the argument from [BDV17] as to why one-way permutations exist relative to \(\mathsf {SDO}\), and then explain why it falls short of establishing the existence of CRHFs.
Consider the oracle \(\varGamma = (f, \mathsf {SDO}^f)\), where f is a random permutation. Showing that f(x) is hard to invert for an adversary \(\mathsf {A}^{f,\mathsf {SDO}^f}(f(x))\) with access to f and \(\mathsf {SDO}^f\) relies on two key observations:
-
1.
Inverting f requires detecting random local changes. Indeed, imagine an alternative experiment where we replace f with a slightly perturbed function \(f_{x'\rightarrow f(x)}\), which diverts a random \(x'\) to f(x). In this experiment, the attacker would not be able to distinguish x from \(x'\) and would output them with the exact same probability. Note, however, that if the attacker can invert f in the real experiment (namely, output x) with noticeable probability, then this means that the probabilities of outputting x and \(x'\) in the original experiment must noticeably differ. Indeed, in the original experiment \(x'\) is independent of the attacker’s view. It is not hard to show that without access to the oracle \(\mathsf {SDO}^f\), such perturbations cannot be detected (this can be shown for example via a coupling argument, as we explain in more detail in Sect. 2.2).
-
2.
The \(\mathsf {SDO}^f\) oracle itself, and thus \(\mathsf {A}^{f, \mathsf {SDO}^f}\), can be made oblivious to random, local changes. Hence, even given access to the \(\mathsf {SDO}^f\) oracle, the adversary cannot invert with non-trivial probability. This is shown based on the idea of “smoothening”: any two circuits \((C_0^{f}, C_1^f)\) can be transformed into new circuits that do not make any specific query x with high probability. This allows arguing that even if we perturb f at a given point, their statistical distance s does not change by much. In particular, if s is moderately far from the random threshold t, chosen by \(\mathsf {SDO}\), \(s'\) the statistical distance of the perturbed circuits remains on the same side of t, which means that \(\mathsf {SDO}\)’s answer will remain invariant. Indeed, such “farness” holds with overwhelming probability over \(\mathsf {SDO}\)’s choice of t.
What About Collision Resistance? The above approach is not sufficient to argue that collisions are hard to find (when f is replaced with a shrinking function). The reason is that collisions are “non-local” — they are abundant, and it is impossible to eliminate all of them in a shrinking function. In fact, as we shall show later on, a similar argument to the one above can be made to work relative to an oracle that trivially breaks CRHFs (this leads to our new proofs of the separations of CRHFs from OWPs and IO [Sim98, AS15]). Accordingly, a different approach is required.
Our Approach: Understanding What Statistical Difference Oracles Reveal. At high level, to show that collisions in f are hard to find, we would like to argue that queries to \(\mathsf {SDO}^f\) leak no information about any f(x), except for inputs x, which the adversary had already explicitly revealed by querying f itself. This would essentially reduce the argument to the standard argument showing that random oracles are collision resistant—each new query collides with any previous query with probability at most \(2^{-m}\), where m is f’s output length. Overall, an attacker making q queries cannot find a collision except with negligible probability \(q^2 2^{-m}\).
However, showing that \(\mathsf {SDO}^f\) reveals nothing is too good to be true. Rather, we show that this is the case with overwhelming probability. That is, with overwhelming probability on any partial execution, the value f(x) of any x not explicitly queried within the execution is uniformly random. Roughly speaking, the property that such partial executions should satisfy is that all queries to \(\mathsf {SDO}^f\) satisfy smoothness and farness conditions similar to those discussed above. The essential observation is that when such conditions hold the answer of \(\mathsf {SDO}^f\) remains invariant not only to a random local change, but to any local change. In particular, a partial execution transcript satisfying these conditions would remain invariant if we change the value f(x) for any x not explicitly queried to any particular \(y\ne f(x)\).
A Note on Leakage from Random Oracles. Our approach is in part inspired by the works of Unruh [Unr07] and Coretti et al. [CDGS18] on random oracles with auxiliary information. They show that revealing short auxiliary information about f (so called leakage), essentially has the effect of fixing f on a small set of values, while the rest of f remains hidden. This does not suffice for us, because it does not restrict in any way which values are fixed. We need to ensure that all values not explicitly queried remain hidden even under the leakage from the oracle \(\mathsf {SDO}\). (Our argument is restricted though to the specific oracle \(\mathsf {SDO}\) and does not say anything about arbitrary leakage.)
2.2 Proving Simon and Asharov-Segev: A Coupling-Based Approach
Next, we sketch the main ideas underlying the new proofs of Simon’s result that OWPs do not imply CRHFs through fully black-box constructions, and the extended result by Asharov and Segev, which consider not only OWPs, but also IO. In this overview, we focus on the simpler result by Simon. We refer the reader to the full version of this paper for the extension to IO.
Simon’s Collision Finding Oracle. The oracle \(\varGamma = (f, \mathsf {Coll}^f)\) introduced by Simon consists of a random permutation f and a collision finding oracle \(\mathsf {Coll}^f\). The oracle \(\mathsf {Coll}^f\) given a circuit \(C^f\) returns a random w along with a random element that collides with w; namely a random \(w'\) in the preimage of \(y=C^f(w)\). In particular, if the circuit C is compressing, then the oracle will output a collision \(w\ne w'\) with high probability, meaning that CRHFs cannot exist in its presence.
Our Proof. To prove that \(\mathsf {Coll}\) does not help inverting f, Simon used careful conditional probability arguments, whereas Haitner et al. [HHRS15], and then Asharov and Segev [AS15] adding also IO to the picture, relied on a compression and reconstruction argument, originally due to Gennaro and Trevisan [GT00]. Our proof is inspired by the [BDV17] proof that the statistical distance oracle \(\mathsf {SDO}\) does not help inverting permutations (discussed above). At high level, we would like to argue that the collision-finding oracle \(\mathsf {Coll}\), like the oracle \(\mathsf {SDO}\), is oblivious to random local changes. Following the intuition outlined for \(\mathsf {SDO}\), an attacker that fails to detect random local changes will also fail in inverting random permutations.
Punctured Collision Finders. To fulfil this plan, we consider a punctured version \(\mathsf {PColl}\) of the oracle \(\mathsf {Coll}\), where the function f can be erased at a given set of values S. Roughly speaking, \(\mathsf {PColl}\) will allow us to argue that \(\mathsf {Coll}\) is not particularly sensitive to the value f(x) of almost any x. To define \(\mathsf {PColl}\), we first give a more concrete description of \(\mathsf {Coll}\) and then explain how we change it.
The oracle \(\mathsf {Coll}\), for any circuit \(C:\{0,1\}^k\rightarrow \{0,1\}^* \), assigns a random input \(w\in \{0,1\}^k\) and a random permutation \(\pi \) of \(\{0,1\}^k \simeq [2^k]\). It then returns \((w,w')\), where \(w'\) is the first among \(\pi (1),\pi (2),\dots \) such that \(C^f(w)= C^f(w')\). The oracle \( \mathsf {PColl}^f_S \) is parameterized by a set of punctured inputs \(S \subseteq \{0,1\}^n\). Like \(\mathsf {Coll}\), for any C, it samples a random input w and a permutation \(\pi \). Differently from \(\mathsf {Coll}\), if \( C^f(w) \) queries any \( x \in S \), the oracle returns \(\bot \). Else, it iterates over the inputs \(\{0,1\}^k\) according to \(\pi \) and finds the first value \(w'\) such that (1) \( C^f(w')\) makes no queries to any \(x\in S\), and (2) \(C^f(w) = C^f(w')\). The oracle outputs the collision \((w,w')\).
The \(\mathsf {PColl}\) oracle satisfies the following essential property. Let \( \tau \) be a transcript generated by the attacker \(\mathsf {A}^{f, \mathsf {Coll}^f}\) and assume that for all \(\mathsf {Coll}\) answers \((w,w')\) in \( \tau \), neither \(C^f(w)\) nor \(C^f(w')\) query any \(x\in S\). Then \(\mathsf {A}^{f, \mathsf {PColl}_S^f}\) generates the exact same transcript \(\tau \). Indeed, this follows directly from the definition of the punctured oracle \(\mathsf {PColl}\).
Proving Hardness of Inversion by Smoothening and Coupling. Equipped with the punctured oracle, we now explain how it can be used argue the hardness of inversion. We first consider a smoothening process analogous to the one considered in the statistical distance separation discussed above. That is, we make sure that (with overwhelming probability) all queries C made to \(\mathsf {Coll}\) are smooth in the sense that \(C^f(w)\) does not query any specific input with high probability when w is chosen at random. We then make a few small perturbations to our oracles, and argue that they are undetectable by a coupling argument. Finally, we deduce univertability.
Step 1: Let x be the preimage that \(\mathsf {A}^{f, \mathsf {Coll}^f}(f(x))\) aims to find. We first consider, instead of \(\mathsf {Coll}\), the punctured oracle \(\mathsf {PColl}^f_{\left\{ x \right\} }\). Due to smoothness, almost every transcript produced by \(\mathsf {A}^{f, \mathsf {Coll}^f}(f(x))\) is such that x is not queried by \(C^f(w),C^f(w')\) for any query C and answer \((w,w')\) returned by \(\mathsf {Coll}\). Any transcript satisfying the latter can be coupled with an identical transcript generated by \(\mathsf {A}^{f, \mathsf {PColl}^f_{\left\{ x \right\} }}(f(x))\), and deduce that the probability of inversion (outputting x) in this new experiment \(E_1\) is close to the probability in the original experiment \(E_0\).
Step 2: We perturb the oracle again. We sample a random \(x'\leftarrow \{0,1\}^n\) and make the following two changes: (1) we change the oracle f to \(f_{x'\rightarrow f(x)}\), which diverts \(x'\) to f(x), and (2) we puncture at \(x'\), namely, we consider \(\mathsf {PColl}^f_{\left\{ x,x' \right\} }\).
We next observe that in this new experiment \(E_2\), x and \(x'\) are symmetric. Accordingly, x and \(x'\) are output with the same probability in the experiment \(E_2\). To complete the proof, we apply a coupling argument to show that x and \(x'\) are output with almost the same probability also in the previous experiment \(E_1\). This is enough as in \(E_1\) the view of the attacker is independent of \(x'\), which will allows us to deduce that the probability of inversion is negligible overall.
Let us describe the coupling argument more explicitly. Both experiments \(E_1\) and \(E_2\) are determined by the choice of \(f,x,x'\) and randomness \(R=\left\{ w,\pi \right\} \) for \(\mathsf {Coll}\). We can look at the events \(X_1=X_1(f,x,x',R)\) and \(X_2=X_2(f,x,x',R)\), where \(X_1\) occurs when the attacker outputs x in the experiment \(E_1\) and \(X_2\) occurs when it outputs x in \(E_2\). Similarly, we can look at \(X'_1\) and \(X'_2\), which describe the events that \(x'\) is output in each of the experiments. Then by coupling, we know that

where \(I_{X_1}\), \(I_{X_2}\) are the corresponding indicators. The same holds for \({X'_1}\), \({X'_2}\). Thus, we can bound:

It is left to see that when fixing f, x, R the outputs in the two experiments \(E_1,E_2\) (and thus also \({X_1,X_2}\) and \({X'_1,X'_2}\)) are identical as long as \(x'\) does not coincide with any of the queries to f, nor with any of the queries induced by any \(\mathsf {PColl}_{\left\{ x \right\} }\) answer \((w,w')\). Since the number of such queries is bounded and \(x'\) is chosen independently at random, this will almost surely be the case.
Organization
In Sect. 3, we provide relevant preliminaries. In Sect. 4, we prove that there are no fully black-box reductions of \({\mathsf {SZK}}\) hardness to CRHFs. In Sect. 5, we reprove Simon’s result that there are no fully black-box reductions of CRHFs to OWPs. The extension of this result to IO can be found in the full version of this paper.
3 Preliminaries
In this section, we introduce the basic definitions and notation used throughout the paper.
3.1 Conventions
For a distribution D, we denote the process of sampling from D by \(x \leftarrow D\). A function \({\mathsf {negl}}:\mathbb {N}\rightarrow \mathbb {R}^{+}\) is negligible if for every constant c, there exists a constant \(n_c\) such that for all \(n > n_c\) \({\mathsf {negl}}(n) < n^{-c}\).
Randomized Algorithms. As usual, for a random algorithm \(\mathsf {A}\), we denote by \(\mathsf {A}(x)\) the corresponding output distribution. When we want to be explicit about the algorithm using randomness r, we shall denote the corresponding output by \(\mathsf {A}(x;r)\). We refer to uniform probabilistic polynomial-time algorithms as PPT algorithms.
Oracles. We consider oracle-aided algorithms (or circuits) that make repeated calls to an oracle \(\varGamma \). Throughout, we will consider deterministic oracles \(\varGamma \) that are a-priori sampled from a distribution \(\varGamma \) on oracles. More generally, we consider infinite oracle ensembles \(\varGamma = \left\{ \varGamma _n \right\} _{n\in \mathbb {N}}\), one distribution \(\varGamma _n\) for each security parameter \(n\in \mathbb {N}\) (each defined over a finite support). For example, we may consider an ensemble \(f=\left\{ f_n \right\} \) where each \(f_n:\{0,1\}^n\rightarrow \{0,1\}^n\) is a random function. For such an ensemble \(\varGamma \) and an oracle aided algorithm (or circuit) \(\mathsf {A}\) with finite running time, we will often abuse notation and denote by \(\mathsf {A}^{\varGamma }(x)\) and execution of \(\mathsf {A}\) on input x where each of (finite number of) oracle calls that A makes is associated with a security parameter n and is answered by the corresponding oracle \(\varGamma _n\). When we write \(\mathsf {A}_1^{\varGamma },\dots , \mathsf {A}_k^{\varGamma }\) for k algorithms, we mean that they all access the same realization of \(\varGamma \).
3.2 Coupling and Statistical Distance
Definition 3.1
(Coupling). Given two random variables X, Y over \( \mathcal {X}, \mathcal {Y}\), a coupling of X, Y is defined to be any distribution \( P_{X'Y'} \) on \( \mathcal {X}\times \mathcal {Y}\) such that, the marginals of \( P_{X'Y'} \) on \( \mathcal {X}\) and \( \mathcal {Y}\) are the distributions X, Y respectively.
Denote by \( \mathcal {P}_{XY} \) the set of all couplings of X, Y.
Lemma 3.2
Given any two distributions X, Y supported on \( \mathcal {X}\),

Furthermore, for distributions over a discrete domain \(\mathcal {X}\) the infimum is attained: that is, there exists a coupling \( P_{XY} \) such that  .
.
The lemma allows us to bound the statistical distance between two random variables (hybrid experiments in our case) by setting up a coupling between two experiments and bounding the probability of them giving a different outcome. Looking ahead, in Lemma 5.6, we describe an explicit coupling for the Simon’s collision finder oracle, of the form above that allows us to bound the statistical distance between hybrids.
4 Separating SZK and CRHFs
4.1 Fully Black-Box Constructions of SZK Problems
The class of problems with Statistical Zero Knowledge Proofs (SZK) [GMR85, Vad99] can be characterized by complete promise problems [SV03], particularly statistical difference, and the transformation is black-box. In order to consider black-box constructions of hard problems in \({\mathsf {SZK}}\), we start by defining statistical difference problem relative to oracles. This modelling follows [BDV17].
In the following definition, for an oracle-aided (sampler) circuit \(C^{(\cdot )}\) with n-bit input and an oracle \(\varPsi \), we denote by \(\mathbf {C}^\varPsi \) the output distribution \(C^\varPsi (r)\) where \(r \leftarrow \{0,1\}^n\). We denote statistical distance by \(\mathrm {SD}\): for two distributions X and Y  .
.
Definition 4.1
(Statistical Difference Problem relative to oracles). For an oracle \(\varPsi \), the statistical difference promise problem relative to \(\varPsi \), denoted as \(\mathrm {SDP}^{\varPsi }=(\mathrm {SDP}_{Y}^{\varPsi }\), \(\mathrm {SDP}_{N}^{\varPsi })\), is given by
Next, we define formally define fully black-box reductions from CRHFs to SZK.
Definition 4.2
(Black-Box Construction of \({\mathsf {SZK}}\)-hard Problems). A fully black-box construction of a hard statistical distance problems (SDP) from CRHFs consists of
-
Black-box construction: A collection of oracle-aided circuit pairs \(\varPi ^{(\cdot )}=\left\{ \varPi _n^{(\cdot )} \right\} _{n\in \mathbb {N}} \) where \( \varPi _n = \left\{ (C_0^{(\cdot )},C_1^{(\cdot )})\in \{0,1\}^{n\times 2} \right\} \) such that each \( (C_0, C_1) \) defines an SDP instance.
-
Black-box security proof: A probabilistic oracle-aided reduction \(\mathsf {R}\) with functions \(q_\mathsf {R}(\cdot ), \varepsilon _\mathsf {R}(\cdot )\) such that the following holds: Let f be any distribution on functions. For any probabilistic oracle-aided \(\mathsf {A}\) that decides \(\varPi \) in the worst-case, namely, for all \(n\in \mathbb {N}\),
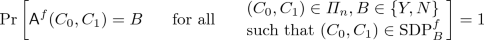
the reduction breaks collision resistance of f, namely, for infinitely many \(n\in \mathbb {N}\),
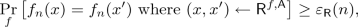
where \(\mathsf {R}\) makes at most \(q_\mathsf {R}(n)\) queries to any of its oracles \((\mathsf {A},f)\) where each query to \(\mathsf {A}\) consists of circuits \(C_0, C_1\) each of which makes at most \(q_\mathsf {R}(n)\) queries to f.
Next, we state the main result of this section: that any fully black-box construction of SDP problems from CRHFs has to either run in time exponential in the security parameter or suffer exponential security loss.
Theorem 4.3
For any fully black-box construction \((\varPi , \mathsf {R}, q_\mathsf {R}, \varepsilon _\mathsf {R})\) of SDPs from CRHFs, the following holds:
-
1.
(The reduction runs in exponential time.) \(q_\mathsf {R}(n) \ge 2^{n/10}\). Or,
-
2.
(Reduction succeeds with exponentially small probability.) \(\varepsilon _\mathsf {R}(n) \le 2^{-n/10}\).
We prove the theorem by describing an oracle \(\varGamma = (f, \mathsf {A})\) such that, \(\mathsf {A}\) solves \(\mathrm {SDP}^f\) but f is a CRHF relative to \(\varGamma \). The rest of the section is devoted to describing this oracle and proving the theorem. We start by describing the adversary that breaks \(\mathrm {SDP}\): the statistical distance oracle.
4.2 The Statistical Distance Oracle
Next we describe the statistical distance oracle \(\mathsf {SDO}\) from [BDV17] that solves \({\mathsf {SZK}}\) instances.
Definition 4.4
(Oracle \(\mathsf {SDO}^\varPsi \)). The oracle consists of \(t=\left\{ t_n \right\} _{n\in \mathbb {N}}\) where \(t_n : \{0,1\}^{2n} \rightarrow (\frac{1}{3},\frac{2}{3})\) is a uniformly random function. Given n-bit descriptions of oracle-aided circuits \(C_0,C_1 \in \{0,1\}^n\), let \(t^\star =t_n(C_0,C_1)\), and let \(s = \mathrm {SD}(\mathbf {C}_0^{\varPsi },\mathbf {C}_1^{\varPsi })\), return
It is immediate to see that \(\mathsf {SDO}^{\varPsi }\) decides \(\mathrm {SDP}^{\varPsi }\) in the worst-case.
Claim 4.4.1
For any oracle \(\varPsi \),
Remark 4.5
(On the Oracle Used). Our separation is sensitive to the oracle used. Subsequent to [BDV17, KY18] observed that the Simon’s collision finding oracle \(\mathsf {Coll}\) can be used to decide \({\mathsf {SZK}}\). Clearly, no separation between CRHFs and SZK holds relative to the Simon’s oracle. It turns out that Simon’s oracle can be used to estimate a different measure of distance between distributions, the Triangular Discrimination,Footnote 2 which like statistical distance also gives an \({\mathsf {SZK}}\)-complete promise problem [BDRV19]. Our separation does hold with a variant of \(\mathsf {Coll}\) and \(\mathsf {SDO}\) that measures triangular discrimination, but does not output a collision.
4.3 Insensitivity to Local Changes
Next, we recall the notions of smoothness and farness from [BDV17] that are used to argue that the \(\mathsf {SDO}^\varPsi \) oracle is insensitive to local changes. Roughly speaking farness says that the random threshold t used for a query \((C_0,C_1)\) to \(\mathsf {SDO}^\varPsi \) is “far” from the actual statistical distance. [BDV17] show that with high probability over the choice of random threshold \(t\), farness holds for all queries \((C_0,C_1)\) made to \(\mathsf {SDO}^{\varPsi }\) by any (relatively) efficient adversary. This intuitively means that changing the distributions \((\mathbf {C}_0^{\varPsi },\mathbf {C}_1^{\varPsi })\), on sets of small density, will not change the oracle’s answer.
Definition 4.6
(\((\varPsi ,t,\varepsilon )\)-Farness). Two oracle-aided circuits \((C_0,C_1) \in \{0,1\}^n\) satisfy \((\varPsi ,t,\varepsilon )\)-farness if the statistical difference \(s= \mathrm {SD}(\mathbf {C}_0^\varPsi ,\mathbf {C}_1^\varPsi )\) and threshold \(t\) are \(\varepsilon \)-far:
For an adversary \(\mathsf {A}\), we denote by \(\mathsf {farness}(\mathsf {A},\varPsi ,\varepsilon )\) the event that every \(\mathsf {SDO}\) query \((C_0,C_1)\) made by \(\mathsf {A}^{\varPsi ,\mathsf {SDO}^{\varPsi }}\) satisfies \((\varPsi ,t,\varepsilon )\)-farness, where \(t= t_n(C_0,C_1)\) is the threshold sampled by \(\mathsf {SDO}\).
Lemma 4.7
([BDV17](Claim 3.7)). Fix any \(\varPsi \) and any oracle-aided adversary \(\mathsf {A}\) such that \(\mathsf {A}^{\varPsi ,\mathsf {SDO}^{\varPsi }}\) makes at most q queries to \(\mathsf {SDO}^\varPsi \). Then

where the probability is over the choice \(t\) of random thresholds by \(\mathsf {SDO}\).
We now turn to define the notion of smoothness. Roughly speaking we will say that an oracle-aided circuit C is smooth with respect to some oracle \(\varPsi \) if any specific oracle query is only made with small probability. In particular, for a pair of smooth circuits \((C_0,C_1)\), local changes to the oracle \(\varPsi \) should not change significantly the statistical distance \(s = \mathrm {SD}(\mathbf {C}_0^{\varPsi },\mathbf {C}_1^{\varPsi })\).
Definition 4.8
(\((\varPsi ,\varepsilon )\)-Smoothness). A circuit \( C^{(\cdot )} \) is \((\varPsi ,\varepsilon )\)-smooth, if every location \( x \in \{0,1\}^*\) is queried with probability at most \( \varepsilon \). That is,

For an adversary \(\mathsf {A}\), we denote by \(\mathsf {smooth}(\mathsf {A},\varPsi ,\varepsilon )\) the event that in every \(\mathsf {SDO}\) query \((C_0,C_1)\) made by \(\mathsf {A}^{\varPsi ,\mathsf {SDO}^{\varPsi }}\) both circuits are \((\varPsi ,\varepsilon )\)-smooth.
Lemma 4.9
([BDV17](Claim 3.9)). Let \(\varPsi \), \(\varPsi '\) be oracles that differ on at most c values in the domain. Let \(C_0 \) and \( C_1\) be \((\varPsi ,\varepsilon )\)-smooth. Let \(s = \mathrm {SD}(C_0^\varPsi , C_1^\varPsi )\) and \(s' = \mathrm {SD}(C_0^{\varPsi '}, C_1^{\varPsi '})\) then \(\left| s-s'\right| \le 2c\varepsilon \).
The above roughly means that (under the likely event that farness holds) making smooth queries should not help the adversary detect local changes in the oracle \(\varPsi \). [BDV17] show that we can always “smoothen” the adversary’s circuit at the expense of making (a few) more queries to \(\varPsi \), which intuitively deems the statistical difference oracle \(\mathsf {SDO}^\varPsi \) useless altogether for detecting local changes in \(\varPsi \).
In what follows, a \((q', q)\)-query algorithm \(\mathsf {A}\) makes at most \(q'\) queries to the oracle \(\varPsi \) and q queries to \(\mathsf {SDO}^\varPsi \) such that for each query \((C_0, C_1)\) to \(\mathsf {SDO}\), the circuits \(C_0, C_1\) themselves make at most q queries to \(\varPsi \) on any input.
Lemma 4.10
(Smoothing Lemma for \(\mathsf {SDO}\) [BDV17](Lemma 3.10)). For any (q, q)-query algorithm \(\mathsf {A}\) and \(\beta \in \mathbb {N}\), there exists a \((q+2\beta q^2, q)\)-query algorithm \(\mathsf {S}\) such that for any input \(z\in \{0,1\}^\star \) and oracles \(\varPsi ,\mathsf {SDO}^\varPsi \):
-
1.
\(\mathsf {S}^{\varPsi ,\mathsf {SDO}^{\varPsi }}(z)\) perfectly simulates the output of \(\mathsf {A}^{\varPsi ,\mathsf {SDO}^{\varPsi }}(z)\),
-
2.
\(\mathsf {S}^{\varPsi ,\mathsf {SDO}^{\varPsi }}(z)\) only makes queries \( (C_0,C_1)\) where both \( C_0, C_1 \) are \((\varPsi ,\varepsilon )\)-smooth queries to \(\mathsf {SDO}^\varPsi \) with probability:

over its own random coin tosses.
4.4 Collision Resistance in the Presence of \(\mathsf {SDO}\) Oracle
In this section, we prove the oracle separation between collision resistant hash functions and \( {\mathsf {SZK}}\).
Let \( \mathcal {F}_{n} \) be the set of all functions from \( \{0,1\}^n \) to \( \{0,1\}^{m(n)} \) where \( m(n) < n\) is a shrinking function. Let \( \mathcal {F}= \left\{ \mathcal {F}_n \right\} _{n\in \mathbb {N}} \) denote the family of these sets of functions. Let \( \mathcal {T}= \left\{ \mathcal {T}_n \right\} _{n\in \mathbb {N}} \) where \( \mathcal {T}_n \) denotes the set of threshold functions \( t: \{0,1\}^n \rightarrow (1/3, 2/3) \).Footnote 3
Definition 4.11
(The Oracle f). The oracle \( f = \left\{ f_n \right\} _{n\in \mathbb {N}} \) on input \( x\in \{0,1\}^n \) returns \( f_n(x) \) where \( f_n : \{0,1\}^n \rightarrow \{0,1\}^m \) is a random function from \( \mathcal {F}_{n} \).
The oracle we consider is \(\varGamma = (f, \mathsf {SDO}^f)\). It is easy to see that all \(\mathrm {SDP}^f \in \mathsf {P}^{f, \mathsf {SDO}^f}\). What remains to show is that f is still collision resistant in the presence of the \(\mathsf {SDO}^f\) oracle. We do so next.
Theorem 4.12
Let \( \mathsf {A}\) be a (q, q)query adversary for \( q= O(2^{m/10})\). Then,

Proof
Fix oracle \( f_{-n} = \left\{ f_k \right\} _{k\ne n}\) arbitrarily. Consider the \((q+ 2\beta q^2, q)\)query smooth version \(\mathsf {S}\), of \(\mathsf {A}\) given by Lemma 4.10 for \(\beta = 2^{m/5}\cdot m\) and \(\varepsilon = 2^{-m/5}\).
We assume w.l.o.g that \(\mathsf {S}\) makes no repeated oracle queries and that whenever \(\mathsf {S}\) outputs a collision \((x,x')\), x is its last oracle query and \(x'\) is a previous query (both to the f oracle).
The first assumption is w.l.o.g because \(\mathsf {S}\) may store a table of previously made queries and answers. The second is w.l.o.g because \(\mathsf {S}\) may halt once its f-queries include a collision and output that collision; also, if one, or both, outputs \(x,x'\) have not been queried, \(\mathsf {S}\) can query it at the end (and if needed change the order of the output so that x is queries last). The latter costs at most two additional queries, and does not affect the smoothness of \(\mathsf {S}\).
Next, we define some notation about transcripts generated in the process.
Transcripts. A transcript \( \pi \) consists of all queries asked and answers received by \( \mathsf {S}\) to the oracle \( (f, \mathsf {SDO}^f) \). Let \(x_i\) denote the i-th query to the f-oracle. We say that \( x\not \in \pi \) if the location x is not among the queries explicitly made in \( \pi \).
The Underlying Joint Distribution. The proof infers properties of the joint distribution \( (f, t, \pi ) \) consisting of the oracle f, the \( \mathsf {SDO}\) oracle’s random thresholds t and the transcript generated by \( \mathsf {S}\). The distribution is generated as follows: \( f \leftarrow \mathcal {F}\) and \( t\leftarrow \mathcal {T}\) and \( \pi \leftarrow \mathsf {S}^{f, \mathsf {SDO}^{f; t} }\) where \( \mathsf {SDO}^{f; t} \) denotes running the \( \mathsf {SDO}\) oracle with random thresholds t. Denote this distribution by \( P_{FT\varPi }\).
Note that given f, t, the transcript \(\pi \) is generated in a deterministic manner as \( \mathsf {S}\) is deterministic and the oracle’s behavior is completely specified. Furthermore, we also consider partial transcripts obtained by running \( \mathsf {S}\) and stopping after i queries. This transcript is denoted by \( \pi _{< i}, x_i \): that is the \( \pi _{< i} \) consists of queries and responses received and \( x_i \) is the next query to the oracle f. Note that \( x_i \) is a deterministic function of \( \pi _{< i} \). Given the distribution \( P_{FT\varPi } \), the conditional distributions \( P_{FT|\varPi = \pi } \) or \( P_{FT|\varPi = \pi _{<i}} \) are well defined: these consist of uniform distribution on pairs (f, t) that when run using \( \mathsf {S}\) result in the transcript being \( \pi \) (or \( \pi _{<i} \)).
The Good Event. We define the concept of Good transcripts. Roughly speaking, these are transcripts \(\pi \) that satisfy sufficient smoothness and farness so to guarantee that the value f(x) at any \(x\notin \pi \) is completely hidden.
Definition 4.13
(Good). A tuple \((f, t, \pi , x, \varepsilon )\) is good, denoted by \(\mathsf {good}(f, t, \pi , x, \varepsilon )\) if the following hold:
-
1.
\(\pi = \mathsf {S}^{f_{x\rightarrow \bot }, \mathsf {SDO}^{f_{x\rightarrow \bot }; t}}(1^n)\), where \(f_{x\rightarrow \bot }\) is the function equal to f everywhere except at x where it takes the value \(\bot \).
-
2.
(x is not explicitly queried:) \(x\not \in \pi \).
-
3.
(Transcript is smooth:) Every \(\mathsf {SDO}\)-query made by \( \mathsf {S}^{f_{x\rightarrow \bot }, \mathsf {SDO}^{f_{x\rightarrow \bot }; t}}(1^n) \) is \((f_{x\rightarrow \bot }, 2\varepsilon ) \)-smooth. Denote this event by \( \mathsf {smooth}(f_{x\rightarrow \bot }, t, \pi , 2\varepsilon ) \).
-
4.
(Transcript is far:) Every \(\mathsf {SDO}\)-query \((C_0,C_1)\) made by \( \mathsf {S}^{f_{x\rightarrow \bot }, \mathsf {SDO}^{f_{x\rightarrow \bot }; t}}(1^n) \), satisfies \((f_{x\rightarrow \bot },t, 12\varepsilon ) \)-farness where \(t = t(C_0,C_1)\). Denote this by \( \mathsf {far}(f, t, \pi , 12\varepsilon ) \).
The key reason for using \( f_{x\rightarrow \bot } \) instead of f in the definition is that when an execution of \( \mathsf {S}^{f_{x\rightarrow \bot }, \mathsf {SDO}^{f_{x\rightarrow \bot }; t}} \) generates a transcript \( \pi \) while making only smooth and far queries, all executions of \( \mathsf {S}^{f_{x\rightarrow z}, \mathsf {SDO}^{f_{x\rightarrow z}; t}} \) for all z, also generate \( \pi \) while not necessarily being smooth or far themselves.
A tuple \( (f, t, \pi , \varepsilon ) \) is good if for all \( x \not \in \pi \), \( \mathsf {good}(f,t,\pi , x, \varepsilon ) \) holds.
Lemma 4.14
Let \( P_{FT\varPi } \) as defined above. Then,

The same holds for i-length partial transcripts generated as well, for all i.
Lemma 4.15
For any transcript \(\pi \) and query \( x \not \in \pi \) such that

it holds that,
Next, we prove Theorem 4.12 assuming Lemmas 4.14 and 4.15. Then, we prove the two lemmas.
Let \( \mathsf {hit}(\pi ) \) denote the event that \( \pi \) contains two queries \( x, x' \) such that \( f_n(x) = f_n(x') \). Then,

We will bound the two terms separately. The first term will involve using Lemma 4.15 while the second term is bound using Lemmas 4.7 and 4.10. We begin by bounding the first term. This is done by decomposing the probability of hitting a collision by the first query that hits a collision:

where \( x_i \notin \pi \) denotes the i-th f query made by \( \mathsf {S}\) and \( \mathsf {hitSet}(\pi _{<i}) \) denotes the answers to f-queries in \(\pi _{<i}\),

The last equality follows from the definition of conditional probability. At this point, we can use Lemma 4.15 to argue that

because \( f(x_i) \) is uniformly random and \( |\mathsf {hitSet}(\pi _{<i})| \le i \). Hence, we get that,

where \(q' = q + 2\beta q^2 + 2\), the number queries that \(\mathsf {S}\) makes to f.
Hence, by Lemma 4.14, the algorithm’s success probability is bounded by

when substituting \(\varepsilon = 2^{-m/5}\), \(\beta = 2^{m/5}\cdot m\), and \(q \le 2^{m/10}\).
Proof
(of Lemma 4.14). The proof follows from the observation if \(\mathsf {S}^{f, \mathsf {SDO}^f}\) outputs \(\pi \) with all the queries being both smooth, and far, then, the same holds for \(\mathsf {S}^{f_{x\rightarrow \bot }, \mathsf {SDO}^{f_{x\rightarrow \bot }}}\) with slightly degraded parameters. That is,

Hence, to complete the proof, we need to show that, for any (f, t) if \(\mathsf {S}^{f, \mathsf {SDO}^f}(1^n)\) outputs \(\pi \) with all the queries being \((f, \varepsilon )\)-smooth, and \((f,t, 16\varepsilon )\)-far, then, \(\mathsf {S}^{f_{x\rightarrow \bot }, \mathsf {SDO}^{f_{x\rightarrow \bot }}}(1^n)\) generates \(\pi \) with all the queries being \((f, 2\varepsilon \)-smooth and \((f,t, 12\varepsilon )\)-far.
First observe that by Lemma 4.9, since \(16\varepsilon \)-farness and \(\varepsilon \)-smoothness hold, answers by \( \mathsf {SDO}^{f_{x\rightarrow \bot }}\) are identical to those by \( \mathsf {SDO}^f\). Accordingly, the transcript \(\pi =\mathsf {S}^{f_{x\rightarrow \bot }, \mathsf {SDO}^{f_{x\rightarrow \bot }}}(1^n)\).
Next, we show that \(2\varepsilon \)-smoothness holds with respect to \(\mathsf {SDO}^{f_{x\rightarrow \bot }}\). Indeed, any \(\mathsf {SDO}\)-query \((C_0^{(\cdot )},C_1^{(\cdot )})\) is \(\varepsilon \)-smooth with respect to f, accordingly the probability that either circuit \(C_b\) queries any individual z is bounded by

Finally, to conclude the proof, we show that \(12\varepsilon \)-farness holds with respect to \(f_{x\rightarrow \bot }\). Indeed, for any query \((C_0,C_1)\), let \(s=\mathrm {SD}(C_0^f,C_1^f)\) be the statistical distance with respect to f, then by \(\varepsilon \)-smoothness with respect to f, the statistical distance \(s^x= \mathrm {SD}(C_0^{f_{x\rightarrow \bot }},C_1^{f_{x\rightarrow \bot }})\) with respect to \(f_{x\rightarrow \bot }\) is at most \(2\varepsilon \)-far from s. Letting \(t= t(C_0,C_1)\) be the threshold chosen by \(\mathsf {SDO}\), we know by \(16\varepsilon \)-farness that \(|s-t| \ge 16\varepsilon \) and thus \(|s^x-t|\ge 12\varepsilon \), which implies the require farness with respect to \(f_{x\rightarrow \bot }\).
The above argument holds unaltered for partial transcripts output by \(\mathsf {S}\) as well. Even there, when a partial trancript is output by \(\mathsf {S}^{f, \mathsf {SDO}^f}\) with all queries being \((f, \varepsilon )\)-smooth and \((f,t, 16\varepsilon )\)-far, then, \(\mathsf {S}^{f_{x\rightarrow \bot }, \mathsf {SDO}^{f_{x\rightarrow \bot }}}(1^n)\) generates the same partial transcript with all the queries being \((f, 2\varepsilon )\)-smooth and \((f,t, 12\varepsilon )\)-far. \(\square \)
Proof
(of Lemma 4.15). Given \( \pi , x\not \in \pi \), for any y

In order to show that, the distribution \(\left\{ f(x) : f\leftarrow P_{F|\varPi =\pi , \mathsf {good}} \right\} \) is uniform, it suffices to show that for all \( y_1,y_2 \in \{0,1\}^m\),

To prove this, it suffices to show that for every (f, t) where \( f(x) = y_1 \),
This follows because as \(\mathsf {good}(f, t, \pi , x, \varepsilon )\) holds, \( \pi = \mathsf {S}^{f_{x\rightarrow \bot }, \mathsf {SDO}^{f_{x\rightarrow \bot }; t}}(1^n) \) and every query made to \( \mathsf {SDO}^{f_{x\rightarrow \bot }; t} \) is both \( 12\varepsilon \)-far and \( 2\varepsilon \)-smooth. Hence, when we change the oracle to \( (f_{x\rightarrow y_2}, \mathsf {SDO}^{x\rightarrow y_2}) \), each query is answered identically to \( f_{x\rightarrow \bot }, \mathsf {SDO}^{f_{x\rightarrow \bot }; t} \). Indeed, for any query \((C_0,C_1)\), let \(s=\mathrm {SD}(C_0^{f_{x\rightarrow \bot }},C_1^{f_{x\rightarrow \bot }})\) be their statistical distance with respect to \(f_{x\rightarrow \bot }\), then by \(2\varepsilon \)-smoothness with respect to \(f_{x\rightarrow \bot }\), the statistical distance \(s' = \mathrm {SD}(C_0^{f_{x\rightarrow y_2}},C_1^{f_{x\rightarrow y_2}})\) is at most \(4\varepsilon \)-far from s. As the threshold \(t = t(C_0,C_1)\) is more than \( 12\varepsilon \) far by farness, the answer will be unchanged to this query.
Hence, \( \mathsf {S}^{(f_{x\rightarrow y_2}, \mathsf {SDO}^{x\rightarrow y_2}) } \) will also return \( \pi \) as the answer. Also, by definition, \( \mathsf {good}(f_{x\rightarrow y_2}, t, \pi , x, \varepsilon ) \) will hold because \( \pi = \mathsf {S}^{f_{x\rightarrow \bot }, \mathsf {SDO}^{f_{x\rightarrow \bot }; t}}(1^n) \) and every query made to \( \mathsf {SDO}^{f_{x\rightarrow \bot }; t} \) is both \( 12\varepsilon \)-far and \( 2\varepsilon \)-smooth. Hence, the claim follows.
\(\square \)
This completes the proof of Theorem 4.12. \(\square \)
5 A New Proof of an Old Separation
In this section, we give a new proofs of a result by Simon [Sim98] ruling out fully black-box reductions of collision-resistant hash functions to one-way permutations.
Fully Black Box Constructions of CRHFs from OWPs. We begin by defining oracle-aided constructions of CRHFs and then specialize it to the setting of OWPs.
Definition 5.1
(Oracle-Aided Collision-Resistant Function Families). A pair of polynomial-time oracle-aided algorithms \( ({\mathsf {Gen}}, \mathsf {Hash}) \) is a collision-resistant function family relative to an oracle \( \varGamma \) if it satisfies the following properties:
-
The index-generation algorithm \( {\mathsf {Gen}}\) is a probabilistic algorithm that on input \( 1^n \) and oracle access to \( \varGamma \) outputs a function index \( \sigma \in \{0,1\}^{m(n)} \).
-
The evaluation algorithm \( \mathsf {Hash}\) is a deterministic algorithm that takes as input a function index \( \sigma \in \{0,1\}^{m(n)} \) and a string \( x\in \{0,1\}^n \), has oracle access to \( \varGamma \), and outputs a string \( y = \mathsf {Hash}^\varGamma (\sigma , x) \in \{0,1\}^{n-1} \).
Definition 5.2
(Black-Box Construction of CRHFs from OWPs). A fully black-box construction of a Collision Resistant Hash Functions (CRHFs) from One-Way Permutations consists of a pair of PPT oracle-aided algorithms \( ({\mathsf {Gen}}, \mathsf {Hash}) \), an oracle-reduction \( \mathsf {R}\) along with functions \( q_\mathsf {R}(n) \), \( \varepsilon _{\mathsf {R}}(n) \) such that the following two conditions hold:
-
Correctness: For any \( n\in \mathbb {N}\), for any permutation f, and for any function index \( \sigma \) produced by \( {\mathsf {Gen}}^{f}(1^n) \), it holds that \( \mathsf {Hash}^{f}(\sigma , \cdot ) : \{0,1\}^n \rightarrow \{0,1\}^{n-1}\).
-
Black-box security proof: For any permutation f and probabilistic oracle-aided algorithm \( \mathsf {A}\) , if
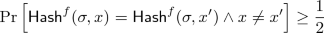
where the experiment is \( \sigma \leftarrow {\mathsf {Gen}}^{f}(1^n) \) and \( (x,x') \leftarrow \mathsf {A}^{f}(1^n, \sigma )\), for infinitely many n, then the reduction breaks f, namely, for infinitely many \(n\in \mathbb {N}\) either

for infinitely many values of n where \(\mathsf {R}\) makes at most \(q_\mathsf {R}(n)\) queries to the oracles \(\mathsf {A}, f\) and for every circuit \(D^{(\cdot )}\) queried to \(\mathsf {A}\) makes at most \(q_\mathsf {R}(n)\) queries to f on any input.
We remark that ruling out black-box reductions as defined above where the reduction has to break the OWP given an adversary that breaks CRHFs w.p. over 1/2 only makes our result stronger. In the standard setting, the reduction has to break OWP given an adversary that succeeds with any noticeable probability.
5.1 Simon’s Collision Finding Oracle and Puncturing
Recall that the Simon’s collision finding oracle is defined as follows:
Definition 5.3
(Simon’s Oracle \(\mathsf {Coll}^\varPsi \)). Given any description of a circuit C with m-bit inputs, the oracle’s randomness contains a random input \( w_C \in \{0,1\}^m \) and a random permutation \( \pi _C : \{0,1\}^m \rightarrow \{0,1\}^m \). The \( \mathsf {Coll}^\varPsi \) oracle returns the following:
W.l.o.g, along with \( (w_C, w_C') \), let \(\mathsf {Coll}\) also return the queries made to \( \varPsi \), and their answers, when evaluating \( C^{\varPsi }(w_C) \) and \( C^{\varPsi }(w_C') \).
The collision-finding oracle breaks any oracle-aided collision resistant hash function.
Lemma 5.4
([Sim98]). Let \(\varGamma = (\varPsi , \mathsf {Coll}^\varPsi )\). Let \(C^{(\cdot )} : \{0,1\}^n \rightarrow \{0,1\}^{n-1}\) be any candidate construction of CRHFs. Then,

where the randomness is over the randomness of \(\mathsf {Coll}\).
Proof
Fix \(\varPsi \) and omit it from the notation. For any string \(y \in \{0,1\}^{n-1}\), let \(a_y = \left| \left\{ x : C(x) = y \right\} \right| \). Then,

where the second inequality follows from the fact that  . \(\square \)
. \(\square \)
Next we define a variant of the Simon’s oracle, dubbed as the punctured Simon’s oracle. This collision finding oracle allows \( \varPsi \) to be punctured, that is, a set of values in \( \varPsi \) are erased. As we will show later, this oracle returns the same answers as \( \mathsf {Coll}^{\varPsi } \) most of the time, and we can characterize when it does not.
Definition 5.5
(Punctured Simon’s Oracle \(\mathsf {PColl}_S^\varPsi \)). Let \( \varPsi : \{0,1\}^* \rightarrow \{0,1\}^* \) be an oracle. Let \( S\subseteq \{0,1\}^* \) be a subset of inputs. The oracle \( \mathsf {PColl}\)’s randomness contains for any circuit C with m-bit inputs, a random input \( w_C \in \{0,1\}^m \) and a random permutation \( \pi _C : \{0,1\}^m \rightarrow \{0,1\}^m \). The \( \mathsf {PColl}_S^\varPsi \) oracle returns the following:
Else,
where \( w_C' = \pi _C(i)\) for the smallest i such that \( C^{\varPsi }(w_C) = C^{\varPsi }(\pi _C(i)) \) and \( C^\varPsi (\pi _C(i)) \) does not query any \( x\in S \). Along with \( (w_C, w_C') \), let it also return the queries made to \( \varPsi \) when evaluating \( C^{\varPsi }(w_C) \) and \( C^{\varPsi }(w_C') \). We refer to these queries as \(\varPsi \) queries induced by the \(\mathsf {Coll}\) oracle.
There are two key properties of the punctured oracle: (1) The answers of \( \mathsf {PColl}^{\varPsi }_S \) are independent of the values of the oracle \( \varPsi \) on all of S; and (2) there is a natural coupling between \( \mathsf {Coll}^\varPsi \) and \( \mathsf {PColl}^\varPsi _S \) such that, as long as there is no explicit query \( x \in S \) to \( \varPsi \), the two oracles return identical answers. This is captured by the following lemma.
Lemma 5.6
Let \( \varPsi : \{0,1\}^* \rightarrow \{0,1\}^* \) be an oracle, let \( S\subseteq \{0,1\}^* \). Consider the coupling of \( \mathsf {Coll}^\varPsi \) and \( \mathsf {PColl}^\varPsi _S \) that instantiates the two oracles with identical randomness. Let \( \mathsf {A}\) be any deterministic oracle-aided algorithm. Let \( \tau \) be the transcript generated by \( \mathsf {A}^{\varPsi , \mathsf {Coll}^\varPsi } \). Then,
where \( \varPsi \hbox {-}\mathsf {set}(\tau ) \) is the set of all queries made to \( \varPsi \) in the execution. This includes the queries to \( \varPsi \) returned by the \( \mathsf {Coll}\) oracle.
Proof
Every direct query to \( \varPsi \) by \( \mathsf {A}\) is returned identically in both the executions. Furthermore, in any transcript \( \tau \), such that \( \varPsi \hbox {-}\mathsf {set}(\tau ) \cap S = \emptyset \), all queries to \( \mathsf {Coll}^\varPsi \) and \( \mathsf {PColl}^\varPsi _S \) are answered identically. This follows from the definition of \(\mathsf {PColl}\) because for every query C to \(\mathsf {Coll}\) and response \((w_C, w'_C)\), all the queries made to \(\varPsi \) when evaluating \(C^\varPsi (w_C)\) and \(C^{\varPsi }(w_C')\) are explicitly made directly to \(\varPsi \), and are thus in \(\varPsi \hbox {-}\mathsf {set}\). In more detail, for any query \(C^{\varPsi }\) made to \(\mathsf {Coll}^\varPsi \) with answer \((w_C,w'_C)\), \(C^{\varPsi }(w_C)\) does not make any queries in S, and thus \(\mathsf {PColl}\), will also return \(w_C\). In addition, any \(w''\) that is lexicographically prior to \(w'_C\) will not be returned because it either induces queries in S, or if it does then it is such that \(C^{\varPsi }(w'')\ne C^{\varPsi }(w_C)\). In contrast, \(C(w'_C)\) does not make any queries to S, and is such that \(C(w'_C)=C(w_C)\). Hence \(w'_C\) will also be returned by \(\mathsf {PColl}\) (and likewise the queries to \(\varPsi \) induced by \(w_C,w'_C\)). \(\square \)
A Word of Caution. In Lemma 4.15, we showed that the distribution f(x) when conditioned on a transcript \(\tau \) is close to uniformly random.Footnote 4
Lemma 5.6 seems to suggest the same for the collision finding oracle. That is, the oracle reveals no information about f(x) for any location x not explicitly queried in \(\tau \). Unfortunately, we do not know how to show this. The key reason for this is that the probability of seeing this transcript \(\tau \) could itself depend on the value of f(x). This issue is not new: it also comes up with the \(\mathsf {SDO}\) oracle. We are able to remedy this issue in the case of the \(\mathsf {SDO}\) oracle in part because of its short output: it allows us to define the notion of farness which shows that the \(\mathsf {SDO}\) oracle is robust to any small changes to the \(\mathsf {SDO}\) oracle. Puncturing only allows us to erase a value, and not set it to a different one.
5.2 Smoothening for the Collision Finding Oracle
Similar to Lemma 4.10, we can show that any algorithm \(\mathsf {A}^{\varPsi , \mathsf {Coll}^\varPsi }\) can be transformed to a smoothened algorithm \(\mathsf {S}^{\varPsi , \mathsf {Coll}^\varPsi }\) that with high probability makes only smooth queries to the \(\mathsf {Coll}^\varPsi \) oracle.
A \((q', q)\)-query algorithm \(\mathsf {A}\) makes at most \(q'\) queries to the oracle f and q queries to \(\mathsf {Coll}^f\) such that each for each query C to \(\mathsf {Coll}\), the circuit C makes at most q queries to f on any input.
Lemma 5.7
(Smoothing Lemma for \(\mathsf {Coll}\)). For any (q, q)-query algorithm \(\mathsf {A}\) and \(\beta \in \mathbb {N}\), there exists a \((q+\beta q^2, q)\)-query algorithm \(\mathsf {S}\) such that for any input \(z\in \{0,1\}^*\) and oracles \(\varPsi ,\mathsf {Coll}^\varPsi \):
-
1.
\(\mathsf {S}^{\varPsi ,\mathsf {Coll}^{\varPsi }}(z)\) perfectly simulates the output of \(\mathsf {A}^{\varPsi ,\mathsf {Coll}^{\varPsi }}(z)\),
-
2.
\(\mathsf {S}^{\varPsi ,\mathsf {Coll}^{\varPsi }}(z)\) only makes queries that are \((\varPsi ,\varepsilon )\)-smooth queries to \(\mathsf {Coll}^\varPsi \) with probability:
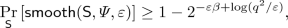
over its own random coin tosses.
The proof of the lemma is identical to that of Lemma 4.10, the bound differs in a factor of 2: \((q + \beta q^2)\) instead of \((q + 2\beta q^2)\) in case of Lemma 4.10 because \(\mathsf {Coll}\) oracle takes only one circuit as input.
5.3 One Way Permutations in the Presence of \( \mathsf {Coll}\)
In this section, we show that CRHFs cannot be constructed from OWPs in a black-box manner (Definition 5.2). That is, we show,
Theorem 5.8
Let \(({\mathsf {Gen}}, {\mathsf {Eval}}, \mathsf {R}, q_\mathsf {R}, \varepsilon _\mathsf {R})\) be a fully black-box construction of CRHFs from OWPs. Then, either
-
1.
(Large Running Time) \(\mathsf {R}\) makes at least \(q_\mathsf {R}(n) \ge 2^{n/6}\) queries. Or,
-
2.
(Large Security Loss) \(\varepsilon _\mathsf {R}(n) \le 2^{-n/6}\).
To prove the theorem, we consider the oracle \(\varGamma = (f, \mathsf {Coll}^f)\) where f is a random permutation. We show that a random permutation f is hard to invert even given access to \( \mathsf {Coll}^f \). We start by defining the oracle. In what follows, \(\mathcal {P}_n\) denotes the set of permutations of \(\{0,1\}^n\).
Definition 5.9
(The Oracle f).\(f = \left\{ f_{n} \right\} _{n\in \mathbb {N}}\) on input \(x\in \{0,1\}^n\) answers with \(f_n(x)\) where \(f_n\) is a random permutation \(f_n\leftarrow \mathcal {P}_n\).
It is clear that \(\mathsf {Coll}^f\) breaks any potential CRHF construction with probability at least 1/2. Our main result states that f cannot be inverted, except with exponentially small probability, even given an exponential number of oracle queries to f and \(\mathsf {Coll}^{f}\). Here, consistently with the previous subsection, we say that an adversary \(\mathsf {A}\) is q-query if \(\mathsf {A}^{f,\mathsf {Coll}^{f}}\) makes at most q queries to f and q queries to \(\mathsf {Coll}^{f}\), and any query made to \(\mathsf {Coll}^{f}\) consists of oracle-aided circuit C that makes at most q queries to f, on any specific input.
Theorem 5.10
Let \(q \le O(2^{n/6})\). Then for any (q, q)-query adversary \(\mathsf {A}\),

Proof
We, in fact, prove a stronger statement: the above holds when fixing the oracles \(f_{-n}:=\left\{ f_{k} \right\} _{k\ne n}\). Let \( \varepsilon = 2^{-n/3} \) and \( \beta = 2^{n/3}\cdot n \). Fix a q-query adversary \(\mathsf {A}\) and let \(\mathsf {S}\) be its smooth \((q + \beta q^2 + 2q^2, q)\) query simulator given by Lemma 4.10. The extra \(2q^2\) queries are incurred by the fact that along with each collision \(w,w'\) from \(\mathsf {Coll}^{f}(C)\), the queries made to f in computing \(C^f(w)\) and \(C^f(w'\)) are also returned. Since \(\mathsf {S}\) perfectly emulates \(\mathsf {A}\), it is enough to bound the probability that \(\mathsf {S}\) successfully inverts. To bound \(\mathsf {S}\)’s inversion probability, we consider six hybrid experiments \(\left\{ \mathbf {H}_i \right\} _{i\in [6]}\) given in Table 1. Throughout, for a permutation \(f \in \mathcal {P}_n\) and \(x,y\in \{0,1\}^n\), we denote by \(f_{x \rightarrow y}\) the function that maps x to y and is identical to f on all other inputs (in particular, \(f_{x \rightarrow y}\) is no longer a permutation when \(x\ne f^{-1}(y)\)).
Hybrid \(\mathbf {H}_1\) is identical to the real world where \(\mathsf {S}\) wins if it successfully inverts the permutation at a random output. We show that the probability that the adversary wins in any of the experiments is roughly the same, and that in hybrid \(\mathbf {H}_6\) the probability that \(\mathsf {S}\) wins is tiny.
Claim 5.10.1

Proof
The difference between the two hybrids is in the collision finding oracle: in \( \mathbf {H}_1 \), \( \mathsf {S}\) gets the standard \( \mathsf {Coll}^f \) oracle, while in \( \mathbf {H}_2 \), punctured oracle \( \mathsf {PColl}^f_{\left\{ x \right\} } \), punctured at x. Note that by coupling the two experiments, we can bound the statistical distance (and hence the winning probabilities) in \(\mathbf {H}_1\) and \(\mathbf {H}_2\) as follows:

Let \(\mathsf {smooth}=\mathsf {smooth}(\mathsf {S}(f(x)),f,\varepsilon )\) be the event that all \(\mathsf {Coll}\)-queries made by \(\mathsf {S}^{f,\mathsf {Coll}^f}(f(x))\) are \((f,\varepsilon )\)-smooth (Definition 4.8). And let \( \mathsf {collHit}= \mathsf {collHit}(\mathsf {S}, f, x, z)\) denote the event that the collision finder oracle \( \mathsf {Coll}^f \) for some query C returns an answer \( (w,w') \) such that \( C^f(w) \) or \( C^f(w') \) queries x during the evaluation. Note that \( \mathsf {collHit}\) does not occur when f is queried at x by \( \mathsf {S}\), but only when its indirectly queried by \( \mathsf {Coll}^f \).
Observe that by Lemma 5.6, as long as punctured set \( \left\{ x \right\} \) is not queried by a collision returned, that is as long as \( \mathsf {collHit}\) event does not occur, the two oracles \( \mathsf {Coll}^f \) and \( \mathsf {PColl}^f_{\left\{ x \right\} } \) would return identical answers. Hence,

We bound the probability of \( \mathsf {collHit}\) as:

By the smoothness Lemma 5.7,

and, when \( \mathsf {smooth}\) holds, we can bound the probability of a \( \mathsf {collHit}\).

This follows from the fact that for any \( (f, \varepsilon ) \)-smooth circuit C, and any x, the following holds:

Hence, as the marginal of each coordinate of a collision returned by the \( \mathsf {Coll}\) oracle is uniformly random, by a union bound, the probability of \( \mathsf {collHit}\) occurring for this particular \( \mathsf {Coll}\) query C is at most \( 2\cdot \varepsilon \). Hence the total probability is bounded by \(q \cdot (2\varepsilon ) \) as desired.
Hence, we can bound the difference between \( \mathbf {H}_1 \) and \( \mathbf {H}_2 \) by
when setting \( \varepsilon = 2^{-n/3} \), \( \beta = 2^{n/3}\cdot n \) and recalling that \( q \le O(2^{n/6}) \). \(\square \)
Claim 5.10.2
 .
.
Proof
The difference between the two hybrids is that in \(\mathbf {H}_2\), \(\mathsf {S}\) receives the normal f oracle, while in \(\mathbf {H}_3\), it receives the planted oracle \(f_{z \rightarrow f(x)}\). And it receives \(\mathsf {PColl}_{\left\{ x \right\} }^f\) in \(\mathbf {H}_2\) while receiving \(\mathsf {PColl}_{\left\{ x,z \right\} }^f\) in \(\mathbf {H}_3\). In what follows, we denote by \(\mathsf {zHit}=\mathsf {zHit}(\mathsf {S},f,x,z)\) the event that \(\mathsf {S}^{f,\mathsf {PColl}_{\left\{ x \right\} }^f}(f(x))\) queries f on z, either directly or indirectly through a collision returned.
Consider the execution of \(\mathsf {S}^{f,\mathsf {PColl}_{\left\{ x \right\} }^f }\) in \(\mathbf {H}_2\), every query \(\mathsf {S}\) makes to the oracle is answered identically in \(\mathbf {H}_3\), unless the event \(\mathsf {zHit}\) occurs. This follows because the f oracle itself differs only at z in the two hybrids, and the \(\mathsf {PColl}\) oracle returns the same value by Lemma 5.6 unless \(\mathsf {zHit}\) occurs. Hence, as \(\mathsf {S}\) receives the same answers and hence asks the same questions in both hybrids, it would have the same output, unless \(\mathsf {zHit}\) occurs. As z is picked uniformly at random, independent of everything else in \(\mathbf {H}_2\),

when setting \( \varepsilon = 2^{-n/3} \), \( \beta = 2^{n/3}\cdot n \) and recalling that \( q \le O(2^{n/6}) \). \(\square \)
Claim 5.10.3
 .
.
Proof
First, by symmetry, observe that in \(\mathbf {H}_3\), the probability of \(\mathsf {S}\) outputting x is the same as that of \(\mathsf {S}\) outputting z, because they are completely symmetrical in this hybrid. Then observe that these two hybrids \(\mathbf {H}_3\) and \(\mathbf {H}_4\) are relabellings of each other: \( z \leftrightarrow x \), \( f(x)\leftrightarrow y \) and \( x \leftrightarrow f^{-1}(y) \). This implies that the probability of the probability of \(\mathsf {S}\) outputting z in \(\mathbf {H}_3\) is the same as that of \(\mathsf {S}\) outputting x in \(\mathbf {H}_4\). This completes the argument. \(\square \)
Claim 5.10.4
 .
.
The difference between the two hybrids is two fold: the f and \(\mathsf {PColl}\) oracles differs at x and are identical otherwise. Note that x is independent of the adversary’s view in \(\mathbf {H}_5\). The proof of this claim is identical to that of Claim 5.10.2 and is omitted.
Claim 5.10.5
 .
.
The only difference between the two hybrids is that the \(\mathsf {Coll}\) oracle from \(\mathbf {H}_6\) is punctured at \(f^{-1}(y)\) in \(\mathbf {H}_5\). The proof of this claim is identical to that of Claim 5.10.1, relies on smoothness, and is omitted.
To conclude the proof of Theorem 5.10, we observe that
Claim 5.10.6
 .
.
Proof
The view of \(\mathsf {S}\) in this hybrid is completely independent of the random choice of x. \(\square \)
This completes the proof of Theorem 5.10. \(\square \)
Notes
- 1.
Simon also ruled out a stronger type of reductions known as semi-black-box reductions [RTV04]. We only rule out the notion of fully black-box reductions described above.
- 2.
The triangular discrimination is defined as
 . This measure also lies in the interval [0, 1] and is a metric.
. This measure also lies in the interval [0, 1] and is a metric. - 3.
While we describe the threshold function as a real valued function, it can be safely discretized because statistical distance for any pair of circuits \(C_0, C_1:\{0,1\}^m \rightarrow \{0,1\}^\star \), takes values that are multiples of \({2^{-(m+1)}}\). We omit the details here.
- 4.
We are using \(\tau \) for transcript here to avoid the ambiguity with the \(\mathsf {Coll}\) oracle randomness \(\pi \).
References
Akavia, A., Goldreich, O., Goldwasser, S., Moshkovitz, D.: On Basing One-way Functions on NP-hardness. In: STOC (2006)
Applebaum, B., Haramaty, N., Kushilevitz, E., Vaikuntanathan, V.: Low-complexity cryptographic hash functions. In: ITCS, Yuval Ishai (2017)
Applebaum, B., Raykov, P.: On the relationship between statistical zero-knowledge and statistical randomized encodings. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 449–477. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_16
Asharov, G., Segev, G.: Limits on the power of indistinguishability obfuscation and functional encryption. In: FOCS (2015)
Bogdanov, A., Brzuska, C.: On basing size-verifiable one-way functions on NP-hardness. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 1–6. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_1
Baecher, P., Brzuska, C., Fischlin, M.: Notions of black-box reductions, revisited. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 296–315. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_16
Berman, I., Degwekar, A., Rothblum, R.D., Vasudevan, P.N.: Multi-collision resistant hash functions and their applications. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 133–161. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_5
Berman, I., Degwekar, A., Rothblum, R.D., Vasudevan, P.N.: Statistical Difference Beyond the Polarizing Regime. In: ECCC (2019)
Bitansky, N., Degwekar, A., Vaikuntanathan, V.: Structure vs. hardness through the obfuscation lens. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 696–723. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_23
Blum, M., Evans, W.S., Gemmell, P., Kannan, S., Naor, M.: Checking the correctness of memories. Algorithmica 12(2/3), 225–244 (1994)
Brakerski, Z., Katz, J., Segev, G., Yerukhimovich, A.: Limits on the power of zero-knowledge proofs in cryptographic constructions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 559–578. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_34
Bogdanov, A., Lee, C.H.: Limits of provable security for homomorphic encryption. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 111–128. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_7
Brakerski, Z., Lyubashevsky, V., Vaikuntanathan, V., Wichs, D.: Worst-case hardness for LPN and cryptographic hashing via code smoothing. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11478, pp. 619–635. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_21
Barak, B., Mahmoody-Ghidary, M.: Merkle puzzles are optimal—an \({O}(n^{2})\)-query attack on any key exchange from a random oracle. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 374–390. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_22
Bogdanov, A., Trevisan, L.: On worst-case to average-case reductions for NP problems. In: FOCS (2003)
Coretti, S., Dodis, Y., Guo, S., Steinberger, J.: Random oracles and non-uniformity. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 227–258. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_9
Damgård, I.B.: Collision free hash functions and public key signature schemes. In: Chaum, D., Price, W.L. (eds.) EUROCRYPT 1987. LNCS, vol. 304, pp. 203–216. Springer, Heidelberg (1988). https://doi.org/10.1007/3-540-39118-5_19
Dodis, Y., Haitner, I., Tentes, A.: On the instantiability of hash-and-sign RSA signatures. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 112–132. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_7
Dachman-Soled, D., Lindell, Y., Mahmoody, M., Malkin, T.: On the black-box complexity of optimally-fair coin tossing. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 450–467. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_27
Damgård, I.B., Pedersen, T.P., Pfitzmann, B.: On the existence of statistically hiding bit commitment schemes and fail-stop signatures. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 250–265. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_22
Fischlin, M.: Black-box reductions and separations in cryptography. In: Mitrokotsa, A., Vaudenay, S. (eds.) AFRICACRYPT 2012. LNCS, vol. 7374, pp. 413–422. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31410-0_26
Goldreich, O., Goldwasser, S.: On the Possibility of basing Cryptography on the assumption that P \(\ne \) NP. IACR Cryptology ePrint Archive (1998)
Goldreich, O., Goldwasser, S., Halevi, S.: Collision-free hashing from lattice problems. IACR Cryptology ePrint Archive, 1996:9 (1996)
Gennaro, R., Gertner, Y., Katz, J., Trevisan, L.: Bounds on the efficiency of generic cryptographic constructions. SIAM J. Comput. 35(1), 217–246 (2005)
Garg, S., Hajiabadi, M., Mahmoody, M., Mohammed, A.: Limits on the power of garbling techniques for public-key encryption. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10993, pp. 335–364. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_12
Goldreich, O., Kushilevitz, E.: A perfect zero-knowledge proof system for a problem equivalent to the discrete logarithm. J. Cryptol. 6(2), 97–116 (1993)
Goyal, V., Kumar, V., Lokam, S., Mahmoody, M.: On black-box reductions between predicate encryption schemes. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 440–457. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_25
Gertner, Y., Kannan, S., Malkin, T., Reingold, O., Viswanathan, M.: The relationship between public key encryption and oblivious transfer. In: FOCS (2000)
Gertner, Y., Malkin, T., Myers, S.: Towards a separation of semantic and CCA security for public key encryption. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 434–455. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_24
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof-systems (Extended Abstract). In: STOC (1985)
Gertner, Y., Malkin, T., Reingold, O.: On the impossibility of basing trapdoor functions on trapdoor predicates. In: FOCS (2001)
Gennaro, R., Trevisan, L.: Lower bounds on the efficiency of generic cryptographic constructions. In: FOCS (2000)
Haitner, I., Holenstein, T.: On the (im)possibility of key dependent encryption. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 202–219. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_13
Haitner, I., Hoch, J.J., Reingold, O., Segev, G.: Finding collisions in interactive protocols-tight lower bounds on the round and communication complexities of statistically hiding commitments. SIAM J. Comput. 44(1), 193–242 (2015)
Holmgren, J., Lombardi, A.: Cryptographic hashing from strong one-way functions (or: one-way product functions and their applications). In: FOCS (2018)
Halevi, S., Micali, S.: Practical and provably-secure commitment schemes from collision-free hashing. In: Koblitz, N. (ed.) CRYPTO 1996. LNCS, vol. 1109, pp. 201–215. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68697-5_16
Hsiao, C.-Y., Reyzin, L.: Finding collisions on a public road, or do secure hash functions need secret coins? In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 92–105. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_6
Ishai, Y., Kushilevitz, E., Ostrovsky, R.: Sufficient conditions for collision-resistant hashing. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 445–456. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_24
Impagliazzo, R.: A personal view of average-case complexity. In: CCC (1995)
Impagliazzo, R., Rudich, S.: Limits on the provable consequences of one-way permutations. In: STOC (1989)
Kilian, J.: A note on efficient zero-knowledge proofs and arguments (extended abstract). In: STOC (1992)
Komargodski, I., Naor, M., Yogev, E.: White-box vs. black-box complexity of search problems: ramsey and graph property testing. In: FOCS (2017)
Komargodski, I., Naor, M., Yogev, E.: Collision resistant hashing for paranoids: dealing with multiple collisions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 162–194. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_6
Kahn, J., Saks, M.E., Smyth, C.D.: The dual BKR inequality and rudich’s conjecture. Comb. Probab. Comput. 20(2), 257–266 (2011)
Kim, J.H., Simon, D.R., Tetali, P.: Limits on the efficiency of one-way permutation-based hash functions. In: FOCS (1999)
Komargodski, I., Yogev, E.: On distributional collision resistant hashing. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 303–327. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_11
Lyubashevsky, V., Micciancio, D.: Generalized compact knapsacks are collision resistant. In: Bugliesi, M., Preneel, B., Sassone, V., Wegener, I. (eds.) ICALP 2006. LNCS, vol. 4052, pp. 144–155. Springer, Heidelberg (2006). https://doi.org/10.1007/11787006_13
Liu, T., Vaikuntanathan, V.: On basing private information retrieval on NP-hardness. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 372–386. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_16
Merkle, R.C.: A certified digital signature. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 218–238. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_21
Megiddo, N., Papadimitriou, C.H.: On total functions, existence theorems and computational complexity. Theor. Comput. Sci. 81(2), 317–324 (1991)
Micciancio, D., Vadhan, S.P.: Statistical zero-knowledge proofs with efficient provers: lattice problems and more. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 282–298. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_17
Mahmoody, M., Xiao, D.: On the power of randomized reductions and the checkability of SAT. In: CCC (2010)
Ogata, W., Kurosawa, K.: On claw free families. In: Imai, H., Rivest, R.L., Matsumoto, T. (eds.) ASIACRYPT 1991. LNCS, vol. 739, pp. 111–123. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-57332-1_9
Pass, R.: Parallel repetition of zero-knowledge proofs and the possibility of basing cryptography on NP-hardness. In: CCC (2006)
Pass, R.: Unprovable security of perfect NIZK and non-interactive non-malleable commitments. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 334–354. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_19
Personal communication with the authors of [KNY18]
Peikert, C., Rosen, A.: Efficient collision-resistant hashing from worst-case assumptions on cyclic lattices. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 145–166. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_8
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_31
Reingold, O., Trevisan, L., Vadhan, S.: Notions of reducibility between cryptographic primitives. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 1–20. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_1
Rudich, S.: Limits on the Provable Consequences of One-Way Functions. Ph.D. thesis, University of California, Berkeley (1988)
Russell, A.: Necessary and sufficient condtions for collision-free hashing. J. Cryptol. 8(2), 87–100 (1995)
Simon, D.R.: Finding collisions on a one-way street: can secure hash functions be based on general assumptions? In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 334–345. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054137
Sahai, A., Vadhan, S.: A complete problem for statistical zero knowledge. J. ACM (JACM) 50(2), 196–249 (2003)
Unruh, D.: Random oracles and auxiliary input. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 205–223. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_12
Vadhan, S.P.: A study of statistical zero-knowledge proofs. Ph.D. thesis, Massachusetts Institute of Technology (1999)
Yu, Y., Zhang, J., Weng, J., Guo, C., Li, X.: Collision resistant hashing from learning parity with noise. IACR Cryptology ePrint Archive, 2017:1260 (2017)
Acknowledgements
Nir Bitansky is a member of the Check Point Institute of Information Security. Supported by the Alon Young Faculty Fellowship, by Len Blavatnik and the Blavatnik Family foundation, and an ISF grant 18/484. Akshay Degwekar did part of this work while visiting the FACT Center in IDC Herzliya, supported in part by ISF grant 1861/16 and AFOSR Award FA9550-17-1-0069. Also supported in part by NSF Grants CNS-1413920 and CNS-1350619, and by the Defense Advanced Research Projects Agency (DARPA) and the U.S. Army Research Office under contracts W911NF-15-C-0226 and W911NF-15-C-0236.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Bitansky, N., Degwekar, A. (2019). On the Complexity of Collision Resistant Hash Functions: New and Old Black-Box Separations. In: Hofheinz, D., Rosen, A. (eds) Theory of Cryptography. TCC 2019. Lecture Notes in Computer Science(), vol 11891. Springer, Cham. https://doi.org/10.1007/978-3-030-36030-6_17
Download citation
DOI: https://doi.org/10.1007/978-3-030-36030-6_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-36029-0
Online ISBN: 978-3-030-36030-6
eBook Packages: Computer ScienceComputer Science (R0)





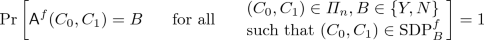
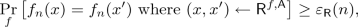

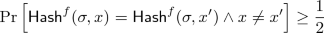

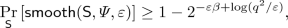
 . This measure also lies in the interval [0, 1] and is a metric.
. This measure also lies in the interval [0, 1] and is a metric.