Abstract
We propose a simple and powerful new approach for secure computation with input-independent preprocessing, building on the general tool of function secret sharing (FSS) and its efficient instantiations. Using this approach, we can make efficient use of correlated randomness to compute any type of gate, as long as a function class naturally corresponding to this gate admits an efficient FSS scheme. Our approach can be viewed as a generalization of the “TinyTable” protocol of Damgård et al. (Crypto 2017), where our generalized variant uses FSS to achieve exponential efficiency improvement for useful types of gates.
By instantiating this general approach with efficient PRG-based FSS schemes of Boyle et al. (Eurocrypt 2015, CCS 2016), we can implement useful nonlinear gates for equality tests, integer comparison, bit-decomposition and more with optimal online communication and with a relatively small amount of correlated randomness. We also provide a unified and simplified view of several existing protocols in the preprocessing model via the FSS framework.
Our positive results provide a useful tool for secure computation tasks that involve secure integer comparisons or conversions between arithmetic and binary representations. These arise in the contexts of approximating real-valued functions, machine-learning classification, and more. Finally, we study the necessity of the FSS machinery that we employ, in the simple context of secure string equality testing. First, we show that any “online-optimal” secure equality protocol implies an FSS scheme for point functions, which in turn implies one-way functions. Then, we show that information-theoretic secure equality protocols with relaxed optimality requirements would follow from the existence of big families of “matching vectors.” This suggests that proving strong lower bounds on the efficiency of such protocols would be difficult.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The power of correlated randomness in secure computation has recently been an active area of research. In the setting of secure computation with preprocessing, two or more parties receive correlated random inputs from a trusted dealer in an offline phase, before the inputs are known. In a subsequent online phase, once the inputs are known, the parties use this correlated randomness to obtain significant speedup over similar protocols in the plain model, either unconditionally or under weaker cryptographic assumptions. Alternatively, in the absence of a trusted dealer, the correlated randomness can be generated via an interactive secure protocol that is executed offline, before the inputs are known, and only the outputs of this protocol need to be stored for later use. For simplicity, we focus in this work on the case of secure two-party computation with security against semi-honest adversaries.Footnote 1
Originating from the work of Beaver [2], who showed how to use “multiplication triples” for secure arithmetic computation with no honest majority, many current protocols for secure computation make extensive use of correlated randomness. Commonly used types of two-party correlations include garbled circuit correlations, OT and OLE correlations, multiplication (“Beaver”) triples and their authenticated version, and one-time truth-tables [2, 4, 11, 13, 14, 22].
Motivated by secure computation applications that involve integer comparisons or conversions between arithmetic and boolean values, we introduce a simple and powerful new approach for secure computation in the preprocessing model. Our approach is based on the general tool of function secret sharing (FSS) [7] and its efficient instantiations from any pseudorandom generator. Informally, a (2-party) FSS scheme splits a function \(f:\mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\) from a function class \({\mathcal {F}}\), where \(\mathbb {G}^{\mathsf{in}}\) and \(\mathbb {G}^{\mathsf{out}}\) are finite AbelianFootnote 2 groups, into two functions, \(f_0\) and \(f_1\), such that (1) each \(f_\sigma \) is represented by a compact key \(k_\sigma \) that allows its efficient evaluation; (2) each key \(k_\sigma \) hides the function f; and (3) for any input \(x\in \mathbb {G}^{\mathsf{in}}\) we have \(f(x)=f_0(x)+f_1(x)\).
The Idea in a Nutshell. Our FSS-based approach for secure computation with preprocessing is very simple. Denote the two parties by \(P_0\) and \(P_1\). We represent the function being evaluated as a circuit C, in which inputs internal wires take values from (possibly distinct) groups. The circuit nodes are labeled by gates, where each gate g maps an input from a group \(\mathbb {G}^{\mathsf{in}}\) into an output from a group \(\mathbb {G}^{\mathsf{out}}\). Note that we can use product groups to capture a gate with multiple input or output wires. To securely evaluate C in the preprocessing model, the dealer generates and distributes the following type of correlated randomness. First, for every wire j in C, the dealer picks a random mask \(r_j\) from the corresponding group. Each party \(P_\sigma \) receives the random masks of the input wires it owns. The online phase evaluates the circuit gate-by-gate in a topological order, maintaining the following invariant: for every wire value \(w_j\) in C, both parties learn the masked value \(w_j+r_j\). This is easy to achieve at the inputs level: if input \(x_i\) is owned by party \(P_\sigma \), this party can simply compute and send \(x_i+r_i\) to the other party.
The key idea is the following FSS-based gate evaluation procedure. For each gate \(g:\mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\), the dealer uses an FSS scheme for the class of offset functions \(\mathcal G\) that includes all functions of the form \(g_{r^{\mathsf{in}},r^{\mathsf{out}}}(x)=g(x-r^{\mathsf{in}})+r^{\mathsf{out}}\). If the input to gate g is wire i and the output is wire j, the dealer uses the FSS scheme for \(\mathcal G\) to split the function \(g_{r_i,r_j}\) into two functions with keys \(k_0,k_1\), and delivers each key \(k_\sigma \) to party \(P_\sigma \). Now, evaluating their FSS shares on the common masked input \(w_i+r_i\), the parties obtain additive shares of the masked output \(w_j+r_j\), which they can exchange and maintain the invariant for wire j. Finally, the outputs are reconstructed by having the dealer reveal to both parties the masks of the output wires.
The above protocol is not only simple, but in a sense is implicit in the literature. It can be viewed as a generalization of the “TinyTable” protocol of Damgård et al. [13], where the novel idea is to use efficient FSS for achieving exponential compression (and speedupFootnote 3) for natural types of gates that are useful in applications. We discuss several useful instances of this approach below.
While the correlated randomness in the above protocol depends on the topology of C, we also present a circuit-independent variant where the input and output masks of different gates are independent of each other. In this variant, for each gate g the dealer chooses additive \(r^{\mathsf{in}}\) offsets only for the input wires of g, and provides FSS shares for the function \(g_{r^{\mathsf{in}},0}(x)=g(x-r^{\mathsf{in}})+0\), together with additive shares of \(r^{\mathsf{in}}\). During the online phase, the parties can “match up” the offsets for adjacent gates, and non-interactively emulate FSS shares of \(g_{r^{\mathsf{in}},r^{\mathsf{out}}}(x)=g(x-r^{\mathsf{in}})+r^{\mathsf{out}}\) using the additive shares, where \(r^{\mathsf{out}}\) is defined to be \((r^{\mathsf{in}})'\) for the appropriate next gate \(g'\). The resulting online communication is one element per wire, as opposed to only one element per computed wire value as in the circuit-dependent version (where circuit fan-out introduces extra wires but not new wire values).
Finally, one could alternatively consider a variant of our protocols in which FSS is used to convert secret-shared inputs to secret-shared outputs rather than common masked inputs to masked outputs. Whereas in the above protocol both parties first apply FSS on the common masked input and then exchange their output shares to obtain a masked output, in the alternative variant they start by reconstructing a common masked input from their input shares, and then apply FSS to directly obtain the output shares.
Application: Simple Derivation of Existing Protocols. By using simple information-theoretic FSS schemes for truth-tables and low-degree polynomials, our FSS-based approach can be used to derive in a simple and unified way several previous protocols for secure computation in the preprocessing model. For instance, protocols from [2, 11, 13, 22, 23] can be easily cast in this framework. We also present useful generalizations of such protocols to broader classes of algebraic computations.
Application: Online-Optimal Secure Equality, Comparison, Bit Decomposition, and More. Our FSS-based technique yields a simple new approach for securely performing useful nonlinear operations on masked or secret-shared values. We first describe the types of nonlinear operations we can efficiently support, and then the efficiency features of our FSS-based solution.
When performing secure arithmetic computations, it is often useful to switch between an arithmetic representation, where the values are secret-shared over a big modulus \(\mathbb {Z}_q\), and a Boolean representation, where the values are secret shared bit-by-bit over \(\mathbb {Z}_2\). Other useful nonlinear operations include zero-testing of a shared value or equality testing of two shared values, comparing between different integer values (i.e., the “greater than” predicate), or checking if an integer value is in an interval. For all of the above predicates, the input is secret-shared over \(\mathbb {Z}_q\) and the 0/1 output is secret-shared for further computations over either \(\mathbb {Z}_2\), \(\mathbb {Z}_q\), or another group. A more general class of nonlinear computations are spline functions that output a different polynomial on each interval. A useful special case is the ReLU function \(g(x)=\max (0,x)\) that is commonly used as an activation function in neural networks. Finally, one can also consider a garbling-compatible variant of the above operations, where the bits of the output select between pairs of secret keys that can be fed to a garbled circuit.
In all of the above cases, we can use computationally secure FSS schemes based on one-way functions [7, 8, 19] to efficiently realize the corresponding offset classes \(\mathcal G\) using only symmetric cryptography. Concretely, for all the above types of gates we can use efficient preprocessing to convert shares of an input into shares of an output with optimal online communication that only involves a single round of exchanging masked input shares and no further interaction. Each party can then directly compute its share of the output given its part of the correlated randomness and the message received from the other party.
The above types of nonlinear “FSS gates” can provide a valuable toolbox for the large body of work on secure machine learning classification, secure implementation of bounded-precision arithmetic, and secure approximations of real-valued functions. In fact, they can even be useful for evaluating standard Boolean circuits. For instance, evaluating an AND/OR gate with fan-in m reduces to a secure equality of m-bit strings.
Comparison with Prior Approaches. There is a long line of work on secure implementation of useful nonlinear computations such as bit-decomposition in different models (see [10, 12, 15, 25] and references therein). As discussed above, our FSS-based technique has an optimal online cost of converting secret-shared inputs to secret-shared outputs. Compared to the commonly used “ABY framework” [15] for performing such operations using garbled circuits, our approach has better round complexity (1 instead of 2 rounds) and, more importantly, it avoids the big overhead of sending a key for each bit of the input. In concrete terms, this improves the online communication complexity by two orders of magnitude. Even in the relatively simple cases of equality testing and integer comparison, where improved special-purpose protocols are known (see [10] and references therein), our FSS-based approach has significant advantages over the best previous protocols.
The low online cost of our FSS-based protocols is inherited from the efficiency of recent constructions of FSS schemes for point functions, intervals, and decision trees [7, 8, 19]. These constructions make a black-box use of any pseudorandom generator, which can be instantiated by AES in practice. Thus, for the type of “gates” supported by such simple FSS schemes, our protocols significantly improve the online communication complexity and round complexity of prior approaches while still being very computationally efficient in the online phase. See Table 1 for comparison.
Realizing the Dealer. We turn to discuss the offline cost of securely generating and storing the correlated randomness. The amount of correlated randomness used by our protocols is dominated by the size of the FSS keys. For equality and comparison gates, this includes a linear number of PRG seeds (e.g., AES keys) in the bit-length of the inputs, and for bit-decomposition it involves a quadratic number of PRG seeds. When the input domain is not too big, the distributed generation of this correlated randomness can be done with good concrete efficiency using a distributed FSS key generation protocol of Doerner and Shelat [16]. Otherwise one can use concretely efficient general-purpose secure computation protocols (such as [24]) for emulating the dealer. Finally, one can avoid the cost of securely distributing the correlated randomness by using a third party as a dealer and settling for security against a single corrupted party. This is similar to the 3-party ABY\(^3\) framework from [25], except that here the third party is only used to generate correlated randomness and can remain offline during the actual computation.
Is FSS Necessary? Our most useful positive results make use of symmetric cryptography. Given that most protocols in the preprocessing model are information-theoretic, one may ask if it is possible to obtain similar results in the information-theoretic model with a polynomial amount of correlated randomness. For simplicity, we consider a shared equality protocol with optimal online complexity. In such a protocol, the parties hold n-bit strings \(x_0\) and \(x_1\), and in a single round of interaction they send an n-bit message to each other. These messages should hide their inputs. Following this interaction, they each locally output a single output bit such that the exclusive-or of the two bits is 1 if and only if \(x_0=x_1\). We show that our FSS machinery is not only sufficient for obtaining this type of protocols, but is also necessary. In particular, any protocol as above implies the existence of a one-way function. (This implication is more subtle than it may seem since unlike our simple FSS-based protocol, a general shared equality protocol may correlate the randomness used to mask the inputs with the randomness used to compute the output shares.) On the other hand, we show that efficient information-theoretic shared equality protocols with constant-size output shares would follow from the existence of big families of “matching vectors” [17, 18, 21], a longstanding open problem in extremal combinatorics. This suggests that strong lower bounds on the efficiency of information-theoretic shared equality protocols would be difficult to obtain.
Organization. In Sect. 2, we provide necessary preliminaries. In Sect. 3, we present our general framework for secure computation with preprocessing via FSS. In Sect. 4, we present applications, instantiating the necessary FSS schemes for specific motivated computation tasks. We conclude in Sect. 5 by exploring negative results and barriers.
2 Preliminaries
2.1 Representing Functions
In order to seamlessly handle both arithmetic and Boolean operations, we will consider all functions to be defined over Abelian groups. For instance, a Boolean function \(f:\{0,1\}^n\rightarrow \{0,1\}^m\) will be viewed as a mapping from the group \(\mathbb {Z}_2^n\) to the group \(\mathbb {Z}_2^m\). Given our heavy use of function secret sharing, we use a similar convention for function representation to the one used in [8] (the only difference being that here we also endow the input domain with a group structure).
Definition 1
(Function families). A function family is defined by \({\mathcal {F}}=(P_{\mathcal {F}},E_{\mathcal {F}})\), where \(P_{\mathcal {F}}\subseteq \{0,1\}^*\) is an infinite collection of function descriptions \({\hat{f}}\) and \(E_{\mathcal {F}}:P_{\mathcal {F}}\times \{0,1\}^*\rightarrow \{0,1\}^*\) is a polynomial-time algorithm defining the function described by \({\hat{f}}\). Concretely, \({\hat{f}}\in P_{\mathcal {F}}\) describes a corresponding function \(f:D_f\rightarrow R_f\) defined by \(f(x)=E_{\mathcal {F}}({\hat{f}},x)\). We require \(D_f\) and \(R_f\) to be finite Abelian groups, denoted by \(\mathbb {G}^{\mathsf{in}}\) and \(\mathbb {G}^{\mathsf{out}}\) respectively. We will typically let \(\mathbb {G}^{\mathsf{in}}\) and \(\mathbb {G}^{\mathsf{out}}\) be product groups, which can capture the case of multiple inputs and outputs. When there is no risk of confusion, we will sometimes write f instead of \({\hat{f}}\) and \(f\in {\mathcal {F}}\) instead of \({\hat{f}}\in P_{\mathcal {F}}\). We assume that \({\hat{f}}\) includes an explicit description of \(\mathbb {G}^{\mathsf{in}}\) and \(\mathbb {G}^{\mathsf{out}}\).
By convention, we denote by \(0 \in \mathbb {G}\) the identity element of \(\mathbb {G}\). We will use the notation \(1 \in \mathbb {G}\) to denote a fixed canonical nonzero element of \(\mathbb {G}\); when \(\mathbb {G}\) is additionally endowed with a multiplicative structure, e.g., when \(\mathbb {G}\) is the additive group of a finite ring, 1 will be set to the multiplicative identity.
2.2 Secure Computation with Preprocessing
We follow the standard definitional framework for secure computation (cf. [9, 20]), except that we allow a trusted input-independent setup phase that distributes correlated secret randomness to the parties. This setup phase can be securely emulated by an interactive preprocessing protocol that can be carried out before the inputs are known. We focus here on protocols with security against a semi-honest adversary who may non-adaptively corrupt any strict subset of parties. For simplicity, we explicitly spell out the definitions for the two-party case, and later explain the (straightforward) extension to the multi-party case.
Functionalities. We denote the two parties by \(P_0\) and \(P_1\) and a party index by \(\sigma \in \{0,1\}\). We consider by default protocols for deterministic functionalities that deliver the same output to the two parties. The general case (of randomized functionalities with different outputs) can be reduced to this case via a standard reduction [9, 20]. A two-party functionality f is described by a bit-string \({\hat{f}}\) via a function family \({\mathcal {F}}\), as in Definition 1. We assume that the input domain \(\mathbb {G}^{\mathsf{in}}\) is split into \(\mathbb {G}^{\mathsf{in}}=\mathbb {G}^{\mathsf{in}}_0\times \mathbb {G}^{\mathsf{in}}_1\), capturing the inputs of the two parties.
Protocols with Preprocessing. A two-party protocol is defined by a pair of PPT algorithms \(\varPi =(\mathsf{Setup},\mathsf{NextMsg})\). The setup algorithm \(\mathsf{Setup}(1^{\lambda },{\hat{f}})\), given a security parameter \({\lambda }\) and functionality description \({\hat{f}}\), outputs a pair of correlated random strings \((r_0,r_1)\). We also consider protocols with function-independent preprocessing, in which \(\mathsf{Setup}\) only receives a bound \(1^S\) on the size of \({\hat{f}}\) instead of \({\hat{f}}\) itself. The next-message function \(\mathsf{NextMsg}\) determines the messages sent by the two parties. Concretely, the function \(\mathsf{NextMsg}\), on input \((\sigma ,j,{\hat{f}},x_\sigma ,r_\sigma ,{\mathbf m})\), specifies the message sent by party \(P_\sigma \) in Round j depending on the functionality description \({\hat{f}}\), input \(x_\sigma \), random input \(r_\sigma \), and vector \(\mathbf m\) of previous messages received from \(P_{1-\sigma }\). We assume both parties can speak to each other in the same round. (In the semi-honest model, one can eliminate this assumption by at most doubling the number of rounds.) If the output of \(\mathsf{NextMsg}\) is of the form \((\mathsf{Out},y)\) then party \(P_\sigma \) terminates the protocol with output y. We denote by \(\mathsf{Out}_{\varPi ,\sigma }({\lambda },{\hat{f}},(x_0,x_1))\) and \(\mathsf{View}_{\varPi ,\sigma }({\lambda },{\hat{f}},(x_0,x_1))\) the random variables containing the output and view of party \(P_\sigma \) (respectively) in the execution of \(\varPi \) on inputs \((x_0,x_1)\), where the view includes \(r_\sigma \) and messages received from \(P_{1-\sigma }\).
Security Definition. We require both correctness and security, where security is captured by the existence of a PPT algorithm \(\mathsf{Sim}\) that simulates the view of a party given its input and output alone. We formalize this below.
Definition 2
(Secure computation with preprocessing). We say that \(\varPi =(\mathsf{Setup},\mathsf{NextMsg})\) securely realizes a function family \({\mathcal {F}}\) in the preprocessing model if the following holds:
-
Correctness: For all \({\hat{f}}\in P_{\mathcal {F}}\) describing \(f:\mathbb {G}^{\mathsf{in}}_0\times \mathbb {G}^{\mathsf{in}}_1 \rightarrow \mathbb {G}^{\mathsf{out}}\), \((x_0,x_1)\in \mathbb {G}^{\mathsf{in}}_0\times \mathbb {G}^{\mathsf{in}}_1\), \({\lambda }\in \mathbb {N}\), \(\sigma \in \{0,1\}\), we have \(\Pr [\mathsf{Out}_{\varPi ,\sigma }({\lambda },{\hat{f}},(x_0,x_1))=f(x_0,x_1)]=1\).
-
Security: For each corrupted party \(\sigma \in \{0,1\}\) there exists a PPT algorithm \(\mathsf{Sim}_\sigma \) (simulator), such that for every infinite sequence \(({\hat{f}}_{\lambda })_{{\lambda }\in \mathbb {N}}\) of polynomial-size function descriptions from \(P_{\mathcal {F}}\) and polynomial-size input sequence \((x^{\lambda }_0,x^{\lambda }_1)_{{\lambda }\in \mathbb {N}}\) for \(f_{\lambda }\), the outputs of the following experiments \(\mathsf{Real}\) and \(\mathsf{Ideal}\) are computationally indistinguishable:
-
\(\mathsf{Real}_{\lambda }\): Output \(\mathsf{View}_{\varPi ,\sigma }({\lambda },{\hat{f}}_{\lambda },(x^{\lambda }_0,x^{\lambda }_1))\)
-
\(\mathsf{Ideal}_{\lambda }\): Output \(\mathsf{Sim}_\sigma (1^{\lambda }, {\hat{f}}_{\lambda },x^{\lambda }_\sigma ,f_{\lambda }(x^{\lambda }_0,x^{\lambda }_1))\)
-
We say that \(\varPi \) realizes \({\mathcal {F}}\) with statistical (resp., perfect) security if the above security requirement holds with statistical (resp., perfect) indistinguishability instead of computational indistinguishability.
2.3 Function Secret Sharing
We follow the definition of function secret sharing (FSS) from [8]. Intuitively, a (2-party) FSS scheme is an efficient algorithm that splits a function \(f\in {\mathcal {F}}\) into two additive shares \(f_0,f_1\), such that: (1) each \(f_\sigma \) hides f; (2) for every input x, \(f_0(x)+f_1(x)=f(x)\). The main challenge is to make the descriptions of \(f_0\) and \(f_1\) compact, while still allowing their efficient evaluation. As in [7, 8], we insist on an additive representation of the output rather than settle for an arbitrary compact output representation. The additive representation is critical for the applications we consider in this work and is achieved by existing constructions.
We now formally define the notion of FSS. While in this work we consider the 2-party case for simplicity, the definitions and the applications can be extended in a natural way to the k-party case.
Definition 3
(FSS: Syntax). A (2-party) function secret sharing (FSS) scheme is a pair of algorithms \((\mathsf{Gen},\mathsf{Eval})\) with the following syntax:
-
\(\mathsf{Gen}(1^\lambda , \hat{f})\) is a PPT key generation algorithm, which on input \(1^\lambda \) (security parameter) and \(\hat{f} \in \{0,1\}^*\) (description of a function f) outputs a pair of keys \((k_0,k_1)\). We assume that \({\hat{f}}\) explicitly contains descriptions of input and output groups \(\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}}\).
-
\(\mathsf{Eval}(\sigma , k_\sigma , x)\) is a polynomial-time evaluation algorithm, which on input \(\sigma \in \{0,1\}\) (party index), \(k_\sigma \) (key defining \(f_\sigma :\mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\)) and \(x \in \mathbb {G}^{\mathsf{in}}\) (input for \(f_\sigma \)) outputs a group element \(y_\sigma \in \mathbb {G}^{\mathsf{out}}\) (the value of \(f_\sigma (x)\), the \(\sigma \)-th share of f(x)).
Definition 4
(FSS: Correctness and Security). Let \({\mathcal {F}}=(P_{\mathcal {F}},E_{\mathcal {F}})\) be a function family (as defined in Definition 1) and \(\mathsf{Leak}\) be a polynomial-time computable function specifying the allowable leakage about \({\hat{f}}\). When \(\mathsf{Leak}\) is omitted, it is understood to output only \(\mathbb {G}^{\mathsf{in}}\) and \(\mathbb {G}^{\mathsf{out}}\). We say that \((\mathsf{Gen},\mathsf{Eval})\) as in Definition 3 is an FSS scheme for the function family \({\mathcal {F}}\) (with respect to leakage \(\mathsf{Leak}\)) if it satisfies the following requirements.
-
Correctness: For all \({\hat{f}}\in P_{\mathcal {F}}\) describing \(f:\mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\), and every \(x \in \mathbb {G}^{\mathsf{in}}\), if \((k_0,k_1) \leftarrow \mathsf{Gen}(1^\lambda ,{\hat{f}})\) then \(\Pr \left[ \mathsf{Eval}(0,k_0,x)+\mathsf{Eval}(1,k_1,x) = f(x) \right] = 1\).
-
Security: For each \(\sigma \in \{0,1\}\) there is a PPT algorithm \(\mathsf{Sim}_\sigma \) (simulator), such that for every infinite sequence \(({\hat{f}}_{\lambda })_{{\lambda }\in \mathbb {N}}\) of polynomial-size function descriptions from \(P_{\mathcal {F}}\) and polynomial-size input sequence \(x_{\lambda }\) for \(f_{\lambda }\), the outputs of the following experiments \(\mathsf{Real}\) and \(\mathsf{Ideal}\) are computationally indistinguishable:
-
\(\mathsf{Real}_{\lambda }\): \((k_0,k_1) \leftarrow \mathsf{Gen}(1^\lambda , {\hat{f}}_\lambda )\); Output \(k_\sigma \).
-
\(\mathsf{Ideal}_{\lambda }\): Output \(\mathsf{Sim}_\sigma (1^\lambda , \mathsf{Leak}({\hat{f}}_\lambda ))\).
-
We refer to the FSS scheme as being statistical (resp., perfect) if the above holds with statistical (resp., perfect) indistinguishability instead of computational indistinguishability.
Definition 5
(Distributed Point Function (DPF)). A point function \(f_{\alpha ,\beta }\), for \(\alpha \in \mathbb {G}^{\mathsf{in}}\) and \(\beta \in \mathbb {G}^{\mathsf{out}}\), is defined to be the function \(f:\mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\) such that \(f(\alpha )=\beta \) and \(f(x)=0\) for \(x\ne \alpha \). A Distributed Point Function (DPF) is an FSS scheme for the family of all point functions, with the default leakage (i.e., \(\mathsf{Leak}({\hat{f}})=(\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}})\)).
Definition 6
(Distributed Interval Function (DIF)). An interval function \(f_{(a,b),\beta }\), for \(a,b\in \mathbb {G}^{\mathsf{in}}\), and \(\beta \in \mathbb {G}^{\mathsf{out}}\), and given an arbitrary total order \(\le \) on \(\mathbb {G}^{\mathsf{in}}\), is defined to be the function \(f:\mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\) such that \(f(x)=\beta \) for \(x \in \mathbb {G}^{\mathsf{in}}, a\le x \le b\), while \(f(x)=0\) for \(x< a\) or \(x>b\). If \(a=0\) (the minimal element of \(\mathbb {G}^{\mathsf{in}}\)) or \(b=|\mathbb {G}^{\mathsf{in}}|-1\) (the maximal element) then we say that \(f_{(a,b),\beta }\) is a special interval function. A Distributed Interval Function (DIF) is an FSS scheme for the family of all interval functions, with the default leakage (i.e., \(\mathsf{Leak}({\hat{f}})=(\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}})\)) and a similar definition holds for Distributed Special Interval Functions.
The following theorem captures the complexity of the best known constructions of DPF and distributed interval functions from a PRG.
Theorem 1
(Concrete complexity of DPF and DIF schemes [8]). Given a PRG \(G:\{0,1\}^\lambda \rightarrow \{0,1\}^{2\lambda +2}\), there exists a DPF for \(f_{\alpha ,\beta }:\mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\) with key size \(m\cdot (\lambda +2) + \lambda + \ell \) bits, where \(m=\lceil \log _2|\mathbb {G}^{\mathsf{in}}|\rceil \) and \(\ell =\lceil \log _2|\mathbb {G}^{\mathsf{out}}|\rceil \). For \(\ell '=\lceil \frac{\ell }{\lambda +2} \rceil \), the key generation algorithm \(\mathsf{Gen}\) invokes G at most \(2(m+\ell ')\) times and the evaluation algorithm \(\mathsf{Eval}\) invokes G at most \(m+\ell '\) times. For special (resp., general) DIF, the above costs are multiplied by at most 2 (resp., 4).
3 Secure Computation with Preprocessing from FSS
In this section, we develop our primary general transformation for using FSS to obtain secure 2PC with preprocessing. We then demonstrate how this approach captures and generalizes existing techniques within this regime.
3.1 Circuit and Offset-Family Notation
We begin by introducing some notation for modeling circuits of computation gates.
Definition 7
(Computation Gate). A computation gate is a function family \(\mathcal {G}\) (Definition 1), where each function describes a pair of Abelian groups \((\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}})\), and a mapping \(g: \mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\). In some cases it will be convenient to interpret \(\mathbb {G}^{\mathsf{in}}\) and \(\mathbb {G}^{\mathsf{out}}\) explicitly as product groups, of the form \(\mathbb {G}^{\mathsf{in}}= \prod _{i \in [\ell ]} \mathbb {G}^{\mathsf{in}}_i\) and \(\mathbb {G}^{\mathsf{out}}= \prod _{i \in [m]} \mathbb {G}^{\mathsf{out}}_i\).
For example, one may consider a zero-test gate, corresponding to the family of zero-test functions parameterized by different input and output groups.
For syntactic purposes, it will be useful to define notation for the following type of (trivial) input and output gates.
Definition 8
(Input and Output Gates). An input gate is a gate \(\mathcal {G}_\mathsf{Inp}\) which syntactically receives no input from other gates \((\mathbb {G}^{\mathsf{in}}=\emptyset )\), and outputs a single value. An output gate is a gate \(\mathcal {G}_\mathsf{Out}\) which syntactically sends no output to further gates \((\mathbb {G}^{\mathsf{out}}=\emptyset )\), and receives as input a single value.
We now define a circuit of input, output, and computation gates, via two parts: (1) the circuit syntax, dictating its topological connectivity amongst gates, and (2) the circuit instantiation, selecting a specific function for each gate, such that the choices of input/output groups are consistent across edges. For example, given multiplication gates followed by a zero-test gate (each corresponding to a family of functions), these gates could be instantiated over any arithmetic ring R followed by zero-test from \(\mathbb {G}^{\mathsf{in}}= R\) to any other space \(\mathbb {G}^{\mathsf{out}}\) with canonical 0 and 1 values.
The syntax of the circuit will be modeled by the structure of a directed acyclic graph, with nodes serving as gates and edges serving as wires. In order to model fan-out, each gate will be associated with both an out-degree (dictated by the graph) and an out-arity \(\ell ^{\mathsf{out}}\), which may not be the same. The out-arity corresponds to the number of values output by the gate computation. Each outgoing edge from the gate corresponds to a wire carrying the value of one of these outputs to another gate, and is labeled with the corresponding index \(j \in [\ell ^{\mathsf{out}}]\).
Definition 9
(Circuit syntax). Let \(\mathcal {B}\) be a finite set (“basis”) of gates. A circuit C over basis \(\mathcal {B}\) specifies a directed acyclic graph (V, E), where each node \(v \in V\) is labeled with an input and output arity \((\ell ^{\mathsf{in}}_v,\ell ^{\mathsf{out}}_v)\), and a gate type \(\mathcal {G}_v \in \mathcal {B}\), such that:
-
Each source node is labeled by an input gate and every sink an output gate (as per Definition 8). We sometimes denote the set of input and output gates of C by \(\mathsf{Inp}\) and \(\mathsf{Out}\).
-
The in-arity \(\ell ^{\mathsf{in}}_v\) of each node \(v \in V\) is equal to its in-degree; each incoming edge into v is associated with a distinct index \(i \in [\ell ^{\mathsf{in}}_v]\). Each outgoing edge from v is labeled with an index \(j \in [\ell ^{\mathsf{out}}_v]\), possibly with repetition (representing fan-out).
-
The depth of C, denoted \(\mathsf{depth}(C)\), is defined as the length of the longest directed path in C.
Definition 10
(Circuit instantiation). Let C be a circuit over basis \(\mathcal {B}\) with graph (V, E). An instantiation  of C is a selection for each \(v \in V\) of a function \(g_v : \mathbb {G}^{\mathsf{in}}_v \rightarrow \mathbb {G}^{\mathsf{out}}_v\) from the gate function family \(\mathcal {G}_v\), subject to the following constraints:
of C is a selection for each \(v \in V\) of a function \(g_v : \mathbb {G}^{\mathsf{in}}_v \rightarrow \mathbb {G}^{\mathsf{out}}_v\) from the gate function family \(\mathcal {G}_v\), subject to the following constraints:
-
1.
\(\mathbb {G}^{\mathsf{in}}_v = \prod _{i \in [\ell ^{\mathsf{in}}_v]} \mathbb {G}^{\mathsf{in}}_{(v,i)}\) and \(\mathbb {G}^{\mathsf{out}}_v = \prod _{j \in [\ell ^{\mathsf{out}}_v]} \mathbb {G}^{\mathsf{out}}_{(v,j)}\) for some abelian groups \(\mathbb {G}^{\mathsf{in}}_{(v,i)},\mathbb {G}^{\mathsf{out}}_{(v,j)}\), where \(\ell ^{\mathsf{in}}_v,\ell ^{\mathsf{out}}_v\) are the arity of v.
-
2.
For every edge \((u,v) \in E\) labeled by \(i \in [\ell ^{\mathsf{out}}_u]\) and \(j \in [\ell ^{\mathsf{in}}_v]\), it holds that \(\mathbb {G}^{\mathsf{out}}_{(u,i)} = \mathbb {G}^{\mathsf{in}}_{(v,j)}\).
We will sometimes refer to edges \((u,v) \in E\) as wires \(w \in C\), denoting \(\mathbb {G}_w := \mathbb {G}^{\mathsf{out}}_{(u,i)} = \mathbb {G}^{\mathsf{in}}_{(v,j)}\).
Remark 1
(Instantiation-dependent topology). In some cases, the circuit topology cannot be completely decoupled from the instantiation. For example, instantiating a bit-decomposition gate with \(\mathbb {G}^{\mathsf{in}}= \mathbb {Z}_{2^k}\) would yield output \(\mathbb {G}^{\mathsf{out}}= \mathbb {Z}_2^k\) of arity k. However, we will attempt to keep syntax and instantiation separate whenever possible for sake of modularity.
Our approach for preprocessing a gate computation relies on FSS sharing of a corresponding family of functions, formed by allowing different additive offset values to both the input and output value. In our application to 2PC, these will serve as the values of random wire masks.
Definition 11
(Offset function family). Let \(\mathcal {G}\) be a computation gate. The family of offset functions \({\hat{\mathcal {G}}}\) of \(\mathcal {G}\) is given by
and where each \(g^{[{r^{\mathsf{in}},r^{\mathsf{out}}}]}\) contains an explicit description of \(r^{\mathsf{in}},r^{\mathsf{out}}\).
3.2 Secure 2-Party Computation with Preprocessing from FSS
We now demonstrate how to apply the ideas from the introduction to obtain a secure 2-party computation protocol in the preprocessing model with cheap online complexity. We restrict our protocol descriptions to the 2-party setting, both for purposes of simplicity, and since this is currently the setting of most efficient FSS constructions. However, the statements generalize to the multiparty case (given corresponding multi-party FSS) with any number of corrupted parties.
The following statement constitutes our core protocol, which leverages the structure of the circuit to provide tailored preprocessing information. Later, in Theorem 3, we extend the approach to support circuit-independent preprocessing, at small extra offline and communication cost. Roughly, the extra communication corresponds to an element communicated for every wire as opposed to every gate output value; note that multiple wires may correspond to the same gate output, in the case of circuit fanout.
Theorem 2
(Circuit-Dependent Preprocessing). Let C be a circuit over basis \(\mathcal {B}\). For each \(\mathcal {G}\in \mathcal {B}\), let \((\mathsf{Gen}_{\hat{\mathcal {G}}},\mathsf{Eval}_{\hat{\mathcal {G}}})\) be an FSS for the offset-function family \({\hat{\mathcal {G}}}\) with key size \(\mathsf{size}_{\hat{\mathcal {G}}}({\lambda },|\mathbb {G}^{\mathsf{in}}|,|\mathbb {G}^{\mathsf{out}}|)\). Then for any instantiation  of C, there exists a 2-party protocol for securely computing
of C, there exists a 2-party protocol for securely computing  with the following properties:
with the following properties:
-
Preprocessing. Given circuit C with gate (“vertex”) indices \(v \in C\), denote the set of gates by \(\mathcal {G}_v\) and their instantiations by \(g_v\), which in particular specify input/output groups \(\mathbb {G}^{\mathsf{in}}_v,\mathbb {G}^{\mathsf{out}}_v\). The preprocessing phase executes \(\mathsf{Gen}_{{\hat{\mathcal {G}}}_v}\) for each \(g_v\) and produces output of size \(\sum _{v \in C} \mathsf{size}_{\hat{\mathcal {G}_v}}({\lambda },|\mathbb {G}^{\mathsf{in}}_v|,|\mathbb {G}^{\mathsf{out}}_v|)\).
-
Online. The online protocol requires local execution of \(\mathsf{Eval}_{\hat{\mathcal {G}}}\) for each gate, yielding the following properties:
-
Rounds: \(\mathsf{depth}_\mathcal {B}(C)\).
-
Communication: \(\sum _{v \in C} \log |\mathbb {G}^{\mathsf{out}}_v|\) bits per party.
-
If the FSS schemes are perfectly (resp., statistically) secure, then the resulting protocol is perfectly (resp., statistically) secure in the preprocessing model.
The proof of Theorem 2 follows the high-level description from the Introduction and appears in the full version.
Remark 2
(Compressing preprocessing output). In some cases, the size of the offline preprocessing information can be compressed, when e.g. FSS keys of neighboring gates contain redundant information. This will be the case, for example, when generating FSS keys for neighboring gates which are each instantiated by degree-2 functions. (Here, the output mask \(r_w\) of the first gate will be identical to the input mask of the second, as they correspond to the same wire; thus including secret shares of \(r_w\) as part of both FSS keys is unnecessary.) See discussion in the following section for further cases.
Circuit-Independent Preprocessing. The protocol construction in Theorem 2 used preprocessing information that was tailored to the topology of the given circuit C. More concretely, we were able to “match up” the input/output offset masks \(r_v\) of every pair of gates sharing a wire, hardcoding the same offset into the FSS keys for the respective functions. In particular, this enabled “for free” a direct translation from masked output of one gate to appropriate masked input to all gates in the next level which accepted this value as input (via fan-out).
In some cases, it may be advantageous to produce generic preprocessing information that depends on the individual gate structure, but which can be used for any circuit built from such gates (independent of the topology linking the gates together). Our approach generalizes to this circuit-independent setting with a small amount of additional overhead, via a few small changes, which we now describe.
The only difference between the two constructions is that the circuit-dependent correlation could directly “match up” the outgoing mask \(r^{\mathsf{out}}\) for a gate to be equal to the incoming mask \(r^{\mathsf{in}}\) of any gate to which it enters. In contrast, when the structure of the circuit C is not a priori known, this can be effectively emulated as follows.
-
For each gate g, we will sample a random input offset mask \(r^{\mathsf{in}}\) (but not \(r^{\mathsf{out}}\)), and provide FSS shares for the offset function \(g^{[r^{\mathsf{in}},0]} = g(x -r^{\mathsf{in}}) + 0\), together with additive secret shares of the mask \(r^{\mathsf{in}}\) (which was not needed previously). Note that a mask per input corresponds directly to a mask per wire in the circuit.
-
Then, once the structure of the circuit C is known (during the protocol), a party \(P_\sigma \) can locally convert his overall collection of preprocessing information over all gates \((k^\sigma _v,(r^{\mathsf{in}}_v)^\sigma )_{v \in C}\) into FSS shares for the desired “matched up” \(g^{[{r^{\mathsf{in}},r^{\mathsf{out}}}]}\) (where \(r^{\mathsf{out}}\) is equal to the input mask \(r^{\mathsf{in}}\) for the next gate that the gate v output value will enter into), by leveraging the additive secret shares of all wire masks \(r^{\mathsf{in}}\) together with linearity of FSS reconstruction: i.e., outputting \(\mathsf{Eval}(\sigma ,k^\sigma _v,x) + (r^{\mathsf{out}}_v)^\sigma \).
This effectively reduces us back to the circuit-dependent version, in terms of correctness and security. Observe, however, that whereas in the circuit-dependent version, \(r^{\mathsf{in}}\) values of all target gates for fan-out wires of the same value could a priori be coordinated, in this setting (when this structure is not a priori known), the parties must send a separate element per fan-out wire. We also must provide the additive shares of the input masks \(r^{\mathsf{in}}\) as part of the correlated randomness.
Theorem 3
(Circuit-Independent Preprocessing). Let \(\mathcal {B}\) be a finite gate basis; for each \(\mathcal {G}\in \mathcal {B}\), let \((\mathsf{Gen}_{\hat{\mathcal {G}}},\mathsf{Eval}_{\hat{\mathcal {G}}})\) be an FSS for the offset-function family \({\hat{\mathcal {G}}}\) with key size \(\mathsf{size}_{\hat{\mathcal {G}}}({\lambda },|\mathbb {G}^{\mathsf{in}}|,|\mathbb {G}^{\mathsf{out}}|)\). Then there exists a 2-party protocol for securely computing any \(\mathcal {B}\)-circuit instantiation  consisting of \(s_\mathcal {G}\in \mathbb {N}\) gates g of type \(\mathcal {G}\) for each \(\mathcal {G}\in \mathcal {B}\), with the following complexity:
consisting of \(s_\mathcal {G}\in \mathbb {N}\) gates g of type \(\mathcal {G}\) for each \(\mathcal {G}\in \mathcal {B}\), with the following complexity:
-
Preprocessing. (Independent of
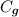 ) The preprocessing phase executes \(s_\mathcal {G}\) executions of \(\mathsf{Gen}_{\hat{\mathcal {G}}}\) for each gate \(\mathcal {G}\in \mathcal {B}\) and produces output size $$\begin{aligned} \sum _{\mathcal {G}\in \mathcal {B}} s_\mathcal {G}\cdot \left( \mathsf{size}_{\hat{\mathcal {G}}}({\lambda },|\mathbb {G}^{\mathsf{in}}|,|\mathbb {G}^{\mathsf{out}}|)+\log |\mathbb {G}^{\mathsf{in}}| \right) \!. \end{aligned}$$
) The preprocessing phase executes \(s_\mathcal {G}\) executions of \(\mathsf{Gen}_{\hat{\mathcal {G}}}\) for each gate \(\mathcal {G}\in \mathcal {B}\) and produces output size $$\begin{aligned} \sum _{\mathcal {G}\in \mathcal {B}} s_\mathcal {G}\cdot \left( \mathsf{size}_{\hat{\mathcal {G}}}({\lambda },|\mathbb {G}^{\mathsf{in}}|,|\mathbb {G}^{\mathsf{out}}|)+\log |\mathbb {G}^{\mathsf{in}}| \right) \!. \end{aligned}$$ -
Online. The online execution takes \(\mathsf{depth}(C)\) rounds (as before), but requires communication \(\sum _{v \in C} \log |\mathbb {G}^{\mathsf{in}}_v|\) bits per party (vs. \(\sum _{v \in C} \log |\mathbb {G}^{\mathsf{out}}_v|\)). Equivalently, one element is communicated per wire, as opposed to only one element per value (where fan-out introduces extra wires but not values).
The proof of Theorem 3 appears in the full version.
3.3 Recasting and Generalizing Existing Protocols
We begin by briefly demonstrating that common existing approaches to 2PC with preprocessing (and even useful extensions) can be cast as instances of the FSS-based framework, for special simple cases of FSS.
Low-Degree Gates. The first category is FSS of low-degree polynomials, which can be attained simply by providing additive secret shares of each coefficient. More broadly:
Observation 4
(FSS via Coefficient-Sharing). For any module M over coefficient ring R, and family of functions of the form \({\mathcal {F}}= \left\{ \sum _{i=1}^m \alpha _i F_i(x) \left. \right| \alpha _i \in R \right\} \) for public functions \((F_i)_{i \in [m]}: \mathbb {G}^{\mathsf{in}}\rightarrow M\), there exists an FSS scheme for \({\mathcal {F}}\) with perfect security and correctness, as follows:
-
\(\mathsf{Gen}(1^{\lambda }, f)\): Parse the description of \(f \in {\mathcal {F}}\) as secret coefficients \((\alpha _i)_{i \in [m]} \in R^m\). The output FSS keys are additive secret shares of each \(\alpha _i\) over R, yielding key size \(m \log |R|\).
-
\(\mathsf{Eval}(\sigma ,k_\sigma ,x)\): Parse \(k_\sigma = (\alpha ^\sigma _i)_{i \in [m]}\). Output \(\sum _{i \in [m]} \alpha ^\sigma _i F_i(x)\).
Note that FSS keys perfectly hide the coefficients \(\alpha _i\), and thus f. Correctness holds by the distributive law within the module M.
As an example of “public functions” \(F_i\), one can consider, e.g., input monomials of a certain degree. Indeed, we can use this approach to instantiate FSS schemes for offset-function classes \({\hat{\mathcal {G}}}\) for the following types of low-degree gates.
Definition 12
(Low-Degree Gates).
-
1.
The degree-d gate \(\mathcal {G}_\mathsf{deg\text {-}d}\) is the class of functions \(g_\mathsf{deg\text {-}d}: R^n \rightarrow R^m\) parameterized by a ring R and \(n,m \in \mathbb {N}\), such that for each \(i \in [m]\), the ith output function \((g_\mathsf{deg\text {-}d})_i(x_1,\dots ,x_n)\) is a polynomial over R of degree no greater than d.
-
2.
The bilinear map gate \(\mathcal {G}_\mathsf{blin}\) is the class of functions \(g_\mathsf{blin}: \mathbb {G}^{\mathsf{in}}_1 \times \mathbb {G}^{\mathsf{in}}_2 \rightarrow \mathbb {G}^{\mathsf{out}}\) such that \(\mathbb {G}^{\mathsf{in}}= \mathbb {G}^{\mathsf{in}}_1 \times \mathbb {G}^{\mathsf{in}}_2,\mathbb {G}^{\mathsf{out}}\) are Abelian groups, and \(g_\mathsf{blin}\) is a bilinear map.
Note that these two classes are incomparable: \(\mathcal {G}_\mathsf{deg\text {-}d}\) addresses higher-order polynomials, beyond degree 2. On the other hand, \(\mathcal {G}_\mathsf{blin}\) captures bilinear operations across different structures beyond a single ring R: e.g., multiplication of non-square matrices, \(\mathbb {G}^{\mathsf{in}}_1 = R^{m_1 \times m_2}\), \(\mathbb {G}^{\mathsf{in}}_2 = R^{m_2 \times m_3}\), and \(\mathbb {G}^{\mathsf{out}}= R^{m_1 \times m_3}\).
Proposition 1
(Information-Theoretic FSS for Low-Degree Gates). Let \(d \in N\). Then there exists perfectly secure FSS for the following offset-function families, with the given complexities:
-
\({\hat{\mathcal {G}}}_\mathsf{deg\text {-}d}\): For \(\mathbb {G}^{\mathsf{in}}= R^n\), \(\mathbb {G}^{\mathsf{out}}= R^m\), key size is \(m{n+d \atopwithdelims ()d}(\log |R|)\) bits.
-
\({\hat{\mathcal {G}}}_\mathsf{blin}\): For \(\mathbb {G}^{\mathsf{in}}= \mathbb {G}^{\mathsf{in}}_1 \times \mathbb {G}^{\mathsf{in}}_2, \mathbb {G}^{\mathsf{out}}\), key size is \((\log |\mathbb {G}^{\mathsf{in}}|+\log |\mathbb {G}^{\mathsf{out}}|)\) bits.
Proof
Consider the following FSS constructions.
-
For \({\hat{\mathcal {G}}}_\mathsf{deg\text {-}d}\): Recall we are sharing offset functions of the form \(g^{[{r^{\mathsf{in}},r^{\mathsf{out}}}]}_\mathsf{deg\text {-}d}\), where \(g=(g_1,\dots ,g_m)\) is a degree-d polynomial \(g: R^n \rightarrow R^m\), and with offsets \(r^{\mathsf{in}}= (r^{\mathsf{in}}_1,\dots ,r^{\mathsf{in}}_n) \in R^n\) and \(r^{\mathsf{out}}= (r^{\mathsf{out}}_1,\dots r^{\mathsf{out}}_m) \in R^m\). By definition, for each \(i \in [m]\),
$$\begin{aligned} (g^{[{r^{\mathsf{in}},r^{\mathsf{out}}}]}_\mathsf{deg\text {-}d})_i(x_1,\dots ,x_n) = g_i(x_1-r^{\mathsf{in}}_1,\dots ,x_m-r^{\mathsf{in}}_m) + r^{\mathsf{out}}_i. \end{aligned}$$In particular, each \((g^{[{r^{\mathsf{in}},r^{\mathsf{out}}}]}_\mathsf{deg\text {-}d})_i\) itself is a degree-d polynomial in the inputs, where the coefficients of each degree \(\le d\) monomial in the variables \(x_i\) depends on the secret values \(r^{\mathsf{in}},r^{\mathsf{out}}\). By Observation 4, we can thus obtain secure FSS by giving additive secret shares of each of these coefficients. There are \({n+d \atopwithdelims ()d}\) distinct monomials of degree \(\le d\) in the n input variables; for each output \(i \in [m]\), the FSS key will contain an additive share of size \(\log |R|\) for each monomial.
-
For \({\hat{\mathcal {G}}}_\mathsf{blin}\): Given an offset function of the form \(g^{[{r^{\mathsf{in}},r^{\mathsf{out}}}]}_\mathsf{blin}\), parse as a bilinear function \(g: \mathbb {G}^{\mathsf{in}}_1 \times \mathbb {G}^{\mathsf{in}}_2 \rightarrow \mathbb {G}^{\mathsf{out}}\), and \(r^{\mathsf{in}}= (r^{\mathsf{in}}_1,r^{\mathsf{in}}_2) \in \mathbb {G}^{\mathsf{in}}_1\times \mathbb {G}^{\mathsf{in}}_2\), and \(r^{\mathsf{out}}\in \mathbb {G}^{\mathsf{out}}\). By definition,
$$\begin{aligned} g^{[{r^{\mathsf{in}},r^{\mathsf{out}}}]}_\mathsf{blin}(x_1,x_2)&= g(x_1-r^{\mathsf{in}}_1,x_2-r^{\mathsf{in}}_2) + r^{\mathsf{out}}\\&= g(x_1,x_2) - g(r^{\mathsf{in}}_1,x_2) - g(x_1,r^{\mathsf{in}}_2) + g(r^{\mathsf{in}}_1,r^{\mathsf{in}}_2) + r^{\mathsf{out}}. \end{aligned}$$Consider the following observations: (1) \(g(x_1,x_2)\) is publicly computable. (2) \(r_3 := g(r^{\mathsf{in}}_1,r^{\mathsf{in}}_2) + r^{\mathsf{out}}\) is a fixed additive term, independent of the input x. (3) Bilinearity of g implies the functions \(g(\cdot ,x_2)\) and \(g(x_1,\cdot )\) are linear in the corresponding second position.
We can thus achieve FSS for this function class by giving out additive secret shares of the values \(r^{\mathsf{in}}_1,r^{\mathsf{in}}_2\), and \(r_3:= g(r^{\mathsf{in}}_1,r^{\mathsf{in}}_2) + r^{\mathsf{out}}\). The corresponding FSS key size is \(\log |\mathbb {G}^{\mathsf{in}}_1|+\log |\mathbb {G}^{\mathsf{in}}_2|+\log |\mathbb {G}^{\mathsf{out}}| = (\log |\mathbb {G}^{\mathsf{in}}|+\log |\mathbb {G}^{\mathsf{out}}|)\) bits.
Plugging these FSS constructions into our protocols from the previous section (Theorems 2 and 3), we obtain secure computation protocols isomorphic to existing protocols from the literature. In addition, the FSS abstraction extends directly to broader classes: e.g., directly supporting general bilinear gates over different rings \(R_i\) (such as matrix multiplications), as well as arbitrary low-degree gates over a ring R.
Note that a degree-d mapping can have circuit complexity \(\sim n^d\). In the corresponding approach, this increases only the size of the FSS preprocessing information (corresponding to more coefficients) whereas the online communication scales just with the input and output size of the gate. Similarly, bilinear operations such as matrix multiplication when expressed as circuits over the base ring R require significantly more small gates as compared to a single matrix input and output when viewed as a single large bilinear gate.
Corollary 1
(2PC with Preprocessing: Low-Degree and Bilinear Gates). Applying our FSS framework (Theorems 2 and 3) for circuits of degree-d and bilinear gates \(\mathcal {G}_\mathsf{deg\text {-}d},\mathcal {G}_\mathsf{blin}\) as above yields perfectly secure protocols in the preprocessing model isomorphic to (and generalizing) the following:
-
Beaver Triples [2]: Applying Theorem 3, yielding circuit-independent preprocessing 2PC for low-degree and bilinear gates.
-
Circuit-Dependent Beaver (e.g., [3, 11, 13, 23]): Applying Theorem 2, yielding circuit-dependent preprocessing 2PC for low-degree and bilinear gates.
Proof
Consider the two approaches.
(Circuit-independent). Applying the protocol framework of Theorem 3, we obtain the following structure. We describe for the case of multiplication gates over a ring R to illustrate the Beaver triple structure (but observe that the construction extends directly to more general degree-d and bilinear gates).
-
For each multiplication gate v with input wires \((w_1,w_2)\) and output wire \(w_3\), sampling random \(r_1,r_2 \leftarrow R\), and generating FSS shares for the gate-offset function will correspond to sharing the function
$$\begin{aligned} g_v^{[(r_1,r_2),0]} (x_1,x_2)&= (x_1-r_1)(x_2-r_2) \\&= x_1x_2 - r_1x_2 - x_2r_1 + r_1r_2. \end{aligned}$$Note that \(x_1x_2\) is always with coefficient 1 and publicly computable. Applying Observation 4 for the remaining (secret) coefficients yields FSS keys that are additive secret shares of 3 values: \(r_1, r_2,\) and \(r_1r_2\).
-
The circuit-independent 2PC preprocessing included FSS keys of each such gate offset function, as well as additive shares of the input masks themselves. In this case, additive shares of the input masks are already included as part of the FSS keys. Thus, the final resulting correlation corresponds directly to Beaver triples: for each gate, additive shares of random \(r_1,r_2\), and \(r_1r_2\).
(Circuit-dependent). Applying Theorem 2 results in an optimization of this approach, as in [11, 13, 23], where the offset masks are correlated across gates.
Truth-Table Gates. The second category is a straightforward FSS of arbitrary functions of polynomial-size domain, formed by simply providing additive secret shares of each element of the truth table. Perfect secrecy and evaluation with additive reconstruction follow in a trivial manner.
Observation 5
(FSS via Shared Truth Table). Let \({\mathcal {F}}\) be any family of functions where for a given \((\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}})\), the truth table of a function \(f \in {\mathcal {F}}\) can be described by \(s=s(\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}})\) elements of the output space \(\mathbb {G}^{\mathsf{out}}\). Then there exists an FSS scheme for \({\mathcal {F}}\) with perfect security and correctness, with key size \(s\cdot \log |\mathbb {G}^{\mathsf{out}}|\) bits.
Note that one can always express the truth table of a function \(g: \mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\) using \(|\mathbb {G}^{\mathsf{in}}|\) many elements of \(\mathbb {G}^{\mathsf{out}}\). However, for some interesting function classes, this can be made even smaller. For example, functions with bounded locality: where  , and each output of the function depends only on a bounded number \(\ell (\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}})\) of fixed coordinates of the input; in such case, the full truth table of the function can be expressed given just
, and each output of the function depends only on a bounded number \(\ell (\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}})\) of fixed coordinates of the input; in such case, the full truth table of the function can be expressed given just  bits, as opposed to
bits, as opposed to  bits.
bits.
In a straightforward way, this translates to the offset-function family \(\hat{\mathcal {F}}\) of any such function family \({\mathcal {F}}\).
Analogous to the case of low-degree functions, plugging these general truth table FSS constructions into our 2PC protocols from Theorems 2 and 3 yields secure computation protocols that reproduce existing protocols from the literature.
Corollary 2
(2PC with Preprocessing: Truth Table Gates). Applying our FSS framework (Theorems 2 and 3) for circuits of arbitrary gates \(\mathcal {G}\) as above rederives perfectly secure protocols in the preprocessing model isomorphic to the following:
-
One-Time Truth Tables [13, 22]: Applying Theorem 3 together with Observation 5 for arbitrary truth tables.
-
Leveled circuits, with sublinear online communication [11]: Applying Theorem 2, together with Observation 5 for circuits with bounded locality.
Proof
(One-Time Truth Tables). For a given gate function g, the truth table of the offset-function \(g^{[r^{\mathsf{in}},0]}\) (recall in the circuit-independent setting, we take \(r^{\mathsf{out}}= 0\)) is simply a randomly shifted version of the original truth table, and FSS shares of this function will be precisely additive shares of the shifted truth table.
(Leveled Circuits). The core technical insight in [11] is that a leveled circuit of size s can be partitioned into large “gates” of depth \(\log \log s\), whose input locality are each bounded by \(\log s\), and thus whose truth tables can each be described in polynomial size. Applying Theorem 2 to such circuit decomposition yields a comparable protocol, with polynomial-size preprocessing information, and where parties need only communicate \(O(s/\log \log s)\) elements, corresponding to just inputs and outputs of these gates, in \(\mathsf{depth}(C)/\log \log s\) rounds.
4 Applications
In this section we explore applications of our technique to useful types of gates for which we can obtain significant improvements over the current state of the art.
4.1 Zero Test/Equality
We start with gates that either compare a single group element to 0 or check that two group elements are equal.
Definition 13
(Equality-Type Gates).
-
1.
The zero-test gate \(\mathcal {G}_\mathsf{zt}\) is the class of functions \(g_\mathsf{zt}: \mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\) parameterized by Abelian groups \(\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}}\) and given by
$$ g_\mathsf{zt}(x) = {\left\{ \begin{array}{ll} 0 \in \mathbb {G}^{\mathsf{out}}~~\text { if } x=0 \in \mathbb {G}^{\mathsf{in}}\\ 1 \in \mathbb {G}^{\mathsf{out}}~~\text { else} \end{array}\right. }. $$ -
2.
The equality-test gate \(\mathcal {G}_\mathsf{eq}\) is the class of functions \(g_\mathsf{eq}: \mathbb {G}^{\mathsf{in}}\times \mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\) parameterized by \(\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}}\) and given by
$$ g_\mathsf{eq}(x,x') = {\left\{ \begin{array}{ll} 0 \in \mathbb {G}^{\mathsf{out}}~~\text { if } x=x' \in \mathbb {G}^{\mathsf{in}}\\ 1 \in \mathbb {G}^{\mathsf{out}}~~\text { else} \end{array}\right. }. $$
Note that the offset function class of the zero-test gate is precisely the class of point functions, where the special input \(\alpha \) corresponds to the input offset and the output value \(\beta \) to the output offset. Hence, realizing a zero-test gate (on a masked input) reduces to a single DPF evaluation.
Proposition 2
(Zero Test from DPF). There is an FSS scheme \((\mathsf{Gen}_\mathsf{zt},\mathsf{Eval}_\mathsf{zt})\) for the offset function family \({\hat{\mathcal {G}}}_\mathsf{zt}\) making black-box use of a PRG. The scheme has the same key size and number of PRG invocations as a DPF with input domain \(\mathbb {G}^{\mathsf{in}}\) and output domain \(\mathbb {G}^{\mathsf{out}}\).
Proof
Consider the following construction, where \((\mathsf{Gen}_\mathsf{DPF},\mathsf{Eval}_\mathsf{DPF})\) is a distributed point function.
-
\(\mathsf{Gen}_\mathsf{zt}(1^{\lambda },g^{[{r^{\mathsf{in}},r^{\mathsf{out}}}]}_\mathsf{zt})\): Parse \(g^{[{r^{\mathsf{in}},r^{\mathsf{out}}}]}_\mathsf{zt}\) to recover \(\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}},r^{\mathsf{in}},r^{\mathsf{out}}\). Sample and output keys \((k'_0,k'_1) \leftarrow \mathsf{Gen}_\mathsf{DPF}(1^{\lambda }, f_{\alpha ,\beta })\), for \(\alpha = r^{\mathsf{in}}\in \mathbb {G}^{\mathsf{in}}\) and \(\beta = 1 \in \mathbb {G}^{\mathsf{out}}\). Sample random additive secret shares \(\langle r_0, r_1 \rangle \) of \(r^{\mathsf{out}}\in \mathbb {G}^{\mathsf{out}}\). Output keys \(k_0 = (k'_0,r_0)\) and \(k_1=(k'_1,r_1)\).
-
\(\mathsf{Eval}_\mathsf{zt}(\sigma , k_\sigma ,x)\): Output \(\mathsf{Eval}_\mathsf{DPF}(\sigma ,k'_\sigma ,x) + r_\sigma \).
Correctness and security can be easily seen to follow from those of the DPF. Moreover, the construction does not involve additional cryptographic operations beyond making a single call to the DPF.
The case of comparing two group elements can be easily reduced to the above case of a zero-test. Indeed, by taking the difference between the two masked inputs, the problem reduces to a zero-test of a masked input whose mask is the difference between the two masks, where the latter are known to the key generation algorithm. We provide an explicit description of the corresponding FSS scheme below.
Theorem 6
(Equality Test from DPF). There is an FSS scheme \((\mathsf{Gen}_\mathsf{eq},\mathsf{Eval}_\mathsf{eq})\) for the offset function family \({\hat{\mathcal {G}}}_\mathsf{eq}\) making black-box use of a PRG. The scheme has the same key size and number of PRG invocations as a DPF with input domain \(\mathbb {G}^{\mathsf{in}}\) and output domain \(\mathbb {G}^{\mathsf{out}}\).
Proof
Consider the following construction, where \((\mathsf{Gen}_\mathsf{DPF},\mathsf{Eval}_\mathsf{DPF})\) is a distributed point function.
-
\(\mathsf{Gen}_\mathsf{eq}(1^{\lambda },g^{[{r^{\mathsf{in}},r^{\mathsf{out}}}]}_\mathsf{eq})\): Parse \(g^{[{r^{\mathsf{in}},r^{\mathsf{out}}}]}_\mathsf{eq}\) to recover \(\mathbb {G}^{\mathsf{in}}= (\mathbb {G}^{\mathsf{in}}_1 \times \mathbb {G}^{\mathsf{in}}_2),\mathbb {G}^{\mathsf{out}},r^{\mathsf{in}},r^{\mathsf{out}}\), where \(r^{\mathsf{in}}= (r^{\mathsf{in}}_1,r^{\mathsf{in}}_2) \in \mathbb {G}^{\mathsf{in}}\). Sample and output keys \((k'_0,k'_1) \leftarrow \mathsf{Gen}_\mathsf{DPF}(1^{\lambda }, f_{\alpha ,\beta })\), for \(\alpha = (r^{\mathsf{in}}_1 - r^{\mathsf{in}}_2) \in \mathbb {G}^{\mathsf{in}}\) and \(\beta = 1 \in \mathbb {G}^{\mathsf{out}}\). Sample random additive secret shares \(\langle r_0, r_1 \rangle \) of \(r^{\mathsf{out}}\in \mathbb {G}^{\mathsf{out}}\). Output keys \(k_0 = (k'_0,r_0)\) and \(k_1=(k'_1,r_1)\).
-
\(\mathsf{Eval}_\mathsf{eq}(\sigma , k_\sigma , (x_1,x_2))\): Output \(\mathsf{Eval}_\mathsf{DPF}(\sigma ,k_\sigma , (x_1-x_2)) + r_\sigma \).
Security follows directly. Correctness holds since the point function \(f_{\alpha ,\beta }(x)\) evaluates to \(\beta = 1\) exactly when \((x_1-x_2) = \alpha = (r^{\mathsf{in}}_1 - r^{\mathsf{in}}_2)\), or equivalently, when \((x_1-r^{\mathsf{in}}_1)=(x_2-r^{\mathsf{in}}_2)\). As before, the only cryptographic operations involve a single call to the DPF.
4.2 Integer Comparison, Interval Membership, and Splines
We turn from equality-type gates to the slightly more involved case of gates related to integer comparisons. The offset functions of such gates can be easily expressed in terms of distributed interval functions (DIFs) as constructed in [8]. See Definition 6 and Theorem 1.
Definition 14
(Comparison-Type Gates).
-
1.
The interval-containment gate \(\mathcal {G}_{(a,b)}\) is the class of functions \(g_{(a,b)}: \mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\) parameterized by Abelian groups \(\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}}\) endowed with a total ordering \(a \le b \in \mathbb {G}^{\mathsf{in}}\), and given by
$$ g_{(a,b)}(x) = {\left\{ \begin{array}{ll} 0 \in \mathbb {G}^{\mathsf{out}}~~\text { if } a \le x \le b \in \mathbb {G}^{\mathsf{in}}\\ 1 \in \mathbb {G}^{\mathsf{out}}~~\text { else} \end{array}\right. }. $$We also sometimes consider the sub-family of “special” (one-sided) intervals, in which \(a= 0\) is set to the minimum element of \(\mathbb {G}^{\mathsf{in}}\) (or, alternatively, the family wherein b is set to the maximum element of \(\mathbb {G}^{\mathsf{in}}\)). For these sub-families, \(\mathsf{Leak}\) is amended to include this information.
-
2.
The comparison gate \(\mathcal {G}_\le \) is the class of functions \(g_\le : \mathbb {G}^{\mathsf{in}}\times \mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\) parameterized by Abelian groups \(\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}}\) endowed with a total ordering, and given by
$$ g_\le (x,x') = {\left\{ \begin{array}{ll} 0 \in \mathbb {G}^{\mathsf{out}}~~\text { if } x\le x' \in \mathbb {G}^{\mathsf{in}}\\ 1 \in \mathbb {G}^{\mathsf{out}}~~\text { else} \end{array}\right. }. $$ -
3.
The spline gate \(\mathcal {G}_\mathsf{spline}\) is the class of functions \(g_{(\mathbf {a}, \mathbf {f})}: \mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\) parameterized by Abelian groups \(\mathbb {G}^{\mathsf{in}},\mathbb {G}^{\mathsf{out}}\) endowed with a total ordering, a list \(\mathbf {a} = a_1< a_2< \cdots < a_k \in \mathbb {G}^{\mathsf{in}}\), and a list of functions \(\mathbf {f} = f_0,\dots , f_k : \mathbb {G}^{\mathsf{in}}\rightarrow \mathbb {G}^{\mathsf{out}}\), given by
$$ g_{(\mathbf {a}, \mathbf {f})}(x) = {\left\{ \begin{array}{ll} f_0(x) \in \mathbb {G}^{\mathsf{out}}~~\text { if } x\le a_1 \in \mathbb {G}^{\mathsf{in}}\\ f_1(x) \in \mathbb {G}^{\mathsf{out}}~~\text { if } a_1< x \le a_2 \in \mathbb {G}^{\mathsf{in}}\\ ~~~\vdots \\ f_k(x) \in \mathbb {G}^{\mathsf{out}}~~\text { if } a_k < x \end{array}\right. }. $$By default, we consider the case where \(\mathbb {G}^{\mathsf{in}}\) and \(\mathbb {G}^{\mathsf{out}}\) are the additive groups of the same finite ring (e.g., \(R=\mathbb {Z}_{2^m}\)), and each \(f_i\) is a degree-d univariate polynomial over R. This is useful in the context of approximating real-valued functions.
We start with the case of interval containment. The key observation is that the offset function of an interval (a, b) is can be expressed as the sum of two special intervals.
Proposition 3
(Interval-Containment from FSS for Intervals). There exists an FSS scheme \((\mathsf{Gen}_{(a,b)},\mathsf{Eval}_{(a,b)})\) for the offset function family \({\hat{\mathcal {G}}}_{(a,b)}\) making black-box use of a PRG. The scheme has the same cost (in key size and number of PRG invocations) as two instances of a special DIF with input domain \(\mathbb {G}^{\mathsf{in}}\) and output domain \(\mathbb {G}^{\mathsf{out}}\), except that each key includes an additional element of \(\mathbb {G}^{\mathsf{out}}\). Moreover, there is an FSS scheme with the same parameters for the offset function family \({\hat{\mathcal {G}}}_\le \) of comparison gates.
Proof
We argue that each function in the offset family \({\hat{\mathcal {G}}}_{(a,b)}\) can be expressed as the sum of two special intervals plus the constant offset \(r^{\mathsf{out}}\). Indeed, the effect of the input offset \(r^{\mathsf{in}}\) is cyclically shifting the interval function \(f_{(a,b),1}\) to the right. There are two possible cases:
-
1.
There is no wrap-around, namely we get another standard interval of the form \(f_{(a',b'),1}\). If \(a'=0\), this is a special interval. Otherwise it can be expressed as the sum of two special intervals: \(f_{(a',b'),1}=f_{(0,b'),1}+f_{(0,a'-1),-1}\).
-
2.
There is a wrap-around, in which case we get a sum of two disjoint special intervals: one starting with \(a+r^{\mathsf{in}}\) and one ending with \((b+r^{\mathsf{in}}) \mod |\mathbb {G}^{\mathsf{in}}|\).
We can now realize FSS for the offset function by letting \(\mathsf{Gen}\) generate independent keys for the two instances of a DIF, and \(\mathsf{Eval}\) output the sum of the two output shares. Finally, given additive shares of the output offset \(r^{\mathsf{out}}\) as part of the key, \(\mathsf{Eval}\) can add \(r^{\mathsf{out}}\) to the output. We can obtain an analogous statement for comparison gates \({\hat{\mathcal {G}}}_\le \) similarly to the reduction of \({\hat{\mathcal {G}}}_\mathsf{eq}\) to \({\hat{\mathcal {G}}}_\mathsf{zt}\).
We turn to the case of spline functions, starting with the default case where \(\mathbb {G}^{\mathsf{in}}\) and \(\mathbb {G}^{\mathsf{out}}\) are the same finite ring R and each function \(f_i(x)\) is a degree-d univariate polynomial over R. Here the high level idea is to use \(2(k+1)\) instances of special DIF to additively share, for each interval, the \(d+1\) coefficients of either the degree-d polynomial \(f'_i(x')=f_i(x'-r^{\mathsf{in}})+r^{\mathsf{out}}\) in case the input \(x'\) is in the shifted i-th interval or the 0 polynomial if \(x'\) is not in this interval. The \(2(k+1)(d+1)\) coefficients can then be linearly combined with public coefficients to yield additive output shares.
Proposition 4
(Splines from FSS for Intervals). There exists an FSS scheme \((\mathsf{Gen}_{{(\mathbf {a}, \mathbf {f})}},\mathsf{Eval}_{{(\mathbf {a}, \mathbf {f})}})\) for the offset function family \({\hat{\mathcal {G}}}_\mathsf{spline}\), where \(\mathbb {G}^{\mathsf{in}}=\mathbb {G}^{\mathsf{out}}=R\) and each \(f_i\), \(0\le i\le k\), is a polynomial of degree at most d over R, making black-box use of a PRG. The scheme has the same cost (in key size and number of PRG invocations) as \(2(k+1)\) instances of a special DIF with input domain R and output domain \(R^{d+1}\).
Proof
We express the shifted spline function as the sum of \(k+1\) cyclically shifted interval functions. As before, each shifted interval can be expressed as the sum of two special intervals. For the shifted interval i, \(0\le i\le k\), the payload \(\beta _i \in R^{d+1}\) is the coefficient vector of the univariate polynomial \(f'_i\), where \(f'_i(x')=f_i(x'-r^{\mathsf{in}})+r^{\mathsf{out}}\). Note that if x is not in the shifted interval, the output of the shifted interval function will be \(\beta _i=(0,0,\ldots ,0)\in R^{d+1}\). Finally, given the \(k+1\) additively-shared coefficient vectors \(\beta _i\), the parties can homomorphically evaluate \(\langle \sum _{i=0}^k \beta _i\, , \,(1,x',(x')^2,\ldots ,(x')^d)\rangle =g^{[r^{\mathsf{in}},r^{\mathsf{out}}]}_{(\mathbf {a}, \mathbf {f})}(x')\), where \(\langle \cdot ,\cdot \rangle \) denotes inner product over R. Since \(x'\) is public, this can be done via a local linear combination of the \((k+1)(d+1)\) ring elements included in the payloads \(\beta _i\).
We note that, with some loss of concrete efficiency, the spline construction can be generalized to accommodate any functions \(f_i\) from a class that supports efficient FSS. Such a construction can be obtained by using the general tensoring operator for FSS from [8] (Theorem 3.2 of full version) to obtain an FSS scheme for functions that output the same output as \(f_i\) on a shifted interval and 0 outside the interval.
4.3 Bit Decomposition
As a concluding item, we turn our attention to the more involved task of bit decomposition.
Definition 15
(Bit-Decomposition Gate). The bit-decomposition gate \(\mathcal {G}_\mathsf{bit}\) is the class of functions \(g_\mathsf{bit}: \mathbb {Z}_M \rightarrow \mathbb {Z}_2^m\) parameterized by \(M \in \mathbb {N}\) (and \(m := \lceil \log M \rceil \)), given by
We now describe how to obtain the required FSS for these gates.
Remark 3
(Bit Decomposition for Special Modulus). For the sake of simplicity, we present in Proposition 5 a construction of bit decomposition for the special case of \(\mathbb {Z}_M\) for \(M = 2^m\). In this setting, modular arithmetic over M does not incur wraparound carries. The same construction and analysis covers also a promise setting where M is arbitrary, but both the input \(x \in \mathbb {Z}_M\) and the secret offset \(r^{\mathsf{in}}\in \mathbb {Z}_M\) are guaranteed to be of low magnitude (bounded by e.g. \(\sqrt{M}\)), as stated in Corollary 3. The general case of \(\mathbb {Z}_M\) with arbitrary inputs and offsets requires a slightly more sophisticated treatment. We discuss the extension of our construction in Remark 4 below.
Proposition 5
(Bit-Decomposition for \(M=2^m\)). There exists an FSS \((\mathsf{Gen}_\mathsf{bit},\mathsf{Eval}_\mathsf{bit})\) for the offset function family \({\hat{\mathcal {G}}}_\mathsf{bit}\) (restricted to \(\mathbb {Z}_M\) with \(M = 2^m\)) making black-box use of a pseudorandom generator \({\mathsf{PRG}:\{0,1\}^{\lambda }\rightarrow \{0,1\}^{2({\lambda }+1)}}\) with the following complexities.
-
\(\mathsf{Gen}_\mathsf{bit}\) for function \(g_\mathsf{bit}: \mathbb {Z}_M \rightarrow \mathbb {Z}_2^m\) (with \(M=2^m\)) makes \(m(m-1)\) calls to \(\mathsf{PRG}\). It outputs keys \(k_0,k_1\) each of size \(({\lambda }+ 4)m(m-1)/2 + m\) bits.
-
\(\mathsf{Eval}_\mathsf{bit}\) makes \(m(m-1)/2\) calls to \(\mathsf{PRG}\).
Proof
Consider the following construction, making use of an FSS for special intervals \((\mathsf{Gen}_\mathsf{SI},\mathsf{Eval}_\mathsf{SI})\). Recall the goal is to recover shares of the (\(r^{\mathsf{out}}\)-shifted) bit representation of \(x + (-r^{\mathsf{in}}) \in \mathbb {Z}_M\), where \(r^{\mathsf{in}},r^{\mathsf{out}}\) are known at time of FSS generation. Let \(\mathbf {r} = (r_{m-1},\dots ,r_{0}) \in \mathbb {Z}_2^m\) denote the bit representation of \((-r^{\mathsf{in}}) \in \mathbb {Z}_M\) (note the additive inverse for notational convenience). For (public) input \(x \in \mathbb {Z}_M\), we similarly denote its bit representation as \((x_{m-1},\dots ,x_{0})\).
Given public input x, we will compute (shares of) each bit of \((x+(-r^{\mathsf{in}}))\) over \(\mathbb {Z}_M\) by computing “grade-school” addition on the bits. Each desired output bit \(y_i\), \(i \in \{0,\dots ,m-1\}\) can be expressed as a sum over \(\mathbb {Z}_2\): \(y_i = x_i\,\oplus \,r_i \oplus \mathsf{carry}_{i,\mathbf {r}}(x)\), where \(\mathsf{carry}_{i,\mathbf {r}}(x) \in \{0,1\}\) is equal to 1 precisely when there is a carry entering into bit i from the lower-order bits, indexes \(j< i\). Note that for \(M = 2^m\), there are no wraparound carries.
The function \(x_i\,\oplus \,r_i\) is linear over the output space \(\mathbb {Z}_2\) and can thus be directly evaluated given the public input x and additive secret shares of \(r_i\) (over \(\mathbb {Z}_2\)). The challenge is in implementing the nonlinear function \(\mathsf{carry}_{i,\mathbf {r}}(x)\), while hiding the value of \(\mathbf {r}\). To do so, we make a simple observation: \(\mathsf{carry}_{i,\mathbf {r}}(x)=1\) if and only if \((\sum _{j=0}^{i-1} 2^j x_j ) \ge 2^i - (\sum _{j=0}^{i-1} 2^j r_j) \in \mathbb {Z}_{2^i}\). That is, there is a carry exactly if the numbers formed by the two truncated bit strings \((x_{i-1},\dots ,x_0)\) and \((r_{i-1},\dots ,r_0)\) sum to greater than \(2^i\) (note they will never reach \(2^{i+1}\)). For each index \(i \in \{0,\dots , m-1\}\), we can thus implement FSS for \(\mathsf{carry}_{i,\mathbf {r}}(x)\) directly by one FSS for a special (one-sided) interval \(f_{(a,2^{i-1})}: \mathbb {Z}_{2^i} \rightarrow \{0,1\}\), which evaluates to 1 on input \(x' \in \mathbb {Z}_{2^i}\) precisely if \(x' > a\).
We thus achieve the desired FSS with the following construction.
-
\(\mathsf{Gen}_{\mathsf{bit}}(1^{\lambda }, g^{[{r^{\mathsf{in}},r^{\mathsf{out}}}]}_\mathsf{bit})\):
-
1.
Parse \(g^{[{r^{\mathsf{in}},r^{\mathsf{out}}}]}_\mathsf{bit}\) to recover \(M, r^{\mathsf{in}}\in \mathbb {Z}_M, r^{\mathsf{out}}\in \mathbb {Z}_2^m\). Parse \(r^{\mathsf{in}}\) as its bit representation \(\mathbf {r} = (r_{m-1},\dots ,r_0)\).
-
2.
For each \(i \in \{0,\dots ,m-1\}\), do the following.
-
(a)
Sample special interval FSS keys \((k^i_0,k^i_1) \leftarrow \mathsf{Gen}_{\mathsf{SI}}(1^{\lambda }, f_{(a,2^{i-1})})\), for \(f_{(a,2^{i-1})}: \mathbb {Z}_{2^i} \rightarrow \{0,1\}\), with \(a = 2^i - (\sum _{j=0}^{i-1} 2^j r_j) \in \mathbb {Z}_{2^i}\).
-
(b)
Sample random additive secret shares \(\langle z^i_0,z^i_1 \rangle \) of \((r_i\,\oplus \,r^{\mathsf{out}}_i)\) over \(\mathbb {Z}_2\).
-
(a)
-
3.
Output keys \(k_0 = (k^i_0, z^i_0)_{i =0}^{m-1} \) and \(k_1 = (k^i_1, z^i_1)_{i =0}^{m-1} \).
-
1.
-
\(\mathsf{Eval}_\mathsf{bit}(\sigma ,k_\sigma , x)\): Parse \(k_\sigma = (k^i_\sigma , z^i_\sigma )_{i =0}^{m-1}\) and \(x = (x_{m-1},\dots ,x_0)\) For each \(i \in \{0,\dots ,m-1\}\), do the following.
-
1.
Execute \(\mathsf{carry}_\sigma ^i = \mathsf{Eval}_{\mathsf{SI}}\left( \sigma , k^i_\sigma , \sum _{j=0}^{i-1} 2^j x_j \right) \).
-
2.
Let \(y_\sigma ^i = \sigma \cdot x_i\,\oplus \,\mathsf{carry}_\sigma ^i\,\oplus \,z^i_\sigma \in \mathbb {Z}_2\). Note that a single party will contribute \(x_i\). (Recall \(z^i_\sigma \) incorporates party \(\sigma \)’s shares of both the \(r_i\) bit itself, as well as output offset bit \(r^{\mathsf{out}}_i\).)
-
1.
-
Output \((y_\sigma ^{m-1},\dots ,y_\sigma ^0) \in \mathbb {Z}_m^2\) as party \(\sigma \)’s output share.
Correctness of the construction holds as argued above; FSS security holds directly by the security of the underlying FSS scheme for special intervals (and additive secret sharing).
As mentioned, this case extends beyond just \(\mathbb {Z}_M\) for \(M=2^m\), if we are in a promise setting of small inputs as compared to the modulus size. This can be useful within applications, e.g., in order to emulate computations over a non-\(2^m\) modulus by emulating over \(\mathbb {Z}_M\) for an artificially large M.
Corollary 3
(Bit Decomposition for Small Inputs). There is an FSS scheme for the family of bit-decomposition functions with small inputs
where the FSS guarantees correctness for inputs \(x \in \mathbb {Z}_M\) of small magnitude \(|x| \le \sqrt{M}\). The complexities of the FSS are as in Proposition 5.
Remark 4
(Bit Decomposition for General Modulus). Our bit-arithmetic approach can be extended to the setting of general modulus M, by combining with an additional branch that either computes the same function as in the \(M=2^m\) case (if no wraparound occurs), or the function with an additional additive offset of \(2^m-M\) (if a wraparound does occur). Ultimately, the computation of each \(\mathsf{carry}_{i,\mathbf {r}}\) can be expressed by the linear combination of two different functions, each an AND of two special intervals (namely, [> value to wraparound] \(\wedge \) [> value to induce carry given wraparound] as well as [< value to wraparound] \(\wedge \) [> value to induce carry without wraparound]).
This can be instantiated via FSS for 2-dimensional intervals, as described in [8]. We leave optimization of such scheme to future work.
4.4 Garbling-Compatible Variants
For the purpose of minimizing round complexity, it can be beneficial to combine FSS-based gate evaluation with garbled circuits, where the outputs of FSS gates are fed into a garbled circuit. This motivates garbling-compatible variants of the above types of gates, where the bits of the output select between pairs of secret keys that correspond to inputs of the garbled circuit.
We can realize this modified functionality with a low additional cost for almost all of the above types of gates (the only exception is spline gates, whose output is not binary). This is done in the following way. The secret keys are incorporated into the function families as part of the function description. The key selection is done by incorporating the keys in the DPF or DIF payload \(\beta \). For instance, in the case of interval membership, the input domain is partitioned into intervals, where for each interval a DIF whose payload is the corresponding key is used to produce an additive secret-sharing of the key corresponding to membership in the (shifted) interval.
5 Negative Results and Barriers
In this section we rule out information-theoretic protocols that achieve the efficiency features of our FSS-based protocols, showing that the machinery we use is in a sense necessary. This should be contrasted with the fact that most positive results on secure computation given a trusted source of correlated randomness are information-theoretic.
We also give evidence that ruling out information-theoretic protocols with slightly relaxed efficiency features is difficult, by establishing a link with the existence of big matching vector families, a well known open problem in extremal combinatorics.
5.1 Online-Optimal Shared Equality Implies DPF
One of the simplest nontrivial instances of our positive results is a secure protocol for string equality with preprocessing and with secret-shared output. Concretely, we consider a protocol that given a pair of n-bit strings \((x_0,x_1)\) and correlated randomness \((r_0,r_1)\) outputs a secret-sharing of a single bit that indicates whether \(x_0=x_1\).
We define an online-optimal protocol to be one that has a single online round in which the message sent by each party is of the same length as its input. (By the perfect correctness requirement, the message length cannot be shorter than the input.) Note that this optimality feature is indeed satisfied by our DPF-based protocol, whose existence can be based on any OWF. We show that any online-optimal protocol can be used to build a DPF, though possibly with an exponential computation overhead in the input length. The latter suffices to prove that an online-optimal shared equality protocol implies a OWF.
Given the very restricted nature of an online-optimal protocol, this converse direction of showing that it implies a DPF may appear to be a mere syntactic translation. However, there are two main challenges that complicate this proof. First, the mapping of the inputs to messages does not necessarily rely on just additive masking. We get around this by requiring this masking to be efficiently invertible. (This requirement is not needed in case the input domain size is polynomial in the security parameter.) Second, the class of online-optimal protocols can deviate from the template of first masking the inputs using a pair of independent random strings and then independently applying an FSS scheme to the offset class defined by mapping the masked inputs to the secret-shared output. Indeed, a general protocol allows an arbitrary dependence between the two parts. As a result of these subtleties, it is not clear how to extend our argument from equality to general functions. Even in the case of equality, we need to assume the protocol to have the extra “efficient inversion” property mentioned above, unless the input domain is small.
We now formalize the notion of an online-optimal shared equality protocol and prove that it implies a DPF.
Definition 16
(Online-optimal shared equality protocol). A protocol \(\varPi =(\mathsf{Setup},\mathsf{Msg},\mathsf{Out})\) is an online-optimal shared equality protocol with inversion algorithm \(\mathsf{Inv}\) if it satisfies the following requirements:
-
Syntax: The protocol has the following structure.
-
1.
\(\mathsf{Setup}(1^{\lambda }, 1^n)\) outputs correlated randomness \((r_0,r_1)\) of size \(\mathsf{poly}({\lambda },n)\).
-
2.
In the online phase party \(P_\sigma \), on input \(x_\sigma \in \{0,1\}^n\), sends a single message \(m_\sigma =\mathsf{Msg}(\sigma ,r_\sigma ,x_\sigma )\) to \(P_{1-\sigma }\), where \(m_\sigma \in \{0,1\}^n\).
-
3.
Party \(P_\sigma \) outputs \(y_\sigma \in \{0,1\}\) where \(y_\sigma =\mathsf{Out}(\sigma ,r_\sigma ,x_\sigma ,m_{1-\sigma })\).
-
1.
-
Correctness: For any \(x_0,x_1\in \{0,1\}^n\), the resulting outputs \(y_0,y_1\) always satisfy \(y_0\,\oplus \,y_1=EQ(x_0,x_1)\), where EQ outputs 1 if the two inputs are equal and outputs 0 otherwise.
-
Security: The protocol \(\varPi \) computationally hides from \(P_\sigma \) the input \(x_{1-\sigma }\). Formally, it satisfies the security requirement of Definition 2 with respect to the constant function \(f(x_0,x_1)=0\).
-
Inversion: The algorithm \(\mathsf{Inv}\) extracts the input from the corresponding randomness and message. That is, for any \(\sigma \in \{0,1\}\) and \(r_\sigma ,x_\sigma ,m_\sigma \) consistent with an execution of \(\varPi \), we have \(\mathsf{Inv}(\sigma ,1^{\lambda },r_\sigma ,m_\sigma )=x_\sigma \).
Note that the correctness requirement implies that \(x_\sigma \) is uniquely determined by \(r_\sigma \) and \(m_\sigma \). Moreover, whenever \(n=O(\log {\lambda })\), one can implement \(\mathsf{Inv}\) in polynomial-time via brute-force search. This will suffice for constructing a DPF on a polynomial-size input domain, which implies a OWF. In our DPF-based shared equality protocol, however, the message is obtained by simply adding (or XORing) the input and a part of the randomness, and thus \(\mathsf{Inv}\) can be implemented in linear time.
We now construct a DPF given oracle access to \(\varPi \) and \(\mathsf{Inv}\) as in Definition 16. The intuition for the construction is the following. Given \(\mathsf{Inv}\), the output of each party \(\sigma \) can be computed from \(r_\sigma ,m_0,m_1\) alone (without relying on the input \(x_\sigma \)). The correlated randomness \((r_0,r_1)\) then defines a pair of tables \(T_\sigma ^{r_\sigma }\), where \(T_\sigma ^{r_\sigma }[m_0,m_1]\) contains the output of \(P_\sigma \) on randomness \(r_\sigma \) and messages \((m_0,m_1)\). The two tables can be viewed as shares of a shifted identity matrix \(T=T_0^{r_0}\,\oplus \,T_1^{r_1}\), where the location \(\varDelta \) of the 1-entry in the first row of T is masked by randomness of both parties. To convert this into a DPF for a point function \(f_{\alpha ,1}\), we include \(\alpha \,\oplus \,\varDelta \) in both keys. This does not reveal \(\alpha \) to either party and yet effectively allows the parties to convert the first row of T into one that contains 1 only in position \(\alpha \) and 0 elsewhere, as required for sharing \(f_{\alpha ,1}\). Finally, to guarantee security even in the case of super-polynomial input domains, we need to replace the first row with a random row \(\rho \), where \(\rho \) is included in both DPF keys.
The construction is formally described in Fig. 1.
Theorem 7
If \((\mathsf{Setup},\mathsf{Msg},\mathsf{Out},\mathsf{Inv})\) form an online-optimal shared equality protocol as in Definition 16, then \((\mathsf{Gen},\mathsf{Eval})\) defined in Fig. 1 is a DPF.
Proof
We separately argue correctness and security.
For correctness, letting \(\pi _\sigma ,T_\sigma ^{r_\sigma }\) be as in Fig. 1 and \(T=T_0^{r_0}\,\oplus \,T_1^{r_1}\), we can write:
as required, where (1) follows from Lines 3–4 of \(\mathsf{Eval}\), (2) from the correctness of the equality protocol, (3) from applying \(\pi _1\) to both sides from the left, (4) from Line 4 of \(\mathsf{Gen}\), (5) from Line 5 of \(\mathsf{Gen}\) and Line 2 of \(\mathsf{Eval}\), and (6) by masking both sides with \(\alpha \,\oplus \,\varDelta \).
We turn to argue security. A key \(k_\sigma \) produced by \(\mathsf{Gen}\) is of the form \(k_\sigma =(r_\sigma ,\rho ,\alpha \,\oplus \,\varDelta )\), where \(\varDelta = \pi _1(\pi _0^{-1}(\rho ))\). From the (computational) security of the equality protocol against \(P_0\), it follows that \((r_0,\rho ,\pi _1(\rho ))\approx (r_0,\rho ,\pi _1(\rho '))\), where \(\rho '\) is distributed uniformly over \(\{0,1\}^n\) independently of \(\rho \), and since \(\pi _1\) is a permutation we have
Similarly, from the security against \(P_1\) it follows that
It follows from (7) that
and hence \(k_0=(r_0,\rho ,\alpha \,\oplus \,\varDelta )\approx (r_0,\rho ,\rho ')\) as required. Similarly, it follows from (8) and from \((\rho ,\pi _0^{-1}(\rho ))\equiv (\pi _0(\rho ),\rho )\) that \(k_1=(r_1,\rho ,\alpha \,\oplus \,\varDelta )\approx (r_1,\rho ,\rho ')\) as required.
Corollary 4
If there exists an online-optimal shared equality protocol as in Definition 16 with efficient \((\mathsf{Setup},\mathsf{Msg},\mathsf{Out})\) (but possibly without an efficient inversion algorithm \(\mathsf{Inv}\)) then a one-way function exists.
Proof
The algorithm \(\mathsf{Inv}\) can be implemented in time \(\mathsf{poly}({\lambda },2^n)\) via a brute-force search that enumerates over all possible choices of \(x_\sigma \). Suppose that the DPF described in Fig. 1 (with oracle to \(\mathsf{Inv}\)) has key size \(|k_\sigma |=O(({\lambda }+n)^c)\) for a positive integer c. Then, letting \(n({\lambda })=(c+1)\log {\lambda }\), we get a DPF with domain size \(N({\lambda })={\lambda }^{c+1}\) and asymptotically smaller key size \(|k_\sigma |=O({\lambda }^c)\). Using Theorem 5 from [19], this implies a one-way function.
5.2 Matching Vectors Imply Shared Equality
In the previous section we have shown that any shared equality protocol that has optimal online complexity implies a DPF, which in turn implies a one-way function. This raises the following question: suppose we relax the optimality requirement by, say, allowing each online message to be of length 10n or even \(\mathsf{poly}(n)\) rather than n. Does such a protocol still imply a DPF? Alternatively, can we get an information-theoretic protocol with this complexity?
We do not know the answer to the above question. However, we show that if we slightly relax the output sharing requirement by allowing a constant-size (rather than single-bit) shares, then the problem of shared equality reduces to finding big families of matching vectors modulo a composite [5, 17, 18, 21], a well studied problem in combinatorics. Given known constructions of matching vectors, this connection implies some unexpected (but rather weak) upper bounds. Perhaps more interestingly, the lack of progress on ruling out much bigger matching vector families suggests that proving strong lower bounds on information-theoretic shared equality protocols would be difficult.
Definition 17
(Matching vectors). [17] Let m be a positive integer and \(S\subseteq \mathbb {Z}_m \setminus \{0\}\). We say that subsets \(U = \{u_1,\ldots ,u_N\}\) and \(V = \{v_1,\ldots ,v_N\}\) of vectors in \(\mathbb {Z}_m^h\) form an S-matching family if the following two conditions are satisfied:
-
For all \(i\in [N]\), \(\langle u_i,v_i\rangle =0\), where \(\langle \cdot ,\cdot \rangle \) denotes inner product over \(\mathbb {Z}_m\);
-
For all \(i,j\in [N]\) such that \(i\ne j\), \(\langle u_i,v_j\rangle \in S\).
The best known constructions of matching vectors over a constant composite modulus m are of quasi-polynomial size. For instance, for \(m=6\) the best known construction is of size \(N=h^{O(\log h/ \log \log h)}\) [21]. Whether bigger sets of matching vectors exist is a well known open problem, and only weak upper bounds are known; see [5] for the current state of the art.
We now show how to use families of matching vectors over a constant-size modulus m to obtain an information-theoretic shared equality protocol that has a single online round and constant-size output shares.
Theorem 8
Let n be a positive integer and \(N=2^n\). Suppose there is a family of matching vectors with parameters m, h, N as in Definition 17. Then there is a perfectly secure shared equality protocol \((\mathsf{Setup},\mathsf{Msg},\mathsf{Out})\) for n-bit inputs with the following efficiency features:
-
\(\mathsf{Setup}\) outputs correlated randomness \((r_0,r_1)\) consisting of O(h) elements of \(\mathbb {Z}_m\);
-
\(\mathsf{Msg}(\sigma ,r_\sigma ,x_\sigma )\) outputs a message in \(\mathbb {Z}_m^h\);
-
\(\mathsf{Out}(\sigma ,r_\sigma ,x_\sigma ,m_{1-\sigma })\) outputs an output share in \(\mathbb {Z}_m\).
Moreover, the two output shares produced by \(\mathsf{Out}\) are equal if and only if \(x_0=x_1\).
Proof
The protocol first encodes each input into a corresponding matching vector, and then computes shares of the inner product using the correlated randomness. In more detail, \(\mathsf{Setup}\) generates a pair of random masks \(R_0,R_1\in \mathbb {Z}_m^h\) and additive shares of their inner product (this can be viewed as a generalized Beaver triple, or an instance of our FSS-based construction for a bilinear gate). \(\mathsf{Msg}\) first encodes \(x_\sigma \) into a corresponding matching vector \(X_\sigma \) (where \(x_0\) is encoded using U and \(x_1\) using V) and outputs \(X_\sigma +R_\sigma \). Finally, \(\mathsf{Out}\) uses the correlated randomness and the two messages to compute subtractive shares of the inner product of \(X_0\) and \(X_1\) (namely, the difference between the outputs is the inner product). Security follows from the masking, and correctness from the definition of a matching vector family.
Generalizing Theorem 8 to other useful predicates beyond equality seems challenging. Indeed, there are strong limitations on the existence of big sets of matching vectors with respect predicates other than equality, even for simple ones such as the “greater than” predicate [1]. This should be contrasted with our (computational) FSS-based protocols, which are not only more efficient for the simple case of equality but also apply almost as efficiently to the “greater than” predicate and other types of simple predicates.
Notes
- 1.
- 2.
Unlike previous applications of FSS, here it is important that the input domain additionally be endowed with group structure. From here on, the term “group” will always refer to a finite Abelian group.
- 3.
A general method for compressing truth-table correlations was recently suggested in [6]. However, the running time still grows linearly with the truth-table size, or exponentially with the gate input length.
References
Bauer, B., Vihrovs, J., Wee, H.: On the inner product predicate and a generalization of matching vector families. In: 38th IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science, FSTTCS 2018, 11–13 December 2018, Ahmedabad, India, pp. 41:1–41:13 (2018)
Beaver, D.: Efficient multiparty protocols using circuit randomization. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 420–432. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_34
Ben-Efraim, A., Nielsen, M., Omri, E.: Turbospeedz: double your online SPDZ! Improving SPDZ using function dependent preprocessing. In: Deng, R.H., Gauthier-Umaña, V., Ochoa, M., Yung, M. (eds.) ACNS 2019. LNCS, vol. 11464, pp. 530–549. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-21568-2_26
Bendlin, R., Damgård, I., Orlandi, C., Zakarias, S.: Semi-homomorphic encryption and multiparty computation. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 169–188. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_11
Bhowmick, A., Dvir, Z., Lovett, S.: New bounds for matching vector families. SIAM J. Comput. 43(5), 1654–1683 (2014)
Boyle, E., Couteau, G., Gilboa, N., Ishai, Y., Kohl, L., Scholl, P.: Efficient pseudorandom correlation generators: silent OT extension and more. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 489–518. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_16
Boyle, E., Gilboa, N., Ishai, Y.: Function secret sharing. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 337–367. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_12
Boyle, E., Gilboa, N., Ishai, Y.: Function secret sharing: improvements and extensions. In: Proceedings of the ACM Conference on Computer and Communications Security, pp. 1292–1303 (2016). Full version: ePrint report 2018/707
Canetti, R.: Security and composition of multiparty cryptographic protocols. J. Cryptol., 143–202 (2000)
Couteau, G.: New protocols for secure equality test and comparison. In: Preneel, B., Vercauteren, F. (eds.) ACNS 2018. LNCS, vol. 10892, pp. 303–320. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-93387-0_16
Couteau, G.: A note on the communication complexity of multiparty computation in the correlated randomness model. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 473–503. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_17
Damgård, I., Fitzi, M., Kiltz, E., Nielsen, J.B., Toft, T.: Unconditionally secure constant-rounds multi-party computation for equality, comparison, bits and exponentiation. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 285–304. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_15
Damgård, I., Nielsen, J.B., Nielsen, M., Ranellucci, S.: The TinyTable protocol for 2-party secure computation, or: gate-scrambling revisited. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 167–187. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_6
Damgård, I., Pastro, V., Smart, N., Zakarias, S.: Multiparty computation from somewhat homomorphic encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 643–662. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_38
Demmler, D., Schneider, T., Zohner, M.: ABY - a framework for efficient mixed-protocol secure two-party computation. In: NDSS 2015 (2015)
Doerner, J., Shelat, A.: Scaling ORAM for secure computation. In: Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, CCS 2017, Dallas, TX, USA, 30 October–03 November, pp. 523–535 (2017)
Dvir, Z., Gopalan, P., Yekhanin, S.: Matching vector codes. SIAM J. Comput. 40(4), 1154–1178 (2011)
Efremenko, K.: 3-query locally decodable codes of subexponential length. SIAM J. Comput. 41(6), 1694–1703 (2012)
Gilboa, N., Ishai, Y.: Distributed point functions and their applications. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 640–658. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_35
Goldreich, O.: Foundations of Cryptography - Basic Applications. Cambridge University Press, New York (2004)
Grolmusz, V.: On set systems with restricted intersections modulo a composite number. In: Jiang, T., Lee, D.T. (eds.) COCOON 1997. LNCS, vol. 1276, pp. 82–90. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0045075
Ishai, Y., Kushilevitz, E., Meldgaard, S., Orlandi, C., Paskin-Cherniavsky, A.: On the power of correlated randomness in secure computation. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 600–620. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_34
Katz, J., Kolesnikov, V., Wang, X.: Improved non-interactive zero knowledge with applications to post-quantum signatures. In: Proceedings of the ACM Conference on Computer and Communications Security, pp. 525–537 (2018)
Katz, J., Ranellucci, S., Rosulek, M., Wang, X.: Optimizing authenticated garbling for faster secure two-party computation. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10993, pp. 365–391. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_13
Mohassel, P., Rindal, P.: ABY\({}^{\text{3}}\): a mixed protocol framework for machine learning. In: Proceedings of the ACM Conference on Computer and Communications Security, pp. 35–52 (2018)
Acknowledgements
Research supported by ERC Project NTSC (742754). E. Boyle additionally supported by ISF grant 1861/16 and AFOSR Award FA9550-17-1-0069. N. Gilboa additionally supported by ISF grant 1638/15, ERC grant 876110, and a grant by the BGU Cyber Center. Y. Ishai additionally supported by ISF grant 1709/14, NSF-BSF grant 2015782, and a grant from the Ministry of Science and Technology, Israel and Department of Science and Technology, Government of India.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Boyle, E., Gilboa, N., Ishai, Y. (2019). Secure Computation with Preprocessing via Function Secret Sharing. In: Hofheinz, D., Rosen, A. (eds) Theory of Cryptography. TCC 2019. Lecture Notes in Computer Science(), vol 11891. Springer, Cham. https://doi.org/10.1007/978-3-030-36030-6_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-36030-6_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-36029-0
Online ISBN: 978-3-030-36030-6
eBook Packages: Computer ScienceComputer Science (R0)





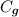 ) The preprocessing phase executes
) The preprocessing phase executes 
