Minimal Representations of Order Types by Geometric Graphs

Abstract

In order to have a compact visualization of the order type of a given point set S, we are interested in geometric graphs on S with few edges that unequivocally display the order type of S. We introduce the concept of exit edges, which prevent the order type from changing under continuous motion of vertices. Exit edges have a natural dual characterization, which allows us to efficiently compute them and to bound their number.

Research supported by the German Science Foundation (DFG), the Austrian Science Fund (FWF), and the Swiss National Science Foundation (SNSF) within the collaborative DACH project Arrangements and Drawings. O.A., I.P., and B.V. were partially supported by Austrian Science Fund (FWF) grant W1230. M.B., J.K., and P.V. are supported by grant no. 18-19158S of the Czech Science Foundation (GAČR). M.B. and J.K. are supported by Charles University project UNCE/SCI/004. M.B. has received funding from European Research Council (ERC) under the European Union’s Horizon 2020 research. M.H. and E.W. are supported by SNSF Project 200021E-171681. A.P. was supported by a Schrödinger fellowship of the Austrian Science Fund (FWF): J-3847-N35. M.S. was partially supported by DFG Grant FE 340/12-1. W.M. was partially supported by ERC StG 757609 and DFG Grant 3501/3-1.

1 Introduction

Let be two sets of n labeled points in general position (no three collinear). We say that S and T have the same order type if there is a bijection $\varphi : S \rightarrow T$ such that any triple $(p, q, r) \in S^3$ of three distinct points has the same orientation (clockwise or counterclockwise) as the image $(\varphi (p), \varphi (q), \varphi (r)) \in T^3$. The resulting equivalence relation on planar n-point sets has a finite number of equivalence classes, the order types [9]. Representatives of several distinct order types of five or six points are illustrated in Fig. 1. Among other things, the order type determines which geometric graphs can be drawn on a point set without crossings. Thus, order types appear ubiquitously in the study of extremal problems on geometric graphs.

Fig. 1.

Left: representatives of the three order types of five points in general position. Right: representatives of two order types of six points. Exit edges are drawn in black.

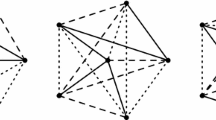
Now, suppose we have discovered an interesting order type, and we would like to illustrate it in a publication. One solution is to give explicit coordinates of a representative point set S; see Fig. 2 left. This is unlikely to satisfy most readers. We could also present S as a set of dots in a figure. For some point sets (particularly those with extremal properties), the reader may find it difficult to discern the orientation of an almost collinear point triple. To mend this, we could draw all lines spanned by two points in S. In fact, it suffices to present only the segments between the point pairs (the complete geometric graph on S). The orientation of a triple can then be obtained by inspecting the corresponding triangle; see Fig. 2 middle. However, such a drawing is rather dense, and we may have trouble following an edge from one endpoint to the other. Therefore, we want to reduce the number of edges in the drawing as much as possible, but so that the order type remains uniquely identifiable; see Fig. 2 right.

Results. We introduce the concept of exit edges to capture which edges are sufficient to uniquely describe a given order type in a robust way under continuous motion of vertices. More precisely, in a geometric drawing of a representative point set with all exit edges, at least one vertex needs to move across an (exit) edge in order to change the order type. We give an alternative characterization of exit edges in terms of the dual line arrangement, where an exit edge corresponds to one or two empty triangular cells. This allows us to efficiently compute the set of exit edges for a given set of n points in $O(n^2)$ time and space.

Using the more general framework of abstract order types and their dual pseudoline arrangements, we prove that every set of $n\ge 4$ points has at least $(3n-7)/5$ exit edges. We also describe a family of n points with $n-3$ exit edges, showing that this bound is asymptotically tight. An upper bound of $n(n-1)/3$ follows from known results on the number of triangular cells in line arrangements [10]. Thus, compared to the complete geometric graph with $n(n-1)/2$ edges, using only exit edges we save at least one third of the edges.

Fig. 2.

Three different representations of an order type of six points.

Identification of Order Types. Let S be a set of n labeled points in the plane. A geometric graph on S is a graph with vertex set S whose edges are represented as line segments between their endpoints. A geometric graph is thus a drawing of an abstract graph. Two geometric graphs G and H are isomorphic if there is an orientation-preserving homeomorphism of the plane transforming G into H. Each class of this equivalence relation may be described combinatorially by the cyclic orders of the edge segments around vertices and crossings, and by the incidences of vertices, crossings, edge segments, and faces. In the following, we will consider topology-preserving deformations. An ambient isotopy of the Euclidean plane is a continuous map such that $f(\cdot , t)$ is a homeomorphism for every $t\in [0,1]$ and $f(\cdot , 0) = \text {Id}$. Note that if there is an ambient isotopy transforming a geometric graph G into another geometric graph H, then G and H are isomorphic.

Definition 1

Let G be a geometric graph on a point set S. We say that G is supporting for S if every ambient isotopy f of that keeps the images of the edges of G straight (thus, transforming G into another geometric graph) and that allows at most three points of f(S, t) to be collinear for every $t\in [0,1]$, also preserves the order type of the vertex set.

Related Work. The connection between order types and straight-line drawings has been studied intensively, both for planar drawings and for drawings minimizing the number of crossings. For example, it is -complete to decide whether a planar graph can be embedded on a given point set [5]. Continuous movements of the vertices of plane geometric graphs have also been considered [2]. The continuous movement of points maintaining the order type was considered by Mnëv [7, 14]. He showed that there are point sets with the same order type such that there is no ambient isotopy between them preserving the order type, settling a conjecture by Ringel [15]. The orientations of triples that have to be fixed to determine the order type are strongly related to the concept of minimal reduced systems [4].

Outline. We introduce the concept of exit edges for a given point set. The resulting exit graphs are always supporting, though they are not necessarily minimal. In Sect. 2 we show that some exit edges are rendered unnecessary by non-stretchability of certain pseudoline arrangements. Despite being non-minimal in general, we argue that exit graphs are good candidates for supporting graphs by discussing their dual representation in pseudoline arrangements (Sect. 3). This connection allows us to both compute exit edges efficiently and give bounds on their number (Sect. 4). Supporting graphs in general need not be connected, and two minimal geometric graphs that are supporting for point sets with different order types can be drawings of the same abstract graph; see Fig. 1 right. Thus, the structure of the drawing is crucial. In Sect. 5 we provide some further properties of the exit graphs. We conjecture that graphs based on exit edges are not only supporting but also they encode the order type, as discussed in Sect. 6.

2 Exit Edges

Clearly, every complete geometric graph is supporting. To obtain a supporting graph with fewer edges, we select edges so that no vertex of the resulting geometric graph can be moved to change the order type while preserving isomorphism.

Definition 2

Let be finite and in general position. Let $a, b, c \in S$ be distinct. Then, ab is an exit edge with witness c if there is no $p \in S$ such that the line $\overline{ap}$ separates b from c or the line $\overline{bp}$ separates a from c. The geometric graph on S whose edges are the exit edges is called the exit graph of S.

Equivalently, ab is an exit edge with witness c if and only if the double-wedge through a between b and c and the double-wedge through b between a and c contain no point of S in their interior; see Fig. 3 left.

Fig. 3.

Characterizing exit edges. Left: If the gray region is empty of points, then the edge ab is an exit edge. Right: An illustration of the proof of Proposition 3.

An exit edge has at most two witnesses. If $|S| \ge 4$ and ab is an exit edge in S with witness c, neither ac nor bc can be an exit edge with witness b or a, respectively. We illustrate the set of exit edges for sets of 5 points in Fig. 1 left.

Exit edges can be characterized via 4-holes. For an integer $k \ge 3$, a (general) k-hole in S is a simple polygon $\mathcal {P}$ spanned by k points of S whose interior contains no point of S. If $\mathcal {P}$ is convex, we call $\mathcal {P}$ a convex k-hole. A point $a \in S$ or an edge ab with $a,b\in S$ is extremal for S if it lies on the boundary of the convex hull of S. A point or an edge in S that is not extremal in S is internal to S.

Proposition 3

Let be a set of points in general position and let $a,\,b \in \,S$. Then, ab is not an exit edge of S if and only if the following conditions hold:

• 1. If ab is extremal in S, then ab is an edge of at least one convex 4-hole in S.

• 2. If ab is internal in S, then there are two 4-holes abxy and bauv, in counterclockwise order, such that their reflex angles (if any) are incident to ab.

We remark that an internal exit edge either has a witness on both sides or is incident to at least one general 4-hole on one side.

Proof

Let ab be an exit edge with a witness c that lies, without loss of generality, to the left of $\overrightarrow{ab}$. Suppose there is a general 4-hole abxy, traced counterclockwise, such that the reflex angle of abxy (if it exists) is incident to ab. We can assume that y lies to the left of $\overrightarrow{ab}$, as in Fig. 3 right. First, suppose that abxy is convex (this must hold if ab is extremal). Since ab is an exit edge with witness c, the line $\overline{ax}$ does not separate c from b and the line $\overline{by}$ does not separate c from a. Thus, c must be inside the 4-hole abxy, which is impossible. Second, suppose that abxy is not convex (then, ab is internal), and x is to the right of $\overline{ab}$. Since ab is an exit edge with witness c, the line $\overline{bx}$ does not separate a from c and the line $\overline{ay}$ does not separate b from c, so c lies inside the 4-hole abxy, again a contradiction.

Conversely, assume that ab is not an exit edge. First, let ab be extremal, and let p be the closest point in $S\setminus \{a,b\}$ to the line $\overline{ab}$. The triangle abp is a 3-hole in S. Since p is not a witness for ab, there is a point $q \in S\setminus \{a,b,p\}$ such that, without loss of generality, the line $\overline{bq}$ separates a from p. Since ab is extremal, q lies on the same side of $\overline{ab}$ as p and, in particular, the polygon abpq is convex. If we choose q so that it is the closest such point to the line $\overline{ap}$, the triangles bpq and abq are 3-holes in S. Altogether, we obtain a convex 4-hole abpq in S.

Second, let ab be internal. Let p be closest in $S\setminus \{a,b\}$ to the line $\overline{ab}$ such that p lies to the left of $\overline{ab}$. The triangle abp is a 3-hole in S. Since p is not a witness for ab, there is a point $q \in S\setminus \{a,b,p\}$ such that either the line $\overline{bq}$ separates a from p or the line $\overline{aq}$ separates b from p. If q lies to the left of $\overline{ab}$, we obtain a convex 4-hole as in the previous case. Thus, we can assume that all such points q lie to the right of $\overline{ab}$. We choose the point q so that it is (one of the) closest to the line $\overline{ab}$ among all points that prevent ab from being an exit edge with witness p. Without loss of generality, we assume that the line $\overline{bq}$ separates a from p. The choice of q guarantees that bpq is a 3-hole in S. Thus, abqp is a 4-hole in S incident to ab from the left. An analogous argument with a point $p'$ from $S\setminus \{a,b\}$ that is closest to $\overline{ab}$ such that $p'$ lies to the right of $\overline{ab}$ shows that there is an appropriate 4-hole in S incident to ab from the right.   $\square$

Proposition 4

Let be finite and in general position and, for every $t\in [0,1]$, let S(t) be a continuous deformation of S at time t. More formally, let be an ambient isotopy and $S(t) = \{f(s,t) \mid s\in S\}$, for $t \in [0, 1]$. Let $S^c\subseteq S$ be the first subset of at least three points to become collinear. Let (a, b, c) be the first triple to become collinear, at time $t_0 > 0$. If c lies on the segment ab in $S(t_0)$, then ab is an exit edge of S(0) with witness c.

Proof

For $t \in [0, t_0)$, the triple orientations in S(t) remain unchanged, and in $S(t_0)$, the point c lies on ab. Thus, for $t \in [0, t_0)$, there is no line through two points of S(t) that strictly separates the relative interior of ab from c. In particular, there is no such separating line through a or b in S(0). Hence, ab is an exit edge with witness c.   $\square$

Corollary 5

The exit graph of every point set is supporting.

The proof of Proposition 4 also shows that if a line separates c from the relative interior of ab, then there is such a line through a or b. This may suggest that the exit edges are necessary for a supporting graph. However, this is not true in general. For example, in Fig. 4 left, we see a construction by Ringel [15]: ab is an exit edge with witness c, but c cannot move over ab without violating Pappus’ theorem. We note that in this situation, we might consider the abstract order type for the triple orientations we would obtain after moving c over ab. Since there is no planar point set with this set of triple orientations, this abstract order type is not realizable. Deciding realizability is (polynomial-time-)equivalent to the existential theory of the reals [14]. We will revisit these concepts in Sect. 4.

We note that there are point sets where two or more other exit edges prevent a witness c from crossing its corresponding exit edge ab; see, for example, Fig. 4 bottom right. Since the two geometric graphs in Fig. 4 right are not isomorphic, they cannot be transformed into each other by a continuous deformation as the one used in Definition 1. However, in this example, while c cannot move to ab without changing the order type in Fig. 4 bottom right, if ab were not present, we could first change the point set to the one in Fig. 4 top right and then move c over ab. Thus, ab indeed has to be in a supporting graph.

Fig. 4.

Left: moving c over ab to orient (a, b, c) clockwise, without changing the orientation of other triples, would contradict Pappus’s theorem [15]. Right: it is not always possible to move a witness c continuously to the corresponding exit edge ab.

3 Exit Edges and Empty Triangular Cells

The (real) projective plane is a non-orientable surface obtained by augmenting the Euclidean plane by a line at infinity. This line has one point at infinity for each direction, where all parallel lines with this direction intersect. Thus, in , each pair of parallel lines intersects in a unique point.

For a point set S in the Euclidean plane, add a line $\ell _\infty$ to obtain the projective plane. We use a duality transformation that maps a point s of  to a line $s^*$ in  . In this way, we get a set of lines $S^*$ dual to S, giving a projective line arrangement ${\mathcal {A}}$. The removal of a line from ${\mathcal {A}}$ does not disconnect  . Since  has non-orientable genus 1, removing any two lines $\ell _1$ and $\ell _2$ from disconnects it into two components. We call the closure of each of the two components a halfplane determined by $\ell _1$ and $\ell _2$. The marked cell $c_{\infty }$ is the cell of ${\mathcal {A}}$ that contains the point $\ell _\infty ^*$ dual to the line $\ell _\infty$. By appropriately choosing the duality transformation, we can assume that $\ell _\infty ^*$ lies at vertical infinity.

The combinatorial structure of ${\mathcal {A}}$, together with the marked cell, determines the order type of S. We show how to identify exit edges and their witnesses in dual line arrangements.

We use the marked cell $c_{\infty }$ to orient the lines from $S^*$: first, we orient the lines on the boundary of $c_{\infty }$ in one direction. Then, we iteratively remove lines that have already been oriented, and we define the orientation for the remaining lines from $S^*$ by considering the new lines on the boundary of $c_{\infty }$. Then, $c_{\infty }$ is the only cell whose boundary is oriented consistently, that is, it can be traversed completely along the resulting orientation. In particular, for an unmarked triangular cell $\triangle$ in ${\mathcal {A}}$, the directed edges of $\triangle$ form a transitive order on its vertices, with a unique vertex of $\triangle$ in the middle. We call this vertex the exit vertex of $\triangle$ and the line through the other two vertices of $\triangle$ the witness line of $\triangle$.

Note that if we consider the duality mapping a point $p=(p_x,p_y)$ from the real plane to the (non-vertical) line $p^*: y=p_xx - p_y$, then the described orientation procedure corresponds to orienting these dual lines from left to right.

Theorem 6

Let be in general position, and let $a, b,c \in S$. Then, ab is an exit edge with witness c if and only if the lines $a^*$, $b^*$, and $c^*$ bound an unmarked triangular cell $\triangle$ in the arrangement $\mathcal {A}$ of lines from $S^*$ so that $c^*$ is the witness line of $\triangle$ and the point $\overline{ab}^*=a^* \cap b^*$ is the exit vertex of $\triangle$.

Proof

For two points $p,q\in S$ and their dual lines $p^*,q^*\in S^*$, we denote by $w(p^*,q^*)$ the halfplane determined by $p^*$ and $q^*$ that does not contain the marked cell. Thus, the boundary of $w(p^*,q^*)$ is not oriented consistently. Since projective duality preserves incidences, the condition that no line spanned by two points of S intersects the edge pq is equivalent in $S^*$ to $w(p^*,q^*)$ not containing any vertex of ${\mathcal {A}}$.

Let $\triangle$ be the triangular region determined by the intersection of the two halfplanes $w(a^*,c^*)$ and $w(b^*,c^*)$. By the projective duality, ab is an exit edge with witness c in S if and only if no line of $S^*$ intersects $a^*$ inside $w(b^*,c^*)$ or $b^*$ inside $w(a^*,c^*)$. In other words, if and only if two sides of $\triangle$, lying on $a^*$ and $b^*$, contain no intersection with lines from $S^*$. This is equivalent to $\triangle$ being a cell of the arrangement $\mathcal {A}$. Moreover, $a^*$ and $b^*$ share the exit vertex of $\triangle$; see Fig. 5. Consequently, the exit vertex $a^* \cap b^*$ is the dual of the line containing the exit edge ab.   $\square$

Fig. 5.

An illustration of the proof of Theorem 6. If ab is an exit edge with witness c in S, then the two bold drawn segments of the corresponding triangular cell are unintersected, and thus, bound an unmarked triangular cell in $S^*$. The exit vertex is represented with a black disk.

Corollary 7

Let S be a set of n points in general position. Then the exit edges of S can be enumerated in $O(n^2)$ time by constructing the dual line arrangement of S and checking which cells are unmarked triangular cells.

4 On the Number of Exit Edges

Line arrangements can be generalized to so-called pseudoline arrangements. A pseudoline is a closed curve in the projective plane  whose removal does not disconnect . A set of pseudolines in  , where any two pseudolines cross exactly once, determines a (projective) pseudoline arrangement. If no three pseudolines intersect in a common point, the pseudoline arrangement is simple. All notions that we have introduced for line arrangements, such as consistent orientations, exit vertices, or witness lines, naturally extend to pseudolines.

A pseudoline arrangement is stretchable if it is isomorphic to a line arrangement, that is, the corresponding cell complexes into which the two arrangements partition are isomorphic. The combinatorial dual analogues of line arrangements and pseudoline arrangements are order types and abstract order types, respectively. Thus, deciding if a pseudoline arrangement is stretchable is (polynomial-time-)equivalent to the existential theory of the reals [7, 14].

As discussed in Sect. 3, the maximum number of triangular cells in a simple projective pseudoline arrangement gives an upper bound on the number of exit edges of a point set. However, one triangular cell could be $c_\infty$, and there could be pairs of triangular cells with the same exit vertex. We call a configuration of the latter type an hourglass; see Fig. 6. We say that the two pseudolines p and q that define the exit vertex of the two triangular cells of an hourglass H slice H and that H is sliced by p and by q.

Fig. 6.

Left: the two triangular cells $\triangle _1$ and $\triangle _2$ do not form an hourglass, because they share a vertex that is not an exit vertex. Right: the two triangular cells $\triangle _1$ and $\triangle _2$ form an hourglass because they share an exit vertex.

Observation 8

A triangular cell can be a part of at most one hourglass.

Observation 9

An exit edge ab with two witness points is dual to an hourglass with exit vertex $\overline{ab}^*$.

Any projective arrangement of $n \ge 4$ lines has at least n triangular cells, as each line is incident to at least three triangular cells [12]. This is known to be tight. Therefore, taking into account the marked cell $c_\infty$ and possible hourglasses, any set of $n \ge 4$ points has at least $\lceil \frac{n - 1}{2} \rceil$ exit edges. We improve this lower bound by bounding from below the difference between the number of triangular cells and the number of hourglasses.

Proposition 10

Any set of $n \ge 4$ points in the plane has at least $(3n-7)/5$ exit edges.

For the proof of Proposition 10 we use the following two lemmas. The first is a theorem by Grünbaum [10, Theorem 3.7 on p. 50], and the second can be derived from the proof of that theorem.

Lemma 11

(Grünbaum [10]). In a simple pseudoline arrangement L every pseudoline from L is incident to at least three triangular cells.

Lemma 12

(Grünbaum [10]). Let L be a simple arrangement of pseudolines, and let H be a closed halfplane determined by two pseudolines $\ell _1, \ell _2 \in L$. If two other pseudolines of L cross in the interior of H, then there is a triangular cell in H that is incident to $\ell _1$ but not to $\ell _2$.

Proof

(of Proposition 10). Let L be a simple projective line arrangement of $n\ge 4$ pseudolines $\ell _1, \ell _2, \dots , \ell _n$. For each pseudoline $\ell _i \in L$, let $t_i$ be the number of triangular cells incident to $\ell _i$ and $h_i$ the number of hourglasses sliced by $\ell _i$. Set $x_i = t_i - h_i/2$. For each pseudoline $\ell _i \in L$, there are three possible cases.

Case (i): there is no hourglass sliced by $\ell _i$. By Lemma 11, every pseudoline is incident to at least three triangular cells. Thus, we have $x_i= t_i \ge 3$.

Case (ii): the pseudoline $\ell _i$ slices an hourglass together with some pseudoline $\ell _j$ and the interior of each of the two halfplanes determined by $\ell _i$ and $\ell _j$ contains at least one crossing of some other pair of pseudolines. By Lemma 12, $\ell _i$ is incident to the two triangular cells of the hourglass plus at least two other triangular cells, one in each closed halfplane. (We ignore here that a cell might be the marked one.) Thus, $t_i\ge 4$. Observation 8 implies $h_i \le t_i/2$. Overall we get $x_i = t_i - h_i/2 \ge t_i - t_i/4 \ge (3/4) \cdot 4 = 3$.

Case (iii): the pseudoline $\ell _i$ slices an hourglass together with some pseudoline $\ell _j$, and one of the two closed halfplanes $H_1$ and $H_2$ determined by $\ell _i$ and $\ell _j$ contains no crossing of any other pair of pseudolines in its interior. Suppose the closed halfplane that contains no further crossing is $H_1$. Then, the hourglass sliced by $\ell _i$ and $\ell _j$ is in $H_1$, as the other two lines defining the hourglass do not cross in that halfplane; see Fig. 7 (left). Since $H_1$ contains no crossing in its interior, it is divided by the other pseudolines into 4-gons and the two triangular cells of the hourglass. In particular, the marked cell is bounded by only four pseudolines, two of them being $\ell _i$ and $\ell _j$; see Fig. 7, right. Thus, there can be at most four pseudolines for which case (iii) applies. Notice that in this case $h_i=1$, since any other hourglass sliced by $\ell _i$ would have one triangular cell in each of the two halfplanes $H_1$ and $H_2$ and the two triangular cells in $H_1$ form the already-counted hourglass (and by Observation 8 they cannot be part of another hourglass). Thus, we can only guarantee that $x_i \ge 3 - 1/2 = 5/2$. However, as we showed, this case can happen at most for two pairs of pseudolines.

Fig. 7.

In case (iii), both $\ell _1$ and $\ell _2$ must bound the marked cell, shown striped on the right picture. Moreover, that cell is bounded by four pseudolines.

Let T be the total number of triangular cells in L and let H be the total number of hourglasses. Summing the contributions of cases (i)–(iii), we have

$$ 3T - H = \sum _{i = 1}^n t_i - \frac{1}{2} \sum _{i = 1}^n h_i = \sum _{i = 1}^n x_i \ge 3\cdot (n-4) + 4 \cdot \left( \frac{5}{2}\right) = 3n - 2. $$

By Observation 8, we have $T\ge 2H$. Combining these inequalities, we get

$$ T-H = \frac{3T-H + 2(T-2H)}{5} \ge \frac{3T-H}{5} \ge \frac{3n-2}{5}. $$

By Theorem 6, the number of exit edges in a point set is equal to the number of exit vertices in its dual line arrangement. In general, the number of exit vertices in a pseudoline arrangement is bounded from below by $T-H-1$. Therefore, there are at least $\frac{3}{5}n - \frac{7}{5}$ exit edges.   $\square$

We do not know if the lower bound in Proposition 10 is tight. The smallest number of exit edges we could achieve is $n - 3$ for $n \ge 9$; see Fig. 8.

Fig. 8.

Construction with $n-3$ exit edges.

The number of triangular cells in a simple arrangement of n lines in the projective plane is at most $n(n-1)/3$ [10], so there are at most $n^2/3+O(n)$ exit edges. This means that representing an order type with the exit graph instead of the complete geometric graph saves at least one third of the edges. Palásti and Füredi [17] showed that for every value of n there are simple arrangement of n lines in with $n(n-3)/3$ triangular cells. Moreover, Roudneff [16] and Harborth [11] proved that the upper bound $n(n-1)/3$ is tight for infinitely many values of n (see also [3]). The point sets that are dual to the currently-known arrangements that maximize the number of triangular cells have $n^2/6+O(n)$ exit edges, since most of their exit edges have two witnesses. This gives a quadratic lower bound in the worst case, but the leading coefficient remains unknown. It is worth noting that there are line arrangements with no pair of adjacent triangular cells [13], which implies the existence of point sets where every exit edge has precisely one witness.

5 Properties of Exit Graphs

We present some further results on supporting graphs and exit graphs.

Theorem 13

Any geometric graph supporting a point set S, with $|S| \ge 9$, contains a crossing.

Proof

Let G be a geometric graph with vertex set S without crossings. There is a point set $S'$ with a different order type that also admits G: Dujmović [6] showed that every plane graph admits a plane straight-line embedding with at least $\sqrt{n/2}$ points on a line; as we have a point set with a collinear triple that admits G, there are at least two point sets in general position with a different order type that admit G. Moreover, one can continuously morph S to $S'$ while keeping the corresponding geometric graph planar and isomorphic to G (see, for example, [2]). Therefore, G does not support S.   $\square$

Proposition 14

Let S be a point set in general position in and let G be its exit graph. Every vertex in the unbounded face of G is extremal, that is, it lies on the boundary of the convex hull of S.

Note that, as shown in Fig. 4 left, an analogous statement does not hold for general supporting graphs. The proof can be found in the full version [1].

6 Concluding Remarks

We conjecture that the geometric graph G of exit edges not only is supporting for S, but also that any point set $S'$ that is the vertex set of a geometric graph isomorphic to G has the same order type as S. One might conjecture that already knowing all exit edges and their witnesses (in the dual line arrangement, all triangular cells and their orientations) is sufficient to determine the order type. Surprisingly, this turns out to be wrong. A counterexample is sketched in Fig. 9 as a dual (stretchable) pseudoline arrangement of 14 lines in the projective plane, based on an example by Felsner and Weil [8]. It consists of two arrangements of six lines in the Euclidean plane that are combinatorially different, but share the set of triangular cells and their orientations. While the exit edges are the same for the two different order types, the corresponding exit graphs are not isomorphic. In the dual of that example the order of the triangular cells along each pseudoline differs, but that extra information is not enough to distinguish the two order types: We can modify the pseudoline arrangements in Fig. 9 by, essentially, duplicating pseudolines 1–6 and making a pseudoline and its duplication cross between the crossings with two green pseudolines (7–14). An illustration is presented in the full version [1].

Fig. 9.

Top: two arrangements of 14 pseudolines with the same set of triangular cells (extending [8, Figure 3]). No triangular cell crossed by the line at infinity. Bottom: corresponding dual point sets. The order types are not the same (see for example the number of extremal points).