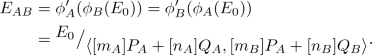Abstract
Oblivious transfer is one of the main pillars of modern cryptography and plays a major role as a building block for other more complex cryptographic primitives. In this work, we present an efficient and versatile framework for oblivious transfer (OT) using one-round key-exchange (ORKE), a special class of key exchange (KE) where only one message is sent from each party to the other. Our contributions can be summarized as follows:
-
We analyze carefully ORKE schemes and introduce new security definitions. Namely, we introduce a new class of ORKE schemes, called Alice-Bob one-round key-exchange (A-B ORKE), and the definitions of message and key indistinguishability.
-
We show that OT can be obtained from A-B ORKE schemes fulfilling message and key indistinguishability. We accomplish this by designing a new efficient, versatile and universally composable framework for OT in the Random Oracle Model (ROM). The efficiency of the framework presented depends almost exclusively on the efficiency of the A-B ORKE scheme used since all other operations are linear in the security parameter. Universally composable OT schemes in the ROM based on new hardness assumptions can be obtained from instantiating our framework.
Examples are presented using the classical Diffie-Hellman KE, RLWE-based KE and Supersingular Isogeny Diffie-Hellman KE.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Remark that a Key Encapsulation Mechanism (KEM) is an A-B ORKE, however the opposite is not known to be true. Note that Key Exchanges (KE) and KEM are not comparable primitives and that some KE are A-B ORKE.
- 2.
The full proof of the theorem is thoroughly described in the full version [10].
References
Alkim, E., Ducas, L., Pöppelmann, T., Schwabe, P.: Post-quantum key exchange—a new hope. In: 25th USENIX Security Symposium (USENIX Security 16), pp. 327–343. USENIX Association, Austin, TX (2016). https://www.usenix.org/conference/usenixsecurity16/technical-sessions/presentation/alkim
Applebaum, B., Cash, D., Peikert, C., Sahai, A.: Fast cryptographic primitives and circular-secure encryption based on hard learning problems. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 595–618. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_35
Asharov, G., Lindell, Y., Schneider, T., Zohner, M.: More efficient oblivious transfer extensions. J. Cryptol. 30(3), 805–858 (2017)
Barreto, P., Oliveira, G., Benits, W.: Supersingular isogeny oblivious transfer. Cryptology ePrint Archive, Report 2018/459 (2018). https://eprint.iacr.org/2018/459
Barreto, P.S.L.M., David, B., Dowsley, R., Morozov, K., Nascimento, A.C.A.: A framework for efficient adaptively secure composable oblivious transfer in the ROM. Cryptology ePrint Archive, Report 2017/993 (2017). https://eprint.iacr.org/2017/993
Bellare, M., Micali, S.: Non-interactive oblivious transfer and applications. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 547–557. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_48
Bergsma, F., Jager, T., Schwenk, J.: One-round key exchange with strong security: an efficient and generic construction in the standard model. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 477–494. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_21
Blazy, O., Chevalier, C., Germouty, P.: Almost optimal oblivious transfer from QA-NIZK. In: Gollmann, D., Miyaji, A., Kikuchi, H. (eds.) ACNS 2017. LNCS, vol. 10355, pp. 579–598. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-61204-1_29
Branco, P., Ding, J., Goulão, M., Mateus, P.: Universally composable oblivious transfer protocol based on the RLWE assumption. Cryptology ePrint Archive, Report 2018/1155 (2018). https://eprint.iacr.org/2018/1155
Branco, P., Ding, J., Goulão, M., Mateus, P.: A framework for universally composable oblivious transfer from one-round key-exchange. Cryptology ePrint Archive, Report 2019/726 (2019). https://eprint.iacr.org/2019/726
Byali, M., Patra, A., Ravi, D., Sarkar, P.: Fast and universally-composable oblivious transfer and commitment scheme with adaptive security. Cryptology ePrint Archive, Report 2017/1165 (2017). https://eprint.iacr.org/2017/1165
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: Proceedings of the 42nd IEEE Symposium on Foundations of Computer Science, FOCS 2001, p. 136. IEEE Computer Society, Washington, DC, USA (2001). http://dl.acm.org/citation.cfm?id=874063.875553
Canetti, R., Fischlin, M.: Universally composable commitments. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 19–40. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_2
Canetti, R., Krawczyk, H.: Analysis of key-exchange protocols and their use for building secure channels. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 453–474. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_28
Canetti, R., Lindell, Y., Ostrovsky, R., Sahai, A.: Universally composable two-party and multi-party secure computation. In: Proceedings of the Thiry-fourth Annual ACM Symposium on Theory of Computing, STOC 2002, pp. 494–503. ACM, New York, NY, USA (2002). http://doi.acm.org/10.1145/509907.509980
Chou, T., Orlandi, C.: The simplest protocol for oblivious transfer. In: Lauter, K., Rodríguez-Henríquez, F. (eds.) LATINCRYPT 2015. LNCS, vol. 9230, pp. 40–58. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22174-8_3
David, B., Dowsley, R., Nascimento, A.C.A.: Universally composable oblivious transfer based on a variant of LPN. In: Gritzalis, D., Kiayias, A., Askoxylakis, I. (eds.) CANS 2014. LNCS, vol. 8813, pp. 143–158. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-12280-9_10
David, B.M., Nascimento, A.C.A., Müller-Quade, J.: Universally composable oblivious transfer from lossy encryption and the McEliece assumptions. In: Smith, A. (ed.) ICITS 2012. LNCS, vol. 7412, pp. 80–99. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32284-6_5
Diffie, W., Hellman, M.: New directions in cryptography. IEEE Trans. Inf. Theory 22(6), 644–654 (1976)
Ding, J., Xie, X., Lin, X.: A simple provably secure key exchange scheme based on the learning with errors problem. Cryptology ePrint Archive, Report 2012/688 (2012). https://eprint.iacr.org/2012/688
Doerner, J., Kondi, Y., Lee, E., Shelat, A.: Secure two-party threshold ECDSA from ECDSA assumptions. In: 2018 IEEE Symposium on Security and Privacy (SP), vol. 00, pp. 595–612 (2018). doi.ieeecomputersociety.org/10.1109/SP.2018.00036
Freedman, M.J., Ishai, Y., Pinkas, B., Reingold, O.: Keyword search and oblivious pseudorandom functions. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 303–324. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_17
Hauck, E., Loss, J.: Efficient and universally composable protocols for oblivious transfer from the CDH assumption. Cryptology ePrint Archive, Report 2017/1011 (2017). https://eprint.iacr.org/2017/1011
Jao, D., De Feo, L.: Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies. In: Yang, B.-Y. (ed.) PQCrypto 2011. LNCS, vol. 7071, pp. 19–34. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25405-5_2
Jeong, I.R., Katz, J., Lee, D.H.: One-round protocols for two-party authenticated key exchange. In: Jakobsson, M., Yung, M., Zhou, J. (eds.) ACNS 2004. LNCS, vol. 3089, pp. 220–232. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24852-1_16
Kilian, J.: Founding cryptography on oblivious transfer. In: Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing, STOC 2088, pp. 20–31. ACM, New York, NY, USA (1988). http://doi.acm.org/10.1145/62212.62215
Kushilevitz, E., Ostrovsky, R.: Replication is not needed: single database, computationally-private information retrieval. In: Proceedings 38th Annual Symposium on Foundations of Computer Science, pp. 364–373, October 1997
Liu, M.m., Krämer, J., Hu, Y.p., Buchmann, J.: Quantum security analysis of a lattice-based oblivious transfer protocol. Front. Inf. Technol. Electron. Eng. 18(9), 1348–1369 (2017). https://doi.org/10.1631/FITEE.1700039
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 1–23. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_1
Parakh, A.: Oblivious transfer based on key exchange. Cryptologia 32(1), 37–44 (2008). https://doi.org/10.1080/01611190701593228
Peikert, C.: Lattice cryptography for the internet. In: Mosca, M. (ed.) PQCrypto 2014. LNCS, vol. 8772, pp. 197–219. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11659-4_12
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_31
Rabin, M.O.: How to exchange secrets with oblivious transfer (1981)
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Proceedings of the Thirty-seventh Annual ACM Symposium on Theory of Computing, STOC 2005, pp. 84–93. ACM, New York, NY, USA (2005). http://doi.acm.org/10.1145/1060590.1060603
Yao, A.C.C.: How to generate and exchange secrets. In: Proceedings of the 27th Annual Symposium on Foundations of Computer Science, SFCS 1986, pp. 162–167. IEEE Computer Society, Washington, DC, USA (1986). https://doi.org/10.1109/SFCS.1986.25
Acknowledgment
The first author thanks the support from DP-PMI and FCT (Portugal) through the grant PD/BD/ 135181/2017. This work was done while visiting the University of Cincinnati. The third author thanks the support from DP-PMI and FCT (Portugal) through the grand PD/BD/135182/2017. This work was funded by the project UID/EEA/50008/2019.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix
A UC-Security and Ideal Functionalities
The Universal Composability (UC) framework, firstly introduced by Canetti [12], allows us to analyze the security of protocols, not just per se, but also when composed with other protocols. Due to the lack of space, only a brief introduction on the UC-framework is presented. For more details on this subject we refer the reader to [12].
In a nutshell, to prove UC security of a protocol \(\pi \) (usually called the real-world execution) one compares it to an ideal version of the primitive, defined a priori (usually called the ideal-world execution). The entities involved in the ideal-world execution are dummy parties which interact via an ideal functionality \(\mathcal {F}\). These dummy parties may or may not be corrupted by an ideal adversary \(\mathsf {Sim}\), usually called the simulator. The functionality works as a trusted party: it receives inputs from all the entities involved and returns to each one something, depending on the primitive being implemented. In this way, each of the parties learns nothing but its own input and output. In the real-world execution, several parties interact between them via some protocol \(\pi \), which implements the desired primitive. These parties may or may not be corrupted by some adversary \(\mathcal {A}\). An entity \(\mathcal {E}\), often called the environment, oversees the executions in both the ideal and the real worlds. At the end of the executions, the environment is asked to distinguish them. The intuition of the UC-framework is that a protocol \(\pi \) is secure if the environment \(\mathcal {E}\) is not able to distinguish the real-world execution of \(\pi \) from the ideal-world execution of \(\mathcal {F}\). If this happens, we can conclude that a real-world adversary \(\mathcal {A}\) does not have more power than an ideal-world adversary \(\mathsf {Sim}\). Hence, whatever strategy a real-world adversary \(\mathcal {A}\) uses to cheat in the execution of \(\pi \), it can also be used by an ideal-world adversary \(\mathsf {Sim}\). Since we define the ideal functionality in order to avoid attacks from any adversary, we can conclude that there is no strategy for the real-world adversary \(\mathcal {A}\) that allows it to know more than its own input and output.
Formally, let \(\pi \) be a protocol where n parties and an adversary \(\mathcal {A}\) are involved. We denote the output of the environment \(\mathcal {E}\) in the end of the real-world execution of \(\pi \) with adversary \(\mathcal {A}\) by \(\mathsf {EXEC}_{\pi ,\mathcal {A},\mathcal {E}}\). The output of \(\mathcal {E}\) at the end of the ideal-world execution of a functionality \(\mathcal {F}\) with adversary \(\mathsf {Sim}\) is denoted by \(\mathsf {IDEAL}_{\mathcal {F},\mathsf {Sim},\mathcal {E}}\). The following definition introduces the notion of a protocol emulating (in a secure way) some ideal functionality.
Definition 11
We say that a protocol \(\pi \) UC-realizes \(\mathcal {F}\) if for every PPT adversary \(\mathcal {A}\) there is a PPT simulator \(\mathsf {Sim}\) such that for all PPT environments \(\mathcal {E}\),
where \(\mathcal {F}\) is an ideal functionality.
Oblivious transfer (OT), firstly introduced by Rabin [33], is a crucial primitive in cryptography. We describe the \(\left( {\begin{array}{c}2\\ 1\end{array}}\right) \)-OT ideal functionality \(\mathcal {F}_\text {OT}\), as presented in [15]. Let \(\lambda \in \mathbb {N}\) be a fixed value known to both parties, \(M_0,M_1 \in \{0,1\}^\lambda \) and \(b\in \{0,1\}\). The value \(\mathsf {sid}\) represents the session ID and the ID of the parties involved in the protocol.

Unfortunately, it is impossible to design universally composable OT protocols in the plain model, that is, without any setup assumption [13]. Hence, we use the random oracle model (ROM) to construct our UC-secure OT protocol. To this end, we work on the \(\mathcal {F}_{\text {RO}}\)-hybrid model in order to model random oracles in the UC framework. The random oracle ideal functionality \(\mathcal {F}_\text {RO}\) is presented below.

The idea behind the \(\mathcal {F}_\text {RO}\)-hybrid model is that every party involved in both the ideal-world execution of \(\mathcal {F}\) and the real-world execution of the protocol \(\pi \) (including the adversary) have access to an ideal functionality \(\mathcal {F}_\text {RO}\), which behaves as a random oracle. The environment can access this ideal functionality through the adversary. We denote by \( \mathsf {EXEC}_{\pi ,\mathcal {A},\mathcal {E}}^{\mathcal {F}_\text {RO}}\) the output of the environment after the real-world execution of the protocol \(\pi \) with an adversary \(\mathcal {A}\) in the real-world, with the ideal functionality \(\mathcal {F}_\text {RO}\). The notion of a protocol securely emulating an ideal functionality can be adapted to this model.
Definition 12
We say that a protocol \(\pi \) UC-realizes \(\mathcal {F}\) in the \(\mathcal {F}_\text {RO}\)-hybrid model if for every PPT adversary \(\mathcal {A}\) there is a PPT simulator \(\mathsf {Sim}\) such that for all PPT environments \(\mathcal {E}\),
In this work, we consider static malicious adversaries. That is, an adversary corrupting any of the parties can deviate arbitrarily as it wishes from the protocol. However the parties are corrupted by the adversary before the beginning of the protocol and they remain so until the end of the protocol.
B Framework Instantiations
In the following section we provide relevant cases of ORKE schemes that can be used to instantiate our framework. More concretely, we show that our framework can be used with Diffie-Hellman, Ding’s KE and Supersingular Isogeny Diffie-Hellman.
1.1 B.1 DH-Based OT
Consider the Diffie-Hellman (DH) KE protocol [19]. Let p be a prime and consider the group \(\mathbb {Z}_p=\mathbb {Z}/p\mathbb {Z}\). Let \(g \in \mathbb {Z}_p\) be a generator of the multiplicative group \(\mathbb {Z}_p^*\). We assume g to be a public parameter of the system (e.g. a standard one), known by all parties. The DH KE is defined by three algorithms:
-
\(\mathsf {Gen}_{\mathrm {DH}}(1^\kappa )\) outputs a secret key \(\mathsf {sk}=x\in \mathbb {Z}_p^*\) and a public key \(\mathsf {pk}\leftarrow g\).
-
\(\mathsf {Msg}_{\mathrm {DH}}(r_i,\mathsf {sk}_i) [= \mathsf {Msg}_{\mathrm {DH}}^\mathsf {A}(r_i,\mathsf {sk}_i) = \mathsf {Msg}_{\mathrm {DH}}^\mathsf {B}(r_j,\mathsf {sk}_j,\cdot )]\) which takes as input the secret \(\mathsf {sk}_i=x_i\) and generator g and outputs \(g^{x_i}\).
-
\(\mathsf {Key}_{\mathrm {DH}}(r_i,\mathsf {sk}_i, m_j)\) which takes as input a message \(m_j \leftarrow g^{x_j}\) and a secret key \(\mathsf {sk}_i=x_i\) and outputs \(m_j^{x_i}\).
Note that DH KE is an ORKE scheme, which means that \(\mathsf {Msg}_{\mathrm {DH}}\) is the same for both parties.
Recall that the Decisional Diffie-Hellman (DDH) assumption assumes that \((g,g^{x},g^y,g^{xy})\) is computationally indistinguishable from \((g,g^{x},g^y,z)\) when  .
.
Using the notation of Sect. 2.1, consider \(\mathcal {M}=\overline{\mathcal {M}}=\mathbb {M}=\mathbb {Z}_p^*\), the operation \(*\) to be the product modulo p and \(\psi :\mathbb {Z}_p^*\times (\mathbb {Z}_p^*,*) \rightarrow \mathbb {Z}_p^*\) to be the action group defined as \(\psi (y,h)=y * h\mod p\).
The properties of \(\psi \)-message indistinguishability and \(\psi \)-key indistinguishability follow directly from the hardness of DDH of base g in the group \(\mathbb {Z}_p^*\). Consider the notation of Definition 5.
Lemma 13
The DH KE protocol is \(\psi \)-message indistinguishable.
Proof
Since g is a generator of \(\mathbb {Z}_p^*\), the message sent by Alice to Bob is a random element from \(\mathbb {Z}_p^*\) when it is computed using \(\mathsf {Msg}_\varPi \) or using \(\psi \). \(\square \)
Lemma 14
The DH KE protocol is \(\psi \)-key indistinguishable, given that the DDH assumption holds.
Proof
Any key obtained using the \(\mathsf {Key}_{\mathrm {DH}}\) algorithm should be of the form \(g^{xy}\), where \(g^x\) is the output of the other party’s \(\mathsf {Msg}_{\mathrm {DH}}\), and y is the secret key of the party running this algorithm. As before, \(g^{xy}\) is a random element in \(\mathbb {Z}_p^*\), and so indistinguishable from a uniform chosen values from \(\mathbb {Z}_p^*\), given that the hardness of the DDH assumption holds. \(\square \)
Therefore, we conclude that the DH KE can be used to instantiate the framework presented in this paper.
1.2 B.2 RLWE-Based OT
The instantiation of this framework using Ding’s KE was presented previously in [9] and this framework can be viewed as a generalization of their work. Here, we present a more generic instantiation using any RLWE-based KE scheme, such as [1, 20, 31].
Let \(q > 2\) be a prime such that \(q\equiv 1\mod 2n\), \(n\in N\) be a power of 2 and \(R_q = \mathbb {Z}_q[x]/\langle (x^n+1)\rangle \). Let \(\chi _\alpha \) be a discrete Gaussian distribution with parameter \(\alpha \).
Let  . The RLWE assumption asks to distinguish \((a,as+e)\) where
. The RLWE assumption asks to distinguish \((a,as+e)\) where  from (a, u) where
from (a, u) where  [29]. The HNF-RLWE assumption is similar to the RLWE assumption, but
[29]. The HNF-RLWE assumption is similar to the RLWE assumption, but  [2].
[2].
Consider an RLWE-based KE scheme, which is secure given that the HNF-RLWE problem is hard. Let \((\mathsf {recMsg},\mathsf {recKey})\) be any reconciliation mechanism, as the ones presented in [20, 31], where \(\mathsf {recMsg}\) receives as input a value \(x_1\in R_q\) and outputs the signal w of \(x_1\) and a key K, and \(\mathsf {recKey}\) receives as input a value \(x_2\in R_q\) and a signal w and it outputs a key K. Recall that a reconciliation mechanism is parameterized by a bound \(\xi _\mathsf {rec}\) such that if \(x_1\) and \(x_2\) are close (meaning that \(|x_1-x_2|\le \xi _\mathsf {rec}\)), then
It is also required that, if \(x_1\) is uniform, then \(K_1\) is indistinguishable from a uniform value, even when given w, where \((w,K_1)\leftarrow \mathsf {recMsg}(x_1)\).
Let  be a public polynomial. The four algorithms that define any RLWE-based KE based are the following:
be a public polynomial. The four algorithms that define any RLWE-based KE based are the following:
-
\(\mathsf {Gen}_{RLWE}(1^\kappa )\) chooses
 and outputs a secret key
and outputs a secret key  and a public key \(\mathsf {pk}\leftarrow a s+2e \mod q\) where
and a public key \(\mathsf {pk}\leftarrow a s+2e \mod q\) where  .
. -
\(\mathsf {Msg}_{RLWE}^\mathsf {A}(r_\mathsf {A},\mathsf {sk}_\mathsf {A})\) outputs the message \(m_\mathsf {A}= \mathsf {pk}_\mathsf {A}\).
-
\(\mathsf {Msg}_{RLWE}^\mathsf {B}(r_\mathsf {B},\mathsf {sk}_\mathsf {B},m_\mathsf {A})\) computes \((w,K)\leftarrow \mathsf {recMsg}(m_A\mathsf {sk}_B+2e')\), where
 , and outputs \(m_\mathsf {B}=(\mathsf {pk}_\mathsf {B},w)\).
, and outputs \(m_\mathsf {B}=(\mathsf {pk}_\mathsf {B},w)\). -
\(\mathsf {Key}_{RLWE}(r_i, \mathsf {sk}_i, m_j)\) computes \(k_i\leftarrow s_i \mathsf {pk}_j + 2e'_i\), where
 , and outputs the shared key \(K \leftarrow \mathsf {recKey}(k_i,w)\).
, and outputs the shared key \(K \leftarrow \mathsf {recKey}(k_i,w)\).
RLWE-based KE schemes [1, 20, 31] are A-B ORKE scheme since Bob’s message depends on Alice message.
Using the notation of Sect. 2.1, consider \(\mathcal {M}\) to be the set of RLWE samples, that is,  and \(\overline{\mathcal {M}}=\mathbb {M}=R_q\), the operation \(*\) to be the sum in \(R_q\) and \(\psi :R_q\times (R_q,+)\rightarrow R_q\) to be the action group defined as \(\psi (y,h)=y+h\).
and \(\overline{\mathcal {M}}=\mathbb {M}=R_q\), the operation \(*\) to be the sum in \(R_q\) and \(\psi :R_q\times (R_q,+)\rightarrow R_q\) to be the action group defined as \(\psi (y,h)=y+h\).
Lemma 15
RLWE-based KE is \(\psi \)-message indistinguishable given that the HNF-RLWE assumption holds.
Proof
The message algorithm of Alice (\(\mathsf {Msg}_{RLWE}^\mathsf {A}\)) in this key exchange protocol outputs messages which are HNF-RLWE samples, thus, it is trivial to reduce the problem of breaking \(\psi \)-message indistinguishability of an RLWE-based KE to the problem of deciding the HNF-RLWE problem. \(\square \)
For the \(\psi \)-key indistinguishability property, let \(K_A\) and \(K_B\) be the output of the algorithm \(\mathsf {Key}_{DingKE}\) when run by party \(\mathsf {A}\) and \(\mathsf {B}\) respectively.
Lemma 16
RLWE-based KE protocol is \(\psi \)-key indistinguishable, given that the HNF-RLWE assumption holds.
Proof
This follows directly from the security of the KE protocol. As proved in [20, Theorem 3], to computationally distinguish \(K_A\) or \(K_B\) from uniformly random in \(R_q\) reduces to the HNF-RLWE assumption. Thus, if the HNF-RLWE assumption holds, the protocol is \(\psi \)-key indistinguishable. \(\square \)
We conclude that RLWE-based KE schemes [1, 20, 31] can be used to instantiate the framework of this article.
1.3 B.3 SIDH-Based OT
Following the work of [4], where it is presented an OT protocol based on the Supersingular Isogeny Diffie-Hellman (SIDH) of [24], we adapt the same techniques to achieve the first UC OT based on Supersingular Isogeny cryptography. Although we use the same techniques to instantiate our framework using this key exchange, we work in the ROM instead of using the secure coin flip they use.
As defined in [24], let \(p=\ell _A^{e_A} \ell _B^{e_B} \cdot f \pm 1\) where \(\ell _A,\ell _B\) are small primes and f is a cofactor such that p is prime. Let \(E_0\) be a supersingular curve defined over \(\mathbb {F}_{p^2}\), and let \({P_A,Q_A}\) be a basis generating \(E_0[\ell _A^{e_A}]\) and \({P_B,Q_B}\) a basis generating \(E_0[\ell _B^{e_B}]\), where \(E[\ell ]\) is the \(\ell \)-torsion group of E, i.e. the set of all points \(P\in E(\overline{\mathbb {F}}_q)\) such that \(\ell P\) is the identity. As in [4], we consider \((P_A,Q_A),(P_B,Q_B)\) as public parameters of the cryptosystem.
Like the DH scheme, this is a vanilla ORKE scheme, since \(\mathsf {Msg}_{SIDH}\) is the same for both parties, and does not depend on the message previously exchanged by the other party. The three algorithms that define the KE are:
-
\(\mathsf {Gen}_{SIDH}(1^\kappa ,r)\) pick \(m_i,n_i \in \mathbb {Z}/\ell _i^{e_i}\mathbb {Z}\), where at most one of them is divisible by \(\ell _i\), and compute an isogeny \(\phi _i: E_0\rightarrow E_i\) with kernel \(K_i = \langle { [m_i]P_i + [n_i] Q_i }\rangle \). Set \(\mathsf {sk}\leftarrow (m_i,n_i,\phi _i)\).
-
\(\mathsf {Msg}_{SIDH}(r_i,\mathsf {sk}_i) [= \mathsf {Msg}_{SIDH}^\mathsf {A}(r_A,\mathsf {sk}_A) = \mathsf {Msg}_{SIDH}^\mathsf {B}(r_B,\mathsf {sk}_B,\cdot )] \) compute images
$$\{ \phi _i(P_j), \phi _i(Q_j) \} \subset E_i$$and outputs the message \(m = (E_i,\phi _i(P_j), \phi _i(Q_j))\).
-
\(\mathsf {Key}_{SIDH}(r_i,\mathsf {sk}_i, m_j)\) since \(m_j \leftarrow (E_j,\phi _j(P_i), \phi _j(Q_i))\), compute an isogeny \(\phi _i': E_j\rightarrow E_{ij}\) considering its kernel \(\langle { [m_i]\phi _j(P_i) + [n_i]\phi _j(Q_i) }\rangle \). Return the j-invariant of
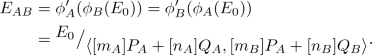
Now, we prove that there exists the group action \(\psi \) as stated in Definition 5. Again, we base our group action on the assumptions of [4] and follow their notation. Consider \(\mathcal {M}= \overline{\mathcal {M}}\) to be the set of elements of the form (E, G, H), where G and H are elements of the \(\ell \)-torsion group of E. In [4], it is assumed that (E, G, H) is computationally indistinguishable from \((E, G+U, H+V)\) when U, V are randomly chosen among \(E[\ell ]\) such that the Weil paring of (G, H) and \((G+U,H+V)\) coincides. Moreover, they also show that such U, V can be sampled in polynomial time among the elements of \(E[\ell ]\), namely \(U \leftarrow \alpha G_B + \beta H_B\), \(V \leftarrow -(\alpha /\beta ) U\), where \(G_B \leftarrow \phi _B(P_A)\), \(H_B\leftarrow \phi _B(Q_A)\), and \(\alpha ,\beta \in \mathbb {Z}/\ell \mathbb {Z}\).
We are now able to propose the required group action \(\psi \). Let \(\mathbb {M}\) be the group of elements of the form \((U,V)\in E[\ell ]\) with group law \(*\) being the coordinate-wise usual sum of the ellipic curve points. This group acts on \(\overline{\mathcal {M}}\), \(\psi :\overline{\mathcal {M}}\times (\mathbb {M},*)\rightarrow \overline{\mathcal {M}}\), by modifying G and H, as \(\psi (y,h) = (E, G+U, H+V)\), where y is of the form of (E, G, H) and h of the form (U, V), and G, H, U, V are all elements in \(E[\ell ]\), such that U, V are sampled accordingly with [4].
Lemma 17
The SIDH KE protocol is \(\psi \)-message indistinguishable given the security assumptions in [24, Section 5] and the parameters are chosen as to prevent any distinguisher based attack [4].
Proof
In order to achieve the property of \(\psi \)-message indistinguishability, we must prevent any distinguisher from figuring out if the first message from the receiver is (E, G, H) or \((E,G+U,H+V)\). As in [4], we can choose the parameters to avoid the paring-based distinguisher using the Weil pairing, and so prevent the sender from finding out the secret bit of the receiver. If their conjecture that there is no other polynomial-time distinguisher for schemes of this form holds, then our OT protocol is \(\psi \)-message indistinguishable. \(\square \)
Note that, differently from [4], in our proposal the receiver sends either (E, G, H) or \((E,G+U,H+V)\), together with the nounce t such that \((U,V)\leftarrow \mathsf {H}(t)\). In fact, [4] uses a secure coin flip procedure to generate U, V, while in this work we obtain U, V from the random oracle. This means that the receiver has the ability to try a polynomial number of queries to the RO in order to choose U, V, in contrast to the single possibility of [4]. Notwithstanding, if it would be possible for the receiver to obtain a good U, V in polynomial many tries, then the probability of the secure coin flip would be non-negligible. Therefore, the two approaches are equivalent with regard to the security of this procedure.
Lemma 18
The SIDH KE is \(\psi \)-key indistinguishable given the assumptions in [24, Section 5].
Proof
This follows from the proof of security of the key exchange in [24]. The shared key must be a j-invariant uniformly random in the set j-invariants, i.e. a random curve in the isogeny graph, which according to the assumptions in [24, Section 5] is difficult to compute without knowledge of the private isogenies. \(\square \)
Therefore, we conclude that SIDH KE protocol of [24] can be used to instantiate the framework in this article.
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Branco, P., Ding, J., Goulão, M., Mateus, P. (2019). A Framework for Universally Composable Oblivious Transfer from One-Round Key-Exchange. In: Albrecht, M. (eds) Cryptography and Coding. IMACC 2019. Lecture Notes in Computer Science(), vol 11929. Springer, Cham. https://doi.org/10.1007/978-3-030-35199-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-35199-1_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-35198-4
Online ISBN: 978-3-030-35199-1
eBook Packages: Computer ScienceComputer Science (R0)


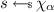 and outputs a secret key
and outputs a secret key  and a public key
and a public key 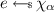 .
.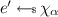 , and outputs
, and outputs  , and outputs the shared key
, and outputs the shared key