Common Subspace Based Low-Rank and Joint Sparse Representation for Multi-view Face Recognition

Abstract

Multi-view face data are very common in real-world application, since different viewpoints and various types of sensors attempt to better represent face data. However, these data have large pose variation, which dramatically degrades the performance of multi-view face recognition. To address this, we propose a common subspace based low-rank and joint sparse representation (CSLRJSR) method, which provides a framework encompassing divergence mitigation and feature fusion. In CSLRJSR method, common subspace is learnt to bridge the view, then low-rank and joint sparse representation are exploited to learn and then fuse the discriminative features. Experiments on multi-view face dataset demonstrate that CSLRJSR outperforms the state-of-the-art methods both in two-view and multi-view situations.

1 Introduction

Multi-view face recognition has been receiving a great deal of attention recently. Multi-view face data provide complementary information of the same object from multiple different views, which have positive effect on multi-view face recognition, compared to single-view face data. Researchers have already realized that fusing multi-view information can greatly improve face recognition performance [1, 2]. However, multi-view face recognition confronts a challenge of the wide variations of pose, illumination, and expression often encountered in realities. Therefore pursing effective methods is still an urgent problem.

Sparse representation is explored extensively in face recognition [3, 4] and super resolution [5] due to its good performance in revealing underlying structure. Some sparse representation based methods are used for multi-view recognition tasks, which improve recognition performance by indirectly exploiting the inherent relationships between multi-view data. Wang et al. [6] assumed one view can be represented sparsely by another view through a pair of dictionaries. Huang et al. [7] combined coupled dictionary and feature space learning (CDL) for two-view recognition and synthesis. Mandal et al. [8] proposed a generalized coupled dictionary learning (GCDL) method which learns dictionaries from two different views in a coupled manner, so that in the two views, the sparse coefficients of corresponding classes are correlated maximally. However, these methods are not suitable for scenarios more than two views, due to that they excessively rely on the coupling between views.

Subspace learning based methods have been introduced in pattern classification and data mining. These methods directly apply a specific low-rank projection to different view data. They can reduce differences between views and flexibly deal with scenarios more than two views. Several recognition approaches based on subspace learning were proposed recently, aiming at seeking for a common subspace where the data from multi-view can be compared [9]. The typical subspace learning method-principal component analysis (PCA) [10], is a technology of seeking a subspace in which the variance of the projected samples is maximized. Supervised regularization based robust subspace (SRRS) [11] presented a unified framework for subspace learning and data recovery. Ding et al. [12] proposed low-rank common subspace for multi-view learning (LRCS), which reserves compatible information among each view, through seeking a common discriminative subspace with a low-rank constraint. Robust multi-view data analysis through collective low-rank subspace (CLRS) proposed by Ding et al. [13] in 2018 complemented LRCS with a regularizer to further maximize the correlation within classes with the help of supervised information. Subspace learning methods perform well when reducing the divergence between views, but ignore the full use of extracted features, which actually limit the performance of recognition.

Recently, low-rank representation [14,15,16,17] and joint sparse [1, 18] are adopted in sparse representation. Low-rank representation based method has shown promising performance in capturing underlying low-rank structure as well as noise robustness. A joint sparse representation (SMBR) was proposed in [18] that enforce joint sparse constraints to the extracted features. SMBR took fully advantage of the extracted feature information to improve recognition performance.

Aforementioned multi-view face recognition methods still exist some intrinsic problems. To address these issues, we propose a novel multi-view face recognition algorithm, the contributions of this work are as follows:

• This paper focuses on the shared information across different views in order to handle the negative situation brought by multi-view face recognition, and puts forward common subspace based low-rank and joint sparse representation (CSLRJSR) method which unifies domain divergence mitigation and feature fusion.

• The method we propose is a more general algorithm that can be easily extended to handle more than two-view scenarios. Different scenarios of experiments were conducted to demonstrate the effectiveness of our algorithm. In many cases, our method outperforms the state-of-the-art multi-view recognition algorithms.

2 The Proposed Algorithm

In this section, we briefly present our motivation, and then propose our CSLRJSR method for the task of multi-view face recognition. Finally, we present the design of the optimization solution.

2.1 Motivation

Multi-view face data are ubiquitous in the real world, as the same objects are usually observed at different viewpoints, or even captured with different sensors. Therefore, the data of the same class but different views will show a big difference, which brings great challenges to the analysis of multi-view data. However, some research work [12, 13, 19] shows that the data of different views of the same class have a close relationship in the feature space. Some algorithms based on sparse representations [6,7,8] handle the task of multi-view recognition by integrating the inherent connection of multi-view data in the algorithm. The main idea of these methods is to learn the dictionary of two views in a coupled way, so that the same classes from the two views are most correlated in some transform space. These algorithms greatly improve the recognition performance of multi-view data. Unfortunately, these algorithms can only handle two views.

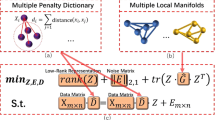
Subspace-based algorithms [12, 13, 20] directly process data from multiple views. The core idea of these methods is to directly apply a specific low-rank projection to different view data. In this way, the low-rank common subspace is learned, so that more shared information in different view data of the same class can be found. These algorithms take advantage of the relationship between multi-view data to improve recognition performance and to generalize the processing of multiple views. However, feature information extracted by these algorithms is not further utilized. Following the core idea of subspace learning, we bridge different view data of the same class based on the common subspace to reduce the divergence between views. And the low-rank and joint sparse constraints are applied to the extracted features to achieve feature fusion, so that the complementary information of the features can be better utilized. Figure 1 shows an overview of the proposed algorithm. Next, we will introduce our algorithm in detail.

Fig. 1.

Framework of our proposed CSLRJSR algorithm. (a) A common projection P for multi-view data to reduce divergences between views. (b) Low-rank and joint sparse constraints are imposed on sparse coefficients to reveal the global structure of multi-view data and fuse extracted features.

2.2 Common Subspace Based Sparse Representation

In multi-view face recognition, each view owns several classes and there are same classes across different views. Between these same classes, there is shared low-rank similar information. Thus, a low-rank common projection ${\mathbf{P}}$ is utilized in our method to preserve this shared information, so that a same class from different views can be aligned into common subspace. Suppose there is $k$-view data ${\mathbf{X}} = [{\mathbf{X}}^{1} , \cdots ,{\mathbf{X}}^{k} ]$, and each view ${\mathbf{X}}^{i} \in {\mathbb{R}}^{{q \times m_{i} }}$ includes $m_{i}$ training samples and $c$ same classes, where $q$ is the original feature dimension of face sample. For each view $i = 1, \cdots ,k$, ${\mathbf{D}}^{i}$ and ${\varvec{\Gamma}}^{i}$ represent the corresponding dictionary and sparse coefficients, respectively. Therefore, the objective function is defined as:

$$ \begin{aligned} \arg & \mathop {\hbox{min} }\limits_{{{\mathbf{P}},{\mathbf{D}}^{i} ,{\varvec{\Gamma}}^{i} }} \sum\limits_{i = 1}^{k} {||{\mathbf{P}}^{T} {\mathbf{X}}^{i} - {\mathbf{D}}^{i} {\varvec{\Gamma}}^{i} | |_{F}^{2} } + rank({\mathbf{P}}) \\ \quad \,\, & s\text{.}t\text{.}\quad {\mathbf{P}}^{T} {\mathbf{P}} = {\mathbf{I}},\quad \, | |{\mathbf{d}}_{j}^{i} | |_{2} \le 1,\quad \left( {i = 1,2, \ldots ,k} \right) \\ \end{aligned} $$

(1)

where $rank(P)$ denotes the rank operator of matrix ${\mathbf{P}} \in {\mathbb{R}}^{q \times p}$ ($p$ is the reduced dimensionality). The orthogonal constraint ${\mathbf{P}}^{T} {\mathbf{P}} = {\mathbf{I}}$ (${\mathbf{I}}$ is a unit matrix) in Eq. (1) is applied to ensure the obtained ${\mathbf{P}}$ is a valid solution. ${\mathbf{d}}_{j}^{i}$ is an atom at the j-th column of dictionary ${\mathbf{D}}^{i}$. $\left\| {\mathbf{M}} \right\|_{F} = \sqrt {\sum\nolimits_{i,j} {{\mathbf{M}}_{i,j}^{2} } }$ denotes the Frobenius norm of matrix ${\mathbf{M}}$. Since rank minimization problem is a NP-hard problem in Eq. (1), recent researches adopt nuclear norm as a good surrogate [17]. However, after reducing the divergence between views and obtaining the ability to deal with scenarios more than two views, we notice that the extracted features haven’t been fully used yet. Thus, we propose a common subspace based low-rank and joint sparse representation method to further exploit them, which is presented in Sect. 2.3.

2.3 Common Subspace Based Low-Rank and Joint Sparse Representation

In order to fully exploit the extracted features and improve the recognition performance, joint sparse constraints are imposed on the representation coefficients to achieve feature-level fusion. Hence, we formulate the final objective function by unifying domain divergence mitigation and feature fusion as

$$ \begin{aligned} & \arg \mathop {\hbox{min} }\limits_{{{\mathbf{P}},{\mathbf{D}}^{i} ,{\varvec{\Gamma}}^{i} }} \sum\limits_{i = 1}^{k} {\left( { | |{\mathbf{P}}^{T} {\mathbf{X}}^{i} - {\mathbf{D}}^{i} {\varvec{\Gamma}}^{i} | |_{F}^{2} + \lambda_{1} | |{\varvec{\Gamma}}^{i} | |_{ *} } \right)} + \lambda_{2} | |{\varvec{\Gamma}} | |_{1,2} + | |{\mathbf{P}} | |_{ *} \\ & \quad \,\,s\text{.}t\text{.}\quad {\mathbf{P}}^{T} {\mathbf{P}} = {\mathbf{I}},\quad | |{\mathbf{d}}_{j}^{i} | |_{2} \le 1,\quad \left( {i = 1,2, \ldots ,k} \right) \\ \end{aligned} $$

(2)

where we concatenate $k$ coefficient matrices as ${\varvec{\Gamma}} = [{\varvec{\Gamma}}^{1} , \cdots ,{\varvec{\Gamma}}^{k} ]$. And $\left\| {\varvec{\Gamma}} \right\|_{1,2}$ denotes a joint sparse constraint calculated via $| |{\varvec{\Gamma}} | |_{1,2} \text{ = }\sum\nolimits_{i} { | |{\varvec{\upgamma}}^{i} | |}_{2}$ (${\varvec{\upgamma}}^{i}$ denotes a vector on the $i$-th row of matrix ${\varvec{\Gamma}}$), which is used to seek sparse nonzero rows so that all views can have similar sparse representations. And features are fused through this way. As for $\left\| \bullet \right\|_{*}$, it denotes a low-rank constraint that is applied to the sparse coefficient ${\varvec{\Gamma}}^{i}$ in order to better expose the global structure of the data, by this way, learnt features become more discriminative. $\lambda_{1}$ and $\lambda_{2}$ are two positive tradeoff parameters. The detailed solution of the proposed algorithm is presented in Sect. 2.4.

2.4 Optimization

In this part, the alternating direction method of multipliers (ADMM) [21, 22] algorithm is used to deal with the optimization problem, as it converges well even several variables are non-smooth. We first introduce three auxiliary variables ${\mathbf{Z}}$, ${\mathbf{L}}^{i}$ and ${\mathbf{W}}$, and then transform Eq. (2) into its equivalent constrained optimization problem as

$$ \begin{aligned} & \mathop {\arg \hbox{min} }\limits_{{{\mathbf{D}},{\mathbf{P}},{\varvec{\Gamma}},{\mathbf{Z}},{\mathbf{L}}^{i} ,{\mathbf{W}}}} \sum\limits_{i = 1}^{k} {( | |{\mathbf{P}}^{T} {\mathbf{X}}^{i} - {\mathbf{D}}^{i} {\varvec{\Gamma}}^{i} | |_{F}^{2} } + \lambda_{1} | |{\mathbf{L}}^{i} | |_{ *} ) + \lambda_{2} | |{\mathbf{Z}} | |_{1,2} + | |{\mathbf{W}} | |_{ *} \\ & \quad \quad \quad \quad \,\,\,\,\,s\text{.}t\text{.}\begin{array}{*{20}c} {} & {{\varvec{\Gamma}} = {\mathbf{Z}},{\mathbf{P}} = {\mathbf{W}},{\varvec{\Gamma}}^{i} = {\mathbf{L}}^{i} } \\ \end{array} ,i = 1, \ldots ,k \\ \end{aligned} $$

(3)

Equation (3) can be addressed using the Augmented Lagrangian Method (ALM) [21]. The Augmented Lagrangian function $f_{{\alpha_{{\mathbf{Z}}} ,\alpha_{{\mathbf{L}}} ,\alpha_{{\mathbf{W}}} }} ({\mathbf{P}},{\mathbf{D}}^{i} ,{\varvec{\Gamma}},{\mathbf{Z}},{\mathbf{L}}_{i} ,{\mathbf{W}};{\mathbf{A}}_{{\mathbf{Z}}} ,{\mathbf{A}}_{{\mathbf{L}}}^{i} ,{\mathbf{A}}_{{\mathbf{W}}} )$ is defined as:

$$ \begin{aligned} & \mathop {\arg { \hbox{min} }}\limits_{{{\mathbf{D}}^{i} ,{\mathbf{P}},{\varvec{\Gamma}},{\mathbf{Z}},{\mathbf{L}}^{i} ,{\mathbf{W}}}} \sum\limits_{i = 1}^{k} {( | |{\mathbf{P}}^{T} {\mathbf{X}}^{i} - {\mathbf{D}}^{i} {\varvec{\Gamma}}^{i} | |_{F} } + \lambda_{1} | |{\mathbf{L}}^{i} | |_{ *} + \left\langle {{\mathbf{A}}_{{\mathbf{L}}}^{i} ,{\varvec{\Gamma}}^{i} - {\mathbf{L}}^{i} } \right\rangle + \frac{{\alpha_{{\mathbf{L}}} }}{2} | |{\varvec{\Gamma}}^{i} - {\mathbf{L}}^{i} | |_{F}^{2} ) \\ & \quad \quad \quad \,\,\, + \,\lambda_{2} | |{\mathbf{Z}} | |_{1,2} + \left\langle {{\mathbf{A}}_{{\mathbf{Z}}} ,{\varvec{\Gamma}} - {\mathbf{Z}}} \right\rangle + \frac{{\alpha_{{\mathbf{Z}}} }}{2} | |{\varvec{\Gamma}} - {\mathbf{Z}} | |_{F}^{2} \\ & \quad \quad \quad \,\,\, + \, | |{\mathbf{W}} | |_{ *} + \left\langle {{\mathbf{A}}_{{\mathbf{W}}} ,{\mathbf{P}} - {\mathbf{W}}} \right\rangle + \frac{{\alpha_{{\mathbf{W}}} }}{2} | |{\mathbf{P}} - {\mathbf{W}} | |_{F}^{2} \\ \end{aligned} $$

(4)

where ${\mathbf{A}}_{{\mathbf{Z}}}$, ${\mathbf{A}}_{{\mathbf{L}}}^{i}$, ${\mathbf{A}}_{{\mathbf{W}}}$ are three Lagrange multipliers and $\alpha_{{\mathbf{Z}}}$, $\alpha_{{\mathbf{L}}}$, $\alpha_{{\mathbf{W}}}$ are the positive penalty parameters, $\left\langle {{\mathbf{A}},{\mathbf{B}}} \right\rangle$ denotes $tr\left( {{\mathbf{A}}^{T} {\mathbf{B}}} \right)$, and ${\mathbf{A}}_{{\mathbf{Z}}} = [{\mathbf{A}}_{{\mathbf{Z}}}^{1} ,{\mathbf{A}}_{{\mathbf{Z}}}^{2} , \ldots ,{\mathbf{A}}_{{\mathbf{Z}}}^{k} ]$.

The truth is that it is difficult to jointly optimize the variables in Eq. (4). Fortunately, we can get optimization results in an iterative way. That is, we solve each variable by keeping the others fixed. Moreover, we denote ${\mathbf{P}}_{t}$, ${\mathbf{D}}_{t}^{i}$, ${\varvec{\Gamma}}_{t}$, ${\mathbf{Z}}_{t}$, ${\mathbf{L}}_{t}^{i}$, ${\mathbf{W}}_{t}$, ${\mathbf{A}}_{{{\mathbf{Z}},t}}$, ${\mathbf{A}}_{{{\mathbf{L}},t}}^{i}$, ${\mathbf{A}}_{{{\mathbf{W}},t}}$, $\alpha_{{{\mathbf{Z}},t}}$, $\alpha_{{{\mathbf{L}},t}}$ and $\alpha_{{{\mathbf{W}},t}}$ as the solutions optimized in the $t$-th iteration $\left( {t > 0} \right)$. Then in the $\left( {t + 1} \right)$-th iteration, those solutions are updated as follows:

Updating ${\mathbf{L}}^{i}$:

$$ {\mathbf{L}}_{t + 1}^{i} = \arg \mathop {\hbox{min} }\limits_{{{\mathbf{L}}^{i} }} \frac{{\lambda_{2} }}{{\alpha_{{{\mathbf{L}},t}} }}||{\mathbf{L}}^{i} ||_{*} + \frac{1}{2} | |{\mathbf{L}}^{i} - ({\varvec{\Gamma}}_{t}^{i} + \frac{{{\mathbf{A}}_{{{\mathbf{L}},t}}^{i} }}{{\alpha_{{{\mathbf{L}},t}} }})||_{F}^{2} $$

(5)

Updating ${\varvec{\Gamma}}^{i}$:

$$ {\varvec{\Gamma}}_{t + 1}^{i} = ({\mathbf{D}}_{t}^{{i^{T} }} {\mathbf{D}}_{t}^{i} + \alpha_{{{\mathbf{Z}},t}} {\mathbf{I}} + \alpha_{{{\mathbf{L}},t}} {\mathbf{I}})^{ - 1} (\alpha_{{{\mathbf{Z}},t}} {\mathbf{Z}}_{t}^{i} + \alpha_{{{\mathbf{L}},t}} {\mathbf{L}}_{{t{ + }1}}^{i} - {\mathbf{A}}_{{{\mathbf{Z}},t}}^{i} - {\mathbf{A}}_{{{\mathbf{L}},t}}^{i} + {\mathbf{D}}_{t}^{{i^{T} }} {\mathbf{P}}_{t}^{T} {\mathbf{X}}^{i} ) $$

(6)

Updating ${\mathbf{D}}^{i}$:

$$ \begin{array}{*{20}c} {{\mathbf{D}}_{t + 1}^{i} = \arg \mathop {\hbox{min} }\limits_{{{\mathbf{D}}^{i} }} | |{\mathbf{P}}_{t}^{T} {\mathbf{X}}^{i} - {\mathbf{D}}^{i} {\varvec{\Gamma}}_{{t{ + }1}}^{i} | |_{F}^{2} } & {s\text{.}t\text{.}} & {\left\| {{\mathbf{d}}_{j}^{i} } \right\|_{2} \le 1} \\ \end{array} $$

(7)

Updating ${\mathbf{W}}$:

$$ {\mathbf{W}}_{t + 1} = \arg \mathop {\hbox{min} }\limits_{{\mathbf{W}}} \frac{1}{{\alpha_{{{\mathbf{W}},t}} }}||{\mathbf{W}}||_{*} + \frac{1}{2}||{\mathbf{W}} - ({\mathbf{P}}_{t} + \frac{{{\mathbf{A}}_{{{\mathbf{W}},t}} }}{{\alpha_{{{\mathbf{W}},t}} }})||_{F}^{2} $$

(8)

Updating ${\mathbf{P}}$:

$$ {\mathbf{P}}_{t + 1} = (\sum\limits_{i = 1}^{k} {{\mathbf{X}}^{i} {\mathbf{X}}^{{i^{T} }} } { + }\alpha_{{{\mathbf{W}},t}} )^{ - 1} (\sum\limits_{i = 1}^{k} {{\mathbf{X}}^{i} {\varvec{\Gamma}}_{t + 1}^{{i^{T} }} {\mathbf{D}}_{t + 1}^{{i^{T} }} } - {\mathbf{A}}_{{{\mathbf{W}},t}} { + }\alpha_{{\mathbf{W}}} {\mathbf{W}}_{{t{ + }1}} ) $$

(9)

Updating ${\mathbf{Z}}$:

$$ {\mathbf{Z}}_{t + 1} = \mathop { \hbox{min} }\limits_{{\mathbf{Z}}} \frac{{\lambda_{1} }}{{\alpha_{{{\mathbf{Z}},t}} }}||{\mathbf{Z}}||_{1,2} + \frac{1}{2}||{\mathbf{Z}} - ({\varvec{\Gamma}}_{t + 1} + \alpha_{{\mathbf{Z}}}^{ - 1} {\mathbf{A}}_{{{\mathbf{Z}},t}} )||_{F}^{2} $$

(10)

We use Singular Value Thresholding (SVT) [23] to solve Eqs. (5) and (8), and a quadratic problem solver [24] to address Eq. (7). Since the structure of Eq. (10) is separable, we solve it separately with respect to each row of ${\mathbf{Z}}$. For each row, we follow the method used in [18] to solve the following sub-problems:

$$ {\mathbf{z}}_{i,t + 1} = \hbox{min} \frac{1}{2}||{\mathbf{n}} - {\mathbf{z}}||_{2}^{2} + \frac{\lambda }{{\alpha_{{\mathbf{z}}} }} | |{\mathbf{z}}||_{2} $$

(11)

where ${\mathbf{n}} = {\varvec{\upgamma}}_{i,t + 1} + \alpha_{{\mathbf{z}}}^{ - 1} {\mathbf{a}}_{{{\mathbf{z}}_{i} ,t}}$, ${\varvec{\upgamma}}_{i,t + 1}$, ${\mathbf{a}}_{{{\mathbf{z}}_{i} ,t}}$, ${\mathbf{z}}_{i,t + 1}$ represent the $i$-th row of matrix ${\varvec{\Gamma}}_{t + 1}$, ${\mathbf{A}}_{{{\mathbf{Z}},t}}$ and ${\mathbf{Z}}_{t + 1}$, respectively.

In conclusion, we present the detailed optimization procedure of CSLRJSR in Algorithm 1, in which $\alpha_{{\mathbf{Z}}}$, $\alpha_{{\mathbf{L}}}$ and $\alpha_{{\mathbf{W}}}$ are set empirically, while tuning the two tradeoff parameters $\lambda_{1}$ and $\lambda_{2}$ via experiments elaborated in the next section. We initialize ${\mathbf{P}}$ randomly in the same way as [12] and initialize dictionary ${\mathbf{D}}$ via an online dictionary learning method that used in [8]. To determine the influence of different initialization methods, we use several traditional methods to initialize ${\mathbf{P}}$, which turns out that the final recognition performance tends to be exceedingly similar.

3 Experiments

In this section, a public multi-view dataset named CMU-PIE face dataset and experimental protocols are first introduced. Secondly, we demonstrate the comparison results of our proposed algorithm and the state-of-the-art algorithms. Lastly, for a comprehensive evaluation, several properties of our CSLRJSR approach are evaluated.

3.1 Dataset and Experimental Setting

The CMU-PIE Face dataset [25] consists of 68 subjects, each of which has multiple poses. Examples for each subject have 21 various illumination variations. In the experiments, we use face images of 7 poses (C02, C05, C07, C09, C14, C27, C29), where there are large differences between every subject in different poses (Fig. 2). Different numbers of poses are selected to build multiple evaluation subsets. Furthermore, face images are cropped into size of $64 \times 64$ and only the raw features are used as the input. We randomly choose 10 samples from each subject each pose to construct the training set, whilst the remaining samples are used for testing.

Fig. 2.

Face samples from different views of one subject in CMU-PIE dataset. We can notice the differences across different views of the same subject.

3.2 Comparison Results

To demonstrate the effectiveness of our approach, we compare the proposed method with sparse representation based methods and subspace learning based methods. All of these methods directly or indirectly exploit the inherent characteristics of the relationship between multi-view data to improve recognition performance. Sparse representation based methods include SCDL [6], CDL [7], GCDL1&GCDL2 [8]; and subspace learning based methods include PCA [10], SRRS [11], LRCS [12] and CLRS [13]. Actually, SCDL, CDL, GCDL1 and GCDL2 are specially designed for two-view cases, thus, only the recognition performances of two-view cases are presented. While PCA, SRRS, LRCS and CLRS are used to process multi-view cases by seeking a robust subspace.

For all comparison algorithms, we adopt the nearest neighbor classifier to evaluate the final recognition performance. We conduct five random selections and average the results. Table 1 depicts recognition performance of different methods on CMU-PIE datasets, where Case1: {C02, C14}, Case2: {C05, C07}, Case3: {C05, C29}, Case4: {C07, C09}, Case5: {C09, C27}, Case6: {C09, C29}, Case7: {C05, C07, C29}, Case8: {C05, C27, C29}, Case9: {C07, C09, C27}, Case10: {C07, C09, C29}, and Case11: {C05, C07, C09, C29}.

Table 1. Comparison results between 9 algorithms on CMU-PIE dataset

From the experimental results, we obtain the following observations. (1) All methods based on sparse representation show good performance. SCDL, CDL, GCDL1 and GCDL2 are to learn the dictionary for the two-view cases in a coupled manner, so that for the corresponding classes from the two views, the sparse coefficients of them are maximally correlated in a certain transformed space. However, these methods are only applicable to two-view cases. While our method is completely compatible for multi-view cases, which applies low-rank common subspace constraint to different views to mitigate the differences between views. And the recognition performance of our proposed algorithm is better than the above algorithms in most case. (2) Comparing with other subspace learning methods, we apply low-rank and joint sparse constraints to learn and fuse discriminative features so that the recognition performance is improved.

3.3 Convergence Analysis and Parameters Analysis

In this part, we analyze several properties of our proposed method, i.e., convergence and parameter influence.

First, we carry out server experiments on convergence curve and recognition performance of different iterations. Specifically, we evaluate on two-view case {C02, C14} and the performance is presented in Fig. 3. From the results, we can see our algorithm converges pretty well. Also, we find that the recognition performance goes up quickly and keeps a relatively stable point.

Fig. 3.

Convergence curve (black ‘o’) and recognition curve (red ‘x’) of the proposed algorithm in two-view Case1 (C02&C14), where the dimensionality is set to 200 and the parameter values $\lambda_{1}$ and $\lambda_{2}$ to 10 and 0.1, respectively. (Color figure online)

Second, because there are two tradeoff parameters $\lambda_{1}$, $\lambda_{2}$ in our method, we simultaneously analyze them on Case1 (C02&C14) and the results are presented in Fig. 4.

Fig. 4.

We evaluate the recognition performance of our proposed algorithm on the two tradeoff parameters influence {$\lambda_{1}$, $\lambda_{2}$} using two-view case (C02&C14). The value from 0 to 6 denotes [0.1, 0.5, 1,5, 10, 20], respectively.

According to the results, we can see that when $\lambda_{1}$ and $\lambda_{2}$ both are set small or large at the same time, the recognition performance is poor. On the contrary, we notice when $\lambda_{1} \in [5,15]$, it provides a much better performance. Therefore, we set $\lambda_{1} \text{ = } 1 0$ and $\lambda_{2} = 0.1$ during the whole experiments.

4 Conclusion

In this paper, a common subspace based low-rank and joint sparse representation for multi-view face recognition method is proposed. Specifically, we apply low-rank common subspace projection to multi-view data to reduce differences between views of the same class, so that the discriminative ability of learnt features is improved. Furthermore, joint sparse is imposed to get a representation consistent across all the views, and then low-rank representation uncovers the global structure of data and further improves the discriminative power of the features. And finally, the discriminative features are learnt and efficiently fused. Experimental results on multi-view dataset, demonstrate the effectiveness and accuracy of the proposed algorithm, compared to several state-of-the-art algorithms.

Our future work will mainly focus on evaluating our method on more different multi-view datasets and improving the accuracy and robustness of our method on noisy datasets which are more common in real-world applications.