1 Introduction

Quality of Service (QoS) mechanisms are necessary in contemporary communication networks in order to provide the required bandwidth needed by calls. In the case of call-level traffic in a single link, modelled as a loss system, such a QoS mechanism is a bandwidth sharing policy [1]. The simplest bandwidth sharing policy is the Complete Sharing (CS) policy. In the CS policy, a new call has full access to all non-occupied bandwidth units (b.u.) of the link and is accepted in the link if the required bandwidth is available. Otherwise, call blocking occurs. Often the terms ‘full accessibility’ or ‘full availability’ are used in the literature instead of the term ‘CS policy’ [1, 2]. However, the term ‘availability’ may also refer to the proportion of time the link is available [3]. Herein, we prefer the term ‘CS policy’.

The simplest teletraffic loss model that adopts the CS policy is the classical Erlang model [1]. In this model, the call arrival process is Poisson while each call requires one b.u. to be accepted in the system. If this b.u. is available then a call remains in the link for a generally distributed service time. Otherwise call blocking occurs. The fact that Call Blocking Probabilities (CBP) are calculated via the classical Erlang B formula has led to numerous extensions of Erlang’s model for the call-level analysis of wired (e.g., [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]), wireless (e.g., [19,20,21,22,23,24,25,26,27,28,29,30]), satellite (e.g., [31,32,33]) and optical networks (e.g., [34,35,36,37,38,39]).

In the recent paper of [27], a two-link loss system is studied that accommodates Poisson arriving calls from a single service-class. Each link may support and provide service to calls offloaded from the other link. An offloaded call is a new call that arrives in a link but will be served (subject to bandwidth availability) by the other link. This offloading mechanism is achieved with the aid of two thresholds per link, a low and a high threshold. Both thresholds refer to the number of in-service calls in each link. The first (low) threshold is the support threshold while the second (high) one is the offloading threshold. The support threshold refers to the point up to which the link can support offloaded calls from the other link. On the other hand, the offloading threshold refers to the point where call offloading can start from one link to the other.

The model of [27] does not have a Product Form Solution (PFS) for the steady state probabilities. This is due to the fact that the offloading mechanism destroys Local Balance (LB) between adjacent states of the system. In order to calculate CBP, either a linear system of Global Balance (GB) equations should be solved or an approximate method that relies on the independence between the links and the classical Erlang B formula can be adopted.

A potential application of the offloading scheme of [27] is in the area of mobile/WiFi networks. To manage the increasing traffic in mobile networks, traffic can be offloaded to WiFi networks [40, 41]. To further increase the available bandwidth of WiFi access links, recent research focuses on the aggregation of backhaul access link capacities and on the bandwidth sharing policies that should be adopted. The impact of such an aggregation to CBP in the case of a single service-class can be well studied by the offloading scheme of [27].

In this paper, we extend the model of [27] to include the case of multirate Poisson traffic, i.e., we consider that the system accommodates calls of different service-classes with different bandwidth requirements. In addition, we incorporate the notion of restricted accessibility. In a restricted accessibility system, a new call may be blocked even if available b.u. do exist at the time of its arrival. Under the general term ‘restricted accessibility’ one may include:

  • bandwidth sharing policies such as the threshold policy [15, 17], the probabilistic threshold policy [28, 42] or even the bandwidth reservation policy [4, 9, 13]. In the threshold policy, a new call (of a particular service-class) is not allowed to enter a system if the number of in-service calls (of that service-class) together with the new call exceeds a predefined threshold. In the probabilistic threshold policy, a new call may enter the system with (a state dependent) probability when the number of in-service calls plus the new call exceeds the threshold. In the bandwidth reservation policy, a new call will be blocked when the only available b.u. at the time of its arrival in one link are already reserved for other calls (e.g., of the same or the other link).

  • the case where each particular state of the system (except from the initial state where the system is empty) is associated with a blocking probability. This means that a new call may be blocked and lost with a certain blocking probability when the system is in a particular state at the time of its arrival. Such an approach is useful when modeling interference between neighbouring cells (e.g., in CDMA systems) [3, 43]. In this paper, we focus on this type of restricted accessibility and study the case where the blocking probability is different for each state. To this end, we provide an approximate method for the CBP determination which is verified via simulation. The CBP calculation in the proposed two-link model is based on the classical Erlang Multirate Loss Model (EMLM) [44, 45], which refers to a single link.

The remainder of this paper is organized as follows: In Sect. 2, we review the system of [27]. In Sect. 3, we propose the extension of [27] which includes the case of multirate traffic and the notion of restricted accessibility. In Sect. 4, we provide analytical and simulation CBP results for the proposed model. We conclude in Sect. 5.

2 Review of the Two-Link System for Single-Rate Traffic

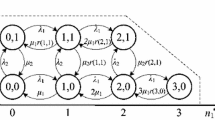
We consider a loss system of two links with capacities \(C_1\) and \(C_{2}\) b.u., respectively. Each link accommodates Poisson arriving calls of a single service-class which require one b.u. in order to be connected in a link. Let \(\lambda _{l}\) be the arrival rate in link l (l = 1, 2). Also let \({j}_{l}\) be the occupied b.u. in link l. Then, \(0\le j_{1} \le C_{1}\) and \(0\le j_{2} \le C_{2}\). Since a call requires one b.u. the value of \({j}_{l}\) also expresses the number of in-service calls in link l.

Each link l (l = 1, 2) has two different thresholds: the support (low) threshold \({\textit{th}}_{1l}\) and the offloading (high) threshold \({\textit{th}}_{2l}\), with \({\textit{th}}_{1l}\mathrm {<}{\textit{th}}_{2l}\) and \(0\le th_{1l}, th_{2l} \le 1\). Assuming that \(\left\lfloor x\right\rfloor \) is the largest integer not exceeding x, then the role of these thresholds, in link l, is described as follows (see Fig. 1):

  1. 1.

    If \(0\le j_{l} <\left\lfloor th_{1l} C_{l} \right\rfloor \) then link l is in a support mode of operation, i.e., it accepts and serves not only new calls that initially arrive in link l but also new calls offloaded from link m \(\left( m=1,2,\, \, m\ne l\right) \).

  2. 2.

    If \(\left\lfloor th_{1l} C_{l} \right\rfloor \le j_{l} <\left\lfloor th_{2l} C_{l} \right\rfloor \) then link l is in a normal mode of operation, i.e., it does not accept calls offloaded from link m. It only accepts calls that initially arrive in link l.

  3. 3.

    If \(\left\lfloor th_{2l} C_{l} \right\rfloor \le j_{l} \) then link l operates in offloading mode of operation, i.e., a new call that initially arrives in link l will be offloaded to link m. If link m operates in support mode (i.e., \(0\le j_{m} <\left\lfloor th_{1m} C_{m} \right\rfloor \)) then the call will be accepted in link m. If link m does not operate in support mode and at the same time \(j_{l} \le C_{l} -1\), the call will be accepted in link l. Otherwise the call will be blocked and lost without further affecting the system.

Fig. 1.
figure 1

The single-rate system of the two links.

Full size image

Based on the above, the call admission of a new call that initially arrives in link l (l = 1, 2) is summarized in the following steps:

(1) If \(\left( 0\le j_{l} <\left\lfloor th_{2l} C_{l} \right\rfloor \right) \) then the call is accepted by the link l and remains for a generally distributed service-time with mean \(\mu ^{-1}\).

(2) If \(\left\lfloor th_{2l} C_{l} \right\rfloor \le j_{l}\) then: (2a) if \(0\le j_{m} <\left\lfloor th_{1m} C_{m} \right\rfloor \) the call is offloaded to link m and remains for a generally distributed service-time with mean \(\mu ^{-1}\), (2b) if \(\left\lfloor th_{1m} C_{m} \right\rfloor \le j_{m} \), then link m is in a normal mode of operation and does not support offloaded calls from link l. In that case, the call will be handled by link l. In addition, if \(j_{l} \le C_{l} -1\), then the call is accepted in link l and remains for a generally distributed service-time with mean \(\mu ^{-1}\). Otherwise, call blocking occurs.

Due to the support and offloading modes of operation of the two links, the corresponding 2-D Markov chain of the system is not reversible and therefore LB between adjacent states is destroyed. Thus, the steady state distribution, \(P({\varvec{j}})=P({ j}_{1} ,j_{2} )\), of this system cannot be described by a PFS. To determine the values of \(P({ j}_{1} ,j_{2} )\) (and consequently CBP) there exist two different methods.

The first method provides accurate results compared to simulation. The drawback of the method is that it requires the knowledge of the system’s state space and the solution of the set of linear GB equations for each state \({\varvec{j}}=({ j}_{1} ,j_{2} )\) expressed as rate into state j = rate out of state j:

(1)

where:

(2)

Before we proceed with the CBP determination, via the first method, we emphasize that this method can be quite complex even for a system with links of small capacity.

Having obtained \(P(j_{1} ,j_{2})\), we can calculate the CBP in each link, \(P_{b_{1} }^{'}\) and \(P_{b_{2} }^{'}\) via (3) and (4), respectively [27]:

(3)
(4)

The rationale behind (3) is that a call can be blocked in the first link if there is no available bandwidth in that link (i.e., if \(\textit{j}_{1}\) = \(\textit{C}_{1}\)) and the second link is not in support mode (i.e, \(\left\lfloor th_{12} C_{2} \right\rfloor \le j_{2} \)). A similar description applies to (4).

In addition, we can calculate the total CBP in the two-link system via the following weighted summation [27]:

(5)

The second method leads to approximate CBP results (compared to the corresponding simulation results) by assuming that both links operate independently from one another. This means that each link l operates as an independent Erlang loss system of capacity \(\textit{C}_{l}\) (l = 1, 2). Such an assumption simplifies (at the cost of accuracy) the necessary calculations for the CBP determination.

The CBP in the first and the second link can be approximated by (6) and (7), respectively:

(6)
(7)

where \(P_{l} \left( C_{l} \right) \) refers to the CBP in link l (l = 1, 2) which can be determined either via the closed form of the classical Erlang B formula (8a), or via its recurrent form, which is appealing for large values of offered traffic-load \(a_{l}\) and capacity \(C_l\) (8b):

(8a)
(8b)

As far as the values of \(P_{l} \left( j_{l} \ge \left\lfloor th_{1l} C_{l} \right\rfloor \right) \) are concerned, they are given by:

(9)

where \(P_{l} (j_{l} )\) is determined via the truncated Poisson distribution:

$$\begin{aligned} P_{l} \left( j_{l} \right) =\frac{\frac{a_{l}^{j_{l} } }{{ j}_{{ l}} !} }{\sum \limits _{i=0}^{C_{l} }\frac{a_{l}^{i} }{{ i}!} } \, ,\, \, \, \, a_{l} =\lambda _{l} /\mu \end{aligned}$$
(10)

Finally, the total blocking probability can be determined via (5), where \(P_{b_{1} }^{'}\) and \(P_{b_{2} }^{'} \) are replaced by \(P_{b_{1} } \) and \(P_{b_{2} }\) (calculated via (6) and (7)), respectively.

An alternative recursive way for the determination of \(P_{l} (j_{l} )\), \({j}_{l}\) =1,...,\(\textit{C}_{l}\), is based on the link independence assumption. In the Erlang loss model, used to describe each link l, there exist LB between the adjacent states \(\textit{j}_{l\ }\)– 1 and \(\textit{j}_{l}\) which has the form [46]:

(11)

Based on (11), we can determine the unnormalized values of \(P_{l}^{'} (j_{l} )\)’s considering an initial value of \(\textit{P}_{l}^{'} (0)\) = 1. The normalized values of \(\textit{P}_{l}^{'} (j_{l} )\) ’s are given by:

(12)

Based on (12), we can calculate \(P_{b_{1}}\), \(P_{b_{2}}\) and the total CBP, via (6), (7) and (5), respectively.

3 The Proposed Model

In the proposed model, we consider again the loss system of the two links. Each link accommodates Poisson arriving calls of K different service-classes. Calls of service-class k (k = 1,..., K) require \(\textit{b}_{k}\) b.u. in order to be connected in a link. Let and be the arrival rates in the first and second link of service-class k calls, respectively. We also denote by j\(_{1}\) and j\(_{2}\) the occupied b.u. in the first and second link, respectively. Similar to Sect. 2, each link l (l = 1, 2) has a support threshold \({\textit{th}}_{1l}\) and an offloading threshold \({\textit{th}}_{2l}\), with \({\textit{th}}_{1l}\) \(\mathrm {<}\) \({\textit{th}}_{2l}\) and \(0\le th_{1l} ,th_{2l} \le 1\). To incorporate the notion of restricted accessibility in the proposed model, we assume that each state \(\textit{j}_{l}\) of link l, except from the initial state where link l is empty (i.e., when \(\textit{j}_{l\ }\) = 0) is associated with a blocking probability, \(pb_{l,k} \left( j_{l} \right) \) which can be different for each service-class k. Clearly, when there is no available b.u. for calls of service-class k in link l (i.e., when \(j_{l} \ge C_{l} -b_{k} +1\)), then \(pb_{l,k} \left( j_{l} \right) \,=\,1\). On the same hand, when the system is empty, then \(pb_{l,k} \left( 0\right) =0\).

The call admission of a new service-class k call that initially arrives in link l (l = 1, 2) is summarized in the following steps:

(1) If \(\left( 0\le j_{l} <\left\lfloor th_{2l} C_{l} \right\rfloor \right) \) then the call will be handled by link l. In addition, if \(j_{l} +b_{k} \le C_{l} \), then the call is accepted in link l with probability \(1-pb_{l,k} \left( j_{l} \right) \) and remains for a generally distributed service-time with mean \(\mu _{k}^{-1}\).

(2) If \(\left\lfloor th_{2l} C_{l} \right\rfloor \le j_{l}\) then:

(2a) if \(\left( 0\le j_{m} <\left\lfloor th_{1m} C_{m} \right\rfloor \right) \) the call is offloaded to link m and assuming that \(j_{m} +b_{k} \le C_{m} \), the call is accepted link m with probability \(1-pb_{{ m},k} \left( j_{m} \right) \) and remains in link m for a generally distributed service-time with mean \(\mu _{k}^{-1} \),

(2b) if \(\left\lfloor th_{1m} C_{m} \right\rfloor \le j_{m} \), then link m is in a normal mode of operation and does not support offloaded calls from link l. In that case, the call will be handled by link l. If \(j_{l} +b_{k} \le C_{l} \), then the call is accepted in link l with probability \(1-pb_{l,k} \left( j_{l} \right) \) and remains for a generally distributed service-time with mean \(\mu _{k}^{-1}\). Otherwise, the call is blocked and lost.

To determine in an approximate but efficient way the CBP of service-class k calls we assume that the two links operate independently from one another. In that case, each independent link behaves as an EMLM system under restricted accessibility [43], and therefore the CBP of service-class k calls in the first and the second link can be approximated by (13) and (14), respectively:

$$\begin{aligned} P_{res,b_{1k} } = P_{res,1k} \left( C_{1} \right) P_{res,2} \left( j_{2} \ge \left\lfloor th_{12} C_{2} \right\rfloor \right) \end{aligned}$$
(13)
(14)

where \(P_{res,lk} \left( C_{lk} \right) \) refers to the CBP of service-class k calls in link l (l = 1, 2) and \(P_{res,{ l}} \left( j_{l} \ge \left\lfloor th_{1l} C_{l} \right\rfloor \right) \) refers to the probability that link l is not in support mode.

The values of \(P_{res,lk} \left( C_{l} \right) \) in (13) and (14) are determined by the formula:

(15)

where \(q(j_{l} )\) refers to the unnormalized values of the link occupancy distribution of link l (l = 1,2) while \(G_{l} =\sum _{j_{l} =0}^{C_{l} }q(j_{l} ) \) is the normalization constant.

In (15), the values of \(q(j_{l})\) can be recursively determined via the following formula:

(16)

where: \(a_{lk} =\lambda _{lk} /\mu _{k} \) is the total offered traffic-load of service-class k calls in link l.

As far as the values of \(P_{res,l} \left( j_{l} \ge th_{1l} C_{l} \right) \), in (13) and (14), are concerned they can be determined by:

$$\begin{aligned} P_{res,l} \left( j_{l} \ge \left\lfloor th_{1l} C_{l} \right\rfloor \right) =\sum _{j_{l} =\left\lfloor th_{1l} C_{l} \right\rfloor }^{C_{l} }G_{l}^{-1} q ({ j}_{{ l}} ) \end{aligned}$$
(17)

where \({ q}(j_{l} )\) is determined via (16).

Finally, we propose the following formula for the total blocking probability of service-class k calls in the system of the two links:

(18)

4 Numerical Examples – Evaluation

In this section, we present an application example and provide analytical and simulation CBP results of the proposed model. Simulation results are mean values of 7 runs and are based on the Simscript III simulation language [47]. In each simulation run a total of ten million calls is generated. To account for a warm-up period, the first 5% of these calls are not taken into account in the CBP results. Furthermore, to increase the readability of figures we do not present reliability ranges. The latter are less than two order of magnitude.

As an application example, consider a two-link system of capacities \(\textit{C}_{1}\) = 24 b.u. and \(\textit{C}_{2}\) = 20 b.u. that accommodates K = 2 service-classes whose calls require \(\textit{b}_{1}\) = 1 and \(\textit{b}_{2}\) = 2 b.u., respectively. For the first link, let:  = 9 calls/min and  = 1 calls/min. Similarly, for the second link let  = 7 calls/min and  = 1 calls/min. Also let \(\mu _{1}^{-1} =\mu _{2}^{-1} =1.0\) min. As far as the values of the thresholds are concerned, we assume that the offloading thresholds are equal to \(\textit{th}_{21}\) = \(\textit{th}_{22}\) = 0.7 and consider two different sets of support thresholds: (1) \(\textit{th}_{11}\) = \(\textit{th}_{12}\) = 0.05 and (2) \(\textit{th}_{11}\) = \(\textit{th}_{12}\) = 0.25. Regarding the restricted accessibility blocking probability factors for each link, we consider two sets: (1) and (2) where l = 1, 2.

In the x-axis of Figs. 2, 3, 4 and 5, and increase in steps of 1.0 and 0.5, respectively. So, point 1 is: (\(\lambda _{11} =9.0,\, \lambda _{12} =1.0,\, \, \lambda _{21} =7.0,\, \lambda _{22} =1.0\)) while point 7 is: (\(\lambda _{11} =15.0,\, \lambda _{12} =1.0,\, \, \lambda _{21} =10.0,\, \lambda _{22} =1.0\)).

Fig. 2.
figure 2

1st service-class - CBP in the first link.

Full size image
Fig. 3.
figure 3

1st service-class - CBP in the second link.

Full size image
Fig. 4.
figure 4

2nd service-class - CBP in the first link.

Full size image
Fig. 5.
figure 5

2nd service-class - CBP in the second link.

Full size image

In Figs. 2 and 3, we present the CBP for the first service-class calls in each link, respectively. In Figs. 4 and 5, we present the corresponding CBP results for calls of the second service-class. Figures  2, 3, 4 and 5 show that the analytical CBP results: (a) are close to the simulation results especially when the values of the support thresholds \(\textit{th}_{11}\) and \(\textit{th}_{12}\) are kept within a reasonable level (e.g., 0.05 to 0.25). Depending on the two-link system, higher values of \(\textit{th}_{11}\) and \(\textit{th}_{12}\) may increase the error between analytical and simulation CBP results. This behavior can also be observed in the model of [27] and is anticipated due to the fact that (6), (7) and consequently (13), (14) imply that both links work independently from one another. (b) The choice of \(pb_{l,k} \left( j_{l} \right) \) greatly affects CBP. The higher values of set 1 result in much higher CBP compared to the lower values of set 2 .

5 Conclusion

We propose a new multirate loss model for the call-level analysis of a two-link system with restricted accessibility that accommodates Poisson arriving calls of different service-class with different bandwidth-per-call requirements. In the two-link system, each link may support and provide service to calls offloaded from the other link. The proposed model does not have a PFS for the steady state probabilities due to the offloading mechanism and the existence of restricted accessibility. However, we show that an approximate method does exist for the determination of CBP that achieves satisfactory accuracy compared to simulation. As a future work, we intend to use the proposed model as the springboard for the analysis of interference between the two links.