Abstract
For the additive channel model and imperfect CSI at the multi-antenna transmitter, rate based beamformer optimizations are difficult to solve directly. The closed-form expressions for ergodic rates involve numeric integrations and are hardly known for other scenarios than Rayleigh or Rician fading (Kang and Alouini, IEEE Trans Wirel Commun 5:112, 143, 2006; Taricco and Riegler, IEEE Trans Inf Theory 57:4123, 2011). This prevents a reformulation of the QoS and RB optimizations into convex form (cf. Chap. 3).
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
In fact, the average SINR results in an upper rate bound for multiplicative fading (see Sect. 3.2).
- 2.
The references about the weighted MSE approximation for weighted sum-rate maximization are only a small subset of the available works. There exist many related publications citing [155].
- 3.
While the MMSE definition in [152] is between the received signal for (interference and) noiseless transmission and the actual received signal with conditional mean estimator, we define the (M)MSE between the intended transmit signal and the corresponding linear MMSE estimate instead.
- 4.
Reference [34] already considers imperfect CSI. Therein, averaging is achieved by a stochastic update rule, which increases the involved samples for the sample average approximations in each iteration. Thereby, the corresponding ACS algorithm still almost surely converges to a KKT point.
- 5.
Each receiver has imperfect knowledge about its corresponding channel, e.g., user k knows the mean and covariance of
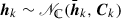 , and the transmitter has this knowledge for all channels.
, and the transmitter has this knowledge for all channels. - 6.
Approximations for moments of ratios of quadratic forms in random variables are shown in [245].
- 7.
- 8.
Derivatives of eigenvalues are detailed in [66, Appendix A.14] and the references therein.
- 9.
- 10.
This is in contrast to the QoS optimization with the average SINR from [118], for example.
- 11.
For example, see [246] for a definition of biconvex functions.
- 12.
Alternatively, one may employ a convex Semidefinite program (SDP) formulation of the dual problem.
- 13.
- 14.
The primal objective \(\sup \limits _{\boldsymbol {\lambda }\geq 0,\boldsymbol {\mu }}L(p,\boldsymbol {t},\boldsymbol {\lambda },\boldsymbol {\mu })\) upper bounds the dual objective \(\inf \limits _{p\geq 0,\boldsymbol {t}}L(p,\boldsymbol {t},\boldsymbol {\lambda },\boldsymbol {\mu })\).
- 15.
The alternative derivation in Sect. A.6 is up to this point. The remaining steps are the same.
- 16.
This follows from \(\hat {\boldsymbol {h}}_k\in \operatorname {range}\{\boldsymbol {R}_k\}\) and the block entries of the block-diagonal matrix Y are \(\boldsymbol {Y}_k=\sum _{j=1}^M\lambda _j\sum _{k\in \mathcal {G}_j}w_k\boldsymbol {R}_k+\boldsymbol {C}_k\) with the matrix \(\boldsymbol {C}_k=\sum _{\ell =1}^L\mu _\ell \boldsymbol {A}_{k,\ell }\succeq \mathbf {0}\).
- 17.
This restriction is without loss of generality for \(\varepsilon <\sum _{k=1}^Kw_k\) and (λ 1, μ) = (0, 0) for \(\varepsilon \geq \sum _{k=1}^Kw_k\).
- 18.
- 19.
- 20.
- 21.
The scalar projection is onto
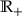 and reads as \([z]^+=\max (0,z)\) for
and reads as \([z]^+=\max (0,z)\) for  .
. - 22.
This follows from the block-diagonal structure of Y .
- 23.
- 24.
Using a sum power constraint for this characterization is without loss of generality. Since the transmit power is unbounded,
 can replace \(\mathcal {P}\) from (1.32).
can replace \(\mathcal {P}\) from (1.32). - 25.
Here, I(λ; ε) is the entrywise minimum of the function I ε(λ, u) = D εM(u)λ + n(u), where \(\boldsymbol {D}_{\boldsymbol {\varepsilon }}=\operatorname {diag}(\varepsilon _1^{-1}-1,\ldots ,\varepsilon _K^{-1}-1)\), \([\boldsymbol {M}(\boldsymbol {u})]_{k,i}=|\hat {\boldsymbol {h}}_k^{\operatorname {H}}\boldsymbol {u}_k|{ }^{-2}\boldsymbol {u}_k^{\operatorname {H}}\boldsymbol {R}_i\boldsymbol {u}_k\), and \([{\boldsymbol {n}}]_k=P^{-1}|\hat {\boldsymbol {h}}_k^{\operatorname {H}}\boldsymbol {u}_k|{ }^{-2}\|\boldsymbol {u}_k\|{ }^{2}\). This reformulation supports the results and algorithms from [89, 90] and many results from [11].
- 26.
Since I ∞(λ ′; ε) =minuD εM(u)λ ′, the fixed point \(\boldsymbol {\lambda }^{{\prime },\star }=\boldsymbol {I}_{\boldsymbol {\varepsilon }}^\infty (\boldsymbol {\lambda }^{{\prime },\star })\) is the eigenvector of D εM(u) with the SIR maximizing equalizers \(\boldsymbol {u}_k=(\sum _{i=1}^K\lambda _i\boldsymbol {R}_i)^{-1}\hat {\boldsymbol {h}}_k\), k = 1, …, K [252, Section 6]. Alternatively, we find λ ′, ⋆ as the limit point of the converging sequence \(\boldsymbol {\lambda }^{{\prime },{(n+1)}}\mspace {-5mu}= \|\boldsymbol {I}_{\boldsymbol {\varepsilon }}^\infty (\boldsymbol {\lambda }^{{\prime },{(n)}})\|{ }_1^{-1}\boldsymbol {I}_{\boldsymbol {\varepsilon }}^\infty (\boldsymbol {\lambda }^{{\prime },{(n)}})\) [92, 226].
- 27.
Both works base their duality derivation on an algorithmic perspective.
- 28.
Only for equal MSE targets, the MSEs for all the users are always equal at the optimum.
- 29.
- 30.
For the general case, we again consider set of weighted sum MSE constraints (4.6).
- 31.
- 32.
This beamformer is also the initialization for equal targets ε k = c and optimal for very low SNR.
- 33.
Assuming fixed v, the optimization problem is convex, because \(\operatorname {AMSE}_k(v_j,\boldsymbol {t})\) is convex quadratic in t for fixed v j and the maximum of convex functions is convex [102, Section 3.2.3].
- 34.
Requiring \(\hat {\boldsymbol {h}}_k^{\operatorname {H}}\boldsymbol {t}_k\) to be real valued does not change the objectives minimum value (cf. Sect. 4.3.1).
- 35.
The same functionality has the test in [79, Algorithm 2], which is for SINR balancing.
- 36.
From (4.98), \(\lambda _j^{(n+1)}\) clearly decreases for increasing ε (n+1) until \(\lambda _j^{(n+1)}=0\) for ε jε (n+1) ≥ m j.
- 37.
The search for M ′ requires less than M ′ iterations for a bisection over the indices i ∈{1, …, M ′′} that halves the number of candidates in each iteration.
- 38.
The LMI constraint is affine in the decision variables μ and ε.
- 39.
The exponential power profile is amongst others used for multi-spotbeam SatCom [255].
- 40.
The alternative updates via a dual SDP formulation provided the same performance.
- 41.
This normalized power iteration is motivated by the complementary slackness conditions for the power constraints, i.e., \(\mu _\ell P_\ell =\mu _\ell \boldsymbol {t}^{\operatorname {H}}\boldsymbol {A}_\ell \boldsymbol {t}\), ℓ = 1, …, L need to be satisfied for any local solution.
References
M. Schubert, H. Boche, QoS-based resource allocation and transceiver optimization. Found. Trends Commun. Inf. Theory 2(6), 383 (2005)
M. Kang, M.S. Alouini, Capacity of correlated MIMO Rayleigh channels. IEEE Trans. Wirel. Commun. 5(1), 143 (2006)
M. Kang, M.S. Alouini, Capacity of MIMO Rician channels. IEEE Trans. Wirel. Commun. 5(1), 112 (2006)
M. Kießling, Unifying analysis of ergodic MIMO capacity in correlated Rayleigh fading environments. Eur. Trans. Telecommun. 16(1), 17 (2005)
M. Razaviyayn, M.S. Boroujeni, Z.Q. Luo, A stochastic weighted MMSE approach to sum rate maximization for a MIMO interference channel, in Proceedings of the 12th IEEE International Workshop on Signal Processing Advances in Wireless Communications SPAWC (2013), pp. 325–329
M. Joham, P. Castro, W. Utschick, L. Castedo, Robust precoding with limited feedback design based on precoding MSE for MU-MISO systems. IEEE Trans. Signal Process. 60(6), 3101 (2012)
R. Hunger, M. Joham, A complete description of the QoS feasibility region in the vector broadcast channel. IEEE Trans. Signal Process. 57(7), 3870 (2010)
R. Hunger, Analysis and Transceiver Design for the MIMO Broadcast Channel. Foundations in Signal Processing, Communications and Networking, vol. 8 (Springer, Berlin/Heidelberg, 2013)
M. Schubert, H. Boche, Solution of the multiuser downlink beamforming problem with individual SINR constraints. IEEE Trans. Veh. Technol. 53(1), 18 (2004)
S. Shi, M. Schubert, H. Boche, Downlink MMSE transceiver optimization for multiuser MIMO systems: duality and sum-MSE minimization. IEEE Trans. Signal Process. 55(11), 5436 (2007)
M. Bengtsson, B. Ottersten, Optimal downlink beamforming using semidefinite optimization, in Proceedings of the 37th Annual Allerton Conference on Communication, Control, and Computing (1999), pp. 987–996
A. Wiesel, Y. Eldar, S. Shamai, Linear precoding via conic optimization for fixed MIMO receivers. IEEE Trans. Signal Process. 54(1), 161 (2006)
W. Yu, T. Lan, Transmitter optimization for the multi-antenna downlink with per-antenna power constraints. IEEE Trans. Signal Process. 55(6), 2646 (2007)
R.D. Yates, A framework for uplink power control in cellular radio systems. IEEE J. Sel. Areas Commun. 13(7), 1341 (1995)
K. Cumanan, J. Tang, S. Lambotharan, Rate balancing based linear transceiver design for multiuser MIMO system with multiple linear transmit covariance constraints, in Proceedings of the IEEE International Conference on Communications ICC (2011)
A. Tölli, M. Codreanu, M. Juntti, Linear multiuser MIMO transceiver design with quality of service and per-antenna power constraints. IEEE Trans. Signal Process. 56(7), 3049 (2008)
M. Schubert, H. Boche, A generic approach to QoS-based transceiver optimization. IEEE Trans. Commun. 55(8), 1557 (2007)
H. Boche, M. Schubert, A superlinearly and globally convergent algorithm for power control and resource allocation with general interference functions. IEEE/ACM Trans. Netw. 16(2), 383 (2008)
N. Vučić, M. Schubert, Fixed point iteration for max-min SIR balancing with general interference functions, in Proceedings of the 36th International Conference on Acoustics, Speech, and Signal Processing ICASSP (2011), pp. 3456–3459
M. Grant, S. Boyd, CVX: Matlab software for disciplined convex programming (2009), http://stanford.edu/~boyd/cvx
S. Boyd, L. Vandenberghe, Convex Optimization, 1st edn. (Cambridge University Press, New York, NY, 2004)
A. Gershman, N. Sidiropoulos, S. Shahbazpanahi, M. Bengtsson, B. Ottersten, Convex optimization-based beamforming. IEEE Signal Process. Mag. 27(3), 62 (2010)
E. Jorswieck, B. Ottersten, A. Sezgin, A. Paulraj, Guaranteed performance region in fading orthogonal space-time coded broadcast channels. EURASIP J. Wirel. Commun. Netw. 2008(39), 1 (2008)
M. Joham, R. Hunger, Feasible rate region of the MIMO broadcast channel with linear transceivers, in Proceedings of the 14th International ITG Workshop on Smart Antennas WSA (2010), pp. 342–349
T. Bogale, L. Vandendorpe, Robust sum MSE optimization for downlink multiuser MIMO systems with arbitrary power constraint: generalized duality approach. IEEE Trans. Signal Process. 60(4), 1862 (2012)
G. Dartmann, X. Gong, W. Afzal, G. Ascheid, On the duality of the max-min beamforming problem with per-antenna and per-antenna-array power constraints. IEEE Trans. Veh. Technol. 62(2), 606 (2013)
G.H. Golub, C.F. van Loan, Matrix Computations, 3rd edn. (The Johns Hopkins University Press, Baltimore, NY, 1996)
S. He, Y. Huang, L. Yang, A. Nallanathan, P. Liu, A multi-cell beamforming design by uplink-downlink max-min SINR duality. IEEE Trans. Wirel. Commun. 11(8), 2858 (2012)
G. Taricco, E. Riegler, On the ergodic capacity of correlated Rician fading MIMO channels with interference. IEEE Trans. Inf. Theory 57(7), 4123 (2011)
R. El Assir, F.A. Dietrich, M. Joham, W. Utschick, Min-max MSE precoding for broadcast channels based on statistical channel state information, in Proceedings of the 7th IEEE International Workshop on Signal Processing Advances Wireless Communications SPAWC, Cannes (2006)
M. Ding, S. Blostein, MIMO minimum total MSE transceiver design with imperfect CSI at both ends. IEEE Trans. Signal Process. 57(3), 1141 (2009)
A. Gründinger, M. Joham, J.P. González-Coma, L. Castedo, W. Utschick, Average sum MSE minimization in the multi-user downlink with multiple power constraints, in Proceedings of the 48th Asilomar Conference on Signals, Systems, and Computers (2014), pp. 1279–1285
D. Guo, S. Shamai, S. Verdú, Mutual information and minimum mean-square error in Gaussian channels. IEEE Trans. Inf. Theory 51(4), 1261 (2005)
P. Stoica, Y. Jiang, J. Li, On MIMO channel capacity: an intuitive discussion. IEEE Signal Process. Mag. 22(3), 83 (2005)
S. Shi, M. Schubert, H. Boche, Rate optimization for multiuser MIMO systems with linear processing. IEEE Trans. Signal Process. 56(8), 4020 (2008)
S. Christensen, R. Agarwal, E. Carvalho, J. Cioffi, Weighted sum-rate maximization using weighted MMSE for MIMO-BC beamforming design. IEEE Trans. Wirel. Commun. 7(12), 4792 (2008)
Q. Shi, M. Razaviyayn, Z.Q. Luo, C. He, An Iteratively Weighted MMSE Approach to distributed sum-utility maximization for a MIMO interfering broadcast channel. IEEE Trans. Signal Process. 59(9), 4331 (2011)
A. Gründinger, M. Joham, W. Utschick, Stochastic transceiver design in point-to-point MIMO channels with imperfect CSI, in Proceedings of the 15th International ITG Workshop on Smart Antennas WSA, Aachen (2011)
A. Gründinger, M. Joham, W. Utschick, Stochastic transceiver design in multi-antenna channels with statistical channel state information, in Proceedings of the 36th International Conference on Acoustics, Speech, and Signal Processing ICASSP, Prague (2011)
F. Wang, X. Yuan, S.C. Liew, D. Guo, Wireless MIMO switching: weighted sum mean square error and sum rate optimization. IEEE Trans. Inf. Theory 59(9), 5297 (2013)
R. Hunger, M. Joham, W. Utschick, On the MSE-duality of the broadcast channel and the multiple access channel. IEEE Trans. Signal Process. 57(2), 698 (2009)
M. Joham, M. Vonbun, W. Utschick, MIMO BC/MAC MSE duality with imperfect transmitter and perfect receiver CSI, in Proceedings of the 11th IEEE International Workshop on Signal Processing Advances in Wireless Communications SPAWC (2010)
J.P. González-Coma, A. Gründinger, M. Joham, L. Castedo Ribas, W. Utschick, On MSE balancing in the MIMO broadcast channel with unequal targets, in Proceedings of the 19th International ITG Workshop on Smart Antennas WSA, Munich (2016)
F. Boccardi, H. Huang, M. Trivellato, Multiuser eigenmode transmission for MIMO broadcast channels with limited feedback, in Proceedings of the 7th IEEE International Workshop on Signal Processing Advances in Wireless Communications SPAWC (2007)
M. Kobayashi, G. Caire, Joint beamforming and scheduling for a multi-antenna downlink with imperfect transmitter channel knowledge. IEEE J. Sel. Areas Commun. 25(7), 1468 (2007)
M. Ding, S.D. Blostein, Maximum mutual information design for MIMO systems with imperfect channel knowledge. IEEE Trans. Inf. Theory 56(10), 4793 (2010)
M. Abramowitz, I.A. Stegun, Handbook of Mathematical Functions, 1st edn. (Dover, New York, 1964)
M. Joham, A. Gründinger, A. Pastore, J. Fonollosa, W. Utschick, Rate balancing in the vector BC with erroneous CSI at the receivers, in Proceedings of the 47th Annual Conference on Information Sciences and Systems, Baltimore, MD (2013)
C. Nuzman, Contraction approach to power control, with non-monotonic applications, in Proceedings of the IEEE Global Communications Conference GLOBECOM (2007), pp. 5283–5287
D.P. Bertsekas, Nonlinear Programming (Athena Scientific, Belmont, MA, 1999)
R. Hunger, D.A. Schmidt, M. Joham, W. Utschick, A general covariance-based optimization framework using orthogonal projections, in Proceedings of the 9th IEEE International Workshop on Signal Processing Advances in Wireless Communications SPAWC (2008), pp. 76–80
A. Bermon, R. Plemmons, Nonnegative Matrices in the Mathematical Sciences (Society for Industrial and Applied Mathematics, Philadelphia, 1994)
M. Grant, S. Boyd, Y. Ye, Disciplined convex programming, in Global Optimization: From Theory to Implementation, Nonconvex Optimization and Its Applications, ed. by L. Liberti, N. Maculan (Springer, New York, 2006), pp. 155–210
X. Zhang, D.P. Palomar, B. Ottersten, Statistically robust design of linear MIMO transceivers. IEEE Trans. Signal Process. 56(8), 3678 (2008)
J. Wang, D.P. Palomar, Robust MMSE precoding in MIMO channels with pre-fixed receivers. IEEE Trans. Signal Process. 58(11), 5802 (2010)
T. Endeshaw, B. Chalise, L. Vandendorpe, MSE uplink-downlink duality of MIMO systems under imperfect CSI, in International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Aruba, Dutch Antilles (2009), pp. 384–387
M. Razaviyayn, M. Hong, Z.Q. Luo, Linear transceiver design for a MIMO interfering broadcast channel achieving max-min fairness, in Proceedings of the 45th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA (2011), pp. 1309–1313
T.M. Kim, F. Sun, A. Paulraj, Low-complexity MMSE precoding for coordinated multipoint with per-antenna power constraint. IEEE Signal Process. Lett. 20(4), 395 (2013)
F. Negro, I. Ghauri, D.T.M. Slock, Sum rate maximization in the noisy MIMO interfering broadcast channel with partial CSIT via the expected weighted MSE, in Proceedings of the 9th International Symposium on Wireless Communication Systems ISWCS (2012), pp. 576–580
D.P. Palomar, V. S., Representation of mutual information via input estimates. IEEE Trans. Inf. Theory 53(2), 453 (2007)
M. Ding, S.D. Blostein, Uplink-downlink duality in normalized MSE or SINR under imperfect channel knowledge, in Proceedings of the IEEE Global Communications Conference GLOBECOM, Washington, DC (2007), pp. 3786–3790
J.R. Magnus, The exact moments of a ratio of quadratic forms in normal variables. Annales D’Économie et de Statistique 1(4), 95 (1986)
Y. Bao, R. Kan, On the moments of ratios of quadratic forms in normal random variables. J. Multivar. Anal. 117, 229 (2013)
O. Lieberman, A Laplace approximation to the moments of a ratio of quadratic forms. Biometrica 81(4), 681 (1994)
J. Gorski, F. Pfeuffer, K. Klamroth, Biconvex sets and optimization with biconvex functions: a survey and extensions. Math. Methods Oper. Res. 66(3), 373 (2007)
M.S. Lobo, L. Vandenberghe, S. Boyd, H. Lebret, Applications of second-order cone programming. Linear Algebra Appl. 284(1), 193 (1998)
S. Shi, M. Schubert, N. Vučić, H. Boche, MMSE optimization with per-base-station power constraints for network MIMO systems, in Proceedings of the IEEE International Conference on Communications ICC (2008), pp. 4106–4110
M. Ulbrich, S. Ulbrich, Nichtlineare Optimierung. Mathematik Kompakt (Springer, Basel, 2012)
J.P. Gonzalez-Coma, M. Joham, P.M. Castro, L. Castedo, Power minimization in the multiuser MIMO-OFDM broadcast channel with imperfect CSI, in Proceedings of the 22nd European Signal Processing Conference EUSIPCO (2014), pp. 815–819
J.P. González-Coma, M. Joham, P.M. Castro, L. Castedo, Power minimization and QoS feasibility region in the multiuser MIMO broadcast channel with imperfect CSI, in Proceedings of the 12th IEEE International Workshop on Signal Processing Advances in Wireless Communications SPAWC, Darmstadt (2013), pp. 619–623
H. Boche, M. Schubert, A general theory for SIR balancing. EURASIP J. Wirel. Commun. Netw. 2006(2), 10 (2006)
S. Shi, M. Schubert, H. Boche, Downlink MMSE transceiver optimization for multiuser MIMO systems: MMSE balancing. IEEE Trans. Signal Process. 56(8), 3702 (2008)
A. Sharpio, D. Dentcheva, A. Ruszczyński, Lectures on Stochastic Programming (Society for Industrial and Applied Mathematics, Philadelphia, 2009)
N. Letzepis, A. Grant, Capacity of the multiple spot beam satellite channel with Rician fading. IEEE Trans. Inf. Theory 54(11), 5210 (2008)
Y. Ye, Interior-Point Algorithm: Theory and Application. Tech. rep., Department of Management Sciences, University of Iowa City (1995)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Gründinger, A. (2020). Mean Square Error Transceiver Design for Additive Fading. In: Statistical Robust Beamforming for Broadcast Channels and Applications in Satellite Communication. Foundations in Signal Processing, Communications and Networking, vol 22. Springer, Cham. https://doi.org/10.1007/978-3-030-29578-3_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-29578-3_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29577-6
Online ISBN: 978-3-030-29578-3
eBook Packages: EngineeringEngineering (R0)


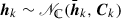 , and the transmitter has this knowledge for all channels.
, and the transmitter has this knowledge for all channels.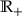 and reads as
and reads as  .
. can replace
can replace